A 7T Spine Array Based on Electric Dipole Transmitters

Abstract

Purpose

In this work the feasibility of using an array of electric dipole antennas for RF transmission in spine MRI at high field is explored.

Method

A 2-channel transmit array based on an electric dipole design was quantitatively optimized for 7T spine imaging and integrated with a receive array combining 8 loop coils. Using B₁⁺ mapping, the transmit efficiency of the dipole array was compared to a design using quadrature loop pairs. The radio-frequency (RF) energy deposition for each array was measured using a home-built dielectric phantom and MR thermometry. The performance of the proposed array was qualitatively demonstrated in human studies.

Results

The results indicate dramatically improved transmit efficiency for the dipole design as compared to the loop excitation. Up to 76% gain was achieved within the spinal region.

Conclusion

For imaging of the spine, electric-dipole based transmitters provided an attractive alternative to the traditional loop-based design. Easy integration with existing receive array technology facilitates practical use at high field.

INTRODUCTION

MRI of the spine at 3T has been found to offer improvement over 1.5T in terms of signal-to-noise ratio (SNR) and tissue delineation, but with new challenges related to B₁ and B₀ inhomogeneity (1). MRI of the spine at 7T is hampered by a lack of commercial radio-frequency (RF) receive coils and a body transmit coil. Development of 7T spine arrays therefore requires implementation of both transmit and receive functions in the same coil assembly, either via transceiver elements or via separate transmit and receive elements. In the past few years, several groups have proposed various designs (2-7) utilizing loop-based transmit structures. However, given the generally large field-of-view (FOV) required for spine imaging in comparison with the RF wavelength at 7T (e.g. ~13 cm in muscle), loop-based transmit elements generally require a rather complicated layout and cabling (2-5). Although it is possible to simplify RF excitation by exploiting the traveling wave phenomenon (e.g. by employing a patch antenna at magnet bore entrance (8,9)), this may result in reduced transmit efficiency when compared with transmitters placed close to the area of interest (10).

In recent studies, use of electric dipole antennas has been explored as an alternative mode of RF transmission at high field (11-18), mostly for small FOV imaging. For head or prostate imaging at 7T, the antennas were shortened to ~20 cm to avoid unnecessary RF deposition outside the region-of-interest (ROI). However, when the conventional “half-wave dipole” (19) is constructed only with conductor strips and without additional lumped elements such as inductors, its length is well-suited for the larger superior-inferior (S-I) FOV required for spine imaging. In one application, the electric dipole was used in a so-called “dark mode” (i.e. only generating longitudinal B₁⁺ field, which is invisible in MRI) to modify the electric field distribution for a cervical spine array based on loop designs (20). But for spine imaging at 7T, the use of electrical dipoles for B₁ transmission has not been reported. In this work, the feasibility of using electrical dipole antennas is explored by evaluating both transmit efficiency and energy deposition, relative to a conventional loop-based design (4).

METHODS

Transmit and receive elements of our spine array were divided between a top layer immediately under the patient surface housing the receive-only loop array and a bottom layer located 4 cm below the patient housing the transmit-only dipole array.

Design and Optimization of the Electric Dipole Array

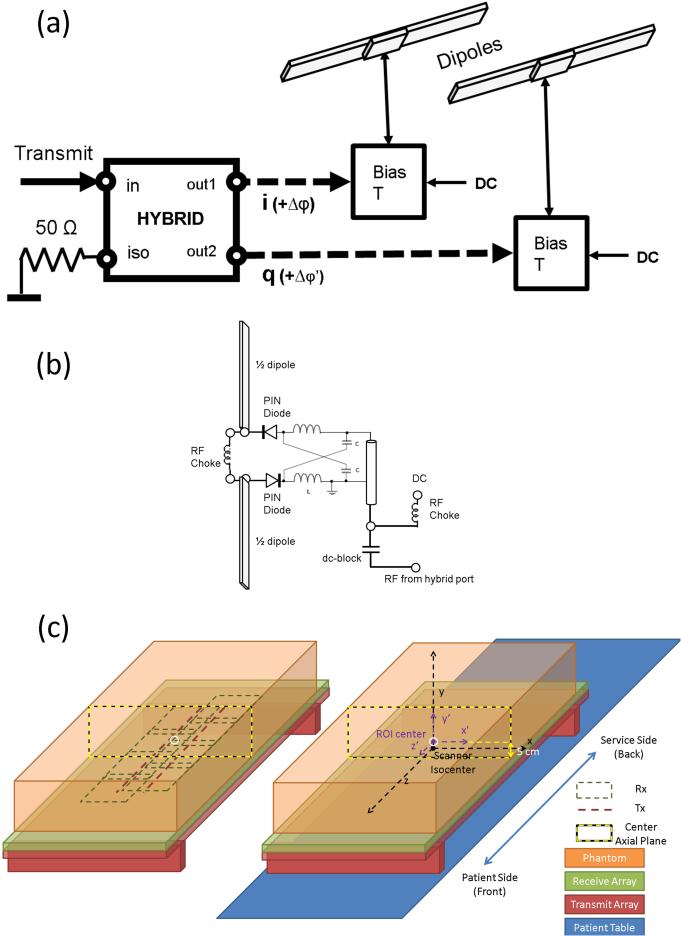
Our transmit-only dipole array (Figure 1a) employed two transmit elements, each consisting of a conventional half-wave dipole. The dipoles were constructed with straight 25 mm wide copper tape and fed at their centers with RF. For each of the two segments of each dipole element, the copper strips mounted on a 5 mm thick acrylic board. The dipoles were positioned 4 cm below the patient surface to allow space for the receive array. As expected, each dipole was found to have a resonance with a wavelength corresponding to twice the total dipole length. The resonant frequency of the dipole shifted lower when it was placed near a highly dielectric and conductive load such as human body. For tuning, a phantom that presented loading characteristics similar to a human body at 297.2 MHz was placed 4 cm above the dipoles. The lengths of the dipole segments were adjusted to bring the resonant frequencies close to the NMR Larmor frequency (297.2 MHz at 7T). Each dipole was fed via a Lorenz (lattice) balun (21) (Figure 1b) matched to ~90 Ω (i.e. two 35 nH inductors and two 8 pF capacitors, consistent with theoretical prediction). Two diodes were added in series with the feeding points of each dipole so that it could be detuned during signal reception (Figure 1b). The RF power of the transmit port of the 7T scanner (Siemens Magnetom 7T, Erlangen, Germany) was split equally between each dipole using a home-built lumped-element quadrature hybrid (22), using a minimal amount of metal to avoid eddy currents in close proximity to the dipoles. Reflected power from the isolation port of the hybrid was terminated with a high-power 50-Ω load (Figure 1a).

Figure 1.

(a) Schematic of the electric dipole array for transmission, (b) circuit diagram for bias T for the PIN control signal, lattice balun for matching, and the detuning circuits, and (c) illustration of the layout of transmit and receive arrays v.s. the loading phantom, and associated coordinates. On the right, the scanner system (x,y,z) is marked in black. Another coordinate system parallel with (x,y,z) system was defined as (x’,y’,z’) (shown in purple) with its origin residing on the center of the ROI at the L-R and S-I center of the phantom, and 5 cm from the bottom on the A-P centerline of the phantom. The (x’,y’,z’) coordinate system, referred as the phantom coordinate system, was always centered at the center of the ROI at the axial center plane of the phantom and was moving with the whole setup, i.e. the phantom and the combined T/R array, whereas the scanner coordinate system (x,y,z) system stayed with the scanner, with its origin always at the scanner iso-center.

A body-mimicking phantom was constructed using a plastic container of 425 mm width, 600 mm length, and 170 mm depth. It was used to optimize coil tuning and perform initial imaging experiments. To mimic the bulk electrical properties of muscle of the back at 7T (σ = 0.79 S/m, ε_r = 59) (23), the phantom was filled to a depth of 110 mm with a sugar-gel recipe developed earlier (24) (available at http://www.amri.ninds.nih.gov/phantomrecipe.html).

Two additional optimization steps were performed on the dipole array before the detuning circuits were added. First, with the elements connected in quadrature (90° inter-channel phase delay), the B₁⁺ fields of the elements were mapped in the central axial plane using a modified Bloch-Siegert approach (25). The separation between the dipoles was empirically minimized until coupling between the elements significantly changed their B₁⁺ distributions. In the next step, the transmit efficiency (defined as B₁⁺ in μT per unit input voltage in V) was measured at the center axial plane by varying the phase delay between the hybrid and individual dipoles. Phase delays were adjusted by inserting additional cable of different lengths between the dipole feeding points and either hybrid output ports. The phase delay was varied in ~30° steps, and the average transmit efficiencies were fit using 6^th order polynomials as a function of inter-channel phase delay. Beside phase delay, the offset in L-R direction between the center of the array and the center of the ROI could also affect the transmit efficiency. Thus similar to (4), the transmit efficiency within a 20 mm diameter circular ROI at 50 mm depth was then numerically maximized over the two variables. After this optimization, the dipole array was converted to a transmit-only configuration by implementing the detuning circuits as mentioned above.

Receive Array Design

Since the main goal of this work was to improve transmit efficiency, a conventional array of overlapping loops was used for reception. Starting with the array described in (4), two columns of 10cm square coils, four per column, were configured in receive-only mode. A third column of transmit-only coil as well as the transmit feature in the center column was removed. Each coil was tuned and matched using the loading phantom. For reception, high reflection, low noise GaAs-FET preamplifiers (type Siemens 10185702 + 10185751; Stark Contrast, Erlangen, Germany) were used, which included active detuning circuits on their circuit boards. For additional protection from RF transmit interference, passive detuning (including an inductor and a pair of cross-diodes) was added to one capacitor of each element. To prevent inter-channel coupling through the RF receive cables, floating cable traps (26) were added on each cable bundle that contains all four coaxial cables connecting the preamplifiers on receive coils to the coil system plug.

Use of the Loop-based Transmit-Receive Spine Array as Reference

In order to compare the transmit efficiency and the RF heating of the dipole-based transmit array to the loop-based design (4), the latter was slightly modified: 1) inline traps were added on the coax cables connecting the four receive-only coils; 2) the bundle traps were replaced with custom-built floating traps (26); and 3) the transmit cables were cut to the determined optimal lengths.

MR Experiments

Phantom measurement of RF transmit efficiency

The experimental setup is illustrated in Figure 1c. A ROI representing the expected location of the spine is marked as a white circle in the center axial plane of the phantom (marked by yellow/black dashed rectangle), centered 5 cm above the bottom of the phantom in anterior-posterior (A-P) direction. Unless specified otherwise, experiments were conducted with the center planes of the phantom (x’=0 plane and z’=0) coinciding with x=0 plane and z=0 plane, as indicated in Figure 1c. For simplicity, we define this position as the “center position”.

Transmit efficiency was measured using Bloch-Siegert B₁⁺ mapping (25) as follows. First, for calibration, the RF envelope voltage required to generate an 11.7 μT (500 Hz) B₁⁺ field was estimated at the center of the ROI (x’=0,y’=0,z’=0) at the center position. After transmitter calibration, axial B₁⁺ maps were acquired. Given the length of the dipole and the increasing gradient nonlinearity in the S-I direction, mapping was performed in sequential axial scans by moving the patient table to cover sections of the FOV. Each section covered a 10 cm region along the long-axis (S-I) of the FOV. Five sections centered on the long-axis of the phantom (S-I) were selected and imaged. The acquired B₁⁺ maps were converted to B₁⁺ efficiency by dividing the measured B₁⁺ amplitudes (in μT) by the RF envelop voltages (in V) used to acquire the data.

Phantom measurement of RF induced heating

To evaluate the RF energy deposition, MR thermometry based on the water proton resonant frequency (PRF) shift was performed for each array. Multi-echo gradient echo (GRE) images were acquired while depositing RF energy with a 32 kHz off-resonance pre-pulse that deposited substantial RF energy deposition without affecting MRI signal. In order to avoid impractically long experiments (due to the required cool-down time between the acquisitions), thermometry was only performed at a single section that covered the area of largest expected temperature increase, which was close to the feeding point (i.e. z’=0) based on the theory (19) and simulation. To minimize the effects of gradient non-linearities, the experiment was performed at the center position, as indicated in Figure 1c. Coronal rather than axial slices were chosen to maximize coverage parallel to the bottom part of the phantom. Duration of the heating was 10 minutes with an average power deposition of approximately 33 W, as measured using the power monitor on the scanner. Temperature changes could be derived from changes in image phase (induced by PRF shift) before and after the heating. As mentioned in (24), the multiple resonances of sucrose, whose resonance frequencies do not change notably with temperature, can confound PRF-based MR thermometry (similar to what is observed in water-lipid environments (27)). Therefore, a nonlinear least squares fitting approach was used to determine changes in water proton resonance frequency in the presence of the known sucrose signal (28), rather than a linear scaling of phase changes as is done in conventional PRF-based MR thermometry (29) .

Anatomical MRI

To demonstrate practical use of the array, anatomical images of the vertebral column and the spinal cord were acquired on two healthy volunteers; all imaging was approved by the Institutional Review Board. On the first volunteer, single slice images were acquired with breathholding and without fat saturation or any saturation band. First, an axial B₁⁺ map with a matching anatomical GRE image was acquired at z=0 to confirm the B₁⁺ efficiency in vivo. Then two additional single slice GRE images in axial and sagittal planes were acquired with imaging parameters similar to what was presented in the literature, e.g. (2,4,5). On the second volunteer, a high-resolution image of the spinal cord was acquired without breathhold using a 2D GRE sequence. Imaging artifacts caused by breathing were corrected based on the built-in navigator echoes, in combination with information about the TE dependence of the artifact, derived from three otherwise identical pre-scan repetitions without phase encoding.

RESULTS

Array Configurations

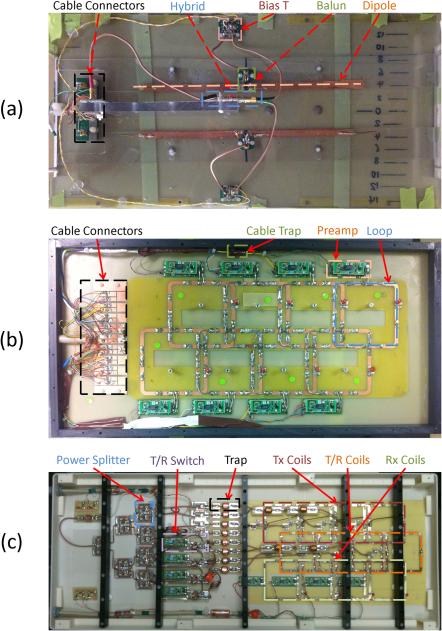
The prototype transmit dipole array, receive array, and transmit/receive (T/R) loop array are shown in Figure 2a, 2b, and 2c respectively. For the transmit array, a length of 370 mm was found to provide the best tuning for the 7T resonance frequency (297.2 MHz in this case), which is shorter than the half wavelength in vacuum (~505 mm). This shortening is attributed to the interaction of the dipole with the high dielectric constant of the body (or the phantom with similar properties). A minimum separation of 6 cm between the dipoles was required to prevent significant inter-element coupling. In this setup, the reflection coefficient S₁₁ for each dipole was < −30 dB, the coupling coefficient S₂₁ between the elements was ~ −12 dB, and the active detuning circuit typically provided better than 20 dB of detuning using an S₂₁ measurement with a pick-up probe. The S-parameters for the loop-based arrays (receive-only and T/R arrays) were typically, S₁₁ = −35 dB for matching, S₂₁ = −24 dB between elements (measured without the present of other electronics), and the detuning circuit typically provided 33 dB of detuning. The unloaded/loaded Q-ratio for each channel was around 7.3. Finally, the preamplifiers typically provided about 17 dB of preamp decoupling on each receive-only element.

Figure 2.

Photos of interior of prototype (a) dipole transmit array (with dipole fine-tuned by copper tape (top) or copper wire (bottom)), (b) loop-based receive array, and (c) an existing loop-based transmit/receive design (4) that was used as a reference, with labeling of major functional component types.

Optimal Positioning and Phasing of the Dipole Array

With the dipole elements connected in T/R configuration, the transmit efficiency of the dipole pair as a function of inter-element phase delay was measured using B₁⁺ mapping. The maps of transmit efficiency (in μT/V) are shown in Figure 3a, with regions of low MRI signal masked out. The capability of “steering” the transmit field by incrementing the phase shift between the elements is clearly demonstrated. Figure 3b shows the dependence of transmit efficiency in the target ROI (at the expected depth of the spine) on the phase delay and on the ROI position relative to the center of the array (i.e. spatial offset in L-R direction). Given that the width of the phantom was much larger than the separation of dipole pair (425 mm v.s. 60 mm), the effect of the spatial offset could be simulated by moving the ROI in the data analysis, as opposed to repeating the B₁⁺ mapping while physically shifting the phantom over the array. The optimum phase delay and spatial offset were found to be 142° and 9 mm, respectively. However, it was found that performance remained within 97% of this optimum value (Figure 3c) if the dipole pair were simply driven in quadrature (90º) and no L-R offset was used. Based on this, in vivo experiments were performed with quadrature drive and with center line of the array in S-I direction approximately aligned with the spinal cord. To further simplify the setup, the centerlines of the receive array (in L-R and S-I) were aligned with those of the transmit array. While this may not be optimal for receiving in the presence of twisting effects in the receive B₁ profile (4), the deterioration in receive sensitivity was expected to be minimal.

Figure 3.

Optimization of the transmit efficiency: (a) Axial B₁⁺ efficiency map (unit μT/V) at the center of the dipole array as a function of inter-channel phase delay. White circles represent the ROI targeting the approximate location of spinal cord; (b) average B₁⁺ efficiency within the ROI as a function of phase delay and spatial offset; (c) measured (red dot) and fitted B₁⁺ efficiency (blue line) with 6^th order polynomial for quadrature drive, assuming no additional spatial offset (i.e. spatial offset = 0).

Performance Comparison between Dipole and Loop Array

Estimated calibration voltages for the RF amplitude were 347 V for the dipole array versus 548 V for the T/R loop array, corresponding to transmit efficiencies as of 0.0338 μT/V and 0.0214 μT/V respectively. The latter is comparable with that reported in (4). Axial B₁⁺ efficiency maps (in μT/V) calculated from B₁⁺ mapping experiments for the two arrays are summarized in Figure 4. It is clear that the dipole-based transmit array has much higher transmit efficiency along the longitudinal centerline (S-I) as compared with the loop-based array. We attribute this to the difference in B₁⁺ field distributions between the two arrays, given that the average B₁⁺ efficiencies over the entire phantom were nearly identical (0.026 μT/V for both arrays).

Figure 4.

Axial B₁⁺ efficiency maps (μT/V) acquired on a phantom in a multi-station fashion, covering 50 cm FOV in the longitudinal (S-I) direction for (a) the detunable dipole-based and (b) the loop-based spine arrays. Imaging parameters for the B₁⁺ mapping were: FOV 200 × 400 mm², image matrix 64 × 128, yielding 3.1 × 3.1 mm² resolution, slice thickness 5 mm, slice spacing 5 mm, repetition time (TR) = 800 ms, echo time (TE) = [13.30, 14.63] ms. The white scale bars in the image represent 5 cm. White circles represent the approximate locations of spinal cord in a human subject.

Maps of temperature change after normalization for input power for the two arrays are shown in Figure 5. The dipole transmitter (Figure 5a) showed ~10% higher maximum RF induced heating as compared to the loop transmitter (Figure 5b) for the 10-minute heating test. Heating for the dipole array is more concentrated on the left side, toward the dipole with 90° phase delay, whereas the heating generated by the loop transmitters is more evenly distributed.

Figure 5.

Coronal normalized temperature change maps (K/W, i.e. temperature change after 10 minute RF heating normalized by the input power) calculated based on MR thermometry data for (a) dipole-based and (b) loop-based spine arrays. The image resolution was 4 × 4 × 3 mm³, FOV = 480 × 480 mm², with 13 coronal slices and 1 mm slice spacing.

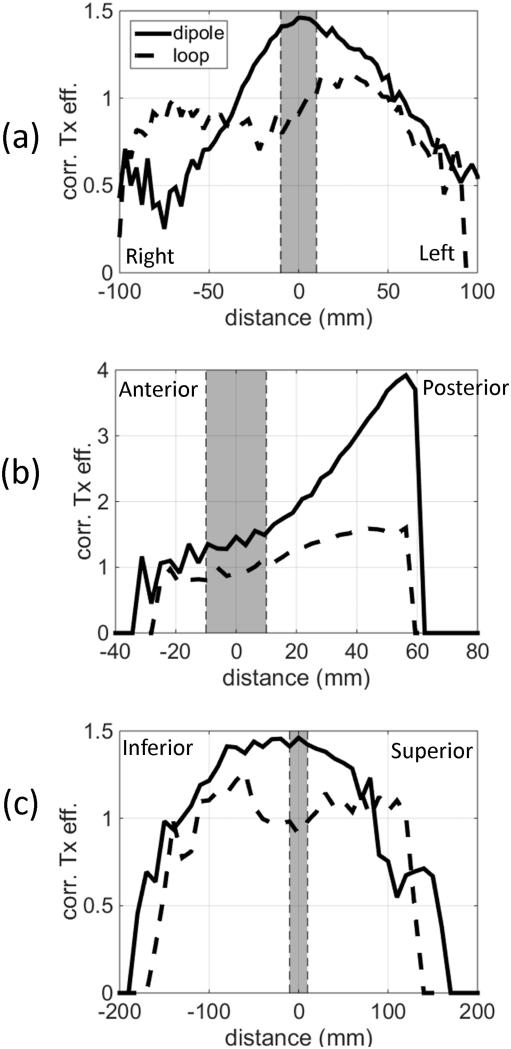
These results suggest that, for a given amount of input power, the dipole array provides a higher B₁⁺ in the region of the spine than the loop-based array, but it also generates higher peak local SAR. Therefore, to properly compare transmit efficiency under SAR-limited conditions, we normalized the B₁⁺ by the square-root of associated maximum local heating for a 10 minute session (from now on referred to as the heating-corrected transmit efficiency, in $\mu \mathrm{T}∕\sqrt{K}$ as temperature change in Kelvin). The square root is needed for the temperature change because B₁⁺ is proportional to the input RF envelope voltage, whereas the local temperature change is proportional to the power (the square of voltage). Figure 6 shows line profiles through the center of the spinal ROI in three orthogonal directions: L-R, A-P, and S-I. These results confirm that the gain in B₁⁺ efficiency by the dipole array is higher than the associated slightly increased peak RF heating. In fact, the gain in these three profiles within 10 cm around the center of the spinal ROI (x’=0,y’=0,z’=0) (highlighted in grey in Figure 6) can be as high as 76%.

Figure 6.

Heating-corrected transmit efficiency profiles (B₁⁺ divided by the square-root of associated maximum local heating in 10 minutes, $\mu \mathrm{T}∕\sqrt{K}$) through the center of the spine ROI in (a) L-R, (b) A-P, and (c) S-I directions. Shaded regions represent the approximate locations of spinal cord.

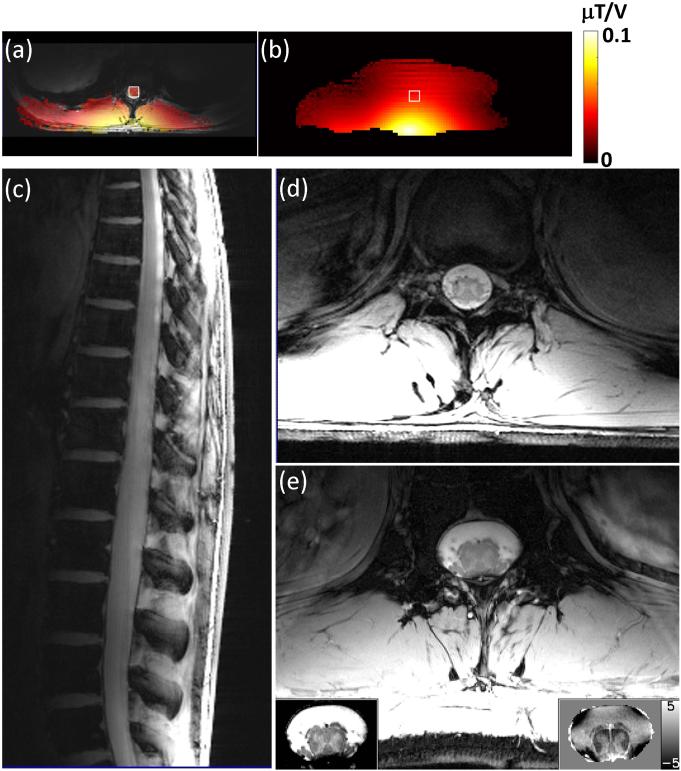
Figure 7a shows an in vivo B₁⁺ efficiency map overlaid on an anatomical image. For comparison, the B₁⁺ efficiency map acquired from the same location on the phantom (center slice in Figure 4a) is shown in Figure 7b, with the ROI corresponding to the cord region marked with white square (about 4cm deep). The average B₁⁺ efficiency within the ROI was 0.0405 μT/V for the in vivo data and 0.0399 μT/V for the phantom. Examples of in vivo images obtained with the dipole array are shown in Figure 7c-e and demonstrate the ability to obtain excellent sensitivity in the region of the spine at high resolution.

Figure 7.

(a) An axial B₁⁺ efficiency map (FOV 112.5 × 300 mm², image matrix 48 × 128, yielding 2.3 × 2.3 mm² resolution, slice thickness 5 mm, TR = 150 ms, TE = [13.28, 14.51] ms) overlaid on a corresponding anatomical slice (TR = 54 ms, TE = 6.9 ms, image matrix 96 × 256, yielding 1.17 × 1.17 mm² resolution) acquired on a healthy volunteer, compared with (b) the one acquired on the phantom (Figure 4a) at the corresponding location. The white square on the in vivo data in (a) represented the cord ROI, which is about 4cm deep. A match ROI (white square) was then draw on the phantom data in (b). Example anatomical spine images acquired in a healthy volunteer using the proposed array at 7T: (c) 2D sagittal GRE image (FOV 234 × 300 mm², image matrix 300 × 384, TR = 20 ms, TE = 3.6 ms, flip angle = 20°, slice thickness 3 mm). (d) 2D axial GRE image (FOV 156 × 200 mm², image matrix 300 × 384, yielding 0.52 × 0.52 mm² resolution, TR = 54 ms, TE = 6.9 ms, flip angle = 20°, slice thickness 3 mm). (e) High resolution GRE cord image acquired on a healthy volunteer (FOV 160 × 320 mm², image matrix 512 × 1024, yielding 0.31 × 0.31 mm² resolution, TR = 33 ms, TE = 9.3 ms, flip angle = 35°, slice thickness 3 mm, and 40 repetitions) after navigator-based artifact correction. The main image was scaled from 0 to 100 a.u. The bottom-left insert is a crop-out magnitude image of the cord region after receiver profile correction then rescaled to [35 65] a.u. for better contrast within the cord. The bottom-right insert is the corresponding phase map (scaled as [−5 5]Hz), showing excellent gray/white matter contrast.

DISCUSSION

In this study, the feasibility of using electric dipole antennae as transmit elements in 7T MR spinal imaging was explored with careful positioning of the dipole elements. Phantom experiments showed that significant gains in transmit efficiency can be achieved without significantly increasing tissue heating. Given the excellent match between the length of the “half-wave dipole” and the expected FOV for spine imaging at 7T, use of electric dipole elements can simplify transmit array design for human spinal applications by reducing total number of channels required to cover a large area (in this example, two dipoles instead of eight loops). Minimizing the number of cables that are used can further reduce potential cable coupling and minimize the parts count for supporting components, such as RF traps and power splitters. One potential drawback with this approach is that the large size of the dipoles used here limits the maximum number of the dipoles that can be used simultaneously without detrimental inter-element coupling. For spine imaging at 7 T, 6 cm separation was found to be necessary to prevent excessive inter-element coupling. Using more half-wave dipoles in parallel with similar separations in L-R direction would place them too far away from the spine ROI. Other dipole configurations would be required to fully take advantage of multi-channel transmission, which usually comes with eight parallel transmit channels. For clinical MRI of the spine, it may be necessary to shorten dipoles (14,18), or combine them with loop transmitters.

The gain in the transmit efficiency at the spinal cord region for the dipole seems mostly due to a different distribution of the B₁⁺ field in comparison with the loop-based design, given the average B₁⁺ efficiency was almost identical. This is probably due to the removal of the return path that is always 180-degrees out-of-phase, i.e. less field cancellation for positions far from the coil. However, the actual mechanism needs further investigation.

In this work, array configurations were optimized experimentally with the help of a modified Bloch-Siegert B₁⁺ mapping method (25). Because this is a laborious approach, only a relatively small portion of the parameter space was explored. Further optimization of the dipole transmitters may be possible by using RF simulations, which readily allow coverage of a larger parameter space. In addition, RF simulations would facilitate the optimization of the dipole configuration using heating-corrected transmit efficiency (or equivalent) rather than RF amplitude normalized transmit efficiency, as was done here, and this may result in further improvement in performance.

CONCLUSION

A coil that employed an efficient transmit array based on electric dipoles and designed for use with a loop-based receive array was constructed for 7T spine imaging. Steering of the B₁⁺ field in the axial plane was accomplished by varying the phase delay between the dipoles, which allowed RF shimming and transmit efficiency optimization for a pre-selected ROI. The transmit efficiency of the dipole array was compared with a previously described design based on quadrature-loop pairs. The dipole antenna provides a much simpler and more efficient transmitter design, and it can be readily combined with standard receive arrays.