Computing interaural differences through finite element modeling of idealized human heads

Abstract

Acoustical interaural differences were computed for a succession of idealized shapes approximating the human head-related anatomy: sphere, ellipsoid, and ellipsoid with neck and torso. Calculations were done as a function of frequency (100–2500 Hz) and for source azimuths from 10 to 90 degrees using finite element models. The computations were compared to free-field measurements made with a manikin. Compared to a spherical head, the ellipsoid produced greater large-scale variation with frequency in both interaural time differences and interaural level differences, resulting in better agreement with the measurements. Adding a torso, represented either as a large plate or as a rectangular box below the neck, further improved the agreement by adding smaller-scale frequency variation. The comparisons permitted conjectures about the relationship between details of interaural differences and gross features of the human anatomy, such as the height of the head, and length of the neck.

I. INTRODUCTION

A. Interaural differences

The human head serves as an obstacle for sound waves, causing the waves to be different at a listener's two ears (Strutt, 1907, 1909). There are interaural differences in sound arrival time and in sound level. The interaural time difference (ITD) and the interaural level difference (ILD) depend upon the location of the source in the azimuthal (horizontal) plane and thereby give auditory cues to the listener about the location of the source of the sound. The interaural differences also depend on the frequency of the sound.

The frequency-dependent character can be usefully divided into two parts: (1) There is a frequency dependence in the structure of the transfer function between 4000 and 16 000 Hz caused by fine details of the listener's anatomy, including the pinnae. This structure is highly individualistic and leads to useful information about the elevation of a source of sound, including differences between a source in front of the listener and a source in back (Roffler and Butler, 1968; Blauert, 1983). This frequency region has been the focus of several computational efforts with special interest in individual pinnae (Gumerov et al., 2010; Mokhtari et al., 2011; Jin et al., 2014). (2) There is also a frequency dependence well below 4000 Hz that depends less on individual differences because longer wavelengths are less sensitive to individual anatomical details. This article concerns the azimuthal dependence and frequency dependence for tones having frequencies <2500 Hz, a range that includes all the useful information in the ITD for waveform fine structure (Zwislocki and Feldman, 1956; Brughera et al., 2013). Such a low-frequency range is amenable to generalized, idealized modeling because the wavelength corresponding to 2500 Hz is ∼14 cm—large compared to small anatomical details. For such long wavelengths, it should be adequate to represent the anatomy by simple shapes, ignoring fine details.

B. Spherical head model

The spherical head model is a mathematically attractive first approach to idealized modeling. It assumes that the head is a perfect sphere suspended in space with the two ears represented by points on an equator. The spherical head model admits an exact series solution, developed by Lord Rayleigh (Rayleigh and Lodge, 1904) for plane wave incidence and made more accessible mathematically by Rschevkin (1963) and Kuhn (1977). This article uses an extension of that solution for finite source distances (Rabinowitz et al., 1993; Duda and Martens, 1998; Brungart and Rabinowitz, 1999) to be consistent with free-field measurements (described in Sec. II) using a source distance of three meters. The calculations in this article also assume that the ears are points and that they are separated by 180 degrees of arc because that is the best angular separation to match the anatomy of a KEMAR manikin (Knowles Electronics Manikin for Acoustics Research, G.R.A.S. Sound and Vibration, Holte, Denmark; Burkhard and Sachs, 1975).

The spherical head model successfully reproduces some features of the interaural differences as measured in free field on real human heads. As shown by Kuhn (1977), the low- and high-frequency limits of the ITD approximately agree with KEMAR measurements. For the ILD, the spherical head model produces a peak as a function of azimuth because of the acoustical bright spot for a source at the extreme left or right side (azimuth of 90 degrees with respect to the forward direction). Such a peak is seen in measurements on human listeners, and it has a strong perceptual effect (Macaulay et al., 2010). However, the spherical head model also has serious deficiencies that become apparent upon detailed comparison with measured interaural differences.

Measured interaural differences can be obtained from a number of databases for head-related impulse responses (HRIRs). We compared the model with four different databases: The CIPIC database (Algazi et al., 2001) was compiled from 45 listeners, including KEMAR. The LISTEN database (Warusfel, 2002) included 51 listeners and improved the impulse-response duration compared to CIPIC. Kayser et al. (2009) used a B&K (Bruel and Kjaer, Naerum, Denmark) head and torso simulator and made some comparisons with the spherical head model. The database by Wierstorf et al. (2011) used a KEMAR manikin in an anechoic room for distances as large as 3 m. These databases provided useful tests of our own measurements. Both the ITD and the ILD functions of frequency obtained from these databases disagree with the predictions of the spherical head model as will be shown in Sec. II.

Many attempts have been made to go beyond the spherical head model using numerical techniques. Most attempts at more realistic models have begun with a geometrical mesh on the surface of the head (or head and torso) and have calculated the scattering of an incoming wave to produce HRIRs or head-related transfer functions (HRTFs). In some cases, these functions have been compared to measurements. Xiao and Liu (2003) used a finite difference model to compute HRTFs starting with a mesh from a scanned KEMAR. Huttunen (2007) performed finite element computations for HRIR and HRTF for a B&K head and torso simulator and compared with the CIPIC database (Algazi et al., 2001). Gumerov et al. (2010) used a modified boundary element method to compute HRTFs starting with a mesh from a scanned manikin. Pollow et al. (2012) used a spherical harmonic decomposition to compute HRTFs for a Head Acoustics (Herzogenrath, Germany) manikin and compared with measured values. None of these attempts has been dedicated to the understanding of the low-frequency region, which is the focus of this article.

C. Plan of the article

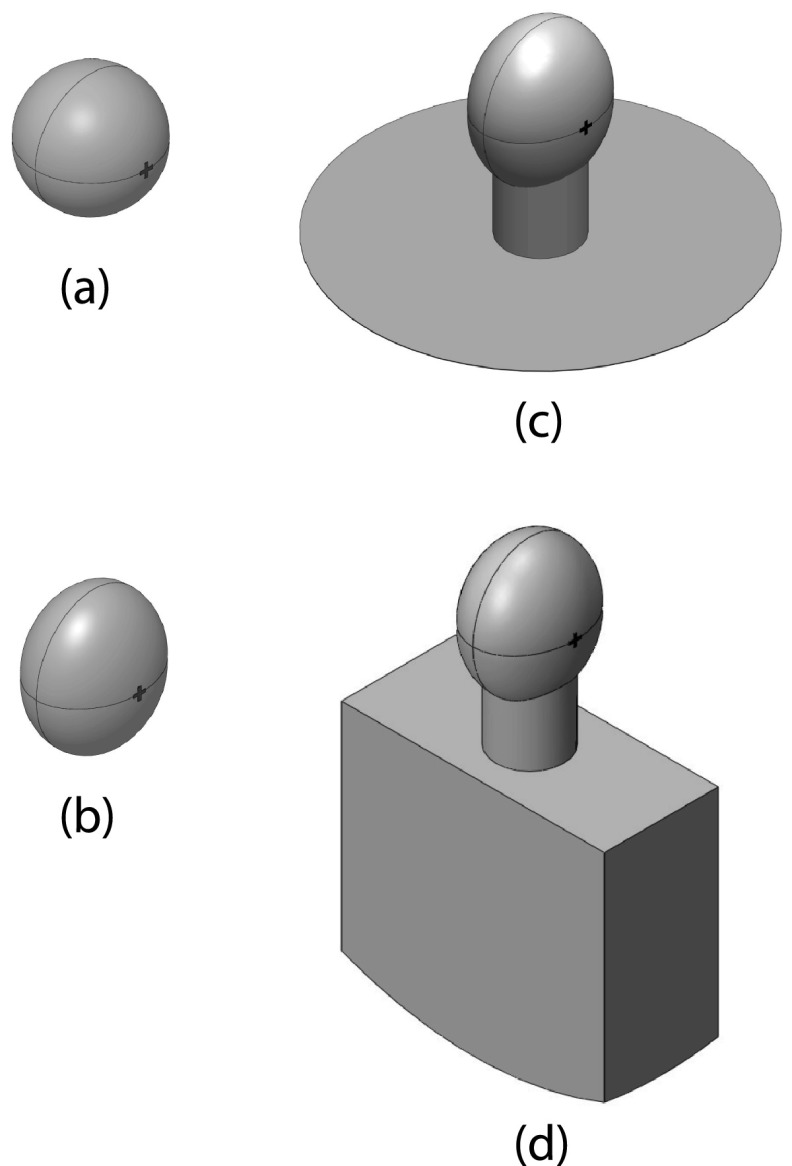
The goal of this article is to improve on the spherical head model for low-frequency interaural differences through a series of geometrical approximations to the human head and torso as shown in Fig. 1. The geometrical models are solved numerically and the predictions are compared with free-field measurements. The models represent only the large scale deviations from a sphere, consistent with the low frequencies and long wavelengths of the numerical calculations and the measurements. The value of this approach is that specific failures of the spherical head model can plausibly be attributed to specific anatomical features.

FIG. 1.

Models for finite element computation: (a) spherical, (b) ellipsoidal, (c) ellipsoidal head with plate torso, and (d) ellipsoidal head with box (deep) torso.

Section II presents our KEMAR measurements of interaural differences for sources in the azimuthal plane and compares them with other databases, as well as with the predictions of the analytic spherical head model. The failures observed for the spherical head model become the targets for the more realistic calculations that follow. It is expected (though not guaranteed) that models with increasing detail will lead to increasingly good agreement with interaural measurements.

Section III begins the finite element calculations by treating the head as an ellipsoid. Subsequent parametric investigations reveal the individual roles for the ellipsoid's height, width, and depth. In Sec. IV, a neck is added to the ellipsoid. Section V adds model torsos to the ellipsoid and neck. The simplest torso is a plate. Improved torsos are rectangular boxes with depth as a parameter. These sections focus on interaural differences. Information on the HRTFs from which the interaural differences were derived appears in the Appendix.

Throughout the modeling, the dimensions are those specified by Burkhard and Sachs (1975) in their original KEMAR article. Inevitably, as the model grows in complexity, the details increasingly represent the KEMAR and lose generality. However, the trends observed as the model changes are expected to apply to much of the population given the low frequencies considered. In addition, as the model grows in physical size, the applicable frequency range needs to be reevaluated. It may not be realistic to expect the larger model to work at frequencies as high as 2500 Hz.

II. MEASUREMENTS

A. Methods

Interaural differences were measured using sine tone signals with 47 frequencies equally spaced by 50 Hz from 200 to 2500 Hz. The KEMAR manikin had the large ears and all its neck rings. Its head faced the forward direction. The manikin ears were fitted with Zwislocki couplers, including Etymotic ER-11 microphones (Etymotic, Elk Grove Village, IL). Preamplifiers matching the microphones were followed by a second stage of amplification (∼40 dB) to reach the range of the analog to digital converters (TDT DD1, Tucker Davis Technologies, Alachua, FL).

Because the frequency was known for each measurement, the signal recording program could use matched filtering to extract the amplitudes and phases of signals in the two ears. ITD and ILD were computed from those measurements. A calibration measurement was made in the forward direction (0-degrees source azimuth), and the results were used as references for measurements at the other azimuths. Therefore, the interaural differences reported here represent the changes induced by rotating the head by stages through ±90 degrees.

Measurements were made in an anechoic room, 4.3 m × 3.0 m × 2.4 m high, with 90-cm foam wedges on all six surfaces. The source of the tones was a single loudspeaker mounted at ear height on a microphone stand. The head was 3 m away along a diagonal of the room, avoiding walls as much as possible. The distance between the head and the nearest foam-wedge wall was 1.1 m and the distance to the other wall was 1.2 m. Because we were concerned about possible reflections, we repeated our measurements for several different locations of the loudspeaker and head, maintaining the 3-m spacing. We report only measurements that were insensitive to location. The different source azimuths were obtained by rotating the manikin about its vertical post. As shown in the Appendix of Hartmann and Macaulay (2014), the displacement of the post from the center of the head had negligible consequences for a source distance of 3 m. Ten measurements were made for each azimuth—five with a rotation to the right and five with a rotation to the left.

Our measurements differed from most of those reported in the literature in several ways: (1) No source array or electromechanical positioner was used, keeping scattering surfaces to a minimum. (2) Because the measuring system was easily moveable, it was possible to test for translational invariance and to accept only invariant measurements. (3) Measurements were made in the frequency domain conferring excellent noise immunity. (4) HRTFs were measured directly with 500-ms segments of sine tones and not by transforming HRIRs. Therefore, frequency resolution was not limited by impulse-response length. (5) The measurements were made at azimuths and frequencies that exactly matched the computations, leading to optimum efficiency in comparing measurements with theory.

B. Results and comparison

The KEMAR measurements for the ITD are shown by symbols in Fig. 2 for six azimuths: 10, 20, 30, 45, 60, and 90 degrees. ITD measurements made below 300 Hz are not reported because extended measurements found that the ITD was sensitive to location in the room. The error bars are two standard deviations in overall length. Similarly, KEMAR measurements for the ILD are shown by symbols in Fig. 3. Our measurements (3 m) can be compared with the mean values from the LISTEN database (2 m) (Warusfel, 2002), consisting of impulse responses to left and right ears for 51 listeners. Those impulse responses were acquired at 15-degree intervals, leading to four opportunities to compare with our measurements when the impulse responses were reduced to interaural differences. At 30, 45, 60, and 90 degrees, the root-mean-square (RMS) discrepancies in ITDs computed over our 47 frequencies were, respectively, 29, 29, 31, and 28 μs. The discrepancies in ILDs were, respectively, 1.3, 1.0, 2.1, and 1.3 dB. These discrepancies were smaller than the standard deviation among listeners in the LISTEN database.

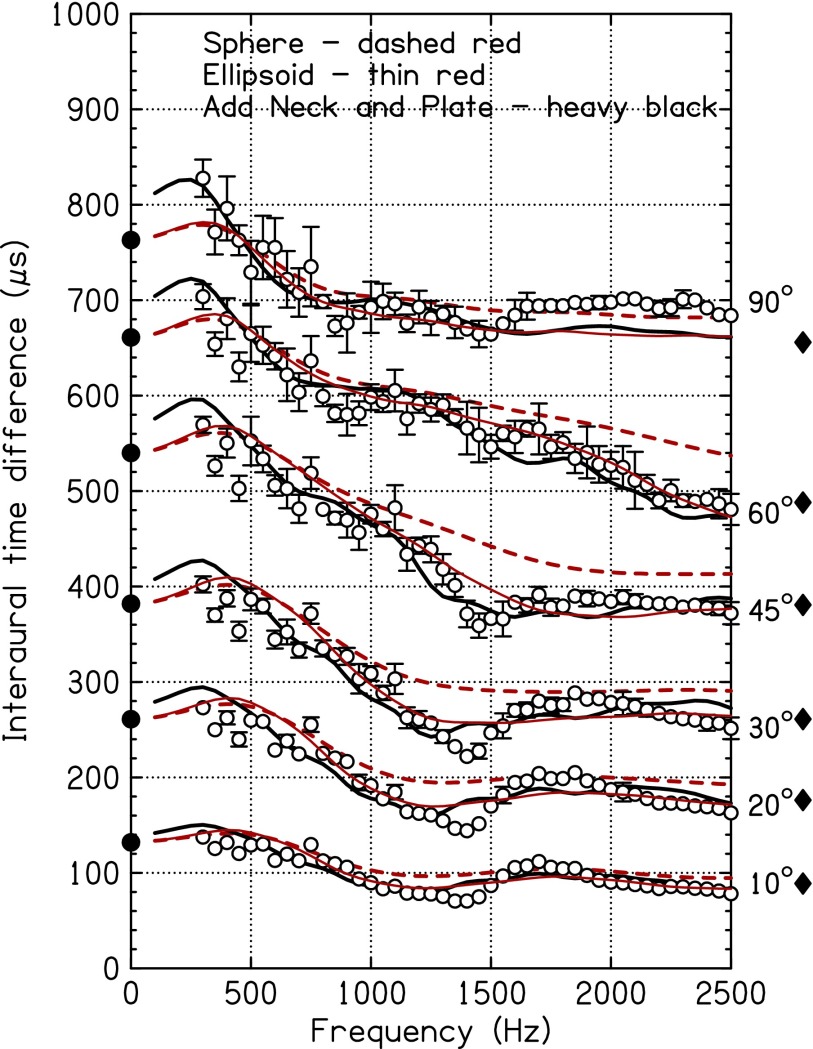
FIG. 2.

ITDs as a function of frequency for six different azimuths. Circles show KEMAR measurements with error bars two standard deviations in overall length. When no error bars appear, the standard deviation was smaller than the circle size. The dashed red lines are the predictions of the spherical head model for 300-cm source distance. Filled circles show the low-frequency limit for infinite source distance. Diamonds show the predictions of the Woodworth (1938) model. The thin red line shows the predictions of the ellipsoidal head model and the heavy black line shows the predictions for an ellipsoid + neck + plate torso.

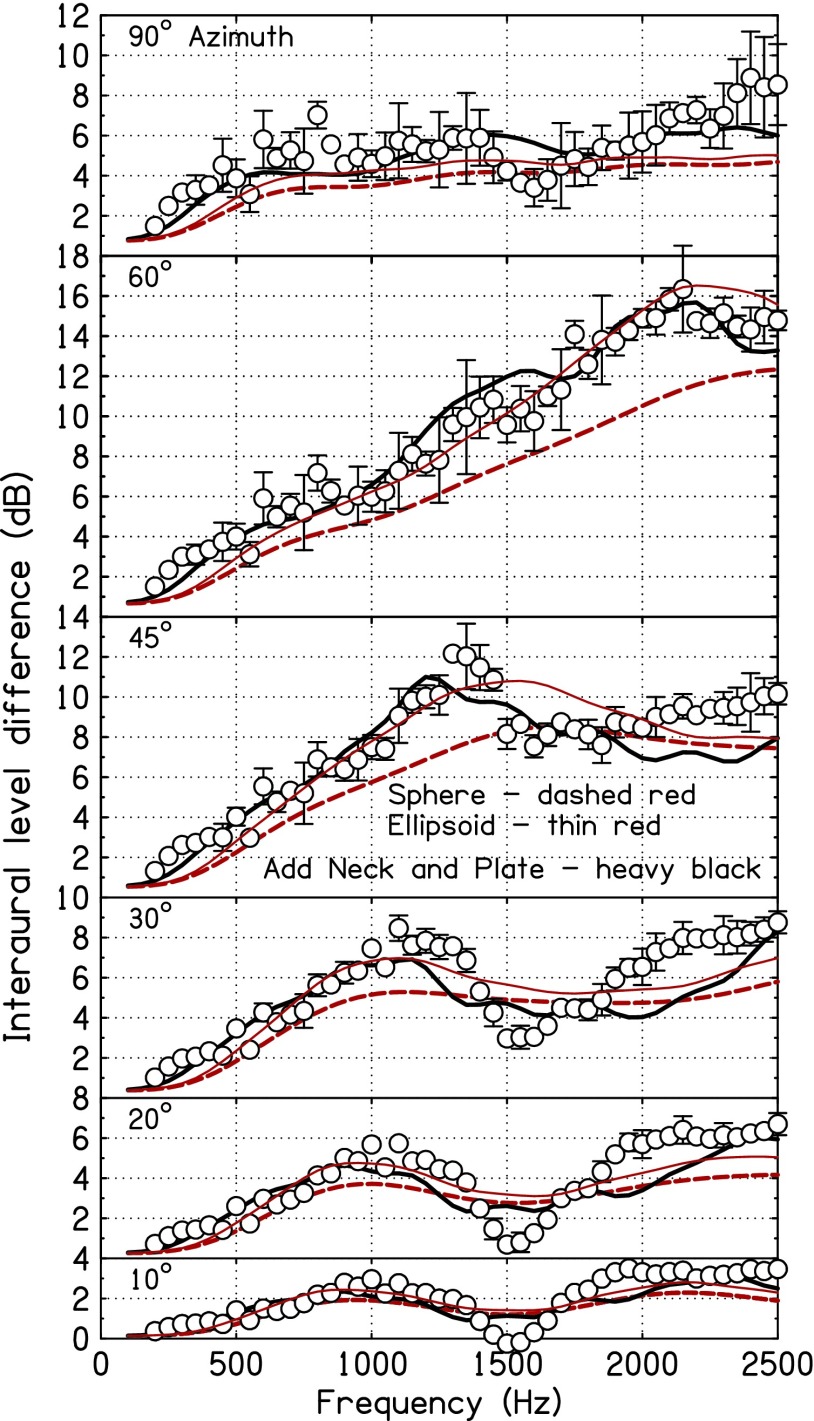
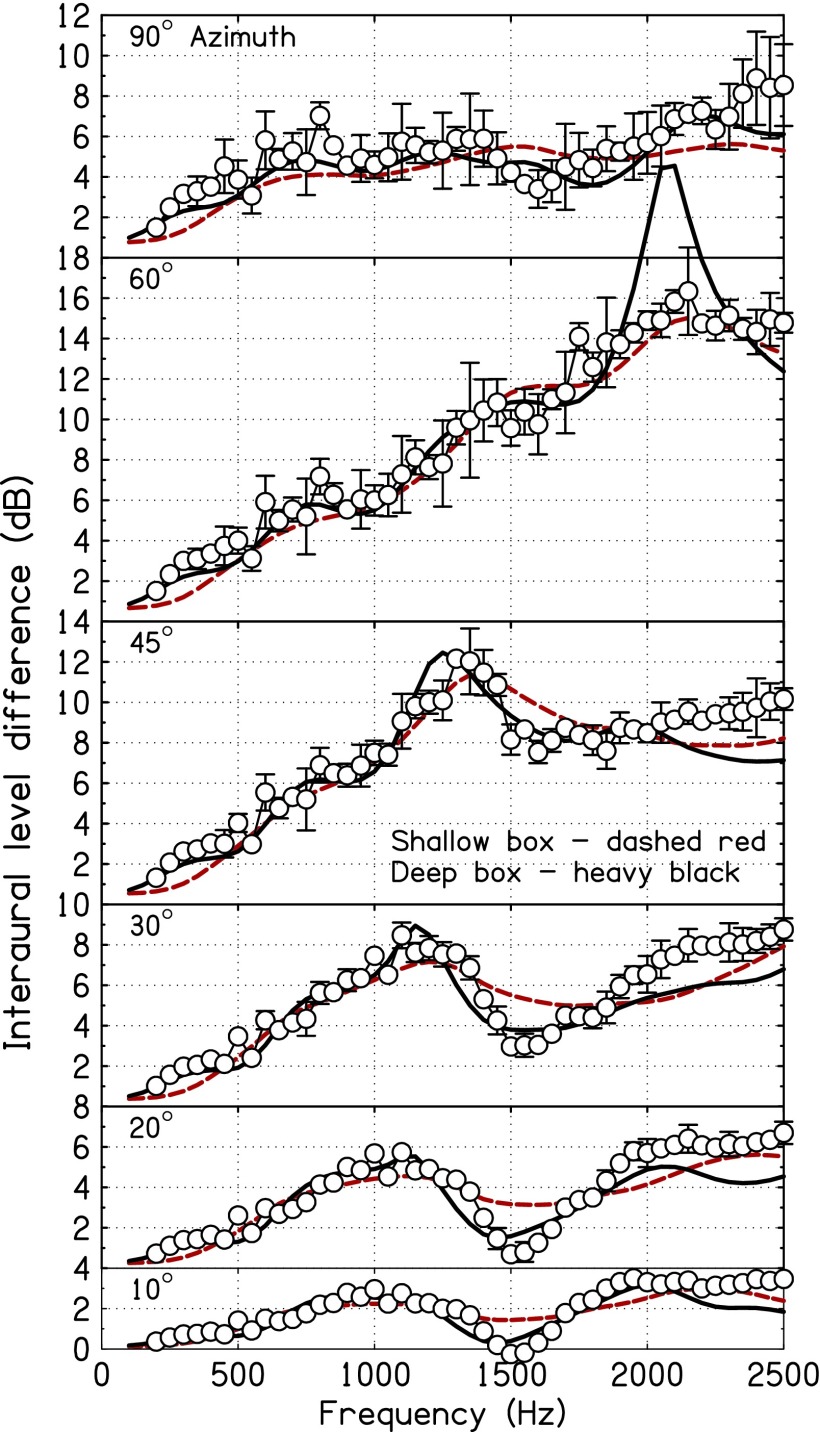
FIG. 3.

ILDs as a function of frequency for six different azimuths. Circles show KEMAR measurements with error bars two standard deviations in overall length. When no error bars appear, the standard deviation was smaller than the circle size. The dashed red lines are the predictions of the spherical head model for 300-cm source distance. The thin red line shows the predictions of the ellipsoidal head model and the heavy black line shows the predictions for an ellipsoid + neck + plate torso.

Predictions of the spherical head model, including low-frequency ITD limits (Kuhn, 1977) and high-frequency ITD limits (Woodworth, 1938), are given in Figs. 2 and 3 where they can be compared with the measurements on ITD and ILD, respectively.

1. ITD

Tables I and II in this article compare model ITDs with measured ITDs using two ITD properties. The first is dispersion, the rapid decrease in observed ITD over a range between ∼500 Hz and ∼1500 Hz. This dispersive property is always a difference in ITDs, usually between an ITD peak and valley. The second property is the actual value of ITDs as measured over the entire frequency range.

TABLE I.

Dispersion between 500 and 1500 Hz. Entries show the difference between the peak ITD near 500 Hz and the minimum ITD near 1500 Hz as measured on the KEMAR and as computed by five different models. If a near peak or valley does not occur, ITDs are those at exactly 500 or 1500 Hz. The RMS discrepancy between models and measurements, averaged over the six azimuths, appears in the last line.

Azimuth (degrees)	KEMAR (μs)	Sphere (μs)	Ellipsoid (μs)	Plate torso (μs)	Shallow box (μs)	Deep box (μs)
10	60	44	61	55	59	68
20	116	83	114	107	112	124
30	165	112	153	149	156	163
45	186	119	172	179	195	172
60	119	91	114	112	126	112
90	91	90	113	80	117	91
RMS	0	40	12	10	12	8

TABLE II.

RMS discrepancies with KEMAR measurements. RMS discrepancies for ten models: Spherical head, ellipsoidal head, three ellipsoids of revolution (ER), ellipsoid + neck, ellipsoid + neck + plate torso, ellipsoid + neck + shallow-box torso, ellipsoid + neck + deep-box torso, ellipsoid + short neck + deep-box torso.

Model	ITD (μs) 300–2500 Hz	ITD (μs) 300–1500 Hz	ILD (dB) 300–2500 Hz	ILD (dB) 300–1500 Hz
Sphere	29	29	1.93	1.70
Ellipsoid	18	20	1.23	1.00
ER tall	35	40	1.36	1.11
ER narrow	30	29	1.84	1.64
ER deep	32	34	1.87	1.63
Added neck	22	26	1.25	1.10
Plate torso	18	20	1.19	0.96
Shallow box	18	18	1.13	0.95
Deep box	15	16	1.28	0.78
Short neck	18	20	1.33	1.06

The measured ITDs showed prominent dispersion in the frequency range near 500–1500 Hz, especially for intermediate source azimuths. The predictions of the spherical head model also showed such dispersion over this frequency range, but, by a much smaller amount. Table I gives the peak-to-valley ITD difference in this frequency range from our measurements and for the spherical head model. The greatest discrepancy occurred at 45 degrees, where it was 36%.

The measurements by Wierstorf et al. (2011), compared with the spherical head model, similarly showed that the greatest discrepancy occurred at 45 degrees—indicating that the spherical head model underestimated the measured dispersion by 43%. Again, at 45 degrees, the spherical head model underestimated the dispersion found in the LISTEN database by 40% and it underestimated the dispersion from the CIPIC database (Algazi et al., 2001) by 27%.

Further, except at 90-degrees azimuth, the spherical head model overestimated the actual ITD values above 1500 Hz, especially at 45 and 60 degrees. The discrepancy was as large as 57 μs (60 degrees, 2500 Hz). The discrepancies with respect to the LISTEN database and the database from Wierstorf et al. (2011) were also largest for 45 and 60 degrees and in the same direction.

2. ILD

The measured ILDs, shown by symbols in Fig. 3, had a complicated frequency dependence with prominent peaks and valleys. The predictions of the spherical head model (red dashed line) often had peaks and valleys at similar frequencies, but they were much less pronounced. In addition, for most azimuths and frequencies, the spherical head model considerably underestimated the ILDs, especially for azimuths >30 degrees. Overall, the discrepancy was 1.93 dB as shown in Table II. Also, for azimuths ≥45 degrees, the spherical head model predicted an ILD peak at a higher frequency than observed.

Kayser et al. (2009) measured interaural differences for a B&K head and torso simulator at 30, 60, and 90 degrees (among others) and compared with a spherical head model. Over the frequency range 200–2500 Hz, their Fig. 6 (like our Fig. 3) showed that the largest discrepancy between measurements and model occurred for an azimuth of 60 degrees—about 5 dB near 2000 Hz. A similar maximum discrepancy occurred in the LISTEN database at this frequency. The ILDs from Kayser et al. (2009) also reproduced the 5-dB dip that we found at 1500 Hz in ILD plots for 30 degrees.

The ILDs derived from the measurements by Wierstorf et al. (2011) showed valleys near 1500 Hz for 10, 20, and 30 degrees azimuth that matched the valleys in our Fig. 3. Those ILDs also showed that the valleys moved to higher frequencies as the azimuth increased to 45 and 60 degrees. The spherical head model underestimated the ILDs from Wierstorf et al. (2011) in the same way that it underestimated the ILDs from our measurements in Fig. 3.

In summary, the measured ITDs and ILDs in Figs. 2 and 3, and the ITDs and ILDs measured in other labs disagree with the spherical head model in similar ways. The main deficiencies in that model are as follows:

• (1)The model ITDs for 20, 30, and 45 degrees of azimuth underestimate the dispersion between 500 and 1500 Hz by as much as 67 μs.
• (2)The model for 30, 45, and 60 degrees considerably overestimates the ITDs from 1200 to 2500 Hz. The discrepancy is as large as 57 μs (60 degrees, 2500 Hz).
• (3)Model ITDs are smooth functions of frequency, but measured ITDs are complicated functions with considerable structure. Also, the model dispersion below 500 Hz has the wrong shape to agree with measured values.
• (4)ILDs from the spherical head model are smooth functions of frequency, but measured ILDs show pronounced peaks and valleys (5 dB at 20 and 30 degrees). The model underestimates the peak to valley differences for 10, 20, 30, and 45 degrees.
• (5)The model for 60 degrees underestimates the ILD at all frequencies—by as much as 5 dB.

III. ELLIPSOIDAL HEAD MODEL

Human heads are better approximated by ellipsoids than by spheres.¹ Duda et al. (1999) studied the ITD as a function of elevation for an ellipsoidal head using a ray tracing approach that is valid at high frequencies. All our calculations below were for an elevation of zero (azimuthal plane) and for low frequencies where the wave properties of sound are important.

A. Methods

Our ellipsoidal head model [Fig. 1(b)] was based on KEMAR head dimensions from Burkhard and Sachs (1975): height 22.4 cm, width 15.2 cm, and depth 19.1 cm. The (point-like) ears were again separated by 180 degrees and were in the azimuthal plane. The ears were symmetrical with respect to ellipsoid height, which we called a “mid-ear” approximation.

Computation was performed using finite element software Abaqus FEA (Dassault Systemes, Velizy Villacoublay, France). First, the incident wave field was pre-generated by a 3-m point source. Then the scattered field was evaluated in the computational spatial domain. In post-processing, the total sound field was obtained by combining the incident wave and scattered wave pressures. Binaural differences were calculated by extracting the sound pressure amplitudes and phases at the ear locations.

Under the assumption that the head is acoustically rigid, only the geometrical characteristics of the head are relevant. The computational domain consisted of a sphere made of air surrounding the model head. The ellipsoidal head was centered in the computational sphere, and its surface formed the inner boundary of the domain. The outer boundary of the computational domain was nonreflecting and had a radius of 0.5 m.

The computational domain was discretized using ten-node quadratic tetrahedral elements with four nodes at the vertices and six nodes midway along the edges (Dassault, 2012). Uniformly meshing the domain produced 0.34 × 10⁶ elements, leading to ∼12 nodes per wavelength for our highest frequency, 2500 Hz. There were 0.95 × 10⁶ degrees of freedom. In computation, the frequency was swept from 100 to 2500 Hz with an increment of 50 Hz.

The computations were done on an eight-processor Linux cluster at the Institute for Cyber-Enabled Research at Michigan State University. The computation for one source azimuth (49 frequencies from 100 to 2500 Hz) required 20 GB of memory and took a few hours to complete.

The finite element procedure was tested by modeling a spherical head and comparing with the analytic series solution in a test of convergence as shown in Table III. The test showed reasonable convergence. The largest discrepancy for the ITD was 1.2 μs and the largest discrepancy for the ILD was 0.13 dB. We concluded that a mesh density of 12 nodes per wavelength led to adequate computational accuracy, and this meshing density was used throughout all our computations.

TABLE III.

Convergence of the finite element calculation. Maximum discrepancies over 6 azimuths and 49 frequencies between finite element calculation for a spherical head and the analytical solution. The number of nodes per wavelength was computed at our maximum frequency of 2500 Hz.

Number of nodes per wavelength	7.4	8.5	11.4	12.6
Maximum ITD error (μs)	2.7	1.9	1.6	1.2
Max ITD error condition (deg, Hz)	90, 2500	90, 2500	90, 2500	45, 400
Maximum ILD error (dB)	0.25	0.23	0.13	0.13
Max ILD error condition (deg, Hz)	90, 2250	90, 2250	90, 2250	90, 2250

B. Comparison with experiment

Interaural differences computed in the ellipsoidal model are plotted as thin red lines in Figs. 2 and 3 where they can be compared with measured values.

1. ITD

Replacing the spherical model head by an ellipsoid greatly improved the agreement between model predictions and measured ITDs in the region of greatest dispersion (∼500 to ∼1500 Hz) for intermediate azimuths, 30–60 degrees, as shown in Fig. 2. Table I is specialized to this frequency region. It shows that the RMS discrepancy between model dispersion and measured dispersion decreased from 40 μs to 12 μs. Further, Fig. 2 shows that the ellipsoidal model better represented the ITDs above 1500 Hz for intermediate azimuths although it underestimated the ITD for 90-degree azimuth. Overall, the ellipsoidal head led to much improved agreement with measured ITDs. The RMS discrepancy from 300 to 2500 Hz over all azimuths decreased from 29 μs to 18 μs, as shown in Table II.

2. ILD

Replacing the spherical model head by an ellipsoid increased the ILD for all azimuths and all frequencies. This increase almost always improved the agreement with the measured ILD, as shown by the thin solid line in Fig. 3 compared to the dashed line for a sphere. The improvement was particularly dramatic for an azimuth of 60 degrees. As noted in the Appendix, it was caused by an increased intensity shadow at the far ear with little change in intensity for the near ear. Further, making the head ellipsoidal increased the predicted differences between peaks and valleys, although these peak–valley differences were still smaller than measured. Figure 3 shows that the ellipsoidal head led to ILD peaks at somewhat lower frequencies, especially above 30-degrees azimuth, improving agreement with measured peaks. Table II shows that the RMS discrepancy in ILD from 300 to 2500 Hz, computed over all azimuths, decreased to 1.23 dB compared with a discrepancy of >1.9 dB for the spherical head model.

Although the ellipsoidal model improved agreement with experiments, the model interaural functions were smoother than the measurements for both ITD and ILD. Specifically, the measurements showed small-scale ripples, oscillations with quasi periodicities from 500 to 800 Hz, not present in the model results. Whether this small-scale structure represents inexplicable variation or patterns that can be captured by more detailed models remained to be tested in Secs. IV and V.

C. Parametric variations

Changing the model head from a sphere to an ellipsoid improved agreement with measured ITD and ILD. The goal of the parametric variations was to determine why that occurred. These variations changed the sphere into three ellipsoids of revolution. In independent calculations, one parameter—the height, the width, or the depth—assumed the value appropriate to the full ellipsoid from Sec. III A while the other two dimensions remained equal to the sphere diameter.

1. Height

With respect to ITD, calculations with an ellipsoid of revolution incorporating only the height from the full ellipsoid (tall head, 22.4 cm) captured most of the dispersion obtained with the ellipsoidal head model. Whereas replacing the sphere with the full ellipsoid reduced the discrepancy in dispersion by 70%, replacing the sphere by the tall head reduced the discrepancy by 62%. However, the tall head caused the overall ITD to become too large because the head width was too large. Therefore, although the predicted ITD for the tall head paralleled the ITD for the ellipsoidal head, the overall RMS discrepancy for the tall head shown in Table II (300–2500 Hz) became 35 μs—almost twice that for the ellipsoidal head.

With respect to ILD, Table II shows that most of the improvement obtained when the sphere was changed to an ellipsoid was captured by the tall head. The effect was striking for 60 degrees, where the spherical head ILD was in greatest disagreement with measurements. At 20, 30, and 45 degrees, the tall head led to helpful changes from the spherical head that were in the same direction as the full ellipsoid but somewhat smaller in size. As noted in the Appendix, the main level difference between the tall head and the full ellipsoid appears in the near ear.

2. Width

With respect to the ITD, an ellipsoid of revolution incorporating only the narrow width of the full ellipsoid (narrow head, 15.2 cm) significantly reduced the ITD compared to the spherical head model or the ellipsoidal head model, especially for larger azimuths. The reduced ITD led to worse agreement with experiment (Table II). Narrow-head ITD functions were parallel to those for a spherical head, indicating that the narrow head did not adequately capture the observed dispersion. Greatly reducing the width (very narrow head, 5.0 cm) continued the trend to smaller ITDs.

With respect to the ILD, the narrow head led to very little difference compared to the spherical head. The small difference that did appear was a surprise. For azimuths of 20, 30, and 45 degrees and for frequencies >1000 Hz, the narrow head led to slightly larger ILDs than the spherical head, even though the narrow head was smaller. Calculations with the very narrow head (5.0 cm) found that further narrowing led to further increase in ILD for frequencies >1000 Hz. Apparently, this very narrow head casts a very deep shadow on the opposite side as the wavelength shrinks to be less than twice the head size (2 × 17.5 = 35 cm). The KEMAR morphing calculations of Mokhtari et al. (2011) generated a shape somewhat like this narrow ellipsoid of revolution. They likewise found major ILD effects on the contralateral side.

3. Depth

With respect to the ITD, incorporating only the depth of the full ellipsoid (deep head, 19.1 cm) led to little change compared to the spherical head, with the largest difference being only ∼10 μs. When the head was given the unphysically large depth of 22.4 cm (deeper head—as deep as the full ellipsoid is tall), there was little difference compared to the deep head—never greater than about 20 μs. Therefore, neither the deep head nor the deeper head agreed with the observed dispersion.

With respect to the ILD, the deep head led to negligible change compared to the spherical head. Only in a few small ranges of azimuth and frequency were the changes as large as 1 dB. The deeper head (22.4 cm) led to little further change—never more than 1 dB except at 60 degrees from 2000 to 2500 Hz where the change was ∼1.5 dB. Therefore, even the deeper head failed to obtain the ILD improvements seen with the full ellipsoid or with the tall head.

4. Conclusion

The three parametric variations indicated that the success of the ellipsoidal head model compared to the spherical head model in computing the ITD was the result of two factors: First, the increased dispersion caused by the increased height of the ellipsoid; second, the decreased ITD overall caused by the narrower width. The depth was not a factor. The success of the ellipsoidal head model in computing the ILD was almost entirely due to the increased height. The width and depth were only minor factors.

IV. ELLIPSOIDAL HEAD PLUS NECK

Replacing a spherical head by an ellipsoidal head increased the height of the model geometry. Adding a neck further increased the height. In this section and Sec. V, the ellipsoid is the full ellipsoid with the three dimensions given by Burkhard and Sachs (1975).

A. Methods

A neck was added, on axis, at the bottom of the ellipsoid. It was modeled as a cylinder, 11.3 cm in diameter (Burkhard and Sachs, 1975) extending down 18.8 cm below the ears. The latter value was obtained by starting with the 17.5-cm ear-to-shoulder distance from Burkhard and Sachs (1975) and correcting by 1.3 cm to compensate for the mid-ear assumption.

The finite element computation for an ellipsoidal head plus neck was similar to that for the ellipsoidal head alone. The radius of the computational domain was increased from 0.5 m to 0.6 m. Therefore, the number of elements became 0.52 × 10⁶, and the number of degrees of freedom became 1.4 × 10⁶. The computation then required 28 GB of memory, and the computation time was about doubled.

B. Comparison

The effect of adding the neck on the computed ITD was to further increase the dispersion between 500 and 1500 Hz. The dispersion became larger than predicted by the ellipsoidal model and also larger than experimentally observed. In addition, the RMS discrepancy computed over all measured frequencies and source azimuths increased from 18 μs to 22 μs (Table II).

As expected, the effect of adding the neck on the computed ILD increased the differences between peaks and valleys. The increased peak–valley variation better matched the measured peak–valley variation. However, the neck also displaced the peaks and valleys in frequency. The frequencies of the peaks in ILD were always decreased by the neck, which usually led to worse agreement with measured peak frequencies. Over the frequency range from 300 to 2500 Hz, the RMS discrepancy between model and measurement was 1.23 dB for the ellipsoidal head and 1.25 dB for the ellipsoidal head plus neck (Table II).

C. Low ears

Contrary to our modeling assumptions, the KEMAR ears are not actually at mid height on the head. To match the dimensions given by Burkhard and Sachs (1975), we reduced the height of the ears by 1.3 cm in the ellipsoid-plus-neck model. The source remained in a horizontal plane bisecting the vertical axis of the ellipsoid and, therefore, the source was above the new ear location.

There was little important effect on the ITD or ILD below 1000 Hz. Above 1000 Hz, and at 20 and 30 degrees of azimuth, the lowered ears increased the frequency of the first peak of the ILD. Also, at 45 and 60 degrees, the lowered ears increased the height of the peak by 10%. Both of these effects improved agreement with measured ILDs. However, lowering the ears resulted in worse agreement with the second peak in the ILD at 10–30 degrees. Duda et al. (1999) also investigated the role of ear height, but only in the high-frequency limit.

D. Spherical head plus neck

For the sake of completeness, we did finite element calculations for a spherical head (as in Sec. II) with a neck. The computational methods were similar to the ellipsoidal head and neck.

The effect of adding a neck to a spherical head was to increase the ITD for low frequencies and decrease the ITD for high frequencies. Described in that way, the boundary between “low” and “high” depended on azimuth. It increased from 600 Hz at 10 degrees azimuth to 900 Hz at 60 degrees. Adding the neck thus captured some of the larger frequency variation observed in the measurements. However, the overall predicted ITD was too high, and adding the neck resulted in worse agreement than obtained with the spherical head by itself.

The effect on the ILD of adding a neck to a spherical head was to increase the variation in predicted ILD as a function of frequency, which better resembled the measurements, but the predicted ILDs were considerably too low—lower than predicted by the ellipsoid plus neck.

V. TORSO

Algazi et al. (2002) computed HRTFs for a spherical head with spherical and ellipsoidal torsos (snowman models). They showed that adding a torso improved agreement with the elevation dependence observed in a KEMAR, but they concluded that there was little effect in the azimuthal plane. In this section, we attempt to determine the effects of a model torso on interaural properties in the azimuthal plane.

As the torso is added, the model grows in size, and the frequency range for comparison with measurements may need revision. With the head alone, the largest dimension (22.4 cm) was equal to one wavelength at 1536 Hz. We chose to compare with measurements over a broader range—up to 2500 Hz. With the torso, the model size was larger and somewhat indefinite in that it extended to the computational boundary. It may be more realistic to compare over a smaller frequency range and, therefore, Table II includes a second range for comparison—only up to 1500 Hz.

A. Plate torso

The plate torso model [Fig. 1(c)] was obtained by placing the ellipsoidal head and neck on a large horizontal surface conveniently terminated by the spherical outer boundary of the computational domain. Because the bottom of the neck was 18.8 cm below the center of the sphere, the plate was circular with a radius of ∼57 cm. Using such a simplified model of the torso led to a computational problem with fewer degrees of freedom—about the same as the ellipsoidal head alone.

Adding the plate torso to the ellipsoid plus neck considerably reduced the tendency of the ellipsoidal head model (with or without neck) to overestimate the ITD between 400 and 800 Hz, as shown by the heavy black line in Fig. 2. Table II shows that the plate improved overall agreement with the measured ITDs, decreasing the RMS discrepancy from 22 μs (ellipsoid plus neck) to 18 μs. Table I shows that adding the plate caused the dispersion in the 500–1500 Hz range to agree better with the measured dispersion. The RMS discrepancy decreased to only 10 μs. Adding the plate thus compensated the overshoot that resulted from an earlier step in the evolution when the neck was added to the ellipsoid.

Adding the plate torso slightly decreased the RMS discrepancy in ILD from 1.25 dB to 1.19 dB. Figure 3 shows that adding the plate led to improvements at all source azimuths, especially below 1200 Hz.

Both the ITD plot in Fig. 2 and the ILD plot in Fig. 3 reveal ripples caused by reflections from the plate. These ripples were apparent in the phases and magnitudes of the model transfer functions at both near and far ears. In fact, the measured data did have irregular ripples of this magnitude, but the details of the peaks and valleys were different from the model. Further, we found that the plate could not be justified as a torso model because of its unrealistic area. However, the plate model taught us that model torso reflections could lead to ripples of about the right magnitude and suggested that a better torso model might also get the details right. Better models were obtained with box-like structures leading to ITD and ILD predictions as shown in Figs. 4 and 5, respectively.

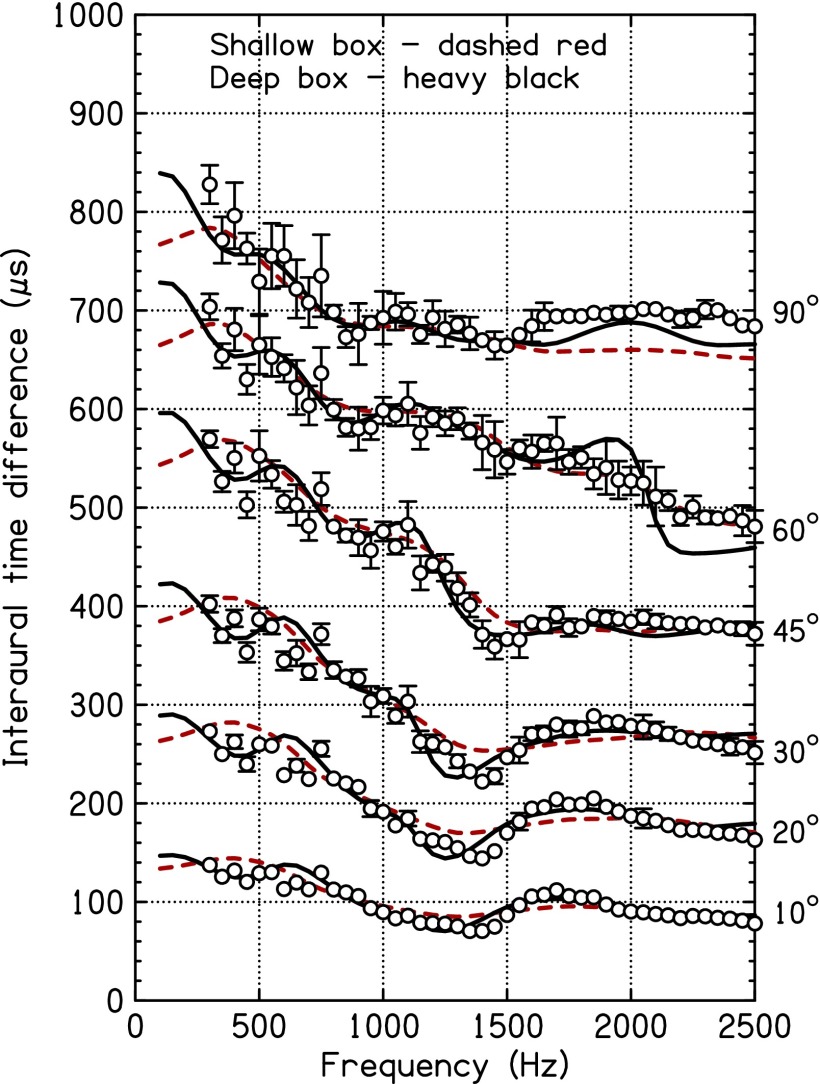
FIG. 4.

ITDs KEMAR measurements (symbols) are compared with two models: Ellipsoid + neck + shallow-box torso (neck depth) and ellipsoid + neck + deep-box torso (chest depth).

FIG. 5.

Same as Fig. 4 except for ILD.

B. Shallow-box torso

The shallow-box torso broke the axial symmetry of the plate torso, and led to a more realistic reflecting surface. The box was mounted below the neck of standard length (18.8 cm). Its width was given by the shoulder width from Burkhard and Sachs (1975), 44 cm, and its depth was only the neck diameter, 11.3 cm.

Reflections from the box caused minor ripples in the ITD function that compensated the excessive dispersion seen for the ellipsoid plus neck alone. Because of the compensation, the ITD resembled the ITD seen for the ellipsoid by itself, as can be seen by comparing the dashed red line in Fig. 4 with the thin solid red line in Fig. 2. There is very little difference between the two curves. Similarly, the shallow box led to minimal changes in the ILD compared to the ellipsoidal model, as can be seen by comparing Fig. 5 with Fig. 3.

C. Deep-box torso

The deep-box torso [Fig. 1(d)] was mounted below the neck of standard length (18.8 cm). Its width was given by the shoulder width from Burkhard and Sachs (1975; 44 cm), and its depth was estimated to be the same as the depth of the chest or head (19.1 cm) based on Fig. 1 in Burkhard and Sachs (1975). As for the plate torso, reflections from the deep-box torso caused ripples in the phases and amplitudes of transfer functions for both ears. Because the ripples were very different in the two ears, the interaural differences were the result of combining two quite different functions. In contrast to the shallow-box torso, the deep-box led to significant interaural effects, as can be seen in Figs. 4 and 5.

The ripples in ITD caused the deep-box torso to obtain better agreement with experiment than obtained for the plate torso, as can be seen in Table II and also can be seen by comparing the heavy dark lines in Figs. 2 and 4. The improvement over the plate torso was particularly striking below 500 Hz, except for an azimuth of 90 degrees. Compared to the ellipsoid, the ripples further improved the dispersion seen between 500 and 1500 Hz for 20, 30, 45, and 60 degrees azimuth. However, the deep-box led to a strange structure near 2000 Hz for 60 degrees. That structure looks like a Kramers–Kronig partner for the equally strange peak that occurred in the ILD at this frequency and azimuth (Fig. 5).² Our interpretation of this effect is that the model had grown too large to be useful over the full range 300–2500 Hz. An alternative evaluation of the effect of the deep-box was obtained by comparing over the smaller range, 300–1500 Hz, where the RMS discrepancy was reduced by 20% compared to the plate torso (Table II).

The deep-box torso led to ripples in ILD that resulted in better agreement with experiment than was obtained for the ellipsoid with the plate torso for all azimuths except 60 degrees, as can be seen by comparing Figs. 3 and 5. For 60 degrees, the deep-box torso led to an anomalous peak in ILD near 2000 Hz, which ruined agreement with experiment, and made the deep-box torso appear to be less successful than the plate torso over the range 300–2500 Hz. (Table II). The alternative evaluation of the deep box over the smaller range, 300–1500 Hz, reduced the RMS discrepancy to <0.8 dB.

The deep-box model, combining the ellipsoidal head, the standard neck, and the deep-box torso, was the most realistic of our models and the most successful, given a reduced frequency range for evaluation. Its advantage over the ellipsoidal head alone came from the torso reflections that created ripples in both the ITD and the ILD. These computed ripples had enough peaks and valleys of the right size and occurring at the right frequencies to improve agreement with measured interaural differences.

As an additional test of these ripples, we calculated characteristic ripple periodicities along the frequency axis. Prominent, consistent periodicities ought to be observable as peaks at characteristic times in the inverse Fourier transforms. Calculated peak times reported in milliseconds correspond to periodic frequency structure observed in ripples per kilohertz. We computed inverse fast Fourier transforms of the ITD and ILD functions for the measured data and the finite element models. Our data permitted horizontal axis times as long as 10 ms (= 0.5 × 1/0.05 kHz) and a resolution of 0.4 ms (= 1/2.500 kHz). For the ITD, small structure appeared with peaks at 1.2 and 2 ms that were similar in both measured data and the deep-box torso model in the sense that the strengths of the peaks as a function of azimuth decreased in the order: 45, 30, 10, 90, 20, and 60 degrees. No such structure appeared in the inverse FFTs for the ellipsoidal model. Gumerov et al. (2010) made similar observations concerning ripples, attributable to torso reflections, in measurements and calculations of HRTFs. However, we were not able to associate the peaks with quantitative geometrical aspects of the KEMAR or the models. The available resolution (14 cm) was inadequate to distinguish small anatomical details.

For the ILD, inverse FFTs of the measured data and the deep-box model were again similar with a dominant peak at 0.8 ms for 10, 20, and 30 degrees, and a broadened peak for 90 degrees. Peaks at 0.8 ms also appeared for the ellipsoidal model for 10 and 20 degrees, though they were somewhat smaller than observed for either the data or the deep-box model. Inverse FFTs for measured data and the deep-box model also found structure between 1.6 and 2.4 ms that was not present for the ellipsoidal model.

Although the deep-box torso led to the smallest discrepancy of any model for dispersion, measured as the ITD difference between the peak near 500 Hz and the valley near 1500 Hz (Table I), the deep box also led to a frequency difference between peak and valley that was smaller than observed for 10, 20, 30, and 45 degrees. Therefore, it overestimated the slopes of the ITD functions for these azimuths, as can be seen in Fig. 4. The frequencies of the peaks and valleys ought to depend on the timing of the reflections from the torso. This timing, in turn, depends on the neck length. In order to observe the effects of different reflection delays, we made a parametric variation on the neck length.

D. Short neck

The short-neck model was identical to the deep-box model above except that the neck length was reduced from 18.8 cm to 14 cm. It was expected that the shorter neck would increase the spacing between peaks and valleys in the interaural differences.

The expected effect was indeed observed in the ITD where the ripples became more widely spaced, especially at 45 and 60 degrees. In addition, the shorter neck increased the amplitude of the ITD ripples. The expected effect was also observed in the ILD, especially at 30, 45, 60, and 90 degrees. The shorter neck sometimes increased the amplitude of the ILD ripples and sometimes decreased the amplitude. The shorter neck resulted in worse agreement with experiment for both ITD and ILD by all of our RMS measures, as shown in Table II.

VI. QUANTITATIVE SUMMARY

Three stages of evolution led to improved agreement with measured interaural differences compared to the spherical head model.

A. Ellipsoidal head

ITD: The dispersion increased (frequency dependence 500–1500 Hz) at all azimuths, reducing the root-mean-square discrepancy (RMSD) by 70%. Improved the ITD fit overall, reducing the RMS discrepancy by 38%.

ILD: The ILD increased at all frequencies and azimuths, especially at middle azimuths of 45 and 60 degrees, and added broad peaks. These changes reduced the RMSD by 36%.

B. Added neck

ITD: The ITD increased at low frequencies.

ILD: The peak–valley structure was enhanced to a magnitude that resembled experiment, but with peaks and valleys badly placed in frequency.

Neither the change in ITD nor the change in ILD was helpful in improving the agreement with measurements, but a neck of the correct length proved to be essential for torso calculations that followed.

C. Added torso

ITD: Small ripples were added, increasing the frequency-dependent structure, which improved agreement with experiment between 450 and 1500 Hz, especially at mid azimuths. The ripples had average quasi periods between 500 and 800 Hz. For the deep-box torso, the added ripples reduced the RMSD (300–1500 Hz) by an additional 20% compared to the ellipsoidal model.

ILD: Ripples were added, which improved the peak and valley agreement with experiment for most azimuths, reducing the RMSD (300–1500 Hz) by an additional 22% compared to the ellipsoidal model.

VII. CONCLUSION

This article began with the observation that the spherical head model failed to represent perceptually important features of ITDs and ILDs as observed for human or humanoid (KEMAR) heads in the frequency range <2500 Hz. To try to understand the discrepancies, we made finite element computations for other idealized shapes that were better than the sphere in representing the head. Idealized shapes potentially lead to easily described insights when restricted to low frequencies and long wavelengths where fine anatomical details are unimportant. Then, a particular example (e.g., KEMAR) may approximately represent the population as a whole, as suggested by our comparison of KEMAR data with the LISTEN database on many subjects.

Our first simple model used an ellipsoidal head. Computations with the ellipsoid matched the observed ITD and ILD better than computations with the sphere, essentially by magnifying the variation of these interaural differences with frequency in the right way. Parametric variations on the ellipsoid showed that it was the increased height of the ellipsoid, compared to the sphere, that was mainly responsible for the improvement. For the ITD, the increased height improved the dispersion while the narrower width of the ellipsoid brought the ITDs themselves back into better agreement with experiment. For the ILD, the increased height was entirely responsible for the improved comparison with experiment. Contributions to the ILD from near and far ears are identified in the Appendix.³

Of course, the improved agreement obtained with the ellipsoidal head did not prove that the discrepancies between the interaural differences observed for the manikin and the interaural differences predicted by the spherical head model were specifically caused by the ellipsoidal shape of the human head rather than some other anatomical feature. It only proved that replacing the sphere by an ellipsoid caused many of the discrepancies to go away. However, attributing failures of the spherical head model to the ellipsoidal shape of the head is plausible for several reasons. First, the discrepancies were at low frequency where large-scale physical features dominate. The overall head shape, neck, and torso have a large physical scale. Noses, eye sockets, and pinnae do not. Based on size alone, the overall shape of the head is a likely origin for the low-frequency interaural discrepancies. Second, the necessary improvements made by the ellipsoid were on a large frequency scale—1000–2000 Hz, as shown in Figs. 2 and 3. Other physical features, such as the torso, are less likely to make changes on this frequency scale because adding a model torso led to changes on a smaller frequency scale (ripples). Third, the ellipsoidal model itself, using the physical dimensions of the KEMAR, successfully accounted for many details of the observed interaural differences, and this was unlikely to be accidental.

Our next step in the evolution of the model added a neck and a torso, represented by a large horizontal plate. Ripples in interaural difference functions predicted by the plate torso encouraged us to try improved models, representing the torso by rectangular boxes, shallow or deep, extending down to the bottom of the computational domain.

All the torso models led to improved agreement with measured ITD and ILD when compared to the ellipsoid or the ellipsoid plus neck, as measured by overall RMS discrepancies (Table II). The deep-box torso predictions for the mid-frequency drop in ITD agreed almost perfectly with the measured dispersion between 500 and 1500 Hz (Table I), although the frequency spacing between peaks and valleys did not.

Our computations showed that adding the neck alone to an ellipsoidal head actually led to worse agreement with measurements. Therefore, we conjecture that the principle role of the neck, so far as interaural differences are concerned, is to serve as a separator between the head and the torso. The effect of the neck is to delay torso reflections leading to ripples in interaural differences. To get the right quasi periods for the ripples, and to get the peaks and valleys at the right frequencies, required that the neck be the right length. Again, our neck length was not optimized, but was taken from Burkhard and Sachs (1975).

Although the final model—ellipsoid, neck, and deep-box torso—improved the agreement with measured interaural differences, the agreement was not perfect. We can speculate about the origins for the remaining discrepancies. Our dimensions for model elements were taken from the dimensions of anatomical features for KEMAR, which were roughly comparable to features in our simple geometries. It is certain that there is some other set of ellipsoid dimensions that would further improve the agreement with measured values. However, the extensive run time for our finite element calculations precluded a parametric search. More important, optimizing geometrical parameters outside the measured dimensions might well obscure discrepancies that ought to be attributed instead to specific geometrical features beyond our final model.

Apart from the model dimensions, there is the tilt of the ellipsoidal head, which we arbitrarily took to be zero. Replacing our box torso by a torso with sloping, or rounded, shoulders might bring the predicted ripples into better agreement with measured values. All of the surfaces in our model were perfectly reflecting; more realistic calculations would use surfaces with appropriate finite impedances, and those would have an effect on the outcome (Treeby, 2007).

Finally, we note that our calculations and measurements were confined to the azimuthal plane. When a spherical head is replaced by a less symmetrical model, the cones of confusion become deformed, and calculations for a source in a single plane lose their generality. The major task of extending the calculations and measurements to encompass sources in the full three dimensions of space would seem to be a particularly interesting problem.

APPENDIX

Whereas the body of this article focuses on interaural differences, this appendix describes the computed HRTFs for near and far ears from which the interaural differences were derived. It deals only with the levels of the signals in the two ears.

1. Spherical head

The signal level in the near ear (near the source) is increased, compared to free field, by reflections from the near surface of the head. For all azimuths, the level in the near ear increases almost monotonically with increasing frequency. These rising functions are, themselves, monotonically increasing functions of azimuth. Therefore, as the azimuth increases from 0 to 90 degrees, the level in the near ear increases because the level boost caused by reflection from the near head surface becomes more effective.

The signal level in the far ear is a broadly oscillating function of frequency. In our restricted frequency range (100–2500 Hz), the most important feature is a dip in level at the far ear that leads to a relatively large interaural difference. The depth of the dip increases with increasing azimuth, and the frequency at which the dip occurs increases with increasing azimuth. For 10, 20, 30, 45, and 60 degrees, the dip-minimum frequency becomes approximately 500, 800, 1000, 1500, and 2500 Hz respectively. The peaks in the ILDs, as shown in Fig. 3, occur at somewhat higher frequencies because of the increasing level in the near ear with increasing frequency as noted above. The exception to these rules is 90 degrees, where the bright-spot effect leads to almost no frequency dependence in the far ear level. For 90 degrees, the ILD is dominated by effects at the near ear. Because we did not do calculations for azimuths between 60 and 90 degrees, we have no details for intermediate azimuths.

2. Ellipsoidal head

The ellipsoidal head is both taller and deeper than the spherical head leading to larger surface area on the near side of the head. The larger area leads to increased reflection compared to the spherical head, and the level at the near ear is always somewhat larger for the ellipsoidal head. The area effect adds 1–2 dB to the ILD.

Most of the ILD difference obtained by making the head ellipsoidal is caused by the far ear. For all azimuths, the dip is deeper for the ellipsoidal head—as much as 5 dB deeper (60 degrees)—and the frequency at which the dip occurs is somewhat reduced. These changes are just what is needed to improve agreement with the measured ILD data, as can be seen in Fig. 3. The exception to these statements is 90 degrees, where the ILD is larger for the ellipsoidal head simply because the near ear level is larger.

3. Tall head

The tall head is not as deep as the ellipsoidal head, and the near surface is not as large. Therefore, the near ear level is not enhanced as much by reflections for the tall head, especially at the larger azimuths. The effect is a little less than 1 dB. That effect appears to be primarily responsible for the fact that the tall head is somewhat less successful than the full ellipsoid in matching the measured ILD because the levels in the far ear are almost identical for those two models.

4. Deeper head

The deeper head has the same dimensions as the tall head except that the deeper head is rotated about the interaural axis to a different orientation with respect to the azimuthal plane. That rotation results in little effect on the near-ear level when the azimuth is large (for an azimuth of 90 degrees there is no effect, by symmetry). When the azimuth is small, the rotation makes the near-ear level smaller for the deeper head.

For the far ear, the rotation leads to a huge difference for 30, 45, and 60 degrees. Whereas the full ellipsoid and the tall head produce much larger level dips than the spherical head, the deeper head produces level dips that are shallower than for the spherical head by as much as 3 dB.

5. Box torso

The HRTFs for the box torso are complicated in both near and far ears with large ripples. At low frequencies, the ripples are somewhat similar in the two ears resulting in some cancellation when the difference is taken. Then the ripples in the HRTFs are larger than the ripples in the ILD. At higher frequencies, the ripples in the two ears seem quite independent.