Abstract
Purpose:
A significant number of patients suffer from craniomaxillofacial (CMF) deformity and require CMF surgery in the United States. The success of CMF surgery depends on not only the surgical techniques but also an accurate surgical planning. However, surgical planning for CMF surgery is challenging due to the absence of a patient-specific reference model. Currently, the outcome of the surgery is often subjective and highly dependent on surgeon’s experience. In this paper, the authors present an automatic method to estimate an anatomically correct reference shape of jaws for orthognathic surgery, a common type of CMF surgery.
Methods:
To estimate a patient-specific jaw reference model, the authors use a data-driven method based on sparse shape composition. Given a dictionary of normal subjects, the authors first use the sparse representation to represent the midface of a patient by the midfaces of the normal subjects in the dictionary. Then, the derived sparse coefficients are used to reconstruct a patient-specific reference jaw shape.
Results:
The authors have validated the proposed method on both synthetic and real patient data. Experimental results show that the authors’ method can effectively reconstruct the normal shape of jaw for patients.
Conclusions:
The authors have presented a novel method to automatically estimate a patient-specific reference model for the patient suffering from CMF deformity.
Keywords: jaw deformity, sparse representation, shape composition, thin-plate spline, treatment planning
1. INTRODUCTION
The field of craniomaxillofacial (CMF) surgery involves the correction of congenital and acquired deformities of the skull and face. It includes dentofacial deformities, congenital deformities, combat injuries, post-traumatic defects, defects after tumor ablation, and deformities of the temporomandibular joint (TMJ). Each year throughout the world, many patients require surgical correction for these deformities.1–3 CMF surgery requires extensive presurgical planning. The success of the CMF surgery depends on not only the technical aspects of the operation but also, to a larger extent, the formulation of a precise surgical planning.4–9 However, CMF surgical planning is extremely challenging due to the complexity of deformity and the absence of a patient-specific reference model. In the conventional CMF surgical planning, a surgeon first acquires a 3-dimensional (3D) model of patient’s skull (which could be either real or electronic) and collects analytical data, and then simulates the surgery by virtually cutting the 3D model and moving and rotating the bony segments to a desired position based on the “averageness” of normal population (so-called “normal values”). However, the outcome of surgical planning is often subjective and highly dependent on the surgeon’s experience.10 We hypothesize that if a surgeon preoperatively knows what the normal CMF shape of the patient should be, the surgical planning process will be more objective and personalized.
Over the past decades, there have been significant improvements in the computer intervention of CMF surgical planning,1 which makes the surgical planning more convenient and efficient. Vannier et al.11 proposed a computer-aided method to delineate abnormal facial soft tissue and bony morphology from CT scans for craniofacial surgical procedure-planning and evaluation. Xia et al.12 developed a 3D computer-aided surgical simulation (CASS) system and clinical protocols to plan different CMF surgeries. With this system, surgeons can generate 3D models of patients’ head bone from multiple modalities, make quantitative analysis (diagnosis), perform “virtual surgery,” and create a 3D prediction of the patient’s surgical outcome, as if performing the surgery in the operating room. Zachow et al.13 proposed a statistical 3D shape model of the human mandible for surgical reconstruction of bone defects. However, to the best of our knowledge, there is no existing surgical planning system that enables the prediction of patient-specific14,15 and anatomically correct reference model for CMF surgery.
In this paper, we present a novel method of preoperatively and automatically estimating what the patient-specific normal CMF shapes should be for individual patients who require CMF surgeries. The estimated explicit patient-specific shape model can be used as a reference to guide the surgical planning. Surgeons will be able to quantitatively determine the difference between the current patient’s deformed shape and the estimated reference shape and then generate a feasible surgical plan. Since CMF surgery includes a large scope of different surgeries for different deformities, our current method focuses on orthognathic surgery, a common type of CMF surgery in which the patient’s deformity is nonsyndromic and only limited to the jaws. In these patients, only the maxilla and mandible are involved in surgery while the midface (the level at zygoma and above) is anatomically correct and does not require a surgery. Figure 1 shows a typical patient requiring a double-jaw orthognathic surgery. The skull surface is divided into two parts: the midface and the jaws. The midface is anatomically correct, while the upper and lower jaws need to be surgically corrected.
FIG. 1.
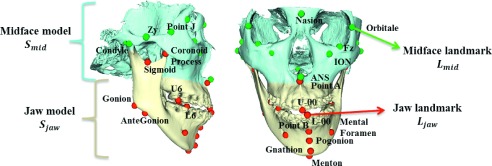
Anatomical landmarks and surface models of a patient requiring orthognathic surgery. The skull surface is divided into two parts: the midface Smid and the jaws Sjaw. Accordingly, the landmarks in the midface and jaw are named as midface landmarks Lmid and jaw landmarks Ljaw.
To predict the normal jaw shape for CMF patients, we adopt a data-driven method inspired by sparse shape composition (SSC) model.16,17 The basic principle of orthognathic surgery is that the midface of a patient is anatomically correct, which allows us to use the anatomy of midface as a prior to predict anatomies of both maxilla and mandible. Thus, given a dictionary of normal subjects, we first use the sparse representation18,19 to approximately represent the midface by those of the normal subjects in the dictionary. Then, the derived sparse coefficients are used to reconstruct a patient-specific normal jaw shape from those of normal subjects. Finally, we validated the proposed approach on both synthetic subject and patient data. Experimental results showed that our method could effectively reconstruct the normal shape of jaw for patients. The results also confirmed that the reconstructed “normal” jaw shapes were within the normal range quantitatively.
A preliminary version of this work was presented at the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI).20 This paper significantly extends the preliminary version with more details on introduction of methodology and also more experimental results, extensive validations, and discussions. The remainder of this paper is organized as follows. Section 2 elaborates the proposed method. Section 3 presents experimental results on both synthetic and real subjects, followed by the discussion and conclusion in Sec. 4.
2. METHOD
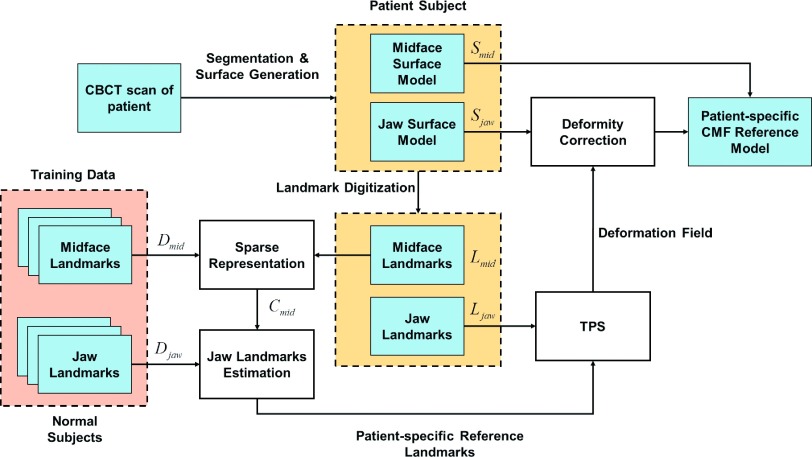
The overall flowchart of the proposed method is shown in Fig. 2. Given a patient with CMF deformity, we first generate the bony surface model that includes two structures: a midface surface Smid and a deformed jaw surface Sjaw. As described above, othognathic surgery only involves the jaws while leaving the midface untouched. Therefore, based on the patient’s midface surface Smid, we can estimate a patient-specific jaw reference model that indicates what the normal shape of the patient’s jaws should be. Thus, given a midface dictionary from normal subjects, we first use the sparse representation18 to approximately represent the midface of the patient. Then, the derived sparse coefficients are used to reconstruct a patient-specific normal jaw shape by weighted combination of the jaw shapes of normal subjects in the dictionary. Finally, the estimated normal jaw shape is combined with the normal midface shape to derive the patient-specific CMF reference model.
FIG. 2.
Flowchart of the proposed work.
2.A. Estimating patient-specific normal CMF shape
In order to utilize the surface model effectively and efficiently, anatomical landmarks are digitized (placed) on the midface and jaw surface models. These landmarks provide several benefits for reconstructing the patient-specific reference model. (1) It is computationally efficient based on a small set of landmarks, instead of tens of thousands of vertices on a discretized surface model (with triangle mesh). (2) All the landmarks have clear and detailed anatomical definitions. Therefore, they have “built-in” correspondence across different subjects. (3) The use of landmarks is clinically relevant since all the cephalometric analyses are landmark-based. In our methods, we select a subset of bony landmarks21 after the 3D model is positioned in the reference system.22 The landmarks are illustrated in Fig. 1. In the development of patient-specific reference model, the surface model is partitioned into two parts: a midface model Smid and a jaw model Sjaw, as illustrated in Fig. 1. Accordingly, we partition the landmarks into midface landmarks Lmid and jaw landmarks Ljaw (Fig. 1). In total, 58 anatomically important points on the head are selected to be landmarks. Among them, 31 points are jaw landmarks and 27 are midface landmarks.
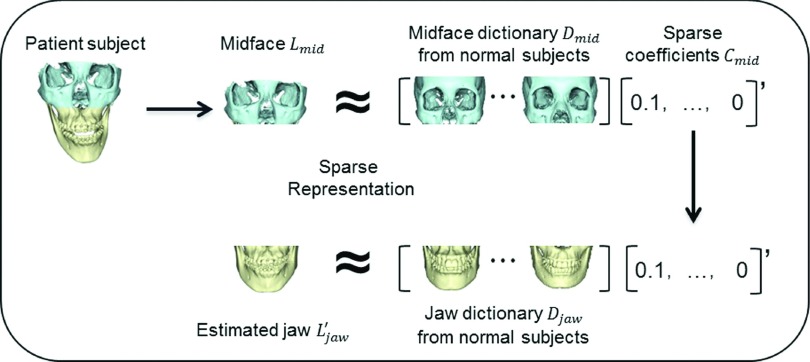
Using digitized anatomical landmarks, we employ the sparse representation technique23,24 to estimate the patient-specific normal jaw shape by referring to the subjects with normal jaw shape. The flowchart of estimating a normal jaw shape is shown in Fig. 3. Specifically, N normal subjects with their corresponding midface landmarks are linearly aligned onto the space of patient subject I (with midface landmarks Lmid) based on their corresponding midface landmarks. For each normal subject or the patient, all coordinates of his/her midface landmarks with size of 58 × 3 are concatenated into a 174-dimensional column vector. Let the aligned midface landmarks be . By gathering all the aligned midface landmarks, we can build a dictionary matrix with size of 174 × N, where each column indicates the aligned midface landmarks of a normal subject. As shown in Fig. 3, we can use dictionary Dmid to sparsely represent the vector of midface landmarks Lmid of a patient. The sparse coefficients Cmid can be estimated by solving the optimization problem below,
| (1) |
where is the l2 norm of vector and is the l0 norm. Intuitively, counts the number of nonzero elements of vector Cmid. k is a parameter to enforce the sparsity of Cmid. It was proven in Refs. 18 and 25 that (1) can be efficiently solved by its l1-norm-relaxed version,
| (2) |
where is the l1 norm of vector, and λ is the parameter controlling the sparsity of representation. Specifically, the first term is the data fitting term, and the second term is the l1 regularization term for enforcing the sparsity of coefficients Cmid. This problem is equivalent to the well-studied LASSO (Ref. 26) and can be numerically solved with the method proposed in Ref. 26. Then, with the estimated sparse coefficients Cmid, the predicted normal patient-specific jaw landmarks can be estimated as
| (3) |
where is the matrix containing all the aligned jaw landmarks from the normal subjects.
FIG. 3.
Flowchart of estimating the patient-specific anatomically correct jaw shape. All the shapes in the figure are in terms of landmarks.
With the estimated patient-specific jaw reference landmarks , we could provide the surgeons a patient-specific CMF reference model. Specifically, we use the thin plate spline24,25 to interpolate the dense deformation field (equally, the dense correspondences) based on correspondences between the patient’s jaw landmarks Ljaw and the estimated patient-specific reference jaw landmarks .27–30 Then, by applying the estimated dense displacement field to the abnormal jaw surface model of patient Sjaw, we can derive the patient-specific jaw reference surface model . Finally, we combine patient-specific jaw reference model with the assumed anatomically correct midface model Smid to get the whole patient-specific CMF reference model, based on which surgeons can use to guide their decision-making during surgical planning.
3. VALIDATION AND RESULTS
We validated our method with experiments designed in both qualitative and quantitative ways. The first two experiments were designed to validate the method with synthetic and real patient data qualitatively, while the third experiment used normality score for the quantitative validation with both the synthetic and real patient subjects.
3.A. Subjects
We utilized 30 normal subjects and 12 patients for both method development and validation. The HIPAA deidentified multislice CT (MSCT) scans of 30 normal subjects were obtained from a digital library31 at the Department of Oral and Craniomaxillofacial Surgery at Shanghai Ninth People Hospital, Shanghai Jiao Tong University School of Medicine. These scans were acquired using a 64-slice GE scanner following a standard clinical protocol: a matrix of 512 × 512, a field of view of 25 cm, and a slice thickness of 1.25 mm.
Twelve sets of CBCT scans of patients with CMF deformity, who had already undergone double-jaw orthognathic surgery, were randomly selected from our clinical archives. The CBCT scans were acquired using an iCAT scanner (Imaging Sciences International LLC, Hatfield, PA) following the standard 0.4 mm isotropic voxel scanning protocol. In the preprocessing, although we could use previously proposed methods32–36 to generate the midface and jaw surface models, we use a CBCT-dedicated method proposed in Ref. 37 to this end. All the subjects were HIPAA deidentified, and IRB approval (IRB0813-0145) was obtained prior to the study. The landmarks were manually digitized by two experienced oral surgeons (Tang and Chen). They first reoriented the whole skull to natural head position (NHP) and manually digitized the landmarks in 3D Studio Max (www.autodesk.com). After that, the digitized landmarks were finally reoriented from NHP to the original space.
3.B. Parameter optimization
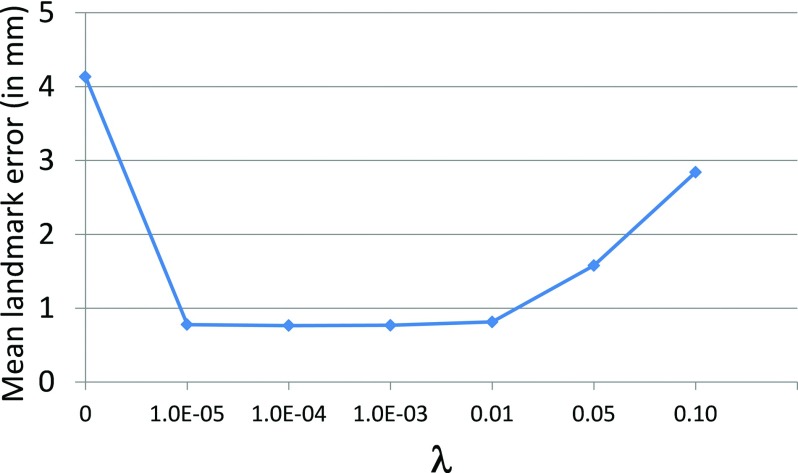
The sparse parameter λ in our proposed method was determined via leave-one-out cross-validation on 30 normal subjects, according to the parameter settings described in Ref. 38. For each testing normal subject, we first employed sparse representation to represent its midface landmarks by the midface landmarks dictionary constructed from the remaining 29 normal subjects. Then, we estimated its jaw landmarks based on the derived sparse coefficients. Finally, we can measure the distance errors between the estimated jaw landmarks and original jaw landmarks (regarded as the ground truth). The mean landmark distance error in terms of using different values of sparse parameter λ ∈ [0 0.1] is shown in Fig. 4. It can be observed that if there is no sparse constraint (λ = 0), which means that all midface landmarks in the dictionary could contribute to the estimation of jaw landmarks, regardless of their similarity to the testing midface landmarks, the errors between the estimated jaw landmarks and the ground truth are very large. When λ is large, such as λ > 0.01, we also found that the errors are large due to the relatively small weight for the data fitting term. On the other hand, when λ ∈ (0 0.01], the errors are much smaller and there is no significant difference among λ = {1 × 10−5, 1 × 10−4, 1 × 10−3, 0.01}, which indicates that our proposed method is relatively robust to the value of λ. In the following experiments, we fixed λ = 0.001.
FIG. 4.
Mean landmark distance error (in mm) in terms of sparse parameter λ.
3.C. Qualitative validation: Patient-specific reference model reconstruction
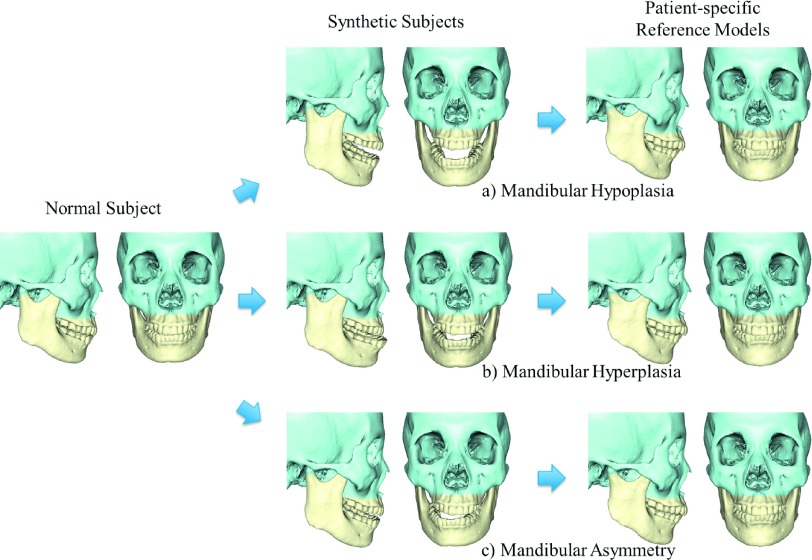
We validated our method using both synthetic subjects and patients. In the validation with synthetic subjects, three common types of the jaw deformity were created (morphed) from a randomly selected normal subject’s 3D surface model: (a) mandibular hypoplasia with severe anterior open-bite; (b) mandibular hyperplasia; and (c) mandibular asymmetry (vertical unilateral condylar hyperplasia) (Fig. 5). The morphing process was completed by two CMF surgeons together to ensure the synthetic deformities correctly mimicking the real clinical conditions. The original normal surface models served as the ground truth. Our method was then used to estimate their normal jaw shapes. During the computational process, the normal subject used to generate synthetic models was excluded from our dictionary during the step of sparse representation. The experimental results showed that all three deformed jaws were successfully recovered to the shape with normal appearance using our method. More importantly, all estimated reference models (i.e., the rightmost of Fig. 5) are very similar to the ground truth, no matter what type of deformity is. Note that only the jaws were “deformed” and “recovered,” mimicking a real orthognathic surgery. The midface is left untouched.
FIG. 5.
Experimental results on synthetic subjects. The left column shows a normal subject, the middle column shows three synthetic patients created from the same subject, and the right column shows our estimated patient-specific reference models. The types of simulated deformity include (a) mandibular hypoplasia, (b) mandibular hyperplasia, and (c) mandibular asymmetry.
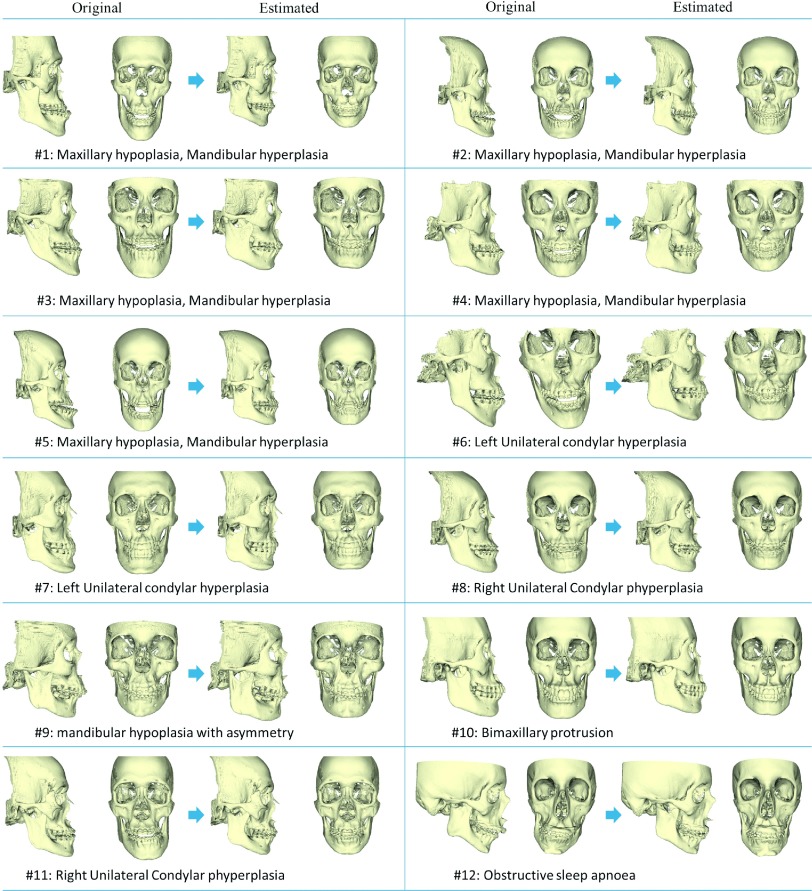
In the validation using patient data, all 30 normal subjects were included in the dictionary and all 12 patients served as the experimental group. The results of the estimated reference models for each patient are shown in Fig. 6. The diagnoses are also shown in the figure. Among them, maxillary hypoplasia and mandibular hyperplasia is one of the most common types of the jaw deformities. This type of deformity was characterized by a protruded mandible and underdeveloped maxilla, as shown in patients #1–#5. For each patient, the original model and estimated patient-specific reference models are shown in the left and right parts, respectively. The results showed that the deformed jaws could be “restored” to the normal shape based on the subject’s midface structure.
FIG. 6.
Experiments on 12 real patients. For each patient, the original abnormal CMF is shown in the left and the estimated CMF reference model is shown in the right. The diagnoses of these patients are also shown in the bottom of each subfigure.
3.D. Quantitative validation
To quantitatively validate our method, we introduced a new measurement, normality score, to quantify the deformity of a subject. Normality score ranges from 0 to 1. A higher score indicates that the patient is more likely to be normal, while a lower score indicates that the patient is more likely to be deformed. This score was computed via sparse representation, similar as described in Sec. 2. The dictionary included both normal and patient subjects, in which each subject was associated with a score (score “1” denotes the normal subjects, while score “0” denotes the patients). If a new subject was mainly represented by normal subjects in the dictionary, the subject’s jaw shape tended to be normal. However, if a new subject was mainly represented by patient subjects, the jaw shape more tended to be deformed. To compute the normality score, we first linearly aligned all training subjects into a common space Scommon based on the landmarks and constructed a dictionary Dall by columnwise stacking all landmarks of training subjects together. To calculate the normality score for a new subject, we first linearly aligned the landmarks of the new subject to the common space Scommon. Then, dictionary Dall was used to sparsely represent this new subject, thus obtaining a sparse coefficient vector C. Finally, the sparse coefficient vector C was used as weights to average the scores from the corresponding training subjects for deriving the normality score of this new subject, i.e., CTv, where v is the score vector with each entry denoting the score (0 or 1) of one training subject.
We calculated the normality score on three groups of subjects, including 30 normal subjects, 12 patients, and their corresponding patient-specific reference models, in a leave-one-out manner, i.e., the testing subject was not included in the construction of dictionary Dall. The statistics of the normality scores from the three groups is summarized in Table I. Statistics showed that typical normal subjects had scores greater than 0.5, while patients had scores less than 0.5. This indicates that the proposed normality score can effectively and quantitatively separate the patients from the normal subjects. We also calculated the normality scores for the reconstructed patient-specific reference model and found that the reconstructed patient-specific reference models have significantly higher normality scores than the original patient models (p-value < 0.0001). This reflects the effectiveness of our method for constructing a normal-looking patient-specific reference model. Furthermore, an interesting observation is that the normality scores of the reference models are slightly better than those of normal subjects. This is due to the fact that human face has about 5% of fluctuating asymmetry even in the normal population with a possibility of less than 2 mm upper dental midline deviation,39–41 while our reference models can be ideally recovered to a perfect facial symmetry with the upper dental midline right on the midsagittal plane.
TABLE I.
The mean and standard deviation of the normality scores for the normal subjects, the patients, the corresponding reference models by our proposed method, and majority voting.
| Group | Normal | Patient | Proposed reference | Majority voting |
|---|---|---|---|---|
| Normality score | 0.787 ± 0.153 | 0.328 ± 0.273 | 0.823 ± 0.085 | 0.7624 ± 0.087 |
To further demonstrate the advantage of the proposed method, we made a comparison with majority voting, which simply averages all the jaw landmarks from the aligned normal subjects. We calculated the normality score for the generated reference model by majority voting, as shown in Table I. It can be seen that its normality score (0.762) is much lower than our result (0.823), which means our proposed reference model is more like a normal one.
3.E. Computational cost
In our implementation, we use the LARS algorithm, which was available in the SPAMS toolbox (http://spams-devel.gforge.inria.fr), to solve the LASSO problem. Given a patient subject with midface and jaw models, the average computational time to estimate the patient-specific reference model is around 2 s on a PC with 2.5 GHz Pentium 4 processor and 4 GB random-access-memory.
4. DISCUSSIONS AND CONCLUSIONS
We have presented a novel method to automatically estimate a patient-specific reference model for the patient suffering from CMF deformity. Specifically, we employ the sparse representation technique to preoperatively estimate a patient-specific CMF reference surface model on what the normal jaw shape should be. Rather than using the measurements from the averageness of normal subjects, the surgery will be planned under the guidance of the patient’s own midface geometry. This is an important step toward personalized medicine.
In this project, we only tested our approach on the patients with jaw deformities that required an orthognathic surgery. It is important to note that the jaws are only undergone rigid transform and not elastically deformed42 to match the shape of reference model in a routine orthognathic surgery. However, it can be immediately extended to the patients with jaw trauma, in which a reconstructive surgery is required to remodel the shattered bony segments. In addition, the current proposed method is only applicable to the jaw deformities, in which the midface is assumed to be normal. However, our method can also be extended to syndromic and complex CMF post-traumatic reconstructive surgeries, in which surgeons can specify and use the normal part of the skull and then estimate the shape of the abnormal and missing bones.
Our future work will include performing cephalometric analysis to further validate our method in a clinic way and integration of the proposed method into the current surgical planning system. We will also further develop our method for syndromic deformities and complex CMF post-traumatic reconstruction.
ACKNOWLEDGMENTS
This work was supported in part by National Institutes of Health/National Institute of Dental and Craniofacial Research Grant Nos. DE022676 and DE021863. Dr. Chen was sponsored by the Taiwan Ministry of Education and Dr. Tang was sponsored by the China Scholarship Council while they were working at the Surgical Planning Laboratory, Department of Oral and Maxillofacial Surgery, Houston Methodist Research Institute, Houston, TX, USA.
REFERENCES
- 1.Xia J. J., Gateno J., and Teichgraeber J. F., “New clinical protocol to evaluate craniomaxillofacial deformity and plan surgical correction,” J. Oral Maxillofac. Surg. 67, 2093–2106 (2009). 10.1016/j.joms.2009.04.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lew T. A., Walker J. A., Wenke J. C., Blackbourne L. H., and Hale R. G., “Characterization of craniomaxillofacial battle injuries sustained by United States service members in the current conflicts of Iraq and Afghanistan,” J. Oral Maxillofac. Surg. 68, 3–7 (2010). 10.1016/j.joms.2009.06.006 [DOI] [PubMed] [Google Scholar]
- 3.Gorlin RJ C. M. and Hennekam R. C. M., Syndromes of the Head and Neck (Oxford University Press, New York, NY, 2001). [Google Scholar]
- 4.Gateno J., Xia J. J., Teichgraeber J. F., Christensen A. M., Lemoine J. J., Liebschner M. A. K., Gliddon M. J., and Briggs M. E., “Clinical feasibility of computer-aided surgical simulation (CASS) in the treatment of complex cranio-maxillofacial deformities,” J. Oral Maxillofac. Surg. 65, 728–734 (2007). 10.1016/j.joms.2006.04.001 [DOI] [PubMed] [Google Scholar]
- 5.Santler G., “3-D COSMOS: A new 3-D model based computerised operation simulation and navigation system,” J. Oral Maxillofac. Surg. 28, 287–293 (2000). 10.1054/jcms.2000.0156 [DOI] [PubMed] [Google Scholar]
- 6.Swennen G. R. J., Barth E. L., Eulzer C., and Schutyser F., “The use of a new 3D splint and double CT scan procedure to obtain an accurate anatomic virtual augmented model of the skull,” Int. J. Oral Maxillofac. Surg. 36, 146–152 (2007). 10.1016/j.ijom.2006.09.019 [DOI] [PubMed] [Google Scholar]
- 7.Swennen G. R. J., Mommaerts M. Y., Abeloos J., De Clercq C., Lamoral P., Neyt N., Casselman J., and Schutyser F., “The use of a wax bite wafer and a double computed tomography scan procedure to obtain a three-dimensional augmented virtual skull model,” J. Craniofac. Surg. 18, 533–539 (2007). 10.1097/scs.0b013e31805343df [DOI] [PubMed] [Google Scholar]
- 8.Troulis M. J., Everett P., Seldin E. B., Kikinis R., and Kaban L. B., “Development of a three-dimensional treatment planning system based on computed tomographic data,” Int. J. Oral Maxillofac. Surg. 31, 349–357 (2002). 10.1054/ijom.2002.0278 [DOI] [PubMed] [Google Scholar]
- 9.Xia J., Ip H. H. S., Samman N., Wang D., Kot C. S. B., Yeung R. W. K., and Tideman H., “Computer-assisted three-dimensional surgical planning and simulation: 3D virtual osteotomy,” Int. J. Oral Maxillofac. Surg. 29, 11–17 (2000). 10.1016/S0901-5027(00)80116-2 [DOI] [PubMed] [Google Scholar]
- 10.Helfrick J., “Modern practice in orthognathic and reconstructive surgery. Edited by William H. Bell. WB Saunders Co, Philadelphia, Pennsylvania, vols. 1, 2, 3, 4, 1992, 2517 pp, $150.00 each,” Head & Neck 15, 587–588 (1993). 10.1002/hed.2880150622 [DOI] [Google Scholar]
- 11.Vannier M. W., Marsh J. L., and Warren J. O., “Three dimensional CT reconstruction images for craniofacial surgical planning and evaluation,” Radiology 150, 179–184 (1984). 10.1148/radiology.150.1.6689758 [DOI] [PubMed] [Google Scholar]
- 12.Xia J. J., Gateno J., and Teichgraeber J. F., “Three-dimensional computer-aided surgical simulation for maxillofacial surgery,” Atlas Oral Maxillofac. Surg. Clin. 13, 25–39 (2005). 10.1016/j.cxom.2004.10.004 [DOI] [PubMed] [Google Scholar]
- 13.Zachow S., Lamecker H., Elsholtz B., and Stiller M., “Reconstruction of mandibular dysplasia using a statistical 3D shape model,” Int. Congr. Ser. 1281, 1238–1243 (2005). 10.1016/j.ics.2005.03.339 [DOI] [Google Scholar]
- 14.Zhang W., Yan P., and Li X., “Estimating patient-specific shape prior for medical image segmentation,” in IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2011 (IEEE, Chicago, IL, 2011), pp. 1451–1454. [Google Scholar]
- 15.Zhu Y., Papademetris X., Sinusas A. J., and Duncan J. S., “Segmentation of the left ventricle from cardiac MR images using a subject-specific dynamical model,” IEEE Trans. Med. Imaging 29, 669–687 (2010). 10.1109/tmi.2009.2031063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang S., Zhan Y., Dewan M., Huang J., Metaxas D. N., and Zhou X. S., “Towards robust and effective shape modeling: Sparse shape composition,” Med. Image Anal. 16, 265–277 (2012). 10.1016/j.media.2011.08.004 [DOI] [PubMed] [Google Scholar]
- 17.Wang G., Zhang S., Li F., and Gu L., “A new segmentation framework based on sparse shape composition in liver surgery planning system,” Med. Phys. 40, 051913 (11pp.) (2013). 10.1118/1.4802215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Donoho D. L., “For most large underdetermined systems of linear equations the minimal,” Commun. Pure Appl. Math. 59, 797–829 (2006). 10.1002/cpa.20132 [DOI] [Google Scholar]
- 19.Zhang S., Zhan Y., and Metaxas D. N., “Deformable segmentation via sparse representation and dictionary learning,” Med. Image Anal. 16, 1385–1396 (2012). 10.1016/j.media.2012.07.007 [DOI] [PubMed] [Google Scholar]
- 20.Ren Y., Wang L., Gao Y., Tang Z., Chen K. C., Li J., Shen S. G. F., Yan J., Lee P. K. M., Chow B., Xia J. J., and Shen D., “Estimating anatomically-correct reference model for craniomaxillofacial deformity via sparse representation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2014, edited by Golland P., Hata N., Barillot C., Hornegger J., and Howe R. (Springer, Boston, MA, 2014), Vol. 8674, pp. 73–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Swennen G. R., Schutyser F. A., and Hausamen J. E., Three-dimensional Cephalometry: A Color Atlas and Manual (Springer, New York, NY, 2005). [Google Scholar]
- 22.Xia J. J., McGrory J. K., Gateno J., Teichgraeber J. F., Dawson B. C., Kennedy K. A., Lasky R. E., English J. D., Kau C. H., and McGrory K. R., “A new method to Orient 3-Dimensional computed tomography models to the natural head position: A clinical feasibility study,” J. Oral Maxillofac. Surg. 69, 584–591 (2011). 10.1016/j.joms.2010.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Donoho D. L. and Elad M., “Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization,” Proc. Natl. Acad. Sci. U. S. A. 100, 2197–2202 (2003). 10.1073/pnas.0437847100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wright J., Yang A. Y., Ganesh A., Sastry S. S., and Ma Y., “Robust face recognition via sparse representation,” IEEE Trans. Pattern Anal. Mach. Intell. 31, 210–227 (2009). 10.1109/TPAMI.2008.79 [DOI] [PubMed] [Google Scholar]
- 25.Starck J. L., Elad M., and Donoho D. L., “Image decomposition via the combination of sparse representations and a variational approach,” IEEE Trans. Image Process. 14, 1570–1582 (2005). 10.1109/TIP.2005.852206 [DOI] [PubMed] [Google Scholar]
- 26.Tibshirani R. J., “Regression shrinkage and selection via the lasso,” J. R. Stat. Soc., Ser. B 58, 267–288 (1996). [Google Scholar]
- 27.Bookstein F. L., “Principal warps: Thin-plate splines and the decomposition of deformations,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 567–585 (1989). 10.1109/34.24792 [DOI] [Google Scholar]
- 28.Lapeer R. J. A. and Prager R. W., “3D shape recovery of a newborn skull using thin-plate splines,” Comput. Med. Imaging Graphics 24, 193–204 (2000). 10.1016/S0895-6111(00)00019-7 [DOI] [PubMed] [Google Scholar]
- 29.Shen D., Wong W.-h., and Ip H. H. S., “Affine-invariant image retrieval by correspondence matching of shapes,” Image Vision Comput. 17, 489–499 (1999). 10.1016/S0262-8856(98)00141-3 [DOI] [Google Scholar]
- 30.Xue Z., Shen D., and Davatzikos C., “Statistical representation of high-dimensional deformation fields with application to statistically constrained 3D warping,” Med. Image Anal. 10, 740–751 (2006). 10.1016/j.media.2006.06.007 [DOI] [PubMed] [Google Scholar]
- 31.Yan J., Shen S. G. F., Fang B., Shi H., Wu Y., Shao Z., Xia B., and Yu D., “Three-dimensional CT measurements for the craniomaxillofacial structure of normal occlusion adult in Jiangsu Zhejiang and Shanghai areas,” China J. Oral Maxillofac. Surg. 8, 2–9 (2010). [Google Scholar]
- 32.Wang L., Shi F., Lin W., Gilmore J. H., and Shen D., “Automatic segmentation of neonatal images using convex optimization and coupled level sets,” NeuroImage 58, 805–817 (2011). 10.1016/j.neuroimage.2011.06.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shen D. and Ip H. H. S., “A hopfield neural network for adaptive image segmentation: An active surface paradigm1,” Pattern Recognit. Lett. 18, 37–48 (1997). 10.1016/S0167-8655(96)00117-1 [DOI] [Google Scholar]
- 34.Jia H., Yap P.-T., and Shen D., “Iterative multi-atlas-based multi-image segmentation with tree-based registration,” NeuroImage 59, 422–430 (2012). 10.1016/j.neuroimage.2011.07.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang L., Shi F., Li G., Gao Y., Lin W., Gilmore J. H., and Shen D., “Segmentation of neonatal brain MR images using patch-driven level sets,” NeuroImage 84, 141–158 (2014). 10.1016/j.neuroimage.2013.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang L., Shi F., Gao Y., Li G., Gilmore J. H., Lin W., and Shen D., “Integration of sparse multi-modality representation and anatomical constraint for isointense infant brain MR image segmentation,” NeuroImage 89, 152–164 (2014). 10.1016/j.neuroimage.2013.11.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang L., Chen K. C., Gao Y., Shi F., Liao S., Li G., Shen S. G. F., Yan J., Lee P. K. M., Chow B., Liu N. X., Xia J. J., and Shen D., “Automated bone segmentation from dental CBCT images using patch-based sparse representation and convex optimization,” Med. Phys. 41, 043503(14pp.) (2014). 10.1118/1.4868455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bach F., Mairal J., and Ponce J., “Task-driven dictionary learning,” IEEE Trans. Pattern Anal. Mach. Intell. 34, 791–804 (2012). 10.1109/tpami.2011.156 [DOI] [PubMed] [Google Scholar]
- 39.Rhodes G., Louw K., and Evangelista E., “Perceptual adaptation to facial asymmetries,” Psychon. Bull. Rev. 16, 503–508 (2009). 10.3758/PBR.16.3.503 [DOI] [PubMed] [Google Scholar]
- 40.Nascimento D. C., Santos Ê. R. d., Machado A. W. L., and Bittencourt M. A. V., “Influence of buccal corridor dimension on smile esthetics,” Den. Press J. Orthodontics 17, 145–150 (2012). 10.1590/S2176-94512012000500020 [DOI] [Google Scholar]
- 41.Jones T. L., “Fluctuation Asymmetry of the Facial Skeleton in a Normal Chinese Population,” Master thesis, School of Dentistry at Houston, The University of Texas, 2013. [Google Scholar]
- 42.Wu G., Jia H., Wang Q., and Shen D., “SharpMean: Groupwise registration guided by sharp mean image and tree-based registration,” NeuroImage 56, 1968–1981 (2011). 10.1016/j.neuroimage.2011.03.050 [DOI] [PMC free article] [PubMed] [Google Scholar]