Acoustic holography as a metrological tool for characterizing medical ultrasound sources and fields

Abstract

Acoustic holography is a powerful technique for characterizing ultrasound sources and the fields they radiate, with the ability to quantify source vibrations and reduce the number of required measurements. These capabilities are increasingly appealing for meeting measurement standards in medical ultrasound; however, associated uncertainties have not been investigated systematically. Here errors associated with holographic representations of a linear, continuous-wave ultrasound field are studied. To facilitate the analysis, error metrics are defined explicitly, and a detailed description of a holography formulation based on the Rayleigh integral is provided. Errors are evaluated both for simulations of a typical therapeutic ultrasound source and for physical experiments with three different ultrasound sources. Simulated experiments explore sampling errors introduced by the use of a finite number of measurements, geometric uncertainties in the actual positions of acquired measurements, and uncertainties in the properties of the propagation medium. Results demonstrate the theoretical feasibility of keeping errors less than about 1%. Typical errors in physical experiments were somewhat larger, on the order of a few percent; comparison with simulations provides specific guidelines for improving the experimental implementation to reduce these errors. Overall, results suggest that holography can be implemented successfully as a metrological tool with small, quantifiable errors.

I. INTRODUCTION

Holography in optics was made famous by Dennis Gabor, who won a Nobel Prize for related work in 1971.¹ The principle underlying holography is that a three-dimensional (3D) wave field can be reconstructed from a 2D distribution of the wave amplitude and phase along some surface transverse to the wave propagation. The difficulty in measuring optical phase directly poses a challenge for recording optical holograms. To solve this problem, fringe patterns created by interference between the optical field of interest and a reference beam are typically recorded. The 3D field is then reconstructed by projecting the reference beam through the recorded hologram. Because sound fields comprise pressure waves and thus possess basic features of wave physics, holography can also be used in acoustics. However, acoustics generally involves much lower frequencies such that phase can be measured directly with common instruments like microphones and hydrophones. Accordingly, acoustic holograms can be easily recorded as a set of numbers; moreover, reconstruction of the full 3D field need not involve a reference beam but can be performed based on straightforward numerical calculations. Such a version of holography was described in detail by Maynard et al.²

The utility of a fundamental formulation of holography is quite broad. Given a hologram measured within a 3D region of interest, the complete sound field within that region can be reconstructed if it is generated by a set of sources distributed over a bounding surface. With a basic assumption that the wave field inside the region satisfies the wave equation, there are no theoretical limitations on the resolution that can be achieved in the reconstructed field. More specifically, Maynard et al.² present a formulation for near-field acoustic holography (NAH) in which linear acoustic propagation is described by the Helmholtz equation. This approach presumes that a suitable Green's function is known and the spatial processing needed for field reconstruction is efficiently accomplished by propagating the angular spectrum of the field in the frequency domain. For NAH, sub-wavelength inhomogeneities in the source can be reconstructed if the corresponding evanescent waves are measured. Such capabilities are often of interest in air acoustics involving structural vibrations and audible frequencies.³

Efforts to characterize ultrasound fields by holography have employed the same angular spectrum formulation utilized for NAH.^4–8 In this work, filtering techniques typically were implemented to remove evanescent waves from the field prior to backward propagation calculations. Such filtering was needed in practice to avoid the amplification of noise introduced by (relatively) coarse sampling of the field.^4,5 Although this approach to backpropagation was driven by practical necessity, we note that it is particularly appropriate for applications involving medical ultrasound and nondestructive testing. For such applications at megahertz frequencies, characteristic dimensions d such as the source aperture and the measurement distance are generally on the order of centimeters, while the acoustic wavelength λ is on the order of a millimeter or less. Such applications are similar to optics in that $d\gg \lambda$, all waves of interest propagate away from the source, and evanescent waves can be neglected.

When $d\gg \lambda$, it is convenient to consider an alternative holography formulation. Rather than reconstructing the source using a direct solution based on the angular spectrum of the measured field, the inverse diffraction problem can be solved by evaluating an integral over the measurement surface or some other approximate technique.⁹ Such an approach based on Rayleigh integrals was presented by Sapozhnikov et al.^10,11 for ultrasound transducers and possesses two useful attributes: First, field reconstructions are inherently well posed in that originally evanescent waves that grow during backprojection are replaced by evanescent waves that decay when backprojected.¹² Second, whereas the approach presented by Maynard et al.² assumes that the source and the measured hologram reside on level surfaces of a prescribed coordinate system, reconstructions based on Rayleigh integrals are more readily adapted to accommodate arbitrary surface geometries—e.g., measurements in a plane in conjunction with a curved transducer surface. Although Rayleigh integrals are exact only for forward projections from flat surfaces,¹³ they provide very accurate solutions for moderately curved surfaces in the $d\gg \lambda$ regime.^14–18

Here we are interested in the holographic characterization of medical ultrasound fields at megahertz frequencies. These fields are generated by centimeter-sized transducers and are projected into tissue at depths also on the order of centimeters. Because evanescent waves in these conditions decay almost completely within a few millimeters from the source, they have no practical significance in medical ultrasound. Consequently, we implement acoustic holography using Rayleigh integrals to perform field reconstructions, thereby taking advantage of the inherent stability and simplicity of the associated calculations.

Medical ultrasound transducers have various shapes, sizes, frequencies, operation modes, and output intensities. Many transducers comprise multi-element arrays that can operate in both continuous-wave and pulsed modes. The corresponding acoustic fields can possess complex 3D structures, including focal regions, parasitic foci, and grating lobes. Such ultrasound fields are created inside the patient's body and thus should be known with the highest accuracy possible, especially for therapeutic applications. Toward this end, measurement standards exist for both diagnostic¹⁹ and high-intensity therapeutic²⁰ fields. The basic approach in these standards is to rely on measurements in water, comprising direct hydrophone measurements of the pressure field and radiation force measurements that determine acoustic power over a range of output levels.^21–23 Pressures and intensities inferred from these measurements are then derated to estimate in situ values that account for acoustic propagation in tissue rather than water.^24,25

In practice, this basic approach can produce incomplete or erroneous results. Collecting measurements throughout a 3D volume is often impractical, making hydrophone measurements at the high-pressure focus may not be feasible, and using typical derating schemes may not adequately account for nonlinear propagation effects. A more complete approach for characterizing medical ultrasound fields combines acoustic holography with modeling of nonlinear propagation.^26–28 With holography, low-amplitude pressure measurements made in water over some surface transverse to the incident beam can be used to reconstruct a hologram of the source. Such a source hologram provides a realistic boundary condition for the wave equation and is therefore an important characteristic of any ultrasound source. The radiated field can then be calculated not only in water but also in tissue if representative values of the physical properties have been estimated.^29–32

A holography-based approach holds particular appeal both for quantifying the expected in situ pressure field for a given treatment and for tracking the performance characteristics of a specific transducer over time. Recognizing the utility of holography, the IEC standard for characterizing high-intensity fields includes a normative annex on acoustic projection methods.²⁰ Implementation of this approach has been reported for a single-element transducer²⁶ and a clinical therapy array with 256 elements.²⁸ These studies demonstrate that many details of the field, including shock formation, are captured quantitatively; however, a detailed study of the uncertainties associated with the technique has not been performed. The purpose of this effort is to analyze the errors associated with acoustic holography to advance it as a metrological tool for medical ultrasound.

The scope of this effort involves the simplest holograms representing linear, steady-state fields with a single temporal frequency. These holograms comprise a single pressure magnitude and phase value at each measurement location. Beyond such continuous-wave (CW) fields, more general transient and nonlinear fields containing many temporal frequencies can be represented by a set of CW holograms.¹¹ Accordingly, the approach presented here for analyzing holography errors could be extended to these more general cases. The sections in the following text describe the methods used to quantify errors in the CW regime with results from both theoretical and experimental implementations. Section II describes a specific holography formulation with details of the Rayleigh integrals and their numerical evaluation included in Appendixes A and B. Explicit error metrics are also defined in Sec. II with ensuing results presented in terms of these metrics.

II. METHODS

The basic configuration of interest is depicted in Fig. 1, which shows a source radiating an ultrasound beam aligned with the z axis of a coordinate system. The radiated beam is characterized from a set of pressure measurements made within a transverse plane at $z=z_{\mathrm{h}}$; the aperture of this measured hologram is defined as $2a_{\mathrm{h}}$. Backward projection of the measured hologram is then performed to reconstruct the source; in turn, forward projection from the source hologram is used to calculate the field at a collection of points in the focal plane at $z=z_{\mathrm{f}}$ and/or in other regions of interest. The accuracy of the holography technique can then be evaluated by comparing the reconstructed field at these points with some independent measure of the “true” field.

FIG. 1.

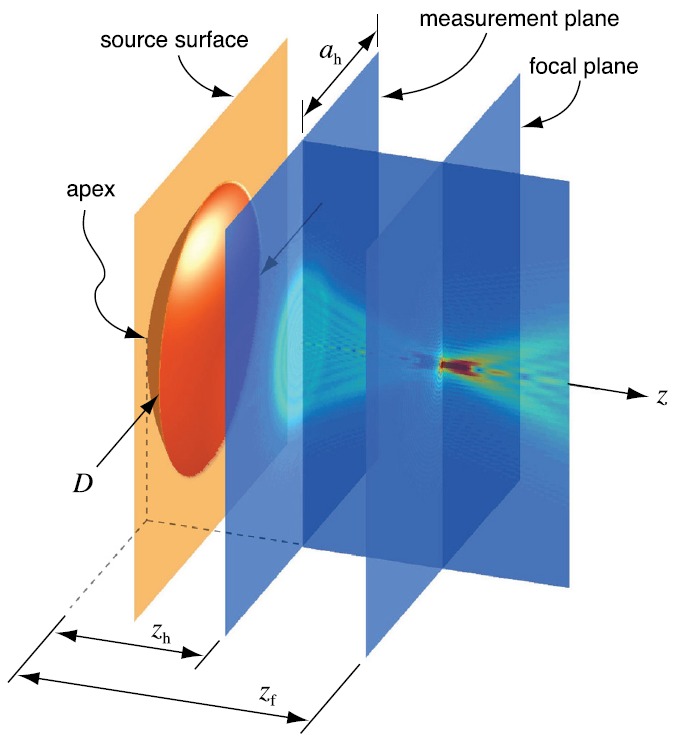
(Color online) Schematic of the relevant geometry. A source with its apex located at the z-axis origin radiates a beam in the $+z$ direction. From this beam, a planar hologram with aperture $2a_{\mathrm{h}}$ is measured at $z=z_{\mathrm{h}}$. This measured hologram is then backprojected to a source surface that comprises the surface of the physical transducer in conjunction with a plane that extends outward from the transducer aperture D. Forward projection from the source hologram can then reconstruct the full 3D field.

In broad terms, we can identify several types of error: Field sampling errors that are inherent in the technique, errors caused by uncertainties in the timing and position at which measurements are made, and additional measurement uncertainties pertinent to a specific experimental arrangement. Here we investigate these errors using both idealized simulations and experiments. First, virtual experiments were conducted in which hydrophone measurements were simulated to generate a hologram representing the ultrasound field radiated by idealized transducers. With this approach, the field reconstructed from hologram projections was compared to the original simulated field. In this way, simulated experiments were used to assess the impacts of field discretization and systematic errors in the position/timing of measurements.

Additional uncertainties associated with actual experimental measurements—e.g., oscilloscope digitization error, noise caused by acoustic reflections in the test tank, etc.—were neglected in the simulations. However, several experimental studies were also conducted, including both measured holograms and independent hydrophone measurements in the focal region. These independent measurements were then used as reference data for comparison with holographically reconstructed fields. In these studies, all experimental measurements for a given source used the same hydrophone over the course of a few days; therefore these comparisons largely neglect the absolute calibration uncertainty of a given hydrophone.

In the following text, we describe details for a practical implementation of holography, including the definition of a hologram from measurements, forward and backward projections of the acoustic field represented by a hologram, and metrics for quantifying the differences between two fields. In addition, details are presented for the virtual and physical experiments conducted in this effort.

A. Holography formulation

1. Definition of notation

To facilitate the description and comparison of measured and calculated fields, it is helpful to define notation. We consider acoustic waves that propagate with a single temporal frequency ω in a medium with uniform density ρ₀ and sound speed c₀. Accordingly, the propagation is characterized by wavenumber $k=\omega /c_0$ and wavelength $\lambda =2\pi /k$. To define the acoustic variables as a function of position $\mathbf{r}$ and time t, we assume that the pressure p varies in time and space as follows:

$$\begin{array}{c}p(\mathbf{r},t)=A_p\hspace{0.17em}\text{cos}(\omega t-{\varphi }_p)\\ =\frac{1}{2}{A}_p\hspace{0.17em}{e}^{-i\omega t+i{\varphi }_p}+\mathrm{c}.\mathrm{c}.=\frac{1}{2}P{e}^{-i\omega t}+\mathrm{c}.\mathrm{c}.,\end{array}$$ (1)

where “c.c.” denotes the complex conjugate. Here the amplitude A_p and the phase delay ${\varphi }_p$ are functions of the spatial coordinate $\mathbf{r}$. Moreover, $P=A_p\hspace{0.17em}{e}^{i{\varphi }_p}$ is the complex pressure magnitude. In an analogous way, we express the component of acoustic velocity normal to a given surface as

$$\begin{array}{c}v(\mathbf{r},t)=A_v\hspace{0.17em}\text{cos}(\omega t-{\varphi }_v)\\ =\frac{1}{2}{A}_v\hspace{0.17em}{e}^{-i\omega t+i{\varphi }_v}+\mathrm{c}.\mathrm{c}.=\frac{1}{2}V{e}^{-i\omega t}+\mathrm{c}.\mathrm{c}.,\end{array}$$ (2)

where $V=A_v\hspace{0.17em}{e}^{i{\varphi }_v}$ is the complex velocity magnitude. Note that we have assumed a time dependence represented by $e^{-i\omega t}$ rather than $e^{+i\omega t}$. As noted by Pierce³³ and Bouwkamp,³⁴ $e^{-i\omega t}$ is advantageous for describing traveling waves, whereas $e^{+i\omega t}$ is generally adopted in electrical engineering where time derivatives are of more concern than spatial derivatives. While either representation of the time dependence can be used, it is important to recognize the choice and apply it consistently.

In practical terms, a hologram based on hydrophone measurements in the CW regime is defined by a set of complex magnitudes P distributed over some surface. Considering the notation defined in the preceding text in Eq. (1), it is evident that the choice of $e^{-i\omega t}$ determines the sign of the phase ${\varphi }_p$. To define a hologram from a set of measured waveforms based on the $e^{-i\omega t}$ convention, the pressure modulus A_p at each location is readily determined as the waveform amplitude at frequency ω, while ${\varphi }_p$ is the corresponding phase in the frequency domain. Although the complex value P is readily obtained using commercial hardware/software to numerically evaluate the Fourier transform of the measured waveform, care should be taken regarding the aforementioned sign convention. For example, many Tektronix oscilloscopes (Beaverton, OR) rely on the $e^{-i\omega t}$ convention, while the “fft” function in matlab (MathWorks, Natick, MA) utilizes the $e^{+i\omega t}$ convention.

2. Numerical projection calculations

Implementation of acoustic holography inherently involves the use of an acoustic propagation model to project the field forward or backward from a given hologram. Common projection methods include both the Rayleigh integral and angular spectrum formulations. Here we use the Rayleigh integral formulation for several reasons: (1) calculations are inherently well posed in that evanescent waves can be neglected without losing information of practical importance; (2) Rayleigh integrals are well suited for the projection of fields onto curved surfaces; and (3) this approach is naturally capable of accounting for the practical conditions under which acoustic measurements are made for recording holograms.

Regarding this last reason, holograms are typically recorded sequentially using a miniature hydrophone that approximates a point receiver. In backprojection calculations based on the Rayleigh integral, the hydrophone measurement at each location in the hologram participates independently in the form of a spherical wave radiated backward to the source. This means that the source's vibrations can be reconstructed even under conditions in which the properties of the propagation medium varied among the different measurement locations. Such conditions may occur if a hologram is recorded by a raster scan that lasts several hours during which the medium temperature changes due to heating from the source transducer or ambient temperature variations in the room. If temperature is measured during the scan, it can be used to correct for sound speed and density variations in the backward propagation calculations. Such compensation can be done only through the Rayleigh integral approach; the angular spectrum approach cannot make such corrections because calculations for each spectral component use hydrophone signals measured at different times.

As noted in the preceding section, the exact mathematical formulations used to define and project acoustic fields is dependent upon the convention chosen for defining harmonic time variations. Using the $e^{-i\omega t}$ convention, the explicit equations used in this effort for forward and backward propagation are presented as Eqs. (A7)–(A10) in Appendix A. In particular, we consider a measured hologram as a time-reversal mirror and project measured pressures backward to reconstruct normal velocities on the surface of the source. We also consider the reverse process, forward projection from normal velocity to pressure. For completeness, relations are also provided for forward and backward projection to field pressures from measured pressures.

While Appendix A provides the relevant integral equations, a complete description of the projection calculations should identify how the integrals are numerically evaluated. Toward this end, Appendix B demonstrates that Rayleigh integrals can be evaluated to exactly represent the acoustic field in the absence of evanescent waves by using a discrete summation with a step size equal to one-half wavelength or less. Such an approach is used here to implement acoustic holography in the regime where propagation distances are much greater than a wavelength and evanescent waves can be neglected.

3. Evaluation of uncertainties: Error metrics

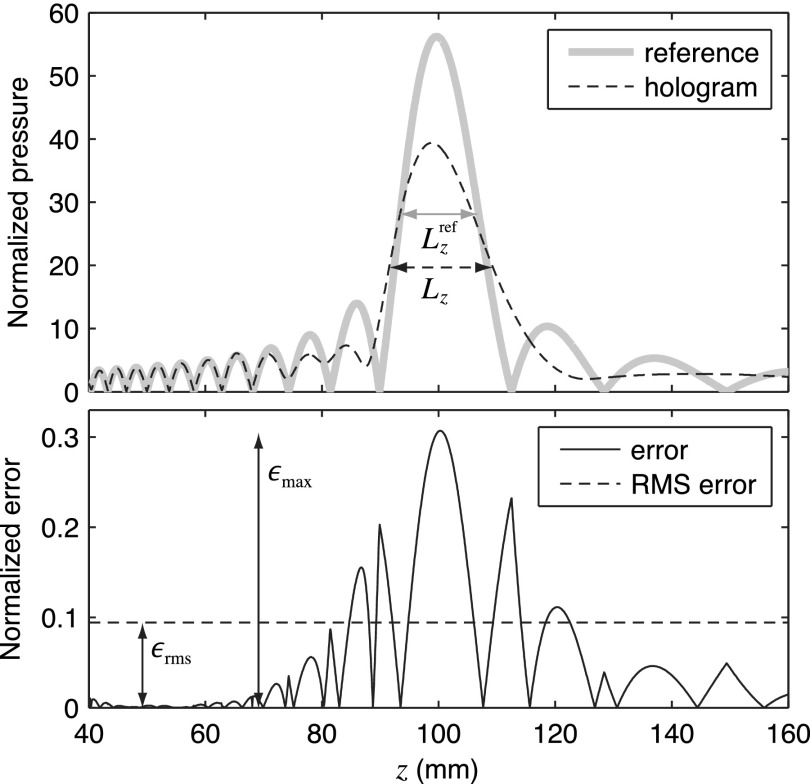
Existing standards for characterizing medical ultrasound fields involve quantification of pressure amplitudes and/or acoustic intensities,^19,20 which are typically calculated from pressure values under the assumption of plane waves. Accordingly, appropriate metrics for the errors associated with holography can be defined in terms of differences in the modulus of complex pressure between a “true” reference field and a field represented by a hologram. Dropping the subscript for convenience, let $A=A_p=\left|P\right|$ be the pressure amplitude as a function of position in the field. Then the deviation from a reference value at the jth point in a collection can be expressed as $\Delta A_j=A_j-A_j^{\text{ref}}$. With this notation, we propose two error metrics to be evaluated over a collection of N field points as follows:

$${\mathrm{ϵ}}_{\text{max}}=\frac{\underset{j}{\max }|\Delta A_j|}{\underset{j}{\max }(A_j^{\text{ref}})},$$ (3)

$${\mathrm{ϵ}}_{\text{rms}}=\frac{\sqrt{\frac{1}{N}\sum _{j=1}^N{\left(\Delta A_j\right)}^2}}{\underset{j}{\max }\left(A_j^{\text{ref}}\right)}.$$ (4)

As implied by the subscripts, ${\mathrm{ϵ}}_{\text{max}}$ describes the maximum error in pressure at any field point and ${\mathrm{ϵ}}_{\text{rms}}$ describes the error over all points in a root-mean-square (RMS) sense. Note that both metrics are normalized by the maximum reference pressure over the collection of all comparison points. While these metrics can be applied to any collection of points, we identify points of particular interest along the acoustic axis of the transducer and in the focal plane (or the transverse plane containing the maximum pressure for a non-focused source). Beyond such comparisons of pressures, we also note the importance of knowing the 3D structure of fields that may contain foci and side lobes. If we define L as the −6 dB beamwidth of the field along a given axis, then another useful error metric can be expressed as the maximum relative error in the beamwidth over all three Cartesian axes passing through the focus,

$${\mathrm{ϵ}}_{\text{bw}}=\underset{m=x,y,z}{\max }\frac{|L_m-L_m^{\text{ref}}|}{L_m^{\text{ref}}}.$$ (5)

These three metrics are illustrated in Fig. 2 for a collection of points along the acoustic axis of a focused source.

FIG. 2.

Definition of holographic reconstruction errors for a collection of points. The top plot shows the axial distribution of pressure magnitude for a uniform, focused source as determined by reference calculations and field reconstruction from a hologram. The −6 dB “beamwidth” corresponding to each field is labeled; these values are used to calculate the error metric ${\mathrm{ϵ}}_{\text{bw}}$. The bottom plot shows the deviation between the two fields in terms of both a peak value ${\mathrm{ϵ}}_{\text{max}}$ and an average value ${\mathrm{ϵ}}_{\text{rms}}$. Both of these error metrics are normalized by the maximum reference pressure magnitude over the collection of points considered.

B. Test configurations for virtual experiments

Simulations were used to conduct virtual experiments to quantify the errors associated with field sampling and systematic uncertainties in the position/timing of measurements. Considering a known source boundary condition, forward projection was performed to determine the pressure field available for measurement. By sampling this “true” field in different ways, measured holograms were recorded and used to reconstruct the field in two steps (see Fig. 1): First the field was projected backward from the measured hologram to a source surface. Then this source hologram was used to project the field forward to some set of points of interest. Finally, the error in the reconstructed field was evaluated at these points in terms of the metrics from Eqs. (3) to (5), using the original “true” field to define the reference values.

To describe a virtual test configuration, it is necessary to define both the “true” reference field and the method used to sample this field to simulate a measured hologram. The first two test configurations explore field sampling effects by varying the aperture and axial position of the measured hologram. For these simulations, two idealized sources were considered to represent transducers used to generate intense ultrasound for medical applications. Both transducers operate at 1 MHz and vibrate uniformly over a diameter of 10 cm. One transducer is a flat disk and the other is a spherical bowl with a 10 cm radius of curvature. Because the flat disk and spherical bowl generate beams with different shapes, consideration of both provides insight for selecting the aperture and position of a measured hologram given some presumed beam shape. For other test configurations, only the spherically focused transducer was considered because it represents the more complicated and interesting case.

In all test configurations, beam propagation occurred along the z axis (see Fig. 1), and the measured hologram was defined from a square grid of measurements in a transverse plane centered at $z=z_{\mathrm{h}}$. The step size between measurements in the grid was always $\lambda /2$. As noted before, this sampling is sufficient to fully represent the field in the absence of evanescent waves. Source holograms were reconstructed using a slightly smaller step size equal to $\lambda /3$ to provide improved visual resolution in images of the source. Beyond the configurations that explicitly varied measurement aperture and axial position, measured holograms were evaluated in the plane $z_{\mathrm{h}}=50$ mm using an aperture of $2a_{\mathrm{h}}=150$ mm. As determined from the initial simulations, this relatively large aperture captured the full width of the focused beam at $z_{\mathrm{h}}=50$ mm. Except for explicit simulations of temperature uncertainties, all projection calculations used the following properties for the propagation medium: density ${\rho }_0=1000$ kg/m³ and sound speed $c_0=1500$ m/s. In the following text, the methods used to simulate hologram recording in different test configurations are described in further detail.

1. Aperture and axial position of the measured hologram

To assess the role of hologram aperture $2a_{\mathrm{h}}$ on accuracy, simulations were performed for both the flat and focused transducers. The measured hologram was recorded at $z_{\mathrm{h}}=50$ mm for apertures ranging from 10 to 150 mm. Given the transducer aperture D, hologram apertures ranged from 0.1D to 1.5D. In addition, simulations for both transducers were conducted to evaluate the impact of the axial location of the measured hologram. Using apertures of both 50 and 150 mm, the measured hologram was recorded at positions $z_{\mathrm{h}}$ ranging from 40 to 160 mm, thereby covering pre-focal through post-focal positions for the spherically focused transducer.

2. Hydrophone size

When a pressure field is measured by a hydrophone of finite size, the measured signal is proportional the average normal velocity of fluid particles impinging on the hydrophone's measuring surface. Accordingly, the hydrophone will possess different sensitivities for plane waves arriving from different directions. Such behavior can affect holography measurements. To investigate these effects, we utilize the reciprocity theorem for acoustic waves. This theorem states that the hydrophone sensitivity to waves arriving from different directions can be inferred from the directivity pattern of the hydrophone when it is used as a source. Thus measured hydrophone signals can be simulated by multiplying the complex amplitude of each incoming wave by the relevant directivity value.

Let us consider a hydrophone with a flat, circular sensing element of radius a₀. If we assume that the hydrophone radiates as a circular piston source, the corresponding directivity pattern is known to be

$$D(\theta )=\frac{2\hspace{0.17em}{J}_1(k{a}_0\hspace{0.17em}\text{sin}\hspace{0.17em}\theta )}{k{a}_0\hspace{0.17em}\text{sin}\hspace{0.17em}\theta }.$$ (6)

Here $J_1(·)$ is the first-order Bessel function, $k=\omega /c_0$ is the wavenumber, and θ is the angle between the hydrophone's axis of symmetry and the direction from which the plane wave arrives. To account for the hydrophone directivity in the angular spectrum approach, the measured field can be simulated by multiplying the angular spectrum amplitudes by $D(\theta )$, where $\text{sin}\hspace{0.17em}\theta =\sqrt{k_x^2+k_y^2}/k$ and the notation defining spatial frequencies k_x, k_y is given in Appendix B.

When holography is based on the Rayleigh integral, hydrophone directivity can also be simulated in a simple way if the ultrasound source points are in the far field of the hydrophone (i.e., the propagation distance to the hydrophone is much larger than the near-field scale $k{a}_0^2/2$). This condition is usually met especially for hydrophones with small sensing elements. Here we use the directivity factor to simulate how the true field would be measured by a hydrophone of finite size. Then directivity effects are neglected in subsequent field reconstructions. More specifically, forward projection from an idealized source based on Eq. (A7) or (A8) in Appendix A is performed by multiplying the relevant integrand by $D(\theta )$. Note that $\text{sin}\hspace{0.17em}\theta$ and $D(\theta )$ can be evaluated directly as a function of the position vectors ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ for each point inside the surface integral (see Fig. 13). Using Cartesian coordinates $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ to describe points on surfaces ${\Sigma }_1$ and ${\Sigma }_2$, respectively, we have

$$\text{sin}\hspace{0.17em}\theta =\frac{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}}{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2+{(z_2-z_1)}^2}}.$$ (7)

This approach was used to simulate directivity effects in recorded holograms for hydrophones with sensing diameters up to 2 mm.

FIG. 13.

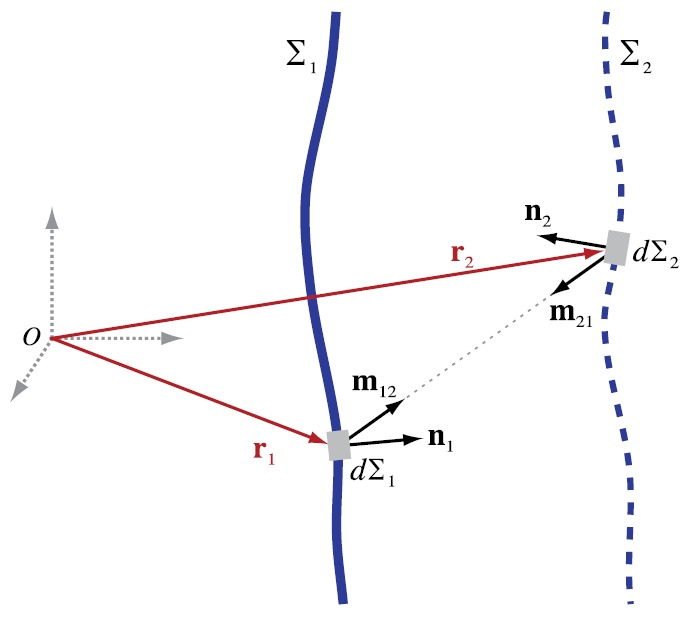
(Color online) As used for field projection calculations, two surfaces ${\Sigma }_1$ and ${\Sigma }_2$ are depicted schematically relative to a coordinate system with origin O. Each surface corresponds to the locus of points represented by position vectors ${\mathbf{r}}_1$ or ${\mathbf{r}}_2$, respectively. ${\Sigma }_1$ represents a boundary surface with an acoustic source that radiates waves into the half-space region that includes ${\Sigma }_2$. This surface is further described by the outward facing unit normal ${\mathbf{n}}_1$ and differential area elements $d{\Sigma }_1$. ${\Sigma }_2$ is described by analogous notation and represents a non-physical surface at which field measurements are made.

It is instructive to note that errors associated with hydrophone directivity can be accounted for in subsequent reconstructions if the directivity pattern is known. The integrand used in backprojection calculations is simply divided by $D(\theta )$. However, for hydrophones that are large relative to the propagation wavelength, averaging over the face of the hydrophone will limit the amount of information that can be recorded. In other words, the directivity pattern will include values near zero for large hydrophones, thereby limiting the ability to record holograms from which the full field can be reconstructed.

3. Non-orthogonality between scan axes

Holography measurements are typically made by moving a single hydrophone in a plane with the help of an automated 3D positioner. If the positioner axes used to move the hydrophone are not exactly orthogonal, then the locations of the measurements will be systematically incorrect. To explicitly describe these conditions, it is convenient to introduce two sets of Cartesian coordinates: (x, y, z) coordinates aligned to the source transducer and $(x\prime ,y\prime ,z\prime )$ coordinates aligned to the axis of a 3D positioner. We take the z axis to coincide with beam propagation as in Fig. 1 with the origin at the transducer apex. In contrast, we naturally assign the origin of the primed positioner coordinates to correspond to some reference point along the beam axis such as the acoustic focus. Here we assume that the z and $z\prime$ axes are perfectly aligned and consider the impact of a lack of orthogonality between the $x\prime$ and $y\prime$ axes. We simulate the case in which the recorded hologram assumes that the scan axes $x\prime$ and $y\prime$ are orthogonal to one another even though the actual angle between them is $90°+{\alpha }_{\mathit{x}\mathit{y}}$. Accordingly, we consider a scan over some desired range of $(x\prime ,y\prime )$ coordinates and sample the true field at the locations actually accessed by the positioner: $x=x\prime -y\prime \hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_{\mathit{x}\mathit{y}}$ and $y=y\prime \hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_{\mathit{x}\mathit{y}}$. Simulations were performed for $0°\le {\alpha }_{\mathit{x}\mathit{y}}\le 3°$.

4. Non-orthogonality between the scan plane and the beam propagation axis

Another situation of practical interest occurs when none of the positioner axes are perfectly aligned with the z axis, which is defined to coincide with the direction of beam propagation. If we consider the same coordinates aligned to the transducer (x, y, z) and the positioner $(x\prime ,y\prime ,z\prime )$, these conditions can be described by a nonzero angle α_z between the z and $z\prime$ axes. In this case, the scan plane defined by the $(x\prime ,y\prime ,z\prime =0)$ plane that intersects the beam axis at $z=z_{\mathrm{h}}$ will not be orthogonal to beam propagation in the z direction.

To simulate such a coordinate misalignment, the measured hologram is determined by sampling the true field over a desired range of positioner coordinates in the $x\prime y\prime$ plane. For an axisymmetric transducer, the orientation of the tilt angle α_z does not matter. For convenience, we consider the misalignment as a rotation of the scan plane around the y axis,

$$\left[\begin{array}{c}x\\ y\\ z-z_{\mathrm{h}}\end{array}\right]=\left(\begin{array}{ccc}\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_z& 0& \hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_z\\ 0& 1& 0\\ -\text{sin}\hspace{0.17em}{\alpha }_z& 0& \hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_z\end{array}\right)\left[\begin{array}{c}x\prime \\ y\prime \\ z\prime =0\end{array}\right].$$ (8)

In this way, angular misalignment of the scan plane was simulated for $0°\le {\alpha }_z\le 3°$. The errors associated with this misalignment were then evaluated by assuming ${\alpha }_z=0$ in field reconstruction calculations. Although this type of misalignment causes errors, we note that the measured hologram still captures the correct 3D field structure; this structure is simply rotated. Accordingly, errors caused by this misalignment can be corrected if the rotation is known.

5. Constant temperature errors

In holography, field reconstruction calculations rely on known characteristics of the propagation medium, namely, the density ρ₀ and sound speed c₀. Although these properties are well known for water, they vary with temperature. For any measured hologram, the temperature of the water should therefore be measured to facilitate accurate field reconstructions. However, temperature measurements may be inaccurate or even omitted from the data collection. In such cases, we seek to quantify how field reconstructions are affected when the temperature used for projection calculations differs by a constant amount from the actual temperature during measurement acquisition.

To simulate such conditions, forward projections of the “true” field were performed with default properties ${\rho }_0=1000$ kg/m³ and $c_0=1500$ m/s; subsequent projection calculations then presumed an erroneous temperature described by the constant shift $\Delta T_0$, using corresponding shifts in density and sound speed. For water between 20 °C and 30 °C, variations of these properties with temperature are approximately linear.^35–37 Accordingly, modified properties were calculated as ${\rho }_0[{\text{kg}/\mathrm{m}}^3]=1000-0.25\Delta T_0$ and $c_0[\mathrm{m}/\mathrm{s}]=1500+2.5\Delta T_0$, where $\Delta T_0$ is expressed in degrees Celsius. Simulations considered temperature errors over the range $-4°\mathrm{C}\le \Delta T_0\le 4°\mathrm{C}$.

6. Temperature drift during a raster scan

Another consideration related to temperature uncertainty in the propagation medium is the potential for temperature changes during the acquisition of holography measurements, which can take several hours. To simulate such conditions, we assume that measurements are acquired by making a raster scan and that the temperature changes the same amount between consecutive measurement points. For total temperature drift $\Delta T_d$, the temperature change for the nth measurement point in a scan containing N total points is then $\Delta T_d\times (n-1)/N$; the temperature shift at each point was used to determine the corresponding density and sound speed from the linear relations given in the preceding text. Errors due to temperature drift were assessed by considering the temperature changes in the forward projection of the “true” field, while subsequent reconstruction calculations used the default values ${\rho }_0=1000$ kg/m³ and $c_0=1500$ m/s. Simulations covered the range $-4°\mathrm{C}\le \Delta T_d\le 4°\mathrm{C}$.

C. Test configurations for physical experiments

Similar to the approach used in virtual experiments, errors associated with holography were evaluated through physical experiments with three focused medical ultrasound transducers (see Fig. 3). In these experiments, a 3D positioner was oriented with one scan axis approximately aligned with the axis of beam propagation from the transducer. Then in a test tank filled with degassed water, a hydrophone attached to the positioner was moved around to locate the acoustic focus and record waveforms in the focal region along the $x\prime ,\hspace{0.17em}y\prime$ and $z\prime$ axes of the positioner. Next the hydrophone was moved a prescribed distance from the focus along the $z\prime$ axis, and a hologram was recorded over an aperture $2a_{\mathrm{h}}$ in the $x\prime y\prime$ plane. Given geometric knowledge of the focal distance of each transducer and the assumption that $z\prime$ was aligned with the beam axis z, the hologram's position at $z=z_{\mathrm{h}}$ was identified.

FIG. 3.

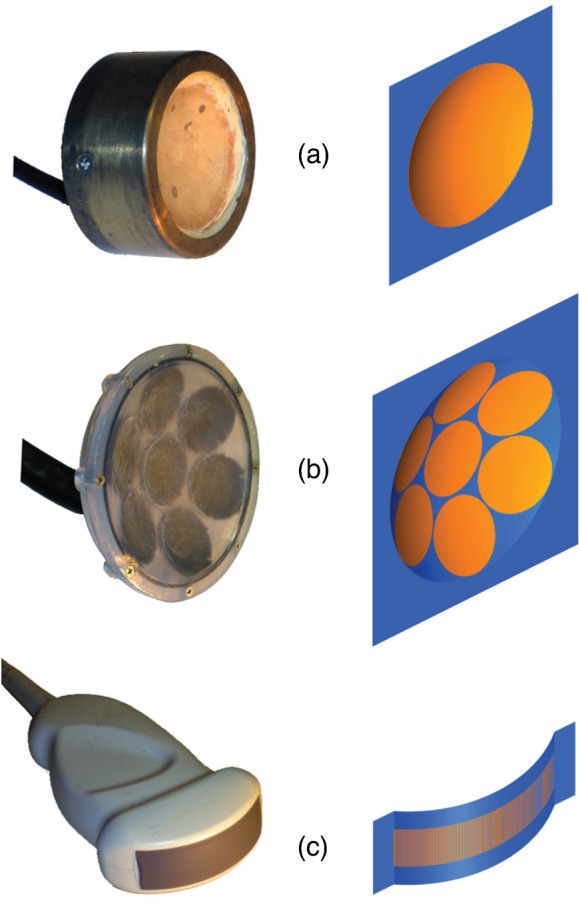
(Color online) Photographs of transducers used in experiments along with depictions of the surfaces on which source holograms were reconstructed. For visual clarity, transducer elements expected to vibrate are depicted on the surfaces of (a) a single-element focused source (2.2 MHz, aperture 45 mm, F-number 1); (b) a focused transducer comprising 7 elements (1 MHz, aperture 147 mm, F-number 0.95); and (c) a convex imaging probe with 128 elements (2.3 MHz, aperture 49.9 × 13.5 mm, elevational lens with approximate focal distance of 50 mm).

For each measurement location, the transducer was excited to radiate pressure waves over a set number of acoustic cycles, and the measured waveform was analyzed to determine pressure magnitude and phase within a specific time window. The number of excitation cycles and the analysis time window were chosen based on the observed “ring up” time for each transducer and geometric considerations to ensure that waves originating from anywhere on the transducer surface were captured at each measurement point. In this way, the recorded holograms represent CW conditions. From each measured hologram, backward projection was used to reconstruct acoustic velocities on the radiating surface with the surface apex at z = 0. Finally, forward projections from source holograms were used to predict field pressures in the focal region that were compared to the independent hydrophone measurements. These comparisons were made at the $x\prime y\prime z\prime$ coordinates at which the independent measurements were made. Because projections propagate the field perpendicular to the $x\prime y\prime$ plane, we note that some misalignment of the compared fields will occur if the positioner axis $z\prime$ is not truly perpendicular to the $x\prime y\prime$ plane. Accordingly, the focal maxima of projected and measured fields were manually aligned to facilitate a quantitative comparison. Further details of the test configuration for each transducer are described in the following text.

1. Single-element transducer

One test transducer comprised a single, spherically curved ceramic element operating frequency of 2.2 MHz. All measurements were made at Moscow State University using a capsule hydrophone (GL-0150-1 A, Specialty Engineering Acoustics, Soquel, CA) with a sensitivity at 2.2 MHz of 0.21 μV/Pa and a sensing region with diameter 0.15 mm. The scan was executed using a Velmex (Bloomfield, NY) positioning system comprising stepper motors and linear slides with a combined positioning resolution of 2.5 μm/step along each axis. At each measurement location, the pressure waveform was recorded by a digital oscilloscope (Tektronix TDS520A, Beaverton, OR). Additional details describing the transducer, the measured hologram, and projection calculations are listed under transducer (a) in Table I. Although the water temperature was not measured directly during measurements, sound speed was measured as $c_0=1495.7$ m/s, implying temperature $T_0=24.7$ °C and density ${\rho }_0=996.9$ kg/m³. These values were used in all projection calculations.

TABLE I.

Experimental holography parameters.

	Transducer from Fig. 3
	(a)	(b)	(c)
Frequency (MHz)	2.2	1	2.3
Transducer aperture (mm)	45	147	$49.9\times 13.5$
Focal distance (mm)	45	140	53
$z_{\mathrm{h}}$ (mm)	30	85	38
Measurement aperture $2a_{\mathrm{h}}$ (mm)	30 × 30	120 × 120	$199.5\times 40.6$
step size (mm)	0.30	0.75	0.35
No. scan points	10 201	25 921	66 807
No. excitation cycles	120	60	160
Time window (μs)	42–44	104–114	88–98
Hydrophone size $2a_0$ (mm)	0.15	0.2	0.2
ρ0 (kg/m3)	997	998	998
c0 (m/s)	1496	1485	1485
Source surface aperture (mm)	$58.8\times 58.8$	$176.8\times 176.8$	$62.8\times 26.4$
Source step size (mm)	0.2	0.4	0.2

2. Seven-element therapy array

The second test transducer was an array of seven flat disks, each 50 mm in diameter. The disks were bonded to a plastic shell, which was shaped to provide an integral acoustic lens for each disk. The lenses focused the field generated by each disk at a distance of 140 mm, and the overall contour of the shell aligned the foci of all seven disks to overlap. Overall geometric details of the transducer and measurements are given under transducer (b) in Table I. All measurements were made at the University of Washington using a capsule hydrophone (HGL-0200, Onda Corp., Sunnyvale, CA) with a sensitivity at 1 MHz of 0.42 μV/Pa and a sensing region with diameter 0.2 mm. The scan was executed using a Velmex positioning system with stepper motors and linear slides that provided a resolution of 6 μm per step. The pressure waveform at each location was recorded using a digital oscilloscope (DSO-X 3034A, Keysight Technologies, Inc., Santa Rosa, CA). For holography measurements, the transducer output level was 1.95 times higher than that used for the independent focal measurements; this elevated output level was used to improve signal-to-noise without the need for waveform averaging at each location. The water properties were not measured directly; instead, a temperature near 20 °C was assumed, with values $c_0=1485$ m/s and ${\rho }_0=998$ kg/m³ used in all projection calculations.

3. Convex imaging probe

The third test transducer was a convex imaging probe driven at 2.3 MHz. The transducer is a phased array consisting of 128 elements with a convex radius of curvature of about 38.5 mm. Elements were phased to generate a beam focused along the central axis of the transducer, 53 mm beyond its apex. Further geometric details of the transducer and measurements are given under transducer (c) in Table I. All measurements were made at the University of Washington using the same instrumentation as described in the preceding text for the seven-element (b) transducer with a hydrophone sensitivity of 0.40 μV/Pa at 2.3 MHz. Again, a higher transducer output level (22.3 times higher) was used for holography measurements to increase the relative signal amplitude without averaging.

III. RESULTS

A. Virtual experiments

The results from virtual experiments are presented in Figs. 4–10, which show how various parameters affect the accuracy of holographic field reconstructions. Each figure plots one or more error metrics as a function of a parameter that quantifies the amount of uncertainty introduced by a practical implementation of acoustic holography. Field points included in the error evaluations are as follows: Points in the xy plane for $-75\le x,y\le 75$ mm with a step size of 0.75 mm; points along the z axis from 40 to 160 mm with a step size of 0.075 mm. Each figure also includes reconstructed source holograms for two specific parameter values to provide some physical insight into the ways in which the associated errors distort the effective source and the field it radiates.

FIG. 4.

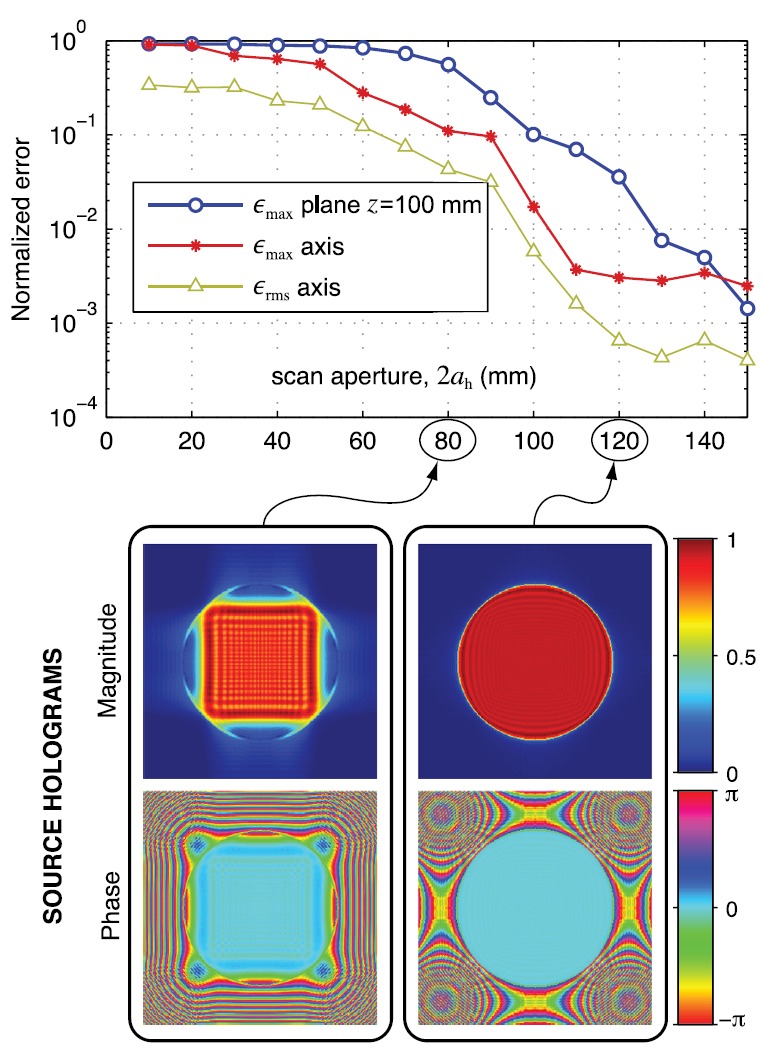
(Color online) Field reconstruction errors (top) for the flat source (100 mm aperture) as a function of the size of the measurement region. This region is a square $2a_{\mathrm{h}}\times 2a_{\mathrm{h}}$ with its center placed on the acoustic axis at $z_{\mathrm{h}}=50$ mm. Bottom images illustrate the reconstructed source hologram in terms of velocity magnitude and phase distributions for two possible sizes of the measurement region (corresponding measurement apertures are circled).

FIG. 5.

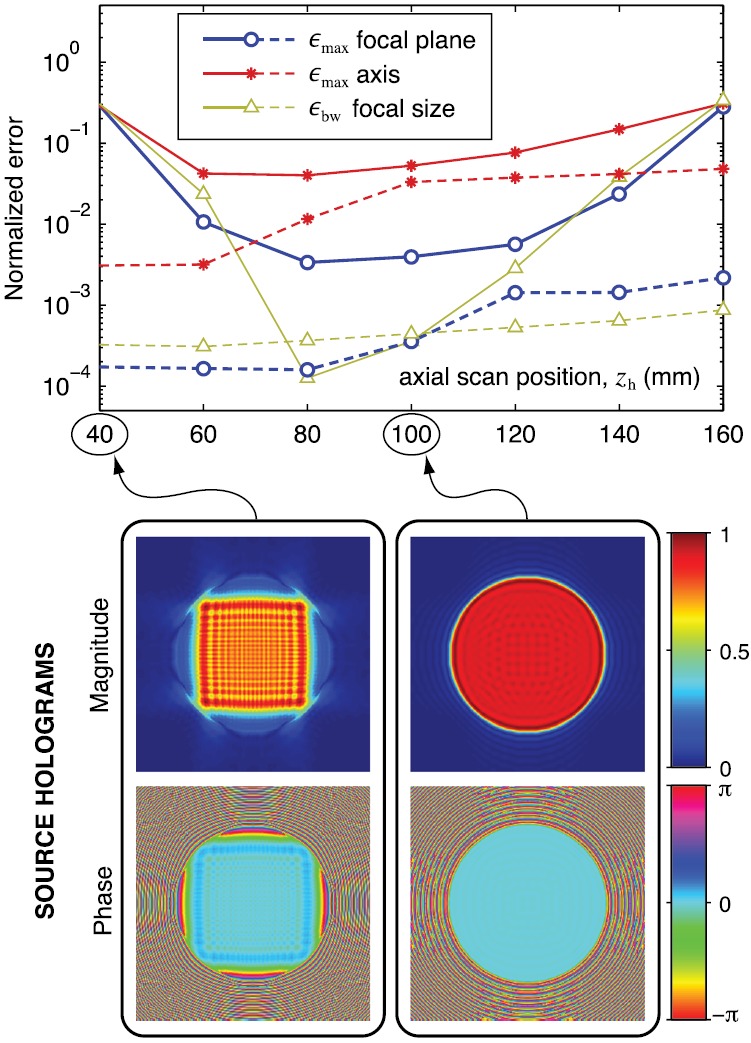
(Color online) Field reconstruction errors (top) for the focused source (100 mm aperture) as a function of the axial position $z_{\mathrm{h}}$ of the measurement region. Solid lines correspond to a measurement region with aperture $2a_{\mathrm{h}}=50$ mm; dashed lines correspond to a region with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate source holograms reconstructed using the smaller measurement aperture at the indicated axial measurement positions.

FIG. 6.

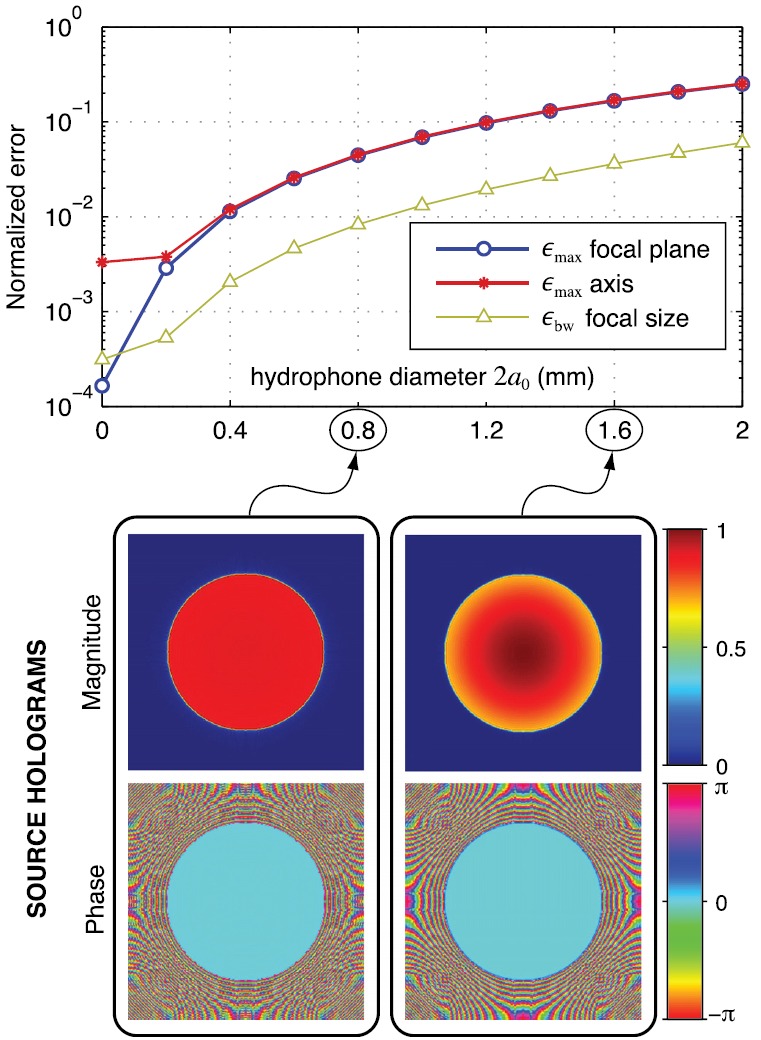
(Color online) Field reconstruction errors (top) for the focused source as a function of the diameter of the hydrophone's sensing element. The measurement region is located at $z_{\mathrm{h}}=50$ mm with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate reconstructed source holograms for the indicated hydrophone diameters.

FIG. 7.

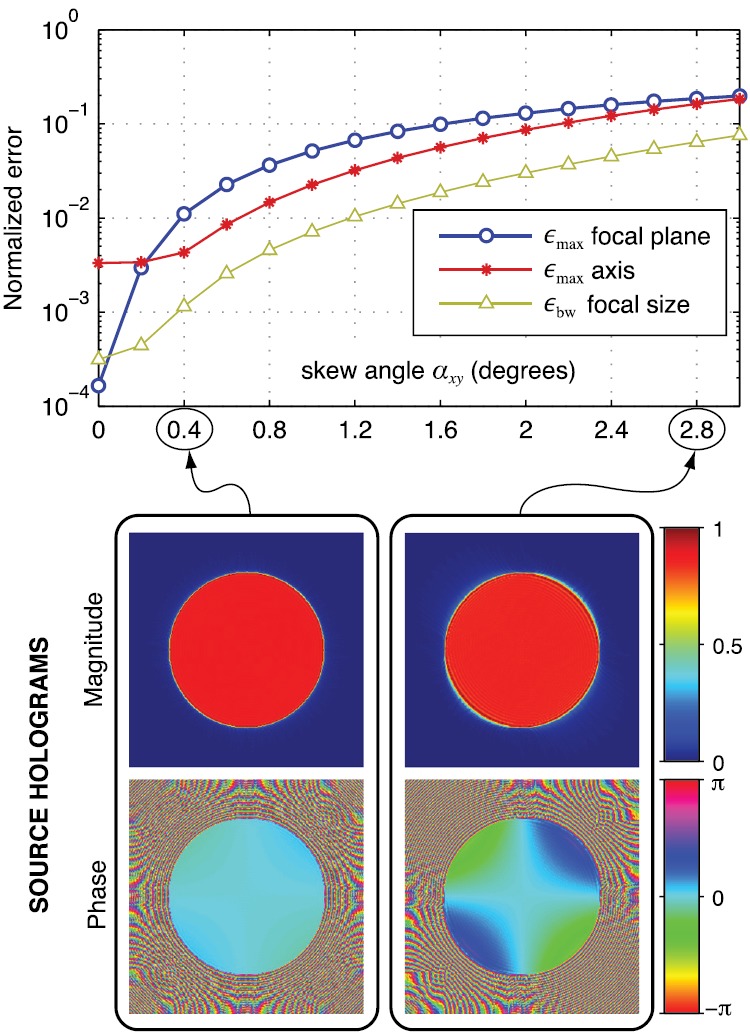
(Color online) Field reconstruction errors (top) for the focused source as a function of the skew angle relative to 90° of the transverse $x\prime y\prime$ coordinate axes used in capturing measurements within the scan plane. The measurement region is at $z_{\mathrm{h}}=50$ mm with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate reconstructed source holograms for the indicated skew angles.

FIG. 8.

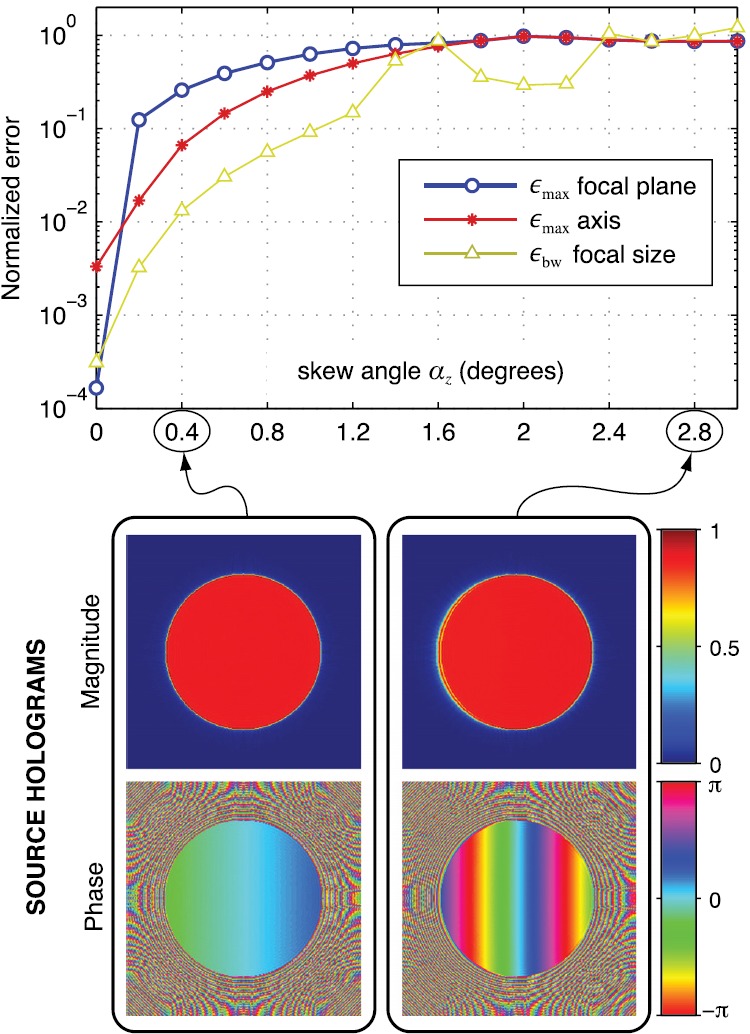
(Color online) Field reconstruction errors (top) for the focused source as a function of the angular misalignment between the source's acoustic axis and the direction normal to the scan plane. The measurement region is at $z_{\mathrm{h}}=50$ mm with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate reconstructed source holograms for the indicated misalignment angles.

FIG. 9.

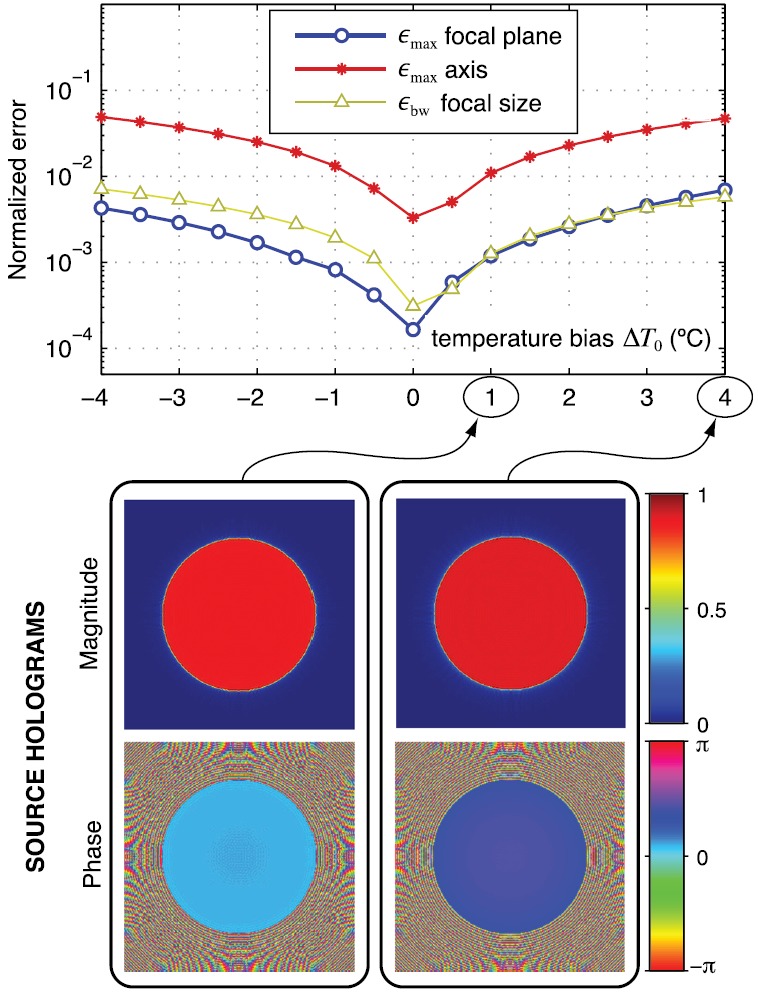
(Color online) Field reconstruction errors (top) for the focused source as a function of the uncertainty in temperature at which the field measurements were made. This uncertainty is presumed to comprise a constant bias in the sound speed used in reconstructing the source hologram. The measurement region is located at $z_{\mathrm{h}}=50$ mm with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate reconstructed source holograms for the indicated temperature biases.

FIG. 10.

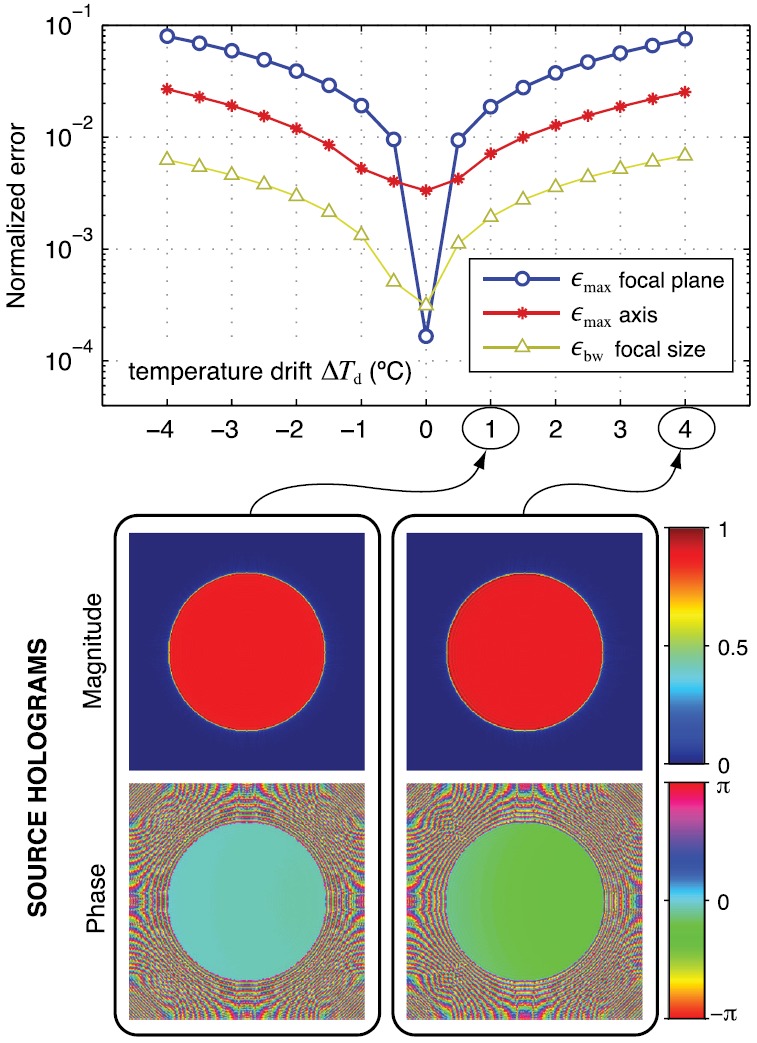
(Color online) Field reconstruction errors (top) for the focused source as a function of the amount of temperature drift that occurs during the acquisition of measurements by a raster scan. Temperature is assumed to change linearly with the scan point number. The measurement region is at $z_{\mathrm{H}}=50$ mm with aperture $2a_{\mathrm{h}}=150$ mm. Bottom images illustrate reconstructed source holograms for the indicated temperature changes.

1. Field sampling errors

A fundamental approximation related to practical implementations of acoustic holography is representation of the whole field by a discrete set of measurements. As noted in Sec. I and in Sec. II A 2, we neglect evanescent waves and therefore can discretize the field without loss of information using a step size between measurements of one-half wavelength. However, because the measurement aperture $2a_{\mathrm{h}}$ must be finite, sampling errors are introduced that depend on this aperture and the relative position $z_{\mathrm{h}}$ of the measured hologram.

In Fig. 4, accuracy as a function of measurement aperture at $z_{\mathrm{h}}=50$ mm is depicted for the flat transducer described in Sec. II B. As expected, the error metrics ${\mathrm{ϵ}}_{\text{max}}$ and ${\mathrm{ϵ}}_{\text{rms}}$ decrease as the measurement aperture gets larger. Considering the more sensitive metric ${\mathrm{ϵ}}_{\text{max}}$ and a target error level of 1% (which is about an order of magnitude less than the uncertainty of hydrophone calibration), a hologram aperture greater than 130 mm is sufficient. Although not shown, a comparable plot for the spherically focused transducer demonstrates that a hologram at $z_{\mathrm{h}}=50$ mm requires an aperture greater than 68 mm to keep ${\mathrm{ϵ}}_{\text{max}}$ less than 1%. Considering the respective beam geometries of these two sources as a cylinder and a cone, we note that a hologram aperture of about 1.3 times the beam diameter is sufficient to achieve sampling error less than 1%. While this rule of thumb can be useful at axial positions relatively close to the source, it loses meaning elsewhere. For example, it is unclear how the rule might apply in the focal plane of a spherically curved source where the geometric beam diameter vanishes.

To explore the impact of the axial measurement position $z_{\mathrm{h}}$, Fig. 5 shows ${\mathrm{ϵ}}_{\text{max}}$ and ${\mathrm{ϵ}}_{\text{bw}}$ for the focused source for both a small measurement aperture ($2a_{\mathrm{h}}=50$ mm, solid lines) and a large one ($2a_{\mathrm{h}}=150$ mm, dashed lines). If measurements are made near the focus where the beam is narrow, it is clear that even a small measurement aperture can accurately capture details in the focal plane. However, corresponding errors on axis grow significantly because waves emanating from the edge of the source are missed by a small scan plane, and these edge waves interfere constructively/destructively to cause peaks/nulls on axis. This result demonstrates that a hologram should capture as much energy as possible from the incident beam to accurately represent the field. Because some waves always diverge from the source, measurements should generally be made fairly close to the source. Indeed analogous simulations for the flat transducer show that errors remain less than 1% only when the large measurement aperture ($2a_{\mathrm{h}}=150$ mm) is positioned at $z_{\mathrm{h}}\le 75$ mm. For both transducers, results suggest that as long as the hologram is large enough to capture most of the radiated wave energy, its exact position is not critical.¹⁰ For a focused source, Fig. 5 demonstrates that a hologram positioned about halfway between the source and focus is useful to achieve small field reconstruction errors with a minimal number of measurements; however, the axial position of measurements can be selected to accommodate a given experimental arrangement if the measurement aperture is also adjusted.

A final aspect of field sampling is the finite size of the hydrophone used to record measurements. Although such errors can be corrected by including reciprocal directivity effects in subsequent projection calculations, such corrections are neglected here. Simulation results are presented in Fig. 6, demonstrating that errors remain less than 1% if the hydrophone diameter remains less than about a quarter wavelength ($\lambda /4$). As depicted in the reconstructed source holograms, uncorrected directivity effects diminish the relative contributions from peripheral regions of the transducer.

Given the results presented in Figs. 4 and 5, simulations to explore the impact of other parameters were conducted for measurements with aperture $2a_{\mathrm{h}}=150$ mm and axial location $z_{\mathrm{h}}=50$ mm for the focused transducer. In addition, virtual measurements were simulated for the idealized case of an infinitesimally small hydrophone.

2. Geometrical errors

Additional errors associated with holography can be attributed to uncertainties in the positions at which measurements are made. In most experimental configurations, a hologram is recorded by a scan over two linear axes that define the $x\prime y\prime$ plane. Although it is typically assumed that the scan axes are perpendicular in defining the coordinate locations of measurements, there will be some error in practice. The impact of such errors is quantified in Fig. 7 as a function of α_xy, the angular deviation from perpendicularity. Results show that errors are less than 1% if the scan axes remain within about 0.4° of perpendicularity. Note that even if such alignment is not achieved, errors can be corrected as long as the actual angle between scan axes is known. Although positioners designed for optics often specify axis alignment tolerances much smaller than 0.4°, other industrial positioners lack such specifications and rely on end users to assemble two or more linear stages. In such cases, alignment error is likely governed by the clearance tolerances for the bolts and holes used in assembly. Based on typical designs for linear stages and standard machining practices for clearances,³⁸ it is plausible that alignment errors on the order of 0.5° could occur.

Another source of geometric uncertainty is the orientation of the $x\prime y\prime$ scan plane relative to the beam axis. Figure 8 illustrates the errors caused by rotation of the scan plane relative to the beam axis when this rotation is neglected in subsequent projection calculations. As is clear from the reconstructed source holograms, the primary effect of misalignment is to make the phase non-uniform at the radiating surface, effectively steering the beam off axis. Although calculated errors are quite sensitive to this type of axial misalignment, such error values are somewhat artificial in that transducer-aligned coordinates were explicitly substituted for positioner-aligned coordinates. Such confusion can be readily avoided in practice given that the measured hologram contains the full 3D beam structure.

As noted by Kreider et al.,²⁸ the orientation of the beam axis relative to measurement coordinates can be inferred from the position of the focus as determined by forward projection from the measured hologram. If the focus does not lie along the positioner's $z\prime$ axis, then the beam and positioner are not aligned and the alignment angle can be determined. Moreover, for both focused and unfocused sources, the angular orientation of the source hologram can be estimated by reconstructing acoustic phase on source surfaces with different orientations relative to the hologram. The true source orientation can then be identified as the one that yields a distribution of phase over the transducer surface that is uniform or follows the transducer's geometric symmetry (e.g., see Fig. 11). These approaches were used in Ref. 28 to verify the relative orientation of the measured hologram within about 0.2°. We conclude that the actual alignment of the scan plane is not critical in practice as long as the scanned region is approximately transverse to the beam and large enough to “catch” most of the radiated energy (see Fig. 5).

FIG. 11.

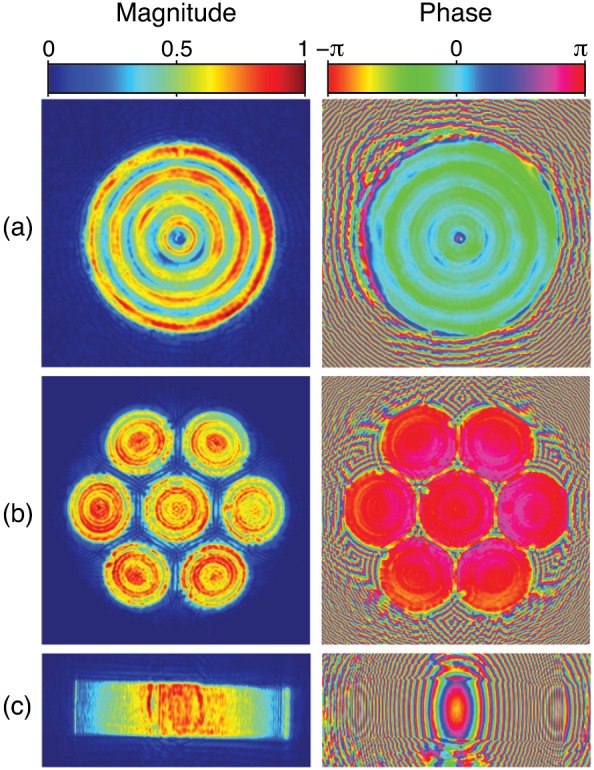
(Color online) Source holograms reconstructed from experimental measurements for the three sources depicted in Fig. 3. Note that velocity magnitudes are normalized relative to the maximum value in the hologram.

3. Temperature errors

Because holography implicitly relies on projection calculations, a final type of error in the reconstructed fields is related to uncertainties in the acoustic properties of the propagation medium (i.e., water). The relevant properties are sound speed and density, which vary as a function of temperature under practical measurement conditions. If a hologram is recorded at one temperature and subsequent projection calculations utilize a different temperature, the reconstructed field will differ from the original one. Beyond such a static temperature bias, other errors can accrue if the temperature drifts during measurements and projection calculations utilize a single temperature. Errors associated with these types of temperature uncertainties are plotted in Figs. 9 and 10, which show that the temperature uncertainty should remain within ±1 °C to keep errors less than about 1%.

B. Physical experiments

To evaluate the accuracy of holography in practice, physical experiments were conducted with the three transducers depicted in Fig. 3. Measurement and reconstruction parameters are listed in Table I; the reconstructed fields for each transducer were compared to independent hydrophone measurements acquired as line scans through the focus. As such, comparisons were made at the following field points along the $z\prime$ axes:

• (a)Single-element transducer: $20\le z\prime \le 90$ mm, 0.5 mm step size,
• (b)Seven-element therapy array: $109\le z\prime \le 169$ mm, 0.1 mm step size,
• (c)Convex imaging probe: $33\le z\prime \le 73$ mm, 0.2 mm step size.

Reconstructed source holograms are shown in Fig. 11. For transducers (a) and (b), surface waves are clearly evident in the form of concentric rings on each ceramic element. For transducer (c), the phase plot shows the effects of both a cylindrical lens for focusing in the elevation direction and element phasing for on-axis focusing in the azimuthal direction. In addition, the magnitude plot shows reduced vibration amplitudes off-axis in the azimuthal direction. This result can be explained by phase averaging: The reconstruction has a spatial resolution on the order of $\lambda /2$, which is larger than the actual width of each array element. Accordingly, when adjacent elements vibrate with different phases, averaging of these phases across the elements yields an apparent reduction in magnitude. Despite this phase averaging, the source hologram has sufficient resolution to accurately represent the field that is radiated more than a few wavelengths away from the transducer.

Direct comparisons of holographic projections with independent measurements along the $z\prime$ axis are plotted in Fig. 12. These plots show that the measured holograms capture on-axis field structures with a high level of detail. To quantify the accuracy, the values of error metrics ${\mathrm{ϵ}}_{\text{max}},\hspace{0.17em}{\mathrm{ϵ}}_{\text{rms}}$, and ${\mathrm{ϵ}}_{\text{bw}}$ are provided in Table II for points along the $z\prime$ axis. For comparison, the table also reports errors from simulated experiments in which the size and axial location of the measured hologram are considered (note that in all cases, the largest simulated errors occur along the z axis).

FIG. 12.

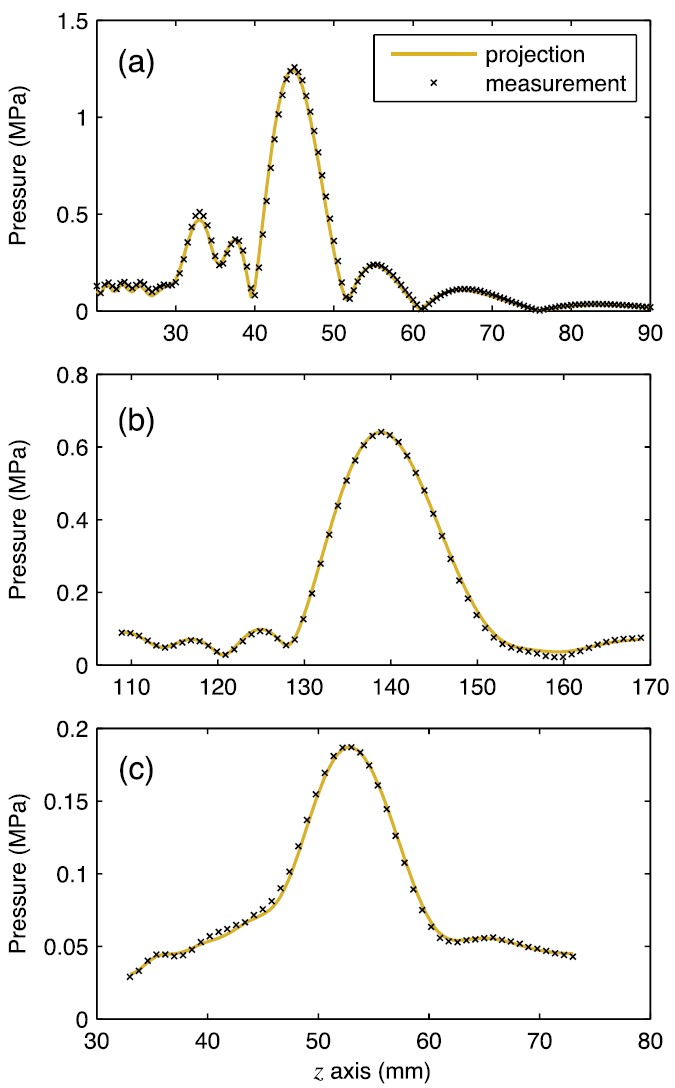
(Color online) Comparison of axial fields measured directly versus those projected from a measured hologram for the three sources depicted in Fig. 3.

TABLE II.

Holography errors associated with physical experiments.

	From experiments	From simulations
	($z\prime$ axis)	(z axis)
(a) Single-element transducer
${\mathrm{ϵ}}_{\text{max}}$	0.053	0.035
${\mathrm{ϵ}}_{\text{rms}}$	0.018	0.005
${\mathrm{ϵ}}_{\text{bw}}$	0.003	<0.001
(b) Seven-element array
${\mathrm{ϵ}}_{\text{max}}$	0.024	<0.001
${\mathrm{ϵ}}_{\text{rms}}$	0.011	<0.001
${\mathrm{ϵ}}_{\text{bw}}$	0.018	<0.001
(c) Convex imaging probe
${\mathrm{ϵ}}_{\text{max}}$	0.033	0.013
${\mathrm{ϵ}}_{\text{rms}}$	0.014	0.004
${\mathrm{ϵ}}_{\text{bw}}$	0.017	0.007

The largest holography errors along the $z\prime$ axis in physical experiments occurred for transducer (a) with ${\mathrm{ϵ}}_{\text{max}}\approx 5\%$. For the other transducers, the values of ${\mathrm{ϵ}}_{\text{max}}$ were smaller at 2%–3%. We note that the simulated errors follow the same trend with the largest ${\mathrm{ϵ}}_{\text{max}}$ of 3.5% for transducer (a). Plausible uncertainties of 1° C–2 °C in water temperature may have contributed several percent error to ${\mathrm{ϵ}}_{\text{max}}$, especially because neither temperature nor sound speed was measured directly for transducers (b) and (c). Moreover, uncertainty in the angle between scan axes α_xy may have also contributed to experimental error.

Although the holographically reconstructed and independently measured axial fields agree very well, it is instructive to note that field reconstructions in the transverse $x\prime$ and $y\prime$ directions can be more sensitive to sources of error not considered in the simulations. For instance, positioning errors can occur due to “dropped” steps when motion is driven by stepper motors without feedback from position encoders. Such errors are particularly likely during transverse scans that comprise a large number of points. We noticed such a problem during transverse scans with transducer (a) for which ${\mathrm{ϵ}}_{\text{max}}$ in the focal plane rose as high as about 20% for points in regions of steep field gradients. This experience demonstrates that special attention should be given to positioner reliability in the test configuration.

IV. CONCLUSIONS

Holography is a technique that permits a steady-state 3D wave field to be collapsed to pressure measurements of magnitude and phase made in 2D. Accordingly, a hologram is an important characteristic of any source because it directly reflects the vibratory behavior of the radiating surface of the transducer. In this effort, we have presented a detailed formulation of acoustic holography that relies on the Rayleigh integral to perform field projection calculations. This formulation neglects evanescent waves, utilizing the typical conditions in medical ultrasound where holograms are measured more than a few wavelengths from the source and projection calculations involve similarly long propagation distances. This formulation has several explicit benefits: Arbitrary geometries, including curved surfaces, can be handled transparently; projection calculations are inherently stable; and point-by-point corrections are possible for temperature changes in the propagation medium.

Beyond the basic holography formulation, we have defined explicit metrics for comparing two ultrasound fields. By comparing holographically reconstructed fields to corresponding reference fields, we have used the metrics to quantify holography errors in both simulated and physical experiments. Simulated experiments demonstrate that measured holograms can represent reference ultrasound fields with maximum errors on the order of 1%. These results provide useful guidance on the selection of fundamental measurement parameters: The measurement aperture should be about 30% wider than the geometric width of the acoustic beam, and measurements should be made with a relatively small hydrophone (sensing diameter less than about $\lambda /4$) to avoid the need for directivity corrections. Other errors related to uncertainties in the timing and position of measurements can be larger than 1% in practice; however, such errors can be minimized by measurement of the water temperature during experiments and/or calibration of the alignment of the 3D positioner axes.

For physical experiments, fields reconstructed from measured holograms were compared with independent hydrophone measurements for three different ultrasound transducers. The maximum error on axis was 3% for two of the transducers and 5% for the third. Although it is beyond the scope of this effort to fully trace the sources of experimental error, it is plausible that errors of 5% can be explained by experimental details not fully taken into account, including changes in the water temperature and misalignment of positioner axes in the scan plane. Overall, these experimental errors associated with holography are comparable to those reported by Clement and Hynynen.⁸ Although Clement and Hynynen used a different normalization for their error metric, we find their metric to be comparable to ${\mathrm{ϵ}}_{\text{max}}$ for our data.

Future work will aim to further identify sources of experimental error. Our results suggest that reconstruction errors in the focal plane can be particularly sensitive to hardware positioning errors, thereby demonstrating the importance of ensuring consistent hardware performance during large scans. However, even for the case with the largest errors, Figs. 11 and 12 demonstrate that the measured hologram captures many details of the source vibrations and the corresponding radiated field. In total, the results of the physical experiments validate the two main assumptions behind the holography formulation: the neglecting of evanescent waves and the adaptation of calculations to non-flat surfaces.

A basic goal of this work was to develop a methodology for designing holography measurements that meet specified error criteria. By presenting such an approach along with practical implementation guidelines, this work advances acoustic holography as a metrological tool. In medical ultrasound, such capabilities can simplify the characterization of therapeutic fields,²⁰ which can otherwise involve an extraordinary number of measurements. Beyond field characterization per se, holography provides unique functionality in that it permits reconstruction of the vibrations at the transducer surface. Quantifying these vibrations can be useful for optimizing and/or monitoring transducer performance as well as for defining a boundary condition for forward projection models that include nonlinear propagation in tissue.

APPENDIX A: RAYLEIGH INTEGRAL FORMULAS

Here we describe explicitly the expressions that were used in reconstructing acoustic fields from holograms. We begin by assuming linear, lossless acoustic propagation in a medium with density ρ₀ and sound speed c₀. Then the problem can be formulated by considering a source located on a boundary surface ${\Sigma }_1$ as depicted in Fig. 13. The outgoing wave field satisfies the Helmholtz equation

$${\nabla }^{2}P+k^{2}P=0,$$ (A1)

where P denotes the complex pressure magnitude as defined in Eq. (1), $k=\omega /c_0$ is the wavenumber, and ω is the angular frequency. Note that we have already introduced the $e^{-i\omega t}$ convention, which affects the equations that follow. Use of the $e^{+i\omega t}$ convention instead would yield equivalent equations in which i is replaced by – i.

If ${\Sigma }_1$ denotes a plane surface with outward unit normal ${\mathbf{n}}_1$ oriented in the direction of wave propagation, the exact solution can then be expressed by Rayleigh's integral formulas that follow from the Kirchhoff–Helmholtz integral,¹³

$$P\left({\mathbf{r}}_2\right)=-\frac{1}{2\pi }{\int }_{{\Sigma }_1}\frac{\partial P\left({\mathbf{r}}_1\right)}{\partial n_1}\hspace{0.17em}\frac{e^{\mathit{i}\mathit{k}\mathit{R}}}{R}\hspace{0.17em}d{\Sigma }_1,$$ (A2)

$$P\left({\mathbf{r}}_2\right)=\frac{1}{2\pi }{\int }_{{\Sigma }_1}P\left({\mathbf{r}}_1\right)\hspace{0.17em}\frac{\partial }{\partial n_1}\left(\frac{e^{\mathit{i}\mathit{k}\mathit{R}}}{R}\right)\hspace{0.17em}d{\Sigma }_1.$$ (A3)

Here $R=|{\mathbf{r}}_2-{\mathbf{r}}_1|$ is the distance between a given observation point at ${\mathbf{r}}_2$ and each surface element $d{\Sigma }_1$ at position ${\mathbf{r}}_1$. As such, R varies over the integrating surface ${\Sigma }_1$ and the normal derivative ($\partial /\partial n_1={\mathbf{n}}_1·\nabla )$ denotes spatial differentiation with respect to the outward normal ${\mathbf{n}}_1$ at the location of each surface element $d{\Sigma }_1$. Bouwkamp termed Eqs. (A2) and (A3) the “Rayleigh solutions” and “Rayleigh's first and second formulas.”¹³ Note that in linear acoustics the normal derivative of pressure is proportional to the component of velocity in the same direction

$$\frac{\partial P}{\partial n}=ik{\rho }_0{c}_{0}V,$$ (A4)

where V is a complex magnitude as defined in Eq. (2). At the surface of a source, it is the normal velocity (not pressure) that characterizes the surface vibrations. To match this physical interpretation, the term “Rayleigh integral” in the acoustics literature typically refers only to Eq. (A2), which is written explicitly in terms of the normal velocity V.

For forward propagating waves, it can be shown that the Rayleigh formulas are equivalent to the angular spectrum solution of Eq. (A1).^13,39 While the angular spectrum approach is readily understood as a direct solution of the homogeneous Helmholtz equation, the Rayleigh solutions have a clear physical interpretation: They provide a rigorous mathematical foundation for the Huygens–Fresnel principle.⁴⁰ Specifically, Eq. (A2) represents the radiated field as a superposition of monopole sources emitting spherical waves inside a bounded half space. Equation (A3) does the same as a sum of dipole sources. Note that the Rayleigh solutions are mathematically exact only for acoustic sources arranged on a plane surface. Considering the Huygens–Fresnel interpretation, it is easy to understand this restriction: The original spherical wave radiated by each differential source element over the surface will “feel” the physical curvature, either reflecting from other parts of a concave surface or diffracting in the shadow of a convex surface.

Although the lack of a planar geometry disrupts mathematical symmetry, the errors in using Rayleigh's formulas are often not significant in practice. For surfaces where the radius of curvature is much greater than a wavelength, errors are only significant very close to the source surface and in directions nearly tangent to this surface; these are the regions to which the self-reflected perturbations are radiated. Consequently, the Rayleigh solutions can be used not only for flat sources, but also for curved ones. As established in the 1940s in acoustics,^41,42 this approach can be employed to calculate the focused fields generated by concave ultrasound sources. The accuracy of the Rayleigh solutions in such cases was examined in several studies, which concluded that for many practical sources (e.g., megahertz transducers used in medicine and nondestructive testing), the errors created by non-flatness of the source are negligible.^14–18

Another important feature of Rayleigh integrals is their ability to elegantly solve the backward propagation problem in which the source is reconstructed from measurements of the radiated field. In optics, the possibility of using these integrals to solve the inverse diffraction problem has long been recognized.¹ It was shown that when the wave field is free of evanescent components, the exact solution of the inverse diffraction problem can be expressed by the Rayleigh integral in which the kernel is complex conjugated.^12,43 Hence using the Rayleigh integral for backpropagation is equivalent to using the angular spectrum approach after filtering out spatial frequencies greater than the wavenumber k, which was the approach used in practice in Refs. 2 and 4. In this sense, the Rayleigh solutions for backward projection have the beneficial property of being inherently stable without the risk of amplifying any noise introduced in the form of evanescent waves.

For backpropagation, Eq. (A3) can be rewritten by integrating over surface ${\Sigma }_2$ and taking the complex conjugate of the kernel $e^{\mathit{i}\mathit{k}\mathit{R}}/R$

$$P\left({\mathbf{r}}_1\right)=\frac{1}{2\pi }{\int }_{{\Sigma }_2}P\left({\mathbf{r}}_2\right)\hspace{0.17em}\frac{\partial }{\partial n_2}\left(\frac{e^{-ikR}}{R}\right)\hspace{0.17em}d{\Sigma }_2.$$ (A5)

Recognizing from Eq. (A4) that the normal velocity at ${\Sigma }_1$ can be obtained by taking a normal derivative of the previous equation, another useful equation for backpropagation is

$$\frac{\partial P\left({\mathbf{r}}_1\right)}{\partial n_1}=\frac{1}{2\pi }{\int }_{{\Sigma }_2}P\left({\mathbf{r}}_2\right)\hspace{0.17em}\frac{{\partial }^2}{\partial n_1\partial n_2}\left(\frac{e^{-ikR}}{R}\right)\hspace{0.17em}d{\Sigma }_2.$$ (A6)

It is instructive to note here the convention used for defining forward and backward propagation. We define forward propagation to be away from the source, and backward propagation to be toward it. Hence in the preceding equations, ${\Sigma }_1$ and ${\Sigma }_2$ are arbitrary surfaces transverse to the ultrasound beam with ${\Sigma }_1$ closer to the source than ${\Sigma }_2$ along the direction of beam propagation. To be explicit, Fig. 1 identifies the $+z$ direction to correspond to the direction of beam propagation away from the source.

To facilitate the practical implementation of projection calculations with consideration of arbitrary surface geometries, we present the Rayleigh integral formulas used in this effort after evaluation of the normal derivatives. Toward this end, it is convenient to introduce unit vectors in the direction of propagation from each surface element $d\Sigma$ to the observation point (see Fig. 13): For forward projection, we have ${\mathbf{m}}_{12}=({\mathbf{r}}_2-{\mathbf{r}}_1)/R$. For backward projection from surface ${\Sigma }_2$, we have ${\mathbf{m}}_{21}=({\mathbf{r}}_1-{\mathbf{r}}_2)/R=-{\mathbf{m}}_{12}$. As depicted in Fig. 1, the conditions of interest involve a set of pressure measurements over a surface with some known geometry. From measured pressures, we want to project the field backwards to reconstruct either the pressure or normal velocity on the source surface. From the reconstructed source hologram, we are then interested in forward projection from either pressure or normal velocity to calculate the pressure field.

For forward projection, we use Eq. (A2) to reconstruct pressure from velocity and Eq. (A3) to reconstruct pressure from pressure

$$\begin{array}{c}P\left({\mathbf{r}}_2\right)={\int }_{{\Sigma }_1}V\left({\mathbf{r}}_1\right)\hspace{0.17em}{K}_{\text{vp}}^{\text{fwd}}({\mathbf{r}}_1;{\mathbf{r}}_2)\hspace{0.17em}d{\Sigma }_1\\ \text{where}\hspace{0.17em}{K}_{\text{vp}}^{\text{fwd}}({\mathbf{r}}_1;{\mathbf{r}}_2)=-\frac{ik{\rho }_0{c}_0}{2\pi }\frac{e^{\mathit{i}\mathit{k}\mathit{R}}}{R},\end{array}$$ (A7)

$$\begin{array}{c}P\left({\mathbf{r}}_2\right)={\int }_{{\Sigma }_1}P\left({\mathbf{r}}_1\right)\hspace{0.17em}{K}_{\text{pp}}^{\text{fwd}}({\mathbf{r}}_1;{\mathbf{r}}_2)\hspace{0.17em}d{\Sigma }_1\\ \text{where}\hspace{0.17em}{K}_{\text{pp}}^{\text{fwd}}({\mathbf{r}}_1;{\mathbf{r}}_2)=\frac{1}{2\pi }\left({\mathbf{m}}_{12}·{\mathbf{n}}_1\right)\left(\frac{-ik}{R}+\frac{1}{R^2}\right)e^{\mathit{i}\mathit{k}\mathit{R}}.\end{array}$$ (A8)

For backward projection, we evaluate the normal derivatives in Eqs. (A5) and (A6) to obtain

$$\begin{array}{c}P\left({\mathbf{r}}_1\right)={\int }_{{\Sigma }_2}P\left({\mathbf{r}}_2\right)\hspace{0.17em}{K}_{\text{pp}}^{\text{bwd}}({\mathbf{r}}_2;{\mathbf{r}}_1)\hspace{0.17em}d{\Sigma }_2\\ \text{where}\hspace{0.17em}{K}_{\text{pp}}^{\text{bwd}}({\mathbf{r}}_2;{\mathbf{r}}_1)=\frac{1}{2\pi }\left({\mathbf{m}}_{21}·{\mathbf{n}}_2\right)\left(\frac{\mathit{i}\mathit{k}}{R}+\frac{1}{R^2}\right)e^{-ikR}.\end{array}$$ (A9)

$$\begin{array}{c}V\left({\mathbf{r}}_1\right)={\int }_{{\Sigma }_2}P\left({\mathbf{r}}_2\right)\hspace{0.17em}{K}_{\text{pv}}^{\text{bwd}}({\mathbf{r}}_2;{\mathbf{r}}_1)\hspace{0.17em}d{\Sigma }_2\text{where}{K}_{\text{pv}}^{\text{bwd}}({\mathbf{r}}_2;{\mathbf{r}}_1)=\frac{1}{2\pi ik{\rho }_0{c}_0}\{\left({\mathbf{n}}_1·{\mathbf{n}}_2\right)\\ \left(\frac{\mathit{i}\mathit{k}}{R}+\frac{1}{R^2}\right)+\left({\mathbf{m}}_{12}·{\mathbf{n}}_1\right)\left({\mathbf{m}}_{21}·{\mathbf{n}}_2\right)\times \left(\frac{3ik}{R}+\frac{3}{R^2}-k^2\right)\}\frac{e^{-ikR}}{R}.\end{array}$$ (A10)

The integration kernels in Eqs. (A7)–(A10) depend upon the geometries of surfaces ${\Sigma }_1$ and ${\Sigma }_2$. A simple example occurs when ${\Sigma }_1$ is the plane z = 0 and ${\Sigma }_2$ is the plane $z=z_{\mathrm{h}}$. Then ${\mathbf{n}}_1=(0,0,1)$ and ${\mathbf{n}}_2=(0,0,-1)$; moreover, the vector dot products within the kernels can be simplified for all integration points: ${\mathbf{n}}_1·{\mathbf{n}}_2=-1$, ${\mathbf{m}}_{12}·{\mathbf{n}}_1=z_{\mathrm{h}}/R$, and ${\mathbf{m}}_{21}·{\mathbf{n}}_2=z_{\mathrm{h}}/R$.

APPENDIX B: NUMERICAL EVALUATION OF RAYLEIGH INTEGRALS OVER PLANE SURFACES

Beyond the formulas in Appendix A, an important practical issue is how these integral expressions should be evaluated numerically to guarantee some specified accuracy. The first question that naturally arises is where measurements should be acquired: If a measured hologram comprises a set of discrete measurements made by scanning a hydrophone over a plane, then what step size h between measurement points should be used to enable accurate reconstruction of the full field? Again using the geometry illustrated in Fig. 1, we consider a measurements within the plane $z=z_{\mathrm{h}}$, and use x and y as the transverse coordinates that span the plane. These measurements then define the complex magnitudes $P(x,y,z_{\mathrm{h}})$, which can be used in the Rayleigh formulas.

Because we are using a version of holography in which the region of interest is located many wavelengths away from the source where evanescent waves are negligible, there is no need for h to be less than a half wavelength. This well-known result is based on the sampling theorem (i.e., the Whittaker–Nyquist-Kotelnikov–Shannon theorem) as applied to the angular spectrum of the field. The angular spectrum can then be written in terms of the spatial sampling frequencies k_x and k_y

$$S(k_x,k_y,z_{\mathrm{h}})=\int {\int }_{-\infty }^{+\infty }P(x,y,z_{\mathrm{h}})e^{-i(k_{x}x+k_{y}y)}\hspace{0.17em}dx\hspace{0.17em}dy\hspace{0.17em}.$$ (B1)

In the absence of evanescent waves, a field with wavenumber $k=2\pi /\lambda$ is fully represented by the portion of the angular spectrum in the k_x-k_y plane that lies within the circle $k_x^2+k_y^2\le k^2$. Consequently, the sampling theorem can be applied to conclude that the field can be exactly discretized with $h\le \lambda /2$ if evanescent waves are neglected.

Although the sampling theorem guarantees that the measurement spacing $h=\lambda /2$ is sufficient to fully capture the relevant part of the angular spectrum, it is still not clear what spatial resolution should be used in the numerical evaluation of Rayleigh integrals. It is instructive to remember how a discretized data set can fully represent a continuous function. We assume that pressure P is measured at discrete points in the xy plane with step size h in both directions. As such, the coordinates (x_m, y_n) of measurement locations can be expressed as x_m = mh, y_n = nh for $m,n=0,\pm 1,\pm 2,\dots$. While the number of points is in practice limited, we assume negligible pressure amplitudes beyond the measurement locations so that an infinite number of points can be defined. Then from the discretized pressure values $P_{\mathit{m}\mathit{n}}=P(mh,nh,z_{\mathrm{h}})$, any value between the measured locations can be obtained exactly by from the Whittaker–Shannon interpolation formula,

$$P(x,y,z_{\mathrm{h}})=\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{P}_{\mathit{m}\mathit{n}}\hspace{0.17em}\text{sinc}\left(\pi \frac{x-mh}{h}\right)\text{sinc}\left(\pi \frac{y-nh}{h}\right)\hspace{0.17em},$$ (B2)

where $\text{sinc}(\alpha )=\text{sin}\hspace{0.17em}\alpha /\alpha$.

In general, the continuous hologram $P(x,y,z_{\mathrm{h}})$ may be projected either backward to reconstruct the physical source or forward to quantify the radiated field in three dimensions. Here we model the diffraction behavior in terms of forward projection to locations with $z>z_{\mathrm{h}}$. Considering the form presented in both Eqs. (A3) and (A8), $P({\mathbf{r}}_1)$ is $P(x,y,z_{\mathrm{h}})$, and we seek to understand what discretization step size h₀ should be used for numerical evaluation of the integral. The answer depends on the proximity of the observation point to the holography plane $z=z_{\mathrm{h}}$. If it is very close, the integration step h₀ should be very small to properly account for variation in the value of the kernel [Eq. (A8)] over surface ${\Sigma }_1$. However, using integration steps h₀ that are much smaller than the hologram step size h is not a problem because Eq. (B2) allows exact resampling wherever needed.

In the following text we explore when it is necessary to use $h_0\ll h$ in the evaluation of Rayleigh integrals. When a hologram is used to project the field over distances much larger than a wavelength, we conclude that it is sufficient to evaluate the integral as a summation with step size $h_0=h$, where $h\le \lambda /2$. As noted in Sec. I, the applications of interest here do not involve evanescent waves or projection distances on the order of a wavelength; hence, all integrals were evaluated as simple summations with the step size $h_0=h$.

To prove this result regarding h₀, we begin with a pressure distribution $P(x,y,z_{\mathrm{h}})$ that is represented by the angular spectrum $S(k_x,k_y,z_{\mathrm{h}})$. Introducing Eq. (B2) into (B1), the angular spectrum can be expressed as

$$S(k_x,k_y,z_{\mathrm{h}})=\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{P}_{\mathit{m}\mathit{n}}\hspace{0.17em}{\int }_{-\infty }^{\infty }\text{sinc}\left(\pi \frac{x-mh}{h}\right)\hspace{0.17em}{e}^{-i{k}_{x}x}\hspace{0.17em}dx{\int }_{-\infty }^{\infty }\text{sinc}\left(\pi \frac{y-nh}{h}\right)\hspace{0.17em}{e}^{-i{k}_{y}y}\hspace{0.17em}dy.$$ (B3)

Given that the integrals in the previous relation are Fourier transforms, we note that a sinc function in the spatial domain equates to a rectangular function in the frequency domain. From this understanding, it is convenient to consider the inverse transform

$$\frac{1}{2\pi }{\int }_{-\pi /h}^{\pi /h}{e}^{-i{k}_{x}mh}{e}^{i{k}_{x}x}\hspace{0.17em}d{k}_x=\frac{1}{2\pi }\hspace{0.17em}\frac{e^{i\pi (x-mh)/h}-e^{-i\pi (x-mh)/h}}{\mathit{i}\mathit{x}}=\frac{1}{h}\hspace{0.17em}\text{sinc}\left(\pi \frac{x-mh}{h}\right),$$ (B4)

from which we conclude that

$${\int }_{-\infty }^{\infty }\text{sinc}\left(\pi \frac{x-mh}{h}\right)\hspace{0.17em}{e}^{-i{k}_{x}x}\hspace{0.17em}dx=\{\begin{array}{ll}h{e}^{-i{k}_{x}mh}& \text{for}\hspace{0.17em}\left|k_x\right|\le \frac{\pi }{h}\\ 0& \text{for}\hspace{0.17em}\left|k_x\right|>\frac{\pi }{h}\hspace{0.17em}.\end{array}$$ (B5)

Now, we can rewrite Eq. (B3) as follows:

$$S(k_x,k_y,z_{\mathrm{h}})=\{\begin{array}{ll}\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{h}^2{P}_{\mathit{m}\mathit{n}}\hspace{0.17em}{e}^{-i(k_{x}mh+i{k}_{y}nh)}& \text{for}\hspace{0.17em}\left|k_x\right|\le \frac{\pi }{h}\hspace{0.17em}\text{and}\hspace{0.17em}\left|k_y\right|\le \frac{\pi }{h}\\ 0& \text{otherwise}.\end{array}$$ (B6)

At this point, it is convenient to remember that we are only interested in fields that are free from evanescent waves; in such cases, only spatial frequencies within the circle $k_x^2+k_y^2\le k^2$ need to be considered. If $\pi /h\ge k$ (i.e., $h\le \lambda /2$) as was originally assumed, then the angular spectrum within the circle is given by the top line in Eq. (B6).

It is well known that an exact projection of the angular spectrum to an arbitrary axial position z is readily accomplished through the following transform:⁴

$$P(x,y,z)=\frac{1}{{(2\pi )}^2}\underset{k_x^2+k_y^2\le k^2}{\iint }S(k_x,k_y,z_{\mathrm{h}})\hspace{0.17em}{e}^{i(k_{x}x+k_{y}y)}{e}^{i\sqrt{k^2-k_x^2-k_y^2}\left(z-z_{\mathrm{h}}\right)}\hspace{0.17em}d{k}_x\hspace{0.17em}d{k}_y\hspace{0.17em},$$ (B7)

where we have limited the integration to the circle of interest $k_x^2+k_y^2\le k^2$. However, it is convenient to rewrite this integral as an integral over all space less an integral over the region outside the circle. Substituting the resampled spectrum from Eq. (B6), we obtain

$$\begin{array}{c}P(x,y,z)=\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{h}^2{P}_{\mathit{m}\mathit{n}}\frac{1}{{(2\pi )}^2}\int {\int }_{-\infty }^{+\infty }{e}^{i\left[k_x\right(x-mh)+k_y(y-nh)+\sqrt{k^2-k_x^2-k_y^2}\left(z-z_{\mathrm{h}}\right)]}\hspace{0.17em}d{k}_x\hspace{0.17em}d{k}_y\\ -\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{h}^2{P}_{\mathit{m}\mathit{n}}\frac{1}{{(2\pi )}^2}\underset{k_x^2+k_y^2>k^2}{\iint }{e}^{i\left[k_x\right(x-mh)+k_y(y-nh\left)\right]}{e}^{-\sqrt{k_x^2+k_y^2-k^2}\left(z-z_{\mathrm{h}}\right)}\hspace{0.17em}d{k}_x\hspace{0.17em}d{k}_y.\end{array}$$ (B8)

So far, this equation is exact. At observation points far from the plane at $z=z_{\mathrm{h}}$, the exponential $\text{exp}[-\sqrt{k_x^2+k_y^2-k^2}(z-z_{\mathrm{h}})]$ effectively vanishes, which is to say, that evanescent waves decay to negligible amplitudes at such distant locations. Hence $P(x,y,z)$ can be approximated by keeping only the first set of summations on the right-hand side of this equation.

Next we recognize that the remaining double integral has a known form that can be represented in terms of a normal derivative over the surface where the angular spectrum is known (see Ref. 40)

$$\frac{1}{2\pi }\int {\int }_{-\infty }^{+\infty }{e}^{i\left[k_x\right(x-x^{\prime })+k_y(y-y^{\prime })+\sqrt{k^2-k_x^2-k_y^2}\left(z-z^{\prime }\right)]}\hspace{0.17em}d{k}_x\hspace{0.17em}d{k}_y=\frac{\partial }{\partial z\prime }\left(\frac{e^{ik|\mathbf{r}-{\mathbf{r}}^{\prime }|}}{|\mathbf{r}-\mathbf{r}\prime |}\right)\hspace{0.17em}.$$ (B9)

For distant observation points, we can now approximate Eq. (B8) by keeping only the first set of summations and substituting the previous relation

$$P(x,y,z)\approx \frac{1}{2\pi }\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{h}^2\hspace{0.17em}{P}_{\mathit{m}\mathit{n}}\hspace{0.17em}\frac{\partial }{\partial n}\left(\frac{e^{ik|\mathbf{r}-{\mathbf{r}}_{\mathit{m}\mathit{n}}|}}{|\mathbf{r}-{\mathbf{r}}_{\mathit{m}\mathit{n}}|}\right)\hspace{0.17em}.$$ (B10)

Here ${\mathbf{r}}_{\mathit{m}\mathit{n}}=(mh,nh,z_{\mathrm{h}})$ are the measurement points. This equation can be compared directly to Eq. (A3) to see that it is simply a discretized approximation of the continuous Rayleigh integral. Therefore numerical evaluation of the Rayleigh integral as a summation over a set of measurement points with step size $h\le \lambda /2$ does not introduce additional errors for observation points positioned many wavelengths away from the measurement plane.