Multiresolution Topological Simplification

Abstract

Persistent homology has been advocated as a new strategy for the topological simplification of complex data. However, it is computationally intractable for large data sets. In this work, we introduce multiresolution persistent homology for tackling large datasets. Our basic idea is to match the resolution with the scale of interest so as to create a topological microscopy for the underlying data. We adjust the resolution via a rigidity density-based filtration. The proposed multiresolution topological analysis is validated by the study of a complex RNA molecule.

Recently, persistent homology has emerged as a new approach for topological simplification of complex data (Patrizio and Claudia, 1999; Vanessa, 1999; Edelsbrunner et al., 2002; Zomorodian and Carlsson, 2005). The essential idea is to create a family of slightly different “copies” for a given dataset through a filtration process so that the topology of each copy can be analyzed. The copies are made different in the filtration process either by the systematic increase in the radius of each sphere of a point cloud data or by the systematic change of the isovalue of volumetric data. During the filtration process, the “birth” and “death” of topological invariants (i.e., Betti numbers) of the underlying copies can be tracked by using either persistent diagrams or barcode representation (Ghrist, 2008). Appropriate mathematical apparatus has been devised to organize simplicial complexes generated via the filtration process into homology groups (Edelsbrunner et al., 2002; Zomorodian and Carlsson, 2005). As such, persistent homology is able to provide a one-dimensional (1D) topological description of a given dataset, in contrast with the zero dimensional (0D) description of the traditional topology and the high dimensional description of geometry. Therefore, persistent homology introduces a geometric measurement to topological invariants, further bridging the gap between geometry and topology. However, most successful applications of persistent homology are focused on topological characterization identification and analysis (CIA).

Recently, we have introduced persistent homology for mathematical modeling and prediction of nanoparticles, proteins, and other biomolecules (Xia and Wei, 2014; Xia et al., 2015). We have proposed the molecular topological fingerprint (MTF) to reveal topology–function relationships in protein folding and protein flexibility (Xia and Wei, 2014). We have employed persistent homology to predict the stability of proteins (Xia and Wei, 2014) and the curvature energies of fullerene isomers (Xia et al., 2015; Wang and Wei, 2014). More recently, we have proposed objective-oriented persistent homology to proactively extract desirable topological traits from complex data, based on variational principle (Wang and Wei, 2014). Most recently, we have developed multidimensional persistent homology to achieve better characterization of biomolecular data (Xia and Wei, 2015b). Persistent homology is found to provide an efficient approach for resolving ill-posed inverse problems in cryo-EM structure determination (Xia and Wei, 2015a).

The direct application of persistent homology analysis to large biomolecules, such as the HIV virus capsid, which has more than four million atoms, is unfeasible at present. One of obstacles is the use of a uniform resolution in the filtration and cross-scale filtration at a high resolution, which is prohibitively expensive in the present persistent homology algorithms. Therefore, there is pressing need for innovative topological methods to deal with excessively large data sets.

The objective of the present work is to introduce multiresolution persistent homology (MPH). Our basic idea is to match the scale of interest with appropriate resolution in the topological analysis. In contrast with the original persistent homology that is based on a uniform resolution of the point cloud data over the filtration domain, the proposed MPH provides a mathematical microscopy of the topology at a given scale through a corresponding resolution. MPH can be employed to capture the topology of a given geometric scale and applied as a topological focus of lens. MPH becomes powerful when it is used in conjugation with the data that has a multiscale nature. Generally, to perform our MPH analysis, we need to introduce an FRI-based density model with an adjustable resolution parameter. The systematic adjustment of this resolution parameter will lead to a multiresolution representation, which incorporates a full spectrum of resolution scales. The detailed method is presented below.

Flexibility–rigidity index (FRI) (Xia et al., 2013; Opron et al., 2014) was originally invented for the flexibility analysis of biomolecules. It provides an excellent prediction of macromolecular Debye–Waller factors or B-factors. The essential idea of FRI is to construct flexibility index and rigidity index by certain kernel functions, and further use them to describe the topological connectivity of protein structures. In the present work, we generalize the FRI method for characterizing the rigidity and flexibility of arbitrary data sets, such as networks, graphs, etc. The generalized FRI method facilitates the multiresolution geometric and topological description of biomolecules. Generally, the rigidity function of the data can be expressed as μ(r)=∑_j w_jΦ(∥ r − r_j ∥; η), where r_j is the coordinate of j-th pseudo-atom, w_j is a weight, and Φ(∥ r − r_j ∥; η) is a kernel function. We use an exponential function 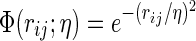in our simulation. The resolution parameter η is systematically changed to generate a series of structures with various resolutions. To construct a filtration process, we linearly rescale all the rigidity function values to the region [0,1] using formula 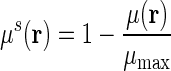, where μ(r) and μ^s(r) are the original and rescaled rigidity density value respectively, and μ_max is the largest density value in the original data. The rescaled density value is then used as the filtration parameter.

A complex RNA molecule 4QG3 is used to demonstrate the utility of the present multiresolution topology analysis for biomolecules. To prepare the structural data, we remove the protein and all ions in the biomolecules, and retain only the RNA part. To construct the rigidity density function, first we take into consideration atom types by setting w_j in the FRI correlation function to be their element numbers. Additionally, we vary the FRI resolution η from 0.3 to 4.0 Å to deliver a full “spectrum” of geometric resolution in our rigidity density map. The RNA molecule extracted from RNA-protein complex 4QG3 has 1723 atoms and large loops in its structure. Since small grid spacing can be prohibitively expensive for this system, we use a grid spacing of 0.3 Å in our study. As a result, some detailed local topological structures may not be fully resolved and may even appear as noise in our persistent barcodes. Therefore, in our barcode results, we removed all the bars with persistent length less than 0.05 with respect to a total length of 1.

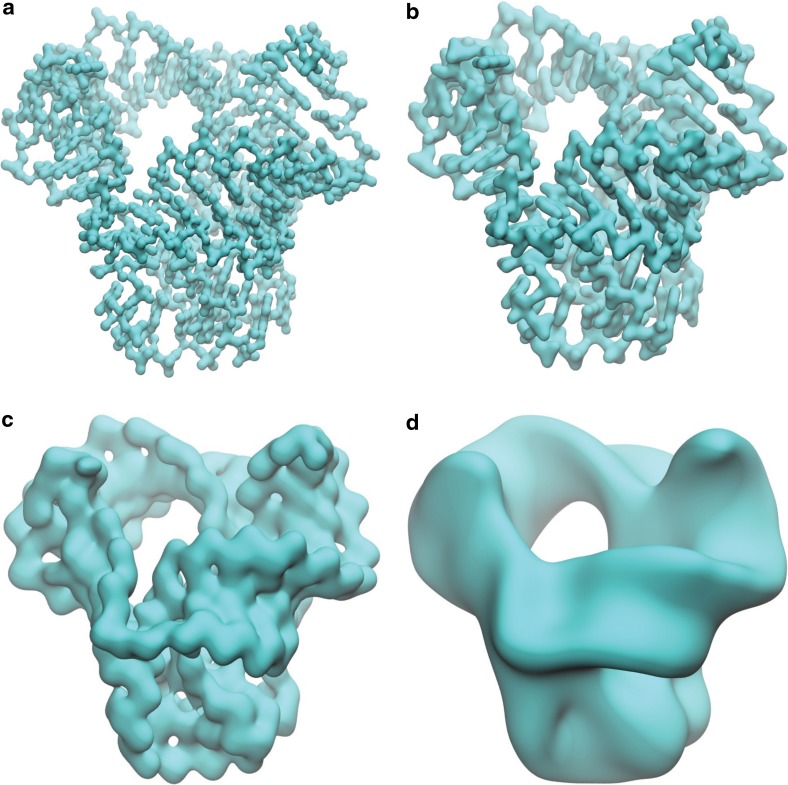
The rigidity density maps generated by various resolutions have dramatically different physical implications. The isosurfaces extracted from these maps give a good explanation of the present multiresolution analysis. Figure 1 demonstrates four isosurfaces from density data generated by η=0.7, 1.0, 2.0, and 4.0Å, respectively. It can be seen that with the increase of η value, isosurfaces gradually shift from a local type of scale to a global type of scale. More specifically, when η is smaller than 0.7Å, generated density maps focus on the scale of atom and atom-bond. When η is increased to around 1.0Å, nitrogenous base or five-carbon sugar scale dominates. The further increase of η to around 2.0Å leads to the major groove and minor groove scale. Finally, when η goes beyond 4.0Å, rigidity map of the RNA gradually “melt” into a single gigantic body. This resolution shifting generates the corresponding topological changes as can be clearly observed from our persistent barcodes. In our multiresolution persistent homology analysis, we systematically change η from 0.3Å to 4.0Å.

FIG. 1.

Multiresolution geometric analysis of RNA 4QG3. At various resolutions, rigidity–density profiles emphasizing on different scales of RNA 4QG3 structure are shown. Panels (a)–(d) are RNA surfaces extracted from density profiles generated with resolutions η=0.7, 1.0, 2.0, and 4.0 Å, respectively. It can be seen from (a) that the rigidity–density map focuses on the atom-and-bond scale. The pentagon and hexagon rings in the base and sugar part are well-captured. More global information begins to reveal when the resolution parameter increases in (b). The RNA double-helix string pattern is visible in (c). The minor grove and major grove can be identified and the loops formed by the helix string are revealed. Further increase in resolution value smears most of the local information, leading to only the intrinsic loop.

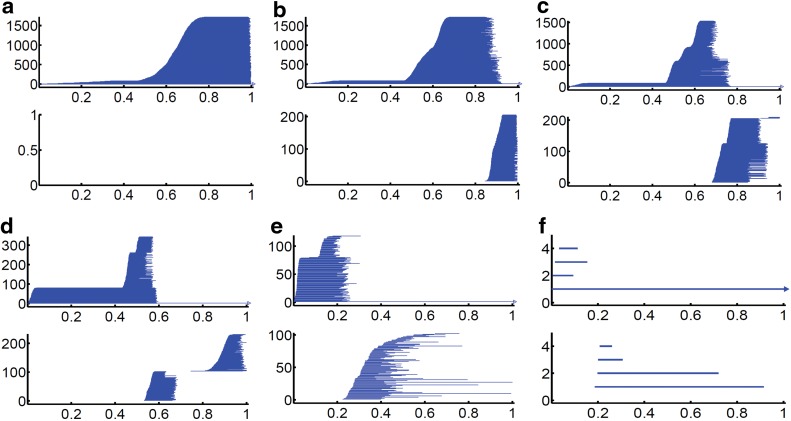
As demonstrated in Figure 2, total PBNs in β₀ panels gradually decrease from 1723 to 4 and will finally dwindle into 1 if we increase the η value further. This phenomenon indicates the inverse relationship between the topological complexity and the resolution value. Additionally, there are 79 β₀ bars that appear much more earlier in the filtration process. These bars are due to 79 phosphorous atoms in the RNA structure, as they have a much larger element number. For β₁ bars, more intriguing patterns can be observed. Originally there were 205 β₁ bars, that is, the total number of PRs and HRs in local nitrogenous bases and five-carbon sugar rings. The number of β₁ bars soars up when more global topological invariants are captured. However, the further increase in the resolution parameter results in the loss of local topological invariants, and thus the PBNs gradually decline. By increasing the resolution parameter, we are able to identify more intrinsic global topological properties in the structure.

FIG. 2.

Multiresolution topological analysis of RNA molecule extracted from RNA–protein complex 4QG3. (a–f) Persistent barcodes for RNA 4QG3 density profiles generated at resolutions η=0.3, 0.5, 0.7, 1.0, 2.0, and 4.0 Å, respectively. Top and bottom panels are for β₀ and β₁ barcodes, respectively. The horizontal axes denote the rescaled rigidity–density value. It can be seen that, at various resolutions, the persistent barcodes give a clear demonstration of various scales existed in the structure. In (a), only the atomic information can be seen. Local pentagon and hexagon ring structure appears in (b). Global topological invariants emerge in (c) and gradually become dominant in (d) and (e). Further increase in the resolution value eliminates most transitional local topological invariants, leaving two largest intrinsic loops as demonstrated in (f). It is obvious that, when the resolution parameter reaches a certain limit, all topological invariants will be gone and the density map of the whole RNA molecule will melt into a featureless body.

It should be noticed that, due to the limited computation resource, the grid spacing in this case is set to be 0.3Å, the smallest resolution value. The results from this resolution may not be accurate enough to capture all the detailed topological properties. For instance, in Figure 2 a and b, if the grid spacing is small enough, the β₀ barcodes should have more steep curves to divide them into several discernable regions corresponding to the atomic types of C, O, P, and N, as they have different atomic numbers thus different density values. However, in this grid spacing, we are still able to maintain the accuracy to distinguish individual atoms, and even tell the difference between phosphor atom and the rest ones.

In summary, we have introduced multiresolution persistent homology through a rigidity density-based filtration. The geometric resolution of the rigidity density is controlled by a resolution parameter, which is appropriately chosen to match the scale of interest. The resulting multiresolution persistent homology is able to handle massive biomolecular datasets that are intractable with conventional persistent homology.

Acknowledgments

This work was supported in part by NSF grants DMS-1160352 and IIS-1302285, and NIH grant R01GM-090208.

Author Disclosure Statement

The authors declare that no competing financial interests exist.