Neural coordination during reach-to-grasp

Abstract

When reaching to grasp, we coordinate how we preshape the hand with how we move it. To ask how motor cortical neurons participate in this coordination, we examined the interactions between reach- and grasp-related neuronal ensembles while monkeys reached to grasp a variety of different objects in different locations. By describing the dynamics of these two ensembles as trajectories in a low-dimensional state space, we examined their coupling in time. We found evidence for temporal compensation across many different reach-to-grasp conditions such that if one neural trajectory led in time the other tended to catch up, reducing the asynchrony between the trajectories. Granger causality revealed bidirectional interactions between reach and grasp neural trajectories beyond that which could be attributed to the joint kinematics that were consistently stronger in the grasp-to-reach direction. Characterizing cortical coordination dynamics provides a new framework for understanding the functional interactions between neural populations.

the focus of cortical motor neuroscience has been shifting from the question of representation to the question of neural dynamics (Cheng and Sabes 2006; Churchland et al. 2012; Scott 2004; Shenoy et al. 2013; Todorov 2004; Todorov and Jordan 2002). To analyze such neural dynamics, a standard approach is the use of state space methods, where a high-dimensional neural signal is described by a trajectory through a low-dimensional space. These methods can also allow us to ask how the trajectories of two neural populations, such as reach- and grasp-related populations, coordinate with one another. The temporal and spatial coordination of transport and grasp components during reach-to-grasp behavior has been studied extensively in psychophysics experiments (Haggard and Wing 1995; Jeannerod 1984), and the development of this coordination has been studied in infants and children (von Hofsten 1984; Kuhtz-Buschbeck et al. 1998; Wimmers et al. 1998). The hand preshapes itself during transport such that when the arm reaches the object, the grasp aperture and orientation of the hand match the required configuration to grasp the object. Other work has posited that during reach-to-grasp, the nervous system is concerned with finding suitable positions for the thumb and fingers on the object's surface and then moving them there (Smeets and Brenner 1999). In both scenarios, populations of motor cortical neurons may need to control the hand and arm in a tightly coordinated fashion.

Previous studies have touched on the cortical basis of coordinating reach-to-grasp movements but have focused on single-neuron responses or pairwise correlations. It has been shown that neurons in primary motor cortex (M1) modulate sequentially during a reach-to-touch task such that shoulder- and elbow-related cells [assessed via intracortical microstimulation (ICMS) effects on the same electrode sites from which the cells were recorded] begin firing on average ∼60 ms before wrist- and finger-related neurons, consistent with the proximal-to-distal sequencing of muscle activation evident in this task as well as in many other multijoint motor behaviors (Murphy et al. 1985). In premotor cortex, pairwise correlations between small groups of neurons have been shown to carry information about particular reaching and grasping combinations even though the constituent neurons' firing rates only carried information about either reaching or grasping (Stark et al. 2008). However, these studies have not examined how the dynamics of large neural ensembles coordinate during this reach-to-grasp behavior.

Here we simultaneously recorded from multiple M1 neurons of two rhesus macaques that performed a reach-to-grasp task to multiple objects in different locations. By measuring temporal fluctuations in single-trial neural trajectories in reach- and grasp-related ensembles, we found evidence of a corrective mechanism that reduced the relative timing between the two ensembles' fluctuations, particularly during the middle of the movement. Using Granger causality analysis on these fluctuations, we also found this coordination to be bidirectional.

MATERIALS AND METHODS

The materials and methods used to collect these data were previously described in Saleh et al. (2012); the same data were used for both studies. All surgical and behavioral procedures involved in this study were approved by the University of Chicago Institutional Animal Care and Use Committee and conform to the principles outlined in the Guide for the Care and Use of Laboratory Animals.

Behavioral task.

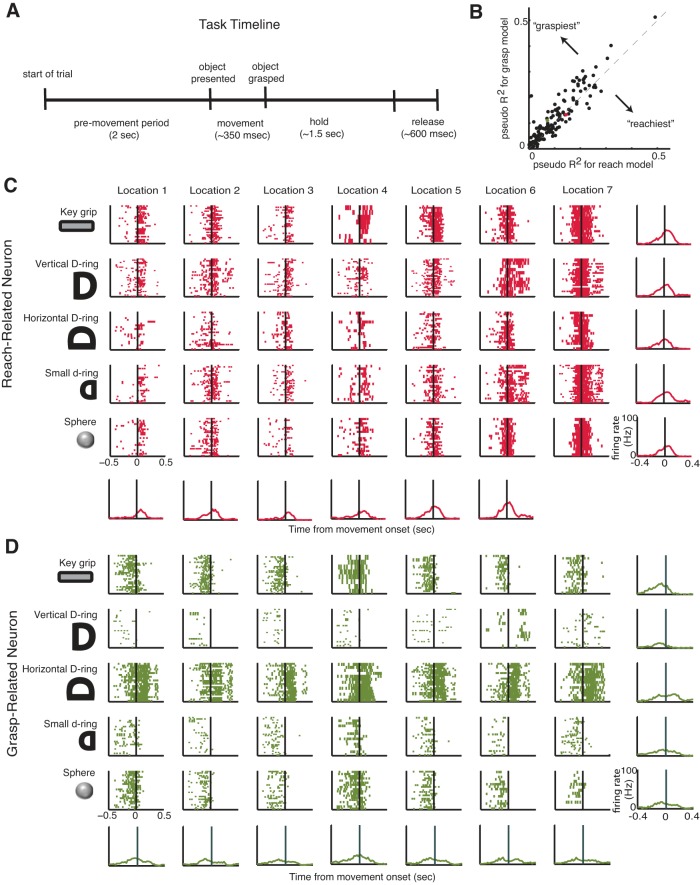
Two female rhesus macaques (monkey O, 6.6 kg, age 7 yr; monkey A, 6.5 kg, age 7 yr) were trained to reach for, grasp, hold, and release objects presented to them by a robot. Each trial was comprised of four periods: a premovement period, a movement period when reaching to grasp the object occurred, a hold period, and a release period, where the robot retracted the object (see Fig. 1A). The animal's vision was blocked during the premovement period, during which the macaque rested its hand on a button. The vision block was then retracted, and the animal proceeded to reach and grasp the object. Once the object was grasped, the animal was required to hold the object until it was retracted by the robot, at which point the object was released. Five different objects/orientations were used for this study, each of which was presented repeatedly in blocks of trials. The first was a keylike object that required a key grip, where the monkey held the object between the thumb and the side of the middle phalanx of the index finger. The second object, the D-ring object, was presented in a vertical and a horizontal configuration that elicited a whole-hand power grip in two different wrist orientations (neutral and pronated). The two configurations were treated as separate objects for the purposes of this study. The fourth object was a smaller D-ring, which elicited a precision grip, where the tips of the index and thumb were opposed. The fifth object, a sphere, required a whole-hand grip with a fanning of the fingers. Objects were presented at seven different locations (at varying azimuthal and elevation angles and depths) in pseudorandom order such that the macaque could not predict the object location on any given trial.

Fig. 1.

Reach- and grasp-related neurons. A: each trial was comprised of 4 periods: a premovement period, reaching to grasp the object, a hold period, and a release period. B: pseudo-R² values for reach-encoding models vs. grasp-encoding models for each neuron in all 4 data sets. C and D: raster plots for 1 exemplary reach-related (C) and 1 exemplary grasp-related (D) neuron for monkey O reaching to grasp each of the different objects at each of the different locations. Perievent time histograms shown for each object at each location.

Neural data acquisition.

Each macaque was chronically implanted with a Utah 100-electrode (400-μm interelectrode distance, 1.5-mm electrode length; Blackrock Microsystems) microelectrode array in the upper limb area of M1 in the left hemisphere. During recording sessions, signals were amplified (gain 5,000×), band-pass filtered between 0.3 Hz and 7.5 kHz, and digitized at 30 kHz with the Cerebus Neural Data Acquisition system (Blackrock Microsystems). A fourth-order, high-pass filter of 250 Hz (single pass) was applied for the spikes. The units were spike sorted off-line with a semiautomated MATLAB routine (MathWorks) developed in our laboratory (courtesy of Jacob Reimer), incorporating some elements of a previously published algorithm (Vargas-Irwin and Donoghue 2007). We used 33 and 42 units for monkey O's first and second data sets, respectively, and 37 and 50 units for monkey A's first and second data sets, respectively.

Motion tracking.

The three-dimensional positions of the macaque's right arm, wrist, and fingers were recorded with a video-based motion analysis system (Vicon Motion Tracking System, Workstation 460); six M2 cameras were used at 1.2-megapixel resolution. Spherical retro-reflective markers (3-mm diameter) were glued to the macaque's fingers, hand, and forearm. A scaled version of a skeletal model of the arm (Holzbaur et al. 2005) was developed with the OpenSim platform (https://simtk.org/home/opensim) and used to compute joint kinematics of the shoulder, elbow, wrist, and fingers. The 17 joint angles are described in detail in Saleh et al. (2012). The joint angles computed for the shoulder were rotation about the coronal plane (abduction/adduction), rotation about the sagittal plane (flexion/extension), and rotation about the upper arm. We computed the angle of flexion/extension for the elbow. For the wrist, we computed the angles of flexion/extension, ulnar/radial deviation, and pronation/supination. We computed flexion/extension at the carpal-metacarpal joint of the thumb, at the metacarpophalangeal joints of the thumb and index and ring fingers, and at the proximal interphalangeal joints of the thumb and index and ring fingers. In addition, we computed the abduction/adduction of the thumb and index and ring fingers (Saleh et al. 2012). A synchronizing pulse was sent to both recording systems every 150 ms with a custom software package (TheGame, version 2) in order to align the kinematics with the neural data. The kinematic data were sampled at 250 Hz and bidirectionally filtered with a fourth-order Butterworth low-pass filter with a 6-Hz cutoff.

Analytical methods: generalized linear models.

We classified neurons as primarily related to either the reach component or the grasp component of movement by fitting generalized linear models (GLMs) with a log link function and Poisson error distributions relating the set of either proximal (shoulder and elbow) or distal (wrist and finger) joint velocities to the firing rates of individual neurons. Neurons whose activity could be better predicted with a model using only proximal joint velocities were labeled as reach related (see Fig. 1C) and those with a model using only distal joint velocities as grasp related (see Fig. 1D). For this part of the analysis, the neural data and the kinematics were downsampled to 50 Hz. For the remainder of the analysis, the neural and kinematic data were both analyzed at 250 Hz or a sampling interval, T, of 4 ms. To allow neural responses to have different latencies with respect to kinematics, we used a stack of kinematics with different delays as regressors. In line with a previous study (Saleh et al. 2012), we used 11 different delays ranging from a lead time of 40 ms (neuron fires after movement) to a delay time of 160 ms (neuron fires before movement). The mean pseudo-R² (Heinzl and Mittlböck 2003) across the runs of a 10-fold cross-validation was used to select the neurons; those with a larger pseudo-R² for the reach model were classified as reach related and vice versa.

Analytical methods: principal component analysis.

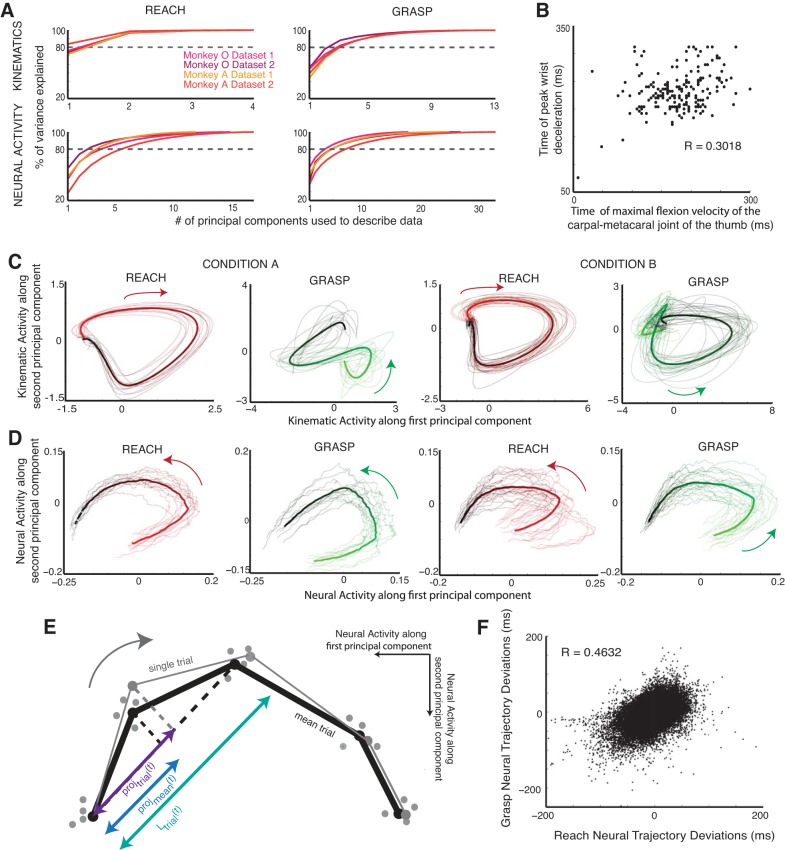
Instead of looking at the firing activity of each of the neurons in a population separately throughout the task, we used principal component analysis (PCA) to reduce the dimensionality of a population's firing activity in order to interpret the interaction between the two populations of neurons. First, each data set was subdivided by condition, defined by the object type and location, for a total of 35 (5 objects × 7 locations) conditions. The firing activities of all of the neurons were smoothed with a Gaussian kernel 100 ms in width, and then all of the trials in the condition were concatenated, resulting in a matrix whose dimensions were the number of neurons by the number of time points in all of the trials for that condition. We applied PCA to reduce the neuronal dimension of this matrix for every condition in each of the data sets. For each data set, we chose between three and eight components to describe the firing activity of the neural population in this reduced subspace, so as to account for at least 80% of the variance in the neural data throughout the course of the trial (see Fig. 2A).

Fig. 2.

Trajectory analysis. A: % of variance explained by reach-related and grasp-related neural and kinematic data for monkey O and monkey A as a function of the number of principal components. B: time of maximal flexion velocity of the carpal-metacarpal joint of the thumb, a proxy for maximum aperture, plotted against time of peak wrist deceleration for all of the trials in 1 data set where monkey O was reaching to grasp the vertical D-ring. C: kinematic trajectories of proximal (reach related) and distal (grasp related) joints in a reduced-dimensional space. Trials shown are for condition A, where 1 monkey reached to grasp a sphere at 1 location, and condition B, where the same monkey reached to the vertical D-ring at a different location. Mean trajectories for the condition are shown as thick lines. D: neural population trajectories of reach-related and grasp-related activity in reduced-dimensional space for the same 2 conditions. Mean trajectories for the condition are shown as thick lines. Color gradients in C and D reflect time from the beginning (red/green) to end (black) of the trial. E: cartoon illustration of a single-trial reach-related trajectory and mean trajectory projected onto a local approximation of the mean trajectory (black dashed line) in 2-dimensional principal component space. The projections are in purple and blue, respectively. (Samples from other trials are also shown as gray dots.) The ratio of the difference between the two projections (i.e., the single trial onto the local approximation to the mean minus the mean onto the local approximation to the mean) and the length of the approximation of the mean trajectory (turquoise) is used to convert the deviations into units of time. F: deviations for reach and grasp neural trajectories plotted against each other for all of the trials in 1 data set (monkey O).

RESULTS

We recorded simultaneously from between 33 and 50 M1 neurons while macaques made reach-to-grasp movements to five different object types presented at seven different locations. Neurons were classified as primarily related to either the reach or grasp component of movement by fitting GLMs. Classifying neurons in M1 as either reach or grasp related on the basis of limb kinematics is challenging because the kinematics of the proximal and distal joints of the upper limb are highly correlated during natural reach-to-grasp movements. In fact, we found that neurons whose activity could be well predicted with a model using only the proximal (i.e., shoulder and elbow, see materials and methods) joint velocities tended to be well predicted by a model using only the distal (i.e., wrist and fingers, see materials and methods) joint velocities (Fig. 1B). Neurons whose activity could be better predicted with a model using only proximal joint velocities were labeled as reach related (Fig. 1C) and those better predicted with a model using only distal joint velocities as grasp related (Fig. 1D). For monkey O, 45% of the neurons were classified as reach related and 55% of the neurons were classified as grasp related for the first data set and 35% reach related and 64% grasp related for the second data set. For monkey A, 32% of the neurons were classified as reach related and 66% were classified as grasp related in the first data set and 34% reach related and 66% grasp related in the second data set.

To study the coordination between populations of M1 neurons during reach-to-grasp, we first verified that the macaques were temporally coordinating arm movement and hand prehension (Fig. 2B). Human psychophysics studies have shown that the time of peak deceleration of the arm is significantly correlated with the time of maximum aperture of the hand (Jeannerod 1984). We found that the time of maximal flexion velocity of the carpal-metacarpal joint of the monkey's thumb, a proxy for maximum aperture, was significantly correlated with the time of peak deceleration of the monkey's wrist, with a Pearson linear correlation coefficient of 0.298 (monkey O, P < 0.001, t = 12.245, DOF = 1,534) and 0.260 (monkey A, P < 0.001, t = 11.788, DOF = 1,918) for each monkey. Observation of this hallmark of coordinated reach-to-grasp allowed us to ask how populations of motor cortical neurons interacted with each other to achieve this coordination.

We examined single-trial neural trajectories of the reach and grasp populations in a reduced subspace using PCA (see materials and methods). For each data set, we chose between three and eight components to describe the population activity so as to account for at least 80% of the variance in the data (Fig. 2A). Each data set was subdivided by condition, defined by the object type and location for a total of 35 (5 objects × 7 locations) conditions. Given that the trajectories of the proximal and distal joints were fairly stereotyped within a particular condition, i.e., the monkey made very similar movements to reach and grasp the same object presented at the same location (Fig. 2C), the neural trajectories of the reach and grasp populations (Fig. 2D) were also fairly stereotyped. We took advantage of this to compute mean reach and grasp neural trajectories for each of the conditions in the reduced dimensional space. The trial-averaged neural trajectory for a particular condition was thus used to represent the ideal, stereotyped dynamics of the neural ensemble when the monkey was reaching to grasp that particular object at that particular location.

Assuming that each of the neural populations would tend toward this stereotyped behavior, we compared the neural population trajectories for each trial to the trial-averaged trajectories by measuring the temporal deviations of each trial's neural trajectory from the mean neural trajectory as a function of time. At each time point during the trial, we projected the single-trial trajectories and mean trajectory onto a local approximation to mean trajectory (Fig. 2E). Thus, for trial i, every time point had an associated temporal deviation, δ_i(t), from the mean, defined as the amount of time the reach or grasp neural trajectory was leading (or lagging) the mean trajectory:

$${\delta }_i(t)=2T\times \frac{[pro{j}_i(t)-pro{j}_{\text{mean}}(t)]}{L_i(t)}$$ (1)

where T is the sampling interval (i.e., 4 ms), proj_i(t) is the projection of trial i at time point t onto a local approximation to the mean trajectory, proj_mean(t) is the projection of the mean trajectory at same time point onto the local approximation to the mean trajectory, and L_i(t) is the length of the local approximation to the mean trajectory from time point t − 1 to t + 1.

Measuring how far both neural populations were along their own stereotyped behavior gives us a window into how synchronized their behavior is. Overall, the reach-related and grasp-related populations' deviations from their respective means were significantly correlated, with correlation coefficients of 0.3856 (P = 0, t = 108.676, DOF = 67,611) and 0.4632 (P = 0, t = 140.585, DOF = 72,343) for monkey O's first (Fig. 2F) and second data sets and 0.107 (P = 0, t = 30.595, DOF = 80,806) and 0.0818 (P = 0, t = 25.167, DOF = 94,092) for monkey A's first and second data sets, indicating that the degree to which each population tends toward stereotyped behavior is linked.

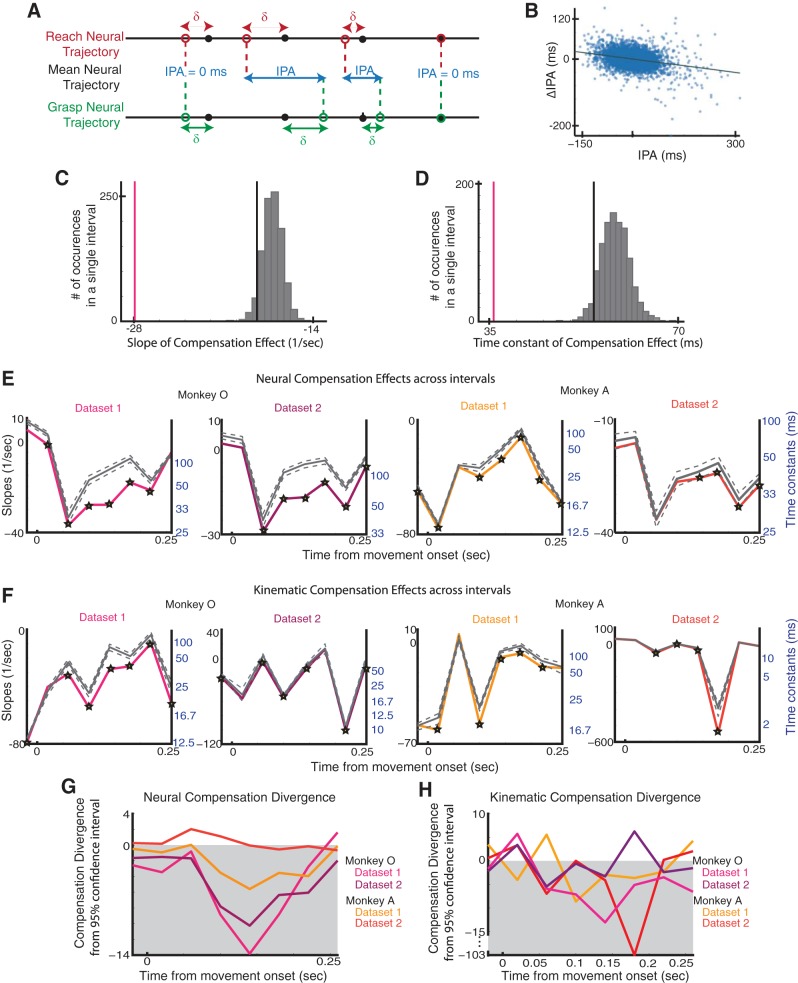
We defined a quantity called the interpopulation asynchrony (IPA) as the difference between the two populations' temporal deviations from their respective means in order to quantify this degree of coupling (Eq. 2). Analogous to previous psychophysical studies that have used perturbations to study the characteristic coupling of the transport and aperture components of reach-to-grasp (Haggard and Wing 1995), we examined fluctuations in IPA_i(t) to examine the temporal coordination between the reach- and grasp-related neural trajectories (Fig. 3A).

$$\mathrm{I}\mathrm{P}{\mathrm{A}}_{\mathit{i}}(t)={\delta }_i^{\text{grasp}}(t)-{\delta }_i^{\text{reach}}(t)$$ (2)

The primary question we addressed in this study was whether a compensatory mechanism existed to correct for transient increases in the asynchrony between the two populations' neural trajectories. That is, if one population's neural trajectory started to lead or lag the other, would either or both populations' neural trajectories compensate such that they would once again become synchronized (i.e., IPA = 0)? To do this, we analyzed how asynchronies tended to diminish in time. We found that an inverse relationship existed between the IPA and its instantaneous temporal derivative, such that larger positive asynchrony was associated with a larger negative derivative in asynchrony and vice versa (Fig. 3B; Eq. 3). That is to say, the larger the difference in the degree to which both neural populations were following their respective stereotyped behavior, the more quickly that both would work to correct for this difference. This compensation effect reflected a proportional control law, indicating an exponential decay in asynchrony (Eq. 4) with a time constant of 1/α inversely proportional to the relationship between the IPA and its instantaneous temporal derivative. To assess how the time constant associated with this decay in IPA varied over the course of movement, we divided trials into intervals and examined the relationship between the IPA and its instantaneous derivative in each interval. Each interval was 40 ms long; there was one interval prior to movement onset and eight intervals after. Although trials were approximately the same length, there was variability in when individual trials ended during the last interval, making the data less interpretable. Thus only the first eight intervals were considered for the remainder of the analysis.

$$\frac{\Delta \text{IPA}(t)}{\text{d}t}=-\alpha \times \text{IPA}(t)$$ (3)

$$\text{IPA}(t)\propto e^{-\alpha t}$$ (4)

Fig. 3.

Interpopulation asynchrony (IPA) and compensation. A: illustration of compensation effect when reach-related trajectory lags grasp-related neural trajectory. B: IPA plotted against change in (Δ)IPA for 1 interval in 1 data set (monkey O). C: slope of compensation (vertical pink line), distribution of shuffled slopes of compensation (gray), and 95% confidence level (vertical black line) for 1 interval in 1 data set (monkey O). D: time constant of compensation (pink), distribution of shuffled time constants of compensation (gray), and 95% confidence level (black) for 1 interval in 1 data set (monkey O) E: slopes of compensation (colored) and mean shuffled slopes of compensation (gray, with 5% and 95% confidence levels after Bonferroni correction) for the neural data plotted throughout the course of movement. Intervals with significant compensation effects are starred; time constants are shown in blue. F: slopes of compensation and shuffled slopes of compensation (gray, with 5% and 95% confidence levels after Bonferroni correction) for the kinematic data plotted throughout the course of movement. Intervals with significant compensation effects are starred; time constants are shown in blue. G: divergence of neural compensation slope from 95% confidence level (after Bonferroni correction) of shuffled slopes for both monkeys. H: divergence of kinematic compensation slope from 95% confidence level (after Bonferroni correction) of shuffled slopes for both monkeys.

Since we collected data from both populations of neurons simultaneously, this patterning could be a result of both populations independently and simultaneously regressing to their respective means. To address this issue, we shuffled the trial order of the reach- and grasp-related neural population trajectories within each reach-to-grasp condition. For example, the reach-related neural population trajectory on a trial where the monkey reached to grasp a sphere at a specific location would be paired with a grasp-related neural population trajectory on a different trial in the same condition. After shuffling, any trial-specific, temporal coordination between the two populations' trajectories would be destroyed. We shuffled the trial order and performed the same analysis 1,000 times, looking at the temporal evolution of the IPA and its temporal derivative over the course of the movement.

The distribution of the slopes generated by the analysis of the shuffled data was compared to the slope generated by the original data for each interval (Fig. 3C). The same comparison was made between the time constants generated by the shuffled data and the original data for each interval (Fig. 3D). If the original slope was <95% of the shuffled slopes for a particular interval after Bonferroni correction, it was considered to be significant. We found that the presence of a significant compensation effect toward the middle of the movement (between 60 ms and 220 ms after movement onset; average movement duration was 324 ms); this effect was present in at least one interval toward the middle of the movement in 88.57% and 80% of the 35 reach-to-grasp conditions for monkey O's data sets and 42.86% and 16% for monkey A's data sets (P < 0.05, 1-tailed, nonparametric shuffling test), respectively. In all of the data sets, all of the significant time constants were 100 ms or shorter (Fig. 3E).

To understand the importance of such interneuronal dynamics during coordinated reach-to-grasp, we analyzed and compared their relationships with kinematics. We performed the same analysis on the kinematic trajectories of proximal and distal joints by examining them in a reduced subspace using PCA; we computed trial-averaged trajectories of the proximal and the distal joint velocities for each condition. As with the neural data analysis, we measured deviations from the mean by projecting single-trial kinematic trajectories onto the trial-averaged kinematic trajectories. Thus, much like the neural trajectories, every point on the kinematic trajectories of either the proximal or distal joints had an associated temporal deviation. By comparing the asynchrony between the proximal and distal joint deviations to its instantaneous temporal derivative, we found patterns of compensation with significant time constants in the kinematic data (Fig. 3F).

To better assess the relationship between the kinematic compensation and the neural compensation, we examined how the slopes of the compensation effect diverged from the 95% confidence level of the slopes generated from the shuffled data by subtracting the 95% confidence level (after Bonferroni correction) from the unshuffled slopes. In both of monkey O's data sets and monkey A's first data set, we found that this divergence increased during the movement, indicating a quicker compensation effect that cannot be explained by both trajectories independently regressing to their own means. This patterning was present in both the neural (Fig. 3G) and the kinematic (Fig. 3H) trajectory dynamics in all four data sets.

As stated above, classifying neurons in M1 as either reach or grasp related on the basis of limb kinematics is challenging because the kinematics of the proximal and distal joints of the upper limb are highly correlated during natural reach-to-grasp movements. Given that this classification is actually a continuum (see Fig. 1B), we reran this analysis on subpopulations of the 10 “reachiest” and 10 “graspiest” neurons; we found significant compensation effects in three of the four data sets (Fig. 4). In addition, to measure how sensitive the compensation dynamics were to this partitioning into reach versus grasp subpopulations, we randomly partitioned the neurons into two subpopulations 100 times, preserving the respective sizes of the subpopulations: one population was the same size as the original reach-related population and the other the same size as the original grasp-related population. We repeated all of the previous analysis for each of the population partitions to generate the slopes and time constants associated with the compensation for each partition; examining the spread of these slopes and time constants gave us an idea of how sensitive our results were to the original reach or grasp population partition. Judging from the mean slopes for all of these partitions it was evident that the compensation dynamics were still present for random partitions of the population, but not to the same extent as the original reach- and grasp-related partition (Fig. 5).

Fig. 4.

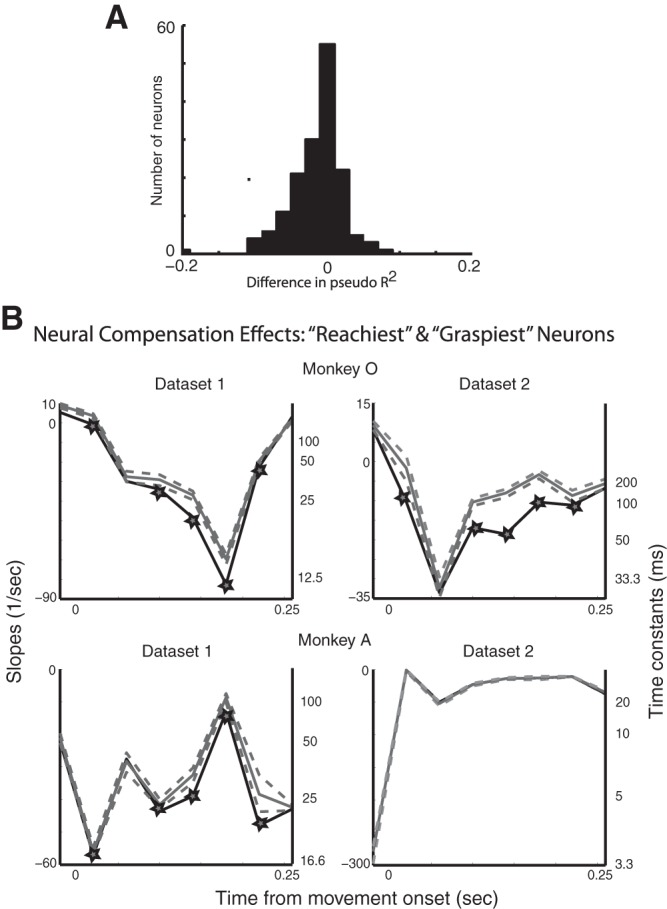
A: histogram of differences between the pseudo-R² values for the models based on reach-related and grasp-related kinematics for all of the data sets. B: the subpopulations were comprised of 10 “reachiest” and 10 “graspiest” neurons. Slopes of compensation (black) and mean shuffled slopes of compensation (gray, with 5% and 95% confidence levels after Bonferroni correction) are plotted throughout the course of movement. Intervals with significant compensation effects are starred; time constants are shown in black.

Fig. 5.

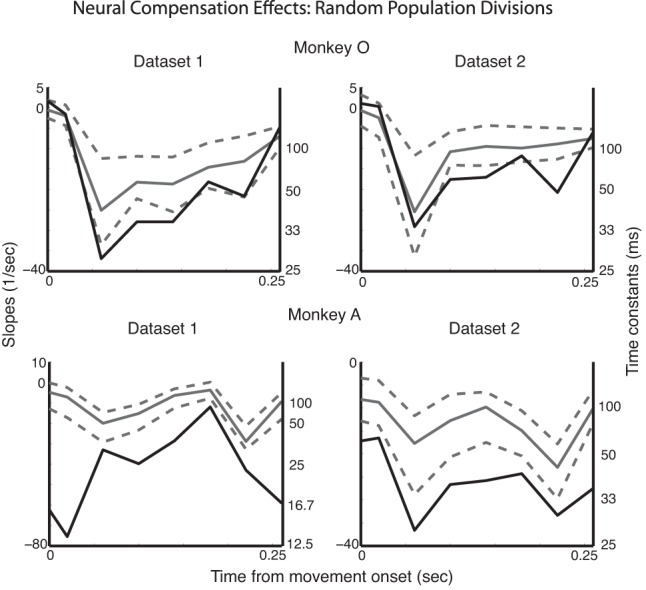
Neurons were randomly partitioned into the 2 subpopulations 100 different times. The original compensation slopes (and time constants) for the reach/grasp partitions are shown in black. The compensation slopes averaged over all random partitions are shown in gray, along with the 5% and 95% spread (after Bonferroni correction).

We next used Granger causality to assess directed causal influences between all combinations of the reach- and grasp-related neural deviations and the reach- and grasp-related kinematic deviations. We quantified the ability of the past deviations of one type to predict the present deviations of another type. We compared a full model that predicted one deviation using regressors that included the past of all four deviation trajectories with a model where the regressor of interest was removed (Seth 2010). We set the maximal model order to 10 lags (40 ms) and used the Bayesian information criterion to select the model order, which resulted in a model order of 10 lags for each data set. We found the significance of the Granger causal relationships with an F-test and then corrected for multiple comparisons with Bonferroni correction. This analysis was done with the Granger Causal Connectivity Toolbox and methods developed by Anil Seth (Seth 2010).

For three of the data sets, we found significant bidirectional Granger causal relationships between the deviations of the reach- and grasp-related neural trajectories [monkey O data set 1 reach to grasp: P < 0.001, F = 7.575, DOF = (1,66866); monkey O data set 1 grasp to reach: P < 0.001, F = 47.625, DOF = (1,66866); monkey O data set 2 reach to grasp: P < 0.001, F = 18.949, DOF = (1,71546); monkey O data set 2 grasp to reach: P < 0.001, F = 25.573, DOF = (1,71546); monkey A data set 1 reach to grasp: P < 0.001, F = 8.731, DOF = (1,79916); monkey A data set 1 grasp to reach: P < 0.001, F = 20.866, DOF = (1,79916)]. For the fourth data set (i.e., second data set from monkey A), we only found a significant Granger causal relationship from the deviations of the grasp-related neural trajectories to the reach-related neural trajectories [monkey A data set 2 grasp to reach: P < 0.002, F = 5.172, DOF = (1,93056)]. In all of the data sets, there was stronger “causal” influence from the grasp-related to the reach-related neural deviations than from the reach-related to the grasp-related neural deviations (Fig. 6A). In addition, using a model that incorporated only the neural deviation trajectories and setting the model order to 2 lags (8 ms), we also found significant bidirectional Granger causal relationships between the deviations of the reach- and grasp-related neural trajectories that were stronger for the first three data sets [monkey O data set 1 reach to grasp: P < 0.001, F = 7.459, DOF = (1,66868); monkey O data set 1 grasp to reach: P < 0.001, F = 198.992, DOF = (1,66868); monkey O data set 2 reach to grasp: P < 0.001, F = 54.9, DOF = (1,71548); monkey O data set 2 grasp to reach: P < 0.001, F = 110.607, DOF = (1,71548); monkey A data set 1 reach to grasp: P < 0.001, F = 39.899, DOF = (1,79918); monkey A data set 2 grasp to reach: P < 0.001, F = 124.684, DOF = (1,79918)] than for the fourth data set [monkey A data set 2 reach to grasp: P < 0.004, F = 9.899, DOF = (1,93058); monkey A data set 2 grasp to reach: P < 0.004, F = 12.606, DOF = (1,93058)]. These “causal” relationships were also stronger from grasp- to reach-related neural deviations than vice versa (Fig. 6B).

Fig. 6.

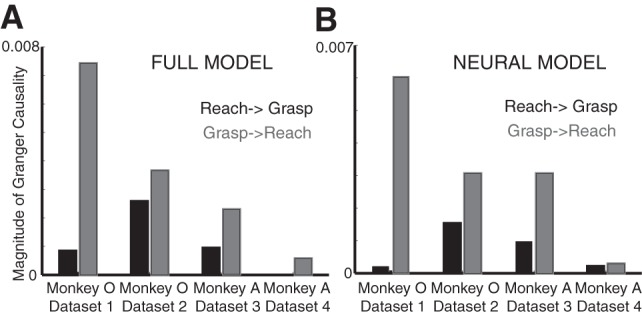
Magnitude of significant Granger causality relationships computed with the full model (A) and the neural model (B). Black bars indicate magnitude of Granger causality directed from reach to grasp neural deviations, whereas gray bars indicate magnitude of Granger causality directed from grasp to reach neural deviations.

DISCUSSION

We have introduced a novel approach to quantifying the coordination dynamics of neural ensembles in the context of reach-to-grasp. We found that the trajectories of the reach-related and grasp-related neural populations were temporally coupled over the course of movement such that any transient asynchrony in time progression between the two trajectories was corrected for by a proportional control mechanism. These coordination dynamics between the two neural populations were observed in a large variety of different types of reach-to-grasp behaviors.

We found that the compensation dynamics were still present for random partitions of the population but were slower compared with the original reach- and grasp-related partition (see Fig. 5). The presence of compensation dynamics even for random partitions is perhaps not surprising given that the upper limb area of M1 forms a highly interconnected network of neurons with highly overlapping movement representations. ICMS studies have shown that nearly half of stimulation sites in M1 evoke twitches in both proximal and distal muscles, particularly on the precentral gyrus where we implanted our electrode arrays (Park et al. 2001, 2004). Several reach-to-grasp studies have shown that the responses of a large percentage of individual M1 neurons were more accurately predicted by considering both proximal and distal kinematics, thereby accounting for the inherent correlations in proximal and distal kinematics in reach-to-grasp (Saleh et al. 2012; Vargas-Irwin et al. 2010). According to this perspective, the neural coordination we observed is a broader property of the entire upper limb area of motor cortex.

The time constant of this compensation effect generally ranged from ∼10 ms to 90 ms. The longer durations in this range were greater than the shortest possible transmission time from motor cortex down to the periphery and back up to cortex as measured by the long-latency loop time (Cheney and Fetz 1984; Witham et al. 2011). However, it is unlikely that the temporal coupling we observed between reach-related and grasp-related populations in M1 is solely mediated by signaling though the periphery. The Granger causality analysis indicated that current temporal deviations in one population's neural trajectory could not be explained solely from the past deviations of limb kinematics but required knowledge of the past deviations of the second population's neural trajectory. This suggests that the temporal coupling between the two populations was not only due to interactions via the periphery. In addition, the Granger causality analysis indicated that causal interactions between the two neural populations' deviations occurred on very fast timescales, on the order of 8 ms.

We also found that these Granger causal relationships were stronger from grasp- to reach-related neural deviations than vice versa, although bidirectional relationships were present in three of the four data sets. The arm and hand constitute a biomechanically linked chain of limb segments, and, as such, motion about one joint induces interaction torques on the other. However, given the larger inertial properties of the arm compared with the hand, interaction torques on the distal limb segments induced by motion of the shoulder and elbow are larger than interaction torques on the proximal limb segments due to motion of the wrist and fingers (Ambike and Schmiedeler 2013; Galloway and Koshland 2002). Therefore, when temporal deviations in the neural state associated with the distal joints occur, it may be particularly important for these deviations to inform the deviations of the proximal joints rather than vice versa. In other words, the asymmetry in interaction torques from proximal to distal joints may be compensated for by an asymmetry in neural communication from distal to proximal joint representations.

The compensation effects were more evident for monkey O's two data sets than for monkey A's two data sets, particularly in the case of monkey A's second data set. One key difference in this data set is that we had more neurons (50 compared with 33, 37, and 42) and needed more principal components to describe this data set, which may have contributed to differences in the results. It is also true that for data sets in which the reach- and grasp-related neural deviations are more strongly correlated, we see a greater degree of neural compensation divergence (Fig. 3G). We hypothesize that a greater correlation between the deviation types could increase the accuracy of our estimation of compensation effects, since we have more data points at which the trajectories are coupled. This effect is evident when we compare the results for data aggregated over all of the conditions to those calculated for each condition. In the aggregate case (Fig. 3E), all of the data sets have between four and six intervals with significant compensation. The difference becomes stark when examining the compensation effects within each condition: monkey A's data sets only have significant compensation present in 42% and 16% of the conditions, while monkey O's data sets have effects present in 80% and 88% of the conditions. We propose that the globally weaker results in the case of monkey A do not necessarily indicate a lesser degree of compensation but a decreased ability to accurately estimate compensation.

Our approach is limited in revealing how these dynamics causally affect coordination. In psychophysics studies, behavioral perturbations are used to establish causality (Haggard and Wing 1995). Similarly, electrical and optogenetic stimulation could be used to establish causality (Diester et al. 2011; Liu et al. 2012). In this study, as a first step toward establishing causality, we incorporated limb kinematics as a proxy for common input and found significant interactions between the two neural populations above and beyond the effects of the common input.

This work extends previous research that has focused on quantifying the dynamics of individual populations (Churchland et al. 2010, 2012; Kaufman et al. 2014; Mante et al. 2013; Shenoy et al. 2013). These approaches characterize the dynamics of neural activity through their trajectories in a low-dimensional projection. Our approach generalizes this approach, by dividing the population into functionally defined subsets and analyzing the relations between trajectories during behavior. This could be adapted to analyze coordination within any brain region and, more importantly, between brain areas. Being able to monitor cortical coordination dynamics is a first step toward understanding how interactions across populations of neurons give rise to coordinated behavior.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke (NINDS) Grant R01 NS-045853, IGERT: Integrative Research in Motor Control & Movement National Science Foundation Grant DGE-0903637, NINDS Grant 5R01 NS-063399, and the Pritzker Fellowship in Neuroscience.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.V., K.K., M.S., and N.G.H. conception and design of research; M.V. and M.S. analyzed data; M.V., K.K., and N.G.H. interpreted results of experiments; M.V. prepared figures; M.V. drafted manuscript; M.V., K.K., and N.G.H. edited and revised manuscript; M.V., K.K., M.S., K.T., and N.G.H. approved final version of manuscript; M.S. and K.T. performed experiments.