Multineuronal activity patterns identify selective synaptic connections under realistic experimental constraints

Abstract

Structured multineuronal activity patterns within local neocortical circuitry are strongly linked to sensory input, motor output, and behavioral choice. These reliable patterns of pairwise lagged firing are the consequence of connectivity since they are not present in rate-matched but unconnected Poisson nulls. It is important to relate multineuronal patterns to their synaptic underpinnings, but it is unclear how effectively statistical dependencies in spiking between neurons identify causal synaptic connections. To assess the feasibility of mapping function onto structure we used a network model that showed a diversity of multineuronal activity patterns and replicated experimental constraints on data acquisition. Using an iterative Bayesian inference algorithm, we detected a select subset of monosynaptic connections substantially more precisely than correlation-based inference, a common alternative approach. We found that precise inference of synaptic connections improved with increasing numbers of diverse multineuronal activity patterns in contrast to increased observations of a single pattern. Surprisingly, neuronal spiking was most effective and precise at revealing causal synaptic connectivity when the lags considered by the iterative Bayesian algorithm encompassed the timescale of synaptic conductance and integration (∼10 ms), rather than synaptic transmission time (∼2 ms), highlighting the importance of synaptic integration in driving postsynaptic spiking. Last, strong synaptic connections were detected preferentially, underscoring their special importance in cortical computation. Even after simulating experimental constraints, top down approaches to cortical connectivity, from function to structure, identify synaptic connections underlying multineuronal activity. These select connections are closely tied to cortical processing.

synaptic connections are fundamental to neocortical computation. They are responsible for instantiating and constraining the multineuronal activity patterns that underlie sensation and behavior (Harvey et al. 2012; O'Connor et al. 2013). If we are to understand information processing, it is crucial to map cortical activity at the level of neurons and their synaptic relationships. For example, paired patch-clamp recordings during quiescence have revealed dense connectivity in local excitatory networks (Song et al. 2005; Neske et al. 2015), yet, circuit spiking activity is sparse and diverse, in ways that are not easily predicted from connection patterns alone (Barth and Poulet 2012). Functional connectivity maps are an important bridge between static connectivity and dynamic information processing.

It is challenging to link activity to underlying connectivity. A large number of presynaptic inputs contribute to the high conductance, depolarized state of postsynaptic neurons during circuit activity (Brunel 2000; Destexhe et al. 2003; MacLean et al. 2005; Watson et al. 2008; Kumar et al. 2008; Neske et al. 2015), limiting the influence of any one synaptic connection (Teramae et al. 2012; Chicharro and Panzeri 2014). The large number of spikes that comprise a multineuronal activity pattern and the impossibility of monitoring all neurons in neocortex mean that correlations in spiking between neurons are not necessarily indicative of a monosynaptic connection (Gerstein and Perkel 1969). Nevertheless, correlation has been shown to indicate an enhanced likelihood that neurons are synaptically connected (Ko et al. 2011). A select fraction of pairwise spike timing relationships are highly reliable (Sadovsky and MacLean 2013) and do not arise by chance. These strong statistical dependencies may be particularly informative of the underlying synaptic connections that produce them.

To establish whether multineuronal activity patterns can be used in a practical way to identify causal synaptic connections, we applied a modified iterative Bayesian algorithm for inferring synaptic connectivity from population activity (Pajevic and Plenz 2009). To evaluate its performance and inform experimental design, we built a neuronal network model comprised of leaky integrate-and-fire units connected via conductance-based synapses with heterogeneous weights. Model activity was poised near criticality, and spiking was sparse, irregular, and asynchronous. Beyond what is expected by chance, we found that model population activity includes reliable lagged timing relationships as a result of its interconnectivity, and we demonstrate that the iterative Bayesian inference method reveals this structure, relating patterned activity to underlying connectivity. Inference improved in the presence of diverse activity, a hallmark of multineuronal patterns in local cortical networks (Harvey et al. 2012; Sadovsky and MacLean 2014). The requirement that a neuron generally must integrate more than one input to achieve threshold (Magee 2000) resulted in inference being most effective when the algorithm considered delays that closely matched the time constant of an excitatory synaptic conductance. Finally, the strongest connections were preferentially detected, consistent with their increased likelihood of driving a postsynaptic action potential.

Despite the fact that there are many impinging synaptic inputs, it is the subset providing drive necessary for the next spike in the pattern that are salient using this method. With temporally proximal pre- and postsynaptic action potentials, these are also the connections that have the capacity to undergo spike-timing-dependent plasticity. Because these connections underlie propagating activity, we propose that they are particularly meaningful in the context of their multineuronal patterns, closely tied to cortical processing and learning.

MATERIALS AND METHODS

Simulated cortical networks with random connection topology.

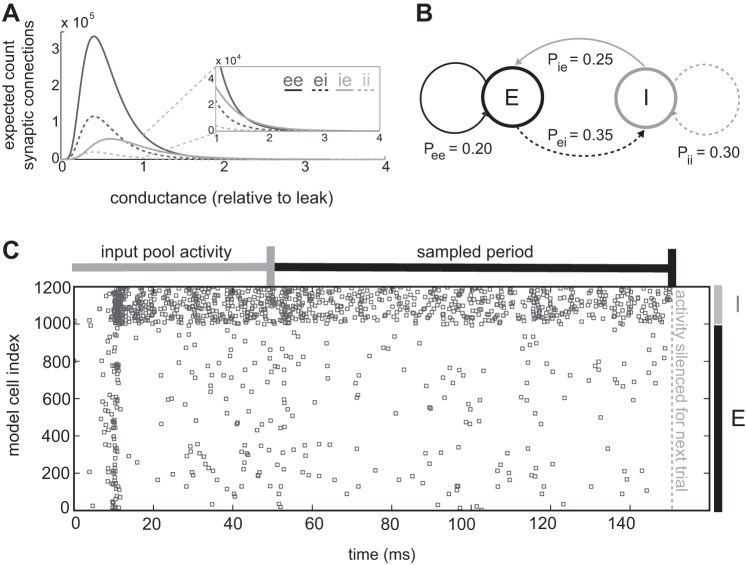
Network simulations were implemented in Python using the Brian Brain Simulator (Goodman and Brette 2009). The model was modified from the integrate-and-fire COBA model (Vogels and Abbott 2005; Brette et al. 2007). In conductance-based models, the depolarizing extent of synaptic bombardments changes with respect to inhibitory and excitatory reversal potentials (Cavallari et al. 2014). Units in the model were divided into two groups, 1,000 excitatory cells (e) and 200 inhibitory cells (i). Synaptic weights were drawn from a lognormal distribution (Fig. 1A). Inhibitory connections to excitatory cells were scaled to be 50% stronger than excitatory connections in the mean. A small tonic excitatory drive g_t to all units helped stabilize sparse spiking. Excitatory and inhibitory conductances g_e and g_i were modeled as decaying exponentials triggered by presynaptic spiking:

$$\frac{\text{d}{g}_{\text{e}}}{\text{d}t}=-\frac{g_{\text{e}}}{{\tau }_{\text{i}}}$$

$$\frac{\text{d}{g}_{\text{i}}}{\text{d}t}=-\frac{g_{\text{i}}}{{\tau }_{\text{i}}}$$

Fig. 1.

Conductance-based integrate-and-fire network with cell-type-dependent connectivity. A: synaptic weights were drawn from a lognormal distribution, with inhibitory-excitatory (ie) conductances scaled 150% relative to other connections. Excitatory connections to other excitatory cells were most numerous and were isolated as the focus of this study. B: 2 populations of integrate-and-fire units with conductance-based synapses, excitatory (black) and inhibitory (gray), were connected sparsely and randomly. Connection probabilities were determined by source and target identity [e.g., individual inhibitory projections to excitatory cells existed with probability of an i unit impinging on an e unit (P_ie) = 0.25]. C: a single simulation epoch of model network activity showing both excitatory and inhibitory spiking. The network was activated via input units firing Poisson spikes at 15 Hz, connected randomly to the excitatory population. After 50 ms, input activity was silenced, and network activity progressed in isolation. During this period, activity was recorded from the excitatory population.

Membrane potential dynamics were defined as follows, where v is voltage across the membrane:

$$\frac{\text{d}v}{\text{d}t}=\frac{g_{\text{e}}(E_{\text{e}}-v)+g_{\text{i}}(E_{\text{i}}-v)+g_{\text{t}}(E_{\text{t}}-v)+g_{\text{leak}}(E_{\text{leak}}-v)}{{\tau }_{\text{m}}}$$

Excitatory reversal potential E_e was 0 mV, as was E_t. Inhibitory reversal potential E_i was −90 mV. Reversal potential for leak current E_leak was −65 mV. Firing threshold was −48 mV, and postspike reset was −70 mV. In addition to afterspike hyperpolarization induced by the reset potential, a 1-ms absolute refractory period was imposed on model neurons. Leak conductance g_leak was fixed at 0.20 mS. Tonic depolarizing conductance g_t was equal in magnitude to the leak conductance.

Collective spiking generated spike-driven conductances that dwarfed the leak conductance, in keeping with definitions of the high-conductance state (Destexhe et al. 2003). Membrane time constant τ_m was 20 ms, excitatory synaptic time constant τ_e was 10 ms, and inhibitory synaptic time constant τ_i was 5 ms.

Excitatory connectivity was topologically random with P_ee = 0.2, in correspondence with measurements of dense local excitatory connectivity from layer 4 in the mouse C₂ barrel (Lefort et al. 2009). Other connection probabilities were chosen to produce overall sparse excitatory spiking and fast promiscuous inhibitory spiking. The probability of an i unit impinging on an e unit P_ie was 0.25, P_ii was 0.3, and P_ei was 0.35 (Fig. 1B).

Simulation protocol.

The model network was stimulated using a pool of 50 input units. Each made uniformly weighted connections on any excitatory cell with probability 1/10 (magnitude 3/5 leak conductance each). To begin a simulation trial, Poisson units spiked over these input connections at 15 Hz (50-ms duration). Network activity was not recorded during the input period. In the recording epoch, input units were silenced, allowing the network to fire according to its internal dynamics (100 ms duration) (Fig. 1C). After 100 ms, activity was silenced, and a new trial was initiated.

The set of connections from input pool to excitatory neurons defined an input topology. After 10 simulated recordings the input topology was randomly regenerated, stimulating the network using a new random pool of network neurons. After 10 input patterns the simulation was terminated, for a total recording time of 100 s.

Finally, replicating experimental constraints, we occluded the majority of the neuronal network and downsampled the remaining spiking activity. Except where otherwise specified, 40% of excitatory cells were visible and used for inference.

Cross-validation of activity differences in relation to input context.

Activity vectors of length N were constructed from segments of recorded activity such that entry N_i was the total number of spikes by neuron i. Distances between activity vectors were computed using the L₁ norm and normalized to mean total firing between the two vectors, quantifying the extent their activity differed as a fraction of total activity. This procedure was repeated across five 100-s simulation trials, each divided into 10-s epochs with shared input projections. Each epoch was subdivided into nonoverlapping 5-s segments. Thus, there were 50 same-input comparisons total. Between-input comparisons were matched in number to same-input comparisons by random selection without replacement.

Reducing the number of possible connection schemes.

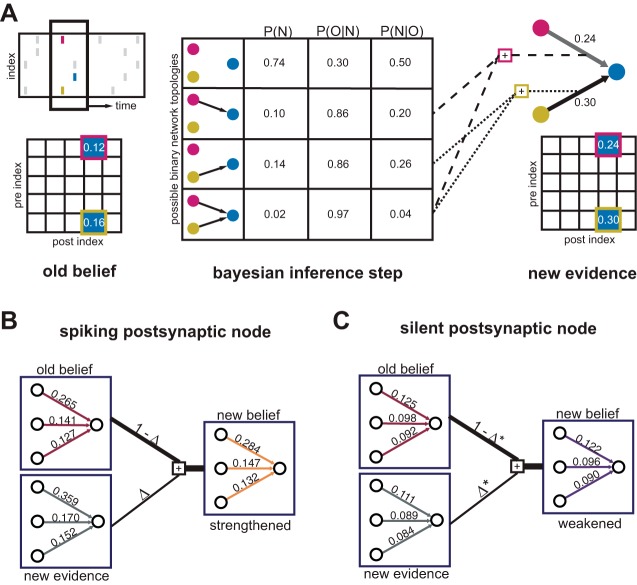
In a network with N nodes where connections can take on m states, the number of possible connection schemes (network topologies) is m^N, a collection too large to consider exhaustively. To simplify the problem, we assume directed pairs fall into two categories, connected or not connected (m = 2). Additionally, during each Bayesian update step (Fig. 2A), only recently active nodes are considered. The number of active nodes in a particular frame (N_active) is small in practice because of sparse spiking and fast frame rates. Depending on computational resources, a cutoff can be imposed on observations where N_active is large; we discarded observations where N_active > 12. With these simplifications a tractable number of possibilities is considered at each update step, despite lacking a polynomial-time algorithm for computing the distribution of posterior probabilities over potential topologies (Pajevic and Plenz 2009).

Fig. 2.

Iterative Bayesian inference for heuristically mapping reliable lagged firing. A: inference step for a single observation. Top left, pick one putative postsynaptic cell and frame (time bin). Consider the active neurons from the previous frame, each of which might have helped recruit the postsynaptic neuron to fire. Bottom left, look up beliefs about connectivity between putative pre- and postsynaptic cells. Middle, consider every binary feedforward connection topology on this subset of neurons. Compute their respective posterior probabilities using a likelihood model and Bayes rule. Right, sum over the posterior distribution to obtain new evidence for the existence of individual connections. B: integrate new evidence with old belief as a weighted sum. In this example, the postsynaptic reference neuron was active, and beliefs about possible presynaptic connectivity increase. C: suppose the postsynaptic reference neuron was quiescent, resulting in decrementing beliefs about connectivity from putative presynaptics. Because quiescence is more common than activity in these recordings, Δ* < Δ. An asymmetric learning rate prevents decrements from rapidly outstripping increments.

Inference of synaptic connectivity.

The matrix W will be a repository for the developing beliefs about synaptic connectivity. At a given iteration, heuristic evidence for the existence of a connection e from potential presynaptic neuron (k) to reference neuron (post) can be found at entry W_e = W_k,post. Before the first observation, entries in W are initialized to a small uniform value. In this work we selected 0.1 for initial mean field belief.

At observation j, choose a random frame t and a random reference neuron post. Let X_post^t describe whether the postsynaptic reference is active or quiescent in that frame. Call the set of neurons firing during the previous frame Pre, potential presynaptic partners to post. Let an observation (O_j) be the conjunction of reference postsynaptic and recently active presynaptic neurons:

$${\text{O}}_j=\left(X_{\text{post}}^t,\hspace{0.17em}\text{Pr}{\text{e}}^{t-1}\right)$$

$$X_{\text{post}}^t=\left\{\begin{array}{ccc}1& \text{if}& \text{neuron post active during frame}\hspace{0.17em}t\\ 0& \text{o}.\text{w}.\end{array}\right\}$$

$$\text{Pr}{\text{e}}^{t-1}=\left\{k|\text{neuron}k\hspace{0.17em}\text{active}\hspace{0.17em}{\text{during frame}}^{t-1}\right\}$$

Consider a vector of ones and zeros representing the connections from Pre to post (N_i) describing the ith possible binary connection scheme between Pre and post. In this simplified framework where synapses can only take two states, zeros represent absent connections, and ones represent existing connections.

$$N_i\in {\left\{0,1\right\}}^{N_{\text{active}}^t}$$

Our objective will be obtaining posterior probability P(N_i|O_j) over all possible binary topologies N_i connecting Pre to post. To that end we define expressions for prior and likelihood using W. Assuming independence among connections for tractability, we compute the prior probability of a given possible topology N_i as

$$P(N_i)={\displaystyle \prod _{\text{e}\in N_i}{W}_{\text{e}}^{j-1}}{\displaystyle \prod _{\text{e}\notin N_i}\left(1-W_{\text{e}}^{j-1}\right)}$$

For the likelihood expression, we define a simple forward model linking binary topology to postsynaptic activity. We imagine an idealized synaptic connection as transmitting a presynaptic spike to postsynaptic partners with probability α. We have used α = 0.8 in this work. In cases of a postsynaptic spike, we model the forward interaction simply as

$$P({\text{O}}_j^{\text{active}}|N_i)=1-{\displaystyle \prod _{\text{e}\in N_i}\left(1-\alpha \right)}$$

Similarly, in the complementary case of postsynaptic quiescence:

$$P({\text{O}}_j^{quiescent}|N_i)={\displaystyle \prod _{\text{e}\in N_i}\left(1-\alpha \right)}$$

It is important that α be <1 so that presynaptic collaboration is recognized in the likelihood computation. This simple model clearly underestimates the potential for collective and nonlinear presynaptic effects. Its corresponding virtue is that it requires very few parameters be fit to data.

From prior and likelihood, the posterior probability P(N_i|O_j) is obtained using Bayes rule:

$$P(N_i|{\text{O}}_j)=\frac{P({\text{O}}_j|N_i)P(N_i)}{P({\text{O}}_j)}=\frac{P({\text{O}}_j|N_i)\text{P}(N_i)}{{\displaystyle {\sum }_{\text{l}}P({\text{O}}_j|N_{\text{l}})\text{P}(N_{\text{l}})}}$$

The marginal P(O_j) is computed as a sum over all binary connection schemes. New evidence w values for individual connection e is obtained by summing across the posterior distribution:

$${w\text{′}}_{\text{e}}^{}=\mathrm{\sum }_{i|(e\in N_i)}P(N_i|O_j)$$

This evidence is integrated into W as a weighted sum (Fig. 2B). Only the subset of edges considered in the Bayesian step are updated (the edges in N_i). The result of linear combination over the course of multiple observations is exponential smoothing on accumulated evidence.

$$W_{\text{e}}^j=\Delta {\text{w}\prime }_{\text{e}}^{}+(1-\Delta )W_{\text{e}}^{j-1}$$

Because firing patterns are sparse, to prevent runaway decrementing toward zero in W, the learning rate Δ takes different values for postsynaptic activity vs. quiescence (Fig. 2C). In this work we used Δ_active = 0.2 and Δ_quiet = 0.05. Because of the asymmetric learning rate, postsynaptic quiescence is a weak source of evidence compared with postsynaptic activity, in correspondence with biological intuitions. Over the course of many repetitions of the inference step, we drew pairs (t, post) without replacement until each visible neuron was sampled for all t > 1.

Evaluating performance.

Precision was defined as the fraction of true positives (TP) to inferred connections [TP/TP + false positive (FP)]. Sensitivity was defined as the fraction of true positives to total connections [TP/TP + false negative (FN)]. The first measure quantifies detection accuracy, whereas the second quantifies extent of coverage. There is a tradeoff between these two factors, varying with choice of threshold on the belief matrix. High thresholds yield high precision but low sensitivity; low thresholds yield low precision but high sensitivity.

An alternative way to quantify the precision-sensitivity tradeoff is to use receiver operating characteristic (ROC) curves, but ROC curves are not a natural metric in this specific context of synaptic detection (Lobo et al. 2008). Specifically, because complete coverage of true positives is out of reach given current experimental methodologies, a large portion of the curve tends to fall on the main diagonal. As a result, measures of area under the curve systematically devalue inferred topologies that do not identify synapses over the entire range of functional weights, even if they perform optimally over a restricted range of thresholds. Area under the ROC curve also fails to differentiate between false positive and false negative errors, which have very different consequences for interpreting inferred connectivity (Lobo et al. 2008). Precision and sensitivity lessen this quantification problem and are additionally appealing because they are intuitive measures of detection performance.

We computed chance-level performance by counting the total number of actual synaptic connections in a category of interest (e.g., falling below a cutoff weight) normalized by the number possible (the set of all directed pairs in the sample population).

Preprocessing for correlation-type activity maps.

For correlation-based inference, simulated spiking was first convolved with a Gaussian function using SD = 10 ms.

Error motifs.

Detection errors were analyzed for systematic features. To quantify the prevalence of errors arising from common inputs, we isolated false positives and counted the frequency with which they shared some hidden third input. We compared that error distribution with the frequency with which randomly selected pairs shared hidden inputs.

Accurate identification of connection direction is important for understanding large-scale features of activity flow (although it is less important for paired patch-clamp experiments where pair identity matters more than direction of interaction, which can be recovered from excitatory postsynaptic potentials instead). We quantified misdirection errors by isolating spuriously inferred pre- and postsynaptic cells and counting the frequency of genuine connection from reference post- to presynaptic. We compared the resulting distribution with randomly chosen directed pairs.

Finally, we hypothesized that slow frame rates might lead to spurious connections spanning multiple synapses. We isolated just the strongest 10% of synaptic connections and computed the frequency that misidentified pre- and postsynaptic cells were connected by a chain (path) of strong connections no more than four cells long (3 edges or fewer). These limits served to constrain the otherwise dense connectivity, where otherwise any two neurons would be connected by a short arbitrary path.

RESULTS

Conductance-based network model with heterogeneous synaptic weights.

A network model was developed to measure performance, i.e., benchmark activity maps in relation to excitatory synaptic connections (see materials and methods). For the model we drew synaptic conductances from a lognormal distribution to ensure that connections were weak on average, with a small number of strong connections (Fig. 1A), matching experimental reports (Song et al. 2005; Perin et al. 2011). Heterogeneity in synaptic efficacy has important consequences for information transmission (Teramae et al. 2012).

Although local neocortical connectivity is highly nonrandom (Perin et al. 2011; Watts and Thomson 2005; Song et al. 2005), we used random connectivity in our model (Fig. 1B). A random network design is appropriate for benchmarking because it is more challenging to reconstruct from activity than more realistic clustered topologies (Kobayashi and Kitano 2013), avoiding biases that inflate apparent performance.

Network activity was initiated from a small Poisson spiking external input pool. Each input unit projected randomly and independently in the excitatory population. By periodically randomizing the small number of input projections, we sought to achieve a diversity of activity within each network model, similar to spontaneous neocortical data (Sadovsky and MacLean 2013, 2014; Luczak et al. 2009) and activity in visual cortex driven by viewing natural scenes (Miller et al. 2014). Except where noted, model network activity was only recorded for inference after cessation of activity in the input population (Fig. 1C). At the end of the recording period we reset the model and began a new trial.

Simulated spike dynamics were asynchronous and irregular (Brunel 2000). Asynchrony was measured with spike-rate correlations, by convolving spike times with a Guassian kernel of width σ = 3 ms. Among excitatory neurons in the recording period, mean correlation coefficient was 0.0019 (Kumar et al. 2008). Irregularity was measured with interspike intervals, which were observed to have mean squared coefficient of variation of 0.81, consistent with other reports of irregular activity (Kumar et al. 2010). Excitatory spiking activity was also characterized by a branching parameter of 0.99 (for 10-ms bins), indicating near-critical dynamics (Beggs and Plenz 2003; Haldeman and Beggs 2005). Firing rates in the excitatory population during the recording period were 1.33 ± 3.15 Hz (mean ± SD) consistent with findings in awake behaving mice (Crochet et al. 2011). According to these criteria, simulated spike dynamics were similar to in vivo recordings.

Iterative bayesian inference to map synaptic recruitment.

We compared activity in cortical circuits with the structure of their underlying connectivity. Functional weights summarize the frequency of recurring firing patterns, producing a map of circuit activity. In particular, we employed an iterative Bayesian inference method (modified from Pajevic and Plenz 2009) that requires few parameters and relatively few epochs of population activity as a result of its simple dynamic model (see materials and methods). In iterative Bayesian inference, information about firing patterns is accumulated by considering small portions of the entire recording, stitched together over the course of many observations. Bayes Rule is used to parse accumulating beliefs about conditional relationships across multiple iterations (Fig. 2, see materials and methods). A single frame lag window was used throughout this work when computing functional relationships.

The algorithm is outlined as follows: in a single observation, choose a random frame t and choose a (putative) postsynaptic neuron post. Consider the set of neurons Pre firing during frame t − 1. These cells are candidates for having driven post to fire. Thus, an observation contains evidence about these potential presynaptic partners. Broadly, if post is spiking, there is new evidence for connectivity from Pre to post. Conversely, if post is silent, the observation is evidence for a lack of connectivity from Pre to post. Silence is only weakly informative of lack of connectivity because synaptic connections are weak in isolation. New evidence is integrated in the prior after each iteration step, gradually updating an overall summary of functional relationships.

Defining recruitment.

Far from recruiting neurons nonspecifically, cortical activity flow at the level of the microcircuit is sparse and precise (Kruskal et al. 2013; Dombeck et al. 2009). Isolating activity within a single input context (trials with the same input projection topology), 36 ± 0.98% of model neurons were never active. With the inclusion of many input contexts over the entire simulation, only 14.5% of model neurons were inactive, recapitulating experimental data (Sadovsky and MacLean 2013). Naturally, unresponsive neurons, which do not participate in propagating circuit activity, do not give rise to functional relationships.

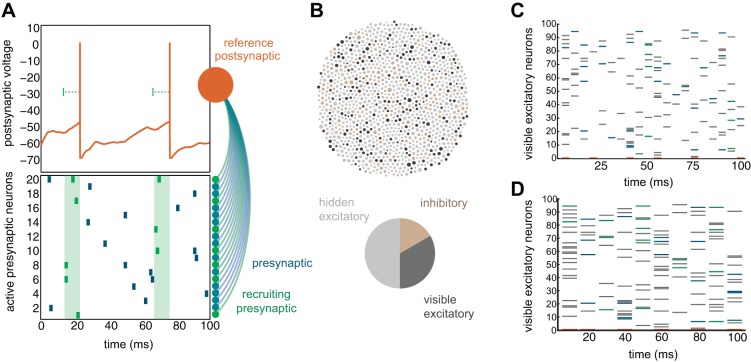
Throughout, lagged firing describes any pair of cells active within one time frame of each other, regardless of their connectedness. We defined active synaptic connections as those connecting pairs where the presynaptic neuron was active at least one time. Surprisingly, many active synaptic connections never resulted in action potential generation in the postsynaptic model neuron. As a result, despite the fact that a synaptic connection was active and produced a subthreshold depolarization, such pre post pairs were not a route for propagating activity (which manifests as a multineuronal activity pattern). Synaptic connections that resulted in an action potential in both the pre- and postsynaptic model neurons were defined as recruiting synaptic connections (Fig. 3A). Specifically, if a presynaptic partner was active in the lag window preceding postsynaptic firing at least one time, the connection was defined as contributing to recruitment. Of course, these functional categorizations depend on the specific multineuronal activity pattern and choice of the lag window that was considered by the algorithm (see below).

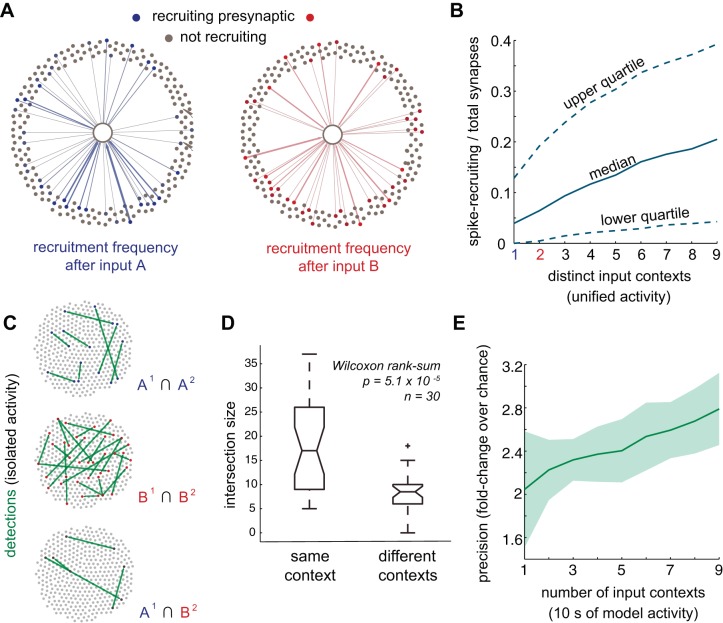
Fig. 3.

Quantifying recruitment and respecting experimental constraints. A: relative to a postsynaptic reference, recruiting presynaptic neurons are those active at least one time during an integration window preceding postsynaptic spiking. B: excitatory cells were sampled randomly for recording, with the majority of neurons hidden (60% of excitatory cells hidden), introducing the challenge of hidden statistical structure. The diameter of each node is proportional to their weighted in degree (sum absolute value of afferent weights). C: activity subsampled in 5-ms bins and categorized using a single-frame integration window. Recruiting presynaptic cells (green) and other active presynaptic cells (blue) were annotated relative to a postsynaptic reference cell (orange, row on bottom). The majority of lagged activity involves cells that are not presynaptic (gray) to the reference. D: activity was also subsampled into 10- and 25-ms bins.

Simulating experimental conditions.

Even with dense uniform sampling within a large field of view (Sadovsky et al. 2011), connected neurons reside above, below, and outside the imaged field. Unobserved activity can lead to ambiguity in the reconstruction of synaptic connectivity from spiking because of misleading statistical dependencies (Chicharro and Panzeri 2014), particularly in resolving true synaptic connections vs. unconnected neurons with shared inputs (Nykamp 2007, 2008). To benchmark the iterative Bayesian algorithm while acknowledging experimental constraints, we occluded 60% of excitatory cells within the network model (except where otherwise noted) (Fig. 3B). Furthermore, we downsampled modeled network activity in time, since even the fastest optics and indicator dyes are slower than an action potential (Fig. 3C). The consequences of estimating spike times from Ca²⁺ signals have been investigated explicitly in a previous study (Lütcke et al. 2013).

Poisson null populations verify significance of timing relationships.

Whenever many neurons are simultaneously active, spurious apparent structure will exist because of chance coincident spike timing. To confirm the presence of genuine pairwise timing in model activity, we created populations of rate-matched Poisson units. A Poisson population can establish chance frequency of activity patterns because it lacks any internal causal interactions (Roxin et al. 2008). Each Poisson unit was paired to a corresponding neuron in the model. Poisson rates were individually determined from the number of spikes their model counterparts fired during the sampling period, on a trial-by-trial basis. Thus, the null population recapitulated firing rate structure and chance interactions without mimicking precise interrelationships in timing.

We applied iterative Bayesian inference to the connected network activity and the independent Poisson activity sampled over 100 s with 5-ms lag windows. Inferred connectivity matrixes from matched Poisson activity were impoverished in total weight (model: 0.17 ± 0.10; Poisson: 0.058 ± 0.074; mean ± SD of individual edge weights). These differences were significant (P = 1.1 × 10⁻⁷, random subset of 100 nonzero edges, Wilcoxon rank-sum) (Fig. 4A). Strong weights reflect reliable spiking relationships between neurons, and they were present in the randomly connected model but not in the Poisson matched null population. These results support the hypothesis that causal connectivity gives rise to reliable functional relationships beyond what is expected by chance. Functional relationships computed with iterative Bayesian inference for an ex vivo dataset collected from mouse somatosensory cortex echoed the simulated-network weight distribution, with a small number of particularly reliable relationships forming an extensive tail (Fig. 4B).

Fig. 4.

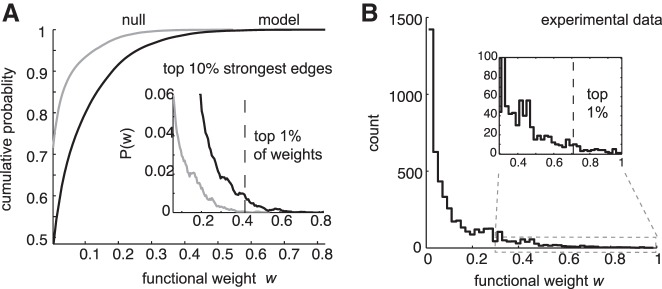
Cortical activity includes reliable pairwise timing relationships. A: cumulative distribution of inferred connection strengths for connected model (black) vs. Poisson rate-matched (gray) populations. Firing rates for each Poisson unit were matched on a trial-by-trial basis to each model neuron. Inset, the corresponding probability distribution function, in zoom. Top percentile of nonzero functional weights (broken line). B: comparison with imaging data. Inferred functional weights for activity recorded in mouse somatosensory neocortex.

Using timing relationships to predict synaptic connectivity.

Applying a threshold to the matrix of functional relationships involved a tradeoff between false positives (type 1 errors) and false negatives (type II errors) (FPs and FNs, respectively). To dissociate these error types, we assessed performance using two metrics: precision (TP/TP + FP) and sensitivity (TP/TP + FN). First, we considered hypothetical conditions where the excitatory population was fully sampled at 100 Hz. As threshold increased, predictions of connectivity became more precise but less sensitive, capturing a smaller fraction of total connections. This tradeoff became particularly visible after isolating synaptic pairs that fired in succession: where presynaptic recruited postsynaptic partner to threshold at least one time (recruiting connections). Applying a top 1%-level threshold informed by Poisson null comparisons, the bulk of chance-level timing relationships was excluded, prioritizing true positives and avoiding false positives.

Correlation is a simple alternative for computing functional relationships, and it has been shown to be informative about synaptic connectivity (Cossell et al. 2015). In fact, when the goal is to maximize the number of detected connections in a low-precision regime, correlation outperforms iterative Bayesian inference. For intermediate scenarios, correlation and iterative Bayesian inference perform comparably. However, when the goal is to identify true positives with minimal ambiguity, iterative Bayesian inference substantially outperforms correlation (in a high-precision regime) (Fig. 5A). Because precision comes at the cost of limited sensitivity, these approaches cannot replace anatomic methods for revealing entire connectomes. Instead, they have the potential to find small active subnetworks of synaptic connections. Inferred iterative Bayesian weights are highly informative of connection probability (Fig. 5B). We find a linear relationship between threshold and precision up to a saturation at perfect performance (r² = 0.98). This relationship between functional weights and the likelihood of a synaptic connection held true regardless of inference method (correlation alone, r² = 0.89).

Fig. 5.

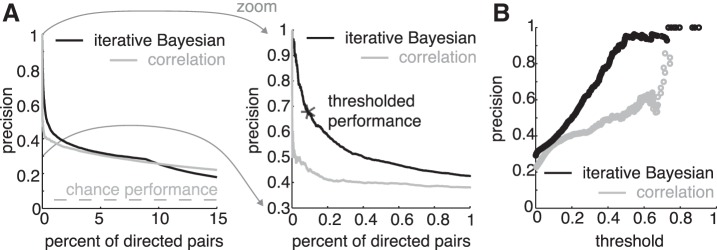
Relationship of inferred weighs to monosynaptic connectivity. A: left, sensitivity [true positive (TP)/TP + false negative (FN)] vs. precision [TP/TP + false positive (FP)] for two activity maps: iterative Bayesian inference (black) and correlation (gray). Right, iterative Bayesian inference substantially outperforms correlation in a narrow high-precision regime. *Thresholded performance. Chance performance reflects the likelihood of identifying a recruiting synapse from a directed pair selected at random. Recruiting connections are a smaller target than synaptic connections at large. B: threshold on functional weight vs. resulting precision, for iterative Bayesian inference (black) vs. correlation (gray). Functional weights reflect probability of connectedness.

Influence of external input on inference.

For evaluating inferred connectivity, we focused on recordings of sustained recurrent activity, after cessation of external Poisson input. To complement those findings, we also quantified performance for simulated activity during the input period, in the presence of ongoing external drive. For this comparison, 10-s samples of activity were recorded under conditions where 300 excitatory neurons were visible. In the absence of external drive, precision reached 62 ± 3.5% (mean ± SD), and sensitivity reached 0.47 ± 0.025%. During external drive under the same conditions, precision reached 60 ± 8.3%, and sensitivity reached 0.37 ± 0.065%. Between the two conditions, precision did not differ significantly (Wilcoxon rank-sum, P = 0.84, n = 5), but sensitivity was higher in the absence of external inputs (Wilcoxon rank-sum, P = 0.032, n = 5).

Diversity of activity between different input contexts.

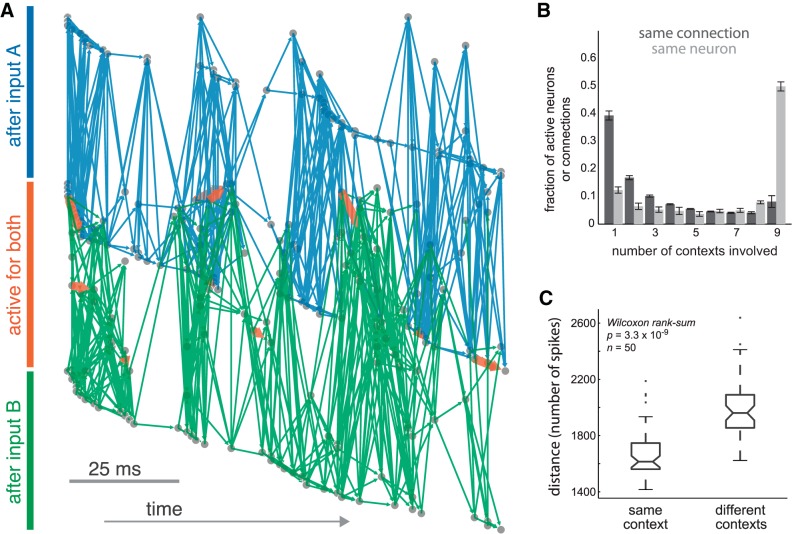
Primary sensory cortexes exhibit diverse multineuronal activity patterns (Sadovsky and MacLean 2013, 2014). Spatially diverse input projections were used to recapitulate these experimental findings. Distinct input projections activated overlapping populations of model neurons (Fig. 6A). However, common neurons were recruited by different presynaptic neighbors and recruited different postsynaptic neighbors in turn, consistent with experimental data (Sadovsky and MacLean 2014). Thus, pairwise relationships differed even where single neuron activity was similar. Single neurons were commonly active after many input contexts, but single recruiting connections were more often unique (Fig. 6B). Cross-validation confirmed that 5-s periods of activity differed substantially more between than within input contexts, in terms of active frames per neuron (Fig. 6C) (P = 3.25 × 10⁻⁹, n = 50, Wilcoxon rank-sum).

Fig. 6.

Activity flow in different input contexts. A: patterns of excitatory recruitment in single trials after input A (blue connections) and after input B (green connections). Rarely, pairwise recruitment recurred across both trials (orange connections). Hidden excitatory and inhibitory neurons are not shown. Rows indicate cell identity. Although pairwise recruitment was largely unique between trials, many single neurons were active in both trials (rows in middle, orange bar). B: single neurons are commonly active at least one time in every input context. In contrast, pairwise recruitment relationships tended to occur in just one or a few input contexts. C: cross-validation verifies that activity across different input contexts genuinely differs, quantified with L₁ distance (city-block distance) for activity vectors within the same input context vs. between different input contexts.

Distinct patterns of recruitment detected after different inputs.

On the pairwise level, recruitment patterns varied from one input pattern to another (Fig. 7A). As a consequence, with increasing numbers of distinct input projections and recording time, increasing numbers of recruitment relationships manifested (Fig. 7B). After a single input context, 8.0 ± 0.21% of connections were involved in recruitment. Across all input contexts, the number of recruiting connections climbed to 24%. Diverse activity exposed additional patterns of activity flow.

Fig. 7.

Mapping diverse activity. A: presynaptic recruitment frequency for a reference postsynaptic neuron after distinct inputs. Within a single context, the majority of presynaptic neurons never recruit the postsynaptic reference. Edge weight proportional to frequency of recruitment. B: input diversity and recording time increases the fraction of presynaptic neurons involved in postsynaptic recruitment. C: a single comparison in the second cross-validation procedure: overlap in detected synapses within shared input contexts (top, middle) and between different input contexts (bottom). Green lines indicate true positives. D: pooling over comparisons, cross-validation verified that different-context overlap in true positives is small, whereas same-context overlap is large. By identifying regularities in recruitment, iterative Bayesian activity maps were linked to the structure of their inputs. ⁺Outlier. E: simulated data were subsampled to establish the role of diversity, for inference while controlling for sample duration. In each case the data analyzed totaled 10 s of recording time. The no. of contexts was the divisor. For inference in the recording period, after inputs were silenced, precision (TP/TP + FP) increases with increasing numbers of diverse inputs.

To verify that distinct inputs gave rise to different patterns of detection, we performed a second cross-validation procedure. Spiking activity was initiated from two distinct populations of input units, input context A and input context B. For each context, simulated activity was divided into two halves, each of which was analyzed separately using iterative Bayesian inference, yielding four functional topologies. Identities of detected synapses were compared within and across contexts (Fig. 7C). Despite variability between individual inference trials, similar detections recurred within same-context activity. Functional relationships were shared between dissimilar contexts less often. Detected synapses were significantly more similar for activity generated from a common input context than for activity between input contexts (P = 5.1 × 10⁻⁵, n = 30, Wilcoxon rank-sum; Fig. 7D). During the period of sustained activity after cessation of inputs, population activity differed depending on input history. These differentiated patterns of spiking gave rise to distinct functional relationships.

To control for the effect of sample duration on inference, we fixed the total amount of time considered by the algorithm to 10 s of activity regardless of the number of different contexts (Fig. 7E). When only one context was analyzed the single context was chosen randomly for each repetition. As we increased the number of contexts considered by the algorithm, while always keeping 10 s of data fixed, we randomly choose the input contexts to be analyzed. After controlling the amount of data analyzed by the algorithm (10 s), inference of underlying connections was substantially better when diverse activity patterns were analyzed. In practice this meant, for example, that 2.5 s of data from four contexts (2.5 s × 4 contexts) were more effective than 10 s of data from one context for the inference of connections.

Enhanced performance at the time course of excitatory synapses.

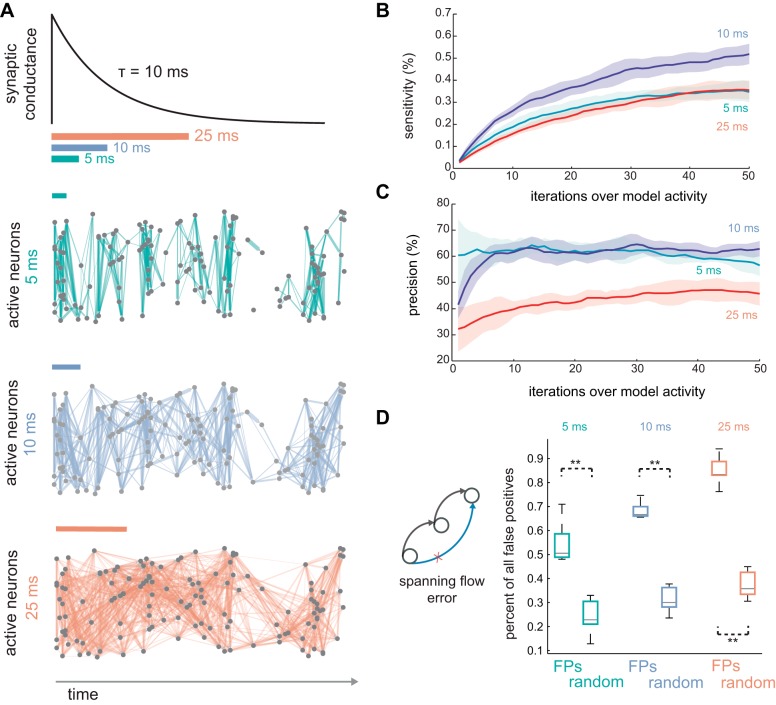
Generally, faster frame rates can be obtained at the cost of smaller population sample sizes. This provides flexibility to select temporal resolution best suited to the detection of causal connections. We considered three potential recruitment windows: 25, 10, and 5 ms (Fig. 8A). With the use of HOPS scanning ex vivo with single-frame recruitment windows, these frame durations correspond to ∼300, 75, and 30 neurons scanned, respectively (Sadovsky et al. 2011). To investigate how choice of single-frame lag window impacts inference without the confound of changing sample size, we obscured 60% of the 1,000 excitatory model cells in each trial. We found that both sensitivity and precision were maximal when a 10-ms recruitment window was used in the inference algorithm. At 10 ms, precision was 63 ± 5.6% (median ± interquartile range), and sensitivity to recruiting synapses was 1.9 ± 0.20%, which was significantly better than 5 ms (precision 57 ± 1.6%: P = 0.011; sensitivity 1.6 ± 0.24%: P = 0.026; Wilcoxon rank-sum, n = 7) and 25 ms (precision 45 ± 0.19%: P = 5.8 × 10⁻⁴; sensitivity 1.1 ± 0.20%: P = 0.0023; Wilcoxon rank-sum, n = 7). Although 25 ms resolution still permitted recovery of monosynaptic connectivity well above chance levels, performance at 5 ms was significantly better than for 25-ms lags (precision: P = 5.8 × 10⁻⁴; sensitivity: P = 0.0041; n = 7, Wilcoxon rank-sum).

Fig. 8.

Detection depends on definition of recruitment window. A: excitatory conductances in the model compared with three definitions of recruitment window. Synaptic interactions appear sparse for short interaction windows and dense for large lag windows. B: sensitivity improved fastest and most extensively when synaptic interactions were mapped with 10-ms recruitment windows (5 ms, blue; 10 ms, purple; 25 ms, red). C: precision improved fastest for 5-ms recruitment windows, whereas the 10-ms windowing resulted in slower increases and a modestly higher plateau (5 ms, blue; 10 ms, purple; 25 ms, red). D: conditioned on false positive detection, the probability of spanning a chain of strong synapses became increasingly likely as recruitment window increased. Spanning errors accounted for the majority of false positives for all recruitment window definitions. **P < 0.001.

For all three sampling rates, best performance was obtained by repeatedly presenting the 100 s of simulated recordings to the inference algorithm. In all cases, sensitivity improved gradually, steadily encompassing increasing numbers of monosynaptic connections (Fig. 8B). Reiteration led to particularly extensive improvement in precision at the slowest frame rates, with 25-ms lag window analyses improving an additional five percentage points in precision after 5- and 10-ms lag window inferences had stabilized (Fig. 8C). In contrast, those faster frame rates stabilized early in precision after 10–20 iterations, with modest subsequent decline for 5-ms lag windows in conjunction with more extensive sensitivity.

Error sources and interaction with choice of recruitment window.

Next, we characterized likely sources of error and their interaction with temporal resolution. For each connectivity pattern, random pairs of model neurons were used to establish chance occurrences, independent of errors in predicting synaptic connectivity. If candidate motifs occurred more frequently at sites of false positives than between random pairs, they were associated with errors in inference.

Shared input between two neurons can induce spurious correlations that appear to indicate causal connectivity when none is present (Gerstein et al. 1978; Keshri et al. 2013). Surprisingly, when synaptic connections were falsely inferred, we did not find elevated numbers of shared hidden inputs. At least under these conditions using iterative Bayesian inference, common hidden inputs did not make significant contribution to false positive detection errors, even at slow frame rates (5 ms: P = 0.976, n = 567; 10 ms: P = 0.989, n = 653; 25 ms: P = 0.776, n = 910; FPs vs. random, 2-way Kolmogorov-Smirnov).

An issue of concern is whether slow frame rates lead to errors resolving connection direction. We evaluated whether the direction of a true synaptic connection was frequently opposite that of an inferred synaptic connection. At baseline, randomly selected directed pairs were connected 20% of the time (as can be predicted from their underlying connection probability). The probability of directionality errors was no different from that of finding a connection between two randomly selected neurons. At the slowest frame rates, we did observe a possible weak association between direction errors and sampling rate (5 ms: P = 0.883, n = 7 trials; 10 ms: P = 0.129, n = 7; 25 ms: P = 0.129, n = 7; FPs vs. random, 2-way Kolmogorov-Smirnov). Nevertheless, these results suggest that slow sampling need not confound measurement of flow direction.

The majority of errors falsely attributed monosynaptic connectivity where there was actually strong polysynaptic connectivity (5 ms: P = 5.8 × 10⁻⁴, n = 7, Wilcoxon rank-sum; 10 ms: P = 5.8 × 10⁻⁴, n = 7, Wilcoxon rank-sum; 25 ms: P = 5.8 × 10⁻⁴, n = 7, Wilcoxon rank-sum; Fig. 8D). As sampling rate decreased, an increasing fraction of errors arose from functional relationships spanning polysynaptic chains. Note that random cells were more likely to be connected in chains at slower frame rates simply because longer recruitment windows (temporal scale) defined more presynaptic cells as participating in recruitment, increasing the density of inferred networks.

Strong synapses are prominent in functional relationships.

Synaptic weights were drawn from a lognormal distribution, matching experimental findings (Perin et al. 2011; Song et al. 2005). Strong connections from the long tail of the weight distribution occurred only infrequently. Thus, at chance level they would be expected to participate in functional relationships only rarely.

In actuality, the effects of strong synapses were particularly detectable from patterned network activity. The distribution of detected synapses was shifted toward higher connection strength values compared with the underlying distribution used to assign synaptic conductances (Fig. 9A). The probability of identifying a recruiting connection was positively correlated with connection strength (r = 0.68, P = 0.0001; Pearson correlation). Furthermore, as stronger subpopulations of structural connections were isolated, precision relative to chance rose dramatically (Fig. 9B).

Fig. 9.

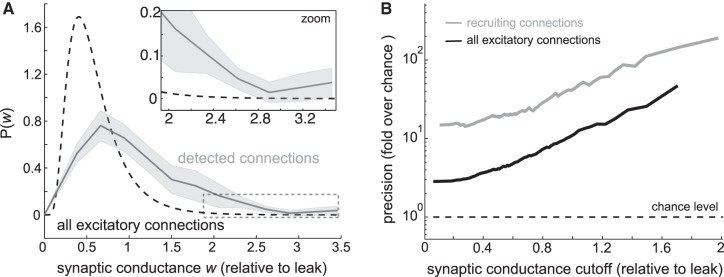
Strong connections are prominent in recruitment. A: distribution of underlying excitatory synaptic conductances compared with synaptic conductances of detected connections. B: precision of inferred connections increases with synaptic strength. Defining chance performance based on all excitatory synaptic connections (black). Defining chance performance more realistically, based on the subset of excitatory connections involved in recruitment (gray).

DISCUSSION

The relationship between connectivity and patterned sequential firing is complex. An average synaptic connection causes only small postsynaptic depolarization, particularly when membrane conductance is high during synaptic bombardments (Teramae et al. 2012; Chicharro and Panzeri 2014; Kumar et al. 2008; Destexhe et al. 2003; Troyer and Miller 1997). As a result, it is difficult to predict sequential firing from synaptic weights alone. To circumvent this complexity, it is necessary to map synaptic activity in emergent contexts generated by ongoing activity.

However, misleading coincidences in spike timing have the potential to confound inference of causal synaptic connectivity (Roxin et al. 2008). We used Poisson populations, lacking interconnectivity, to establish how frequently lagged firing, which would be interpreted by our inference approach to be indicative of a connection, appears by chance. We found that the null, which matched rate statistics, did not reproduce the same lagged firing relationships found in network activity. Connected populations gave rise to strong and reliable pairwise timing relationships where Poisson firing did not. By applying a threshold to inferred weights, we were able to exclude many spurious relationships.

The modified iterative Bayesian inference algorithm applied here results in sparse connectivity matrixes that relate synaptic connectivity to a small number of particularly precise timing relationships. These inferred connections map routes of activity through the synaptic network. By isolating only the most precise pairwise timing relationships, iterative Bayesian inference identifies a small number of synaptic connections with higher precision than can be achieved using correlation-based inference, a common alternative approach (e.g., Cossell et al. 2015). For applications requiring high sensitivity but only modest precision, correlation or other inference approaches may be more appropriate; but, for accurate inference of a synaptic connection with very few type I errors, iterative Bayes should be the algorithm of choice.

A constellation of methods for inferring connectivity from imaged activity is emerging, reflecting a growing consensus that bridging function and structure is a crucial long-term goal in neuroscience (e.g., Mishchenko et al. 2011; Stetter et al. 2012; Gerhard et al. 2013). This study complements related work by emphasizing performance under the conditions of realistic optical experiments (constrained recording durations and restricted sampling) (Sadovsky et al. 2011). We purposefully designed our simulations to pose substantial challenges to inference, including weak conductance-based synapses, random connectivity, occlusion of 60% of the neurons in the network, and limited recording times. We included these challenges to mimic experimental constraints.

For network simulations, input units made random connections on the recorded population. To mimic diverse inputs, their random projections were periodically redrawn. Thus, between different contexts, inputs were matched in average temporal structure but differed in their vectors of projection weights. The result was a diversity of model network spike patterns, echoing our experimental observations (Sadovsky and MacLean 2013, 2014). Differences in recruitment manifested even though inputs were completely silent during the recording period, when network activity evolved in isolation. These results demonstrate a simple way that recent history impacts network activity, with context-dependent recruitment situated to play an important role in neuronal computation (Buonomano and Maass 2009; Kumar et al. 2010).

Because each input context gave rise to new patterns of activity, detection of synaptic connections improved after diverse inputs. The importance of diverse activity suggests that mapping be carried out using statistical rich sensory stimuli such as natural movies. Spontaneous activity is also a good source of diverse activity, having been demonstrated to broadly traverse network activity patterns (Luczak et al. 2007; MacLean et al. 2005). Independent driving stimulations are likely to generate even higher sensitivity (Van Bussel et al. 2011), at the cost of potentially nonnaturalistic patterns of emergent activity in the cortical network. We found that inference was somewhat more sensitive during the recording period, when external inputs were silent, than in the presence of external Poisson spiking. This difference may arise from the addition of common hidden inputs.

Interaction times between neurons are not dominated by fast synaptic delays, so that millisecond resolution is not necessary for resolving monosynaptic connectivity. We found it better to use a 10-ms lag window than a 5-ms lag window, measuring functional relationships that closely mirrored the time course of excitatory synaptic conductances in our model. With the use of HOPS scanning (Sadovsky et al. 2011), a 10-ms frame duration corresponds to ∼75 neurons imaged. Note that equal or better precision could be obtained by considering lags spanning multiple 5-ms frames rather than a single 10-ms frame. However, in practice, the doubled scan rate would necessitate more than halving the imaged population size. At slower frame rates, reliable timing relationships were still predictive of monosynaptic connectivity. However, they also increasingly corresponded to misidentification of a single connection where in fact there was a chain of strong connections, a spanning error. Regardless of temporal resolution, polysynaptic spanning errors may help explain why random networks are harder to reconstruct than clustered architectures (Kobayashi and Kitano 2013). In clustered networks, strong chains are more likely to be crisscrossed with additional connections, resulting in neighbors-of-neighbors arrangements (Perin et al. 2010). These results suggest designing experiments with fast population scan rates if the aim is to infer causal monosynaptic connectivity from activity. This consideration must be balanced with the need to sufficiently sample the network numerically to see enough spiking relationships to detect statistical dependencies (Gururangan et al. 2014). The membrane time constant is also relevant to the interval within which integration can occur, and slow metabotropic conductances may extend integration time even farther in real cortical neurons.

Strong cortical connections are a desirable experimental target because of their proposed roles in information processing (Song et al. 2005; Litwin-Kumar et al. 2011; Teramae et al. 2012; Gururangan et al. 2014). However, they are rare in the population of all connections. Consistent with their importance, we have shown that in patterned spiking the strongest synapses are particularly salient and detectable: 10- to 100-fold more so than predicted by chance detection levels. These results suggest combining imaging and inference with paired-patch experiments to study the role of strong synapses in local circuit dynamics, enabling higher success rates in searching for strongly connected pairs.

Our findings highlight a feature of structure-function relationships that is discussed surprisingly little: in realistic activity, a synaptic connection need not imply the existence of sequential firing; that is, in a given recording, a synaptic connection may contribute to depolarizing its target without ever preceding a postsynaptic action potential. Similarly, a single connection may function as a route for propagating activity in one network context, but not in another (Fisher et al. 2013). These different functional roles have important consequences for activation of projection neurons. Relatedly, propagating activity establishes the connections that can be potentiated through Hebbian mechanisms because of proximal pre- and postsynaptic spiking. Yet, for arbitrary input and network history, the problem of predicting routes of propagation from the collective interaction of many synapses is exceedingly hard. Activity-mapping approaches sidestep this daunting problem by isolating connections underlying multineuronal firing, potentially linking specific synaptic connections to computation in the neocortex.

GRANTS

This work was supported by National Science Foundation CAREER Award No. 095286 and National Science Foundation Grant No. DGE-0903637 IGERT (Integrative research in motor control and movement).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: B.C. and J.N.M. conception and design of research; B.C. performed experiments; B.C. analyzed data; B.C. and J.N.M. interpreted results of experiments; B.C. and J.N.M. prepared figures; B.C. and J.N.M. drafted manuscript; B.C. and J.N.M. edited and revised manuscript; B.C. and J.N.M. approved final version of manuscript.