Dynamic Transmission of Protein Allostery without Structural Change: Spatial Pathways or Global Modes?

Abstract

We examine the contrast between mechanisms for allosteric signaling that involve structural change, and those that do not, from the perspective of allosteric pathways. In particular we treat in detail the case of fluctuation-allostery by which amplitude modulation of the thermal fluctuations of the elastic normal modes conveys the allosteric signal, and address the question of what an allosteric pathway means in this case. We find that a perturbation theory of thermal elastic solids and nonperturbative approach (by super-coarse-graining elasticity into internal bending modes) have opposite signatures in their structure of correlated pathways. We illustrate the effect from analysis of previous results from GlxR of Corynebacterium glutamicum, an example of the CRP/FNR transcription family of allosteric homodimers. We find that the visibility of both correlated pathways and disconnected sites of correlated motion in this protein suggests that mechanisms of local elastic stretch and bend are recruited for the purpose of creating and controlling allosteric cooperativity.

Introduction

Allostery is most broadly described as a mechanism by which ligand binding at one site on a protein affects the binding strength for an alternative molecule at a distant site and is a fundamental mechanism underpinning both normal and pathological molecular cellular processes (1,2). A positive allosteric ligand enhances the affinity for a molecule at the distant site, while a negative allosteric ligand will reduce the affinity. The two earliest models for protein allostery were couched in terms of a ligand-induced switch between distinct protein conformations with differing activities. The two-state Monod-Wyman-Changeux model (MWC, or symmetry model) described allostery as arising from the equilibrium between two conformational states. This equilibrium is altered by ligand binding and all subunits in a multisubunit protein change state together (3). The Koshland-Nemethy-Filmer model (sequential model) replaces the conformational symmetry of the MWC model with an application of induced-fit ligand binding with distinct protein conformations in the bound and unbound state and permits a description of negative allostery (4). Implicit in both the MWC and Koshland-Nemethy-Filmer models is the idea of protein structural change initiated by ligand binding. This led, for many years, to a view of allostery in which protein conformational change was the underlying mechanism and that ligand binding permitted the interconversion between stable ground state structures.

Less high-profile has been the development of, and discussion around, an alternative allosteric mechanism that does not require structural switching, but instead exploits the physical consequence of thermal fluctuations around the mean structure. In this mechanism, substrate binding modulates the amplitude of thermal fluctuations by altering the local effective elastic modulus of the protein. Such a restriction of random motion has thermodynamic consequences: it constitutes a change in entropy on ligand binding because, in general, the entropic contribution from a single harmonic mode of motion with modulus k_α is (see, for example, Huerta and Robertson (5))

$$S_{\alpha }=-\frac{k_{\text{B}}}{2}\text{ln}{k}_{\alpha }.$$ (1)

Furthermore, if at least one global mode so affected extends from the effector-binding site to the allosteric site, then its effective modulus can be altered by purely local (binding-event related) changes at either site. In this way, the full allosteric free energy may contain components that arise purely by this route. The powerful idea emerges that proteins have evolved to take functional advantage of not only the mean conformation, but also the inherent thermal fluctuations about this mean, in the generation of allosteric cooperativity. It was found that root-mean-square shifts of only 1% of the interatomic distance, when summed over an entire protein, could permit changes to the allosteric free energies of experimental order of magnitude purely through alterations in this entropy of fluctuations in internal conformations (6).

A feature of this mechanism of fluctuation allostery is that, to contribute to nonlocal allosteric interaction, the longer-wavelength slow-relaxation global modes of motion are recruited, rather than the higher-frequency and more local motions (such as side-group oscillation). This is because small-scale inhomogeneities in the elastic properties of a material (such as typically arise in globular proteins) tend to localize normal modes to within a few wavelengths, an example of a general phenomenon known in physics as Anderson localization (7–9). This is in distinction from homogenous media, which support extended normal modes of all wavelengths across their entire domains (the classic example is of sinusoidal standing waves on a taut string). The new length-scale of localization, which is a function of the spatial frequencies and amplitudes of the inhomogeneities and the wavelength of the normal mode, is termed its correlation-length ξ. Mathematically, ξ appears in an approximately exponential envelope-function of the normal mode localized at a general position r′, so that the amplitude from the mode at another position r is reduced by exp(−|r – r′|/ξ). Now allosteric signaling by modulation of thermal fluctuation requires, as a necessary condition, the presence of correlated motion at effector and allosteric sites, because it is by modulating the amplitude of thermal fluctuations at the second through a mechanical perturbation at the first, that the signal is transmitted. This condition combined with the localization condition then restricts the class of relevant supporting normal modes to those whose own correlation lengths are of the order of the spatial separation of the communicating sites, which are in turn typically of the same order of magnitude as the entire protein. Hence, by this logic, we arrive from the referenced results on localization that the global modes are primary carriers of the effect.

This essential action of large-scale correlated motions in fluctuation-allostery means that successful models of protein dynamics that capture the effect are therefore coarse-grained rather than necessarily atomically resolved. Indeed, because of the long correlation times of some of the global modes responsible, it is in general not possible to simulate their equilibrium fluctuations in realistic computation times using fully atomistic molecular dynamics. Specific models of particular protein systems at various degrees of coarse-graining have been constructed (10–13) that show the orders of magnitude of real allosteric free energies can be generated by such restriction of dynamical correlations alone. More recently, elastic network models (ENMs) that are more faithful to experimentally determined protein structures, have been able to capture thermodynamic effects in wild-type and mutant protein homodimers (14). Although ENMs take the apparently crude approximation that all C_α carbons within a fixed cutoff radius (of typically a nanometer) are effectively coupled by a universal spring constant, the models reproduce normal mode and local dynamical structures remarkably well (for an example, see Yang et al. (15)).

Insights from these models have been combined with theoretical statistical mechanics applied to perturbative and nonperturbative models of elastic media to show that the elastic inhomogeneities that localize the faster global modes are actually necessary for the transmission of fluctuation allostery (16). A perfectly uniform elastic medium has, surprisingly, no far-field allosteric effect from modulated fluctuations. This is true even though there are still globally extended normal modes. In this limiting case, however, the interference from the many extended modes tends to cancel positively and negatively cooperative contributions.

Some of the literature on this mechanism of allosteric interaction without structural change uses the term “population shift model” (17,18). The terminology here arises from viewing the fluctuation structure around the mean as equivalent to a population of closely neighboring states (in phase space) whose width is modified by both effector and ligand binding (19–22). The population of states momentarily occupied through thermal fluctuations around a mean state can be restricted or widened by increasing or decreasing the effective local elastic modulus, respectively. Modifications of the ENM approach include methods for systematic coarse-graining, enhancing the model with stronger main-chain C_α bonds than off-chain, and capturing of both aspects of population shift—in both mean and fluctuation of coordinates (23).

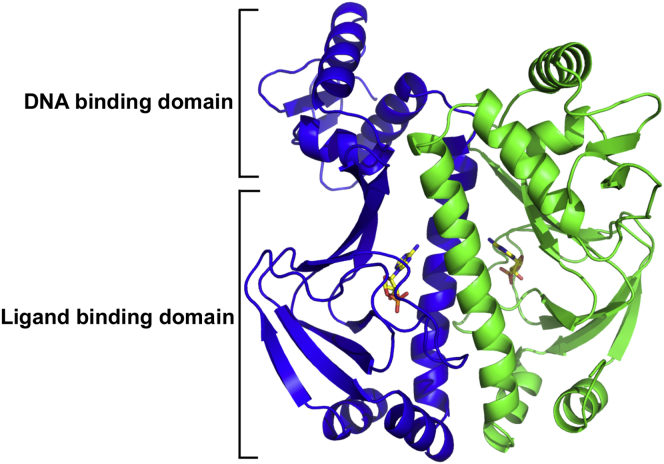
Theoretical considerations of fluctuation-based allostery without mean conformational change need naturally to be investigated and tested by experimental example, ideally through the testing of model predictions. The CRP/FNR family transcription factor CAP of Escherichia coli has been used by us, and by others, as a core exemplar (14,16,24). CAP is a 210-amino-acid homodimeric transcription factor that binds cAMP generated by adenylyl cyclase in response to the phosphorylated form of Enzyme IIA^Glc (phosphorylated in response to the phosphoenolpyruvate-carbohydrate phosphotransferase system) (25). The CAP-cAMP complex (see Fig. 1) regulates the transcription of >100 genes required for the metabolism of diverse carbon sources through its binding to a specific promoter region and recruitment of RNA polymerase (26).

Figure 1.

(Ribbon diagram) Crystal structure of CAP homodimer determined at 1.48 Å resolution (PDB: 4HZF) with the cAMP ligand bound (in ball-and-stick representation). To see this figure in color, go online.

An NMR- and thermodynamics-based analysis of the isolated cAMP-binding domains of CAP demonstrated entropically driven negative allostery between the cAMP-binding sites in the absence of any observable conformational change (24). A subsequent combined experimental analysis employing NMR techniques, and theoretical analysis of CAP using ENMs, demonstrated that negative allostery arises from modulation of the global low-frequency modes on cAMP binding (14,27,28).

The extensive literature on allostery that invokes conformational change has developed an extended discussion of the idea that effector and allosteric sites can be connected by allosteric pathways of local structural change. So, rather than the entire protein becoming implicated in a switch from one conformation to another, a restricted sequence of more local structural shifts, beginning at the effector site, creates a domino effect of sequential changes, eventually modifying the allosteric binding site. Some recent work has identified such allosteric pathways within the elastic normal modes, which we review briefly and selectively in the following.

Balabin et al. (29) identified allosteric signaling pathways via a hypothesis that combines the approaches of structural and fluctuation mechanisms. A normal mode analysis on coarse-grained models of the G-protein coupled receptors, bovine rhodopsin, and the human β² adrenergic receptor for which high-resolution crystal structures have been determined, identified candidate allosteric pairs of sites whose local structural distortions, from the activation of normal modes, were correlated. One dominant mode that conveys 50% of the allosteric signal was identified in these proteins. In this case, the allosteric pathway (in a very generalized sense) is essentially this dominant normal mode. More local treatments of activated or repressed dynamics have discussed physically connected pathways between allosteric sites (30–32).

In contrast, Gerek and Ozkan (33) performed a similar analysis by perturbation response scanning (34). This method takes an elastic network or atomistic model of a protein and imposes a perturbation of local structure at an arbitrary region. When the entire protein model has been equilibrated to the new minimum energy subject to the constraint of this perturbation, all regions with correlated elastic perturbations are identified. Because, at least in linear response, the pattern of response is controlled by the same nonlocal elastic interactions that correlate fluctuations, this method must be equivalent to the correlation method of Balabin et al. (29) via the fluctuation-dissipation theorem. Gerek and Ozkan (33) found that in two PDZ domain proteins, regions exhibiting elastic perturbations correlated with those around allosteric sites that formed spatially connected pathways through the globular structures, connecting in both cases to the effector sites. Furthermore, although the proteins were similar, the pathways connecting allosteric and effector sites differed markedly. The PDZ proteins are small and single-domain, in contrast with the multidomain membrane proteins studied by Balabin et al. (29).

In a third case, Ribeiro and Ortiz (35) found that such displacement correlation measures performed poorly in identifying residues critical for allosteric signaling in the enzyme imidazole glycerol phosphate synthase. The allosteric signaling pathways were better predicted by a network analysis of the strength of local covalent and noncovalent bonding. In this case, the propagation of the allosteric signal from the HisF glutaminase to the HisH cyclase domain proceeds by local structural rearrangement.

The mechanism of allostery arising from fluctuation-modification without mean structural change, as in the case of CAP, has no such structure of pathways, for at least two reasons. The first is that the coarse-grained structure of the protein that fluctuation effects draw upon, and which can be captured by such crude models as the ENM, appears initially not to have the resolution to capture the local structural rearrangements that are typically constitutive of allosteric pathways. However, the fluctuation-allosteric mechanism does not depend on such structural rearrangements. This distinguishes it from the alternative mechanism of allostery by conformational change. So any pathways that appear may do so at the large length scales, greater than the minimal C_α-C_α unit, which are captured by ENM models. The second reason is that we need, in any case, to redefine what the notion of an allosteric pathway would mean in the fluctuation case without structural change. The only candidate would be the appearance of spatially connected correlated patterns of motion that take the form of connected pathways. Such structures seem unlikely because, as discussed, the fluctuation-modification mechanism involves delocalized and long-range global modes of motion, rather than local modes that might connect. However, when applied to such inhomogeneous elastic objects as proteins, it is not obvious that pathways of communication do not arise in this case as well. The form of global modes in highly inhomogeneous elastic media can be very different from the isotropically extended forms of uniform sheets or solids.

Here we explore the relevance of allosteric pathways in the case of allostery in the absence of structural change. We first extend the model calculations of McLeish et al. (16) in both perturbative elastic field theory calculation and in nonperturbative coarse-grained models to establish general criteria for when and how such pathways of correlated fluctuation can arise through elastic inhomogeneities in protein structure. We then analyze our previous results on the CRP/FNR homodimer family as an example.

Materials and Methods

ENM simulations

These simulations were performed using our own code (27) based on the regular implementation (36). Only the Ca atoms in the protein were considered and joined together with a simple harmonic spring with spring constants set to a constant value of 1 kcal mol^–1 Å^–2 and with a cutoff radius of 8 Å. The presence of cAMP effector at the binding site was treated by the addition of one node at the mass weighted average coordinate for each ligand. The allosteric free energy was calculated by summing over modes 1 to n. The value n was determined by examining where values for the ratio of binding constants for the first and second cAMP-binding events, K₂/K₁, converged (14). The Protein Data Bank (PDB) file for constructing the GlxR ENM was PDB: 3R6S.

Theoretical statistical mechanics

These employed Gaussian field theory using a scalar field model of continuum elasticity and a perturbation analysis of the partition function and free energy (16) to second-order in three terms: 1) elastic perturbation at the allosteric site; 2) perturbation at the effector site; and 3) perturbation to the continuum elastic modulus. Highly coarse-grained model structures were treated with low-dimensional normal mode analysis with exact enumeration of the partition function.

Structure determination

Materials and Methods involved in extracting the structure and allosteric properties of mutant and wild-type GlxR CRP/FNR homodimer, to which we refer, can be found in the original publications (14,27,37).

Results

We obtained theoretical results for the connectivity and possible pathway structure of allosteric fluctuations by extension of previous calculations departing from two extreme limits (12). The first starting point is a minimal, uniform, model of local homogenous elasticity, penalizing positional deformation with a harmonic potential. The second starts from a highly nonuniform structure of stiff rods, where higher-order bending elasticity dominates.

Results from simplified models: perturbation approach in elastic fields

We begin with general theoretical considerations of when fluctuation pathways may arise. The existence of elastic inhomogeneity turns out to be essential for the existence of long-range fluctuation allostery. In previous work (16), we showed that there is a general relation in a simplified model of scalar elasticity between the allosteric free energy ΔΔG and the correlations of the gradient in elastic deformation (notated by the action of the spatial gradient operator on the scalar field: ${\nabla }_x\phi \left(x\right)$ at the effector (x₁) and allosteric (x₂) sites (16)):

$$\text{Δ}\text{Δ}G=-\frac{\beta }{4}{\tilde{\kappa }}^2\left[{\langle {\left({\nabla }_x\phi \left(x_1\right)\right)}^2{\left({\nabla }_x\phi \left(x_2\right)\right)}^2\rangle }_0-{\langle {\left({\nabla }_x\phi \left(x_1\right)\right)}^2\rangle }_0{\langle {\left({\nabla }_x\phi \left(x_2\right)\right)}^2\rangle }_0\right]$$ (2)

(this equation is reproduced from McLeish et al. (16)). The allosteric free energy is defined as the difference in the two binding free energies ΔG of one ligand in the cases where the other ligand is bound and not bound (hence the two deltas in ΔΔG). In the calculation of Eq. 2, the form of the perturbation to the local elasticity on substrate binding at either site x_i, within a general elastic medium, is assumed to be $\tilde{\kappa }\delta \left(x-x_i\right)$. The coefficient of this δ-function becomes a coefficient of Eq. 2. The field φ(x) describes in a simplified way the local displacement of the structure at site x (in a full model there would be three component fields of vector displacement, but the vectorial version retains the structure of the scalar theory described here). The angular brackets indicate averaging over the equilibrium ensemble, and β = 1/k_BT. Equation 2 just expresses the physical statement made in the Introduction above, that in order for the local modifications of thermal fluctuations to convey allosteric signaling (ΔΔG), equilibrium correlations must exist in the fluctuations between the communicating sites (the averages on the right-hand side of Eq. 2). This powerful result is independent of the form of elastic energy of any specific theory. So to complete the calculation of the allosteric free energy requires just a Hamiltonian for the energy of the field φ(x). Taking the linear-response case of Gaussian energy penalty for the fluctuating elastic energy,

$$\mathsf{H}=\frac{1}{2}{\int \kappa \left(x\right)\left({\nabla }_x\phi \right)}^2\text{d}x,$$ (3)

with a uniform elastic medium of local modulus κ(x) = κ₀, the correlator in the square brackets of Eq. 2 is identically zero, unless the two positions are coincident (16).

To generate a long-range effect requires inhomogeneous elastic structure. This is a fundamental requirement. It clarifies two observations from previous theoretical work on allostery without structural change. First, it clarifies that the toy models such as scissor-molecules (16) and paired plates (10), which usefully showed how large fluctuation-induced allosteric free energies could in principle be induced in protein-sized objects at ambient temperatures, clearly invoke inhomogeneous elastic structure. The scissor-molecule, for example (see below in a generalized calculation), can be thought of as two stiff rods with very high internal elastic modulus connected by much weaker springs, or equivalently by connecting regions of much lower elastic modulus. Second, it suggests an explanation for the large elastic inhomogeneities observed in real proteins. In building ENM models of real proteins, the elastic springs are generated by the rule that every C_α atom is connected to every other within a cutoff range of about a nanometer. When this is done, it is evident that proteins possess very strongly inhomogeneous elastic structures; the density of springs is visibly highly nonuniform. An example is given in Fig. 1 of Rodgers et al. (27).

The next level of calculation, motivated by the observation that proteins have indeed evolved highly nonuniform elastic structures, and by the possible appearance of pathway-like structures even in the case of allostery via delocalized normal modes, is to examine the effect of nonuniform perturbations to the elastic background of an otherwise continuous elastic medium, irrespective of the local changes on effector binding. So, following McLeish et al. (16), we write again the elastic Hamiltonian of Eq. 3, but now with a spatially modulated background elasticity:

$$\kappa \left(x\right)={\kappa }_0+{\kappa }_1\left(x\right).$$ (4)

Now in the modified calculation of the allosteric free energy, the averages of Eq. 2 are taken perturbatively with respect to the inhomogeneous elastic field κ₁(x) so that, when the Boltzmann factor for the equilibrium distribution exp(−βH) is expanded, they generate the functional-integral forms for the averages in Eq. 2:

$${\langle \dots \rangle }_0=\int D\left[\phi \left(x\right)\right]\text{exp}\left(\frac{\beta }{2}\int {\kappa }_0\left(x\right){\left({\nabla }_x\phi \right)}^2\text{d}x\right)\mathrm{....}\left(1-\frac{\beta }{2}\int {\kappa }_1\left(x\right){\left({\nabla }_x\phi \right)}^2\text{d}x\right).$$ (5)

The first nonzero and nonlocal terms in the allosteric free energy now pick up sixth-order averages at lowest order in the elastic field, rather than the fourth-order averages, which gave the null result of McLeish et al. (16) in purely homogenous media. The calculation proceeds, as in McLeish et al. (16), via Fourier transforms using the transformed functions $\tilde{\kappa }\left(q\right)$ and $\tilde{\phi }\left(q\right)$ (the tilde generally indicates a Fourier transform), but now generating a nonlocal form for the perturbative term in Eq. 5. This is a straightforward consequence of the convolution theorem applied to the product of functions κ₁(x) and ∇_xφ(x):

$${\int {\kappa }_1\left(x\right)\left({\nabla }_x\phi \right)}^2{\text{d}}^{3}x=\frac{1}{{\left(2\pi \right)}^6}\iint {\tilde{\kappa }}_1\left(q_5\right)\left(q_5-p\right).p\tilde{\phi }\left(q_5-p\right)\tilde{\phi }\left(p\right)d^3{q}_5{d}^{3}p.$$ (6)

Likewise, the fourth-order correlator in Eq. 2 is also expressed in Fourier transform:

$${\left({\nabla }_x\phi \left(x_1\right)\right)}^2{\left({\nabla }_x\phi \left(x_2\right)\right)}^2=\frac{1}{{\left(2\pi \right)}^4}\int \int \int \int q_1{q}_2{q}_3{q}_4{e}^{i\left(q_1+q_2\right).x_1}{e}^{i\left(q_3+q_4\right).x_2}\tilde{\phi }\left(q_1\right)\tilde{\phi }\left(q_2\right)\tilde{\phi }\left(q_3\right)\tilde{\phi }\left(q_4\right)d{q}_{1}d{q}_{2}d{q}_{3}d{q}_4.$$ (7)

Finally, the nonzero and nonlocal terms in the expression for the allosteric free energy (2) are found by taking the Gaussian averages in Eq. 5 with (without loss of generality because other choices are symmetric among the indices) the identifications q₁ = q₅ −p; q₂ = p; q₃ = −q₄; q₃ = q₅ −p; q₄ = p; and q₁ = −q₂. The final result, after multiple use of the standard result for Gaussian integrals, for the lowest order term in the allosteric free energy is

$$\text{Δ}\text{Δ}G=-\frac{{\beta }^2}{4{\left(2\pi \right)}^7}{\tilde{\kappa }}^2\left[{\kappa }_1\left(x_1\right)+{\kappa }_1\left(x_2\right)\right].$$ (8)

We note straight away from Eq. 8 that the translational symmetry of the system is now broken—the result is not a function of (x₁−x₂), but picks up the local differences in elastic modulus around the two communicating sites. This is an expected result of introducing the spatially nonuniform modulus field κ₁(x). More significantly, the result of Eq. 8 is significant for the discussion of pathways: at this order the allostery does not require a continuous pathway of special elastic structure perturbed away from the uniform background. Instead, it responds to local perturbations at the allosteric and effector sites. The result shows that, as anticipated, it is possible for fluctuation allostery to arise without any structure of pathways at all, supporting previous detailed findings by Balabin and others.

However, the magnitude predicted by Eq. 8 is very small in perturbation, and it is advisable to approach the problem from the opposite direction of a starting point of highly anisotropic elasticity, already identified as effective in the highly simplified models of scissors (16), plates (10), and coils (12).

Results from simplified models: nonperturbative modification of bending energies

The elastic field theory of McLeish et al. (16), extended above to account for inhomogeneous elasticity, can generate a finite-ranged fluctuation allostery by the alternative route of including bending elasticity in the Hamiltonian (fourth order, rather than second order, in spatial gradient ∇_xφ(x)), as well as the simple displacement elasticity described in Eq. 3. Even in homogenous media, this now results in an allosteric interaction with finite (exponentially damped) range. This higher-order bending elasticity can emerge in further coarse-graining of, for example, an ENM model. It is also appropriate in the modeling of some secondary structural elements in globular proteins, such as α-helices. The pair of helices at the dimer interface of the CAP protein constitutes an example of such structures with a high density of C_α-C_α bonds, and which exhibit bending dynamics within global modes of protein motion (16). The presence of such linear and relatively stiff structures within proteins motivates highly simplified and very coarse-grained models of fluctuation allostery that begin with such highly inhomogeneous structures rather than perturbations in the case of uniform elasticity (16).

The simplest, and instructive, example is the two-rod model, in which mutual displacements and rotations of stiff rods, interacting via local harmonic potentials at their extremities and midpoint, is modified by binding events at the rod ends. In the simplest case, completely stiff rods generate a system with just two degrees of freedom (mutual displacement x, and mutual rotation θ) whose free energy can be calculated exactly. If the strength of the harmonic interactions at the extremities are modified upon binding from a stiffness λ₁ to δλ₁, then the allosteric free energy becomes a function of just two model parameters, δ and the ratio of the central harmonic spring strength to those at the extremities, λ₀ (this result is reproduced from McLeish et al. (16):

$$\text{Δ}\text{Δ}G=\frac{1}{2}{k}_{\text{B}}T\text{ln}\left(\frac{\left(2{\lambda }_0+4\delta \right)\left(2\delta {\lambda }_0+4\delta \right)}{{\left[4\delta +{\lambda }_0\left(1+\delta \right)\right]}^2}\right).$$ (9)

This nonperturbative model is instructive as a limiting case of an allosteric pathway, as was defined above in the case of fluctuation allostery without conformational change. The motion of all the segments of the rods are, by construction, both correlated and connected—these connected correlations constitute a pathway between the allosteric sites. In stark contrast to the case of displacement elasticity discussed above, which does not require spatially connected correlations to generate allostery, if bending elasticity is involved (in the case of the simple stiff-rod model, the bending elasticity is present but formally infinite), connected pathways of correlations are generated naturally. As a consequence, the extremities of the fluctuating rods, which in the model we assume to be the allosteric sites, are just one of a continuous family of possible pairs of allosteric sites, uniformly distributed along the length of the rods. This characteristic property of the fluctuation allostery of bending/rotational modes of embedded rods contrasts markedly with the disconnected topology of allosteric sites generated by inhomogeneous perturbations to the smooth background of displacement elasticity we found in the last section.

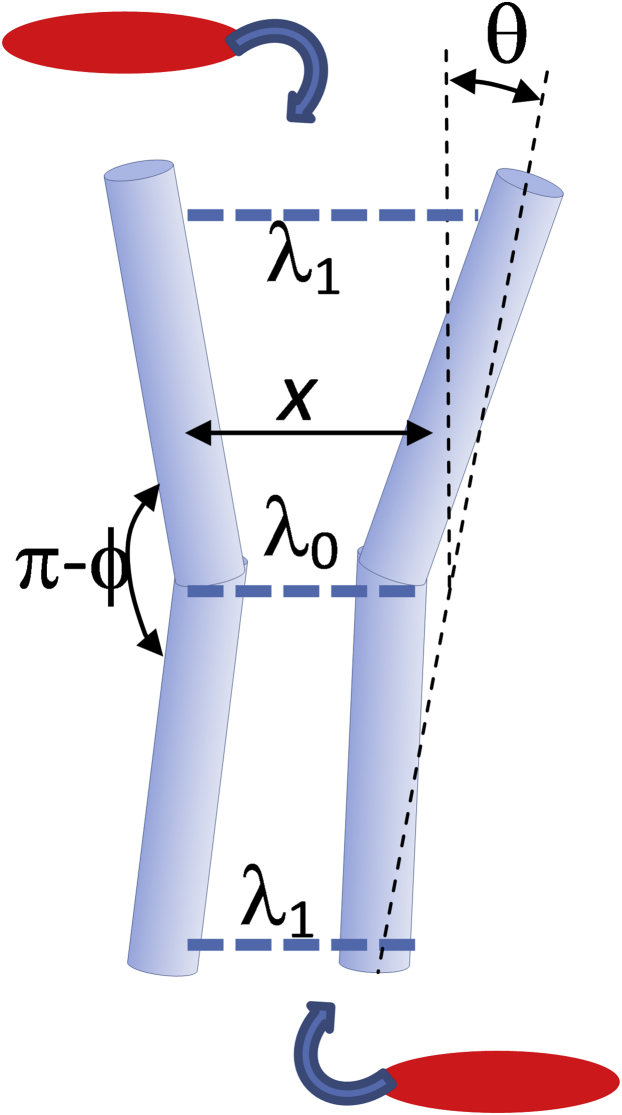
To explore this behavior of bend-dominated elastic deformation, in contrast to the case of simple, local displacement elasticity, we here generalize the two-rod model to permit finite bending of the two rods at their midpoint. To the coordinates x and θ we add a bending mode, with associated angular degree of freedom ϕ (see Fig. 2).

Figure 2.

The modified two-rod model of fluctuation allostery in which the degree of freedom of mutual displacement x, and rotation θ, of the rods is supplemented with a bending angle at their midpoint ϕ. Binding events by substrates at the extremities of the rod-pair is modeled by a modification to their interaction potential at those points. The spring constants λ_i are indicated for each location i. The binding of small molecules at the positions of springs λ₁ and λ₂ is modeled by modifying the local spring constants by a factor δ. To see this figure in color, go online.

By introducing a quadratic potential energy term for the internal, now finite, bend ϕ of the rods (μ/2) ϕ², we can analyze the effect on the allosteric free energy of decorrelating the fluctuations of the communicating sites. In the limit of μ→∞, we expect the result of Eq. 9 for stiff rods to be recovered. Writing the total potential energy Φ in terms of the coordinate system x and Hessian matrix (for the pairwise elastic interactions between residues) $\mathbb{K}$ as Φ = (x⋅$\mathbb{K}$ ⋅x) in the three cases of ${\mathbb{K}}_0$, ${\mathbb{K}}_1$, and ${\mathbb{K}}_2$ for the apo, holo-1, and holo-2 cases, respectively:

$$\begin{array}{c}\mathbf{x}=\left(\begin{array}{c}x\\ \theta \\ \phi \end{array}\right),\\ \mathbb{K}=\left(\begin{array}{ccc}{\lambda }_1+{\lambda }_0+{\lambda }_2& {\lambda }_2-{\lambda }_1& {\lambda }_2+{\lambda }_1\\ {\lambda }_2-{\lambda }_1& {\lambda }_2+{\lambda }_1& {\lambda }_2-{\lambda }_1\\ {\lambda }_2+{\lambda }_1& {\lambda }_2-{\lambda }_1& {\lambda }_2+{\lambda }_1+\mu \end{array}\right).\end{array}$$ (10)

We now use the general result for the allosteric free energy

$$\text{Δ}\text{Δ}G=\frac{1}{2}{k}_{\text{B}}T\text{ln}\frac{\left|{\mathbb{K}}_0\right|\left|{\mathbb{K}}_2\right|}{{\left|{\mathbb{K}}_1\right|}^2}$$ (11)

(where the vertical straight brackets signify determinants of the Hessian matrices) to find, finally, a closed form expression in terms of the model parameters, defining in dimensionless form λ ≡ λ₁/λ₀ = λ₂/λ₀ for the holo values of the spring constants at the effector and allosteric sites and δ,

$$\text{Δ}\text{Δ}G=\frac{1}{2}{k}_{\text{B}}T\text{ln}\left(\frac{\left[2\lambda \left(2\lambda +\mu \right)+4{\lambda }^2\mu \right]\left[\left(2\delta \lambda (2\delta \lambda +\mu \right)+4{\delta }^2{\lambda }^2\mu \right]}{{\left[4\left(1+\mu \right)\delta {\lambda }^2+\lambda \mu \left(1+\delta \right)\right]}^2}\right).$$ (12)

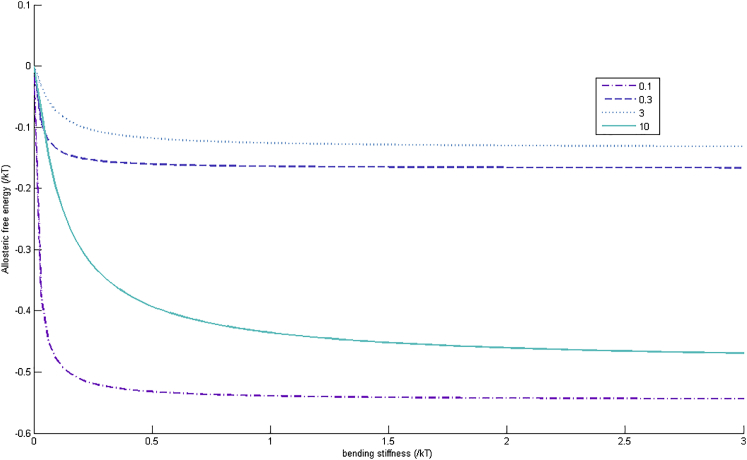
In the limit μ→∞, Eq. 12 just reduces, as it must, to the expression for completely stiff rods in Eq. 9. But for finite stiffness there is a considerably richer structure. In Fig. 3, we show the dependence on stiffness for four values of the local binding elasticity change (δ), covering the cases of softening and stiffening. We choose to fix the baseline ratio of the binding-site springs λ₁ and λ₂ to the internal spring λ₀ to 0.01, within the range of the model that gives significant allosteric free energies.

Figure 3.

Allosteric free energy ΔΔG from Eq. 12 in terms of the dimensionless bending constant, μ, of the two-rod model. The legend gives the values of the four different values of δ, the change of local stiffness on binding. The limiting values for simple stiff rods are recovered at high stiffness. To see this figure in color, go online.

The result, for this simplest case of allostery through fluctuations transmitted by bending elasticity, differs markedly from the case of local displacement elasticity. Now when the bending potential drops to zero, breaking the pathway of correlated motion between the sites, the allosteric cooperativity disappears. This is simple to check from the expression in Eq. 12. Interestingly, in the case of softening on binding (δ < 1 cases in Fig. 3), the limiting value for allosteric free energy is regained as the bending constant increases much faster than in the case of stiffening on binding.

The two cases of coarse-grained elasticity—local displacement and local bending—generate very different structures when employed to generate fluctuation allostery. In the first case, there is no requirement to connect the effector and allosteric sites with a continuous pathway of local elastic stiffness that differs from the surrounding medium. This may be the case, but the only necessary condition is that the elasticity is perturbed in the vicinity of the two sites. In the presence of bending structures, however, the situation is different, and the allosteric effect does require a connected pathway of correlated motion.

With these interpretive tools to hand, we can now turn to the case of the family of allosteric CRP/FNR homo-dimers (so named after the first two discovered members of the family) in which we have identified the controllable presence of allostery without conformational change.

An example: fluctuation correlation pathways in GlxR

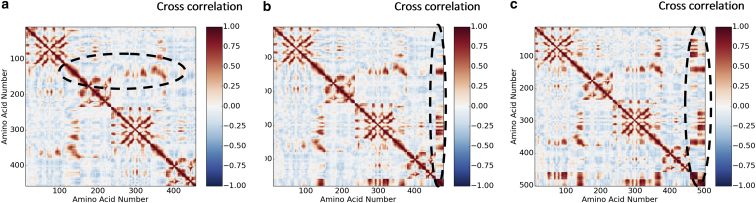
Insight into both the original allosteric cooperativity and the third-order allosteric control via fluctuation modification can be obtained by plotting correlation maps of motions in phase, or in anti-phase, in apo and holo forms of the protein, as calculated within the ENM model. This is done for the case of GlxR homodimer in Fig. 4, using the ΔΔPT Toolkit and methods as described in Rodgers et al. (27). We note the appearance of highly nonlocal correlations from specific residues. For example, the helix interface residues 125–140 (and corresponding residues in the other monomer) sustain correlated motions that extend far into the opposite monomer (in the diagrams this appears as strongly off-diagonal vertical and horizontal signals—indicated within a dashed ellipse in Fig. 4a). These deep pathways of correlations increase in strength with successive binding of the two cAMP molecules. They also become strongly correlated with the fluctuations of the cAMP nodes of the network (additional residues 460–500 in Fig. 4, b and c). Other correlations change their nature on cAMP binding—the anticorrelation between residues in the regions of 100 and 320 in the apo dimer becomes a correlation in the holo-2.

Figure 4.

Correlated motions in ENMs for apo-GlxR (a) (dashed ellipse indicates a region of intermonomer correlation; see text), holo1-GlxR (b), and holo2-GlxR (c). Both the x and y axes represent amino-acid numbers in CAP for the first (1–220) and the second (221–440) cAMP-binding monomer. (b and c) Residues beyond 440 correspond to the ENM representation of the cAMP molecule itself (dashed ellipses). The color chart represents the degree of correlation and anticorrelation in motion. To see this figure in color, go online.

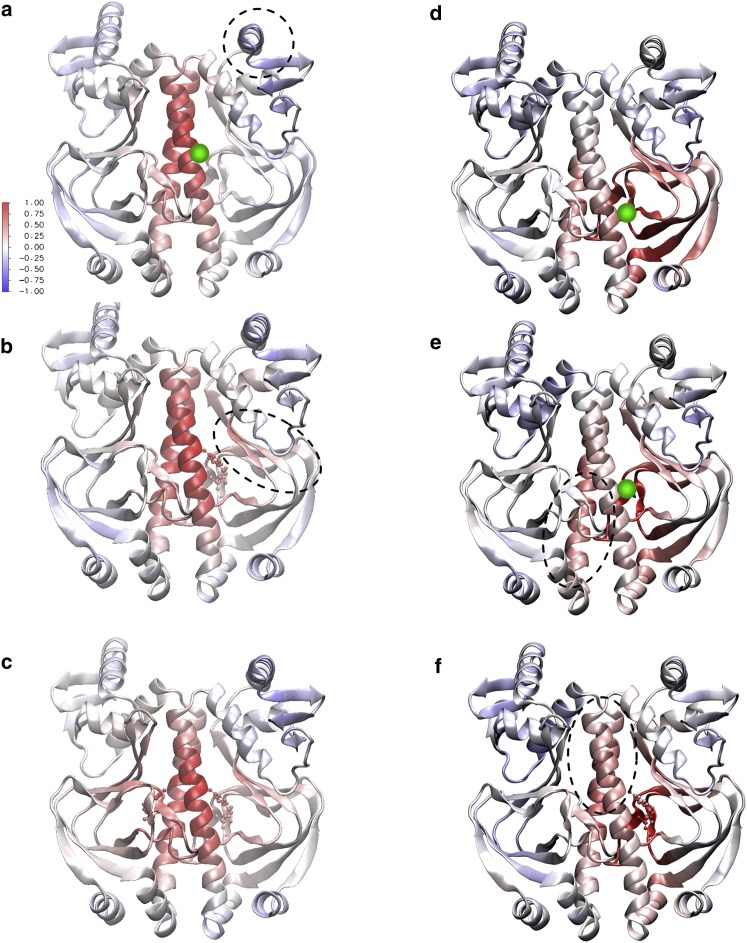
The pathways of correlation in Fig. 4 are necessarily spatially connected if they follow consecutive residues, but may also constitute physically connected pathways even if correlated regions are localized in residue number. To identify spatially continuous and discontinuous correlation patterns requires a real-space representation. To do this, however, we cannot retain all the information of the cross-correlation plots of Fig. 4, but must choose one residue at a time, whose fluctuation correlations can then be plotted spatially. In Fig. 5, a–c, the choice is made of 127 close to the interfacial helix (as this is strongly implicated in a highly nonlocal band of correlations identified in Fig. 4) in all three bound states, as well as 71 (Fig. 5d) and 82 (Fig. 5, e and f)—residues located more deeply within the elastically coherent non-DNA-binding block domain. These three base residues for correlation were also selected for their implication in distant correlated dynamics from the large calculation of Fig. 4.

Figure 5.

A real-space representation of the correlations in apo-GlxR from Fig. 4. (Red indicates correlated, blue is anticorrelated, and white is uncorrelated motion, with respect to the chosen reference residue.) For (a)–(f), the reference residue and bound state of the dimer is given: (a) 127 apo, (b) 127 holo-1, (c) 127 holo-2, (d) 71 apo, (e) 82 apo, and (f) 82 holo-1. The green circle shows the correlated residue in each case. To see this figure in color, go online.

Although the total allosteric interactions operate via a sum of delocalized normal modes, the real-space representation of the correlated fluctuations is instructive: we conclude in the case of correlations from 127 that the signal proceeds into the opposite monomer principally via a pathway of the type discussed above in terms of the twin-rod model. The effective rods are generated by the two central helices. Furthermore, their finite effective stiffness is reflected in the progressive loss of correlation along their lengths. We note that this qualitative pattern of correlations is identified independently of choice of correlated monomer within the helices. Other weaker correlations appear at more distant sites, for example within the helices of the DNA binding domains in the opposite monomer where an anticorrelated region is not connected to the 127 residue by any spatially connected pathway of correlations in the three cases (dashed circle in Fig. 5a). Finally, as first one, then two, cAMP molecules bind so new connected pathways appear, involving the binding sites themselves, and sites immediately adjacent to them, as they are occupied. β-strands containing next-nearest residues then also become correlated. So the two-strand β-sheet, adjacent to the binding sites and opposite the central helix domains, initially uncorrelated with the helices in the apo dimer, become positively correlated when the cAMP binds (dashed ellipse in Fig. 5b).

Fig. 5d shows the correlations with the motions of residue 71 across both monomers. The coherent blocklike elastic property of its domain is signaled by correlations throughout the domain, sustained especially by the β-sheet secondary structure (this is also clear from the strong correlations in Fig. 4 perpendicular to the main diagonal). The domain is contiguous with the interface helices, which are able to convey correlated motion continuously into the opposite monomer. This structure illustrates the continuous pathway case of relatively rigid units. However, residue 71 is mildly anticorrelated with the helices in both DNA-binding domains (dashed circle of Fig. 5d). These are not connected by bending elasticity to the domain of the residue, as the domain interface is a relatively weak hinge (corresponding to a low value of μ in the coarse-grained two-rod model). In this case there is no connected pathway of correlation between the two sites. The small anticorrelation is an example of the transmission by inhomogeneous displacement elasticity, which avoids the need of a connected correlation pathway.

Fig. 5, e and f, shows the correlations from residue 82, in the same domain as 71 but closer to the interfacial helix, in apo and holo-1 states. This example is instructive as it illustrates an example of pathway shift on binding. The apo form transmits correlations from residue 82 mostly away from the DNA binding regions (dashed ellipse in Fig. 5e), but the holo-1 form shifts the correlated pathway toward them (dashed ellipse in the upper region in Fig. 5f) especially in the helix of the opposite domain. Residue 82 is adjacent to the cAMP-binding site, and this pathway shift is clearly a major contributor to the anticooperative binding of the second cAMP. The mild anticorrelation of the DNA binding regions follows a very similar pattern to that evinced by residue 71.

The GlxR example is instructive as it contains both examples of the elastically transmitted fluctuation allostery discussed in the case of approximate models. Spatially connected pathways do exist, and others emerge on effector binding. But some potentially allosteric regions are spatially disconnected from each other, primarily when they are separated by weak domain interfaces. The method is sensitive to and discriminatory of the two cases. This is exemplified by the disconnected correlations between binding-site adjacent residues and the DNA binding regions (stretch) and the connected correlations along the helices (bend). So the method can identify the type of elasticity both from the connectivity of the correlations and from their sign. Disconnected (stretch-induced) regions may be negatively correlated, while bend-induced correlations are positive.

Discussion

We have explored the presence, meaning, and implication of allosteric pathways in the case of allostery without conformational change or fluctuation allostery. In this case, pathways may emerge from connected regions of correlated motion. The discussion has led us to identify two different types of coarse-grained elastic structures within proteins, both of them able to transmit allostery without conformational change, through modification of the correlations of thermal fluctuations. They correspond to the two different elastic deformations of stretch (or displacement elasticity) and bend. At the level of quadratic approximation for their energies, these local deformations create energetic potentials proportional to the second and fourth power of the gradient of local displacements, respectively.

Very coarse-grained calculations, perturbing from two base state elastic structures that are in the first case homogenous and in the second highly inhomogeneous, show that stretch and bend elasticity generate very different behaviors in terms of allosteric pathways. Stretch elasticity requires the introduction of elastic inhomogeneities at the effector and allosteric sites with respect to the rest of the protein. However, it does not require a connected spatial pathway of stiffer regions to convey the allosteric signal. In this case, the pathway can be thought of as a complex sum of normal modes of motion, delocalized spatially so that no preferred pathway emerges. In the case of bend elasticity, there does emerge a continuous spatial pathway of correlated fluctuations between the communicating sites.

We examined the GlxR homodimer within the ENM coarse-grained approach, using structures and models developed in our previous work, but now focusing on correlated fluctuations and the emergence of connected pathways of correlations. We found evidence that both types of fluctuation transmission arise, resulting in connected pathways and disconnected regions for correlations from three representative residues.

The correlation patterns and mechanisms give additional insight into the mechanism of binding cooperativity and its control. We found in earlier work (14) that both the strength and the sign of allosteric interaction between binding sites can be controlled by mutating the elastic strength locally at a number of third sites. These control sites tended to occupy isolated regions. Now we can see this to be symptomatic of the recruitment of stretch elastic energy, which does not need connected correlation pathways to generate allosteric effects. It also helps to clarify the disparate findings of work on the existence of allosteric pathways where there is no structural change. Further mutation experiments on the lines of Rodgers et al. (14) may deliberately modify bend- or stretch-rigidity locally, and test the general predictions made in this work.

The existence of more than one strategy to create allosteric signaling, even in the case of fluctuation allostery, has clear consequences for protein evolution. Very recently (38), we found significant bias within historical evolution of CRP/FNR homo-dimers in which double mutations tended to correlate to maintain the value of allosteric cooperativity. The relative occurrence of mutations that control stretch and bending elasticity is of relevance both to past evolution and to applications of engineered proteins.

Author Contributions

T.C.B.M. performed the mathematical calculations and cowrote the article; M.J.C. cowrote the article; and T.L.R. performed the numerical calculations.

Editor: Ivet Bahar.