Variable Ventilation as a Diagnostic Tool for the Injured Lung

Abstract

Mechanical ventilation of patients with acute respiratory distress syndrome (ARDS) is a necessary life support measure which may lead to ventilator induced lung injury, a complication that can be reduced or ameliorated by using appropriate tidal volumes and positive end-expiratory pressures. However, the optimal mechanical ventilation parameters are almost certainly different for each patient, and will vary with time as the injury status of the lung changes. In order to optimize mechanical ventilation in an individual ARDS patient, therefore, it is necessary to track the manner in which injury status is reflected in the mechanical properties of the lungs. Accordingly, we developed an algorithm for assessing the time-dependent manner in which different lung regions open (recruit) and close (derecruit) as a function of the pressure waveform that is applied to the airways during mechanical ventilation. We used this algorithm to test the notion that variable ventilation provides the dynamic perturbations in lung volume necessary to accurately identify recruitment/derecruitment dynamics in the injured lung. We performed this test on synthetic pressure and flow data generated with established numerical models of lung function corresponding to both healthy mice and mice with lung injury. The data were generated by subjecting the models to a variety of mechanical ventilation regimens including variable ventilation. Our results support the hypothesis that variable ventilation can be used as a diagnostic tool to identify the injury status of the lung in ARDS. I.

Introduction

The current standard of care for acute respiratory distress syndrome (ARDS) dictates use of the low tidal volume (V_t) of 6 ml/kg ideal body weight to reduce ventilator induced lung injury (VILI) caused by over-distention (volutrauma) [1] together with positive end-expiratory pressure (PEEP) to maintain airway patency [2, 3]. These guidelines are based on the aggregate characteristics of ARDS patients in general, which constitute a rather heterogeneous patient population [1] in which the best average strategy is very unlikely to be best in any particular case. It seems reasonable to suppose, therefore, that optimizing mechanical ventilation for individual patients should improve outcomes beyond the current universally applied low-V_t approach. However, personalized management of mechanical ventilation must conceptually involve the minimization of a cost function describing the injury that different ventilatory settings would cause. Any such injury prediction will inevitably depend on the current injury status of the lung [4], and thus must be based on diagnostic parameters that can be tracked continuously in time.

It is reasonable to believe that such diagnostic parameters must relate to lung mechanical function, since we have shown that acute lung injury is typically accompanied by substantial changes in lung derecruitability, reflected in the propensity of a recruited lung to derecruit over time [4–10]. Assessing the derecruitability of the lungs thus requires that lung volume be periodically perturbed in a manner sufficient to cause a significant degree of recruitment, so that the dynamics of subsequent derecruitment can be observed. We have previously achieved this in mouse models of lung injury by recruiting the lungs with a large inspiration and then tracking lung elastance while low-Vt ventilation is applied at various levels of PEEP [6, 7, 11, 12]. This provides a set of elastance time profiles to which we can fit a computational model that recapitulates the regionally distributed time-dependent nature of derecruitment [10]. Previous in vitro [13] and computational [14–16] studies suggest that our model fits can be used to infer the extent to which lung injury affects surface tension at the air-liquid interface. However, the ventilatory maneuvers we have employed in mice to determine derecruitability do not resemble any of the conventional regimens of mechanical ventilation employed for managing ARDS patients, and thus are very unlikely to be considered clinically acceptable methodologies by the medical community.

We therefore seek a means of perturbing lung volume in a manner that will be safe for ARDS patients while at the same time allowing the dynamics of recruitment and derecruitment (R/D) to be observed. These requirements are potentially met by variable ventilation (VV) [17], which attempts to recapitulate the breath-to-breath changes in V_t and breathing frequency seen during spontaneous breathing. VV has been shown to be protective in animal models of lung injury [18–20], and we have previously shown that this therapeutic efficacy may be related to the dynamics of R/D [21]. Here we investigate the use of VV in a different role, namely as a diagnostic modality that provides the volume perturbations necessary to identify lung derecruitability. In order to perform this investigation in a precisely controlled environment, we estimated derecruitability from synthetic airway pressure and flow data generated by subjecting our previously developed computational model of R/D dynamics [4, 8, 10, 22] to regimens of VV.

I. MATERIALS AND METHODS

A. Generation of synthetic data

We simulated pressure and flow at the airway opening during mechanical ventilation using a simulation model consisting of N_Units = 48,000 parallel elastic lung units. Each lung unit had an elastance E_Unit that was constant at low volumes but which increased quadratically with volume above a critical volume V_Crit thus:

$$E_{\mathit{\text{Unit}}}(V_{\mathit{\text{Unit}}})=N_{\mathit{\text{Units}}}\{\begin{array}{cc}\hfill E_{\mathit{\text{Base}}},\hfill & \hfill \mathit{\text{if}}{V}_{\mathit{\text{Unit}}}\le V_{\mathit{\text{Crit}}}/N_{\mathit{\text{Units}}}\hfill \\ \hfill E_{\mathit{\text{Base}}}+E_{\mathit{\text{Fac}}}{((V_{\mathit{\text{Crit}}}/N_{\mathit{\text{Units}}})/N_{\mathit{\text{Units}}})}^2,\hfill & \hfill \mathit{\text{if}}{V}_{\mathit{\text{Unit}}}>V_{\mathit{\text{Crit}}}/N_{\mathit{\text{Units}}}\hfill \end{array},$$ (1)

where E_Base, E_Fac (= 13E_Base), V_Unit are constants. The elastance E_mod of the entire model was a function of the number of open units N_open according to

$$E_{\mathit{\text{mod}}}(t)={\left[{\sum }_{i=1}^{N_{\mathit{\text{Units}}}}\right\{\begin{array}{cc}\hfill 0\hfill & \hfill \mathit{\text{closed unit}}\hfill \\ \hfill 1/E_{\mathit{\text{Unit}}}^i(V_{\mathit{\text{Unit}}}^i)\hfill & \hfill \mathit{\text{open unit}}\hfill \end{array}]}^{-1}$$ (2)

The airflow resistance of each unit was R_unit = N_UnitsR_aw, with R_aw = 0.47 cm H₂O·s·ml⁻¹ to match experimental observations [22]. The total resistance R_mod of the model was therefore

$$R_{\mathit{\text{mod}}}(t)=R_{\mathit{\text{Unit}}}{[N_{\mathit{\text{open}}}(t)]}^{-1}.$$ (3)

Flow into the model for each breath was driven by a volume waveform buffered by a gas elastance E_gas = 130 cm H₂O·ml⁻¹ [22], representing the ventilation delivered by the small animal ventilator we used in our previous studies [10]. Inspiration was sinusoidal, while expiration from the model was driven by the difference between the elastic recoil pressure within each open lung unit and the prescribed level of PEEP. The rate of expiration from each unit was governed by the ratio of this pressure difference to the sum of R_Unit and the resistance of the ventilator tubing R_eq = 0.4 cm H₂O·s·ml⁻¹.

The dynamics of R/D of each lung unit was simulated using virtual trajectories as we have described previously [4, 8–10, 22] which provide an empirical approximation to the pressure dependence and latency of these phenomena. Each lung unit was associated with a trajectory represented by a variable 0 ≤ y ≤ 1 that decreased in value at a rate given by dy/dt = S_C(P−P_C) if the airway pressure P was less than the critical closing pressure P_C; S_C is the closing velocity constant. Conversely, if P was greater than the critical opening pressure P_O then dy/dt = S_O (P−P_O). The opening velocity constant S_O = 10S_C, causing reopening to occur an order of magnitude more quickly than closure, as we have previously determined to be the case in injured mice [10]. The model equations were integrated using the forward Euler method at a simulation frequency of 150 Hz.

The dynamics of the model were thus governed by statistical distributions used to assign values of P_O, S_O, P_C and S_C to each lung unit. Closing and opening pressures have previously been reported to follow Gaussian distributions [23, 24], and we have used these distributions in previous model fitting studies [8, 10]. Accordingly, P_C in the present study was drawn from a Gaussian distribution having a mean μ specified to correspond to a particular clinical situation. The standard deviation of the Gaussian was 3 cm H2O in all cases. P_O was also drawn from a Gaussian distribution such that P_O = P_C + ΔP with ΔP = 4 cm H₂O in all cases. We have also found in previous model fitting studies [5, 10] that monotonically decreasing probability density functions (PDFs) are appropriate for S_O and S_C, so in the present study we selected these parameters from exponential PDFs.

We initialized the simulation model by ventilating it for 1 min with V_t = 0.25 ml at 200 breaths/min followed by two deep inspirations (DI, V_t = 1.0 ml, 0.8 Hz). This ventilation sequence was applied to provide a standardized volume history for the virtual trajectories for each iteration of the model, and the two large DIs were included to fully recruit the simulation model.

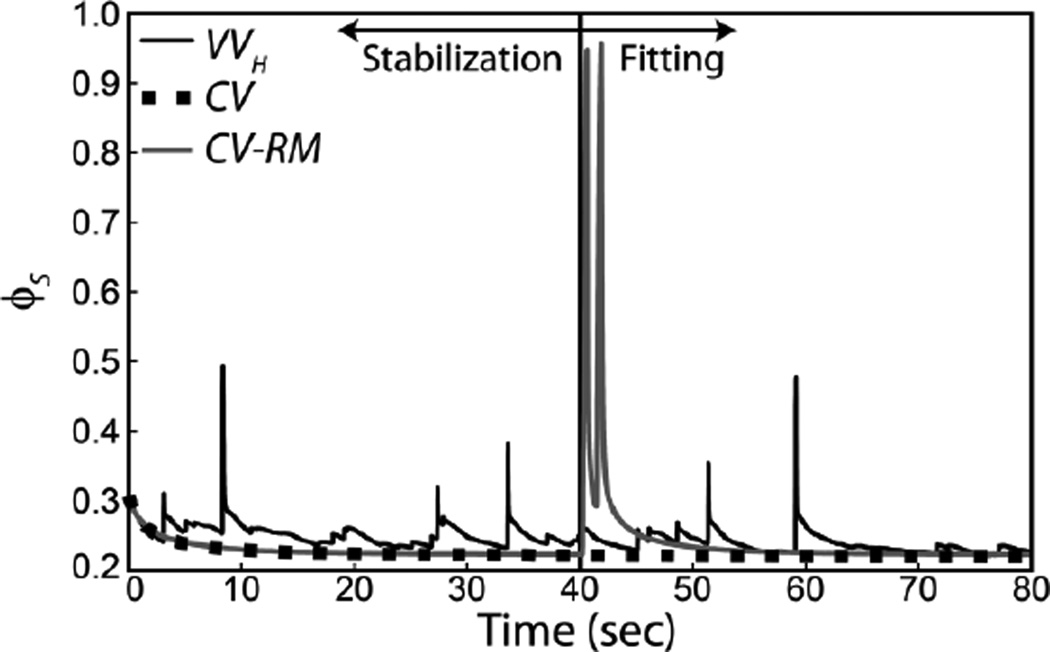
Eighty sec sequences of mechanical ventilation were then applied at a respiratory rate of 240 breaths/min (appropriate for a 20 g mouse) in the four patterns listed below. The first 40 sec were used to establish a standardized volume history, while the pressures and flows in the later 40 sec (the fitting period) were used to estimate derecruitability as described in §IIB.

VV_H: VV for healthy mice. The tidal volume of each breath was chosen using the probability density function defined by Thammanomai et al. [25, 26]

$$p(V_t)=\{\begin{array}{cc}\hfill g_0\hfill & \hfill \mathit{\text{for}}V{t}_{\mathit{\text{Min}}}\le V_t\le V_P\hfill \\ \hfill g_0{(V_t/V_P)}^{-\delta }\hfill & \hfill \mathit{\text{for}}{V}_P\le V_t\le V_{\mathit{\text{Max}}}\hfill \end{array}.$$ (4)

where Vt_Mean is mean tidal volume (8.0 ml/kg), Vt_Min is the minimum tidal volume (0.7 Vt_Mean), V_Max is maximum tidal volume (3.5 Vt_Mean), V_P = 0.9 Vt_Mean, the decay constant δ = 5.1, and PEEP = 3 cm H₂O. The normalization constant g₀ = 3.35 was chosen so that ${\int }_{\mathrm{V}{\mathrm{t}}_{\text{Min}}}^{{\mathrm{V}}_{\text{Max}}}\mathrm{p}({\mathrm{V}}_{\mathrm{t}})\mathrm{d}{\mathrm{V}}_{\mathrm{t}}=1$.

VV_I: VV for mice with HCl-induced lung injury. This was identical to VV_H except with V_Max = 2.25 Vt_Mean [25] and g₀ = 3.31.

CV: Constant volume ventilation with V_t = 8.0 ml/kg and PEEP = 3 cm H₂O.

CV-RM: Constant volume ventilation with V_t = 8.0 ml/kg and PEEP = 3 cm H₂O with two successive 50 ml/kg inspirations at 0.8 Hz applied at the onset of the fitting period.

We simulated pressure and flow at the airway opening during VV_H, VV_I, CV, and CV-RM in a healthy BALB/c mouse and a mouse with VILI [22] to enable calibration of the model to previously collected experimental data. The model parameters for these two conditions are listed in Table II. We have found previously that the progression of VILI is accompanied by changes in lung derecruitability that can be characterized in terms of two injury-dependent populations of lung units with markedly different R/D characteristics [22]. Accordingly, in the present study we separated the lung units in the VILI simulations into two groups, one containing 30% of the units that opened and closed relatively slowly with low critical opening and closing pressures, and the remaining 70% that opened and closed more rapidly at higher pressures (Table II). This gave bimodal PDFs for P_O and P_C for the injured mice as shown in Figure 3 (black line). These P_C PDFs are similar to the distributions of regional compliance at low inflation pressures in dogs with oleic acid injury reported by Kaczka et al [27], suggesting that acid injury increased P_C in a subset of lung units resulting in derecruitment and decreased compliance. Furthermore, at higher inflation pressures the compliance distributions were similar to those of healthy dogs. This indicates that recruitment in the injured lung occurred between 15 and 20 cm H₂O which is in agreement with the 18 cm H₂O upper peak of our bimodal P_C distribution.

Table II.

Parameter Values for Healthy and Injured Mice.

Variable	Healthy Mouse	VILI Mouse
EBase (cm H2O)	11.5	14
VCrit (ml)	0.6	0.55
RU Group 1 Membership	100%	30%
RU Group 1 µ (cm H2O)	0	3
RU Group 1 λC	4	4
RU Group 2 Membership	0%	70%
RU Group 2 µ (cm H2O)	N/A	18
RU Group 1 λC	N/A	0.5

Figure 3.

Probability density of the closing pressure for injured mice prescribed in the simulation model (black line) and computed using the estimation model. Gray area shows the mean ± standard deviation of 16 iterations of the estimation model.

B. Estimation of lung derecruitability

We estimated lung derecruitability and elastance from the simulated airway pressure and flow data generated by the simulation model using an estimation model that was similar in many ways to the simulation model but significantly simpler in structure so that its parameters could be determined uniquely by model fitting. The estimation model contained N_Units = 512 lung units. The PDF for P_C in the estimation model consisted of the superposition of four Gaussian distributions having means at 0, 6, 12, and 18 cm H₂O each with a standard deviation of 3 cm H₂O. The amplitudes of these four Gaussians were specified by a weighting vector α = [α₁, α₂, α₃, α₄]. Similarly, PDFs for S_C for each of these four Gaussian P_C distributions were chosen from exponential distributions of the form λ_ce^−λ_cz, where the value of λ_c for each distribution was specified in the four element vector λ.

To fit the estimation model to data generated by the simulation model, we had to determine n_param = 10 parameters that together minimized the objective function f = RMS(P_sim − P_est) when the estimation model was driven by the corresponding ventilation waveform. Here, P_sim and P_est are the airway pressures predicted by the simulation and estimation models, respectively, and RMS indicates the root mean square. The parameters are the four components of α, the four components of λ, E_Base and V_Crit (Table III). Model fitting was achieved iteratively using a constrained parallel pattern search (PPS) algorithm [28–32] that functions by repeatedly simulating pressure and flow data with the estimation model using sets of parameter values selected from within a specified bounded domain. The lower (l) and upper (u) bounds on this domain, listed in Table III, were selected to include parameters values that we have observed in our previous experimental studies in mice [4, 10, 22, 33]. To standardize the volume history of the estimation model prior to each run through the iterative fitting algorithm we first ventilated it for 40 sec using the prescribed ventilation pattern. A second 40 sec period of ventilation was then applied and these data were used to compute the value of the objective function.

Table III.

Initial Conditions.

Variable	Lower Bound (l)	Upper Bound (u)	Initial Step Size (Δ0)	Mean Starting Value $(x_0^{\mathit{\text{mean}}})$
EBase	8	18	1.5	15
VCrit	0.4	0.7	0.05	0.575
α [1–4]	0.0	1.0	0.125	[1.0,0.1,0.1,0.1]
λ [1–4]	0.025	2.5	1	0.8

The initial guess for the parameter values was $x_0=x_0^{\mathit{\text{mean}}}+{\mathrm{\Delta }}_{0}B$ where $x_0^{\mathit{\text{mean}}}$ is the average parameter starting value (Table III), B is a random number from a uniform distribution −1 ≤ B ≤ 1, and Δ₀ is the initial step size vector. This random variation was included to avoid bias in the solution due to the prescribed initial conditions which would be unknown in clinical or laboratory scenarios.

We defined a set of search directions 𝒟 = {d⁽¹⁾, …, d^(p_max)} where each d⁽ⁱ⁾ is a vector of length n_param and superscripts indicate the direction index. The maximum number of search directions $p_{\mathit{\text{max}}}=n_g^{n_{\mathit{\text{param}}}}=59049$, and n_g = 3 is the number of possible values for each variable in x. The search directions were defined as

$$\begin{array}{c}\hfill d^{(i)}(j)=\lfloor \frac{i}{n_g^j}\rfloor -n_g\lfloor \lfloor \frac{i}{n_g^j}\rfloor /n_g\rfloor -1\hfill \\ \hfill 0\le i<p_{\mathit{\text{max}}}\mathit{\text{and}}0\le j<n_{\mathit{\text{param}}}\hfill \end{array}.$$ (5)

Each iteration of the pattern search algorithm 0 ≤ k ≤ 30 consisted of three steps:

1. Generate a set of trial points which correspond to the search directions

   $${\mathbf{X}}_k^{(\mathit{i})}=\{x_k+{\mathrm{\Delta }}_k{d}^{(i)}:0\le i<p_{\mathit{\text{max}}}\}$$ (6)

   where Δ_k is the step size vector and x_k is the solution vector from the previous step. The four (out of n_param) elements for each ${\mathbf{X}}_{\mathbf{k}}^{(\mathit{i})}$ corresponding to the weighting vector α are scaled to a magnitude of 1 and duplicate trial points resulting from this transformation are removed. Likewise, any direction index which contains points outside the constrained domain $l\le {\mathbf{X}}_k^{(\mathit{i})}\le u$ is also eliminated. Finally, only a single value of λ_C is included for any entry of α = 0, where the remainder of the trial parameter values are identical. The remaining trial points in X_k are evaluated in a queue.

2. If a trial point z_k ∈ X_k exists so that f(z_k) < f(x_k) then the iteration is deemed successful, and we set x_k+1 = z_k, Δ_k+1 = Δ_k, and return to step 1 if k ≤ 30. Otherwise, the algorithm is terminated.

3. If a trial point z_k ∈ X_k does not exist so that f(z_k) < f(x_k) then the iteration is deemed unsuccessful and we set x_k+1 = x_k and Δ_k+1 = 0.5 Δ_k. If k ≤ 30 and Δ_k+1 > 0.025 Δ₀ the algorithm returns to step 1. Otherwise, the algorithm is terminated.

The pattern search algorithm is readily parallelized [28–31] because once X_k is calculated the objective function evaluation for each trial point is independent of the others. Accordingly, we implemented the above algorithm using the compute unified device architecture on a graphics processing unit (GPU) (Tesla K20, NVIDIA, Santa Clara CA) as suggested by Zhu [34, 35]. Each trial point was assigned to an independent thread on the GPU and dynamic parallelism was used to branch each trial point into 512 additional threads (1 per RU) which were then used to evaluate the dynamics of R/D. This novel approach provided a substantial performance improvement, particularly when polling smaller parameter spaces near the bounds of the search domain.

II. RESULTS

Figure 1 shows E_Unit as a function of total lung volume in the fully recruited lung for the healthy and injured simulation models (circles), as well as the corresponding E_Unit curves for selected cases provided by the estimation model (the latter are the averages of 16 estimations obtained using different random initial guesses for the parameter values of the estimation model). The gray areas in Figure 1 show the mean ± standard deviation, demonstrating the repeatability of these estimates. These results show that we are able to accurately estimate the volume dependence of E_Unit from the airway pressure and flow data recorded during various modes of mechanical ventilation in mice, including two different types of VV.

Figure 1.

Lung unit elastance prescribed in the simulation model (black circles) and determined with the estimation model using VV_H (a) and VV_I (b) for healthy and injured mice. Gray area shows mean ± standard deviation over 16 runs.

The PDF for P_C used for simulating data from a healthy mouse is shown in Figure 2 (gray circles), together with the PDF produced by the estimation model, again showing good agreement. The area of the black lines in Figure 2 represents the mean ± standard deviation. Corresponding plots for the injured mouse are shown in Figure 3, and demonstrate that the estimation model is able to recover the bimodal distribution we used in the simulation model to generate the airway pressure and flow data. Note that the position of the lower peak in the PDF for P_C (at 3 cm H₂O) does not align with positions of any of the four Gaussians comprising the composite P_C distribution used in the estimation model, demonstrating the capacity of the composite distribution to estimate the PDF for P_C.

Figure 2.

Probability density of P_C for healthy mice prescribed in the simulation model (gray circles) and the mean ± standard deviation of 16 iterations of the estimation model.

We quantified the accuracy of the elastance fit as

$${\epsilon }_E=\frac{E_{\mathit{\text{Base}}}^{\mathit{\text{Est}}}-E_{\mathit{\text{Base}}}^{\mathit{\text{Sim}}}}{E_{\mathit{\text{Base}}}^{\mathit{\text{Sim}}}}+\frac{V_{\mathit{\text{Crit}}}^{\mathit{\text{Est}}}-V_{\mathit{\text{Crit}}}^{\mathit{\text{Sim}}}}{V_{\mathit{\text{Crit}}}^{\mathit{\text{Sim}}}},$$ (7)

where superscript Sim and Est indicate the simulation and estimation models, respectively. Likewise, the accuracy of the P_C fit was described by

$${\epsilon }_P={\int }_{-50}^{50}|{\sum }_{i=1}^4{\alpha }_i{\kappa }_i(P_C)-K(P_C)|d{P}_C$$ (8)

where K is the P_C PDF in the simulation model and κ_i is the PDF for P_C for the i^th Gaussian distribution in the estimation model. Statistically significant differences in ε_E and ε_P, determined using a 1-way analysis of variance (p = 0.05) and Tukey’s honestly significant difference criterion, are indicated with symbols in Figure 4.

Figure 4.

Mean error between the simulation and estimation models for 16 estimation model runs, light gray bars show error in P_C and dark gray bars show errors in elastance. Lines shows the standard error. * indicates a significant difference from CV-RM and ‡ indicates a significant difference from CV (p=0.05). Dashed line shows the lowest possible value of ε_P for the injured mouse due to the composite P_C PDF.

The performance of the estimation algorithm was proportional to the degree to which the applied ventilation waveform perturbed the model system. Figure 5 shows that CV-RM spanned the widest range of open fractions and, as shown in Figure 4, provided the best parameter estimate. The dashed line in this figure shows the minimum possible value for ε_P due to the composite PDF used in the estimation model.

Figure 5.

Open fraction predicted by the simulation model for an injured mouse. The first 40 sec of the simulation is used to initialize the model and the second 40 sec is used to fit the estimation model.

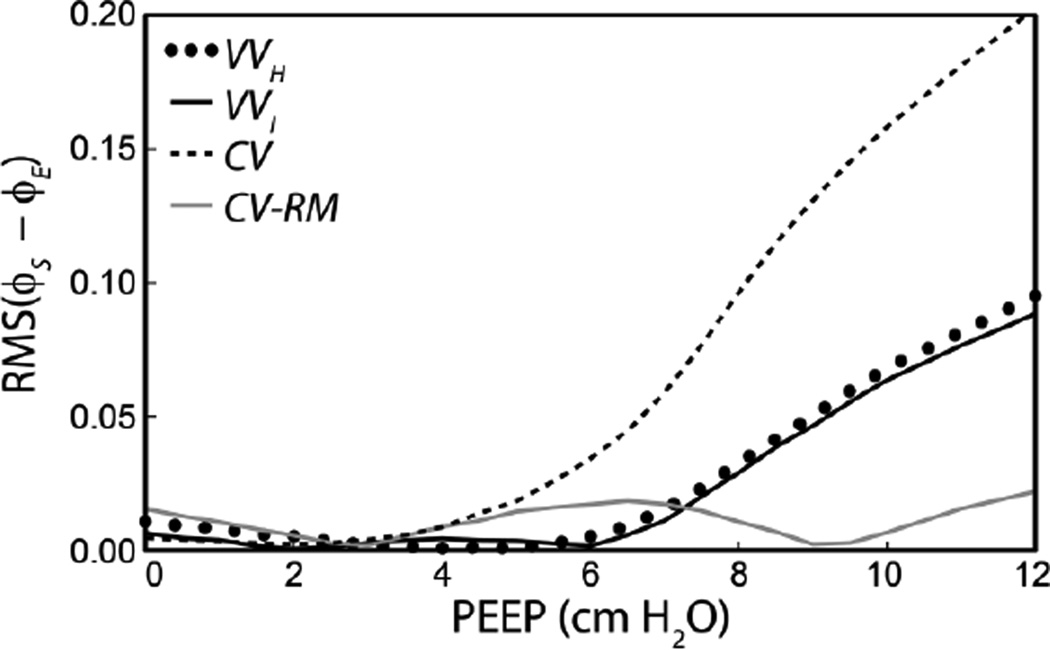
To evaluate the efficacy of the fitting method in recovering data which could be used to evaluate injury or optimize mechanical ventilation, we determined the open fraction φ during ‘derecruitability tests’ which we have previously demonstrated are a sensitive measure of lung injury [6–8, 10, 12, 22]. We utilized φ to test the performance of the estimation model because changes in the open fraction of the lung that occur as a result of R/D play a pivotal role in the genesis of VILI. The derecruitability tests consisted of a 1 min stabilization period (V_t = 0.25 ml, 200 breaths/min) followed by a recruitment maneuver (2 breaths of V_t = 0.25 ml, 50 breaths/min) as described above for the simulation model. The predicted open fraction was then monitored during 3 min of ventilation at 8 ml/kg and 240 breaths/min. This procedure was repeated for a range of PEEPs. The root mean square (RMS) difference in φ predicted using the average parameters determined with the estimation model (φ_E) and prescribed in the simulation model (φ_S) was used to quantify the model accuracy during the derecruitability tests. Figure 6 shows the average RMS(φ_S − φ_E) for 10 simulations of the VILI mice at ½ cm H₂O PEEP increments. Here we note that at low PEEPS all modes of ventilation resulted in excellent approximations to the parameters used in the simulation model. However, as PEEP increased, the accuracy of the φ predictions decreased.

Figure 6.

Average error in the open fraction during derecruitability tests at different PEEPs using parameters determined via the estimation algorithm and compared to the simulation model for injured mice.

III. DISCUSSION

The pulmonary edema that characterizes ARDS impairs surfactant function and causes increased derecruitment of small airways and alveoli. This, in turn, increases the susceptibility of the lung to VILI as a result of the excessive fluid-mechanical and tissue stresses that invariably accompany mechanical ventilation. The current standard of care in ARDS is a one-size-fits-all approach employing low V_t to reduce volutrauma, and is based on the reduction in mortality reported with 6 ml/kg compared to the nominal prior standard of 12 ml/kg [1]. However, the seminal clinical trial on which the low-V_t approach is based employed a large number of patients at multiple sites and at huge expense. Gaining new evidence to further refine the 6 ml/kg target is probably beyond the practical limits of randomized clinical trials because of the large number of patients that would be required to obtain statistical significance.

Currently, PEEP and the fraction of inspired oxygen (FiO₂) are both frequently prescribed based on blood oxygenation, and thus provide some degree of personalized management aimed at optimizing the efficacy of gas exchange. However, while decrements in oxygenation are readily measured in the clinic, they lag behind the lung derecruitment that is responsible for them, suggesting that better personalized control of VILI would be achieved by monitoring lung function. In addition, lung function measurements potentially reflect the repetitive R/D events and the tissue over-distension that constitute the fundamental injurious processes behind VILI. Accordingly, we hypothesize that further improvements in the ventilatory management of ARDS patients will demand a personalized approach that adapts to the changing lung mechanics of individual patients. This approach would use continuous monitoring of lung function to adjust the parameters of a predictive computational model which is then used to determine the least injurious mode of ventilation.

In a series of previous studies in mice, we have demonstrated that the dynamics of R/D are sensitive and specific indicators of lung injury, and that they can be used to follow the progression of VILI [6–8, 10, 12, 22]. Accordingly, we believe that the dynamic derecruitability of the lung constitutes the appropriate readout on which to base an adaptive and personalized strategy for mechanical ventilation of the ARDS lung. The question we address in the present study is how to determine derecruitability in a manner that could potentially be applied safely to a human patient with ARDS. In our prior mouse studies, we estimated derecruitability from the transient responses in lung elastance observed during episodes of mechanical ventilation at different levels of PEEP, each episode being preceded by a large inflation to recruit closed lung units [6, 7, 10–12]. These maneuvers provided the volume perturbations necessary for identifying the lung’s propensity to derecruit, but they would almost certainly be unacceptable in the clinical arena; very large inflations may themselves cause VILI, and ventilation for even a few minutes at a low level of PEEP may be highly inadvisable for severely injured lungs because it would promote atelectrauma.

Our goal in the present study was therefore to determine if VV imposes a set of volume perturbations that is rich enough to allow accurate identification of the dynamic R/D characteristics of the lung. Actually, the extent to which this can be done is a matter of degree; even conventional mechanical ventilation perturbs lung volume, and so should itself be able to reveal R/D dynamics to some extent. The problem with conventional ventilation, however, is that its perturbations are completely regular and rather modest, and thus can only reveal the derecruitability characteristics of the lung over a limited range of operating conditions. By contrast, the explicit goal of VV is to impose a varied volume perturbation to the lung [17], so we reasoned that it would be much better suited to the identification of lung derecruitability. Also, VV has shown potential as a therapy for ARDS [36] in both animals [20, 37, 38] and humans [36, 39] due to increased surfactant secretion [19, 26] and recruitment [21, 26, 40, 41].

In the present study, we used simulated airway pressure and flow data to test the use of various ventilation patterns in the assessment of lung derecruitability. The data were generated by an established computational model of R/D dynamics [4, 8, 10, 22], which allowed us to make objective comparisons of the performances of the various ventilation patterns since the true R/D characteristics represented by the data were known precisely. Our results show that the ability to determine derecruitability accurately is closely linked to the range over which volume is perturbed. Thus, for example, CV-RM gave the best estimates of the true parameter values (Figures 2, 3, and 4), no doubt because of the very large degree of derecruitment that was induced by the initial deep inspirations in this scenario (Figure 5). By contrast, the very limited amount of recruitment produced by CV resulted in the least accurate parameter estimates. These differences occurred because the peak pressures did not exceed approximately 10 cm H₂O with CV, so the open fraction varied, on average, by less than 1% as shown in Figure 5. Consequently, changes in α and λ did not substantially impact the objective function. On the other hand, with CV-RM the airway pressures reached almost 30 cm H₂O causing φ to span from an average of 0.22 to 0.96. Therefore, even minor changes in R/D properties are reflected in the objective function obtained with CV-RM.

The two VV ventilation patterns were intermediate in performance between these two extremes, as shown in Figure 4. The predicted open fraction for VV_H in the injured mouse is shown in Figure 5, demonstrating that a sufficient period of low-V_t ventilation must follow a deep breath for derecruitment to occur and provide information for the parameter fitting. The timing between these recruitment events is implicit in the definition of the VV tidal volume PDF (Eq. 4). Interestingly, all four ventilation patterns provided good estimates of the nonlinear elastance for the injured mouse simulations. This was likely due to the fact that all the ventilation patterns perturbed lung volume enough to cause V_Unit to exceed V_Crit in those lung units that remained open. In contrast, V_Unit did not exceed V_Crit during CV and VV_I in the healthy mouse simulations due to the greater degree of recruitment.

The accuracy of the estimation model was further assessed by simulating derecruitability tests in injured mice over a range of PEEP using the best-fit parameters. At low PEEP, there were only minor differences in φ between the estimation and simulation models (Figure 6), as expected due to the good agreement in the P_C distributions (Figure 3). However, with increasing PEEP, the estimated φ diverged progressively from that of the simulation model for all ventilation modes except CV-RM (Figure 6). This deviation at high PEEP is proportional to the peak pressures during the fitting period and is also reflected in the pressure and elastance errors (Figure 4). These findings demonstrate the tradeoff between the ability of a ventilation mode to avoid damaging the lung (i.e. not causing large volume excursions) versus providing the information necessary to assess derecruitability. On balance, we believe that VV achieves a useful compromise between these competing factors.

The real-world efficacy of our parameter estimation algorithm could be impaired by noise in the measured pressure response to a prescribed flow. A full analysis of the effects of noise on the fitting performance is beyond the scope of the current investigation. We have, however, compared the results of the estimation model in the absence and presence of random noise in the pressure signal using VV_I in an injured mouse. The noise in P_sim was drawn from a Gaussian distribution with a standard deviation of 0.22 cm H₂O, equal to 1% of the peak-to-peak pressure amplitude. We evaluated 8 iterations of the estimation algorithm, for each iteration the initial conditions were identical in the noisy and noise-free cases. The addition of noise did not significantly change the mean of the fitted values for α, λ, E_Base or V_Crit (paired t-test, p= 0.01). However, the mean of the standard deviation of the 10 predicted parameter values did increase by 53%. These findings suggest that the estimation algorithm is robust enough to provide accurate parameter estimates in the presence of noise.

In summary, we have developed a numerical optimization algorithm that uses pressures and flows evaluated at the trachea to identify a distributed model of the lung that encapsulates its intrinsic stiffness as well as the dynamics of R/D. The performance of this algorithm was evaluated using simulated data representing healthy and injured mice subjected to four types of mechanical ventilation. Our results indicate that the spectrum of lung volume perturbations provided by VV is rich enough for the ongoing assessment of lung derecruitability. This potentially gives VV a useful diagnostic capability to complement its emerging role as a therapeutic modality.

Table I.

Nomenclature.

Parameter	Description
NUnits	Number of respiratory units
NOpen	Number of open units
VUnit	Respiratory unit volume
EUnit	Respiratory unit elastance
EBase	Low-volume elastance
EFac	Elastance increase rate in nonlinear regime
VCrit	RU transition volume between linear and nonlinear elastance
Emod	Total model elastance
Rmod	Total model resistance
RUnit	Unit resistance
y	Virtual trajectory
λC	Constant which defines exponential PDF for SC
SC	Virtual trajectory closing velocity constant
SO	Virtual trajectory opening velocity constant
PC	Virtual trajectory closing pressure
PO	Virtual trajectory opening pressure
μ	Mean virtual trajectory closing pressure
ΔP	Difference between PC and PO
P	Airway pressure
Vt	Ventilation tidal volume
α	Closing pressure distribution weighting vector
λ	Vector of closing velocity constant PDFs [λC]
	Variable Ventilation Parameters
p(Vt)	Volume PDF for VV
g0	VV normalization constant
VtMean	VV mean tidal volume
VtMin	VV minimum tidal volume
VMax	VV maximum tidal volume
VP	Peak Vt for uniform portion of VV PDF
δ	VV decay constant
	Pattern Search Algorithm Parameters
nparam	Number of parameters to fit with PPS
ng	Number of possible values for each fit parameter
pmax	Maximum number of search directions
l	Lower bound of parameter space
u	Upper bound of parameter space
k	Pattern search algorithm iteration number
xk	kth vector of best-fit parameters
Δk	kth step size vector
𝒟	Set of search directions for PPS
d(i)	ith search direction vector of length nparam
pmax	Maximum number of search directions
Xk	Set of trial points for the kth PPS search step
	Analysis Parameters
ϕS	Respiratory unit open fraction for simulation model
ϕE	Respiratory unit open fraction for estimation model
K	Composite PC PDF in the simulation model
κi	ith of the four PC PDFs in the estimation model
εP	PC PDF error between simulation and estimation models
εE	Elastance error between estimation and simulation models