antaRNA: ant colony-based RNA sequence design

Abstract

Motivation: RNA sequence design is studied at least as long as the classical folding problem. Although for the latter the functional fold of an RNA molecule is to be found, inverse folding tries to identify RNA sequences that fold into a function-specific target structure. In combination with RNA-based biotechnology and synthetic biology, reliable RNA sequence design becomes a crucial step to generate novel biochemical components.

Results: In this article, the computational tool antaRNA is presented. It is capable of compiling RNA sequences for a given structure that comply in addition with an adjustable full range objective GC-content distribution, specific sequence constraints and additional fuzzy structure constraints. antaRNA applies ant colony optimization meta-heuristics and its superior performance is shown on a biological datasets.

Availability and implementation: http://www.bioinf.uni-freiburg.de/Software/antaRNA

Contact: backofen@informatik.uni-freiburg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Engineered RNA molecules are of growing importance with applications ranging from biotechnology to medicine and synthetic biology. In biotechnology, several applications use engineered RNAs as scaffolds to optimize reactions or to deliver drugs. For example, RNA aptamers can serve as protein-docking sites within scaffolds to organize intracellular reactions (Delebecque et al., 2011, 2012). Or the bacteriophage phi29 DNA packaging motor can be used to generate RNA nanoparticles for delivering therapeutic compounds (Guo, 2010). However, biotechnology applications are not restricted to scaffold design, but often involve intriguing RNA-based pathways. For instance, Penchovsky and Breaker (2005) computationally designed ribozymes to sense oligonucleotides. Last but not least, the application of the CRISPR/cas9 system for genetic engineering is emerging and complementing the well established RNAi technology. This requires the design of specific RNA-molecules, see the review of Terns and Terns (2014).

Another important and growing area is RNA synthetic biology, as reviewed in (Benenson, 2012; Isaacs et al., 2006). Design examples include RNA-based regulators of translation (Mutalik et al., 2012), a general, RNA-based framework for microbial engineering on the level of DNA, protein or mRNA (Qi and Arkin, 2014), sRNA-based cellular circuits (Rodrigo et al., 2012), the improvement of functional sRNAs by scaffold engineering (Sakai et al., 2014) or the de novo design of synthetic, transcriptional riboswitches (Wachsmuth et al., 2013).

Many of these approaches use rational design, based on a secondary structure model of the targeted RNA molecule, and an increasing number of applications use computational methods for filtering the initial design. In principle, this is an instance of the inverse folding problem, which consists of finding a sequence that fits some secondary structure constraints. RNAinverse (Hofacker et al., 1994) pursues seed sequence generation with a subsequent optimization based on local search. The objective function is either to maximize the similarity of the minimum free energy (MFE) structure to the target, or to maximize the probability of the target structure in the ensemble. Several other programs follow the idea of RNAinverse and try to provide better strategies for either finding seed sequences or the local refinement step. For instance, in InFoRNA (Busch and Backofen, 2006, 2007) the seeding was improved by generating a sequence that is maximally stable for the target structure and thus has high probability to fold into that structure. RNA-SSD (Andronescu et al., 2004) extends this by using stochastic local search. In more recent approaches, new strategies have been used in order to find sequence solutions: NUPACK (Zadeh et al., 2011) is using efficient ensemble defect optimization; RNAfbinv (Weinbrand et al., 2013) employs simulated annealing for a fragment-based design; fRNAkenstein (Lyngso et al., 2012) applies a genetic algorithm approach. Similarly, the approach by Dromi et al. (2008), MODENA (Taneda, 2011) and ERD (Ali et al., 2014) also apply evolution inspired principles to solve the inverse folding problem.

There are two necessary conditions an up-to-date inverse folding tool must fulfill. First, the tool must be able to handle sequence constraints, in order to capture specific elements like a ligand binding pocket in riboswitches or RNA aptamers binding a specific protein. This is provided by most methods available. But second, the tool has to provide a sequence with a defined guanine-cytosine (GC)-content since the GC-content has drastic influence on the function of the designed molecule. For example, it is known that CRISPR/cas9 elements with too low or too high GC-content do not function optimally (Wang et al., 2014). Another example is given in (Isaacs et al., 2004, 2006), where the authors engineered an RNA-based regulatory activator system for bacterial gene expression. They report that altering the GC-content and further increasing the stability of the designed element did result in a 19-fold activation. In contrast to this biological requirements, most of the first generation tools have an intrinsic GC-bias (Reinharz et al., 2013) that cannot be compensated by GC-filtering (see Supplementary Material). Recently, programs have been developed, which allow to declare a target GC-value or to constrain the GC-range for solution sequences. So far, the only known tools providing this functionality are RNA-SSD (Andronescu et al., 2004), IncaRNAtion (Reinharz et al., 2013), which is a seed sequence generator for RNAinverse, and RNAiFold (Garcia-Martin et al., 2013), a constraint programming approach.

Here we introduce antaRNA, which uses the ant colony optimization (ACO) meta heuristic to solve the inverse folding problem of RNA to produce sequences with controlled target GC-composition. Furthermore, sequence constraints are incorporated. Accessorily, the introduction and application of implicit structure constraints allows a design principle that enables the declaration of RNA structure in a ‘fuzzy’ mode.

Sequences designed by antaRNA show high agreement of their MFE-structures with the targeted structures independently of the additional objective GC-content constraints.

2 Methods

antaRNA is based on the ACO heuristic, which was already successfully applied to solve a broad collection of classical optimization problems, such as routing (Gambardella and Dorigo, 2000), scheduling (Socha et al., 2002), assignment (Merkle and Middendorf, 2003), subset partitioning/clustering (Blum and Blesa, 2005), constraint satisfaction (Solnon, 2000), classification rules (Parpinelli et al., 2002) and Bayesian networks (de Campos et al., 2002). Also directly biologically motivated problems such as protein structure folding (Shmygelska and Hoos, 2005) and docking simulations (Korb et al., 2006) as well as RNA secondary structure prediction methods (McMillan, 2006) have been investigated with ACO.

Generally, ACO is a self-adjusting local search strategy, which automatically adapts to the specific problem instance optimized. Because RNA structure formation is very sensitive to sequence changes, ACO should be able to learn the importance of local sequence features, which is an essential aspect when solving the RNA inverse folding problem.

Thus in the following, we present the adaptation of ACO to the RNA inverse folding problem and describe the necessary basic RNA notations to subsequently describe the algorithm. The algorithm is depicted on a conceptual level. Please consult the supplement material for more detailed formal definitions.

2.1 Ant colony behavior

Ants, while foraging for food or exploring new terrain, use pheromones to indicate the quality of a certain path on their return. They apply a quality-dependent amount of pheromone to the just examined path (Pasteels et al., 1987), while the quantity is defined by many (here abstracted) factors according to the situation: Does the path yield food? Is the amount of food large/small? What is the quality of the food? Other ants sense the pheromone on a path and are influenced in their decision whether to follow the same path or to continue exploring new paths (Goss et al., 1989). The pheromone itself evaporates over time, such that, if no ant follows the indicated path and renews its pheromone trail, the path becomes ‘silent’ or ‘unknown’ to the colony (Deneubourg et al., 1990).

The general principle of ACO (Dorigo and Stützle, 2004; Dorigo et al., 2006) simulates an ant colony and its foraging behavior on a modeled terrain to solve optimization problems. Here, ACO is incorporated and exerted to the problem of RNA inverse folding to generate RNA sequences, which are optimized to fold into a targeted structure under additional constraints. In the developed application, the ants of a colony walk subsequently over the simulated terrain and assemble and evaluate RNA solution sequences. According to the quality of each solution, the solution generating parts of the terrain are marked with pheromone, such that the information of prior solutions contributes to the decisions of subsequent ants. Each pheromone update also covers ‘environmental’ exposure of the whole terrain, i.e. globally the pheromone information evaporates with a certain rate. Over time, one pheromone trail will dominate the terrain and will indicate the best solution, which is in accordance with the user defined constraints. The underlaying ACO principle of antaRNA is depicted within Algorithm 1.

2.2 RNA input

The aim of the heuristic is to obtain an RNA sequence $\mathcal{S}$ that is comprised of n nucleotides. Each sequence position ${\mathcal{S}}_1\dots {\mathcal{S}}_n$ derives from the RNA nucleotide alphabet $\Sigma =\{\text{A},\text{C},\text{G},\text{U}\}$. A base pair (i, j) is an interaction, in which hydrogen bonds between two nucleotides at sequence positions ${\mathcal{S}}_i$ and ${\mathcal{S}}_j$ within the sequence $\mathcal{S}$ were established. antaRNA considers canonical Watson-Crick and G-U base pairs. A set of base pairs defines a secondary structure $P=\{(i,j)|i<j\}$ of $\mathcal{S}$. We consider only nested secondary structures, i.e. all base pairs fulfill $\text{∄}(i,j),(k,l)\in P:i<k<j<l$. In addition, a minimal loop size of 3 is enforced, i.e. $\forall (i,j)\in P:j-i>3$.

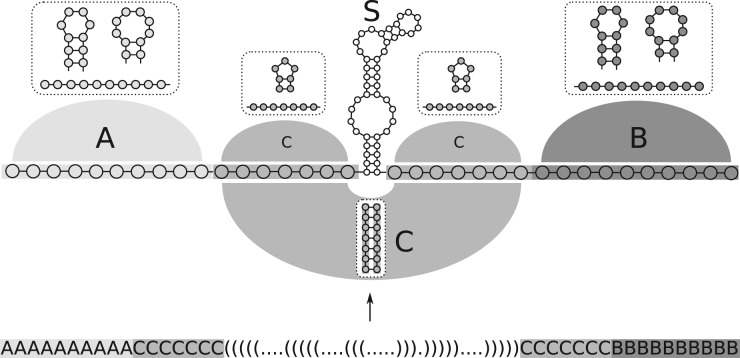
The user can define three types of constraints: The structure constraint ${\mathbb{C}}^{\text{str}}$ is used to provide the explicit and implicit secondary structure constraints, which is encoded in an extended dot-bracket notation. The explicitly targeted structure parts define the base pairs and single stranded positions that have to be formed as they are defined. If the definition of an explicit structure is too rigid for a design problem, more ‘fuzzy’ implicit structural constraints can be encoded to restrict base interactions to specific regions. Those regions can be declared by capital letters within the extended dot-bracket string. One region does not necessarily have to be formed by consecutive positions, but can also stretch over two or more disjoint areas (see Fig. 1). All base pairs emerging in the same type of region (same letter) are implicitly allowed and not penalized during structural distance evaluation (as discussed later).

Fig. 1.

Implicit structure constraint: structure constraint example for a SECIS-like design of Kossinova et al. (2013) Here, the structurally explicitly constrained SECIS element (S) is further embedded within implicit structure constraint regions (labeled A–C). Additional base pairs may occur within individual regions A, B and C but are not allowed to cross them. This allows a highly flexible context design to minimize the likelihood of interactions between the context and the functional hairpin. In the given example, region C allows for the extension of S, while region A and B ensure this extension to be limited. The implicit constraint patterns allow a multitude of substructure combinations. For each region, possible valid substructures are exemplified in the insets

The sequence constraint ${\mathbb{C}}^{\text{seq}}$ can restrict certain sequence positions to specific nucleotides. Furthermore, the GC-content constraint ${\mathbb{C}}^{\text{GC}}\in [0,1]$ provides the targeted GC-ratio within the sequence.

2.3 ACO of inverse-folded RNA—antaRNA

During the optimization a large set of sequences $\mathcal{S}$ is assembled. The best solution sequence ${\mathcal{S}}^{\text{sol}}$ is returned, if a termination criterion is reached.

In order to obtain a sequence $\mathcal{S}$, the ants search sequentially in the simulated terrain represented as a directed graph $T=(\mathcal{V},\mathcal{E})$. Each ant investigates one terrain path, which corresponds to a sequence assembly based on the visited vertices. The set of vertices $\mathcal{V}$ contains a non-emitting start vertex $v_{•}$ and nucleotide ($\sigma \in \Sigma$) emitting vertices $v_{i\sigma }$ for each sequence position ${\mathcal{S}}_i$. These are connected by the set of directed edges $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$, where each edge $e_{(i\sigma ,j\sigma )}=(v_{i\sigma },v_{j\sigma \prime })\in \mathcal{E}$ resembles an available path within the terrain. The vertices $v_{1\sigma }$ are accessible from the start vertex $v_{•}$ while vertices $v_{i\sigma }$ ($1<i\le n$) can be reached from all preceding nucleotide emitting vertices $v_{(i-1)\sigma }$. Each edge holds pheromonic (τ) and heuristic (η) information. The resulting terrain graph contains $|\mathcal{V}|=1+|\Sigma |n$ vertices and $|\mathcal{E}|=|\Sigma |+|\Sigma {|}^2(n-1)$ edges when optimizing a sequence of length n. Figure 2 illustrates the composition of the terrain graph $T$.

Fig. 2.

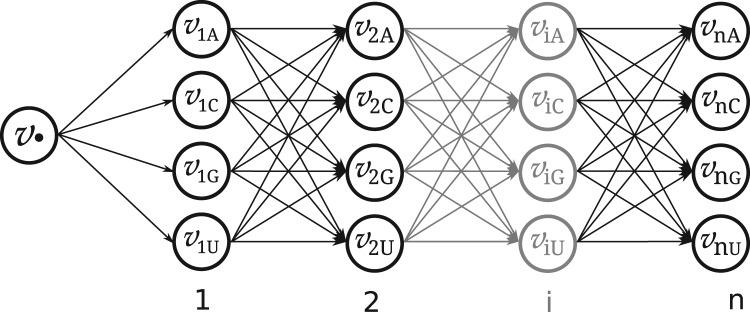
Terrain $T=(\mathcal{V},\mathcal{E})$: Starting from vertex $v_{•}$, an ant selects probability-dependent an outgoing edge until it reaches a final node $v_{n\sigma }$. Hereby, all visited vertices $v_{i\sigma }$ emit the encoded nucleotide σ to the respective sequence position ${\mathcal{S}}_i$. The assembled solution sequence $\mathcal{S}$ is evaluated and the pheromone information of the corresponding path in the graph is updated according to the solution’s quality

2.4 Solution generation

2.4.1 Graph initialization

Because each solution sequences $\mathcal{S}$ is assembled by the ants according to the information embedded within the terrain, the terrain must encode the requested constraints. The constraint information is split into the dynamic pheromonic τ and the static heuristic η contribution of the edges. Herein, we define the pheromonic contingent to be controlled by the structure and sequence constraints, ${\mathbb{C}}^{\text{str}}$ and ${\mathbb{C}}^{\text{seq}}$, whereas the heuristic part is encoding the targeted GC-content ${\mathbb{C}}^{\text{GC}}$. The weight of an edge is the sum of both contingents weighted by two parameter α and β, respectively.

The pheromone τ initialization is of binary character. The pheromone value of an edge $e_{(i\sigma ,j\sigma \prime )}$ is set to 0, if the emitted nucleotide σ of the target vertex $v_{j\sigma \prime }$ is not in accordance with the sequence constraint ${\mathbb{C}}_j^{\text{seq}}$ at position j. Otherwise, we set $\tau (e_{(i\sigma ,j\sigma \prime )})=1$. Note, we also encode implicit sequence constraints that arise from the combination of ${\mathbb{C}}^{\text{str}}$ and ${\mathbb{C}}^{\text{seq}}$ as follows. If a position is constrained by a specific nucleotide, e.g. ${\mathbb{C}}_i^{\text{seq}}=\text{U}$, and also part of an explicitly requested base pair $(i,j)\in {\mathbb{C}}^{\text{str}}$, we derive an implicit complementarity sequence constraint for the pairing partner, in our example ${\mathbb{C}}_j^{\text{seq}}\in \{\text{A},\text{G}\}$.

The heuristic information η is defined for all edges with $\tau >0$ by a target GC-content ${\mathbb{C}}^{\text{GC}}$ dependent static edge weighting. Hereby, a differentiation between edges leading to AU-emitting nodes $v_{j\left\{\text{AU}\right\}}$ and edges leading to GC-emitting nodes $v_{j\left\{\text{GC}\right\}}$ is enabled. The heuristic contribution of an edge is defined by the deviation of ${\mathbb{C}}^{\text{GC}}$ from a basis GC-value of 50% and depends on the edge’s target node.

2.4.2 Sequence assembly

Each ant compiles a solution sequence $\mathcal{S}$. This is achieved by the ant’s walk over the terrain. Starting from vertex $v_{•}$, n edges are traversed and n vertices in the graph are visited. An edge $e_{(i\sigma ,j\sigma \prime )}$ is selected according to it’s probability $p(e_{(i\sigma ,j\sigma \prime )})$. The probability of an edge is the relative weight of its terrain information among all edges originating in its start vertex $v_{i\sigma }$, as given in Equation (1).

$$p(e_{(i\sigma ,j\sigma \prime )})=\frac{\alpha *\tau (e_{(i\sigma ,j\sigma \prime )})+\beta *\eta (e_{(i\sigma ,j\sigma \prime )})}{{\displaystyle \sum _{{\sigma }^{*}\in \Sigma }\left(\alpha *\tau (e_{(i\sigma ,j{\sigma }^{*})})+\beta *\eta (e_{(i\sigma ,j{\sigma }^{*})})\right)}}$$ (1)

Each visited vertex $v_{i\sigma }$ emits its assigned nucleotide, i.e. the solution sequence position is updated by ${\mathcal{S}}_i=\sigma$ (see Fig. 2).

2.4.3 Sequence evaluation

The actual evaluation of the assembled sequence is done via a combination of different measures: a structural distance $d_{\text{str}}$, a GC-content aberration distance $d_{\text{GC}}$ and a sequence distance $d_{\text{seq}}$ are transformed into a score, with which the terrain is updated.

The structural distance $d_{\text{str}}$ computation is based on the program RNAfold of the ViennaRNA-package v2.1.3 (Lorenz et al., 2011). In a first step RNAfold calculates the MFE-structure $P^{\text{sol}}$ of the sequence $\mathcal{S}$.

Given $P^{\text{sol}}$, next a solution dependent target structure $P^{\mathbb{C}}$ is composed, since ${\mathbb{C}}^{\text{str}}$ allows for explicit and implicit structure constraints. Initially, $P^{\mathbb{C}}$ contains all explicitly requested base pairs from ${\mathbb{C}}^{\text{str}}$. In the following, the handling of lonely base pairs, implicit structure constraint and sequence constraint contributions are discussed.

During the evaluation, explicitly requested lonely base pairs are temporarily removed from $P^{\mathbb{C}}$, since they are usually energetically unfavorable and thus counteract the MFE-based design principle. For their ‘soft’ integration into the design, a distance penalty is added for each lonely base pair that cannot be formed by the current solution sequence $\mathcal{S}$. Lonely ‘2 base pair stacks’ are handled equivalently for the same reason.

The ‘fuzzy’ implicit structure constraint allows for all base pairs that are within one of its defined regions (see Fig. 1). Thus, all base pairs of the current solution structure $P^{\text{sol}}$ that are confined to such blocks of implicit structure are temporarily added to the target structure $P^{\mathbb{C}}$.

Finally, in some cases, the sequence constraint ${\mathbb{C}}^{\text{seq}}$ induces base pairs under certain structural folding context. If both positions ${\mathcal{S}}_i$ and ${\mathcal{S}}_j$ of a base pair of the current solution $(i,j)\hspace{0.17em}\in P^{\text{sol}}$ are constrained by ${\mathbb{C}}^{\text{seq}}$, this base pair is added to the target structure $P^{\mathbb{C}}$.

In a final step, the length-normalized base pair distance $d_{str}$ between $P^{\text{sol}}$ and the compiled target structure $P^{\mathbb{C}}$ is determined.

The GC-aberration $d_{\text{GC}}$ between the objective and the actual GC-content of $\mathcal{S}$ is determined by subtracting the actual from the target GC value. Due to the discrete nature of sequence lengths, it is often not possible to precisely reach the objective GC-content ${\mathbb{C}}^{\text{GC}}$. Thus, sequence length dependent correction terms are added to the actual GC value for $d_{\text{GC}}$ computation.

The sequence constraint distance $d_{\text{seq}}$ encodes the violation of the sequence constraint ${\mathbb{C}}^{\text{seq}}$ given the current solution sequence $\mathcal{S}$. It reflects the ratio of sequence positions that do not respect ${\mathbb{C}}^{\text{seq}}$.

The overall quality score Q of the sequence’s features is the weighted sum of the inverted distance measures. Thus, lower distances result in higher quality estimates.

2.4.4 Pheromone update

Given the quality Q of a solution $\mathcal{S}$, the pheromone information of the solution-associated edges in the terrain graph is increased by Q. Hereby, only those edges are rewarded that correspond to positions where the structure information is identical between the resulting solution $P^{\text{sol}}$ and the target structure $P^{\mathbb{C}}$. In order to limit the memorization and influence of previous solutions, a global evaporation of pheromone is applied. According to the evaporation rate ρ, the pheromone information of all edges is reduced. The pheromone information encodes the compliance of paths in the terrain with all constraints. This way, the solution sequence assembly of subsequent ants is tuned towards correct sequence designs, since the local decisions are based on the combination of pheromone and heuristic information (see earlier).

2.4.5 Termination

Although the ants walk over the terrain, edges, which have been involved in good solutions get promoted over those, which have not contributed to good solutions. This solidifying behavior results in convergence towards optimal or suboptimal quality in respect to the given constraints. antaRNA uses three termination criteria to stop the ACO: maximal number of generated solutions, a termination potential and a reset potential.

The termination potential is initialized and increased every time subsequent solutions show a structural distance of zero. As soon as a termination threshold is exceeded, the algorithm is stopped and the best solution according to Q is returned.

Another possibility to terminate is based on a maximal number of internal terrain resets. The terrain and all initial values are reset, if the reset potential exceeds the reset threshold. The reset potential is increased, if the structural distance of a current solution is not zero but the GC quality is within a margin of the momentarily best solution, i.e. $d_{\text{GC}}\le 1.5*d_{\text{GC}}^{\text{bestSoFar}}$.

3 Datasets

The underlaying dataset of this study is an extract from the Rfam database v11.0 (Burge et al., 2013). A training subset has been used to evaluate and adjust antaRNA’s parameters. A distinct and larger test set was used to benchmark and compare antaRNA with other tools. We evaluated the behavior of the algorithms concerning different complexities of structure and sequence constraints and their influence and impact on the solution sequences and their characteristics.

For each selected Rfam family, structure and sequence information of conserved positions within the respective Rfam family’s seed alignment were extracted to define ${\mathbb{C}}^{\text{str}}$ and ${\mathbb{C}}^{\text{seq}}$. We applied the following protocol to derive the dataset.

For each Rfam seed-alignment with at least 20 entries, the shortest ungapped sequence was selected. Subsequently, the alignment’s consensus structure was mapped to that sequence. The obtained structure defines the explicit structure constraint ${\mathbb{C}}^{\text{str}}$. No implicit structural constraints were derived. We further ensured a minimal structural confinement, i.e. a family was discarded, if the fraction of base pair forming positions within ${\mathbb{C}}^{\text{str}}$ was below 20%.

For each position i within such a structure, a sequence constraint ${\mathbb{C}}_i^{\text{seq}}$ was set depending on a minimal conservation ratio MR. If a nucleotide in the according column of the seed alignment shows a relative abundance larger than MR, the nucleotide is used as sequence constraint. Otherwise, the position is unconstrained (${\mathbb{C}}_i^{\text{seq}}=\text{N}$). A family-specific MR threshold was used such that the fraction of ${\mathbb{C}}^{\text{seq}}$-constrained sequence positions was in the range of 20–30%. The GC-content of the ${\mathbb{C}}^{\text{seq}}$-constrained positions was not allowed to exceed 15%, to ensure enough flexibility within the sequence constraint to reach the targeted GC-values of the benchmark.

In total, this resulted in 83 derived targets from the Rfam database. The lengths of the obtained constraints range from 34 to 274 nucleotides with varying constraint complexities. The training subset contains constraints with lengths not longer than 200 nucleotides and length differences of at least five nucleotides to the rest of all training set members. The remaining entities define the test set. The training set contains 20, the test set 63 entities. Further information about the sets can be found in the (Supplementary Materials).

4 Results and Discussion

In order to identify the best default parameter values and to study their robustness, we investigated antaRNA performance for various settings using a grid search on the training data set. Within the grid search we optimized: the weighting factors α and β of the path weight computation, the evaporation rate ρ, the three distance weighting factors for solution quality Q calculation, and the termination parameters (see Supplementary Materials for details).

For each parameter setting, we designed for each test set family 10 sequences with and without sequence constraint ${\mathbb{C}}^{\text{seq}}$ targeting three different objective target GC values ${\mathbb{C}}^{\text{GC}}$ of 25, 50 and 75%. The resulting 1200 sequences (20 × 10 × 2 × 3) were used to calculated a benchmark score for the parameterization.

The score sums the mean structural distance, the mean GC aberration and a mean of the normalized runtime, i.e. it is in the range $[0,3]$. The parameter set with the lowest score (0.219) was chosen as default parameter set for antaRNA and was used for all following comparisons. The values are listed in the Supplementary Material.

4.1 Targeting arbitrary GC-content distributions

The parameter optimization revealed for antaRNA a high precision concerning targeted GC values while it also robustly fulfills structural and sequence constraints. Thus, we investigated antaRNA’s potential to produce pools of sequences, whose GC values are resembling a user defined distribution rather than a single value. A possible application is the design of sequences that show a GC-distribution similar to prototype sequences or the organism of interest.

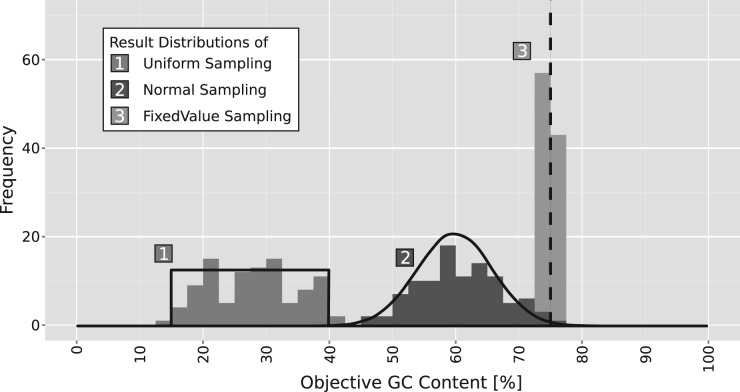
Here, the application is exemplified and tested for a uniform (15–40% GC-content) and a normal distribution ($\mu =60\%,\hspace{0.17em}\sigma =6\%$) and compared with a fixed value (70%) sampling. For each given GC-content target distribution, a set of individual target GC values is sampled from the distribution and antaRNA is run for each. Figure 3 presents the results. In all three cases, the achieved distributions agree very well with their respective targets. Only the single target shows a small bias towards lower GC-content values. Distribution distortions derive from the limited sample size and the aforementioned length-dependence of achievable GC value (see GC distance computation).

Fig. 3.

antaRNA high-precision GC-content distribution compliance given antaRNA’s precision, it is possible for the first time to design sequences for arbitrary targeted GC-content distributions. The figure provides three examples, each comprises 100 designs for a tRNA-like structure (Supplementary Materials). The targeted distributions are drawn in gray scale [left: uniform (within interval 15–40%), middle: gaussian ($\mu =60\%,\hspace{0.17em}\sigma =6\%$)]. The 75% target value can be found on the right side. The respective achieved values are given as histograms: uniform distribution (left/1), gaussian distribution (middle/2), and single target GC value (right/3)

4.2 Comparison to existing tools

All recent RNA inverse folding tools are able to design sequences for a given structure with or without sequence constraints. In contrast to that, RNA-SSD, IncaRNAtion and RNAiFold are, beside antaRNA, the only known tools so far that can also constrain the GC-content at the same time. Here, we compare IncaRNAtion, RNAiFold and antaRNA and benchmark their design quality for various target GC values with and without sequence constraints using our test dataset. RNA-SSD is not included into this comparison, since Reinharz et al. (2013) have shown its inferiority compared with IncaRNAtion.

Please note, the presented RNAiFold data has been kindly computed externally by the maintainers of RNAiFold, since a local installation and application was not possible. antaRNA and IncaRNAtion have been run locally on the same computer cluster. Note further, RNAiFold is based on the ViennaRNA-package v1.8.5. Hence, we used the same version to compute the MFE-structures in order to evaluate the structural distance $d_{\text{str}}$ of the corresponding predictions. Both, antaRNA and IncaRNAtion employ the ViennaRNA-package v2.1.3 that was applied for $d_{\text{str}}$ evaluation accordingly. Finally, RNAiFold requires the definition of an allowed range around the targeted GC value, which was set to 2% to ensure correct designs. Due to these different setups, only limited comparisons can be made.

For each structural constraint ${\mathbb{C}}^{\text{str}}$, three different objective GC-content target values ${\mathbb{C}}^{\text{GC}}\in \{25,\hspace{0.17em}50,75\%\}$ have been addressed in this benchmark, each targeted with and without sequence constraint ${\mathbb{C}}^{\text{seq}}$. To illustrate length-dependencies, the test dataset was separated into length categories (L1:1–100, L2:101–200 and L3:201–300 nucleotides) for visualization. Each tool was executed 100 times per constraint set, to enable statistics. Different time limitations were used: maximal 1 hour for RNAiFold and 10 min for antaRNA/IncaRNAtion per single sequence design.

We observe a length dependency for the runtimes of antaRNA and IncaRNAtion (see Supplementary Materials), i.e. longer sequences require more time, which is expected. The current antaRNA implementation is about one order of magnitude slower compared with IncaRNAtion. This might result from the different programming languages used. antaRNA is completely encoded in Python, while IncaRNAtion uses the C-based RNAinverse for the time expensive optimization and only generates seed sequences in Python. A runtime comparison to RNAiFold is not possible due to the external computations. When investigating the effect of sequence constraints on runtime, we observe a target GC dependency. Although predictions with low target GC values (25%) seem to be slightly faster when sequence constraints are applied, the counter-effect is observed for high GC target values (75%). For moderate GC-values no effect is found.

We encountered strong differences in the success rate of the different tools, i.e. the rate of successful design attempts that produce a solution sequence within the given time limits. Both antaRNA and IncaRNAtion always provide a solution sequence, independent from time limits, since they are heuristic optimization approaches that successively improve solutions. RNAiFold, in contrast, is based on constraint programming techniques, which produce only solutions that completely comply with all given constraints. Otherwise no solution is produced at all. Furthermore, solution generation in constraint programming frameworks strongly depends on the used search heuristics, which directly influence the runtime behavior. Figure 4a depicts the limited success rates for RNAiFold. It becomes clear that some constraint sets seem to be too confining to enable a sequence design for RNAiFold within 1 h. Notably, for some categories the tool fails completely in its design attempts.

Fig. 4.

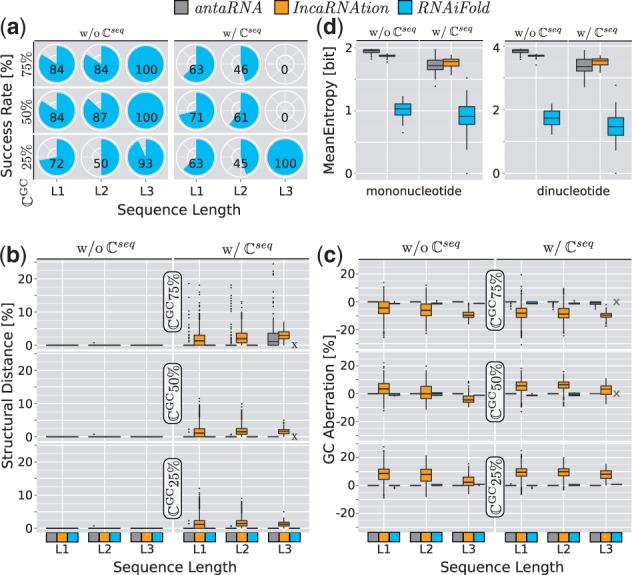
Constraint compliance quality summary of the sequences produced by the programs antaRNA (gray), IncaRNAtion (yellow) and RNAiFold (blue). The runs have been performed with and without the respective Rfam sequence constraints ${\mathbb{C}}^{\text{seq}}$. Different target GC-content value ${\mathbb{C}}^{\text{GC}}$ have been tested (top 75%, middle 50%, bottom 25%). For each constraint set, 100 sequences have been generated targeting the respective GC-content. The datasets have been split according to sequence length categories (L1:1–100; L2: 101–200; L3:201–300). (a) Success rates of RNAiFold for each setting. (b) Structural distance of the sequences’ MFE-structures to the targeted Rfam family derived RNA secondary structures. (c) GC-aberrations of the sequences. Reference values are the appointed target GC values.(d) The mean Shannon-Entropy H of unconstrained sequence positions indicating design diversity for each program with and without ${\mathbb{C}}^{\text{seq}}$

To evaluate the tools’ structure and sequence compliances, we compare the individual distributions of structural distances $d_{\text{str}}$, GC aberrations $d_{\text{GC}}$ and sequence distances $d_{\text{seq}}$.

Figure 4b summarizes the measured structural distances $d_{\text{str}}$ for all three tools. If no sequence constraint is applied, all tools show a very good compliance with the target structure. When sequence constraints are applied, the tools show different behaviors. antaRNA still shows $d_{\text{str}}$ medians of 0 deviation; except for the L3 sequences, where the median is 2 and the upper quartile is about 4. In comparison, the deviations of IncaRNAtion always show a median of ∼2%, but their upper quartiles vary between 2 and 4%. With increasing target GC values, IncaRNAtion shows increasing variance in its distributions. RNAiFold also exhibits good structure compliance in the sequence constrained cases, if solution sequences have been returned. In the case of ${\mathbb{C}}^{\text{GC}}=75\%$ and 50%, RNAiFold fails to return sequences (Fig. 4d) that fulfill the specified constraints.

Figure 4c presents the observed GC aberrations $d_{\text{GC}}$. The sequences designed by antaRNA show a very good target ${\mathbb{C}}^{\text{GC}}$ compliance (mean $|d_{\text{GC}}|=0.02$%). Only for the extreme setting ${\mathbb{C}}^{\text{GC}}$ = 75% including sequence constraints ${\mathbb{C}}^{\text{seq}}$, the median $d_{\text{GC}}$ drops to −0.7% and the corresponding lower quartile is at −1.8%. The results for RNAiFold are all within the allowed 2% variance around the respective ${\mathbb{C}}^{\text{GC}}$ while it slightly deviates in almost all cases (mean $|d_{\text{GC}}|=0.7$%).

Almost all IncaRNAtion designs do not fulfill the target ${\mathbb{C}}^{\text{GC}}$ constraint (mean $|d_{\text{GC}}|=7.1$%). Only one constraint set (${\mathbb{C}}^{\text{GC}}$ = 50%, no ${\mathbb{C}}^{\text{seq}}$) shows a $d_{\text{GC}}$ median of zero. All sets show wide distributions (interquartile ranges are about 5–8% $d_{\text{GC}}$) and in most cases the interquartile range does not even come close the targeted ${\mathbb{C}}^{\text{GC}}$. In extreme cases, the $d_{\text{GC}}$ median deviate up to 10%.

The sequence constraints ${\mathbb{C}}^{\text{seq}}$ are completely respected by antaRNA and RNAiFold. Both only design sequences that totally comply with the respective ${\mathbb{C}}^{\text{seq}}$ ($d_{\text{seq}}=0$). The sequences designed by IncaRNAtion do not always comply with their constraints (mean $d_{\text{seq}}=0.9\%$; data not shown).

So far, we only studied the constraint compliance of the designed sequences. In the following, we evaluate the sequence diversity of the designed sequences. This is an important feature to enable further successive filtering of the designs, e.g. for experimental use.

To this end, we computed the mean Shannon-Entropy for each sequence position over all according sequences. Positions constrained by ${\mathbb{C}}^{\text{seq}}$ have been excluded. The resulting mean mononucleotide entropy is presented in Fig. 4d for designs with and without ${\mathbb{C}}^{\text{seq}}$. Here, a high entropy implies that for unconstrained positions, most of the possible sequence combinations have been used. Low entropy implies a sequence bias, which is a undesired feature for a design tool. antaRNA shows the highest entropy if no sequence constraint is applied, followed by IncaRNAtion. This is swapped in the presence of ${\mathbb{C}}^{\text{seq}}$, but still very high for both tools. antaRNA sequences have a mean entropy of 1.95 (of maximally 2) in the sequence unconstrained setup and 1.72 among ${\mathbb{C}}^{\text{seq}}$-constrained sequences. For IncaRNAtion the respective values are 1.87 and 1.77. Thus, both tools produce very diverse sequences. In contrast, RNAiFold shows mean entropy of 1.01 in the unconstrained setup and 0.9 for sequence constrained instances. In general, the respective entropies decline, if sequence constraints are applied.

A manual inspection of the sequences produced by RNAiFold revealed stretches of common subsequences, which is depicted by dinucleotide entropies in Fig. 4d). That is, instead of single positions the entropy of neighbored position pairs was measured. Again, IncaRNAtion and antaRNA both show high entropy values (>3 of maximally 4) with and without sequence constraints revealing the same relations observed for mononucleotide entropy. That is, both tools show high diversity also concerning dinucleotides. In contrast, the dinucleotide entropies of RNAiFold range below 2 bits, indicating that the respective sequences have a bias towards common subsequences. Furthermore, note that the dinucleotide entropy is in relation even lower compared with the mononucleotide entropy, which even highlights the observation. We expect this to be an artifact of the constraint programming framework applied within RNAiFold.

5 Conclusion

Within this work we present antaRNA, which solves the RNA inverse folding problem for given secondary structures under additional side constraints using an ACO approach. Besides the explicit target structure features, specific target GC-content values, sequence constraints, and newly developed implicit structural constraints are incorporated and presented. Target GC-content constraints allow to request sequences with a desired specific GC-content or from arbitrary controlled GC-content distributions, while the latter is unique to antaRNA. The results show that the tool produces on average sequences that exactly show the targeted GC-content, even when additional sequence constraints are enforced. The MFE-structures of the designed sequences respect the provided structural constraints for almost all targets tested. This holds for a broad range of targeted GC values with and without sequence constraints.

The program was optimized, compared and evaluated on various sets of constraints derived from the Rfam database. The assessment revealed the superior quality of antaRNA produced sequences over IncaRNAtion and RNAiFold. The prime feature of a sequence and its biological functionality is the structure. Thus, it should be the central objective for sequence design tools. IncaRNAtion does not achieve this objective and produced on average high structural distances in our experiments. Although it was tailored to enable specific GC-content optimization, it also shows poor performance in fulfilling the targeted GC values. Only its high-sequence diversity partially outperforms other compared methods. IncaRNAtion applies a two stage-optimization approach that first produces GC-optimized seed sequences that are subsequently optimized towards the target structure by RNAinverse. Thus, often the GC-unaware RNAinverse MFE-structure optimization counters the GC-optimization.

In contrast, the sequences designed by RNAiFold and antaRNA show both very good structural as well as GC compliance. Although qualitative comparable on the level of constraint violation, the tools show significant differences concerning reliability and sequence diversity. RNAiFold is not always producing sequence solutions within the allowed runtime. This might be due to the used constraint programming techniques and results in missing sequence designs for many constraint sets. In contrast, antaRNA is based on ACO and applies a parallel optimization of all constraints. Thus, it always reports a solution sequence with no qualitative loss. Furthermore, antaRNA produces more diverse sequence sets compared with RNAiFold, which shows a trend to non-diverse subsequences.

Summarizing, the capability of antaRNA to reliably produce highly diverse sequences for a given structure, coupled with the precise GC targeting, will help to explore the sequence space for RNA design problems.

The introduced implicit structure constraints enable the user to define parts of the structure in a very vague way. This can be of use when the structural context of a specific design target is less important as long as it does not interact with the important and maybe explicitly defined structure domains. The improvement and application of the ‘fuzzy’ constraint concept (e.g. details about position or constraint type specific weighting) is a focus of our ongoing work.

In total, the results are promising and encourage further work, which will include runtime optimization e.g. based on parallelization approaches. In addition, the implicit structure constraint is of great use in future work when modeling multi-structure constraints or pseudo-knot structures. Furthermore, improving and developing new internal scoring mechanisms and evaluation patterns is subject of ongoing work, such that the tool can also handle more complex input structures and their constraints in an adequate way. This inevitably results in potentially new parameter setups for which we have to update our understanding of their synergistic effects on antaRNA.

Funding

This work was supportively funded by the Baden-Württemberg Ministry of Science, Research and Arts [MWK grant (7533-7-11.6.1) Ideenwettbewerb Biotechnologie und Medizintechnik Baden-Württemberg, Germany].

Conflict of Interest: none declared.