Response to Comments on “Magnetic Resonance Spectroscopy Identifies Neural Progenitor Cells in the Live Human Brain”

Abstract

We reported on a neural progenitor cell biomarker, a lipid-based metabolite enriched in these cells, which we detected using spectroscopy both in vitro and in vivo, and singular value decomposition–based signal processing. The study provided an outline of our computational methodology. Herein, we report more extensively on the method of spectrum analysis used, demonstrating the specificity of our findings.

Manganas et al. (1) described a metabolic biomarker for the detection and quantification of neural progenitor cells (NPCs) in the human brain in vivo. Most of the concerns of Hoch et al. (2), Friedman (3), and Jansen et al. (4) relate to the reported spectral processing methods and their validity. The methodology used to detect NPCs in (1) is based on singular value decomposition (SVD) and relies on the assumption that the metabolite signals are modeled as decaying complex sinusoids. As such, the method belongs to the category of parametric methods. In general, provided that the model of the data is correct, parametric methods can often achieve much better performance than nonparametric ones (5). For instance, excellent quantitation results have been recently reported for an algorithm that is based on decaying complex sinusoids (6). Various versions of SVD-based methods have been reported, and their accuracy demonstrated (7, 8). For example, it has been shown that, for sufficiently high signal-to-noise ratios (SNRs), the SVD-based methods achieve the Cramér-Rao bound, which provides the smallest variance of an estimate that can be obtained by an unbiased estimator (7, 9). However, if the acquired data do not follow the assumed signal and noise models or if the SNRs are below a certain level, the performance of the method degrades and reliable estimates become impossible. The robustness of the SVD method is a complex problem, and the fact that the method is iterative makes the evaluation of its robustness even more challenging. Thus, in a series of test experiments, we extensively analyzed the validity of our method and quantified the false discovery rates.

To test the detection/estimation performance of our method as a function of SNR, we performed experiments on both fully synthesized and semi-synthesized data. The SNR was defined by

$$\mathit{\text{SNR}}=10log\frac{{\left|a\right|}^2}{{\mathrm{\sigma }}^2}+10log\frac{1-e^{-2dN}}{N(1-e^{-2d})}$$ (1)

where a and d are the initial amplitude and damping factor of the decaying sinusoid, respectively, σ² is the noise variance, and N is the number of samples. When the damping factor d is zero, the SNR is equal to the first term of the above equation. As a metric for accuracy in estimation performance, we used the relative root mean square estimation error (RRMSE), defined by

$$\mathit{\text{RRMSE}}\triangleq 100\sqrt{\frac{1}{K}\sum _{k=1}^K\frac{{(\mathrm{\theta }-{\widehat{\mathrm{\theta }}}_k)}^2}{{\mathrm{\theta }}^2}}$$ (2)

where K is the number of Monte Carlo trials, θ is the true value of the unknown parameter, andθ̂_k is the estimate of θ in the k-th trial.

The testing with fully synthesized data was done as reported by Stern et al. (10). Figure 1 shows the results of detection/estimation of two close components, where component 1 had frequency 0.15 and damping factor 0.01, and component 2 had frequency 0.2 and damping factor 0.005 (the sampling frequency was normalized to 1; note that the frequencies are not expressed in ppm). The number of samples in each data set was 1024. We tested the detection/estimation performance of the method as a function of SNR by setting the amplitude of component 1 to be 100 times stronger than that of component 2. With this choice of parameters, the power spectral density of component 1 at frequency 0.2 was about 2.5 times as large as the power spectral density of component 2. We simulated circular complex white Gaussian noise and varied the SNR in the range from −25 dB to 5 dB, where important changes in performance are expected (the SNR was defined with respect to component 2). For each SNR, we simulated 200 independent realizations. As shown in Fig. 1A, for SNRs > −14 dB, the weaker signal is always detected (100% detection). Figure 1B demonstrates how the RRMSE decreases with the increase of SNR. For example, the graph shows that the RRMSE of the estimated amplitude of the second signal is almost 20% at −14 dB.

Fig. 1.

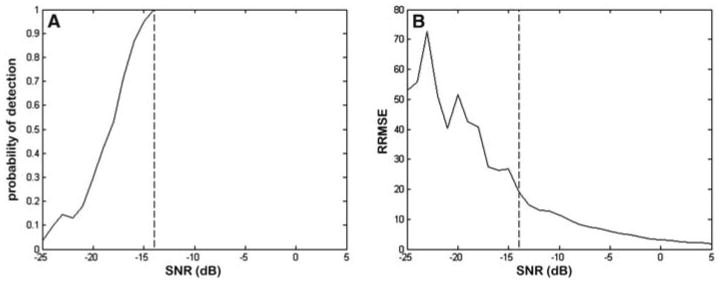
Detection/estimation performance of the SVD-based method on fully synthesized data. (A) Probability of detection as a function of SNR. (B) RRMSE of the estimated amplitude of the weaker signal as a function of SNR.

It is well known that when the noise is sufficiently strong, the applied model may incorrectly register a noise component in the proximity of the signal component and falsely consider it as a true signal, leading to a false positive detection. We tested the rate of false positive events on simulated data where we removed the component 2 at frequency 0.2 and searched for a signal component in the bandwidth 0.195 to 0.205. Component 1 was still present in the data. It was assumed that the number of signal components was M = 15. In 2000 trials, a signal was detected 306 times, which implies that the estimated false positive rate was about 0.15, a rather high rate of false discovery. However, the histogram of detected false positives as a function of SNR (Fig. 2) demonstrates that the maximum SNR of a false positive signal was around −18 dB and that most of the false positive signals had SNRs < −20 dB. Therefore, when we detect a signal that yields an SNR < −20 dB, we can dismiss it and consider it as a false positive, with the probability of making a mistake of at least about 0.2. In addition, for an SNR of −20 dB, the RRMSE of the estimated amplitude is about 40% or higher. Therefore, the results show that with a combined detection-estimation strategy, one can get reliable results in the range of SNR that is of interest.

Fig. 2.

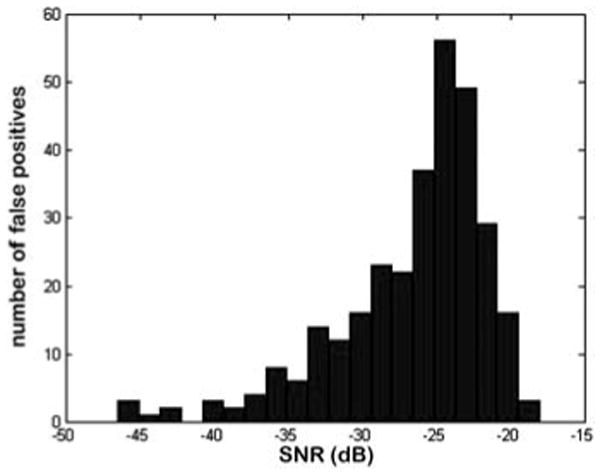
Histogram of false positives as a function of SNR.

The testing on semisynthesized data consisted of injecting a computer-generated signal into the acquired human ¹H-MRS data, thereby mimicking the presence of a metabolite. This allowed us to work with realistic data (i.e., actual amplitudes for common metabolites and actual noise characteristics) but under conditions where we had the ground truth for the fictitious metabolite. The injected signal of the fictitious metabolite had one of five different amplitudes with relative values, as compared to the creatine level, of 0.01, 0.05, 0.1, 0.5, and 1. In all experiments, the damping factor equaled 0.0045. To determine the absolute amplitude of the fictitious signal, we estimated the absolute amplitude of creatine. The frequency of the fictitious signal was not always the same, but was known. The obtained results from 22 sets of data analyzed with Monte Carlo simulations demonstrate that we could rely on our method (Table 1) for all creatine/fictitious metabolite ratios except 0.01, for which SVD-based estimates were unreliable. Furthermore, the fitted spectra and the shape of the fitted signals were verified for plausibility using independent approaches [as suggested in (11)]. The presence of the 1.28-ppm biomarker was checked not only with a single number of assumed signal components but also with a set of different components M. We took special care that the operator was always unbiased and had no knowledge of the source of the data and that we always analyzed control data in parallel. In summary, we have developed and extensively tested our SVD-based algorithm on fully synthesized and semisynthesized data. We have defined the boundaries of our algorithm in order to prevent detection of false positive signals. Our results give us strong confidence in our original claims (1).

Table 1.

SVD-based analysis of semisynthesized data.

Relative amplitude	0.01	0.05	0.1	0.5	1
Mean estimate	0.028	0.049	0.098	0.501	0.993
RRMSE	244.0	15.8	11.3	5.5	2.8

Hoch et al. (2) and Jansen et al. (4) raise concerns about the cell preparations used to obtain our ¹H-NMR spectra. Our data represent the ¹H-NMR spectra of whole-cell suspensions, as described for various settings (12, 13), and not the high-resolution magic angle spinning (HRMAS) spectra of cell extracts used in (14). It has been suggested that HRMAS of cell extracts provides highly resolved spectra (15). However, it has also been recognized that the extraction procedures, as well as different solubilities of metabolites, may not accurately represent the in vivo neuro-chemical profiles of cells analyzed (16, 17). For instance, perchloric acid extraction may lead to damage of tissue lipids and profound distortions in the representation of lipids in the cell extracts (18–21). Overall, HRMAS of cell extracts is clearly different from the spectra of whole cells (22). One of the major differences reported is the presence of lipid resonances in the whole-cell spectra but not in the spectra of extracts (22). Therefore, the whole-cell spectra and cell extract HRMAS are not readily comparable. Frequently, the whole-cell ¹H-NMR gives spectral broadening, as pointed out by Friedman (3), and this may interfere with quantification when peak area is used. Therefore, we employed the SVD-based processing, taking into account not the area of the peak but the amplitude of the peak at a given frequency (1.28 ppm) in the time domain. To accurately determine the position of all metabolites observed in all spectra, we calibrated them in vitro with tetramethylsilane (TMS), which oscillates at 0.00 ppm (1). Therefore, the calibration in vitro did not depend on the NAA or any other metabolite that could shift the frequency oscillation values. We performed the whole-cell in vitro spectroscopy on different cell types, isolated and grown in culture with a high level of purity. For each cell type, all preparations for spectroscopy were done the same way. All cells were trypsinized before spectroscopy, and in all of the spectra there is a distinct lactate doublet, clearly discernible from the 1.28-ppm peak [figure 1A in (1)]. Our results also indicate that the 1.28-ppm peak is not due to trypsin-induced cell necrosis, as suggested by Friedman (3), because one would expect the peak to be present in all cell samples, whereas it clearly was not [figure 1A in (1)]. Furthermore, the NAA peak is minimally present in the NPC preparation, which is expected because it predominates in neurons [figure 1B in (1)]. Therefore, our whole-cell spectra, calibrated with TMS and analyzed for the amplitude of the peak, overcome the potential pitfalls of whole-cell ¹H-NMR.

Jansen et al. (4) note additional concern about our findings in whole embryonic stem cells (ESCs). The variability of the ¹H-NMR acquisition was always controlled by performing spectroscopy of NPCs in parallel with other samples studied, and the amplitude of the 1.28-ppm peak in ESCs was always significantly lower than in NPCs [figure 1D in (1)]. Furthermore, whereas Jansen et al. (14) examined the extracts of ES-derived NPCs, for our whole-cell studies we used the NPCs derived from the mouse brain. Such ES-derived and somatic neural stem cells are different in their transcriptional and signaling profiles. A recent comparison of the ES-derived and brain-derived NPCs, which correspond closely to the preparations used in (14) and in our study (1), respectively, reveals numerous differences between the two cell types, including the proliferation ability, RNA profiles, enhanced mitogen-activated protein kinase signaling, and up-regulation of the insulin-like growth factor pathway in the ES-derived versus somatic neural stem cells (23). Thus, the differences between our NPC spectra (1) and spectra obtained from extracts of NPCs differentiated from ESCs (14) may arise from the difference in the experimental conditions (whole cells versus extracts, respectively), the nature of cells analyzed (ES-derived versus somatic neural stem cells), and the type of acquisition (regular spectroscopy versus HRMAS spectroscopy), and such differences do not contradict the published data (14). In addition, Jansen et al. (14) noted that they observed a broad line next to the lactate resonance (1.33 ppm), particularly in the NPCs, which might actually represent the metabolite we clearly detect in the whole NPC spectra using the SVD-based signal processing method. Our further experiments employ alternative analytical methods for analysis of both in vitro and in vivo data and have already provided encouraging preliminary results.

To summarize, we performed whole-cell ¹H-NMR of a variety of different cell types exposed to the same conditions throughout every step, from sample preparations for the ¹H-NMR acquisition to signal analysis. The breadth of our control experiments, as well as numerous additional in vitro data we have acquired, gives us the confidence that the 1.28-ppm metabolite is enriched in NPCs. Furthermore, we have performed alternative methodologies for data analysis that confirm our findings and emphasize the robustness of our analysis and the accuracy of our claims. The ultimate resolution of the concerns raised lies in identification of the precise molecular composition of the 1.28-ppm peak of NPCs, and such studies are under way.

Regarding the concerns raised by Friedman (3) about the processing of the raw in vivo data, our studies indicate that the exogenous NPC 1.28-ppm biomarker could be observed even when the raw data were processed using Fourier transform [figure 3B in (1)]. To detect the bio-marker, the raw data had to be processed using SVD-based algorithms [figure 3, A and C, in (1)]. For each in vivo case in (1), we provided spectra obtained by both Fourier transform (insets) and SVD-based algorithms [figures 3 and 4 in (1)]. However, the comparison of spectra obtained by the Fourier transform and spectra obtained by the SVD-based methods can be misleading if conclusions are drawn only by their visual inspection. An excellent example of this problem is demonstrated in a classic textbook on spectral analysis (24). There, two seemingly different spectra are shown, one that clearly suggests the presence of two harmonics in the data and another with a very broad peak and high-level noise in the background. In fact, the two spectra are equivalent and contain exactly the same information; that is, one spectrum is a monotonic transformation of the other. In our case, the reported NPC 1.28-ppm SVD-based quantification was calculated based on the estimated amplitude, with reduced influence from neighboring spectral tails. In addition, because of the differences in spectral acquisition, the constraints of signal processing of the in vitro, animal, and human data are different. Overall, while both the acquisition and signal processing of in vivo data are far more challenging than signal processing of in vitro data, our results make us confident that our algorithm generates reliable and reproducible data.

Finally, we agree with the comment of the authors (2–4) that more studies are essential before more complex investigations of NPCs in human brain disease can proceed. We are confident that our conclusions will endure the test of time and will advance our understanding of NPC biology and biochemistry and the role of these cells in health and disease.