Significance
We here demonstrate that we can resolve the seasonality of the hydrologic cycle in the Amazon using an approach, opposite to general circulation models, in which we resolve convection and parameterize large-scale circulation as a function of the resolved convection. The results emphasize the key role of cloud albedo feedback and, in particular, of the morning fog layer in determining the diurnal course of surface heat fluxes and seasonality of the surface and atmospheric heat and water cycles. These results indicate that our understanding of tropical climates over land can be considerably advanced by using coupled land−atmosphere models with explicit convection and parameterized large-scale dynamics.
Keywords: land−atmosphere interactions, Amazon, hydrologic cycle, fog, cloud-resolving models
Abstract
The diurnal and seasonal water cycles in the Amazon remain poorly simulated in general circulation models, exhibiting peak evapotranspiration in the wrong season and rain too early in the day. We show that those biases are not present in cloud-resolving simulations with parameterized large-scale circulation. The difference is attributed to the representation of the morning fog layer, and to more accurate characterization of convection and its coupling with large-scale circulation. The morning fog layer, present in the wet season but absent in the dry season, dramatically increases cloud albedo, which reduces evapotranspiration through its modulation of the surface energy budget. These results highlight the importance of the coupling between the energy and hydrological cycles and the key role of cloud albedo feedback for climates over tropical continents.
Tropical forests, and the Amazon in particular, are the biggest terrestrial CO2 sinks on the planet, accounting for about 30% of the total net primary productivity in terrestrial ecosystems. Hence, the climate of the Amazon is of particular importance for the fate of global CO2 concentration in the atmosphere (1). Besides the difficulty of estimating carbon pools (1–3), our incapacity to correctly predict CO2 fluxes in the continental tropics largely results from inaccurate simulation of the tropical climate (1, 2, 4, 5). More frequent and more intense droughts in particular are expected to affect the future health of the Amazon and its capacity to act as a major carbon sink (6–8). The land surface is not isolated, however, but interacts with the weather and climate through a series of land−atmosphere feedback loops, which couple the energy, carbon, and water cycles through stomata regulation and boundary layer mediation (9).
Current General Circulation Models (GCMs) fail to correctly represent some of the key features of the Amazon climate. In particular, they (i) underestimate the precipitation in the region (10, 11), (ii) do not reproduce the seasonality of either precipitation (10, 11) or surface fluxes such as evapotranspiration (12), and (iii) produce errors in the diurnal cycle and intensity of precipitation, with a tendency to rain too little and too early in the day (13, 14). In the more humid Western part of the basin, surface incoming radiation, evapotranspiration, and photosynthesis all tend to peak in the dry season (15–17), whereas GCMs simulate peaks of those fluxes in the wet season (10, 11). Those issues might be related to the representation of convection (1, 2, 4, 5, 13, 14) and vegetation water stress (6–8, 15–17) in GCMs.
We here show that we can represent the Amazonian climate using a strategy opposite to GCMs in which we resolve convection and parameterize the large-scale circulation (Methods). The simulations lack many of the biases observed in GCMs and more accurately capture the differences between the dry and wet season of the Amazon in surface heat fluxes and precipitation. Besides top-of-the-atmosphere insolation, the simulations require the monthly mean temperature profile as an input. We demonstrate that this profile, whose seasonal cycle itself is a product of the coupled ocean−land−atmosphere dynamics, mediates the seasonality of the Amazonian climate by modulating the vertical structure of the large-scale circulation in such a way that thermal energy is less effectively ventilated in the rainy season.
Results and Discussion
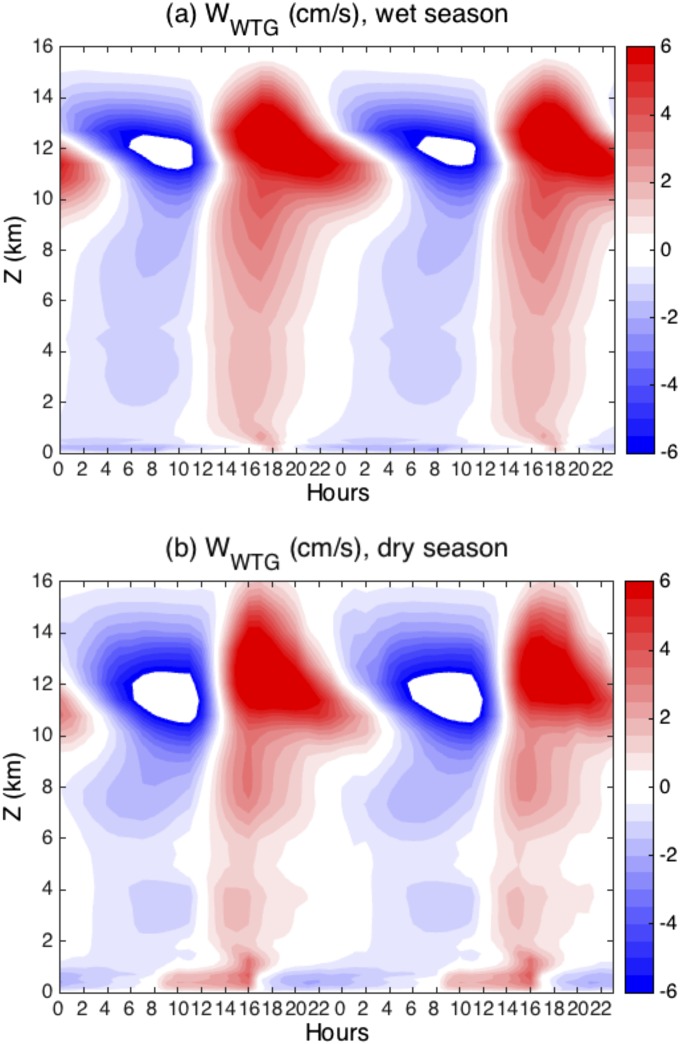
We use the Weather Research and Forecasting (WRF) model at 2-km horizontal grid spacing (see Methods for details of the runs). This resolution has been shown to be sufficient to resolve deep convection (no convective parameterization is used) and to correctly represent the sign and magnitude of the land−atmosphere interaction feedback (18), contrary to GCMs, which tend to exhibit soil moisture−precipitation feedbacks of opposite sign to that observed (19). We parameterize the time-dependent large-scale vertical motion as a function of internally resolved convection using the weak temperature gradient (WTG) approximation (Methods). The WTG approach has been used in many previous studies of tropical atmospheric dynamics to represent the feedback between locally resolved convection and larger-scale circulation (Methods) (10, 11, 20–23). Under WTG, we diagnose the horizontal average large-scale vertical motion (Fig. S1) so as to induce a vertical advective potential temperature tendency, which relaxes the model’s domain-averaged potential temperature toward that of the target profile. The same large-scale vertical motion is then also used for vertical advection of moisture (Methods).
Fig. S1.
The 2-d cycle of the modeled large-scale vertical velocity anomalies from the monthly mean (Fig. 2) in the (A) wet season and (B) dry season. Note the strong transients (diurnal cycles) exporting/importing energy that strongly modulate the moist and static energy budgets.
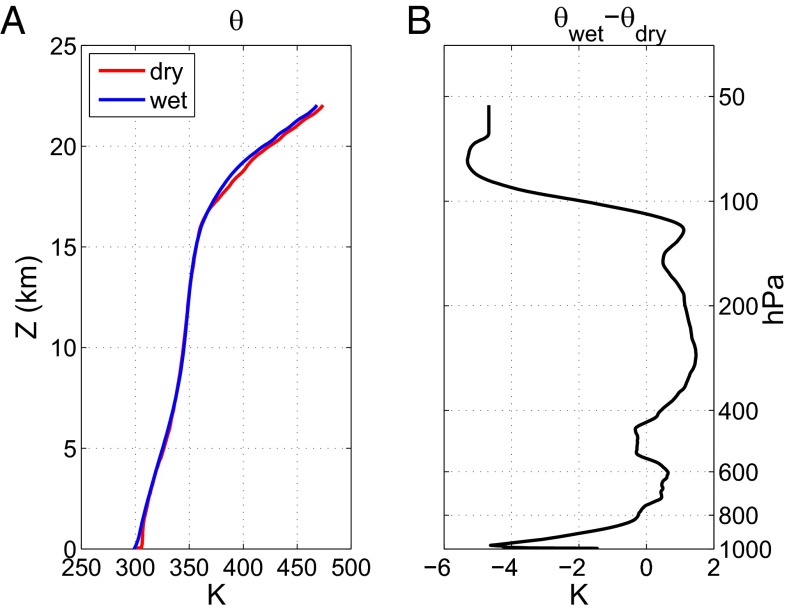
The target potential temperature profiles we use, representative of the wetter part of the Amazon, are taken from the 2014 Atmospheric Radiation Measurement mobile facility located at Manacapuru, near Manaus, Brazil (3°12'46.70”S, 60°35'53.0”W). The profiles are averaged over the month of February for the wet season, and September for the dry season, as shown in Fig. 1A. At the surface (where WTG is not directly applied; see Methods), the dry profile is warmer by about 5 K, reflecting the influence of higher surface heat fluxes (Fig. 1B). In the midtroposphere, the wet profile is warmer by more than 1 K. In the stratosphere, the wet profile is colder by more than 5 K due to the seasonal elevation of the tropopause. All these differences are consequences of the seasonal cycle itself; the warmer troposphere and cooler lower stratosphere are typical differences between states of stronger and weaker deep convection (24). Here the ultimate cause of the wet−dry season temperature difference is presumably the stronger insolation in the wet season, but the temperature differences are in part an outcome of land−atmosphere interactions, as the tropospheric temperature difference between the two seasons in the nearby oceanic regions shows no such signal (Fig. S2). Because we assume this seasonal difference in temperature profiles, our simulations do not predict the seasonal changes purely as a function of external boundary conditions and forcing. Rather, we predict part of the solution—including precipitation, clouds, and surface fluxes—given another, the free atmospheric temperature. This allows us to understand the mediation of convection and land−atmosphere interaction by the atmospheric temperature, similar to what has been done in studies of tropical cyclones and the Madden−Julian oscillation (24, 25).
Fig. 1.
(A) Monthly mean observed atmospheric potential temperature profile in the wet (February) and dry (September) season observed at Manacapuru, near Manaus, Brazil (3°12'46.70”S, 60°35'53.0”W) using radiosonde and used as reference profiles for the WTG method. (B) Atmospheric potential temperature difference between the wet and dry seasons.
Fig. S2.
Monthly mean tropical potential temperature at seven pressure levels from near surface to lower stratosphere, averaged during the period from 1979 to 2014 using the ERA-Interim global reanalysis dataset. Mean potential temperature in (Left) February and (Middle) September; (Right) difference between February and September. Over the Amazon, the wet season is generally cooler than the dry season near the surface and the tropopause but warmer in the free troposphere, consistent with observation (Fig. 1).
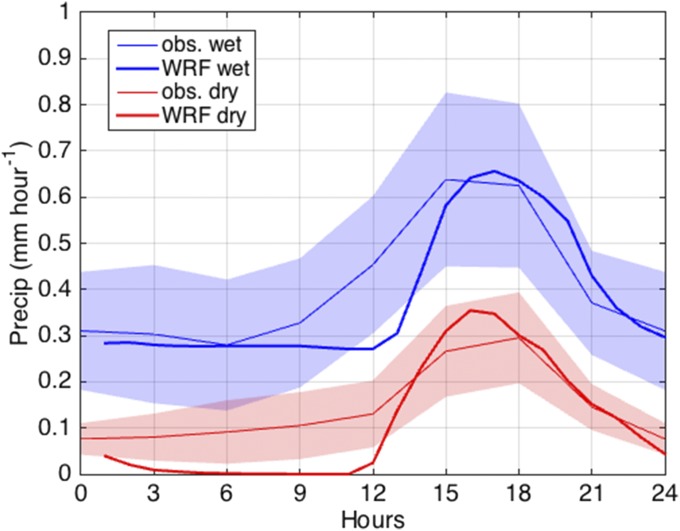
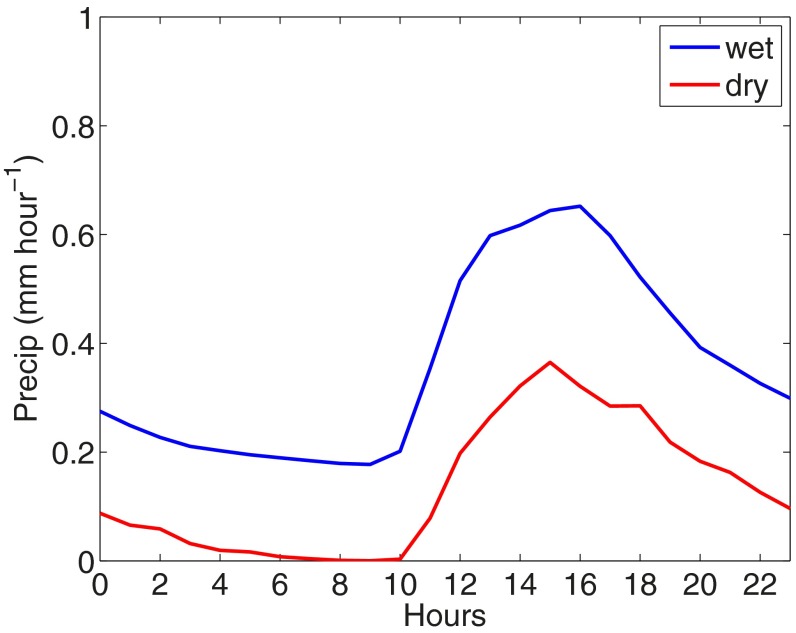
The increase in precipitation in the wet season relative to the dry season (Fig. 2) can be attributed to the reduction in the export of moist static energy by the large-scale circulation (see Supporting Information), which is a consequence of the more stable temperature profile (25), despite the absence of an increase in surface fluxes or radiative heating. This increase, in turn, moistens the land surface, an important factor leading to the differences in cloud between the wet and dry seasons. In agreement with observations [here Climate Prediction Center Morphing Technique (CMORPH) (26, 27) data averaged over 10 y (2004−2014) for the months of February and September for the wet and dry seasons, respectively], our simulated precipitation maxima occur in the early to late afternoon in both seasons, with greater absolute amplitude in the wet season.
Fig. 2.
Diurnal cycle of modeled (thick line) and observed (thin line) precipitation from CMORPH along with one-third of the SD (shaded area) in the local time zone.
In both seasons, rapid precipitation transitions from minima in the morning local hours to maxima in the afternoon are associated with transitions from shallow to deep convection (Fig. 3). In the dry season (Fig. 3A), convection starts in the morning (1000 hours time zone local time) manifesting first as a sharp increase in midlevel cloud at that time coverage, and then a more gradual transition to deep convection in the afternoon associated with the timing of rainfall maxima. Midlevel cloud cover dissipates overnight into the early morning. The overall cloud cover is relatively small during daytime and higher in the afternoon and evening, as observed, but contrary to what GCMs predict as mentioned above. The smaller cloud cover during daytime drives greater surface fluxes, and, in particular, evapotranspiration and photosynthesis, by allowing more solar radiation to reach the surface.
Fig. 3.
Composite of the WRF simulated 2-d cycle of fractional cloud cover for the (A) wet and (B) dry season. Note the fog layer above the surface in the wet season.
In the wet season (Fig. 3B), the diurnal cycle of cloud cover exhibits a different behavior. In addition to the increase in cloud cover, there is now a distinct layer of fog above the surface that is maintained by radiative cooling from the wet surface and lasts from midnight until noon, as observed in the Amazon (Figs. S3 and S4) and other rainforests. This morning fog layer blocks shortwave radiation from reaching the surface and reduces daytime net surface shortwave radiation and evapotranspiration. Such morning fog was also shown to be critical in the maintenance of distinct diurnal climate equilibrium regimes by a previous modeling study (28, 29).
Fig. S3.

Time series of observed surface relative humidity (%) in (A and C) February and (B and D) September at eddy covariance tower K34 in the Amazon (A and B, located 50 m above the ground, latitude −2.61° and longitude −60.21°) and at a tower in Fazenda Nossa Senhora (FNS) in Rondonia (C and D, located 4 m above the ground, latitude −10.77° and longitude −62.34° acquired in 2000). Relative humidity reaches 100% nearly every night and early morning in February in both the Amazon and Rondonia, indicative of the near omnipresence of nighttime fog in the wet season. LBA, Large-Scale Biosphere and Atmosphere in the Amazon.
Fig. S4.
Ceilometer data from the LBA campaign in Rondonia. The presence of fog at night and early morning in February (Top) is clearly apparent with a stronger backscattering response (in red−brown) due to the presence of water droplets (also during precipitation events—vertical red lines). Fog is almost absent in the dry season (Bottom).
As a result, the latent heat flux (Fig. 4A) and surface temperature are smaller in the wet season than in the dry season, because surface shortwave radiation is reduced by the fog layer (Fig. 4B), which more than compensates for the higher soil water availability and lower Bowen ratio in the wet season (from diurnal average of 0.4 in the dry season to 0.32 in the wet season based on eddy covariance data). We note that surface observations are difficult to correctly measure in the presence of dew (eddy covariance measurements cannot correctly record measurements) so that most days with fog are not captured by surface observations; thus clear days (infrequent in the wet season; Figs. S3 and S4) with higher latent heat flux are overrepresented in the observations. Because the diurnal rise of the surface turbulent fluxes is delayed in the wet season by the fog layer, the transition from shallow to deep convection occurs later in the day compared with the dry season.
Fig. 4.
Diurnal cycle of (A) latent heat flux, and (B) net shortwave at the surface, for WRF modeled (thick) and observed (thin) fluxes. Observed fluxes are taken from the climatology of eddy covariance fluxes observed at K34 station in Reserva Biológica do Cuieiras. We note that surface observations are difficult to obtain in the presence of dew (eddy covariance measurements typically cannot correctly record measurements) so that the observations typically omit fog situations, with an overrepresentation of relatively clear days compared with fog days.
Although the downward solar insolation at the top of the atmosphere in the wet season exceeds that in the dry season by more than 20 W⋅m−2, the net shortwave radiation at the surface is greater in the dry season (Fig. 4B). This results from a strong negative cloud albedo feedback in the wet season and greater reflection of shortwave radiation to space. The fog layer is an important contributor to this albedo. We further quantify the cloud albedo feedback by computing cloud radiative forcing (CRF), as the clear-sky minus all-sky upwelling flux at the top of the atmosphere (Fig. 5). Weaker convection in the dry season induces a smaller longwave CRF component compared with that induced in the wet season. However, the shortwave CRF in the wet season is much more negative than in the dry season due to the presence of the fog layer. Because the shortwave CRF dominates in the wet season, and longwave CRF dominates in the dry season, the net CRF is negative in the wet season and positive in the dry. Comparison with CRF obtained from the Clouds and the Earth’s Radiant Energy System (CERES) [the CERES SYN1deg daily radiative fluxes (30, 31)] shows a reasonable agreement with our simulations, although some biases exist.
Fig. 5.
Cloud radiative forcing, shortwave (SWCRF), longwave (LWCRF), and net (NETCRF) for the wet and dry seasons as simulated (squares) and observed from CERES (circles).
Perhaps surprisingly, the seasonal difference in the top of the atmosphere seasonal mean insolation is not the dominant control that determines the differences in seasonal climate, even though it is ultimately what controls the seasonal cycle in nature. In our simulations, the differences in the target potential temperature profiles are primarily responsible for the seasonal differences described above. We performed sensitivity experiments in which the insolation from the wet season is used with the target potential temperature profile from the dry season and vice versa (see Figs. S5−S7). We also performed sensitivity experiments over Rondonia (10.7°S, 62.7°W), where the seasonal difference in insolation is greater (Figs. S8−S10). When insolation is varied while holding the potential temperature profile fixed, no significant difference is found in terms of the typical pattern of diurnal and seasonal patterns of precipitation. Again, the cloud albedo adjusts so that the surface shortwave radiation is always higher in the case of the dry season profile, leading to higher evapotranspiration flux (Fig. S9). This behavior differs from convection over oceans, where stronger seasonal insolation leads to higher surface fluxes (and sea surface temperature), and cloud albedo is not so tightly coupled to atmospheric convection because, unlike land, the ocean can both substantially store and transport heat reducing the coupling of evaporation with shortwave incoming radiation.
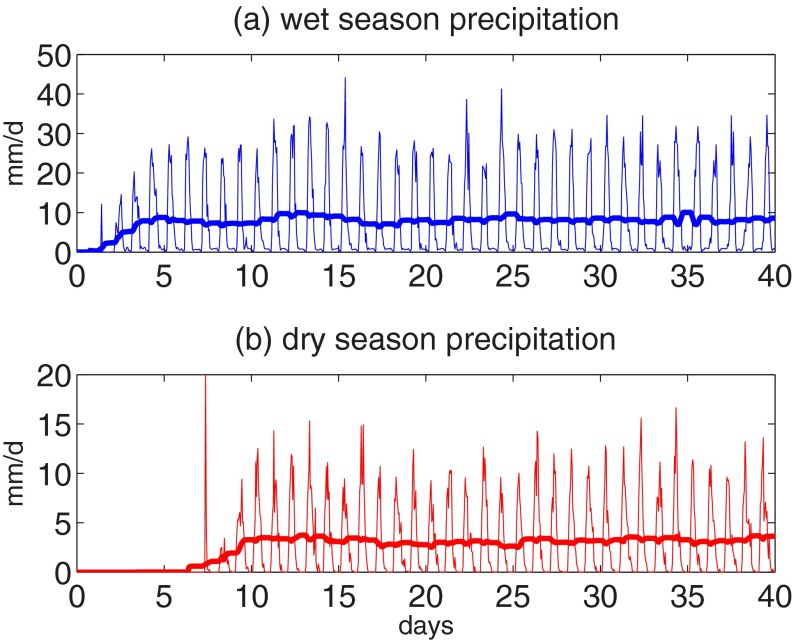
Fig. S5.
Time series of modeled precipitation, hourly (thin line) and 2-d running average (thick line), in the (A) wet and (B) dry seasons.
Fig. S7.
Simulated diurnal cycle of precipitation with correct insolation (continuous line) and from sensitivity experiment in which insolation is switched (dashed line) in the wet (blue) and dry (red) seasons. Sensitivity experiment produces slightly more precipitation in the mean (∼0.5 mm/d).
Fig. S8.
Same as Fig. 1 but for the 1999 radiosoundings observed in Santarem, Brazil. Sounding taken from the LBA.
Fig. S10.
As in Fig. 4 but for Rondonia. Surface observations are taken from eddy covariance observations in FNS (latitude −10.77° and longitude −62.34°; acquired in 2000).
Fig. S9.
Diurnal cycle of simulated precipitation using sounding for Rondiona for the wet (blue) and dry (red) seasons.
Fig. S6.
As in Fig. S5 but for sensitivity experiment with insolation being switched between the wet and dry seasons with everything else the same.
Methods
Model Configuration.
We use the WRF model version 3.3, in three spatial dimensions, with doubly periodic lateral boundary conditions. The experiments are conducted with Coriolis parameter f = 0. The horizontal domain size is 192 × 192 km2 with a grid spacing of 2 km. There are 50 vertical levels total, with the top level at 22 km, and 10 levels in the lowest 1 km. Gravity waves propagating vertically are absorbed in the top 5 km to prevent unphysical wave reflection off the top boundary by using the implicit damping vertical velocity scheme (32). The 2D Smagorinsky first-order turbulent closure scheme is used to parameterize the horizontal transports by subgrid eddies. The Yonsei University first-order closure scheme is used to parameterize nonlocal boundary layer turbulence and vertical subgrid-scale eddy diffusion (33). The surface fluxes of moisture and heat are parameterized following Monin−Obukhov similarity theory. Microphysics is simulated using the Purdue−Lin bulk scheme (34), which has six species: water vapor, cloud water, cloud ice, rain, snow, and graupel. Radiative fluxes are determined interactively using the National Center for Atmospheric Research Community Atmosphere Model version 3.0 scheme for shortwave and longwave radiation. Both surface and radiative fluxes are fully interactive.
The atmospheric model is coupled to the Noah land surface model (LSM) (35) that has four soil layers at 10, 30, 60, and 100 cm depth. The LSM provides four quantities to the atmospheric model: sensible heat flux, latent heat flux, upward longwave radiation, and upward shortwave radiation off the ground. The LSM prognostic land states are surface skin temperature, volumetric total (liquid and frozen) soil moisture at each layer, soil temperature at each layer, and canopy water content. Vegetation type is evergreen forest, surface albedo is 0.12, and the wind field is left unnudged.
Parameterized Large-Scale Circulation and Initial Conditions.
The large-scale vertical velocity is dynamically parameterized using the WTG method (20, 21). The WTG vertical velocity WWTG is obtained by a Newtonian relaxation with a relaxation time scale (over which gravity waves propagate out of the domain) taken here as 2 h (20, 21),
| [1] |
where is the domain mean potential temperature, and is the observed potential temperature profile obtained from radiosondes averaged over 1 mo of observations. WWTG is then linearly interpolated in the boundary layer to zero at the surface because gravity waves are not the main mode of buoyancy adjustment in the boundary layer. The impact is negligible in the daytime boundary layer as it is well-mixed so that the vertical gradients are null. Boundary layer height is determined interactively in the WRF model using the bulk Richardson number method and varies diurnally.
Once WWTG is obtained, it is used to define the domain-average large-scale tendencies of potential temperature and specific humidity over the computational domain,
| [2] |
| [3] |
respectively, where is the domain mean water vapor mixing ratio.
Initial conditions are seasonally averaged quantities in the dry and wet seasons using the ERA-Interim data set. The model is run for about 40 d and the analysis conducted on the equilibrium part only, which is the last 30 d. We have performed a sensitivity test on the soil moisture initial conditions, by switching the seasonal magnitudes, and they had no influence on the results. The reference, target temperature profile is time-independent in each season and does not include diurnal variations (21). The modeled diurnal cycles of surface fluxes, clouds, and precipitation are driven solely by the diurnal cycle of radiation at the top of the atmosphere. Daily mean insolation in the dry season is held fixed at 415 W⋅m−2 and, in the wet season, at 439 W⋅m−2, reflecting values at Manacapuru.
Surface Observations.
We used eddy covariance data from the K34 station located in Estação Experimental de Silvicultura Tropical 02°37'S, 60°09'W, located around 60 km from Manaus. We have used data from 2000 to 2006 available at Oak Ridge National Laboratory (36). We used quality-controlled eddy covariance data, based on outliers comparison, wind speed (acceptable variation is two SD units from the linear regression), and unresponsive sensor checks. Eddy covariance measurements typically cannot correctly measure in the presence of dew; thus fog conditions are undersampled, which implies that the latent heat flux in Fig. 4 is an overestimate of the true latent heat flux (an average of fog conditions with little radiation and nonfog conditions with higher radiation).
Conclusion
We have shown that, when given the top of the atmosphere insolation and the monthly mean free-atmospheric temperature profile, the seasonal and diurnal cycles of cloud, precipitation, and surface fluxes can be simulated by a limited domain cloud-resolving model with parameterized large-scale forcing without the biases commonly found in global climate models.
We can view the seasonality in the Amazon as mediated by the atmospheric temperature profile. That profile itself results from the stronger convection in the wet season, but the increased wet season precipitation in the model is still a nontrivial prediction of the model. It can be explained by the reduced ventilation of moist static energy from the column, which is a consequence of the warmer tropospheric temperature profile in the wet season.
The surface fluxes, on the other hand, are strongly controlled by the diurnal cycle of cloud albedo, and especially of wet season fog, which blocks shortwave radiation from reaching the surface in the early morning. This fog is an essential regulator of the Amazon climate.
We demonstrate that a high-resolution cloud-resolving model with parameterized large-scale circulation offers a new window onto the dynamics of climate in the Amazon. In the future, this approach may allow new insights into the Amazon’s changes under anthropogenic influence and the capacity of the basin to act as a CO2 sink in the future.
Budget Analysis and the Normalized Gross Moist Stability
The budgets of the column-integrated moist static energy h (sum of the thermal, potential, and latent energy) and the dry static energy s (sum of the thermal and potential energy) in statically steady state can be written as
| [S1] |
| [S2] |
where is the mass-weighted vertical integral from the bottom to the top of the domain. E, H, P, W, and are the latent heat flux, sensible heat flux, precipitation, large-scale vertical velocity, and column-integrated radiative heating, respectively. Overbars denote time and domain mean.
Combining Eqs. S1 and S2, we can obtain a diagnostic equation for precipitation in the steady state (32),
| [S3] |
where is the normalized gross moist stability, a dimensionless quantity that encapsulates the influence of divergent atmospheric circulation on moist and dry static energy budgets in the way relevant to precipitation (37, 38). It may also be viewed as a measure of precipitation efficiency. The overbar in Eq. S3 is a time and horizontal mean, so NGMS is determined both by the time mean profiles of the quantities under the overbars and the correlations of deviations from the time mean. Calculation of the NGMS as a residual from Eq. S3 above gives 0.63 in the dry season and 0.061 in the wet season, indicating much less efficient ventilation of moist static energy from the column during the wet season. Some of the much smaller NGMS in the wet season is attributable to the diurnal mean vertical profile of W (e.g., refs. 37 and 39), which is less top-heavy in the wet season. However, the strong diurnal variations in the large-scale vertical motion, shown in Fig. S1, contribute significantly to the export of moist static energy and thus to NGMS, so that the diurnal mean budget cannot be explained only in terms of the diurnal mean profile of W.
Acknowledgments
P.G. thanks Florian Cochard for preliminary radiosonde and profile analysis. P.G. was supported by Department of Energy Grants GoAmazon DE-SC0011094 and DE-FOA-0000885 on the transition between shallow and deep convection. U.A., S.W., and A.H.S. acknowledge support from the National Science Foundation under Grant AGS-1008847 and the Office of Naval Research under MURI Grant (N00014-12-1-0911). Weather Research and Forecasting experiments were performed on the YETI cluster at Columbia University. Data profiles at the Atmospheric Radiation Measurement site were obtained at www.arm.gov/sites/amf/mao/. Surface flux observations were obtained at dx.doi.org/10.3334/ORNLDAAC/1174.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1505077112/-/DCSupplemental.
References
- 1.Achard F, Eva HD, Mayaux P, Stibig H-J, Belward A. Improved estimates of net carbon emissions from land cover change in the tropics for the 1990s. Global Biogeochem Cycles. 2004;18(2):GB2008. [Google Scholar]
- 2.Hoffman FM, et al. Causes and implications of persistent atmospheric carbon dioxide biases in Earth system models. J Geophys Res. 2014;119(2):141–162. [Google Scholar]
- 3.Cai W, et al. Improved estimations of gross primary production using satellite-derived photosynthetically active radiation. J Geophys Res. 2014;119(1):110–123. [Google Scholar]
- 4.Todd-Brown KEO, et al. Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations. Biogeosciences. 2013;10(3):1717–1736. [Google Scholar]
- 5.Cox PM, et al. Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability. Nature. 2013;494(7437):341–344. doi: 10.1038/nature11882. [DOI] [PubMed] [Google Scholar]
- 6.Lee JE, et al. Forest productivity and water stress in Amazonia: Observations from GOSAT chlorophyll fluorescence. Proc Biol Sci. 2013;280(1761):20130171. doi: 10.1098/rspb.2013.0171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reichstein M, et al. Climate extremes and the carbon cycle. Nature. 2013;500(7462):287–295. doi: 10.1038/nature12350. [DOI] [PubMed] [Google Scholar]
- 8.Gatti LV, et al. Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements. Nature. 2014;506(7486):76–80. doi: 10.1038/nature12957. [DOI] [PubMed] [Google Scholar]
- 9.de Arellano JV-G, van Heerwaarden CC, Lelieveld J. Modelled suppression of boundary-layer clouds by plants in a CO2-rich atmosphere. Nat Geosci. 2012;5(10):701–704. [Google Scholar]
- 10.Pascale S, Lucarini V, Feng X, Porporato A, Hasson SU. Analysis of rainfall seasonality from observations and climate models. Clim Dyn. 2014;44(11-12):3281–3301. [Google Scholar]
- 11.Martins G, Randow von C, Sampaio G, Dolman AJ. Precipitation in the Amazon and its relationship with moisture transport and tropical Pacific and Atlantic SST from the CMIP5 simulations. Hydrol Earth Syst Sci Discuss. 2015;12(1):671–704. [Google Scholar]
- 12.de Gonçalves LGG, et al. Overview of the Large-Scale Biosphere−Atmosphere Experiment in Amazonia Data Model Intercomparison Project (LBA-DMIP) Agric For Meteorol. 2013;182-183:111–127. [Google Scholar]
- 13.Dai A. Precipitation characteristics in eighteen coupled climate models. J Clim. 2006;19(18):4605–4630. [Google Scholar]
- 14.Bechtold P, et al. Representing equilibrium and nonequilibrium convection in large-scale models. J Atmos Sci. 2014;71(2):734–753. [Google Scholar]
- 15.Da Rocha HR, et al. Patterns of water and heat flux across a biome gradient from tropical forest to savanna in Brazil. J Geophys Res. 2009;114(G1):G00B12. [Google Scholar]
- 16.Fisher JB, et al. The land−atmosphere water flux in the tropics. Glob Change Biol. 2009;15(11):2694–2714. [Google Scholar]
- 17.Restrepo-Coupe N, et al. What drives the seasonality of photosynthesis across the Amazon basin? A cross-site analysis of eddy flux tower measurements from the Brasil flu network. Agric For Meteorol. 2013;182-183:128–144. [Google Scholar]
- 18.Taylor CM, et al. Modeling soil moisture-precipitation feedbacks in the Sahel: Importance of spatial scale versus convective parameterization. Geophys Res Lett. 2013;40(23):6213–6218. [Google Scholar]
- 19.Guillod BP, Orlowsky B, Miralles DG, Teuling AJ, Seneviratne SI. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat Commun. 2015;6:6443. doi: 10.1038/ncomms7443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Anber U, Wang S, Sobel A. Response of atmospheric convection to vertical wind shear: Cloud-system-resolving simulations with parameterized large-scale circulation. Part I: Specified radiative cooling. J Atmos Sci. 2014;71(8):2976–2993. [Google Scholar]
- 21.Wang S, Sobel AH, Kuang Z. Cloud-resolving simulation of TOGA-COARE using parameterized large-scale dynamics. J Geophys Res. 2013;118(12):6290–6301. [Google Scholar]
- 22.Sobel AH, Bretherton CS. Large-scale waves interacting with deep convection in idealized mesoscale model simulations. Tellus, Ser A. 2003;55(1):45–60. [Google Scholar]
- 23.Sobel AH, Nilsson J, Polvani L. The weak temperature gradient approximation and balanced tropical moisture waves. J Atmos Sci. 2001;58(23):3650–3665. [Google Scholar]
- 24.Holloway CE, Neelin JD. The convective cold top and quasi equilibrium. J Atmos Sci. 2007;64(5):1467–1487. [Google Scholar]
- 25.Raymond DJ, Sessions SL. Evolution of convection during tropical cyclogenesis. Geophys Res Lett. 2007;34(6):L06811. [Google Scholar]
- 26.Dirmeyer PA, et al. Simulating the diurnal cycle of rainfall in global climate models: Resolution versus parameterization. Clim Dyn. 2011;39(1-2):399–418. [Google Scholar]
- 27.Joyce RA, Janowiak J, Arkin PA, Xie P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J Hydrometeorol. 2004;5(3):487–503. [Google Scholar]
- 28.Ramos da Silva R, Avissar R. The hydrometeorology of a deforested region of the Amazon basin. J. Hydrometeorol. 2006;7(5):1028–1042. [Google Scholar]
- 29.Rochetin N, Lintner BR, Findell KL, Sobel AH, Gentine P. Radiative convective equilibrium over a land surface. J Clim. 2014;27(23):8611–8629. [Google Scholar]
- 30.Wielicki BA, et al. Clouds and the Earth’s Radiant Energy System (CERES): An Earth observing system experiment. Bull Am Meteorol Soc. 1996;77(5):853–868. [Google Scholar]
- 31.Loeb NG, et al. Advances in understanding top-of-atmosphere radiation variability from satellite observations. Surv Geophys. 2012;33(3-4):359–385. [Google Scholar]
- 32.Klemp JB, Dudhia J, Hassiotis AD. An upper gravity-wave absorbing layer for NWP applications. Mon Weather Rev. 2008;136(10):3987–4004. [Google Scholar]
- 33.Hong S-Y, Pan H-L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon Weather Rev. 1996;124(10):2322–2339. [Google Scholar]
- 34.Chen S-H, Sun W-Y. A one-dimensional time dependent cloud model. J Meteorol Soc Jpn. 2002;80(1):99–118. [Google Scholar]
- 35.Ek MB. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J Geophys Res. 2003;108(D22):8851. [Google Scholar]
- 36. Saleska SR, da Rocha HR, Huete AR, Nobre AD, Artaxo P, and Shimabukuro YE (2013) LBA-ECO CD-32 Flux Tower Network Data Compilation, Brazilian Amazon: 1999−2006. Available at daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1174. Accessed December 25, 2014.
- 37.Sobel AH. 2007. Simple models of ensemble‐averaged precipitation and surface wind, given the SST. The Global Circulation of the Atmosphere, eds Schneider T, Sobel AH (Princeton Univ Press, Princeton, NJ), pp 219–251.
- 38.Neelin JD, Held IM. Modeling tropical convergence based on the moist static energy budget. Mon Weather Rev. 1987;115(1):3–12. [Google Scholar]
- 39. Raymond DJ, Sessions SL, Sobel AH, Fuchs Z (2009) The mechanics of gross moist stability. J Adv Model Earth Syst 1(3):9.