Resilient 3D hierarchical architected metamaterials

Significance

Fractal-like architectures exist in natural materials, like shells and bone, and have drawn considerable interest because of their mechanical robustness and damage tolerance. Developing hierarchically designed metamaterials remains a highly sought after task impaired mainly by limitations in fabrication techniques. We created 3D hierarchical nanolattices with individual beams comprised of multiple self-similar unit cells spanning length scales over four orders of magnitude in fractal-like geometries. We show, through a combination of experiments and computations, that introducing hierarchy into the architecture of 3D structural metamaterials enables the attainment of a unique combination of properties: ultralightweight, recoverability, and a near-linear scaling of stiffness and strength with density.

Abstract

Hierarchically designed structures with architectural features that span across multiple length scales are found in numerous hard biomaterials, like bone, wood, and glass sponge skeletons, as well as manmade structures, like the Eiffel Tower. It has been hypothesized that their mechanical robustness and damage tolerance stem from sophisticated ordering within the constituents, but the specific role of hierarchy remains to be fully described and understood. We apply the principles of hierarchical design to create structural metamaterials from three material systems: (i) polymer, (ii) hollow ceramic, and (iii) ceramic–polymer composites that are patterned into self-similar unit cells in a fractal-like geometry. In situ nanomechanical experiments revealed (i) a nearly theoretical scaling of structural strength and stiffness with relative density, which outperforms existing nonhierarchical nanolattices; (ii) recoverability, with hollow alumina samples recovering up to 98% of their original height after compression to ≥50% strain; (iii) suppression of brittle failure and structural instabilities in hollow ceramic hierarchical nanolattices; and (iv) a range of deformation mechanisms that can be tuned by changing the slenderness ratios of the beams. Additional levels of hierarchy beyond a second order did not increase the strength or stiffness, which suggests the existence of an optimal degree of hierarchy to amplify resilience. We developed a computational model that captures local stress distributions within the nanolattices under compression and explains some of the underlying deformation mechanisms as well as validates the measured effective stiffness to be interpreted as a metamaterial property.

Hierarchy is ubiquitous in the natural world; characterizing it, understanding its origins, and discovering its role in enhancing material properties are essential to designing new advanced materials (1–4). Natural structural materials, like Euplectella sponges, radiolarians, and bone, are exceptionally resilient against extreme mechanical environments and seem to draw their robustness from intricate mechanical networks that contain multiple levels of hierarchy (3–7). Hierarchical engineered structures are used in modern architecture, with notable examples being the Eiffel tower and the Garabit viaduct (8); today, hierarchy is seen commonly in construction cranes and building scaffolding. Both natural and engineered structures use the concept of hierarchical design to minimize material use while optimizing structural integrity.

The hierarchical scale of a material is defined by its order, which represents the number of distinct structural length scales (2). Design principles and theories describing hierarchical structural materials exist (2, 9), and macroscopic second- and third-order 2D cellular solids, like honeycombs (10, 11) and corrugated core sandwich panels (12–14), have been designed and tested experimentally. Theories that describe the design and optimization of 3D hierarchical trusses have been proposed (15–18); until recently, their fabrication presented a challenge. Modern fabrication breakthroughs have enabled the creation of 3D architected materials. These techniques include self-propagating photopolymer waveguides used to create Ni-based ultralight microlattices (19), microstereolithography capable of fabricating simultaneously strong and ultralight metal- and ceramic-based microlattices (20), and two-photon lithography direct laser writing, which enabled the creation of nanolattices with features sufficiently in the nanometer regime to capitalize on size-affected material properties in addition to structural effects (21–23).

We report the fabrication, mechanical characterization, and computational analysis of hierarchical nanolattices made out of three different materials: (i) solid polymer IP-Dip (Nanoscribe GmbH), (ii) a core-shell composite with a polymer core and a 20-nm-thick Al₂O₃ coating, and (iii) hollow 20-nm-thick Al₂O₃. In situ nanomechanical deformation experiments were performed on a number of different geometries and showed that hierarchically designed nanolattices exhibit enhanced recoverability over simple periodic ones (22) and have a close to linear scaling of yield strength and stiffness with relative density. These findings were confirmed by computational predictions, and they are consistent with theoretical predictions for stretching-dominated solids (24). Simulations were performed to further elucidate the local stress distributions within the nanolattices, which confirm the effective experimental nanolattice response and help shed light on the distribution of loadbearing components that are responsible for the overall observed nanolattice performance.

Various sample geometries were tested to quantify the effect of geometry and relative density on mechanical behavior (Materials and Methods and SI Appendix, Tables S1–S3). Samples were designed using a recursive method, where a unit cell is patterned along the length of the beams of a self-similar unit cell, resulting in a fractal-like geometry (Fig. 1A and SI Appendix, Fig. S1). This design concept can be extended to create hierarchical metamaterials of any order with previously unobserved combinations of properties across multiple length scales—for example, high strength to weight ratios, tunable mass density, near-infinite bulk to shear modulus ratios (25, 26), and negative Poisson’s ratios (27, 28). The versatility of this fabrication method is shown in Fig. 1 and SI Appendix, Fig. S2, which show examples of designed and fabricated hierarchical nanolattice geometries.

Fig. 1.

Computer-aided design (CAD) and scanning electron microscopy (SEM) images of various hierarchical nanolattices show the versatility of the nanolattice fabrication technique. (A) CAD images illustrating the process of making a third-order hierarchical nanolattice. A zeroth-order repeating unit, an elliptical beam, is arranged into a first-order octahedron; it becomes the repeating unit for a second-order octahedron of octahedra, which is then arranged to create a third-order octahedron of octahedra of octahedra. (B, Upper, C, Upper, D, Upper, and E, Upper) CAD and (B, Lower, C, Lower, D, Lower, and E, Lower) SEM images of the various second-order samples. (Scale bars: 20 µm.) (F) SEM image of a second-order octahedron of octahedra lattice. (Scale bar: 50 µm.) (G) A zoomed-in image of the second-order octahedron of octahedra lattice showing the first-order repeating units that make up the structure. (Scale bar: 10 µm.) (H) SEM image of a third-order octahedron of octahedra of octahedra. (Scale bar: 25 µm.)

Results

Strength and Stiffness.

All fabricated samples were compressed uniaxially in an in situ nanoindenter (InSEM; Nanomechanics Inc.) to 50% strain before unloading. The load displacement data for each of the samples showed an initial linear region from which the effective loading stiffness was determined followed by an inelastic region with behavior that varied depending on the constituent material (Figs. 2 and 3). Failure strength and modulus were calculated as defined in Materials and Methods. Linear elastic finite element simulations were performed on representative nanolattices to predict stiffness and local stress distributions.

Fig. 2.

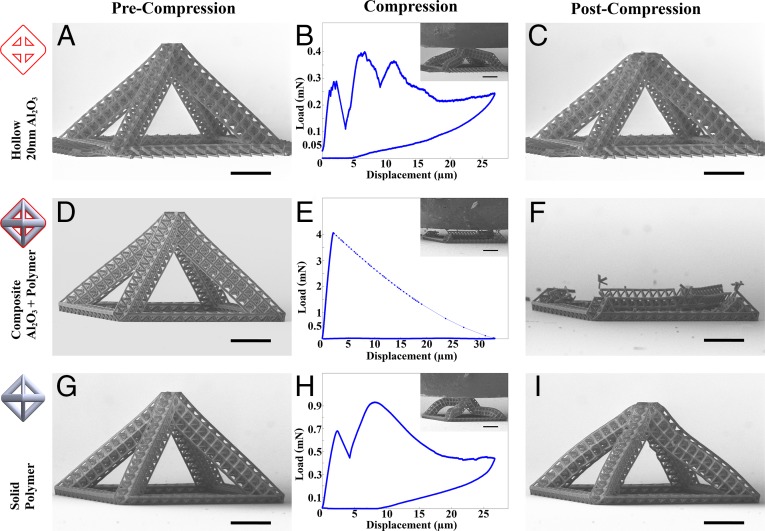
Compression experiments on second-order octahedron of octet half-cells with N = 15 and L = 8. (A) Image of the hollow 20-nm walled Al₂O₃ sample before compression. (B) Load displacement data that show compression to 50% strain. Inset corresponds to 50% strain. (C) Postdeformation image of the hollow sample. (D) Image of the composite polymer and 20-nm Al₂O₃ sample before compression. (E) Load displacement data that show compression to 65% strain. Inset corresponds to the sample after the occurrence of a strain burst. (F) Postdeformation image of the composite sample. (G) Image of the polymer sample before compression. (H) Load displacement data that show compression to 50% strain. Inset corresponds to 50% strain. (I) Postdeformation image of the polymer sample. (Scale bars: 20 µm.)

Fig. 3.

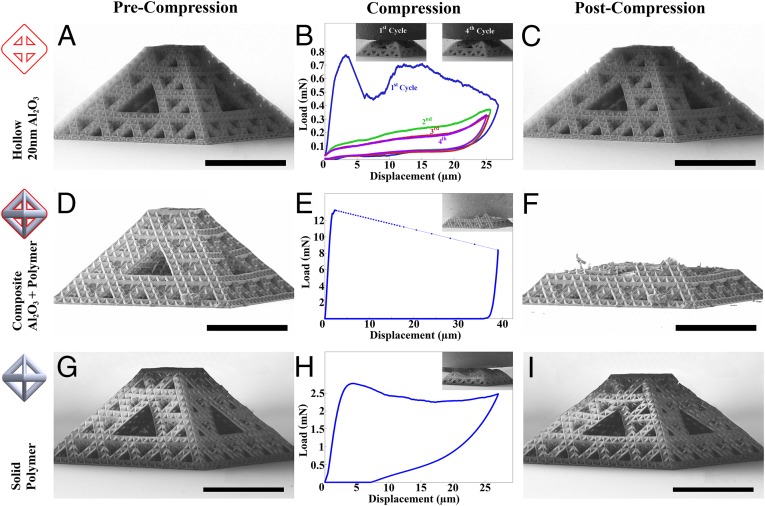
Compression experiments on third-order octahedron of octahedra of octahedra half-cells with N = 5 and L = 8. (A) Image of the hollow 20-nm walled Al₂O₃ sample before compression. (B) Load-displacement data that show cyclic compression to 50% strain. Insets correspond to 50% strain at various loading cycles. (C) Postcompression image of the hollow sample. (D) Image of the composite polymer and 20-nm Al₂O₃ sample before compression. (E) Load-displacement data that show compression to 65% strain. Inset corresponds to the sample after the occurrence of a strain burst. (F) Postdeformation image of the composite sample. (G) Image of the polymer sample before compression. (H) Load displacement data that show compression to 50% strain. Inset corresponds to 50% strain. (I) Postdeformation image of the polymer sample. (Scale bars: 50 µm.)

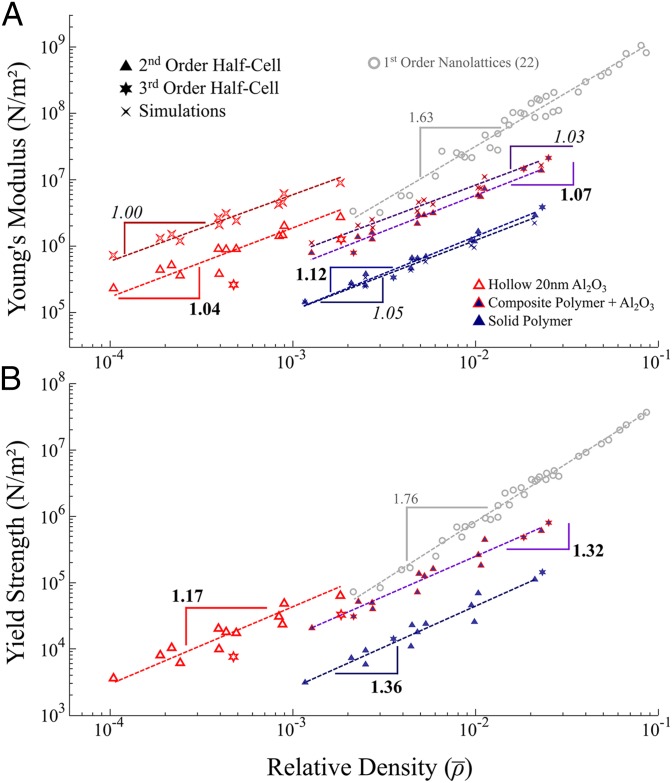
Second-order half-cell samples of varying material compositions were tested with densities spanning over two orders of magnitude from $\rho =0.30\hspace{0.17em}\hspace{0.17em}\text{kg}\hspace{0.17em}{\text{m}}^{-3}$ to $\rho =33.2\hspace{0.17em}\hspace{0.17em}\text{kg}\hspace{0.17em}{\text{m}}^{-3}$. Individual material systems had relative densities that spanned more than one order of magnitude. Strength and modulus in architected materials scale with relative density as

$$E=B{E}_s{\overline{\rho }}^{\beta }$$ [1]

and

$${\sigma }_y=C{\sigma }_{ys}{\overline{\rho }}^{\gamma },$$ [2]

where $E_s$ and ${\sigma }_{ys}$ are the constituent material’s Young’s modulus and yield strength, respectively; $B$ and $C$ are geometry-dependent proportionality constants, and $\beta$ and $\gamma$ are scaling constants (24). We found the experimentally measured stiffness in the hollow second-order half-cells to scale nearly linearly, with relative density as $E=0.015\hspace{0.17em}{E}_h{\overline{\rho }}^{\hspace{0.17em}1.04}$ and strength as ${\sigma }_y=0.026\hspace{0.17em}{\sigma }_{yh}{\overline{\rho }}^{\hspace{0.17em}1.17}$. We found similar scaling relations for polymer and composite second-order half-cell samples. Table 1 provides a full list of the constituent material properties used and the observed scaling parameters; polymer and composite properties can be found in SI Appendix, SI Materials, and Al₂O₃ properties were taken from refs. 29–33.

Table 1.

Material properties and proportionality and scaling constants for second-order half-cells as obtained from experiments and simulations

Material type	${\mathit{E}}_{\mathit{s}}$ (GPa)	${\mathit{\sigma }}_{\mathit{ys}}$ (MPa)	$\mathit{B}\left(\mathit{B}\mathit{*}\right)$	$\mathit{\beta }\left(\mathit{\beta }\mathit{*}\right)$	$\mathit{C}$	$\mathit{\gamma }$
Polymer	2.10	62.7	0.110 (0.071)	1.12 (1.05)	0.316	1.36
Polymer + 20 nm Al2O3	15.8	509	0.050 (0.062)	1.07 (1.04)	0.236	1.32
20 nm Al2O3	165	5,200	0.015 (0.036)	1.04 (1.00)	0.026	1.17

^*Stiffness constants in parentheses represent simulation results.

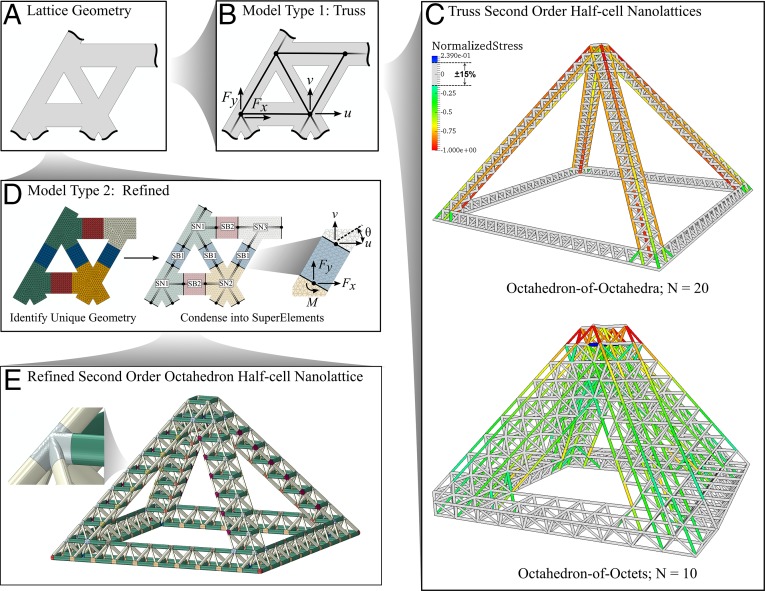
The definition of stiffness in experiments on structural metamaterials has been ambiguous because of various competing deformation mechanisms at each level of hierarchy ranging from elastic deformation to hinge-like phenomena to elastic–plastic buckling. We performed simulations on the elastic response of all tested second-order hierarchical nanolattices to calculate the stiffness of polymer, composite, and hollow ceramic nanolattices using an efficient finite element substructuring technique (Fig. 4 and SI Appendix, SI Materials) with the constituent properties listed in Table 1. Computed scaling exponents are included in Table 1 and show good agreement with experiments, differing by only 6.1%, 3.3%, and 3.9% for polymer, composite and hollow trusses, respectively. The absolute computed stiffnesses were, on average, 10.7% lower for polymer, 30.2% higher for composite, and 68.5% higher for hollow samples compared with experimental data (Fig. 5), which hints that geometric and/or material imperfections contribute significantly to a reduction in the effective stiffness.

Fig. 4.

Model flowchart showing truss and refined model generation. (A) Representative lattice geometry section. (B) Creation of a truss model lattice. (C) Example compression of truss model half-cell nanolattices. Stress is normalized by the maximum compressive stress in the sample, and stresses $\left|\sigma \right|\le 15\%$ of the maximum stress have been grayed out to help illustrate the beams with high stresses. (D) Refined model creation process containing geometrically unique supernodes (SN) and superbeams (SB). (E) Example refined model half-cell nanolattice colored by unique geometry beam or node.

Fig. 5.

Comprehensive data plot of all tested hierarchical nanolattices. (A) Effective Young’s modulus of the hierarchical structures plotted against their relative density. Data are plotted for experimental (slope values are in bold) and refined node simulations (slope values are italicized) results. (B) Experimentally derived effective yield strength of the hierarchical nanolattices plotted against their relative density.

We found that the strength and stiffness of the equivalently dense hollow third-order half-cell samples were approximately a factor of two lower than those of second-order half-cells; under the same metric, polymer and composite samples had equivalent strength and stiffness for second- and third-order samples. Experimental and computational results for all second- and third-order half-cells are summarized in Fig. 5. Experiments on full second-order nanolattices revealed that the strength and stiffness align with second-order half-cell experiments (SI Appendix, SI Materials).

Failure, Deformation, and Recoverability.

The characteristic failure and postyield deformation of each sample were observed to correlate with (i) material system and (ii) architecture. We found that the material system (i.e., polymer vs. composite vs. hollow alumina) most strongly influenced the global deformation behavior and that the architecture directly affected the localization of failure within the hierarchical beams and the global recoverability of the samples. Examples of all three material systems for samples with two different orders of hierarchy are provided in Figs. 2 and 3 (Movies S1–S6).

The postyield deformation behavior of hollow ceramic samples was ductile-like with continuous serrated flow (Figs. 2 A–C and 3 A–C). Failure occurred through a combination of localized elastic beam buckling in the first-order beams, shell buckling in individual hollow tubes, and microcracking at the nodes. Of all material systems, the hollow ceramic samples had the highest average recovery, with samples recovering up to 85–98% of their original height after compressions exceeding 50% strain. Failure in the hollow samples initiated and localized primarily in individual first-order beams oriented along the axis of second-order beams, or referred to here as axially oriented beams. Buckling of these axially oriented first-order beams creates a compliant region in the higher-order beams that accommodates most of the ensuing displacement. We observed that first-order beams that did not buckle at the onset of failure remained completely intact during compression. On unloading, most of the beams within the cross-section of the higher-order beams remained intact, allowing significant global recovery. This effect is present in all hierarchical nanolattices and does not seem to correlate with hierarchical order. The recoverability mechanism described above is present in all material systems to varying degrees and most pronounced in hollow samples.

The postyield deformation of polymer samples was ductile and continuous, with samples recovering to ∼75–90% of their original height after unloading (Figs. 2 G–I and 3 G–I). Failure in polymer samples was governed primarily by buckling in first- and second-order beams. Most of the composite samples failed catastrophically by fracture of the second-order beams (Figs. 2 D–F and 3 D–F), except for the most slender samples, which showed some recoverability (SI Appendix, Fig. S6E).

Simulations reveal the local stress distribution and expose the load-carrying members of the hierarchical nanolattices. One prominent feature revealed by computations is that the first-order axially oriented beams, which comprise ∼8.1% of all of the beams in an individual sample, carry an average of 91% of the load, which corroborates the observation of failure initiating in these beams. Fig. 4C illuminates the regions of high local stress revealed by computations in second-order samples with varying degrees of slenderness. Samples with low slenderness have stress concentrations highly localized to the topmost first-order beams and are more likely to experience failure there. Samples with high slenderness have a more even stress distribution throughout their length and are more likely to have failure initiate away from the topmost region. This stress localization trend agrees well with experimental observations (SI Appendix, Fig. S6).

Fig. 3 A–C shows cyclic experiments on a third-order hollow ceramic half-cell, which revealed, after the initial loading cycle, that the stiffness dropped from $420$ to $39\hspace{0.17em}\text{\hspace{0.17em}N/m}$ and that the applied load at yield decreased from $0.77$ to $0.089\text{\hspace{0.17em}mN}$. In the first loading cycle, the sample recovered to 96% of the original height on unloading; all subsequent cycles showed nearly complete 100% recovery to this initial deformed height. The load displacement data quickly reached a stable hysteretic cycling behavior, with minimal degradation after the second loading cycle (Fig. 3 A–C and Movie S6).

Discussion

Strength and Stiffness Scaling.

Compression experiments revealed the strength and stiffness of the second-order hierarchical half-cells to scale nearly linearly with relative density, which follows analytical and computational predictions for stretching-dominated cellular solids (24). These results show a factor of 1.5 improvement in the scaling relationship for strength and a factor of 1.6 improvement for modulus over nonhierarchical hollow Al₂O₃ nanolattices, and they are brought about by increasing the hierarchy from first to second order (22) (Fig. 5). Simulations reveal that the load in hierarchical nanolattices is carried primarily through axially oriented first-order beams in uniaxial compression, with little contribution to the deflection from bending. Analytical models for architected materials predict a linear scaling of strength and stiffness with density for structures with members that are primarily in uniaxial compression and tension (34). This linear scaling behavior has not been previously observed in hollow tube stretching-dominated nanolattices (22). We postulate that the near-linear strength and stiffness scaling observed in hierarchical nanolattices in this work arises from the combination of axially loaded first-order beams and the reduced effects of bending on global compliance. One key observation that arises from the nearly linear scaling of strength and stiffness is that the density of the samples can be varied indefinitely with only minor changes in the stiffness to weight and strength to weight ratios.

Simulations show that axially oriented beams, which comprise 8.1% of the macroscopic sample mass, carry 91% of the axial load (Fig. 4C). This low percentage of load carrying beams suggests that the remaining beams within the structure are underused. The underutilization of nonaxially oriented beams is likely a major factor in the observed reduction of the proportionality constants $B$ and $C$ (Eqs. 1 and 2) from what is predicted analytically for an ideal stretching-dominated solid, which have $B=C\approx 0.3$ (24) (Table 1). The negative impact of underused beams could be improved through better optimization of the hierarchical geometries.

Recoverability.

The underutilization of nonaxially oriented beams plays a significant role in the ability of hierarchical nanolattices to recover. Axially oriented beams undergo failure at the point of highest stress in a sample; in the absence of a catastrophic failure event, nonaxially oriented beams are able to remain intact. Under global compression, the undamaged nonaxially oriented first-order beams either (i) efficiently distribute strain through bending or (ii) undergo local elastic buckling to accommodate large global deformation without failure. A large number of elastically deformed first-order beams enables the hierarchical samples to globally recover. In the absence of residual strain in the buckled beams, such as is the case in hollow nanolattices, samples show excellent recovery behavior. The residual plastic strain in the buckled beams of polymer nanolattices impedes their ability to fully recover. In samples that undergo multiple loading cycles, most of the first-order beam buckling modes are activated in the first loading cycle; multiple loading cycles serve to reactivate the same buckling modes, which leads to near-perfect recoverability of the initially deformed samples. It may be possible to remove underused beams through better optimization of the hierarchical geometries, but such a reduction in the nonloadbearing beams may reduce the postyield recoverability by impeding the recovery mechanism.

Deformation and Failure.

Hierarchical nanolattices failed by a combination of different mechanisms: elastic beam buckling, shell wall bending, brittle fracture, and viscoplastic yielding. Failure initiates in beams through the weakest mechanism; equating the energy necessary to activate each mechanism enables the prediction of the dominant deformation mode. Previous work by Meza et al. (22) showed enhanced recoverability in hollow Al₂O₃ nanolattices when shell buckling acts as the preferential mechanism over fracture. Calculations performed on the hollow hierarchical samples in this work show that global (Euler) beam buckling acts as a dominant mechanism over shell buckling and that shell buckling acts preferentially over fracture (SI Appendix, SI Materials). This formulation implies that incipient failure initiates through beam buckling, and subsequent deformation is accommodated through shell buckling, leading to ductile-like behavior. This prediction agrees well with experimental observations (Figs. 2 A–C and 3 A–C). The brittleness of the Al₂O₃ causes large local strains to be relieved by either elastic buckling or fracture, and because shell buckling acts as a dominant mechanism, no residual strains are generated in the beams after unloading, which enables the samples to globally recover their original shape after unloading. In polymer samples, Euler buckling of the first-order beams is the dominant failure mechanism; the substantial postbuckled deformations generate nonnegligible residual stress in the beams, which impedes global recovery (Figs. 2 G–I and 3 G–I). The viscoelasticity of the polymer likely gives rise to the observed ductile load displacement behavior. The presence of the polymer–ceramic interface in composite samples suppresses buckling failure of either material and leads to a brittle fracture of the tube walls that results in the observed catastrophic collapse (Figs. 2 D–F and 3 D–F).

The large number of available failure modes in the hierarchical samples serves to reduce the yield strength. The activation of both beam and shell buckling causes the nanolattices to fail at a lower load than the yield limit, which decreases the global strength of samples and the proportionality constant C in Eq. 2 when these mechanisms are dominant. Shell wall bending in hollow samples generates stress concentrations near the nodes and along the beams. The negative impact of hollow nodes manifests itself in a twofold reduction in strength and stiffness in the third-order hollow samples, likely brought on by the higher-volume fraction of nodes in these samples.

The transition to buckling failure in nanolattices normally correlates with a significant reduction in the scaling of strength with relative density caused by the nonlinear dependence of buckling on slenderness in low-density samples (35). In this work, the length and aspect ratio of the first-order beams remains unchanged for different relative density samples; the relative density is modulated by the number of unit cells in a hierarchical beam $N$, which does not negatively affect the strength scaling with relative density.

Role of Imperfections.

The marked overestimation of the absolute stiffness obtained by the refined model simulations compared with experiments can be explained by the presence of geometric imperfections in the fabricated samples. Defects, like misaligned nodes, prebending of the beams, and variations in the wall thickness negatively impact the mechanical performance of nanolattices (21, 22). One dominant imperfection that was observed in all tested samples is sinusoidal waviness of the first-order beams caused by the external vibrations during the two-photon writing process. Simulations of the compression of beams with varying degrees of waviness and material compositions showed that, for a wave amplitude of 50 nm and a wavelength of 1 µm, the calculated effective stiffness of polymer beams decreased by 5%, that of the ceramic–polymer composites decreased by 32%, and that of the hollow ceramic beams decreased by 70%, which serve to illustrate the increased sensitivity to defects in the composite and hollow beams. The simulations overpredicted the stiffnesses of composite and hollow ceramic hierarchical lattices by 30.2% and 68.5%, respectively, which suggests that waviness-induced defects significantly contribute to this reduction. Model inaccuracy in underpredicting solid polymer stiffness by 10.7% can likely be attributed to the uncertainty in the polymer modulus.

We created hierarchical architected metamaterials with exceptional strength, stiffness, and damage tolerance and have architectures comparable with those of hard biomaterials, which derive their resilience from hierarchically arranged constituents. We show that adding a single level of hierarchy in nanolattices enhances the mechanical properties over simple periodic lattices, enables more efficient load transfer, and suppresses global failure but that the addition of additional levels of hierarchy does little to improve the mechanical properties and in some cases, degrades them. This ability to engineer material structure on the most fundamental length scales opens up a new design space where material properties—mechanical, thermal, electrical, photonic, etc.—can be controlled and tuned independently by properly choosing (i) atomic-level microstructure, (ii) critical material dimensions, and (iii) architecture.

Materials and Methods

Fabrication.

Hierarchical nanolattices were fabricated from solid polymer, ceramic–polymer core-shell composites, and hollow ceramic tubes. Solid polymer lattices were written in negative photoresist (IP-Dip 780) using the Photonic Professional TPL-DLW System (Nanoscribe GmbH). Core-shell composites were created by depositing a conformal coating of 20 nm Al₂O₃ onto the polymer nanolattices using atomic layer deposition in a Cambridge Nanotech S200 ALD System with H₂O and trimethylaluminum (TMA) precursors. Hollow structures were made by removing the edges of the coated nanolattices using focused ion beam milling with the FEI Nova 200 Nanolab and then etching out the internal polymer structure with oxygen plasma using the Zepto Plasma Etcher (Diener GmbH), resulting in the hollow ceramic nanolattice. More details on this process can be found in ref. 22 (SI Appendix, SI Materials).

Two sets of samples were created: (i) half-unit cells (half-cells) and (ii) full nanolattices. Three different types of half-cells were fabricated and tested: a second-order octahedron of octahedra (Fig. 1B), a second-order octahedron of octets (Fig. 1C), and a third-order octahedron of octahedral of octahedra (Fig. 1H). For the second-order structures, two different base unit cell sizes (L) were used (8 and 12 µm), with three numbers of unit cells per fractal beam (N): 10, 15, and 20. For the third-order samples, two different octahedron of octahedral of octahedra were fabricated and tested with different geometric configurations: a unit cell with L = 3 µm and N = 10 and one with L = 8 µm and N = 5. Three different second-order octahedron of octahedra full nanolattices were fabricated and tested: a unit cell with L = 8 and N = 10, one with L = 6 and N = 15, and one with L = 4 and N = 20. The inherent limitations of the two-photon lithography fabrication methodology used to create the nanolattices render it impractical to create materials with more than three orders of structural hierarchy. A full list of samples and structural parameters can be found in SI Appendix, Tables S1–S3.

Experimental Methods.

In situ nanomechanical experiments were performed in a Quanta SEM (FEI Co.) using an InSEM Nanomechanical Module (Nanomechanics Inc.). All samples were compressed to 50% strain at a strain rate of 10⁻³ s⁻¹. The structural stiffness was estimated based on the loading slope of the load displacement curve in the linear regime, and failure strength was taken to be the peak applied load before failure. We calculated the Young’s modulus by normalizing the measured loading stiffness by the sample height divided by the footprint area. Yield strength was determined by dividing the measured peak load by the sample footprint area. Scaling relations were obtained using an exponential best fit of the stiffness data; the scaling is computed as the average of the fits of the two second-order half-cell geometries: the octahedron of octets and the octahedron of octahedra.

Simulations.

Modeling of hierarchical nanolattices ultimately requires simulating thousands or millions of truss members while accurately resolving local deformation and failure mechanisms at the smallest scales. For elastic loading and stiffness predictions, simulations were performed based on a two-step computational strategy (using Abaqus and an in-house variational-based solid mechanics code). First, the characteristic elastic response of individual beams and representative lattice junctions was determined by finite element calculations using linear elastic shell and solid elements and a detailed representation of the CAD-generated geometry of individual truss members and junctions as shown in Fig. 4. This procedure was applied to monolithic, hollow, and composite beams and junctions. To dramatically reduce the number of degrees of freedom, we assume that the cross-sections of both ends of a beam deform rigidly through kinematic constraints. Thus, the deformation of each beam is reduced to depend only on the displacements and rotations of its end points. Similarly, truss junctions are reduced to depend only on the orientations of the attached truss members. Second, the thus-obtained load-displacement relations and stiffness matrices are input into an efficient simulation of the complete hierarchical structure based on the reduced degrees of freedom of all beam members and junctions in the lattice. The response of 12 second-order lattices of varying architecture was modeled by the aforementioned procedure. Constituent Young moduli were taken from Table 1. Poisson’s ratios of the polymer and alumina were chosen as ${\nu }_p=0.49$ and ${\nu }_{A{l}_2{O}_3}=0.3$, respectively.

To show the importance of the exact deformation mechanisms through fully resolved geometric models, we alternatively simulated the effective lattice response using bar elements (for solid beams) or shell elements (for hollow beams) without the aforementioned multiscale strategy and with the same base material properties. Calculations of first-order beam utilization in second-order beams were completed using the bar element model. Percentages of the axially aligned force carried in first-order beams relative to the whole second-order beam were calculated by sampling the middle 40% length of the second-order lattice beam. Axially aligned beam fractions were taken by dividing the number of axially oriented beams by the number of beams in the sample.

CAD Design/Relative Density.

CAD Solidworks models were used to determine the relative density of structures. The model uses measured voxel dimensions from each structure as design parameters in conjunction with base unit cell size and fractal number of structures. Each hierarchical repeating unit is patterned to construct higher-order structures, and similarly, higher-order unit cells were patterned to compose full nanolattices. The relative densities were calculated by evaluating the ratio of the volume of the structure by that of the solid from which the cell walls are made. A full illustration can be found in SI Appendix, Fig. S4.