Significance
Mechanical interactions between cells, mediated by the elastic response of the extracellular matrix to active applied forces, play a critical role in developmental biology, wound healing, and cancer progression. This work applies sophisticated technical means, both in experiment and computational modeling, to investigate the micron-scale mechanics of a popular model of this medium, a collagen gel. The results obtained show clearly that on the cellular scale, there are significant spatial variations in the micromechanics due to network heterogeneities.
Keywords: micromechanics, collagen, fiber network
Abstract
Collagen gels are widely used in experiments on cell mechanics because they mimic the extracellular matrix in physiological conditions. Collagen gels are often characterized by their bulk rheology; however, variations in the collagen fiber microstructure and cell adhesion forces cause the mechanical properties to be inhomogeneous at the cellular scale. We study the mechanics of type I collagen on the scale of tens to hundreds of microns by using holographic optical tweezers to apply pN forces to microparticles embedded in the collagen fiber network. We find that in response to optical forces, particle displacements are inhomogeneous, anisotropic, and asymmetric. Gels prepared at 21 °C and 37 °C show qualitative difference in their micromechanical characteristics. We also demonstrate that contracting cells remodel the micromechanics of their surrounding extracellular matrix in a strain- and distance-dependent manner. To further understand the micromechanics of cellularized extracellular matrix, we have constructed a computational model which reproduces the main experiment findings.
The mechanical properties of the extracellular matrix (ECM) play a central role in developmental biology (1), tissue homeostasis, and remodeling (2). Alteration of the ECM elasticity is a signature of many diseases such as pulmonary and atrial fibrosis, Ehlers–Danlos syndrome, and infantile cortical hyperostosis (3). The mechanical cues from the ECM also strongly correlate with the clinical prognosis of various types of cancers (4).
In recent years, many studies have shown that to mimic the physiological conditions in vitro, mechanical cues from a truly 3D ECM are necessary (5). Type I collagen gel has gained popularity as arguably the most used in vitro model of a 3D ECM (2). As the most abundant protein in animal tissue and accounting for 25% of the human whole-body protein content (6), type I collagen is the major component of the ECM in skin, tendon, and organs. Despite its lack of biochemical complexity compared with live tissue, reconstituted type I collagen gel has been successfully used to provide mechanistic insights into processes such as morphogenesis (7), wound repair (8), and cell migration (9). In particular, the rheology and especially the rigidity of collagen gel have been shown to tune the growth and migratory phenotypes of cancer cells in vitro (10, 11).
Structurally, collagen gels are formed by fibrous networks and typically have pore sizes of a few to tens of microns (12–14). The typical size of these structural discontinuities is comparable to the size of cells and is much larger than cell–ECM adhesion complexes (15, 16). It is therefore expected that a cell senses the micromechanical properties of its surrounding matrix, rather than the macroscopic rheology of the ECM (16, 17). Although many studies have focused on the (nonlinear) bulk rheology of empty and cellularized collagen ECM (18–22), the micromechanics of the porous biopolymer network is largely unexplored, presumably due to the lack of direct experimental measurements.
In this paper, we report direct experimental measurements and computational models on the mechanical response of empty and cellularized type I collagen gel of different architectures. Previously, we have demonstrated that as the gelation temperature increases, the resulting collagen gel experiences a phase transition from highly heterogeneous long fiber clusters to homogeneously distributed short fiber mesh (23). As we demonstrate, the microscopic architecture strongly affects the micromechanics of the collagen gel. Furthermore, we study the effects of embedded fibroblast cells and breast cancer cells on the micromechanics of collagen fiber networks. These experimental measurements have led us to develop a computational model of realistic biopolymer networks. Our results provide a largely overlooked perspective on the studies of 3D cell–ECM mechanical interactions.
Results
To measure the micromechanical response of the collagen gel, we apply optical forces to 3-μm-diameter polystyrene beads embedded in the gel and record the resulting motion with holographic video microscopy. We use a computer-controlled spatial light modulator to manipulate the laser beam (1,064-nm wavelength) and displace the optical trap away from the equilibrium position of the embedded particle. We turn the optical trap on and off using an external shutter while recording video microscopy of the bead’s motion. The beads are illuminated with a partially coherent light source at 625 nm, which generates concentric diffraction patterns that allow us to track the particle trajectories at high resolution (24, 25).
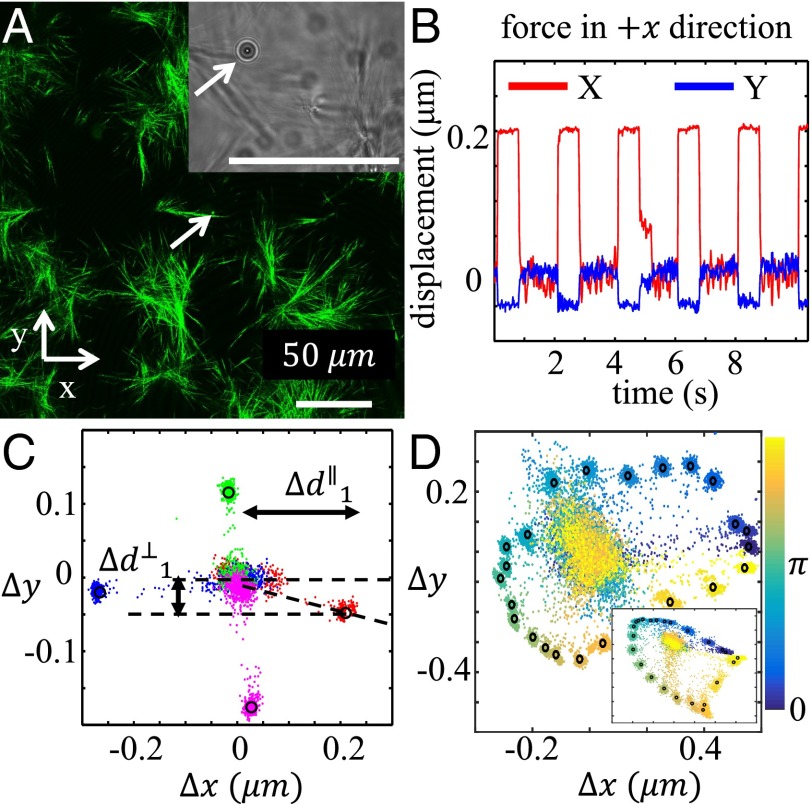
Fig. 1A shows a confocal reflection microscopy (CRM) (23, 26) image of a bead embedded in a collagen gel (prepared at room temperature; Materials and Methods), and the Fig. 1A, Inset, shows one frame of the transmitted light video microscopy for the same bead. We analyze each video frame to obtain a time series of the bead’s mechanical response in two dimensions, as shown in Fig. 1B. In this case, the particle is manipulated by displacing the optical trap 0.725 μm in the direction relative to the equilibrium position of the particle. This time series illustrates several features of our system and of the collagen mechanical response: particle displacements are determined with sub–10-nm resolution; particle displacement has components parallel and perpendicular to the direction of the trap displacement; and the residual motion during the displaced (trap on) times is smaller than the residual motion during the equilibrium (trap off) times, indicating that the trap suppresses the particle’s Brownian motion.
Fig. 1.
A typical micromechanical measurement of collagen gel. (A) Confocal reflectance image of a 3-μm-diameter particle embedded in a collagen matrix. The collagen gel was formed at 21 °C and featured distinct fiber clusters dispersed in a fluid medium. Inset shows one frame of the video used to track the particle displacement. (B) Time series showing the particle displacement in response to a pulsed 22 pN/μm optical trap placed 0.725 μm away from the particle equilibrium position in the direction. (C) Two-dimensional trajectory map of the particle response to optical traps positioned 0.725 μm away (from the particle equilibrium position) in the (red), (green), (blue), and (pink) directions. The circles represent the mean displacements determined by fits of the time series to a pulse function. (D) Two-dimensional trajectory map of a particle response to optical traps positioned in 24 evenly distributed orientations. (Inset) Two-dimensional trajectory map of another particle in the same sample. These measurements are done in the same way as in C except for more directions probed instead of only four. Colors of the particle trajectories represent the orientations of the trap positions. See also SI Appendix, section S1, for more information.
To complete our characterization of the micromechanical response of an embedded bead, we repeat the above measurements with the optical trap displaced in the , , and directions in the image plane. The collected results for the four directions are shown in Fig. 1C, where each dot represents data from one video frame. Most frames correspond to either the displaced case (trap on) or the equilibrium case (trap off), but some frames do record transition states in between. By fitting the time series to a pulse function, we reduce the influence of these transition states with the result that each video yields one data point representing the mean displacement of the particle from its equilibrium position. The displacement includes components both parallel and perpendicular to the trap displacement. The data for this particle illustrate that the response of the collagen gel is off-axis, anisotropic, and asymmetric. As shown in Fig. 1D, these features are not a result of particular choice of measurement axis but indeed represent the complex micromechanical properties of the collagen network.
We repeat the measurements described in Fig. 1 A–C for 100 particles in each collagen gel sample. The particles are seeded at a density of , and all measured particles are within a 200 × 150 × 20 μm3 volume. The particle density is chosen to minimize particle aggregation and disruption of the native gel structure, while still offering high resolution of the spatial variations of the network micromechanics.
To characterize the distribution of micromechanical properties in each gel sample, we define three quantities that summarize the results. For a given particle and trap location, we define the compliance as
| [1] |
where refers to one of the four trap locations, 1.5 μm is the particle radius, is the component of the particle displacement along the direction of the trap displacement, is the parallel component of the applied force, 22 pN/μm is the harmonic optical trap stiffness, and 0.725 μm is the distance of the trap from the particle’s equilibrium position (see SI Appendix, section S1, for trap calibration). The average of the four measurements gives the local compliance:
| [2] |
For a linear elastic material, this definition reduces to the standard definition of compliance, which is the inverse of the shear modulus.
To quantify the anisotropic response, we define the anisotropy A as the dimensionless quantity
| [3] |
To quantify the off-axis response of the particles to the applied forces, we define the directional off-axis angle
| [4] |
where positive angles are measured counterclockwise from the trap displacement to the particle displacement. We also define the off-axis angle for a given particle to be the maximum of its directional off-axis angles:
| [5] |
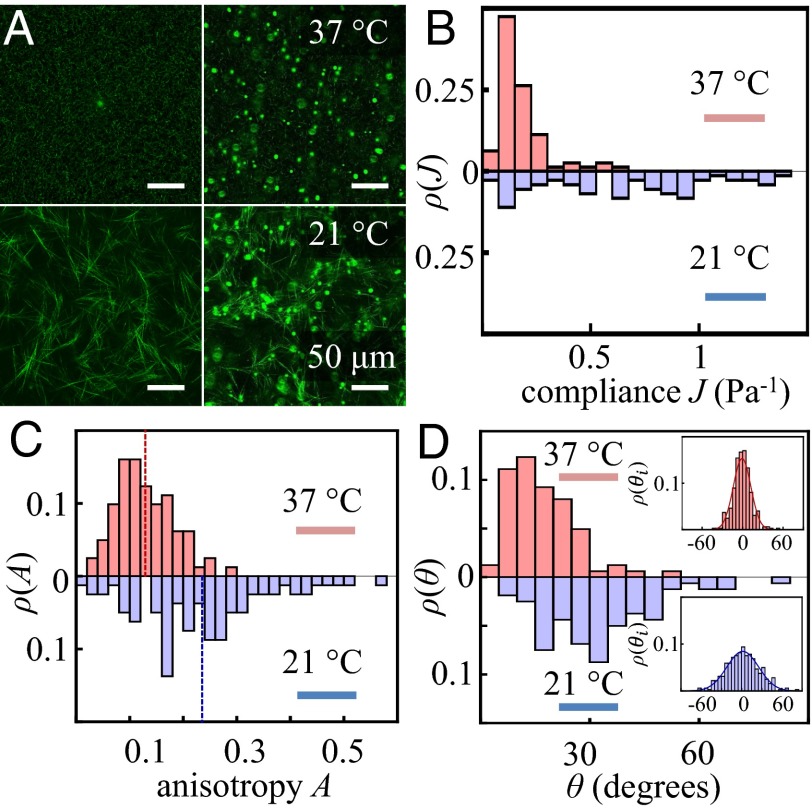
To investigate the effect of network architecture on collagen gel micromechanics, we examine two types of collagen gels prepared under different conditions: one with collagen concentration of 1.5 mg/mL and grown at 37 °C and the other with the same concentration but grown at 21 °C with increased ionic strength. Fig. 2 shows the representative results for one gel of each type. Sample to sample variations do not change the qualitative behaviors reported below (for more examples, see SI Appendix, section S2). Consistent with our previous results (23), different gelation temperatures lead to visible differences in the microstructure of the collagen fiber network, as seen in Fig. 2A. At 37 °C, the collagen network is composed of short and thin fibers that form a nearly homogeneous mesh with a typical pore size of . At 21 °C, the collagen gel contains thick fiber clusters, and the gaps between fiber clusters are on the order of tens of microns.
Fig. 2.
Statistical distributions of micromechanical properties. (A) Confocal reflection images of 1.5 mg/mL collagen gels grown at 37 °C and 21 °C, with (Right) and without (Left) the embedded probing particles. (B) Normalized histograms of compliance J for collagen gels grown at 37 °C (Upper; red) and 21 °C (Lower; blue). (C) Normalized histograms of anisotropy A for collagen gels grown at 37 °C and 21 °C. Gels formed at 37 °C are more isotropic. (D) Normalized histograms of off-axis angles θ for collagen gels grown at 37 °C and 21 °C. Inset shows normalized histograms of directional off-axis angles . are fit well by a normal distributions (mean and SD: , ; , ; see SI Appendix, section S2, for more details).
These structural differences cause the two gels to have significantly different micromechanical properties. Fig. 2B shows normalized histograms (probability distribution) for the local compliance J of the two gels. The gel formed at 37 °C has a compliance J that is narrowly distributed around the average value. The gel formed at 21 °C, in contrast, has a broadly distributed local compliance.
In addition to the compliance J, the anisotropy of the local mechanical response also exhibits a systematic dependence on the collagen network architecture. As shown in Fig. 2C, the distribution of the anisotropy A peaks at 0.1 for gels formed at 37 °C. For 21 °C gels, the anisotropy peaks around 0.18 and may take extreme values as high as 0.5. For both gels, the directions of maximum (or minimum) compliance are evenly distributed among , , suggesting that the gels are macroscopically isotropic random networks. Note that in our definition, an anisotropy of 0.5 means the compliance measured locally along different directions may differ by twice as much as the average. Also note that because we are measuring displacement in only four directions, A is a lower bound of the compliance anisotropy. As a result, the large discrepancies between compliances measured in different directions further demonstrate the rich micromechanical properties beyond the expectations for a continuous elastic medium.
When probing an isotropic random biopolymer network at scales much larger than its structure discontinuity, we expect the mechanical response to be parallel to the probing force, or . This is no longer true in the case of micromechanics. As shown in Fig. 2D, for gels formed at 37 °C, the off-axis angles tend to be smaller, and the distribution peaks around 10° and has a tail extending to more than 30°. For gels formed at 21 °C, the off-axis angles tend to be greater. The distribution peaks at 30° and broadly covers the range from 0 to extreme values as high as 70°. Unlike θ, the probability distributions of are symmetric and well approximated by normal distributions, as shown in Fig. 2D, Inset. A surprising observation revealed by Fig. 2D is that there is a significant fraction of probes with off-axis displacements larger than on-axis displacements ( 45°), suggesting that the ECM may be locally auxetic. Because many types of cells have mechanosensitive membrane receptors that are sensitive to shear stress (27), a large off-axis angle means the cellular contraction force in the normal direction may activate these shear-sensing receptors as well. To our knowledge this is a new type of mechano-feedback between cells and their ECM. Further investigation is necessary to uncover its implications for 3D cellular dynamics. Another observation from comparing Fig. 2 C and D is that the shapes of the distribution functions for A and θ are similar. The normalized correlation coefficients between A and θ are higher than 0.4 for both types of gels, suggesting that micromechanical anisotropy and off-axis response in collagen are closely related. On the other hand, neither A nor θ is strongly correlated with the local compliance J (correlation coefficients 0.1 for both types of gels). These results suggest that A and θ are good measures of the geometric configuration of the ECM network, whereas J is mainly determined by the elastic modulus of fibers and their cross-links.
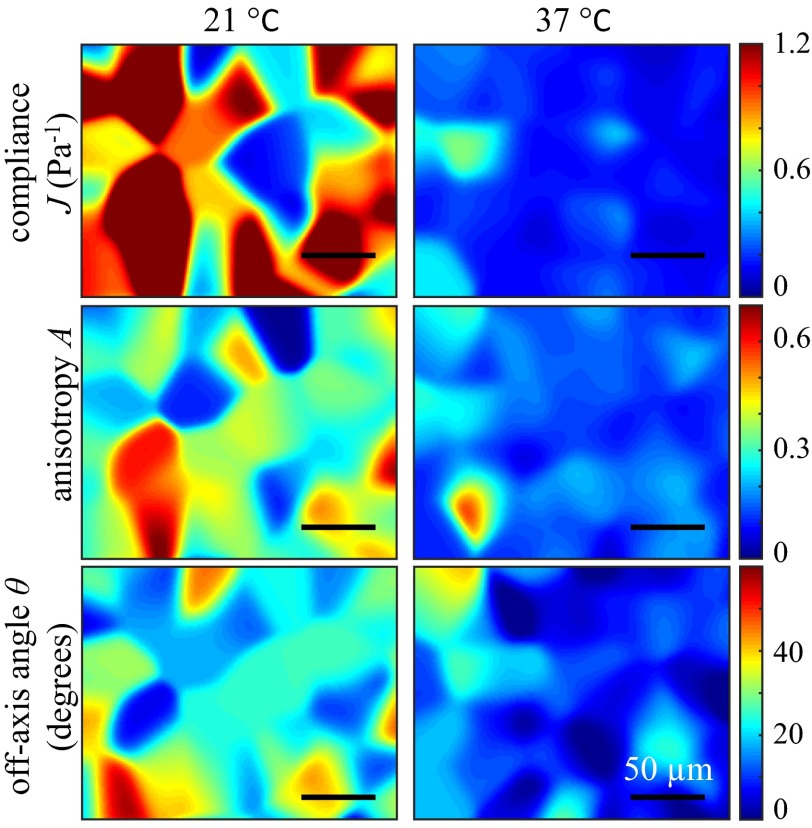
To further investigate the spatial fluctuations of the micromechanical properties of collagen gel, we generate spatial maps of J, A, and θ with a Gaussian kernel. For each gel, we use particles within a 10-μm range in z direction to generate spatial maps using Gaussian weighted averages:
| [6] |
where , represent the position of probing particle i; represents one of the micromechanical properties (J, A, or θ) measured for particle i; and 10 μm. Fig. 3 compares the spatial maps for gels formed at 37 °C and 21 °C. Due to the finite density of probing particles, these maps are low-pass–filtered representations of the spatial distributions. Nonetheless, it is evident that gels formed at lower temperature have greater spatial variations compared with gels formed at higher temperature. Also note that the anisotropy A and the off-axis angle θ are spatially correlated.
Fig. 3.
Spatial maps of compliance (Top), anisotropy (Middle), and off-axis angle (Bottom) of collagen networks grown at 21 °C (Left) and 37 °C (Right). Scale bar is 50 μm. The value at the location of each particle is fixed and the region between particles is interpolated using a Gaussian kernel as a function of the distance from each particle. Gels formed at 21 °C network demonstrate greater spatial fluctuations of all three micromechanical properties.
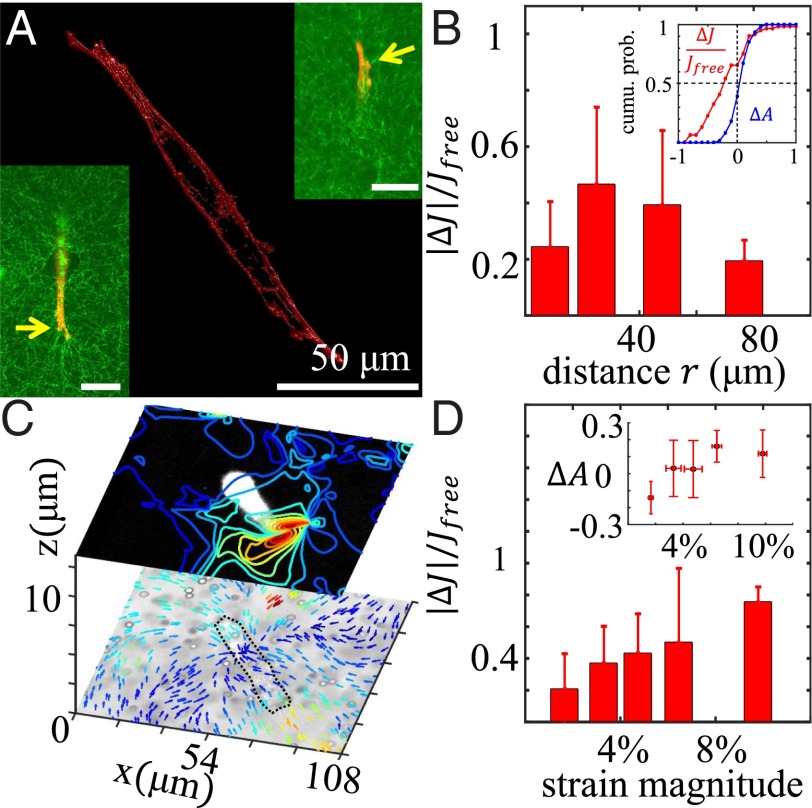
When the collagen matrix is populated by cells, the cellular contraction forces may deform the local network microstructures. Therefore, we expect the micromechanical properties of a cellularized collagen gel to be remodeled by embedded cells (28–30). To test this hypothesis, we seed strongly contracting mesenchymal cells (mouse fibroblast cells NIH 3T3 and human breast cancer cells MDA-MB-231) in the collagen matrix at low density and measure the micromechanical response around a single isolated cell. Fig. 4A shows the actin cytoskeleton of a MDA-MB-231 cell in a 3D collagen matrix. Unlike in 2D cultures, stress fibers are not apparent, and polymerized actin (as labeled by phallotoxins) is concentrated at the cell membrane. The cell exhibits small membrane protrusions that are actin-rich and presumably stabilized by cell–ECM adhesions (Fig. 4A, arrows). We measure the displacement of probing particles around each cell when perturbed by holographic optical tweezers as described above. To further elucidate the role of the cell contraction forces, we measure the mechanical response of each particle before and after we biochemically disrupt the cell actin cytoskeleton with cytochalasin D, which suppresses the contraction forces and restores the collagen network to a stress-free state. From these measurements, we calculate the local compliance and before and after cytochalasin D treatment, as well as , , , and . We have repeated the experiment on seven samples (three NIH 3T3 and four MDA-MB-231) with more than 100 probing particles in total.
Fig. 4.
ECM micromechanical properties are remodeled by cell contraction forces. (A) Three-dimensional reconstruction of a MDA-MB-231 cell embedded in a collagen matrix based on its F-actin immunofluorescence. Left Inset and Right Inset show the confocal slices with simultaneous imaging of actin (red) and collagen fibers (green) of the same cell. (Scale bars: 50 μm.) (B) Relative change of local compliance () as a function of probe-to-cell distance (r). (Inset) Cumulative probability of (red) and (blue). A vertical line intersects the two curves at and . (C) Two confocal slices of a typical sample. The slices are separated by 12.5 μm along the optical axis. The top slice shows the fluorescently labeled cell (white on black background) and the strain magnitude contours. The bottom slice shows the bright-field (nondescanned channel) image of the same cell (outlined in black curve) and the deformation field caused by cell contraction forces. The color of the contours and the arrows are scaled linearly (blue to yellow) with the magnitude of strain field (0–11%) and the deformation field (0–3 μm). (D) Relative change of the local compliance () as a function of local strain magnitude. (Inset) as a function of local strain magnitude. Error bars in B and D are SDs.
We find that the effect of cells on the local compliance is spatially dependent. Fig. 4B shows the spatial variation of the change of local compliance , where and r is the distance between the probing particle and cell membrane as determined from confocal image stacks. The change of compliance gradually decrease as r increases and remains significant () as far as 80 μm away from the cell. When r is small (10 μm), the change of local compliance is suppressed by the mechanical property of the cell itself, which is more rigid than the local collagen matrix. This explains the nonmonotonic trend shown in Fig. 4B and is also confirmed by numerical simulations below. We have also obtained statistics of changes in the local mechanical properties. As shown in Fig. 4B, Inset, from the cumulative probability of (red) and (blue), we find that the cells tend to stiffen their local ECM ( 65% probes) and increase ECM anisotropy ( 62% probes).
To further elucidate the role of cell contraction forces in remodeling the local mechanics of the ECM, we have measured the strain field generated by the cells embedded in collagen gels with 3D particle tracking velocimetry (SI Appendix, section S3). A typical result is shown in Fig. 4C. Two confocal slices at different depths are plotted with (2D projections) contours of strain magnitude and arrows of deformation field. To facilitate imaging, we have fluorescently labeled the cells (Materials and Methods) as shown in the top slice. The strain field is not symmetric and is strongly correlated with the cell morphology (31). The magnitude of the strain field represents the change of microstructure, and we expect that larger strain correlates with more significant changes of micromechanical properties. Indeed, as shown in Fig. 4D, the relative change of compliance increases monotonically with strain magnitude. At the same time, larger strain also increases the micromechanical anisotropy (Fig. 4D, Inset). From these results, it is evident that cells actively remodel the micromechanics of their 3D ECM. These effects propagate as far as 80 μm away from the cell, mediated by the strain fields generated by cellular contraction forces.
To provide fundamental understanding of the micromechanical measurements, we have developed a 2D lattice-based computational model. Our model is constructed on a triangular lattice. As described previously (21, 32, 33), triangular lattice models have successfully reproduced many bulk mechanical features of biopolymer networks, such as strain stiffening, the bending–stretching transition, and shear-induced fiber alignment. However, the utility of triangular lattice models in understanding ECM micromechanics has not been reported to our knowledge.
The network construction has been described in detail previously (32, 34). Briefly, on a regular triangular lattice, each bond is of length a and is present with probability p. Straight lines in this lattice, which have average length , are identified as fibers with stretching stiffness k and bending stiffness κ. The lattice sites are freely rotating crosslinks. The Hamiltonian of the entire network is
| [7] |
where for bonds that are present and 0 for removed ones. The first term is the stretching energy; is the distance between sites i and j in the deformed state. The second term is the bending energy; labels three consecutive sites along a straight line in the reference state, and is the change of angle along the fiber. We vary the value of the relative bending stiffness , ranging from to . This is consistent with what is expected for actual collagen fibers because the ratio is of the order of , where d and a are the diameter and mesh size obtained when modeling the fibers as simple elastic rods (22). Previous studies report an average connectivity (number of fiber segments meeting at a junction) of ; therefore, we set in our model (19, 35). To simulate collagen networks of qualitatively different microstructures, following the above construction, we apply the Metropolis–Hastings algorithm (SI Appendix, section S4), which controls network heterogeneity through an effective temperature . Consistent with our previous experimental results (23), at higher effective temperature, the network consists of short and thin fibers. At low effective temperatures, the network contains thick fiber clusters. Generally, the heterogeneity of the network monotonically decreases as increases.
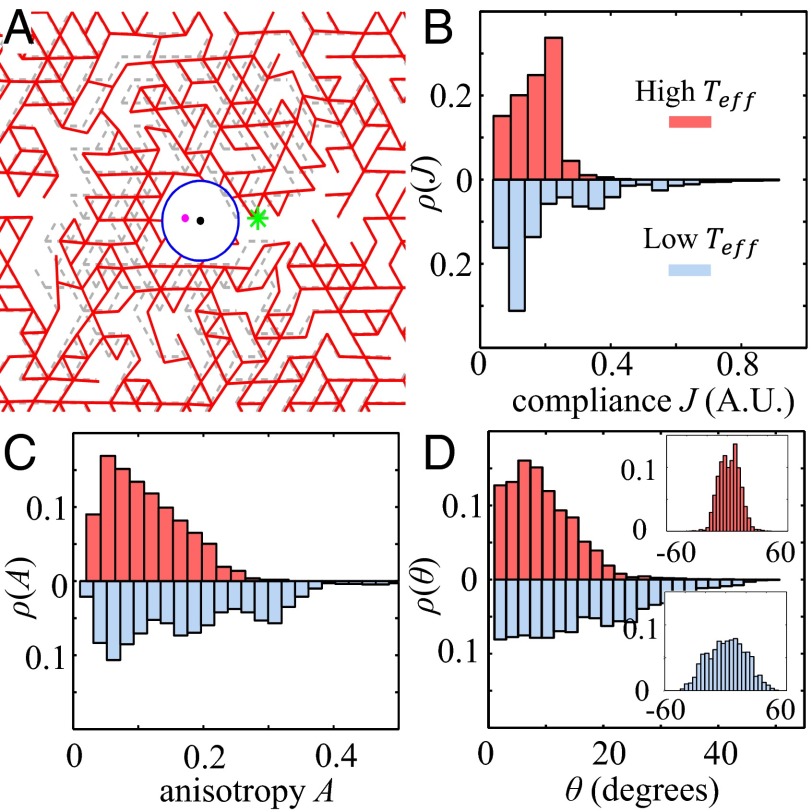
We model a probing particle as a circular hole in the lattice network with its boundary connecting to neighboring bonds (Fig. 5A) and the optical trap as a quadratic potential well: . Thus, the total Hamiltonian becomes . The equilibrium state of the network is calculated by applying the conjugate gradient method, which allows us to extract particle displacements analogous to those measured directly in the experiments. As shown in Fig. 5 B–D, the distributions of compliance J, anisotropy A, and off-axis angle θ for networks formed at two different effective temperatures demonstrate the same trends as the experimental results and to some extent agree quantitatively with Fig. 2 B–D. Moreover, we find in our simulations that networks formed at lower have greater spatial variations in their micromechanical properties (SI Appendix, section S4), which is consistent with the experimental measurements.
Fig. 5.
Simulation results of the micromechanics of biopolymer networks. (A) The micromechanical response of the network. Whole simulation network is 150 150 bound length. A probing particle (centered at the pink dot) embedded in a stress-free network (gray dashed lines) moves to a new equilibrium position (black dot and blue circle) and deforms its surrounding matrix (red lines) in response to the force of an optical trap (centered at green star). (B) Normalized histogram of compliance J for lattice network grown at high effective temperature (; Upper) and at low effective temperature (; Lower). (C) Normalized histogram of anisotropy A for a lattice network grown at (Upper) and (Lower). (D) Normalized histogram of off-axis angles θ for a lattice network grown at (Upper) and (Lower).
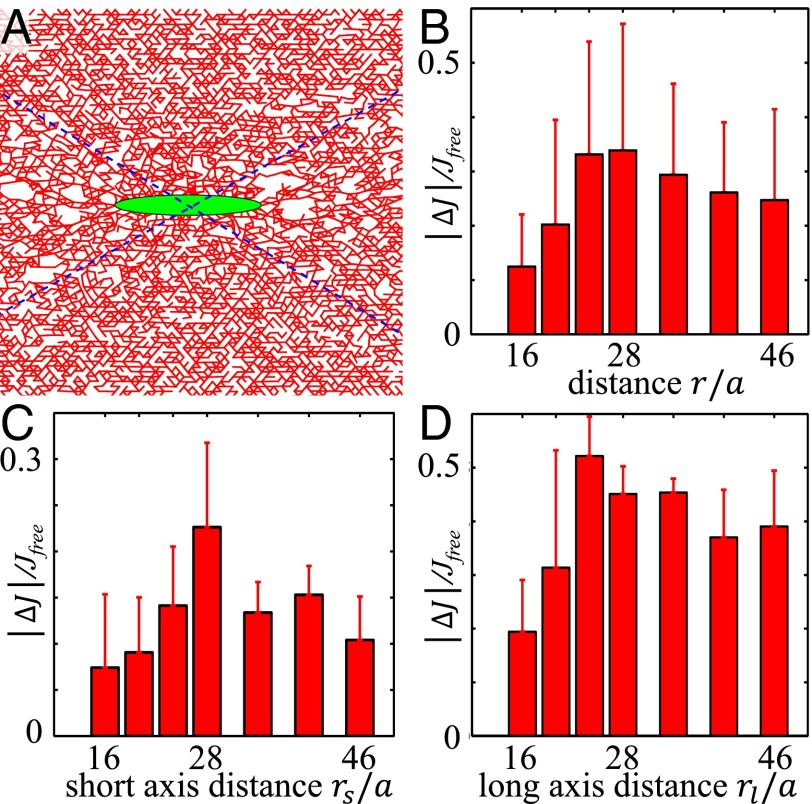
To simulate a cellularized collagen network, we model a contracting cell as an ellipse (aspect ratio 5:1 as obtained from typical cell morphology in experiments) embedded in the network and shorten the bond lengths isotropically of any bonds inside the ellipse (36, 37) (Fig. 6A). Similar to our experimental measurements, we have compared the micromechanical compliance with () and without cell contraction (). As shown in Fig. 6B, the relative change of compliance measured at varying distances from the cell agrees well with the experimental results. As detailed in SI Appendix, section S5, this nonmonotonic behavior can be explained by the intrinsic rigidity of the cell, which exists even in the absence of contractive forces. Using our computational model, we have further examined the directional dependence of . As shown in Fig. 6 C and D, similar trends are observed along both the long and short axes. However, the magnitudes differ by as much as 50%. This difference explains the relatively large error bar in Fig. 6B.
Fig. 6.
Simulation results of the cellularized collagen network micromechanics. (A) The equilibrium configuration of a cellularized network. The green ellipse in the center stands for a contractive cell. The blue dashed lines divide the whole space into four parts. Top and bottom parts are in the short axis direction, and left and right parts are in the long axis direction. (B) Relative change of compliance J, as a function of distance r (in units of bound length a) from the cell. (C) as a function of distance in the short axis direction (). (D) as a function of distance in the long axis direction ().
The above results demonstrate that triangular lattice models and their extensions capture the main features of the micromechanics of cellularized collagen gel. The rich micromechanical properties are intrinsically tied to the microstructure of the fiber network, as well as the stress states determined by the dynamic cell–ECM interactions.
Discussion
We have reported on the experimental and computational studies to elucidate the micromechanics of cellularized collagen networks. We have demonstrated that when probing scales smaller than the structure discreteness, rich mechanical properties are observed beyond the predictions of micro or bulk rheology. Although these properties are microscopic measurables, they are determined by the network configuration on a larger scale ( 20 times the mesh size determined from simulation). Therefore, the ECM microstructure has a significant effect on ECM micromechanical characteristics, as we have confirmed both experimentally and by simulation. In particular, the sharply distributed micromechanical compliance J for collagen gels grown at 37 °C agrees with the value measured from bulk rheology (such as in ref. 35). In these cases, gel pore sizes are typically smaller than the probing particles, and we expect the continuous medium assumption together with Eq. 1 to be a good approximation. However, for collagen gels which have large spatial heterogeneities and pore sizes, the bulk rheology becomes a poor predictor of micromechanics. Indeed, although gels grown at 21 °C typically have a smaller bulk compliance compared with 37 °C gels (18, 35), the average of micromechanical compliance shows the opposite. The breakdown of continuum assumption is evident from the broad distribution of J shown in Fig. 2. In this case, we expect that bulk rheology and micromechanics probe different physical properties of the collagen network.
We have shown that a relatively simple model of collagen gels can capture many features of the experimental data. The model is based on a 2D lattice and is not meant to be a precise match to the 3D sample. Instead, it serves as a way to make sense of the general properties of fiber-based bending-dominated elastic systems. These systems have well-understood macroscopic properties such as strain stiffening and nonlinear differential Poisson ratios that emerge from this model class, and we show here for the first time to our knowledge that the micromechanical properties can also be successfully modeled, both with and without embedded cells. Of particular interest is the difference between high- and low-temperature gels, seen both in the data and in our simulations; there is a pronounced increase in local mechanical variability for the gels that are created at low temperature, connected to their increased structural variability. We should note that the model underpredicts the extent of this variability for the compliance data. This may be due to the fact that in our model the bonds have a fixed elastic response independent of temperature, which results in a temperature-independent average compliance, as opposed to the net change in mean compliance seen in the data. Our focus here is on the variance for which the model does reflect the correct physics resulting from the differing network heterogeneity.
We have applied a 2D model rather than 3D in this study for computational complexity consideration. It is worth noting that continuum elasticity in 2D allows mechanical perturbation to propagate longer range than its counterpart in 3D. This possibly suggests an overestimation of the range of the effects shown in Fig. 6. However, previous studies on the breakdown of continuum elasticity in fiber matrices have shown anomalous, long-range deviations from continuum elasticity in 2D matrices (38, 39). Therefore, it is natural to expect the fiber nature could also result in long-range noncontinuum effects in 3D. In this sense, our 2D model is enlightening to understand micromechanics of real 3D biopolymer networks.
When collagen gels are populated by contractive cells, the micromechanical properties are significantly altered locally. For NIH 3T3 and MDA-MB-231 cells, the effects can be seen as far as 100 μm away for gels at collagen density of 2 mg/mL This is consistent with the observation that bulk rheology of collagen gels is modified at high embedding cell densities (20). The micromechanical remodeling is highly correlated with the strain field created by the cellular contraction forces, thus further illustrating the close structure–property relation at microscopic scales. Reciprocally, micromechanics, more directly than the bulk rheology of ECM, regulates the morphology, migration, proliferation, and differentiation of embedded cells (40, 41). Therefore, we expect that micromechanical heterogeneity is a key factor that contributes to the heterogeneous cellular behaviors observed even in the same 3D culture environment (42, 43). Our experimental and computational approaches provide a way of further investigating these effects.
Materials and Methods
Preparing and Imaging Collagen Gel.
Collagen gels are prepared from high-concentration rat tail collagen I in acetic acid (Corning; 10–11 mg/mL). The collagen is diluted with dH2 O (for 21 °C gel) or DMEM growth medium (for 37 °C gel), 10 PBS, and 0.1 N NaOH to a final concentration of 1.5 mg/mL and a pH of 7.4. Confocal reflection microscopy images of the collagen gels are taken using an inverted laser scanning confocal microscope (Leica TCS SPE) with either a 20 or 40 oil immersion objective.
Three-Dimensional Cell Culture and Staining.
NIH 3T3 mouse fibroblast and MBA-MB-231 human breast cancer cells are suspended at very low density in neutralized collagen solutions. The suspension is then immediately transfered to gridded glass bottom dishes (ibidi μ-dish Grid-50) and incubated in a tissue culture incubator [37 °C, 5% (vol/vol) CO2] for at least 24 h before staining or micromechanical measurements. Actin staining is done using Alexa Fluor 488 phalloidin dye (Life Technologies) on fixed samples. For cellularized collagen gel, micromechanical measurements with active contraction forces are followed by staining the cell using CellTracker Green dye (Life Technologies). We then perform confocal imaging before and after cytochalasin D (Sigma Aldrich; 10 μg/mL in PBS) treatment for 1–2 h. Micromechanical measurements are then conducted again with the same probing particles.
Holographic Optical Tweezers.
See SI Appendix, section S1, for more details.
Supplementary Material
Acknowledgments
We are thankful to Prof. Skip Rochefort for helpful discussions and access to a rheometer. We also thank L. Sander and X. Mao for useful discussions of the lattice modeling framework. This research was supported in part by the Office of Naval Research via the Oregon Nanoscience and Microtechnologies Institute Nanometrology and Nanoelectronics Initiative (Grant N00014-07-1-0457). C.A.R.J. is partially supported by the National Science Foundation Grant PHY-1400968. J.F. is supported by the National Science Foundation Center for Theoretical Biological Physics (Grant PHY-1308264). H.L. is supported in part by the Cancer Prevention and Research Institute of Texas Scholar Program of the State of Texas at Rice University.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1509663112/-/DCSupplemental.
References
- 1.Mammoto T, Ingber DE. Mechanical control of tissue and organ development. Development. 2010;137(9):1407–1420. doi: 10.1242/dev.024166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brown RA. In the beginning there were soft collagen-cell gels: Towards better 3D connective tissue models? Exp Cell Res. 2013;319(16):2460–2469. doi: 10.1016/j.yexcr.2013.07.001. [DOI] [PubMed] [Google Scholar]
- 3.Matheson WJ, Markham M. Infantile cortical hyperostosis. BMJ. 1952;1(4761):742–744. doi: 10.1136/bmj.1.4761.742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pickup MW, Mouw JK, Weaver VM. The extracellular matrix modulates the hallmarks of cancer. EMBO Rep. 2014;15(12):1243–1253. doi: 10.15252/embr.201439246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Griffith LG, Swartz MA. Capturing complex 3D tissue physiology in vitro. Nat Rev Mol Cell Biol. 2006;7(3):211–224. doi: 10.1038/nrm1858. [DOI] [PubMed] [Google Scholar]
- 6.Lodish H, et al. 2000. Molecular Cell Biology (W. H. Freeman, New York), 4th Ed.
- 7.Hotary K, Allen E, Punturieri A, Yana I, Weiss SJ. Regulation of cell invasion and morphogenesis in a three-dimensional type I collagen matrix by membrane-type matrix metalloproteinases 1, 2, and 3. J Cell Biol. 2000;149(6):1309–1323. doi: 10.1083/jcb.149.6.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Grinnell F. Fibroblast biology in three-dimensional collagen matrices. Trends Cell Biol. 2003;13(5):264–269. doi: 10.1016/s0962-8924(03)00057-6. [DOI] [PubMed] [Google Scholar]
- 9.Petrie RJ, Gavara N, Chadwick RS, Yamada KM. Nonpolarized signaling reveals two distinct modes of 3D cell migration. J Cell Biol. 2012;197(3):439–455. doi: 10.1083/jcb.201201124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Paszek MJ, et al. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8(3):241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 11.Petrie RJ, Yamada KM. At the leading edge of three-dimensional cell migration. J Cell Sci. 2012;125(Pt 24):5917–5926. doi: 10.1242/jcs.093732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.O’Brien FJ, et al. The effect of pore size on permeability and cell attachment in collagen scaffolds for tissue engineering. Technol Health Care. 2007;15(1):3–17. [PubMed] [Google Scholar]
- 13.Yang YL, Motte S, Kaufman LJ. Pore size variable type I collagen gels and their interaction with glioma cells. Biomaterials. 2010;31(21):5678–5688. doi: 10.1016/j.biomaterials.2010.03.039. [DOI] [PubMed] [Google Scholar]
- 14.Lang NR, et al. Estimating the 3D pore size distribution of biopolymer networks from directionally biased data. Biophys J. 2013;105(9):1967–1975. doi: 10.1016/j.bpj.2013.09.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.O’Brien FJ, Harley BA, Yannas IV, Gibson LJ. The effect of pore size on cell adhesion in collagen-GAG scaffolds. Biomaterials. 2005;26(4):433–441. doi: 10.1016/j.biomaterials.2004.02.052. [DOI] [PubMed] [Google Scholar]
- 16.Baker BM, Chen CS. Deconstructing the third dimension: How 3D culture microenvironments alter cellular cues. J Cell Sci. 2012;125(Pt 13):3015–3024. doi: 10.1242/jcs.079509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wong S, Guo WH, Wang YL. Fibroblasts probe substrate rigidity with filopodia extensions before occupying an area. Proc Natl Acad Sci USA. 2014;111(48):17176–17181. doi: 10.1073/pnas.1412285111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang YL, Leone LM, Kaufman LJ. Elastic moduli of collagen gels can be predicted from two-dimensional confocal microscopy. Biophys J. 2009;97(7):2051–2060. doi: 10.1016/j.bpj.2009.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lindström SB, Vader DA, Kulachenko A, Weitz DA. Biopolymer network geometries: Characterization, regeneration, and elastic properties. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(5 Pt 1):051905. doi: 10.1103/PhysRevE.82.051905. [DOI] [PubMed] [Google Scholar]
- 20.Raub CB, Putnam AJ, Tromberg BJ, George SC. Predicting bulk mechanical properties of cellularized collagen gels using multiphoton microscopy. Acta Biomater. 2010;6(12):4657–4665. doi: 10.1016/j.actbio.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Broedersz CP, Mao X, Lubensky TC, MacKintosh FC. Criticality and isostaticity in fiber networks. Nat Phys. 2011;7(12):983–988. [Google Scholar]
- 22.Feng J, Levine H, Mao X, Sander LM. 2014. Alignment and nonlinear elasticity in biopolymer gels. arXiv:1402.2998.
- 23.Jones CA, Liang L, Lin D, Jiao Y, Sun B. The spatial-temporal characteristics of type I collagen-based extracellular matrix. Soft Matter. 2014;10(44):8855–8863. doi: 10.1039/c4sm01772b. [DOI] [PubMed] [Google Scholar]
- 24.Cheong FC, et al. Flow visualization and flow cytometry with holographic video microscopy. Opt Express. 2009;17(15):13071–13079. doi: 10.1364/oe.17.013071. [DOI] [PubMed] [Google Scholar]
- 25.Parthasarathy R. Rapid, accurate particle tracking by calculation of radial symmetry centers. Nat Methods. 2012;9(7):724–726. doi: 10.1038/nmeth.2071. [DOI] [PubMed] [Google Scholar]
- 26.Brightman AO, et al. Time-lapse confocal reflection microscopy of collagen fibrillogenesis and extracellular matrix assembly in vitro. Biopolymers. 2000;54(3):222–234. doi: 10.1002/1097-0282(200009)54:3<222::AID-BIP80>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 27.White CR, Frangos JA. The shear stress of it all: The cell membrane and mechanochemical transduction. Philos Trans R Soc Lond B Biol Sci. 2007;362(1484):1459–1467. doi: 10.1098/rstb.2007.2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kotlarchyk MA, et al. Concentration independent modulation of local micromechanics in a fibrin gel. PLoS One. 2011;6(5):e20201. doi: 10.1371/journal.pone.0020201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kniazeva E, et al. Quantification of local matrix deformations and mechanical properties during capillary morphogenesis in 3D. Integr Biol (Camb) 2012;4(4):431–439. doi: 10.1039/c2ib00120a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gjorevski N, Nelson CM. Mapping of mechanical strains and stresses around quiescent engineered three-dimensional epithelial tissues. Biophys J. 2012;103(1):152–162. doi: 10.1016/j.bpj.2012.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Koch TM, Münster S, Bonakdar N, Butler JP, Fabry B. 3D traction forces in cancer cell invasion. PLoS One. 2012;7(3):e33476. doi: 10.1371/journal.pone.0033476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Das M, MacKintosh FC, Levine AJ. Effective medium theory of semiflexible filamentous networks. Phys Rev Lett. 2007;99(3):038101. doi: 10.1103/PhysRevLett.99.038101. [DOI] [PubMed] [Google Scholar]
- 33.Broedersz CP, MacKintosh FC. Modeling semiflexible polymer networks.+ Rev Mod Phys. 2014;86(3):995–1036. [Google Scholar]
- 34.Mao X, Stenull O, Lubensky TC. Effective-medium theory of a filamentous triangular lattice. Phys Rev E Stat Nonlin Soft Matter Phys. 2013;87(4):042601. doi: 10.1103/PhysRevE.87.042601. [DOI] [PubMed] [Google Scholar]
- 35.Licup AJ, et al. 2015. Stress controls the mechanics of collagen networks. arXiv:1503.00924.
- 36.Wang H, Abhilash AS, Chen CS, Wells RG, Shenoy VB. Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys J. 2014;107(11):2592–2603. doi: 10.1016/j.bpj.2014.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Abhilash AS, Baker BM, Trappmann B, Chen CS, Shenoy VB. Remodeling of fibrous extracellular matrices by contractile cells: Predictions from discrete fiber network simulations. Biophys J. 2014;107(8):1829–1840. doi: 10.1016/j.bpj.2014.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Head DA, Levine AJ, MacKintosh FC. Mechanical response of semiflexible networks to localized perturbations. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72(6 Pt 1):061914. doi: 10.1103/PhysRevE.72.061914. [DOI] [PubMed] [Google Scholar]
- 39.Heussinger C, Frey E. Force distributions and force chains in random stiff fiber networks. Eur Phys J E Soft Matter. 2007;24(1):47–53. doi: 10.1140/epje/i2007-10209-1. [DOI] [PubMed] [Google Scholar]
- 40.Rehfeldt F, Engler AJ, Eckhardt A, Ahmed F, Discher DE. Cell responses to the mechanochemical microenvironment--implications for regenerative medicine and drug delivery. Adv Drug Deliv Rev. 2007;59(13):1329–1339. doi: 10.1016/j.addr.2007.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cuerrier CM, Pelling AE. Cells, Forces, and the Microenvironment. CRC Press; Boca Raton, FL: 2015. [Google Scholar]
- 42.Baharvand H, Hashemi SM, Kazemi Ashtiani S, Farrokhi A. Differentiation of human embryonic stem cells into hepatocytes in 2D and 3D culture systems in vitro. Int J Dev Biol. 2006;50(7):645–652. doi: 10.1387/ijdb.052072hb. [DOI] [PubMed] [Google Scholar]
- 43.Kenny PA, et al. The morphologies of breast cancer cell lines in three-dimensional assays correlate with their profiles of gene expression. Mol Oncol. 2007;1(1):84–96. doi: 10.1016/j.molonc.2007.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.