Substantial increase in concurrent droughts and heatwaves in the United States

Significance

Climatic extremes cause significant damage to the environment and society, and can cause even more damage when multiple extremes occur simultaneously. This study shows that although there is no significant trend in meteorological drought, the concurrence of meteorological droughts and heatwaves shows statistically significant increases across the United States. We show that the tail of the distribution of concurrent drought and heatwave conditions has shifted toward more frequent and extreme concurrent extremes. Our study outlines a statistical approach for investigating continuous change in the cumulative distribution functions of climatic extremes.

Abstract

A combination of climate events (e.g., low precipitation and high temperatures) may cause a significant impact on the ecosystem and society, although individual events involved may not be severe extremes themselves. Analyzing historical changes in concurrent climate extremes is critical to preparing for and mitigating the negative effects of climatic change and variability. This study focuses on the changes in concurrences of heatwaves and meteorological droughts from 1960 to 2010. Despite an apparent hiatus in rising temperature and no significant trend in droughts, we show a substantial increase in concurrent droughts and heatwaves across most parts of the United States, and a statistically significant shift in the distribution of concurrent extremes. Although commonly used trend analysis methods do not show any trend in concurrent droughts and heatwaves, a unique statistical approach discussed in this study exhibits a statistically significant change in the distribution of the data.

Heatwaves cause severe damage to society and the environment (1), with impacts on human health, air quality, and vegetation (2, 3). In 2003, for example, European countries faced an unprecedented heatwave, which in turn caused unusually high ozone concentrations (3) and severe health problems, particularly in France, where 15,000 extra deaths occurred (3–5). United Nations Environment Programme considers the European heatwave the world’s most costly weather-related disaster in 2003. Impacts were exacerbated because the region was in a drought (6).

Heatwaves have a variety of direct, indirect, immediate, and delayed impacts, including higher water loss via evapotranspiration, lower yields of grains and other agricultural products (7), increased energy consumption, a decrease in efficiency of power plants (8), air pollution, and adverse effects on human health (3, 6). Heatwaves have also contributed to an increase in the duration, size, and intensity of wildfires, causing economic losses and catastrophic environmental impacts (8).

Droughts also have pronounced impacts on society and the environment, such as significant reductions in gross primary productivity, leading to shortages in food production and increases in global food prices (2). The annual economic damage caused by droughts is estimated to be approximately $7 billion globally (9), with potential impacts on livestock, transportation by river, hydropower production, bioenergy, and energy consumption (8, 10–12).

Extreme climatic events can occur simultaneously, exacerbating environmental and societal impacts. Environmental hazards often result from a combination of climatic events (13, 14) over a range of spatial and temporal scales (15, 16). A wildfire, for example, may occur on a hot, dry, and windy day, although each of these individual conditions may not necessarily be extreme by themselves (16). In the Intergovernmental Panel on Climate Change special report on managing the risks of extreme events and disasters, the combination of multiple climate extreme events is termed a compound event (14, 16). Most analyses of climate and weather extremes typically tend to focus on a single climatic condition; however, this univariate approach may underestimate the effects of concurrent and compound extremes (16).

Sustained precipitation deficit in summer can be a contributory factor to hot summer days (17). Heatwaves reduce the total energy transfer to the atmosphere, resulting in a decrease in convective precipitation (7). This in turn causes a soil−precipitation feedback loop that tends to extend or intensify drought conditions (7). The interaction between precipitation and temperature has been widely recognized in numerous studies (18, 19). Heatwaves concurrent with droughts can intensify individual impacts of heatwaves or drought on society, the environment, and the global economy (19, 20). Studies suggest that changes in the relationship between precipitation and temperature may be more important than the changes in each of the variables individually (16, 21). This study investigates changes in concurrent droughts and heatwaves in the United States using several different statistical techniques.

A heatwave is typically defined as a period of consecutive extremely hot days (22, 23), such as five consecutive days with temperature above the 90th percentile. Here, we use the 85th, 90th, and 95th percentiles of the warm season (May–October) temperature as extreme thresholds, and three heatwave durations (3 d, 5 d, and 7 d). A 5-d heatwave with a 90th percentile threshold is defined as five consecutive days with the maximum temperature exceeding the 90th percentile of the long-term climatology for that month. In this study, meteorological droughts are defined as precipitation deficits relative to the climatology using the Standardized Precipitation Index (SPI) (24). Throughout this study, a drought is defined as an event that leads to SPI < −0.8 (approximately the 20th percentile precipitation). We use daily temperature and monthly precipitation information to identify historical droughts and heatwaves in the United States (see Data).

Results

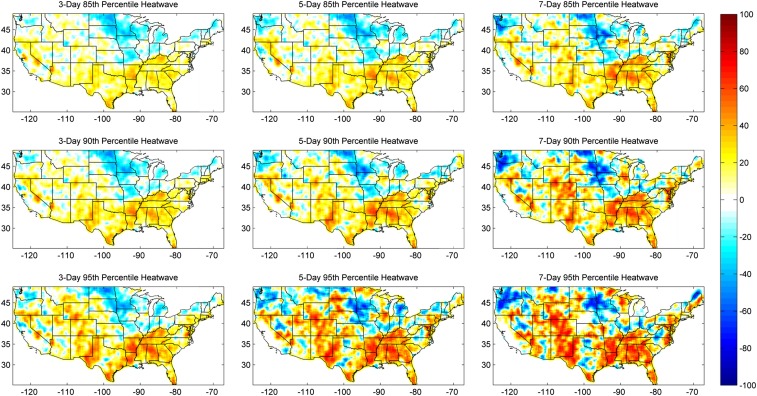
We evaluated the changes in concurrent droughts and heatwaves during 1990–2010 relative to the baseline period 1960–1980. Fig. 1 displays percent change in the occurrences of concurrent drought and heatwave events in each grid box (see also Figs. S1 and S2). Here, the percent change is based on the difference in the number of events in 1990–2010 relative to 1960–1980, divided by the total number of events. We present results for different durations (3-, 5-, and 7-d heatwaves) and extreme temperature thresholds (85th, 90th, and 95th percentiles). Fig. 1 shows that concurrences of all combinations of drought and heatwave intensities and durations have increased substantially in the south, southeast, and parts of the western United States, and have decreased in parts of the Midwest and northern United States. Notably, the longer and more severe (7-d 95th percentile) drought and heatwave concurrences have increased more than shorter, less severe concurrences (e.g., compare 7-d 95th percentile with the 3-d 85th percentile panels). This indicates that longer heatwaves (i.e., 7 d) have become more frequent in 1990–2010 compared with the shorter heatwaves (i.e., 3 d).

Fig. 1.

Percent (%) change in concurrent droughts and heatwaves during 1990–2010 relative to 1960–1980 for each grid box. The rows change in heatwave severity (85th percentile, 90th percentile, and 95th percentile), and the columns change in heatwave duration (3 d, 5 d, and 7 d).

Fig. S1.

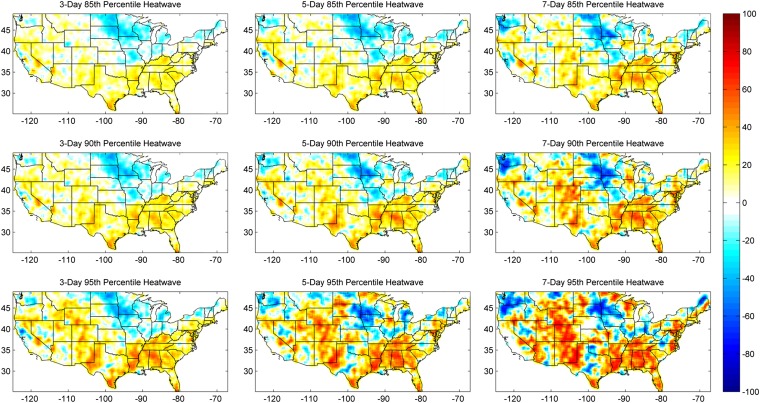
Percent (%) change in concurrent droughts (SPI < −0.5) and heatwaves during 1990–2010 relative to 1960–1980 for each grid box. The rows change in heatwave severity (85th percentile, 90th percentile, and 95th percentile), and the columns change in heatwave duration (3 d, 5 d, and 7 d).

Fig. S2.

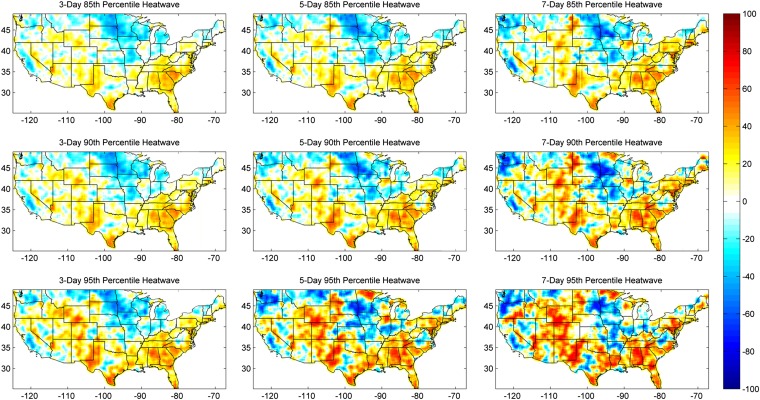
Percent (%) change in concurrent droughts (3-mo SPI < −0.8) and heatwaves during 1990–2010 relative to 1960–1980 for each grid box. The rows change in heatwave severity (85th percentile, 90th percentile, and 95th percentile), and the columns change in heatwave duration (3 d, 5 d, and 7 d).

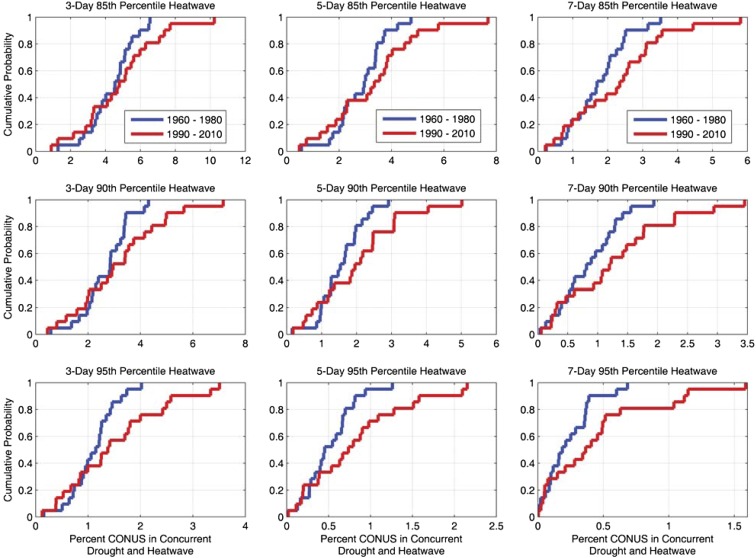
Investigating the empirical cumulative distribution function (CDF) of the concurrent droughts and heatwaves reveals a substantial change in extremes in 1990–2010 relative to 1960–1980 (Fig. 2). The x axes represent the percent (%) of the contiguous United States in concurrent drought and heatwave. The y axes show the corresponding cumulative probability. In each panel, the blue line is the CDF for the baseline period and the red line represents the CDF for 1990–2010. The CDF is based on data from the continental United States. As shown, for all intensities and durations during 1990–2010, the upper tail of the CDF has shifted to the right, indicating more extreme events in 1990–2010 relative to the baseline period (compare the red and blue lines in Fig. 2). Notice that the shift is far more pronounced in the more extreme 7-d 95th percentile drought and heatwave concurrence compared with other combinations. The two-sample Kolmogorov−Smirnov (KS) test (Methods) confirms that the CDFs of the concurrent droughts and heatwaves in the second period (1990−2010) are substantially different from those in the baseline period (1960−1980) at 0.05 significance level (95% confidence) for all heatwave durations and intensities except for 3-d 85th percentile heatwaves (Table 1).

Fig. 2.

The empirical CDF of drought and heatwave concurrences from 1960 to 1980 (blue) and 1990 to 2010 (red). The x axes represent the percent (%) of CONUS in concurrent drought and heatwave (see SI Data Sources and Processing for more information on percent of CONUS). The rows change in heatwave severity (85th percentile, 90th percentile, and 95th percentile), and the columns change in heatwave duration (3 d, 5 d, and 7 d).

Table 1.

Change in distribution functions between 1960–1980 and 1990–2010 based on the KS test

Drought and heatwave	P value
3-d, 85th percentile	0.53090
5-d, 85th percentile	∼0
7-d, 85th percentile	∼0
3-d, 90th percentile	∼0
5-d, 90th percentile	∼0
7-d, 90th percentile	∼0
3-d, 95th percentile	∼0
5-d, 95th percentile	∼0
7-d, 95th percentile	∼0

Column 2 shows the corresponding P values, where P values smaller than 0.05 indicate the distribution functions are drawn from different distributions at a 0.05 significance level. Smaller P values represent higher confidence in rejecting the null hypothesis that the distributions come from the same distribution.

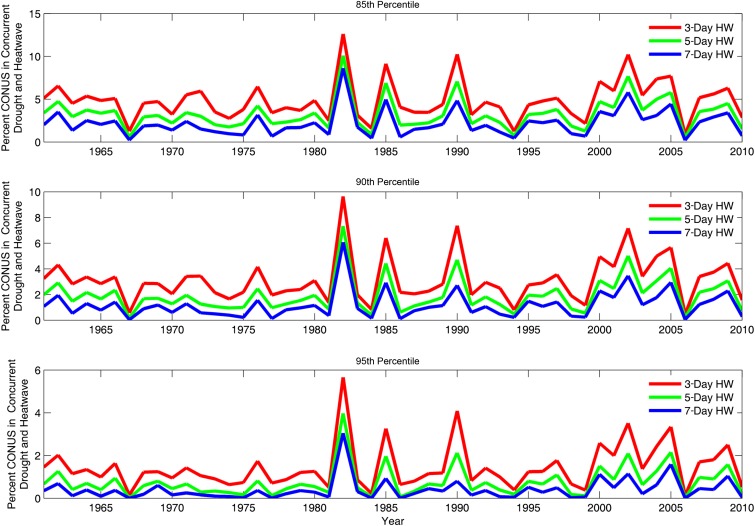
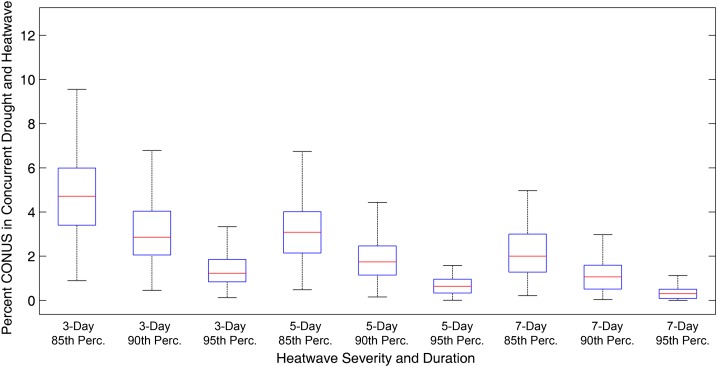
Past studies focused on changes in drought trends report conflicting results (9, 21, 25, 26). Here, we investigate the percent of the continental United States in concurrent droughts and heatwaves for different durations and intensities from 1960 through 2010 (Fig. 3; see also Fig. S3). For the 90th percentile threshold, the percent of the country in drought and heatwave can range between 6% (7-d heatwave) and 9.6% (3-d heatwave); see the boxplots of the percent contiguous United States (CONUS) in concurrent drought and heatwave for all durations and severities in Fig. S4. Although the CDFs clearly indicate changes in concurrent droughts and heatwaves, the commonly used Mann−Kendall (MK) trend test (see Methods) does not show a statistically significant trend (95% confidence) in the fraction of CONUS under concurrent drought and heatwave (Table S1 provides the test statistics results). This can be attributed to limitations of statistical trend tests discussed in previous studies (27) or to lack of sensitive tools for change detection.

Fig. 3.

Percent (%) of CONUS in concurrent drought and heatwave from 1960 to 2010.

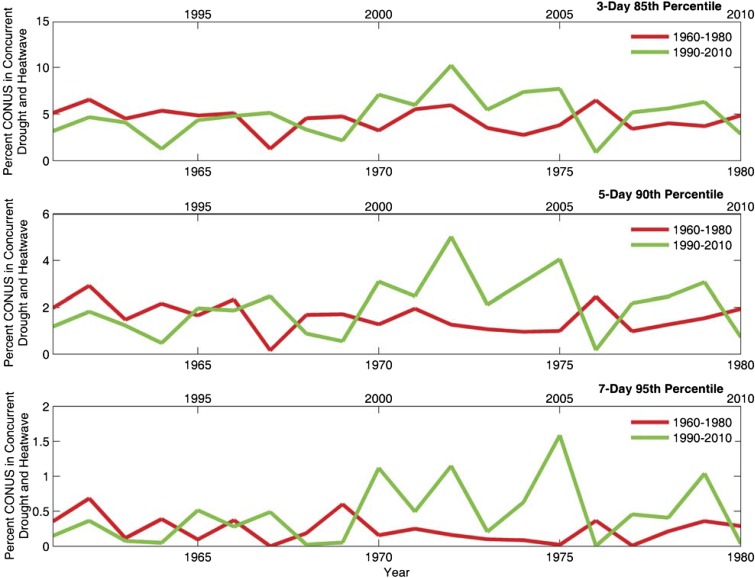
Fig. S3.

Percent (%) of CONUS in concurrent drought and heatwave from 1960 to 1980 (bottom x axes) relative to 1990–2010 (top x axes) for three different heatwave durations and severity thresholds.

Fig. S4.

Box plots of the percent (%) of CONUS in concurrent drought and heatwave from 1960 to 2010 (based on data presented in Fig. 3) for three different heatwave durations (3 d, 5 d, and 7 d) and severity thresholds (85th, 90th, 95th percentiles). The central marks (red lines) are the medians, and the edges of the boxes are the 25th and 75th percentiles. The whiskers show the most extreme values not identified as outliers.

Table S1.

Trends in drought and heatwave concurrence from 1960 to 2010 based on the MK trend test

Drought and heatwave	P value	Trend line slope
3-d, 85th percentile	0.9095	0.0021
5-d, 85th percentile	0.871	0.0032
7-d, 85th percentile	0.5919	0.0053
3-d, 90th percentile	0.7576	0.0044
5-d, 90th percentile	0.6492	0.0048
7-d, 90th percentile	0.4355	0.005
3-d, 95th percentile	0.6728	0.0049
5-d, 95th percentile	0.4452	0.0038
7-d, 95th percentile	0.4452	0.0027

A P value > 0.05 indicates that the null hypothesis of no trend cannot be rejected at a significance level of 0.05 (95% confidence). Column 2 shows the corresponding P values, and column 3 shows the trend line slope for the best linear fit.

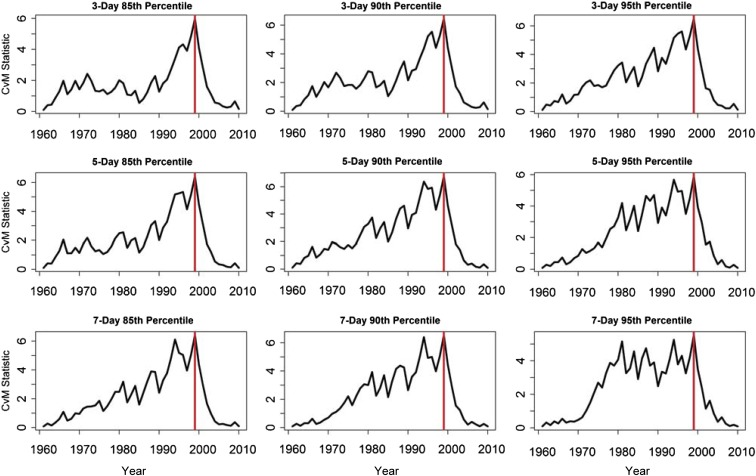
Here, we explore an approach based on the Cramér–von Mises change point detection test statistic (see Methods and Supporting Information) to investigate changes in concurrent droughts and heatwaves. We argue that this method is more sensitive to potential changes in time series and is well suited to investigate climate time series. This method, primarily used in economics and finance, evaluates different periods of data and determines statistically significant changes throughout time series. Fig. 4 shows the Cramér–von Mises statistics for drought and heatwave concurrences during 1960–2010. The y axes indicate a dimensionless measure of divergence between the empirical distributions of data before and after any given year as a continuous function (see Methods). For all plots, the maximum divergence occurs between 1998 and 1999, indicating substantial departure of the drought and heatwave CDFs before and after the red line in Fig. 4. This information cannot be achieved from the commonly used trend analysis method or distribution change evaluation approaches.

Fig. 4.

The Cramér−von Mises (CvM) change point statistic from 1960 to 2010. The rows change in heatwave severity (85th percentile, 90th percentile, and 95th percentile), and the columns change in heatwave duration (3 d, 5 d, and 7 d). The red lines indicate the point of maximum divergence between the distributions of concurrent drought and heatwave events.

Recent reports suggest an apparent hiatus or so-called pause in global warming since 1999–2000 (28). Possible explanations include a long-lasting solar energy output minimum, low stratospheric water vapor, an increase in early 21st century volcanic activity, and a more frequent La Niña phase since the major El Niño event of 1997–1998 (28). However, analyses show no pause in the occurrence of hot extremes over land since 1997 (29), or even in the mean global temperature (30). Rather, during the hiatus, exceedances of 30 extreme warm days per year have increased (29). The results in Figs. 2 and 4 indicate a statistically significant (at the 0.05 significance level) change in concurrent drought and heatwave events across many regions. Fig. 2 indicates more extreme drought and heatwave concurrences in the latter two decades. This is consistent with the increase in extreme warm days during this period (29). However, this conclusion cannot be reached using the commonly used statistical trend analysis techniques (e.g., MK trend test) used in hydrology and climate literature. Unlike the MK trend test, which investigates monotonic changes in the ranks of variables over time, the Cramér–von Mises test focuses on changes in the distributions of subsamples of the data (Table S2 provides the test statistics results). Typically, climatologists evaluate a certain period against a baseline. The Cramér–von Mises test is a flexible approach that allows investigators to examine different subsamples (e.g., projected and baseline periods) for potential distributional changes. The methodology outlined in this paper shows statistical changes in extremes beyond those achieved with commonly used methods.

Table S2.

P values of the Cramér−von Mises test for concurrent drought and heatwaves in 1990–2010 relative to 1960–1980

Drought and heatwave	P value
3-d, 85th percentile	0.43242
5-d, 85th percentile	∼0
7-d, 85th percentile	∼0
3-d, 90th percentile	∼0
5-d, 90th percentile	∼0
7-d, 90th percentile	∼0
3-d, 95th percentile	∼0
5-d, 95th percentile	∼0
7-d, 95th percentile	∼0

A P value < 0.05 indicates that the null hypothesis of no change can be rejected at a 0.05 significance level (95% confidence).

Data

Both precipitation and temperature data sets are from the observation-based forcings developed for the North American Land Data Assimilation System Variable Infiltration Capacity simulations over CONUS (31, 32). Daily temperature and monthly precipitation data with a spatial resolution of 1/8° are used for detecting droughts and heatwaves (see Supporting Information for more information on the data).

Methods

Here, the two-sample KS test assesses differences between the CDFs of the concurrent drought and heatwave events. KS is a nonparametric test that can evaluate two distribution functions (two-sample) based on the distance between their empirical distribution functions. The null hypothesis is that the two distribution functions are drawn from the same distribution at a certain significance level (here, α = 0.05). We use the two-sample KS test to compare different types of droughts and heatwaves (e.g., 3-d 85th percentile, 5-d 90th percentile) in 1990–2010 relative to 1960–1980. The test indicates whether the data from the two periods come from the same distribution at a 0.05 significance level.

The MK trend test (33) here assesses the presence of a statistically significant (0.05 significance level) trend in the time series of the fraction of CONUS in concurrent drought and heatwave. The MK test is a nonparametric approach based on the empirical ranks of time series widely used in hydrology and climatology.

We use a framework based on the Cramér–von Mises change point detection to evaluate temporal changes in the concurrent drought and heatwave events (34–37). This approach detects changes in the empirical CDF by comparing two subsamples [${\widehat{F}}_S\left(x\right)$ and ${\widehat{F}}_T\left(x\right)$] of the original time series,

$${\widehat{F}}_S\left(x\right)=\frac{1}{\tau }{\displaystyle \sum }_{i=1}^{\tau }I\left(X_i\le x\right)$$

$${\widehat{F}}_T\left(x\right)=\frac{1}{n-\tau }{\displaystyle \sum }_{i=\tau +1}^{n}I(X_i\le x),$$

where ${\widehat{F}}_S\left(x\right)$ and ${\widehat{F}}_T\left(x\right)$ are the empirical CDF of the two subsamples, I is the indicator function, n denotes sample size, and the terms 1/τ and 1/(n - τ) are adjustment factors for the length of each subsample. The test measures the divergence between the empirical distributions as

$$W_{\tau ,n}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\left|{\widehat{F}}_S-{\widehat{F}}_T\right|}^{2}d{F}_t\left(x\right)$$

where $W_{\tau ,n}$ can be computed as the square of the mean distance between the empirical distributions (37, 38),

$$W_{\tau ,n}={\displaystyle \sum }_{i=1}^n{\left|{\widehat{F}}_S\left(X_i\right)-{\widehat{F}}_T\left(X_i\right)\right|}^2.$$

Larger divergence values, W, indicate greater changes in the cumulative distributions. Here, the null hypothesis is that there is no change in the data over time and the two subsamples come from the same distribution. The null hypothesis is rejected if at an unspecified point τ, ${\widehat{F}}_S\left(x\right)$ and ${\widehat{F}}_T\left(x\right)$ come from statistically different distributions. Because we do not have any prior information on the position of $\text{τ}$ in the time series, the test involves computing ${\text{W}}_{\text{τ},\text{n}}$ for all $1<\text{τ}<n$ (39). However, for different values of τ, the variance of the two subsamples will be different. For this reason, the $W_{\tau ,n}$ statistics are adjusted so that both periods exhibit equal mean and variance for all values of τ (39) (see Supporting Information for more). The methods in this study should be applied to independent and identically distributed time series. Supporting Information provides more information on the sampling approach and temporal autocorrelation of the data (see Fig. S5 and the corresponding discussion).

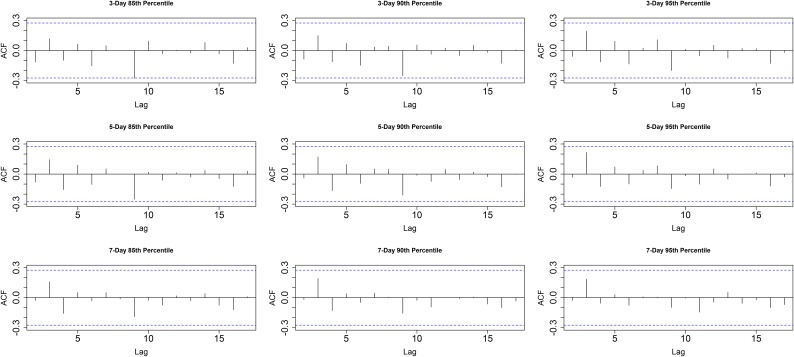
Fig. S5.

Autocorrelation function (ACF) of the time series used in Fig. 3. The dashed lines represent the 95% confidence intervals (0.05 significance level).

SI Data Sources and Processing

We used daily temperature and monthly precipitation data from a unique long-term and observation-based data set that provides forcings for land surface models (31, 32). In this data set, daily precipitation is based on data from more than 10,000 precipitation gauges available from the National Oceanic and Atmospheric Administration (NOAA) Cooperative Observer Program (COOP). Using the synergraphic mapping system approach (40, 41), the precipitation observations are gridded to 1/8° resolution. Monthly precipitation fields are daily precipitation accumulations. Maximum daily temperature data are also from NOAA’s COOP stations and are regridded using the same approach.

Information about the NOAA COOP data can be found at www.ncdc.noaa.gov/data-access/land-based-station-data/land-based-datasets/cooperative-observer-network-coop. The 1/8° gridded daily temperature data are available at hydro.engr.scu.edu/files/gridded_obs/daily/ncfiles/. The 1/8° gridded monthly precipitation data are available at hydro.engr.scu.edu/files/gridded_obs/monthly/ncfiles/.

This study focuses on warm season (May–October) temperature extremes (i.e., 85th, 90th, and 95th percentiles of the maximum temperature) and the corresponding monthly precipitation. We derive the percent (%) of CONUS in concurrent drought and heatwave by summing the number of concurrent events in the warm season normalized by CONUS’s area (sum of the pixels in concurrent drought and heatwave in each year’s May−October, divided by the total number of pixels in CONUS). More than one heatwave can occur during a warm season, and, by using this approach, we can account for multiple concurrent drought and heatwave events in any given pixel.

SI Results and Discussion

Fig. 1 shows percent change in concurrent drought and heatwave events during 1990–2010 relative to 1960–1980. We present the results for 1-mo SPI < −0.8 (approximately, 20th percentile precipitation), different heatwave durations (3 d, 5 d, and 7 d), and extreme temperature thresholds (85th, 90th, and 95th percentiles). To show consistent patterns of percent change in concurrent drought and heatwave events, we show similar figures for SPI < −0.5 (Fig. S1) and 3-mo SPI < −0.8 (Fig. S2). The general patterns remain similar to Fig. 1 for different drought definitions. For better visualization, the percent change values are smoothed using a 3 $\times$ 3-pixel running mean.

Fig. 3 displays the percent of CONUS in concurrent drought and heatwave for different durations and intensities from 1960 to 2010. For a better visualization, Fig. S3 shows the percent (%) of CONUS in concurrent drought and heatwave from 1960 to 1980 (bottom x axes) relative to 1990–2010 (top x axes) for three different heatwave durations and severity thresholds. The results show more concurrent drought and heatwaves during 1990–2010 (top x axes), consistent with the findings of Fig. 2. However, the MK trend test does not indicate any statistically significant change in the concurrent drought and heatwave time series in Fig. 3.

Both droughts and heatwave events exhibit dependence across space (see Fig. 1). However, the statistical tests in this paper require independent and identically distributed time series (27). Basically, multiple pixels that belong to one event should not be counted as multiple independent occurrences. To address this issue, at any given time step, we extracted one value: the fraction of CONUS in concurrent drought and heatwave. In other words, we identify all concurrent droughts and heatwaves. Then, instead of using the count of the events (or pixels), we evaluate the fraction of the country. As shown in Fig. S5, the values extracted at each time step, used in Figs. 2–4, do not exhibit any statistically significant temporal correlation at 0.05 significance level.

SI Methods

In the Cramér–von Mises change point detection method, the $W_{\tau ,n}$ statistics are adjusted to ensure the two subsamples [${\widehat{F}}_S\left(x\right)$ and ${\widehat{F}}_T\left(x\right)$] have equal mean and variance for all values of τ (42). This can be achieved using a standardization approach as (43)

$${\sigma }_{W_{\tau ,n}}=\sqrt{\frac{(n+1)\left(\left(1-\frac{3}{4}\hspace{0.17em}\tau \right)n^2+\left(1-\tau \right)n-\tau \right)}{45n^2(n-\tau )}}$$

$${\mu }_{W_{\tau ,n}}=\frac{(n+1)}{6n}$$

where ${\mu }_{W_{\tau ,n}}$ and ${\sigma }_{W_{\tau ,n}}$ are the mean and SD of $W_{\tau ,n}$. The so-called maximized test statistic can then be defined as (42)

$$W_n=\underset{\tau }{\max }\frac{W_{\tau ,n}-{\mu }_{W_{\tau ,n}}}{{\sigma }_{W_{\tau ,n}}}.$$

This method of standardizing $W_{\tau ,n}$ and maximizing $W_n$ for all values of τ gives a single test statistic for significance analysis and hypothesis testing. A bootstrap sampling approach outlined in refs. 42 and 44–46 can determine the P value and hypothesis testing. The approximate P value is computed using a multiplier approach as

$$\frac{(0.5+\hspace{0.17em}{{\displaystyle \sum }}_{i=1}^N{1}_{\{W_i\ge W\}})}{N+1}$$

where W and W_i are the test statistic and a multiplier replication, respectively. In a bootstrap process with n = 1,000 replications, if the result falls in the α-tail (α = 0.05) of the N simulations, the test is statistically significant at a 0.05 significance level. The bootstrapping approach is known as the sequential block bootstrapping procedure, and can be used for both independent and serially dependent variables (38, 47). Given that our data are independent and identically distributed (Fig. S5), we use a unit block length, which leads to independent and identically distributed multiplier sequences. In addition to the above approximate P value, the so-called two-sample Cramér−von Mises test (CMTest2) can compare two different periods (data records). This test evaluates whether independent samples from two periods (here, 1960–1980 and 1990–2010) are drawn from the same population (43, 48). In this test, the P value can be derived similar to the two-sample KS test (43). Table S2 summarizes the P values of CMTest2 for drought and heatwaves during 1990–2010 relative to 1960–1980. The table confirms a statistically significant change in the distribution of concurrent drought and heatwaves at 0.05 significance level (95% confidence) for all heatwave durations and intensities except for 3-d 85th percentile heatwaves. For more information on the procedure and statistical significance analysis and bootstrapping approach, refer to the “cpm” (cran.r-project.org/src/contrib/Archive/cpm/) and “npcp” (cran.r-project.org/web/packages/npcp/index.html) R packages.