Significance
Recent behavioral research has made rapid progress toward revealing the processes by which we make choices based on judgments of subjective value. A key insight has been that this process unfolds incrementally over time, as we gradually build up evidence in favor of a particular preference. Although the data for this ‟evidence-integration” model are compelling, they derive almost entirely from single-step choices: Would you like chocolate or vanilla ice cream? Decisions in everyday life are typically more complex. In particular, they generally involve choices between sequences of action, with accompanying series of outcomes. We present here results from two experiments, providing the first evidence to our knowledge that the standard integration model of choice can be directly extended to multistep decision making.
Keywords: reward-based decision making, drift-diffusion model, reinforcement learning
Abstract
Research on the dynamics of reward-based, goal-directed decision making has largely focused on simple choice, where participants decide among a set of unitary, mutually exclusive options. Recent work suggests that the deliberation process underlying simple choice can be understood in terms of evidence integration: Noisy evidence in favor of each option accrues over time, until the evidence in favor of one option is significantly greater than the rest. However, real-life decisions often involve not one, but several steps of action, requiring a consideration of cumulative rewards and a sensitivity to recursive decision structure. We present results from two experiments that leveraged techniques previously applied to simple choice to shed light on the deliberation process underlying multistep choice. We interpret the results from these experiments in terms of a new computational model, which extends the evidence accumulation perspective to multiple steps of action.
Imagine a customer standing at the counter in an ice cream shop, deliberating among the available flavors. Such a scenario exemplifies “simple choice,” a decision situation in which the objective is to select among a set of individual, immediate outcomes, each carrying a different reward. Simple choice, in this sense, has provided a convenient focus for a great deal of work in behavioral economics and decision neuroscience (1–5). However, it would be an obvious mistake to treat it as an exhaustive model of reward-based decision making. The decisions that arise in everyday life are of course often more complicated. One important difference, among others, is that everyday decisions tend to involve sequences of actions and outcomes.
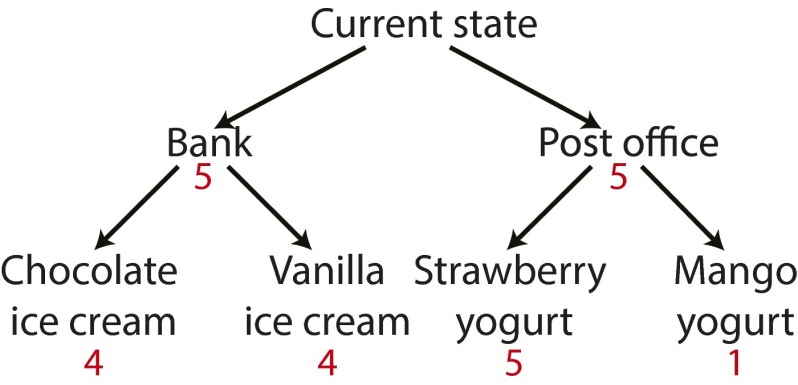
As an illustration, let us return to the ice cream customer, picturing him at a point slightly earlier in the day, exiting his home in quest of something sweet. Upon reaching the sidewalk, he faces a decision between heading left toward the ice cream shop, or heading right toward a frozen yogurt shop. If he wishes to fully evaluate the relative appeal of these two options, he must answer a second set of questions: Which flavor would he choose in each shop? Furthermore, it may be relevant for him to consider more immediate consequences of the left–right decision. For example, the leftward path might pass by a bank, allowing him to deposit a check along his way, whereas the rightward path might lead by the post office, giving him the opportunity to mail a package.
Rather than selecting among individual and immediate outcomes, the decision maker in this scenario finds himself at the root of a decision tree (Fig. 1A), with nodes corresponding to value-laden outcomes or states, and edges corresponding to choice-induced state transitions. Deciding among immediate actions, even at the first branch point, requires a consideration of all of the paths that unfold below. Decision making thus assumes the form of reward-based tree search (6–10).
Fig. 1.
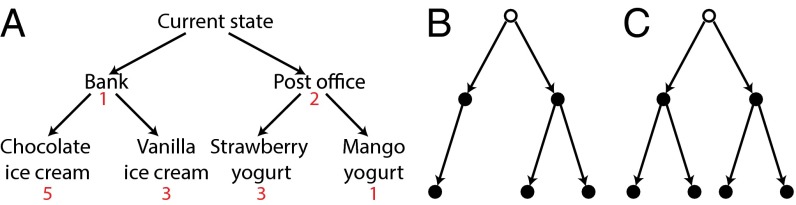
(A) Reward-based tree search entails both cumulative and recursive structure. Choosing between the first-stage outcomes in isolation (bank vs. post office) would lead to suboptimal behavior: Although the post office is more rewarding (2 vs. 1), the optimal path entails going through the bank to get to the chocolate ice cream (total reward of 6). However, choosing the bank is optimal only if chocolate ice cream is going to be selected in the ice cream shop, or vanilla ice cream is going to be selected in the ice cream shop and mango yogurt in the yogurt shop. If vanilla ice cream and strawberry yogurt are to be selected, the path through the post office is preferable. (B) Decision tree used in experiment 1. Each node is a state, and each arrow an action. Participants start in the state marked by an open circle. States marked by a closed circle contain reward. (C) Decision tree used in experiment 2.
Note that decision making in this setting cannot be reduced to a collection of independent simple-choice problems. In particular, deciding between first-stage outcomes (bank vs. post office) may backfire if one fails to consider the later choices to which they lead; one must consider total rather than piecewise reward. Furthermore, to choose among immediate actions, one must do more than merely consider later decisions. One must actually make those decisions, because the expected value of immediate behavior depends on plans for subsequent action. For example, the post office route may be preferable to the bank route if the anticipated food choices are vanilla ice cream and strawberry yogurt, but this might reverse if the choices are vanilla ice cream and mango yogurt (Fig. 1A). Thus, unlike simple choice, reward-based tree search entails both cumulative and recursive structure.
The problem of reward-based tree search has long provided a central focus for work in control theory, operations research, artificial intelligence, and machine learning. Only more recently has it begun to receive due attention in psychology and neuroscience. In the most salient work along these lines, reward-based tree search has been conceptualized in terms provided by model-based reinforcement learning, a computational framework in which reward-based decisions are based on an explicit model of the choice problem, a “cognitive map” of the decision tree itself (11). Under this rubric, recent work has illuminated several aspects of reward-based tree search, providing an indication of how representations of decision problems are acquired and updated (12–14), where in the brain relevant quantities (e.g., cumulative rewards) are represented (15–17), and how model-based decision making interacts with simpler, habit-based choice mechanisms (15, 18–22).
Despite such advances, however, comparatively little progress has so far been made toward characterizing the concrete process by which model-based decisions are reached, that is, the actual procedure through which a representation of the decision problem is translated into a choice (9, 10, 23). This situation contrasts sharply with what one finds in the literature on simple choice, where a number of detailed process models have been proposed. Although important differences exist, current models of simple choice converge on a common evidence-integration paradigm (1–5, 24–26). Here, each choice option is associated with a specific utility, but this quantity can only be accessed through a noisy sampling procedure. This procedure involves collecting a series of samples for each choice option and integrating across them until the accumulated evidence in favor of one option is significantly greater than the rest. This evidence-integration framework, often implemented in the form of a drift-diffusion process, accounts for detailed behavioral data, both at the level of reaction times and choice probabilities (2–4).
In the present paper, we aim to extend these advances to the domain of reward-based tree search, by introducing and testing a process model of multistage decision making. Our specific proposal is that the evidence-integration framework that has been so successful in explaining simple choice can in fact be directly extended to reward-based tree search. We begin by sketching an evidence-integration model for sequential decision making. We then present results from two behavioral experiments that provide an empirical foundation for evaluating the proposed computational account. Leveraging the resulting reaction time and choice proportion data, we compare the proposed model with a range of variants and alternatives.
Results
Computational Model.
As in previous studies of decision dynamics, we aimed to develop a model that can simultaneously capture the pattern of choices and reaction times. Although the complexity of moving from one-stage to multistage choice seems formidable, one particularly simple solution is to treat the problem as a single-stage decision between the paths of the corresponding decision tree. Here, by “path” we mean a single trajectory down from the top of the tree to a terminal node at the bottom of the tree. Although it is simple, we will show that this model provides a better description of the data than a number of appealing alternatives.
More concretely, at the root of a decision tree, each path is treated as an independent competitor. The evidence for each begins at zero and on each iteration of the deliberation process grows in proportion to the sum of all of the single-stage rewards that can be accumulated along the path. As in models of simple choice (2–4), the reward information retrieved for each individual item is noisy, and multiple samples have to be collected to make a decision. A decision is made when the evidence in favor of one path is significantly greater than the evidence for all of the other paths [“best vs. next” (4, 27)].
Because competition is between paths, the model thus far makes the prediction that participants make a decision once at the root of the tree and then play out the entire sequence of chosen moves. To foreshadow the results, however, the data suggest that decisions are further revised at subsequent stages. As such, we amend the model to output each stage of the decision separately, with surviving paths continuing to compete at the next stage until a higher evidence threshold is reached.
A formal description of the model can be found in Supporting Information. Presently, we describe two experiments that were designed to test the model.
Experiment 1.
Our strategy in both experiments was to directly extend methods that have been successfully applied to simple choice. Participants started by rating a set of 270 items (board games, electronics, etc.) on a five-point scale (0–4 in experiment 1 and 1–5 in experiment 2). This was followed by a series of decision trials in which participants were asked to choose the items they would most prefer to receive given the structure of the decision problem. The structure used in experiment 1 is illustrated schematically in Fig. 1B and represents what is perhaps the simplest possible extension of one-stage binary choice to the multistage domain. Participants made either one or two binary (left/right) decisions on each trial. The first decision committed them to at least one item on the corresponding side of the screen. One side had a further left/right decision, allowing participants to select a second item from among two others. The other side had a forced left/right “decision” committing participants to a particular item. An example is shown in Fig. 2. Importantly, participants had access to the full structure of the problem, including reward information at both stages, when making their first-stage decision. The first-stage decision should thus, in principle, reflect the influence of all of this information.
Fig. 2.
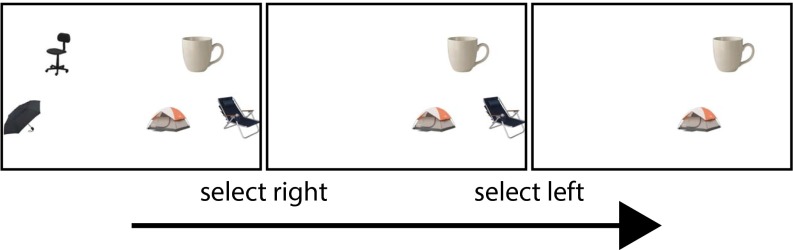
Example of a trial in experiment 1 (compare with Fig. 1B). Participants start with the screen on the far left and are faced with a left/right decision. If they select the right side, they would be committing to the mug, and would then have to input a second decision choosing between the tent and beach chair. The choice is confirmed on the last screen (in this case, the participant chose left, committing to the tent). If they choose left at the first stage, they would be committing to the office chair and would be forced to input left again to get the umbrella.
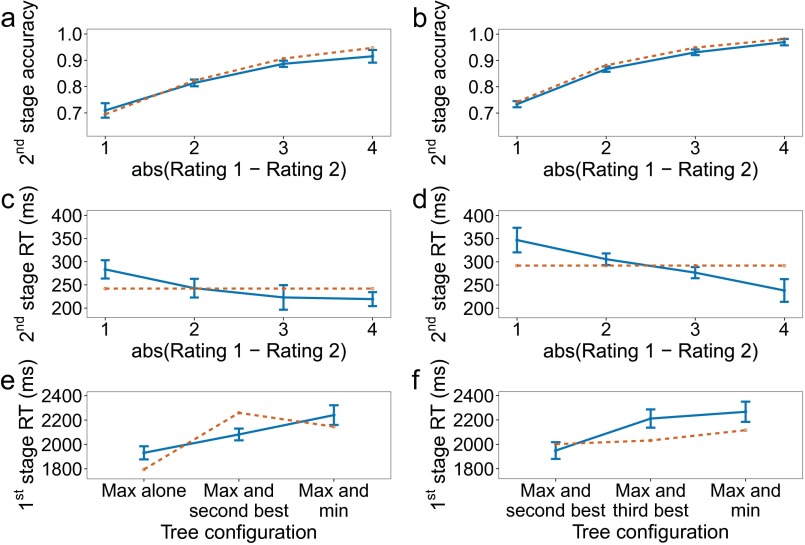
Similar to studies of simple choice, the dependent variables that are of interest are choice accuracy (or consistency, that is, how often participants chose the higher rated items) and reaction time. However, the independent variable must be specified with care. The first impulse is to use the full structure of the decision tree (i.e., the conjunction of all item ratings). However, if one notes that it is possible for five different ratings to appear in each of the five positions, even when the symmetry of the branches at both stages is taken into account, this yields very few trials for each tree configuration. Work on simple binary choice has focused on using the difference between item ratings as the independent variable. This represents a measure of decision difficulty, with larger differences resulting in faster and more accurate decisions (2, 3). We derive a similar measure for our two-stage problem by collapsing across time and treating the problem as a comparison between the three pairs of items, as assumed in the process model proposed above. The value of each pair is taken to be the sum of the ratings in that pair. One measure of difficulty then, following work on multialternative simple choice (4), is the difference between the maximum value and the mean of the other two values. The solid lines in Fig. 3 A and D plot choice accuracy and reaction time for the first-stage decision as a function of this measure. Accuracy increases and reaction time decreases as decisions get easier, suggesting that the measure we adopted provides a valid index of decision difficulty.
Fig. 3.
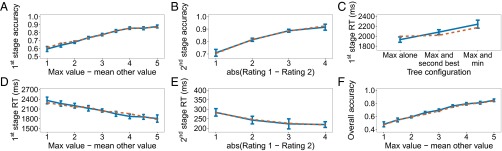
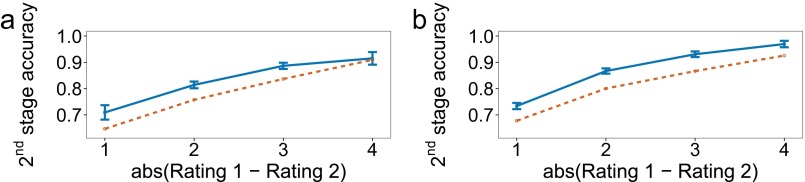
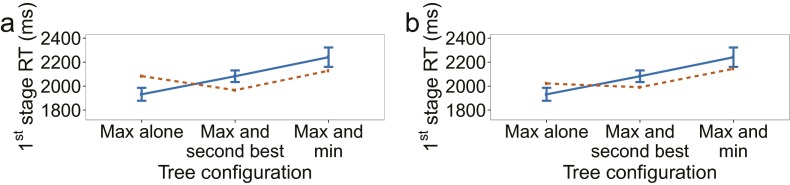
Results of experiment 1. Empirical data appear in blue with solid lines and the winning model in orange with dashed lines. Bars represent within-subject confidence intervals (28). In the figure and in the following description, “value” refers to the sum of the ratings along one path of the decision tree. (A) First-stage choice accuracy as a function of the difference between the maximum value and average of the other two values. A trial is considered correct if the first-stage choice does not rule out the optimal path. (B) Second-stage choice accuracy as a function of the absolute difference between the ratings of the items remaining at the second stage. A trial is considered correct if the higher-rated item is selected. Only trials where a second-stage choice had to be made are included. (C) First-stage reaction time for correct trials. A trial is considered correct if the best overall path was selected. (D) Second-stage reaction time for correct trials. A trial is considered correct if the best overall path was selected. (E) First-stage reaction time for correct trials, as defined in C and D, as a function of the paths that appear together in the tree. For example, “Max and second best” means that the two paths with the two largest values were grouped on one side (pressing left or pressing right at the first stage, depending on the paths’ location, would leave both of them in play), and the smaller-valued path was on the other side by itself. (F) Overall choice accuracy, taking both stages into account.
We can look at choice accuracy and reaction time for the second-stage decision as a function of the difference in ratings for the remaining two items. They are plotted in Fig. 3 B and E, which resemble the pattern of results typically seen in simple binary choice. Although small, the reaction time effect is significant []. Importantly, the reaction time effect suggests that the second stage involves further deliberation and not simply playback of a motor plan prepared at the first stage. We further test this possibility below by comparing a number of one-stage deliberation models that can potentially mimic this effect with our primary model.
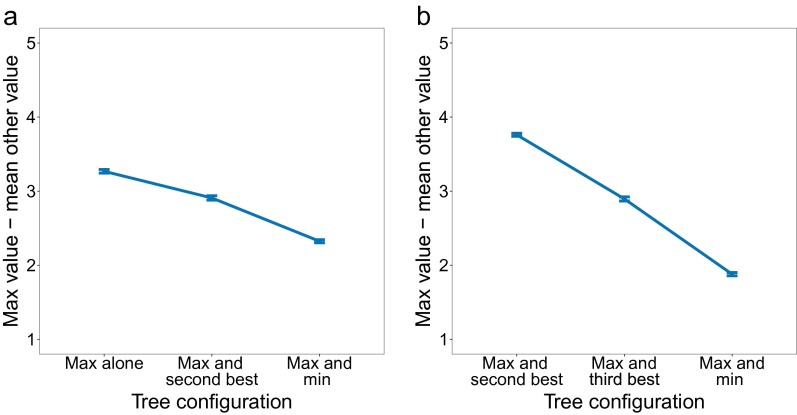
Fig. 3C provides a different look at first-stage reaction times, plotting them as a function of the internal organization of the decision tree. We distinguish between three configurations: (i) The most valuable path appears by itself on one side of the tree; (ii) the most valuable and the second most valuable paths appear on the same side of the tree, sharing the same first-stage choice; and (iii) the most valuable and least valuable paths appear on the same side. The differences in reaction times across these cases reflect differences in the distribution of decision difficulties for these three groupings of the data (Fig. S1). However, there may be an additional contributing factor: When most of the “mass” is on one side of the tree (e.g., when the most valuable and second most valuable paths lie on the same side), participants may complete their decision at the first stage before deciding what to do at the second stage. This window into the data serves as an additional constraint for model evaluation, as discussed below.
Fig. S1.
The difference between the value of the best path and the average of the other paths’ values as a function of which paths appear together in the tree. Decision difficulty differs across different tree configurations as a result of the two-stage structure. For example, consider the “Max and min” case vs. the “Max and second best” case. Because paths are correlated at the first stage, the value of the minimum path is on average closer to the maximum in the former compared with the latter. However, the second-best path in the former, which is on the other side, has to be even higher and is even more correlated. This makes the decision harder on average. (A) Experiment 1. (B) Experiment 2.
Finally, Fig. 3F plots overall choice accuracy, taking both stages of action into account.
Experiment 2.
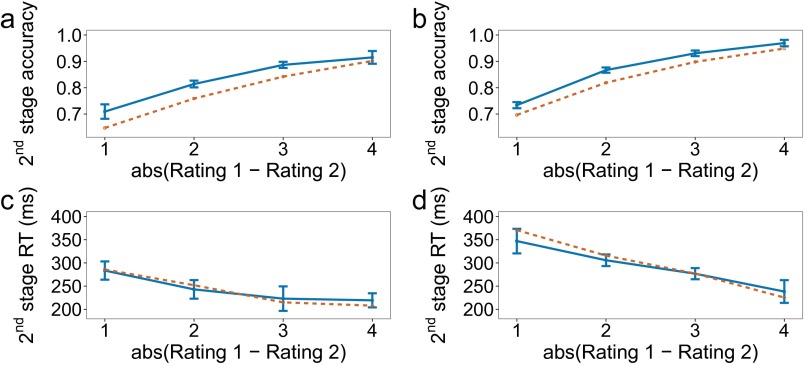
The second experiment was similar to the first, except that both sides of the decision tree had a second-stage decision (Fig. 1C). The goal was to replicate the first set of findings and modeling results with a new set of participants, while also testing the model’s ability to account for an additional path in the tree. The data are shown in Fig. 4, with results closely paralleling those shown in Fig. 3 for experiment 1. The second-stage reaction time effect is again significant [].
Fig. 4.
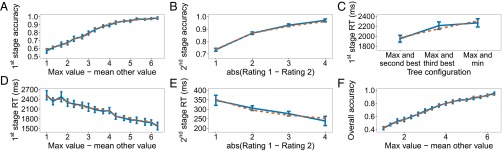
Results of experiment 2. (A–F) The panels parallel those of Fig. 3 for experiment 1.
Model Evaluation.
A straightforward implementation of the proposed model provides tight fits to the data for both experiments (Figs. 3 and 4). It should be noted that although the figures display summary statistics, the model is simulating 1,304 different conditions (tree configurations) in experiment 1 and 2,043 different conditions in experiment 2. Best fitting model parameters are displayed in Table S1.
Table S1.
Best-fitting parameters of the winning model
| Parameter | Exp. 1 | Exp. 2 |
| 0.000107600 | 0.000122600 | |
| 0.727058500 | 0.738474100 | |
| 394.9164580 | 188.2272950 | |
| 0.002418200 | 0.001776700 | |
| 0.746330100 | 0.778294900 | |
| 205.2812689 | 236.5221880 |
We used Bayesian model comparison to test the model against a number of alternatives and variants, which we briefly describe next. Details can be found in Supporting Information. Each model was fit separately to each experiment, with the resulting BIC (29) (Bayesian information criterion) values displayed in Table S2.
Table S2.
Bayesian information criterion values
| Model | Exp. 1 | Exp. 2 | Parameters |
| Two-stage, independent paths (primary model) | −265 | −431 | 6 |
| Forward greedy | −204 | −395 | 6 |
| Backward search | −222 | −399 | 8 |
| Backward search, same first-stage parameters | −129 | −207 | 6 |
| Backward search with reset | −257 | −375 | 8 |
| Backward search with reset, same first-stage parameters | −247 | −415 | 6 |
| One-stage with vigor | −199 | −330 | 6 |
| One-stage with single vigor | −202 | −331 | 5 |
| One-stage with single vigor and rating noise | −236 | −373 | 6 |
| Two-stage, correlated paths | −226 | −360 | 6 |
| Two-stage, independent paths, with pruning | −262 | −418 | 7 |
| Two-stage, correlated paths, with pruning | −249 | −408 | 7 |
| Two-stage, independent paths, single drift | −207 | −351 | 5 |
Forward Greedy Search.
The presence of a reaction time effect at both stages leaves open the possibility that participants make decisions one stage at a time, rather than in parallel. Decisions seem informed in the aggregate because values and single-stage rewards are correlated (values are summed single-stage rewards). Although this seems unlikely given the very fast reaction times at stage two, we formally test this possibility. In particular, the first model assumes that decisions are made in a greedy fashion: Participants decide only between the top-level items during the first stage and then decide between the remaining two items during the second stage. The search is “greedy” in that the best decision is made at each stage without looking ahead.
Backward Search.
Forward search is an example of a typical search strategy in classic artificial intelligence formulations of planning (30). Another strategy is backward search, which reasons backward from potential goal states to the current state. Unlike forward greedy search, this approach is optimal because it takes into account information at all levels: It starts by asking what is best at the end, and then reasons about the best way to get there.
Neither forward nor backward search provides a better fit than the primary model (Table S2).
One-Stage Parallel Integration with Vigor.
Both response (31, 32) and movement (33, 34) vigor (the speeds at which participants initiate and carry out an action) are thought to be modulated by reward. The next set of models test the possibility that the second-stage reaction time effect can be explained based on these principles alone, without the need for continued deliberation. The first model is similar to the primary model during the first stage, with parallel deliberation between decision paths. However, no further processing takes place during the second stage. Reaction time at both stages is negatively modulated by the reward associated with the chosen item, with larger rewards resulting in faster decisions. We tested versions of the model with the slope of the vigor effect constrained to be the same between the two stages, and with the slope allowed to vary.
One-Stage Parallel Integration with Vigor and Rating Noise.
All of the models considered so far treat the rating for each item as the ground truth representation of reward. However, preferences are likely to be noisy, and this noise may contribute to accuracy effects at both stages. The next model is equivalent to the above vigor model with a single slope parameter, but the reward associated with each item is drawn on each trial from a Gaussian distribution centered on the item’s rating. This allows for a simultaneous test of the two likely alternative explanations driving stage-two effects if no deliberation takes place there.
None of the three one-stage parallel integration models provided a better fit than our primary model (Table S2). The reason can be seen in Fig. S2: Because there is no deliberation at stage two, the models underestimate the level of choice accuracy seen there in both experiments.
Fig. S2.
Simulation of both experiments using the best-fitting parameters of the one-stage parallel integration with vigor model. The model underestimates second-stage choice accuracy due to the lack of deliberation there. (A) Experiment 1. (B) Experiment 2.
Two Stages with Correlated Paths.
We now turn to a series of more subtle variations of our primary model. The primary model treats each path as an independent competitor, but this ignores the structure of the decision tree. Because each item at the top level appears in two paths, it could be the case that reward for these items is sampled only once per iteration, with the samples contributing to both of the corresponding paths. This means that noise is correlated between the paths: Paths that remain after going left at the first stage share noise from sampling the top left item, and similarly on the right.
This variant also performs worse for both experiments (Table S2). Because only the bottom-level items drive the resolution between paths on each side of the tree, these items have to be relatively disentangled before progressing to the second stage (with uncorrelated noise, noise at the top level can also push the evidence for a path above threshold). Furthermore, the amount of noise affecting competition between paths on each side of the tree is half that affecting competition between paths on opposite sides. These features of the model predict higher-than-expected second-stage choice accuracy even without additional deliberation (Fig. S3 A and B), and this in turn predicts a flat second-stage reaction time curve (Fig. S3 C and D).
Fig. S3.
Simulation of both experiments (A, C, and E, experiment 1; B, D, and F, experiment 2) using the two-stage model with correlated noise. Because noise is correlated at the top level, the model forces a resolution at the first stage between the bottom-level items on the winning side. However, the level of resolution required to match the first-stage accuracy and reaction time effects overestimates second-stage accuracy without additional deliberation. This in turn predicts a flat second-stage reaction time curve. The reduction in noise at the first stage differentially affects different tree configurations, also resulting in a poor fit to this aspect of the data.
Two Stages with Pruning.
Both the uncorrelated and correlated noise versions of the primary model posses another potential inefficiency: For some trials, it is possible to make a first-stage decision and prune away part of the decision tree before the second-stage decision is complete. This is especially easy to imagine when paths corresponding to the maximum and second-best values appear together on the same side. Participants may decide they will select one of these paths before deciding which one, allowing them to prune away the other side of the tree. For example, consider again the trial shown in Fig. 2. If the umbrella has a relatively low rating, the participant may decide after some time that it is the worst option, and that having the office chair does not compensate for it. This path could then be discarded from further consideration, allowing the deliberation process to concentrate on the difference between the tent and the beach chair on the right side.
The next two models implement this idea. They are identical to the independent and correlated noise versions of the primary model discussed above, but they have a second decision rule for the first stage. It says that a decision is made when the minimum integrator on one side of the tree is a threshold amount greater than the maximum integrator on the other side of the tree. A decision is rendered when either the new or old rule applies, whichever occurs first.
Both pruning models make a qualitatively different prediction for experiment 1 compared with what is seen in the data. They suggest that deliberation is fastest when the best and second-best paths appear on the same side of the tree (Fig. S4, compare with Fig. 3C). The reason is intuitive: When the two best paths are on the same side of the tree, the pruning mechanism is more likely to end the first-stage deliberation early. In contrast, the pruning mechanism cannot fire at all on correct trials when the best path is by itself (“Max alone”).
Fig. S4.
Simulation of experiment 1 using the two-stage integration model with (A) pruning and (B) pruning and correlated noise. The pruning mechanism predicts that first-stage decisions should be fastest when the best and second-best paths appear on the same side of the decision tree, contrary to the data.
Two Stages with Single Drift Rate.
The primary model presented first beat out all of the variants considered so far. We attempted to simplify the model further by having one rather than two separate drift rates for evidence accumulation. The simplified version suggests that exactly the same integration process continues during the second stage, similar to work on simple choice that shows that evidence can continue to accumulate and affect decisions after an initial response is initiated (35). However, this version of the model underestimates choice accuracy at the second stage (Fig. S5), where a different and faster rate of accumulation is necessary to explain the data.
Fig. S5.
Simulation of both experiments (A and C, experiment 1; B and D, experiment 2) using the primary model with a single drift rate for both stages. The model underestimates second-stage choice accuracy because the drift rate required to fit the first-stage data is much lower than that required to fit the second-stage data.
Finally, we tested a model in which the average of the second-stage rewards is accrued at the first stage. For more information, see Supporting Information and Fig. S6.
Fig. S6.
Example of a max/mean conflict trial. Here the maximum overall path is on the right side (); however, the average value of the two paths on the right [5 + (5 + 1)/2 = 8] is less than the average of the two paths on the left [5 + (4 + 4)/2 = 9].
Discussion
In this paper we have provided an initial account of how the class of evidence-integration models, previously applied to data on simple choice, can be directly extended to multistage decision problems. In two experiments involving tree-structured decisions, we have shown that the dynamics of the deliberation process can be understood as integrating evidence in parallel, across time, with competition between the paths of a decision tree. The evidence-integration perspective links multistage reward-based decision making to other cognitive domains where the same form of decision process has been implicated, including memory retrieval (36–38) and perceptual (26, 27, 39) and lexical (40) decision making. It may also help to guide hypotheses regarding neural mechanisms. Previous work (41) has begun to address implementation-level questions by building detailed biophysically plausible models of evidence integration. Our results suggest that such models may be directly translatable to the types of problems we study here.
The processes involved in our parallel integration model bear a striking resemblance to Monte Carlo tree search (42–45) (MCTS), a set of planning algorithms that work by sampling trajectories and computing value functions and policies by averaging over the samples. In our model, the integrators represent the sum of noisy rewards (i.e., unnormalized mean values). However, the number of samples in MCTS is usually a free parameter. It would be of significant interest to integrate this body of work with a theory of reaction time.
Understanding this relationship would be especially welcome in the context of larger state spaces, where MCTS is usually applied. Many real-world problems are still more complicated than the ones we study here: They may have larger depth (more time steps) and breadth (more actions available at each time step) and may involve probabilistic, rather than deterministic, transitions. Although pruning proved unnecessary for the two-stage trees we studied, previous work has shown that human participants do in fact prune larger trees (9, 10) (however, this form of pruning is more reflexive than the deliberate style of pruning studied here; see refs. 9 and 10 for details). MCTS works by exploiting the sparsity inherent to many problems using a form of soft pruning: sampling randomly at first, and then slowly redirecting the effort to the most promising parts of the state space. This perspective may provide insight into how people make decisions in large state spaces.
A complementary approach to dealing with large state spaces is to take advantage of the hierarchy present in many complex problems. In particular, it would be of interest to integrate ideas from hierarchical reinforcement learning, which have recently been applied to human decision making (10, 46–50), with the evidence accumulation framework.
Another parallel that warrants exploration is the relationship to Bayesian accounts of decision making. We previously suggested (23) that the brain may solve the model-based reinforcement learning problem by treating it as a Bayesian inference problem (51). The components of the model (i.e., the transition and reward function) are encoded together with the policies in a joint probability distribution, and decision making amounts to computing the posterior over the policy variables conditional on (maximizing) the reward. We used the framework to explain a number of qualitative behavioral and neural findings from the literature. The goal of the present work was to begin a more detailed quantitative study of these issues, and we opted instead for an approach that more closely resembles what has previously been done in the context of simple choice. However, the Bayesian approach is not necessarily far removed from the model proposed here. As detailed by Solway and Botvinick (23), the evolving posterior over policy variables can be understood as integrating reward information over time. Future work will need to more formally address this potential parallel.
An important aspect our model does not consider is that of attention. Previous work has shown that visual fixations can bias the evidence-integration process in simple choice, promoting the currently fixated option at the expense of the others (3, 4, 52). Integrating eye tracking with our model would open the door for interesting new predictions. For example, fixating on a top-level item should promote both of the paths in which it participates. This would lead to neglect of the alternative side of the tree but provide no advantage for disambiguating the paths in which the item is embedded. In contrast, fixating on a second-level item should promote only a single path.
Incorporating internal fluctuations of attention and the dynamics of memory retrieval into the model is also an important long-term goal. This is perhaps even more pertinent in the context of multistage decision making, where the transition and reward structure are seldom visible (consider again planning a route). Recent work has begun to address this issue (13, 53).
Finally, the current work assumes that each node in the decision tree is independent of the rest. This is not true of many real-world problems, where the same state may appear in multiple paths, or be visited multiple times within a single path. Future research will need to resolve how such contingencies complicate (or simplify) the decision problem.
Materials and Methods
Participants.
Thirty different participants completed each experiment in its entirety. A few participants were dismissed after the item-rating phase. For more information on participant inclusion criteria, see Supporting Information. Participants were compensated either 12 dollars per hour or with course credit. All experimental procedures were approved by the institutional review board of Princeton University.
Task.
Experiments were programmed in MATLAB (MathWorks, Inc.) using the Psychophysics Toolbox (54). Each experiment consisted of two parts. The first part was nearly identical for both experiments and involved rating a set of 270 items, including electronics, clothing, books, nonperishable foods, kitchen items, jewelry, and various novelties. Participants were first shown pictures of all of the items they would later encounter and were then asked to rate each item within the context of all of the other items on the list. A scale of 0–4 was used in experiment 1 and a scale of 1–5 was used in experiment 2.
The second part of each experiment consisted of a series of decision trials. The structure of the decision problem differed slightly between experiments (Fig. 1 B and C), but the order of events within each trial remained the same. Each trial started with a 500-ms fixation cross, followed by a self-paced decision phase (Fig. 2), and ended with a 750-ms “feedback” phase where only the selected items remained on the screen. The intertrial interval was 500 ms with a 0- to 250-ms jitter.
Experiment 1 consisted of a two-stage decision. One item appeared on the top left of the screen, and another appeared on the top right. Below each of these items, either one or two additional items appeared in a horizontal orientation (Fig. 2). Two items appeared on the bottom left and one on the bottom right in a random half of the trials, and the other half of the trials had the reverse orientation. Participants made up to two left/right decisions on each trial. The first committed them to the top item on the corresponding side, and to possibly making a second decision between the two bottom items on that side. If participants chose the side with a single item on the bottom, they were forced to select it by pressing the corresponding keyboard key. The item was offset slightly to the left or to the right of the one above it, as if a second item was next to it. The same two left/right keyboard keys were used as input for both stages. Experiment 2 was similar to experiment 1 except that both sides of the screen had a second-stage decision.
Participants did not actually receive any of the items at the end of the experiment, nor did they receive any kind of performance bonus for selecting items that were rated higher during the first phase. Instead, they were told to simply choose the items they would most prefer to receive as if they would actually get them after each trial.
Trials with first-stage reaction times faster than 500 ms, or first or second-stage reaction times slower than 10 s, were discarded from analysis both in the data and in the model.
Model Fitting.
Model predictions were obtained through simulation. Models were fit using differential evolution (55), as implemented in the DEoptim (56) package in R (57). Each generation consisted of 10 times the number of members as parameters in the model, and the search procedure was stopped when the value of the objective function remained unchanged for 100 generations. Because differential evolution has an element of stochasticity, each model was fit 10 times, and the best fit was used. Each trial in the data was simulated once for each parameter set. The objective function consisted of the residual sum of squares of the group psychometric curves in Figs. 3 A–E and 4 A–E (overall choice accuracy, shown in Figs. 3F and 4F, was not explicitly fit). First-stage reaction times were divided by 10,000 and second-stage reaction times by 1,000 to put them on more equal footing with the accuracy data.
BIC values were computed as follows:
| [1] |
Here, k is the number of parameters, n is the number of data points (29 in experiment 1 and 45 in experiment 2), and RSS is the residual sum of squares. This relationship holds if we assume that model errors are normally distributed with zero mean.
SI Materials and Methods
Participant Selection.
Thirty participants were targeted for each experiment. As described in the main text, each experiment consisted of two parts. The first involved rating items and the second making decisions about them. To progress to the second part, participants had to rate a minimum number of items at each rating level (although they were not told about this requirement, discussed below). Recruitment continued until there were 30 valid participants for each experiment. Overall, 31 participants were recruited for experiment 1, and all progressed to the second part. One participant was dismissed with credit before completing the experiment because they did not finish 30 min after the allotted time. Thirty-six participants were recruited for experiment 2, and 30 of them progressed to the second part.
Participants had to rate at least 10 items at each rating level for experiment 1 and 12 for experiment 2. Participants were not told of this specific requirement beforehand but were instructed to give relative ratings by considering each item in the context of all of the other items on the list, and to try to use all of the numbers during the rating period. Participants who did not meet this requirement were dismissed with two hours’ worth of compensation. This requirement was enforced to reduce carryover effects between consecutive trials. Because five items were displayed on each trial of the decision phase in experiment 1, and each could be associated with the same rating, having 10 items at each rating level ensured that the same item would not have to appear on two consecutive trials. This same reasoning applies to experiment 2, which had six items per trial.
Item Selection and Experiment Duration.
The set of items for each participant was trimmed to have the same number for each rating level. For example, if 90 items were rated 0, 50 were rated 1, 30 were rated 2, 50 were rated 3, and 50 were rated 4, the 30 items rated a 2 were all kept together with a random subset of 30 items from each other rating level. This helped put items associated with different ratings on more equal footing.
Experiment 1.
The items on each trial were pseudorandomly chosen such that (i) the same item did not appear on consecutive trials and (ii) the difference between the value of the best path and the average of the values of the other two paths was between 1 and 5, in increments of 0.5. The latter is the primary measure of trial difficulty described in the main text, and value is defined as before as the sum of the ratings in a single path of the tree. For example, if the rating of the item on the left top was 4, left bottom left 5, left bottom right 3, right top 1, and right bottom left 5, the values were computed to be left top + left bottom left = 9, left top + left bottom right = 7, and right top + right bottom left = 6. The difficulty of the trial in this case was . Each participant completed 900 trials, 100 at each difficulty level, with four unlimited breaks offered evenly spaced throughout the experiment.
Experiment 2.
Items were similarly chosen on each trial, with difficulty measured based on four pairs of items instead of three. Difficulty levels between 1 and 6 were included, rounded to the nearest integer. Seventeen participants completed 660 trials, 110 at each difficulty level, and the remaining 13 participants completed 780 trials, 130 at each difficulty level. Both groups were offered four unlimited breaks evenly spaced throughout the experiment. The number of trials was increased to reflect the amount that fit within a 2-h window. Note that in Fig. 4 difficulty level is rounded to the nearest 10th decimal place rather than to the nearest integer.
Statistical Analysis.
Second-stage reaction time effects were analyzed by log-transforming the data, computing the mean for each participant and absolute difference in ratings, and subjecting the results to a repeated measures ANOVA.
Computational Models.
We present the modeling details in terms of the second experiment. However, the implementation of the first experiment is exactly the same, with one fewer item (and path) being compared.
Two stages with independent paths (primary model).
The primary model treats each path through the tree as an independent competitor. The evidence for each begins at zero and on each iteration of the deliberation process is updated according to the rewards (ratings) along that path:
| [S1] |
E refers to the amount of evidence associated with a single path. For example, is the evidence for the path corresponding to going “left” and then “left” again. R is the reward associated with a particular position, with and referring to the left and right rewards at the first stage, to the left reward at the second stage after going left at the first stage, and so on. ε is a Gaussian random variable with mean 0 and SD 0.01, and is a free parameter. A decision is made when the difference between the largest integrator and the next largest integrator (“best vs. next”) exceeds threshold (, a free parameter).
Although the model thus far is able to render a decision for both stages of action (the winning path implies what to do at both stages), it predicts a constant reaction time for the second stage. This contrasts with Figs. 3E and 4E in the main text, which show an effect of difficulty. To capture this effect, we amend the model to output only the first-stage decision and allow the remaining paths to continue integrating until the difference between them exceeds another threshold. For example, if the right side was selected during the first stage, the second stage continues according to
| [S2] |
is a free parameter, and a decision is made when the difference between the larger and smaller integrator exceeds .
Each stage of action also has an additional parameter, and , respectively, specifying the amount of nondecision time. This includes time spent processing the stimuli and issuing a response.
Two stages with correlated paths.
The correlated paths model is exactly the same as above, except the noise term (ε) is correlated for and . That is, on each iteration is sampled once and the sample contributes to both and , and likewise for .
Two stages with pruning.
Each of the two models above was also instantiated with a second decision rule, which says that a first-stage decision can be made when either
| [S3] |
or
| [S4] |
is an additional free parameter. A decision is made as soon as either this rule or the max-vs.-next-best rule applies, whichever occurs first.
Two-stage average.
Rather than individual paths competing at the first stage, this model posits a single integrator for each first-stage action, with its value incremented according to the average of the (noisy) rewards below:
| [S5] |
A decision is made when the difference between and exceeds threshold. This simplification comes at a cost. First, to capture the second-stage reaction time effect, these samples also contribute to integrators for second-stage items (which compete after the first stage ends, as in the models above), resulting in an increase in the total number of integrators. Second, the model is suboptimal on trials like the one shown in Fig. S6, which we call “max/mean conflict” trials. On such trials, the overall maximum path is on one side of the tree, whereas the average of the pairs of paths is higher on the other side. For example, in the tree shown in Fig. S6, the best path is on the right, but the average of the two paths on the right [5 + (5 + 1)/2 = 8] is less than that on the left [5 + (4 + 4)/2 = 9]. The model prefers the side with the maximum average rather than the maximum overall path.
Considering the average best may be a useful heuristic when the decision tree is deep and only one or two steps need to be executed quickly. Although our experiments did not directly address this scenario, and max/mean conflict trials make up a small portion of our data (less than 3% of experiment 1 and less than 2% of experiment 2), we performed an exploratory analysis fitting this and the primary model not only to the data discussed in the main text, but also to first-stage choice accuracy and reaction time as a function of trial type (max/mean conflict vs. no max/mean conflict). The baseline model provided a more parsimonious fit for both experiments (experiment 1, primary model BIC , average model BIC ; experiment 2, primary model BIC , average model BIC ).
Forward greedy search.
In forward greedy search, items at each stage compete independently. The top-level items compete first:
| [S6] |
A decision is made when the difference between the integrators exceeds . The remaining items compete at the second stage. For example, if the right side was chosen, the items on the right compete as in Eq. S2, but both start with zero evidence. Each stage of action also has an additional parameter specifying the amount of nondecision time, as in the models above.
Backward induction.
First, items at the second level compete in parallel:
| [S7] |
A decision is made on the left when one integrator exceeds the other by , and likewise on the right. This contributes the length of the longer of the two competitions to the first-stage reaction time. The top level items then enter the competition:
| [S8] |
The integrators for the second-level items remain frozen during this time. A decision is made when the sum of the integrators for the left top-level item and the winning left second-level item exceeds the sum of the integrators for the right top-level item and the winning right second-level item, or vice versa, by . In other words, when
| [S9] |
The model thus far does not predict a reaction time effect at the second stage. To allow the model to capture this effect, the second-stage integrators are unfrozen and continue integrating (with drift , until the difference between them exceeds ). As above, each stage of action has an additional parameter specifying the amount of nondecision time.
We also fit a version of the model where was constrained to equal and was constrained to equal .
Backward induction with reset.
This version of the backward induction model begins the deliberation process according to Eq. S7. However, the losing items are then pruned away, and evidence for the winning items is reset. The remaining branches compete in parallel, with evidence accruing for items at both levels:
| [S10] |
is the rating associated with the winning item at the second level on the left, and likewise for and the winning item on the right. These two competitions constitute the first-stage deliberation. The second-stage deliberation proceeds as in the above model.
One-stage parallel integration with vigor.
The one-stage parallel integration model is similar to the primary model during the first stage and proceeds according to Eq. S1. Upon choosing a path, the first-stage reaction time is further incremented by . is a free parameter, is the maximum rating (4 in experiment 1 and 5 in experiment 2), and is the rating associated with the top-level item of the winning path. No deliberation takes place during the second stage. The second-stage reaction time is incremented by , where is a free parameter and is the rating associated with the second-level item of the winning path. Each stage has an additional parameter that captures the sum of the time spent looking at the stimuli and the intercept term for the motor response.
One-stage parallel integration with vigor and rating noise.
This model is exactly the same as the model above, except that the reward associated with each item is sampled once at the beginning of the trial from a Gaussian distribution centered on the item’s rating. For example, reward for the top left item is sampled according to
| [S11] |
and similarly for the other items. is a free parameter. The sampled ratings are used in place of the actual ratings in Eq. S1.
Acknowledgments
The authors thank Debbie Yee and Jin Hyun Cheong for their help with data collection. This project was made possible through grant support from the National Science Foundation (CRCNS1207833) and the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the funding agencies.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1505483112/-/DCSupplemental.
References
- 1.Busemeyer JR, Townsend JT. Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev. 1993;100(3):432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- 2.Milosavljevic M, Malmaud J, Huth A, Koch C, Rangel A. The drift diffusion model can account for the accuracy and reaction time of value-based choices under high and low time pressure. Judgm Decis Mak. 2010;5(6):437–449. [Google Scholar]
- 3.Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nat Neurosci. 2010;13(10):1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- 4.Krajbich I, Rangel A. Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proc Natl Acad Sci USA. 2011;108(33):13852–13857. doi: 10.1073/pnas.1101328108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Woodford M. Stochastic choice: An optimizing neuroeconomic model. Am Econ Rev. 2014;104(5):495–500. [Google Scholar]
- 6.Daw ND. Model-based reinforcement learning as cognitive search: neurocomputational theories. In: Todd PM, Hills TT, Robbins TW, editors. Cognitive Search: Evolution Algorithms and the Brain. MIT Press; Cambridge, MA: 2012. pp. 195–208. [Google Scholar]
- 7.Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat Neurosci. 2005;8(12):1704–1711. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
- 8.Dolan RJ, Dayan P. Goals and habits in the brain. Neuron. 2013;80(2):312–325. doi: 10.1016/j.neuron.2013.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Huys QJM, et al. Bonsai trees in your head: How the pavlovian system sculpts goal-directed choices by pruning decision trees. PLOS Comput Biol. 2012;8(3):e1002410. doi: 10.1371/journal.pcbi.1002410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huys QJM, et al. Interplay of approximate planning strategies. Proc Natl Acad Sci USA. 2015;112(10):3098–3103. doi: 10.1073/pnas.1414219112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sutton RS, Barto AG. Reinforcement Learning: An Introduction. MIT Press; Cambridge, MA: 1998. [Google Scholar]
- 12.Bornstein AM, Daw ND. Dissociating hippocampal and striatal contributions to sequential prediction learning. Eur J Neurosci. 2012;35(7):1011–1023. doi: 10.1111/j.1460-9568.2011.07920.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bornstein AM, Daw ND. Cortical and hippocampal correlates of deliberation during model-based decisions for rewards in humans. PLOS Comput Biol. 2013;9(12):e1003387. doi: 10.1371/journal.pcbi.1003387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gläscher J, Daw N, Dayan P, O’Doherty JP. States versus rewards: Dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron. 2010;66(4):585–595. doi: 10.1016/j.neuron.2010.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Daw ND, Gershman SJ, Seymour B, Dayan P, Dolan RJ. Model-based influences on humans’ choices and striatal prediction errors. Neuron. 2011;69(6):1204–1215. doi: 10.1016/j.neuron.2011.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Simon DA, Daw ND. Neural correlates of forward planning in a spatial decision task in humans. J Neurosci. 2011;31(14):5526–5539. doi: 10.1523/JNEUROSCI.4647-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wunderlich K, Dayan P, Dolan RJ. Mapping value based planning and extensively trained choice in the human brain. Nat Neurosci. 2012;15(5):786–791. doi: 10.1038/nn.3068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Otto AR, Gershman SJ, Markman AB, Daw ND. The curse of planning: Dissecting multiple reinforcement-learning systems by taxing the central executive. Psychol Sci. 2013;24(5):751–761. doi: 10.1177/0956797612463080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Otto AR, Raio CM, Chiang A, Phelps EA, Daw ND. Working-memory capacity protects model-based learning from stress. Proc Natl Acad Sci USA. 2013;110(52):20941–20946. doi: 10.1073/pnas.1312011110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Smittenaar P, FitzGerald THB, Romei V, Wright ND, Dolan RJ. Disruption of dorsolateral prefrontal cortex decreases model-based in favor of model-free control in humans. Neuron. 2013;80(4):914–919. doi: 10.1016/j.neuron.2013.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Smittenaar P, Prichard G, FitzGerald THB, Diedrichsen J, Dolan RJ. Transcranial direct current stimulation of right dorsolateral prefrontal cortex does not affect model-based or model-free reinforcement learning in humans. PLoS One. 2014;9(1):e86850. doi: 10.1371/journal.pone.0086850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wunderlich K, Smittenaar P, Dolan RJ. Dopamine enhances model-based over model-free choice behavior. Neuron. 2012;75(3):418–424. doi: 10.1016/j.neuron.2012.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Solway A, Botvinick MM. Goal-directed decision making as probabilistic inference: A computational framework and potential neural correlates. Psychol Rev. 2012;119(1):120–154. doi: 10.1037/a0026435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Diederich A. Dynamic stochastic models for decision making under time constraints. J Math Psychol. 1997;41(3):260–274. doi: 10.1006/jmps.1997.1167. [DOI] [PubMed] [Google Scholar]
- 25.Roe RM, Busemeyer JR, Townsend JT. Multialternative decision field theory: A dynamic connectionist model of decision making. Psychol Rev. 2001;108(2):370–392. doi: 10.1037/0033-295x.108.2.370. [DOI] [PubMed] [Google Scholar]
- 26.Usher M, McClelland JL. The time course of perceptual choice: The leaky, competing accumulator model. Psychol Rev. 2001;108(3):550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- 27.Teodorescu AR, Usher M. Disentangling decision models: From independence to competition. Psychol Rev. 2013;120(1):1–38. doi: 10.1037/a0030776. [DOI] [PubMed] [Google Scholar]
- 28.Morey RD. Confidence intervals from normalized data: A correction to Cousineau (2005) Tutor Quant Methods Psychol. 2008;4(2):61–64. [Google Scholar]
- 29.Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6(2):461–464. [Google Scholar]
- 30.Boutilier C, Dean T, Hanks S. Decision-theoretic planning: Structural assumptions and computational leverage. J Artif Intell Res. 1999;11(1):1–94. [Google Scholar]
- 31.Niv Y, Daw N, Dayan P. 2005. How fast to work: Response vigor, motivation and tonic dopamine. Advances in Neural Information Processing Systems, eds Weiss Y, Schölkopf B, Platt J (MIT Press, Cambridge, MA), Vol 18, pp 1019–1026.
- 32.Niv Y, Daw ND, Joel D, Dayan P. Tonic dopamine: Opportunity costs and the control of response vigor. Psychopharmacology (Berl) 2007;191(3):507–520. doi: 10.1007/s00213-006-0502-4. [DOI] [PubMed] [Google Scholar]
- 33.Kawagoe R, Takikawa Y, Hikosaka O. Reward-predicting activity of dopamine and caudate neurons--a possible mechanism of motivational control of saccadic eye movement. J Neurophysiol. 2004;91(2):1013–1024. doi: 10.1152/jn.00721.2003. [DOI] [PubMed] [Google Scholar]
- 34.Takikawa Y, Kawagoe R, Itoh H, Nakahara H, Hikosaka O. Modulation of saccadic eye movements by predicted reward outcome. Exp Brain Res. 2002;142(2):284–291. doi: 10.1007/s00221-001-0928-1. [DOI] [PubMed] [Google Scholar]
- 35.Resulaj A, Kiani R, Wolpert DM, Shadlen MN. Changes of mind in decision-making. Nature. 2009;461(7261):263–266. doi: 10.1038/nature08275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ratcliff R. A theory of memory retrieval. Psychol Rev. 1978;85(2):59–108. [Google Scholar]
- 37.Polyn SM, Norman KA, Kahana MJ. A context maintenance and retrieval model of organizational processes in free recall. Psychol Rev. 2009;116(1):129–156. doi: 10.1037/a0014420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sederberg PB, Howard MW, Kahana MJ. A context-based theory of recency and contiguity in free recall. Psychol Rev. 2008;115(4):893–912. doi: 10.1037/a0013396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Comput. 2008;20(4):873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wagenmakers E-J, Ratcliff R, Gomez P, McKoon G. A diffusion model account of criterion shifts in the lexical decision task. J Mem Lang. 2008;58(1):140–159. doi: 10.1016/j.jml.2007.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. 2006;26(4):1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Coulom R. Efficient selectivity and backup operators in Monte-carlo tree search. In: van den Herik HJ, Ciancarini P, Donkers HHLM, editors. Computers and Games. Springer; New York: 2007. pp. 72–83. [Google Scholar]
- 43.Gelly S, Silver D. Monte-carlo tree search and rapid action value estimation in computer Go. Artif Intell. 2011;175(11):1856–1875. [Google Scholar]
- 44.Kocsis L, Szepesvári C. 2006. Bandit based Monte-Carlo planning. Proceedings of the 17th European Conference on Machine Learning, eds Fürnkranz J, Scheffer T, Spiliopoulou M ( Springer, Berlin), pp 282–293.
- 45.Kearns M, Mansour Y, Ng AY. A sparse sampling algorithm for near-optimal planning in large Markov decision processes. Mach Learn. 2002;49(2-3):193–208. [Google Scholar]
- 46.Barto AG, Mahadevan S. Recent advances in hierarchical reinforcement learning. Discrete Event Dyn Syst. 2003;13(4):341–379. [Google Scholar]
- 47.Botvinick MM, Niv Y, Barto AC. Hierarchically organized behavior and its neural foundations: A reinforcement learning perspective. Cognition. 2009;113(3):262–280. doi: 10.1016/j.cognition.2008.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Diuk C, Tsai K, Wallis J, Botvinick M, Niv Y. Hierarchical learning induces two simultaneous, but separable, prediction errors in human basal ganglia. J Neurosci. 2013;33(13):5797–5805. doi: 10.1523/JNEUROSCI.5445-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ribas-Fernandes JJF, et al. A neural signature of hierarchical reinforcement learning. Neuron. 2011;71(2):370–379. doi: 10.1016/j.neuron.2011.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Solway A, et al. Optimal behavioral hierarchy. PLOS Comput Biol. 2014;10(8):e1003779. doi: 10.1371/journal.pcbi.1003779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. MIT Press; Cambridge, MA: 2009. [Google Scholar]
- 52.Towal RB, Mormann M, Koch C. Simultaneous modeling of visual saliency and value computation improves predictions of economic choice. Proc Natl Acad Sci USA. 2013;110(40):E3858–E3867. doi: 10.1073/pnas.1304429110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wimmer GE, Shohamy D. Preference by association: How memory mechanisms in the hippocampus bias decisions. Science. 2012;338(6104):270–273. doi: 10.1126/science.1223252. [DOI] [PubMed] [Google Scholar]
- 54.Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
- 55.Price K, Storn RM, Lampinen JA. Differential Evolution: A Practical Approach to Global Optimization. Springer; New York: 2006. [Google Scholar]
- 56.Mullen KM, Ardia D, Gil DL, Windover D, Cline J. DEoptim: An R package for global optimization by differential evolution. J Stat Softw. 2009;40(6):1–26. [Google Scholar]
- 57.R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna: 2013. [Google Scholar]