Random Forest Classification of Depression Status Based On Subcortical Brain Morphometry Following Electroconvulsive Therapy

Abstract

Disorders of the central nervous system are often accompanied by brain abnormalities detectable with MRI. Advances in biomedical imaging and pattern detection algorithms have led to classification methods that may help diagnose and track the progression of a brain disorder and/or predict successful response to treatment.

These classification systems often use high-dimensional signals or images, and must handle the computational challenges of high dimensionality as well as complex data types such as shape descriptors.

Here, we used shape information from subcortical structures to test a recently developed feature-selection method based on regularized random forests to 1) classify depressed subjects versus controls, and 2) patients before and after treatment with electroconvulsive therapy. We subsequently compared the classification performance of high-dimensional shape features with traditional volumetric measures. Shape-based models outperformed simple volumetric predictors in several cases, highlighting their utility as potential automated alternatives for establishing diagnosis and predicting treatment response.

1. Introduction

High resolution structural magnetic resonance brain imaging (MRI) has offered a rich description of the brain differences associated with a wide variety of disorders affecting the central nervous system including Alzheimer's [1, 2], Parkinson's [3] and Huntington's disease [4, 5]. Recent developments in pattern recognition and machine learning have been applied to brain imaging data to aid in the diagnosis and staging of numerous diseases and their progression [6, 7].

Computer assisted diagnosis (CAD) of disease progression or remission may have several key advantages over standard radiologic assessment of MRI. CAD is not as susceptible to human errors and provides an unbiased, consistent outcome. Additionally, a CAD system is better suited to observing patterns that may exist in higher dimensions or at more subtle thresholds than a human eye could discern. Brain differences are still poorly understood in many disorders, across their different stages of onset and recovery and often present subtle alterations across a set of brain regions. It is therefore of major value to public health to develop biomarkers of disease progression and algorithms capable of discerning the stage of a disease or future response to treatment.

Global volume and thickness measures for various brain regions are most commonly used to characterize neurological disease. While volume and thickness often reveal robust group differences, these are summary measures that lack detailed local information. Several surface-based shape metrics have been developed to provide descriptions of a brain region's local morphometry. Subtle changes in local morphometry of a brain structure may provide additional information to classification systems about the diagnosis and stage of a disease.

The choice of classifier is critical when incorporating local shape descriptors. Volume and thickness both provide a single measure for each sub-structure volume of interest (VOI), but shape descriptors are most commonly defined locally at each vertex of a given surface. Therefore, the set of shape descriptors describing a single VOI may exist in a very high dimensional space, as a function of the resolution of the surface mesh. Different classification algorithms have differing degrees of susceptibility to overfitting high dimensional data.

The prevalence of major depressive disorder (MDD) is approximately 10-20% in the U.S. [8, 9] with an estimated lifetime suicide risk of about 15–20% and an average annual cost of $42 billion dollars in the U.S. alone [10]. Antidepressant drugs and behavioral therapy are the most frequently prescribed treatments for MDD. However, due to its rapid onset of action and efficacy, electroconvulsive therapy (ECT) is commonly used in cases of treatment-resistant depression and in cases of imminent risk for suicide [11].

In this study we implement a recent extension of the random forest algorithm, termed guided regularized random forests (GRRF) to classify depression and treatment status in a matched cohort of participants with and without MDD in which the MDD participants received an index treatment series of ECT. We report the accuracy of 1) volumetric and 2) surface-based shape metrics derived from the same set of subcortical VOIs to classify participants as pre- or post-ECT. We similarly report the accuracies of classification of MDD versus control participants.

2. Materials and Methods

2.1. Participants

43 patients meeting DSM-V criteria for MDD and eligible to receive ECT (mean age, 40 years [SD 11.57]; range 20-64) and 32 controls (mean age, 40 years [SD 12.44]; range 20-74) were recruited as part of an ongoing study examining biomarkers of treatment response in patients with MDD. Patients and controls were evaluated at two separate time points: prior to ECT or at baseline (T1) and within a week of completing the ECT treatment index series (T2) at transition to a maintenance therapy. 35 MDD and 30 control participants continued to T2. Written informed consent was obtained from all participants. The study protocol was approved by the University of California, Los Angeles Institutional Review Board.

2.2. Image acquisition and segmentation

High-resolution motion-corrected multi-echo T1-weighted MPRAGE images [12, 13] were acquired on a Siemens 3T Allegra system (Erlangen, Germany) for all subjects and time points (TEs/TR= 1.74, 3.6, 5.46, 7.32/2530 ms, TI=1260 ms, FA=7°, FOV=256 × 256 mm, 192 sagittal slices, voxel resolution = 1.3 × 1.0 × 1.0 mm³)

Previously validated FreeSurfer [14] workflows, which include removal of non-brain tissue, intensity normalization and automated volumetric parcellation based on probabilistic information from manually labeled training sets, were used to segment the following VOIs in each hemisphere: the nucleus accumbens, amygdala, caudate, hippocampus, pallidum and thalamus. Each segmented image was visually inspected to ensure its quality.

2.3. Surface parameterization and registration

The parameterization of each VOI's surface was obtained via a conformal mapping to a holomorphic 1-form as detailed in [15]. Here, the conformal parameterization of the surface is mapped to a rectangular Euclidean domain. This mapping has the advantage of maximizing the uniformity of the resultant mesh grid [16].

2.4. Morphological descriptors

Three descriptors were used: 1) volume, 2) the Jacobian determinant (JD) and 3) radial distance (RD) maps of the parametric surfaces.

Volume was computed directly from FreeSurfer. The Jacobian matrix at each vertex is given by the following: Take φ: S₁ → S₂ to be the conformal mapping of the VOI surface to the rectangular holomorphic 1 -form. In a discretized setting, the derivative map of φ can be approximated by the linear mapping between two triangular faces, [υ₁, υ₂, υ₃] →[w₁, w₂,w₃], embedded in ℝ². The Jacobian matrix, dφ, is then simply given by,

$$d\phi =[w_3-w_1,w_2-w_1]{[{\upsilon }_3-{\upsilon }_1,{\upsilon }_2-{\upsilon }_1]}^{-1},$$ (1)

The local JD at each vertex is given by taking the determinant of dφ. Local surface dilation is indicated by a JD > 1 while JD < 1 indicates local atrophy.

The local RD of the surface mesh is calculated by first computing a 3D medial core which traverses the volume's local center. The radial distance from each vertex to the nearest point of the medial core provides the index of radial distance, an approximation of the structure's local thickness [1, 17].

2.5. Feature selection and classification

Prior to submitting surface-based morphometric data to a classification model, we opted to perform feature selection to reduce the risk of overfitting to our training data. Each surface mesh was composed of 15,000 vertices with each having RD and JD as an attribute. Recently, a three-step feature selection and classification procedure called guided regularized random forests (GRRF) [18] was proposed, to handle high-dimensional data within the RF framework. The GRRF algorithm uses importance scores associated with each variable obtained from a standard RF to inform a regularized RF in the feature selection process. Features selected by GRRF are then submitted to a standard RF for classification. The process is detailed in [18, 19] and summarized below.

2.5.1. Random forests and importance scores

RFs are supervised classifiers built on an ensemble of classification and regression trees (CART) [20]. Each CART is constructed of a bootstrapped sample of the total observations. At each node of the CART a random subset of features is selected and the Gini index is calculated for each feature at the present node, v. Gini(v) is given by:

$$\mathit{\text{Gini}}(\upsilon )={\sum }_{C=1}^C{\widehat{p}}_c^{\upsilon }(1-{\widehat{p}}_c^{\upsilon }),$$ (2)

where ${\widehat{p}}_c^{\upsilon }$ is the proportion of observations belonging to class C at node v. The RF algorithm aims to split each CART node by the feature X_i which maximizes the class purity of the resultant child nodes, υ^r and υ^l. This is achieved by selecting the maximum Gain (X_t, υ) where,

$$\mathit{\text{Gain}}(X_i,\nu )=\mathit{\text{Gini}}(X_i,\upsilon )-{\omega }_l\mathit{\text{Gini}}(X_i,{\upsilon }^l)-{\omega }_r\mathit{\text{Gini}}(X_i,{\upsilon }^r),$$ (3)

and ω_l and ω_r are the proportions of observations in node v assigned to child nodes and υ^r and υ^l , respectively. The forestwise importance, I, of feature X_i is given by the summation of the decreases in the Gini index at each node where the CART was partitioned by X_i [7]. Concretely,

$${\mathit{I}}_{X_i}=\frac{1}{\mathit{\text{total tree number}}}{\sum }_{\upsilon \in S_{{\mathit{X}}_i}}\mathit{\text{Gain}}(X_i,\upsilon ),$$ (4)

where S_Xi denotes the set of all nodes split by X_i.

Each CART is allowed to grow to its full extent, unpruned. As an ensemble classifier, the RF uses the majority vote of its constituent CARTs terminal nodes to predict the class label of a new observation.

The bootstrap resampling process of RFs leaves about one third of the observations out of each CART. Referred to as out-of-bag (OOB) data, these observations classified and used as an intrinsic measure of the tree's performance. The classification error of the OOB observations is referred to as OOB error.

2.5.2. Guided regularized random forests

GRRFs are an extension of RFs that use normalized importance scores, I_n, from an ordinary RF to parameterize the regularization of Gain (X_i, υ) in a secondary RF. This allows GRRF to apply a unique penalty to each feature,

$${\mathit{\text{Gain}}}_{\mathit{\text{reg}}}(X_i,\upsilon )=\{\begin{array}{cc}{\lambda }_i\mathit{\text{Gain}}(X_i,\upsilon )& X_i\notin \mathrm{F}\\ \mathit{\text{Gain}}(X_i,\upsilon )& X_i\in \mathrm{F}\end{array},$$ (5)

where F is the set of feature indices used to split previous nodes in previous trees and λ_i is the regularization coefficient for feature X_i. λ_i is given by,

$${\lambda }_i=(1-\gamma )+\gamma {\mathit{I}}_{n_i},$$ (6)

where γ ∈ [0, 1], is a constant argument to GRRF to control the degree of gain penalization.

2.6. GRRF-RF parameters

Within each training subset (described in section 2.7), the 15,000 vertices of each VOI mesh were separately submitted to the GRRF feature selection algorithm. This ensured that the final classification would be based on information from each surface and that classification based on each of the three metrics would draw from the same set of VOIs.

The features selected by GRRF were submitted to a standard RF. For the purposes of our study, we included 10,000 trees in each GRRF-RF model. We set the base penalization coefficient, γ, to 0.5 for GRRF feature selection. The number of variables included in the random subset at each tree node was the standard √M, where M is the total number of input variables to the RF. A unique random bootstrapped sample of two-thirds of the training sample was used for each tree.

To compare the efficacy of shape-based and volumetric features, separate RFs were formed using each of the three feature sets: Volume, RD and JD. Finally, we combined the three sets in a final RF model to investigate whether the full compliment of information would enhance diagnostic accuracy.

2.7. Training and testing data

We investigated the discrimination of three pairings: (Group 1) MDD participants prior (Tl_D,) to and following ECT (T2_D), (Group 2) T1_D and unaffected controls imaged at the same time point (Tl_C) and (Group 3) MDD participants following ECT (T2_D) and unaffected controls at the same time point (T2_C). Each of the three comparisons was assessed using a two-fold cross validation, with 50% of subjects used for training and the remaining for testing. Table 1 outlines the partitioning of subjects for cross validation.

Table 1.

Count of subjects in the training and testing partitions, by comparison group.

Group	Train	Test
G1	22T1 : 15T2	21T1 : 14T2
G2	22D : 16C	21D : 16C
G3	15D : 15C	14D : 15C

3. Results

3.1. Classification of group 1: T1_D and T2_D

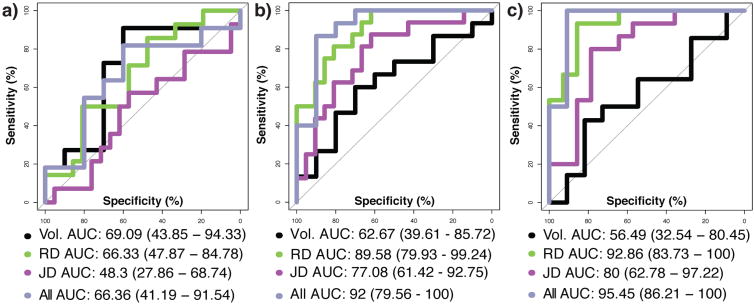
Volumetric and RD measures were most accurate in distinguishing T1_D and T2_D from each other, and volumetric measures slightly outperformed RD. The JD performed more poorly than volume and RD. DeLong's test [21] for two correlated receiver operating characteristic curves (ROC) detected no significant differences in the area under (AUC) of the ROCs given by the various metric-specific RF models. Combining all metrics to predict ECT status did not significantly outperform models built from individual feature sets. Figure 1 plots ROCs for each model by comparison group.

Fig. 1.

ROC curves and associated AUC (95% C.I.) by feature set used in model and by group comparison: (a) T1_D and T2_D, (b) T1_D and T1_C and (c) T2_D and T2_C.

Table 2 outlines the AUC for the ROC for each group and model and summarizes the out-of-bag classification error and percentage of features retained by the GRRF feature selection process among the shape metrics, RD and JD.

Table 2.

Outline of classification accuracies by comparison group and metrics (Model ‘All’ is formed by the combination of volumetric, RD and JD features). ‘Percent M’ indicates the percentage of the original 1.8×10⁵ features retained by GRRF.

Group	Model	OOBE	AUC (95% CI)	Percent M
G1	Vol.	69%	69.0 (43.8 - 94.3)	NA
	RD	5.9%	66.3 (47.8 - 84.7)	0.06%
	JD	8.2%	48.3 (27.8 - 68.7)	0.06%
	All	3.6%	66.3 (41.1 - 91.5)	NA
G2	Vol.	57.3%	62.6 (39.6 - 85.7)	NA
	RD	5.2%	89.5 (79.9 - 99.2)	0.05%
	JD	5.1%	77.0 (42 - 92.7)	0.05%
	All	4.5%	92.0 (79.5 - 100)	NA
G3	Vol.	32.9%	56.4 (32.5 - 80.4)	NA
	RD	6.1%	92.8 (83.7 - 100)	0.04%
	JD	0.14%	80.0 (62.7 - 97.2)	0.04%
	All	3.8%	95.4 (86.2 - 100)	NA

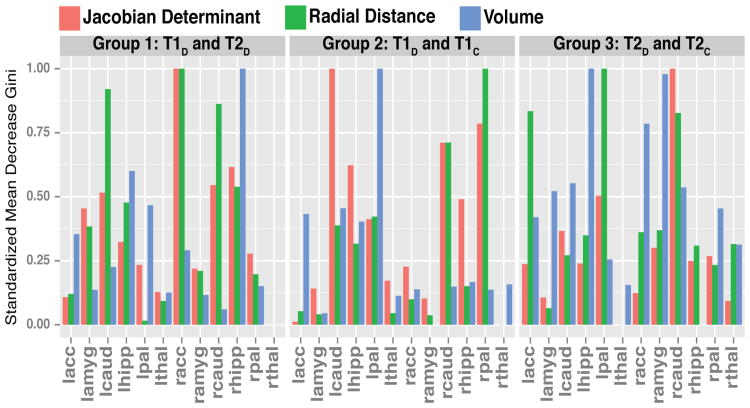
Figure 2 illustrates the relative importance of each VOI to each RF model by comparison group by plotting the scaled sum of the mean decrease in Gini score for each VOI within its model. Higher scores of the mean decrease in Gini score indicate a relatively higher importance for that variable in classification [20].

Fig. 2.

Mean decrease in Gini scores by VOI by group comparison. Larger scores indicate a variable is more important when classifying the two groups of interest.

Here, the right hippocampus is the most important VOI in the volume-only model while the right accumbens is the most influential VOI among the shape-feature models. The bilateral caudate is also reported to have a strong influence on the RD model.

3.2. Classification of group 2: T1_D and T1_C

RD and JD both outperformed volume in classifying T1_D and T1_C with RD having the largest AUC. Here, the combined information from all metrics in a single RF outperformed each single-metric RF. There were no significant differences in AUC following FDR correction for multiple comparisons [22].

The left pallidum was the most influential VOI in the volumetric model. The right pallidum was most predictive VOI in the RD model while the left caudate was most important in the JD model.

3.3. Classification of group 3: T2_D and T2_C

In the classification of T2_D and T2_C RD again had the highest overall accuracy with JD performing nearly as well. Here, volume only performed slightly above the level of chance with an AUC of 56.49%. The combined metric model slightly outperformed all other single-metric models. After FDR correction, the AUC for the RD (DeLong's Z = 2.90, p < 0.005) and combined (DeLong's Z = 2.83, p < 0.05) models were both significantly greater than for the volumetric model.

The left hippocampus followed closely by the right amygdala were the most predictive VOIs for the volumetric model. The left pallidum was most distinguishing in the RD model while the right caudate informed the JD model most heavily.

4. Discussion

Automated diagnosis and tracking of a disorder's progression or remission is a central goal in medical imaging and pattern recognition. CAD systems that employ high dimensional feature spaces pertaining to subtle phenotypes may offer the most accurate information.

Our study demonstrated an effective method to reduce high-dimensional shape features derived from subcortical brain structures to a feature set amenable to classification in a standard RF model. Our results highlight the importance of investigating both volumetric and shape-based features in the analysis of brain or mood disorders.

Applied to the treatment of MDD with ECT, we found that shape metrics are nearly as sensitive as traditional volumetric measures in detecting short-term changes in MDD participants following ECT. In distinguishing MDD from controls however, shape-based changes significantly outperform solely volumetric measures. Importantly, the most effective approach was to combine all feature sets, suggesting that the diagnosis of MDD was added by the multiple brain measures.