INFERENCE FOR INDIVIDUAL-LEVEL MODELS OF INFECTIOUS DISEASES IN LARGE POPULATIONS

Abstract

Individual Level Models (ILMs), a new class of models, are being applied to infectious epidemic data to aid in the understanding of the spatio-temporal dynamics of infectious diseases. These models are highly flexible and intuitive, and can be parameterised under a Bayesian framework via Markov chain Monte Carlo (MCMC) methods. Unfortunately, this parameterisation can be difficult to implement due to intense computational requirements when calculating the full posterior for large, or even moderately large, susceptible populations, or when missing data are present. Here we detail a methodology that can be used to estimate parameters for such large, and/or incomplete, data sets. This is done in the context of a study of the UK 2001 foot-and-mouth disease (FMD) epidemic.

1. Introduction

The spatio-temporal modelling of infectious diseases is an area of great importance. Accurately modelling the infectious dynamics of a disease enables scientists to understand risk factors associated with transmission and, through this, develop viable control strategies for potential future outbreaks. There are obvious public health and/or economic benefits in understanding the infectious dynamics of diseases in humans, animals, and plants. Furthermore, it is well understood how important the spatial aspect to these dynamics is in understanding disease spread (e.g., Lawson, 2001).

The focus of this paper is on modelling infectious disease epidemics through time and space at the level of individuals in a population. Here, individuals are represented as discrete points in time and space. In the resulting ‘individual-level model’ (ILM) (sometimes known as an individual-based model), the probability of a susceptible individual being infected from the infectious pressure exerted upon it from the surrounding infectious population is quantified. The resulting models are highly intuitive and flexible (e.g., Gibson, 1997; Keeling, Woolhouse, Shaw, Matthews, Chase-Topping, Haydon, Cornell, Kappey, Wilesmith and Grenfell, 2001; Jamieson, 2004). However, they are also typically computationally costly to parameterise.

Examples of such models are not readily found in the literature. Lawson (2001) develops an approach wherein infectious individuals are modelled explicitly as individuals, and the susceptible population through a random field. Gibson and Austin (1996) detail the use of an ILM in plant epidemiology. Gibson (1997) and Marion, Gibson and Renshaw (2003) use Markov chain Monte Carlo (MCMC) methodology and importance sampling, respectively, to develop inference for this model. Neal and Roberts (2004) detail a two-level ILM to study a localised outbreak of measles in school children in a village in Germany. Also, Jamieson (2004) develops an ILM to study the spatio-temporal dynamics of citrus canker.

There are a number advantages to setting such models within a Bayesian MCMC framework. First, there are the obvious desirable mathematical and philosophical properties of the Bayesian approach itself (e.g., Robert, 2001). MCMC affords us a very powerful tool for carrying out inference on highly complex models, and hence great flexibility in our choice of model. Another highly desirable feature of this framework is the ability to easily impute missing data, which is a major cause for concern in spatial epidemiology, and to estimate marginal posterior densities for these data. In terms of practical outcomes, using the full-posterior Bayesian approach also allows parameter (and, in theory, model) uncertainty to be incorporated into simulation studies used to test control strategies. This can be especially important when looking at extremes (e.g., worst-case scenario problems).

However, a major problem with using ILMs can be the computational difficulty in calculating the full likelihood. This is especially the case in epidemics in large populations (examples cited above are all for relatively small epidemics) or if imputing a large amount of missing data. Approximate techniques can be considered (e.g., Filipe and Gibson, 2001; Diggle, 2006) although these tend to have case specific downsides, as well as losing some or all of the advantages mentioned above.

In this paper we show how to carry out full posterior computation for ILMs by separating the likelihood into a small component, which needs to be recalculated as parameters vary, and a large component which remains constant as parameters vary. This may require care in choosing our ILM model, as we shall see, as the inference techniques here developed are applied to data from the UK 2001 foot- and-mouth disease (FMD) epidemic.

In Section 2 we introduce the type of data we are interested in analysing, and the general form of the ILM which is to be used. In Section 3 we present some background information about the 2001 UK FMD epidemic, and the original model of Keeling et al. (2001) from which our models are developed. In Section 4 we detail an extension of the model of Keeling et al. (2001) and the motivation behind the extension. In Section 5 we discuss the Bayesian framework in which the model is set, along with the computational problems in calculating the full likelihood for ILMs and the computational methodology used to make the likelihood computable within a non-prohibitive time span. In Section 6 we discuss an example of the methodology which can be used in the context of missing data in ILMs; in this case, that used to impute the infection dates of certain high risk farms. We then present some results regarding parameter estimation for the UK 2001 FMD epidemic in Section 7, and go on to discuss some possible future directions for research into infectious disease epidemics in Section 8.

Additionally, the results of a small simulation study carried out in the context of using the Bayesian model to optimise a particular FMD control policy is contained in Section 12 of the supplementary material.

2. Infectious Disease Data and the General Model

The models with which we are concerned are formulated as discrete-time SEIR models (here we use the notation . This means that at any given point in time an individual i can be in one of four states: i ∈ 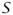implies individual i is susceptible to the disease; I ∈ implies that individual i has been exposed to the disease (i.e., has been infected, but is not yet infectious); i ∈ implies that individual i is infectious; i ∈ implies that individual i has been removed from the population (e.g., through recovery accompanied by gained immunity to the disease). Models within other compartmental frameworks (e.g., ) could also be parameterised using the methodology of this paper, but we do not cover this here.

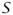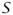In order to parameterise the ILMs it is necessary to have knowledge (actual or estimated) about the event history of individuals. That is, for t = 1, …, ∞, it is necessary to know if individual i is in state , , or . We refer to an individual i in one of these four states at a given time t as being in the sets (t), (t), (t) or (t) respectively. Note that here we discretise time so that an event which occurs in the continuous time interval [t, t + 1) is referred to as occurring at time t.

2.1 The general model

In this section we present the general form of the epidemic ILM. Here we consider that the transitions from to and to , defined by the rates and , respectively, are fixed and known. However, it would be quite possible to extend this model to the case where we estimate and .

Letting P (i, t) denote the probability that previously uninfected (susceptible) individual i

$$P(i,t)=1-exp\left[\left\{-{\mathrm{\Omega }}_S(i)\sum _{j\in \mathcal{I}(t)}{\mathrm{\Omega }}_T(j)\kappa (i,j)\right\}+\epsilon (i,t)\right],$$ (2.1)

is newly exposed within the time interval [t, t + 1), the general ILM is given by where (t) is the set of infectious individuals at time t; Ω_S (i) represents risk factors associated with susceptible i (i.e., susceptibility); Ω_T (j) represents risk factors associated with infectious individual j (i.e., transmissibility); κ(i, j) is an infection kernel representing risk factors involving both the infected and susceptible individuals (often based upon their separation distance, d_ij); and ε(i, t) is some infection process which describes some other random behaviour (this might represent infections from outside the population considered, or those not explained by the basic framework of the model).

Ω_S (i) and Ω_T (j) could be functions of various risk factors; for example, they could represent social interaction measures, genetic information, the size of sub-population (if an individual refers to a sub-population of susceptibles such as on a farm), or environmental risk factors associated with the location of the individual.

The infection kernel κ(i, j) is often used to characterise the risk of infection over some distance measure. For example, κ(i, j) could be a function of Euclidean or road distance (Savill, Shaw, Deardon, Tildesley, Keeling, Brooks, Woolhouse and Grenfell, 2006). Alternatively, it could represent traffic flows between towns, cities or farms.

The term, ε(i, t), that represents infections which are not well explained by the model structure as given by Ω_S (i), Ω_T (j) and κ(i, j), could be a purely random infection sparks term (ε(i, t) = ε). Alternatively, it could be a function of susceptible factors (e.g., ε(i, t) = ε(i) = ∈Ω_S(i)), or could be a function of the current size of the epidemic.

Given a record of infection events at discrete time points t = 0, …, T during the epidemic, the likelihood is simply a product over those time points so that

$$f(\mathcal{S},\mathcal{E},\mathcal{I},\mathcal{R}\mid \mathit{\theta })=\prod _{t=0}^T{f}_t(\mathcal{S},\mathcal{E},\mathcal{I},\mathcal{R}\mid \mathit{\theta }),$$ (2.2)

where

$$f_t(\mathcal{S},\mathcal{E},\mathcal{I},\mathcal{R}\mid \mathit{\theta })=\left[\prod _{i\in \mathcal{E}(t+1)\backslash \mathcal{E}(t)}P(i,t)\right]\left[\prod _{i\in \mathcal{S}(t+1)}\{1-P(i,t)\}\right],$$

$\mathcal{S}={\{\mathcal{S}(t)\}}_{t=1}^T,\mathcal{E}={\{\mathcal{E}(t)\}}_{t=1}^T,\mathcal{I}={\{\mathcal{I}(t)\}}_{t=1}^T,\mathcal{R}={\{R(t)\}}_{t=1}^T$, and θ is the vector of unknown parameters. That is, f_t( |θ) is the probability of all observed new infections in time interval [t, t + 1) being infected, and all observed non-infected individuals in time interval [t, t + 1) not being infected.

The primary purpose of this paper is to present a general methodology for parameterising infectious disease ILMs when large datasets are being used. This is done using the 2001 UK FMD epidemic as a case study.

3. Case Study: Foot and Mouth Epidemic of 2001

To illustrate the application of the general ILM of Section 2.1 in a large population, we look to the UK foot-and-mouth disease (FMD) epidemic of 2001.

The UK foot-and-mouth epidemic of 2001 is thought to have entered the UK in early February of that year. By the time it had been discovered and movement restrictions imposed, around 70 farms had been infected (Anderson, 2002). The epidemic resulted in recorded known infections and culls at Infected Premises (IPs) across the UK. Over 10,000 other farms with unknown infection status, but determined to be at high risk, had animals slaughtered. In total over four million animals were slaughtered as part of the control program to eradicate the disease.

The additional (non-IP) slaughter policy had two main components. One was the slaughtering of animals on farms designated Contiguous Premises (CPs), which were farms judged to have shared a common border with an IP. The second was the slaughtering of animals on farms designated Dangerous Contacts (DCs). These were farms in which there had been known contact of some sort with an IP (e.g., a milk tanker had visited a DC shortly after visiting an IP).

There is evidence to show that at least some aspects of the slaughter policy used were critical in controlling the epidemic (Keeling et al., 2001; Ferguson, Donnelly and Anderson, 2001a,b; Morris, Wilesmith, Stern, Sanson and Stevenson, 2001). However, there is little evidence to suggest that this slaughter policy was optimal in terms of disease control. Work has been carried out (Keeling, Woolhouse, May, Davies and Grenfell, 2003; Tildesley, Savill, Shaw, Deardon, Brooks, Woolhouse, Grenfell and Keeling, 2006) to develop improved control strategies to inform future culling and/or vaccination policies. (DEFRA’s current policy on vaccination and control is detailed in DEFRA, 2005). However, in order to devise a good control policy based on the 2001 UK epidemic, as good a model of that epidemic, and as rigorous an approach to the problem of parameterisation as possible, are required.

The data which we use to parameterise the models come from two sources. The first is the UK census of June 2000 which gives a list of all farms contained in the set (i.e., potential susceptibles). The census lists the number of different types of animals at each farm, as well as an X and Y ordnance survey location for the farmhouse of the farm. The second is the dataset of farms which were directly involved in the 2001 epidemic, all farms known to have been infected (IPs) and farms on which animals were culled. This data set directly gives the cull-dates of each farm on which animals were culled. Dates of exposure and infectiousness for IPs are inferred from disease reporting dates, expert veterinary opinion about the extent of disease progress at reporting, and assumptions about the length of the disease latency period (the time from exposure to infectivity). 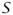Thus, we have a data set from which the sets, (t), (t), (t), and (t), t = 1, …, ∞ can be inferred in the case of IPs and farms not exposed to FMD.

Of course, this is not the case for CPs and DCs for which the date of removal from the population is known, but the dates of exposure (and on which infectivity began) are not. This is dealt with in Section 6. We also assume that farms on which animals were culled that were not CP or DC culls (e.g., welfare cull farms; see Anderson, 2002) were uninfected before slaughter. For farms on which animals were not culled the assumption is made that they were never exposed to FMD; that is, there was no exposure to FMD in 2001 which died out naturally without being observed.

(N.B. The data has been extensively cleaned for the analyses of this paper, as well as that of Tildesley et al., 2006 and Savill et al., 2006; this will be detailed in work to be published.)

3.1. The Keeling model

Keeling et al. (2001) details an explicitly spatial ILM and the general form of Section 2.1 holds as follows. Individuals, here, are farms rather than animals upon the farms. Time, here, is measured in days. It is assumed that once exposed to FMD, the farm would remain in that exposed state for five days, and then become infectious for four days. After this point, it is assumed that symptoms would be visible and so the farm would be reported and subsequently removed from the population through animal slaughter (state ).

Under this model, which we refer to as the Keeling model, the probability of susceptible farm i being infected during time period [t, t + 1) is given by (2.1), where Ω_S (i) = SN_i, Ω_T (j) = TN _j, κ(i, j) = K_T (d_ij), and ε(i, t) = 0. Here, S denotes a susceptibility vector, (S_s S_c), where S_s and S_c describe the rate of increase in susceptibility of a susceptible farm per additional sheep and cow, respectively. Similarly, T denotes the transmissibility vector, (T_s T_c), where T_s and T_c denote parameters describing the rate of increase in infectious pressure per additional sheep and cow, respectively, that an infectious farm exerts on the susceptible population. N_i denotes the number of animals vector, (N_i,s N_i,c)^T, where N_i,s is the number of sheep on farm i, and N_i,c is the number of cattle on farm i. Finally, K_T(d_ij) denotes a distance-based kernel estimated from DEFRA tracing data (Keeling et al., 2001), where d_ij denotes the distance between the farmhouses of farms i and j. The tracing kernel is described in Section 4.1 and is shown in Figure 1. To ensure identifiability, S_s = 1.0 is fixed and, thus, the only free parameters in the Keeling model are T and S_c.

Figure 1.

Distance kernels for models P_T and P_B.

Parameterisation of the model was originally carried out using a mixture of maximum likelihood estimation and fine tuning by running forward simulations, and using a goodness-of-fit measure. This procedure produces forward simulations that mimic important characteristics of the 2001 epidemic, suggesting a reasonable model. However, it is well known that such conditional parameterisation can lead to misleading results. Also, parameterisation via forward simulations and goodness-of-fit requires the mimicry of the 2001 culling policy which is difficult, and may introduce some bias in the parameterisation. There is obviously a case for carrying out a more rigorous attempt at the parameterisation, although, of course, the approach of Keeling et al. (2001) (as well as that of Diggle, 2006 and Ferguson et al., 2001a,b) has the advantage of relatively simple and quick parameterisation methods which a more rigorous approach does not necessarily allow.

4. Extending the Model

We extend the basic model of Keeling et al. (2001) in several key ways: we introduce a geometric change-point transmission kernel whose parameters will be estimated along with other key model parameters; we introduce a sparks term which allows for spontaneous unexplained infection; and we allow for a non-linear relationship between animal numbers and both infectivity and susceptibility. The purpose of these extensions is given in Sections 4.1–4.3.

4.1. Distance kernel

The DEFRA tracing data distance kernel was estimated by veterinarians on the ground considering the event history at the time of an IP being reported and making a best guess at the source of the infection. The distances between IPs and their tracing data source were then normalised to form the kernel, K_T (d_ij). However, it could be argued that such a subjectively-based distance kernel would overestimate the effect of short distance infections and underestimate the effect of the long distance infections. We therefore extend the Keeling model by introducing a more general kernel whose parameters are estimated using the infection data described in the previous section.

A geometric distance kernel was chosen, although it would be possible to use an exponential-based kernel. The geometric kernel was preferred since it has more mass in the tails of the kernel, and thus allows for the possibility of longer distance infections.

Experimentation with the FMD data suggested that the geometric kernel failed to adequately describe short range transmissions as the geometric shape was largely determined by a tail that describes the longer-range transmissions. Over shorter distances, different disease transmission dynamics come into play with close farms tending to share boundaries. Also, the assumption that the distance between farmhouses adequately reflects the distance between the location of farm animals begins to break down. Thus, we introduce a change-point to our model at some distance δ₀, to be determined, within which we assume a constant disease transmission rate, k₀.

Thus, we have a disease transmission kernel of the following form:

$$\kappa (i,j)=K_A(d_{ij})=\{\begin{array}{ll}{k}_0\hfill & 0<d_{ij}\le {\delta }_0\hfill \\ d_{ij}^b\hfill & {\delta }_0<d_{ij}\le {\delta }_{\mathit{max}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

with parameters k₀, δ₀ and b. δ_max is fixed a priori and restricts the maximum distance over which infections can occur. Here we set δ_max = 30km. The selection of δ_max clearly has some bearing on the results, with more of the epidemic being generated by infection sparks (Section 4.3) as δ_max is reduced. However, increasing δ_max above 30km produces relatively little change in other parameters.

Clearly if δ₀ = 0, the kernel simplifies to $K_A(d_{ij})=d_{ij}^b$, a kernel that roughly describes the shape of the tracing data kernel, K_T (d_ij). We use the tracing data kernel to provide the prior information for b. This is described in Section 7.1.

4.2. Introducing non-linearity

In the original model of Keeling et al. (2001) the assumption was made that the relationships between numbers of animals on infecting, and susceptible, farms and the infection rate was linear. To test this assumption we redefine the ΩS and ΩT functions so that

$${\mathrm{\Omega }}_S(i)=\mathit{S}\left(\begin{array}{c}{N_{i,s}}^{{\psi }_{S,s}}\\ {N_{i,c}}^{{\psi }_{S,c}}\end{array}\right)\text{and}{\mathrm{\Omega }}_T(j)=\mathit{T}\left(\begin{array}{c}{N_{i,s}}^{{\psi }_{T,s}}\\ {N_{i,c}}^{{\psi }_{T,c}}\end{array}\right).$$

Clearly, the original linear model is a special case of this more general specification.

It might be expected that transmissibility and susceptibility as defined here would be, at least in part, surrogates for the risk of animals from different farms mixing (e.g., due to animal movements). If this is so, it would seem unlikely that the linear assumption would be an accurate one to make, since we might expect that the risk of mixing does not increase by the same degree when a given increase in animal numbers starts from a low number, as when the increase starts from a high number.

4.3. Infection sparks

Finally, we introduce a new parameter which allows for spontaneous infections that is unexplained by the susceptibility, transmissibility and kernel components of the model. This term traditionally allows for infectious pressure from outside the study area. In our case, it allows for infection beyond the δ_max limit (e.g., long distance movement of vehicles or people, for example).

Though other choices are possible, we assume that the risk of spark infection on farm i at time t is directly affected by the susceptibility, Ω_S(i), and by the number of infectious farms during the interval [t, t + 1), |I(t)|. In this way, the risk of infection through the ε term increases with the underlying susceptibility of the farm, but also follows the course of the epidemic so that a spark-based infection will be most likely when there are large numbers of infectious farms, and will tend to zero as this number decreases. Thus, we take ε(i, t) = −∈Ω_S(i) | I(t)|.

4.4. Resulting model

These extensions together give us a new model with associated probability of susceptible farm i being infected during time period [t, t + 1) given by

$$P_A(i,t)=1-exp\left(-\mathit{S}{\mathit{N}}_i^{{\psi }_S}\left[\left\{\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_A(d_{ij})\right\}-\epsilon \mid \mathcal{I}(t)\mid \right]\right).$$ (4.1)

As before, we set S_s = 1 to make the model identifiable and so the vector of model parameters to be estimated is given by θ_A = (T_s, T_c, S_c, b, ∈, δ₀, k₀, ψ_S,_s, ψ_S,_c, ψ_T,_s, ψ_T,_c).

Some examples of possible distance kernels and susceptibility/transmissibility curves are given in Figures 4 and 5, which can be found in the on-line supplementary material.

5. Bayesian Computation

5.1. The posterior and simulation

Parameter estimation is carried out here within a Bayesian framework. The likelihood for our model is obtained by the substitution of (4.1) into (2.2) to give

$$f_A(\mathcal{S},\mathcal{E},\mathcal{I},\mathcal{R}\mid \mathit{\theta })=\prod _t\left[\prod _{i\in \mathcal{E}(t+1)\backslash \mathcal{E}(t)}{P}_A(i,t)\right]\left[\prod _{i\in \mathcal{S}(t+1)}\{1-P_A(i,t)\}\right].$$ (5.1)

We assume priors for our parameters (Section 7.1) to obtain our posterior distribution π_A(θ | ) up to a constant of proportionality. We explore the posterior via Markov chain Monte Carlo (MCMC) with Metropolis Hastings parameter updates (Section 7.2). For a more detailed description of MCMC within a Bayesian framework see, for example, Gammerman and Lopez (2006).

5.2. Minimising computational expense

Bayesian computation via Metropolis-Hastings MCMC requires the recalculation of π_A(θ | ) many, many times, with varying θ, to obtain a dependent sample from the posterior. The 2001 FMD dataset records over 160,000 farms, with just over 10,000 of those being directly affected by FMD either through being infected or culled. Thus, for any given t, the set 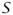(t + 1) consists of around 150,000 elements. This means that the calculation of (5.1) at every MCMC iteration becomes prohibitive due to the need to compute, for each t, the right-hand product

$$\begin{array}{l}{\chi }_A(t)=\prod _{i\in \mathcal{S}(t+1)}\{1-P_A(i,t)\}\\ =exp\left(\sum _{i\in \mathcal{S}(t+1)}-\mathit{S}{\mathit{N}}_i^{{\psi }_S}\left[\left\{\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_A(d_{ij})\right\}-\epsilon \mid \mathcal{I}(t)\mid \right]\right).\end{array}$$ (5.2)

(The set (t) will, of course, comprise far fewer elements for any given day of the epidemic than 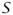(t + 1), so the left-hand product of (5.1) is much more manageable.)

To facilitate the computation for large data sets we seek to avoid recalculating (5.2) in its entirety at every MCMC iteration. In this section, we assume that the infection status of all farms is known from the start of the simulation and remains fixed throughout. (Dates of infection may be considered variable in the case of CP and DC-culled farms, however, and this case is discussed in Section 6.) We then show how, by linearising the model, we are able to split the time-consuming summations in the likelihood into two groups: those which are computationally expensive but need to be calculated only once; and those which are much quicker to compute but change with the parameter values and therefore need to be recalculated throughout the simulation.

5.3. Linearising the model

The model is linearised by taking Taylor series expansions of the appropriate terms in (4.1) so that the summations are split into two distinct groups. In our case the Ω_S(i), and κ(i, j) terms require linearisation. Let (f; x, x₀) denote the kth-order Taylor series expansion of the function f(x) around the point x₀. Then the probability of susceptible farm i being infected during time period [t, t + 1) is given by

$$P_B(i,t)=1-exp\left(-\mathit{S}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S},{\psi }_S,{\varphi }_S)\left[\left\{\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_B(d_{ij})\right\}-\epsilon \mid \mathcal{I}(t)\mid \right]\right),$$ (5.3)

where

$$\begin{array}{ll}\hfill {\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)& =\left(\begin{array}{c}{\mathcal{L}}^2({N_{i,s}}^{{\psi }_{S,s}};{\psi }_{S,s},{\varphi }_{S,s})\\ {\mathcal{L}}^2({N_{i,c}}^{{\psi }_{S,c}};{\psi }_{S,c},{\varphi }_{S,c}),\end{array}\right),\hfill \\ \hfill {\mathcal{L}}^2({N_{i,q}}^{{\psi }_{S,q}};{\psi }_{S,q},{\varphi }_{S,q})& ={N_{i,q}}^{{\varphi }_{S,q}}+{N_{i,q}}^{{\varphi }_{S,q}}({\psi }_{S,q}-{\varphi }_{S,q})ln(N_{i,q})+\frac{1}{2}{N_{i,q}}^{{\varphi }_{S,q}}{({\psi }_{S,q}-{\varphi }_{S,q})}^2{ln}^2(N_{i,q})\hfill \end{array}$$

for q ∈ (s, c}; here K_B (d_ij) is a linearised version of distance kernel K_A (d_ij),

$$K_B(d_{ij})=\{\begin{array}{ll}{k}_0\hfill & 0<d_{ij}\le {\delta }_0\hfill \\ {\mathcal{L}}^2(d_{ij}^b;b,\beta )\hfill & {\delta }_0<d_{ij}\le {\mathit{delta}}_{\mathit{max}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},$$

and ${\mathcal{L}}^2(d_{ij}^b;b,\beta )=d_{ij}^{\beta }+d_{ij}^{\beta }(b-\beta )ln(d_{ij})+(1/2)d_{ij}^{\beta }{(b-\beta )}^2{ln}^2(d_{ij})$.

So, for the new model, P_B(i,t) → P_A(i,t) as b → β, ψ_S,s → φ_S,s and ψ_S,c → φ_S,c. The choice of β, φ_S,s and φ_S,c is discussed in Section 5.5.

5.4. Partitioning the summations

We now consider how to partition the likelihood in such a way as to make the calculation computationally feasible. Replacing P_A(i, t) by P_B (i, t) in (5.2) gives

$${\chi }_B(t)=\prod _{i\in \mathcal{S}(t+1)}\{1-P_B(i,t)\}$$ (5.4)

and, substituting (5.3) into (5.4),

$$\begin{array}{l}{\chi }_B(t)=exp\left(\sum _{i\in \mathcal{S}(t+1)}-\mathit{S}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\left[\left\{\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_B(d_{ij})\right\}-\epsilon \mid \mathcal{I}(t)\mid \right]\right)\\ =exp\left\{\sum _{i\in \mathcal{S}(t+1)}\mathit{S}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\epsilon \mid \mathcal{I}(t)\mid \right\}\times exp\left\{\sum _{i\in \mathcal{S}(t+1)}-\mathit{S}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_B(d_{ij})\right\}\\ ={\chi }_B^{(L)}(t){\chi }_B^{(R)}(t),\end{array}$$

say.

We now show how the sums in these expressions can be separated into those which either depend on the model parameters, and therefore require calculation throughout the simulation, or depend only on the data and therefore can be calculated just once at the outset.

Consider the term $X_B^{(L)}(t)$ which can be rewritten as

$$\begin{array}{l}{\chi }_B^{(L)}(t)=exp\left\{\epsilon \mid \mathcal{I}(t)\mid \mathit{S}\sum _{i\in \mathcal{S}(t+1)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\right\}\\ =exp\left\{\epsilon \mid \mathcal{I}(t)\mid (S_s{S}_c)\sum _{i\in \mathcal{S}(t+1)}\left(\begin{array}{c}{\mathcal{L}}^2({N_{i,s}}^{{\psi }_{S,s}};{\psi }_{S,s},{\varphi }_{S,s})\\ {\mathcal{L}}^2({N_{i,c}}^{{\psi }_{S,c}};{\psi }_{S,c},{\varphi }_{S,c})\end{array}\right)\right\}\\ =exp\left\{\epsilon \mid \mathcal{I}(t)\mid (S_s{S}_c)\left(\begin{array}{l}{\zeta }_{1,1}^{(s)}(t)+({\psi }_{S,s}-{\varphi }_{S,s}){\zeta }_{1,2}^{(s)}(t)+{({\psi }_{S,s}-{\varphi }_{S,s})}^2{\zeta }_{1,3}^{(s)}(t)\hfill \\ {\zeta }_{1,1}^{(c)}(t)+({\psi }_{S,c}-{\varphi }_{S,c}){\zeta }_{1,2}^{(c)}(t)+{({\psi }_{S,c}-{\varphi }_{S,c})}^2{\zeta }_{1,3}^{(c)}(t)\hfill \end{array}\right)\right\}.\end{array}$$ (5.5)

where the $\zeta \frac{(q)}{1,x}$ for x ∈ {1, 2, 3} and q ∈ {s, c} are given in the Appendix in the supplementary material.

It is clear that each of the ζ_1,x terms are independent of the model parameters and can therefore be calculated at the start of the simulation. Similarly, we can split the summations in $X_B^{(R)}(t)$, though this is complicated somewhat by the dependence of the kernel on δ₀.

First, note that we can rewrite the definition of $X_B^{(R)}(t)$ as

$$\begin{gathered} {\chi }_B^{(R)}(t)=exp\left(-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\mathit{S}\sum _{i\in \mathcal{S}(t+1)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)K_B(d_{ij})\right) \\ =exp(-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\mathit{S}[\sum _{i\in {\mathcal{A}}_1(j,t)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S){\mathcal{L}}^2(d_{ij}^b;b,\beta ) \\ -\sum _{i\in {\mathcal{A}}_2(j,t)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\left\{{\mathcal{L}}^2(d_{ij}^b;b,\beta )-k_0\right\}]) \\ =\left(exp\left[-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\mathit{S}\sum _{i\in {\mathcal{A}}_1(j,t)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S){\mathcal{L}}^2(d_{ij}^b;b,\beta )\right]\right) \\ \times {\left(exp\left[-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\mathit{S}\sum _{i\in {\mathcal{A}}_2(j,t)}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S) \\ \times \left\{{\mathcal{L}}^2(d_{ij}^b;b,\beta )-k_0\right\}\right]\right)}^{-1} \\ =\frac{{\chi }_{B1}^{(R)}(t)}{{\chi }_{B2}^{(R)}(t)}, \end{gathered}$$ (5.6)

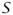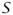Where (j, t) = {i : i ∈ (t + 1) and d_ij ∈ [0, δ_max]}, and (j, t) = {i : i ∈ (t + 1) and d_ij ∈ [0, δ₀]}.

Now we can rewrite $X_B^{(R)}(t)$ as

$$\begin{array}{l}{\chi }_{B1}^{(R)}(t)=exp\left[-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\mathit{S}\left\{\sum _{i\in \mathcal{S}(t+1)}{\mathcal{L}}^2({{\mathit{N}}_i}^{{\psi }_S};{\psi }_S,{\varphi }_S){\mathcal{L}}^2(d_{ij}^b;b,\beta )\right\}\right]\\ =exp\left[-\mathit{T}\sum _{j\in \mathcal{I}(t)}{\mathit{N}}_j^{{\psi }_T}\left\{(S_s{S}_c)\left(\begin{array}{c}{\zeta }_2^{(s)}(j,t)\\ {\zeta }_2^{(c)}(j,t)\end{array}\right)\right\}\right],\end{array}$$

where,

$$\begin{array}{l}{\zeta }_2^{(q)}(j,t)={\zeta }_{2,1}^{(q)}(j,t)+(b-\beta ){\zeta }_{2,2}^{(q)}(j,t)+{(b-\beta )}^2{\zeta }_{2,3}^{(q)}(j,t)\\ +({\psi }_{S,q}-{\varphi }_{S,q}){\zeta }_{2,4}^{(q)}(j,t)+(b-\beta )({\psi }_{S,q}-{\varphi }_{S,q}){\zeta }_{2,5}^{(q)}(j,t)\\ +{(b-\beta )}^2({\psi }_{S,q}-{\varphi }_{S,q}){\zeta }_{2,6}^{(q)}(j,t)\\ +{({\psi }_{S,q}-{\varphi }_{S,q})}^2{\zeta }_{2,7}^{(q)}(j,t)+(b-\beta ){({\psi }_{S,q}-{\varphi }_{S,q})}^2{\zeta }_{2,8}^{(q)}(j,t)\\ +{(b-\beta )}^2{({\psi }_{S,q}-{\varphi }_{S,q})}^2{\zeta }_{2,9}^{(q)}(j,t),\end{array}$$ (5.7)

with the $\zeta \frac{(q)}{2,x}(j,t)$, for x ∈ {1, … 9} and q ∈ {s, c} as defined in the Appendix. As before, it is clear that each of the $\zeta \frac{(q)}{2,x}$ terms are independent of the model parameters and can therefore be calculated once at the start of the simulation.

Of course, $X_{B2}^{(R)}(t)$ cannot be made independent of all parameters in the same way as $X_{B1}^{(R)}(t)$, because it explicitly depends on the change point, δ₀, in the range of summation. However, assuming the number of elements in (j, t) is relatively small (which is the case for the UK 2001 FMD data), $X_{B2}^{(R)}(t)$ can be fairly cheaply calculated with careful programming. The algorithm used here requires a maximum value of δ₀, ${\delta }_0^{(\mathit{max})}$, to be set. Here ${\delta }_0^{(\mathit{max})}=3,000\mathrm{m}$ was found to be adequate.

Of course, these Taylor series expansions require the specification of an appropriate centering point which we briefly consider in the next section.

5.5. Values of β, φ_S,s and φ_S,c

The computational methodology of this section provides a way of forming a likelihood which is computationally feasible within the framework of full-posterior sampling. Unfortunately, the parameter space of the linearised model, P_B (i, t), is different from that of model P_A(i, t), except when b = β, ψ_S,s = φ_S,s and ψ_S,c = φ_S,c. This difference means that as b deviates from β, ψ_S,s deviates from φ_S,s, and ψ_S,c deviates from φ_S,c, the parameters b, ψ_S,s, and ψ_S,c, become harder to interpret, respectively. Thus, it is useful to try and find sensible values for these parameters that approximate the values we might expect for the true parameter values.

The availability of the tracing data kernel, K_T (d_ij), provides an obvious means for selecting a suitable value of β. Here β̂ was obtained by fitting the model

$$\alpha d_l^{\beta +1}=d_l{K}_T+{\epsilon }_l,\forall l\in L,$$ (5.8)

where L denotes the set of discretised distances over which the tracing data kernel is defined and ε_ι ~ N(0, σ²). Along with the scale parameter estimate α̂ = 1,284.2, the rate parameter estimate was given by β̂ = −1.62, and the variance parameter by σ̂² = 0.000350.

Various settings of φ_S,c ∈ (0, 1.5) and φ_S,s ∈ (0, 1.5) were tested. It was found that the setting φ_S,c = φ_S,s = 1.0 produced high levels of likelihood and good MCMC mixing properties. These values of φ_S,c and φ_S,s also resulted in marginal mean posterior estimates of ψ_S,s and ψ_S,c for which ψ_S,s ≈ φ_S,s and ψ_S,c ≈ φ_S,c, thus aiding interpretation of ψ_S,s and ψ_S,c.

6. Imputing the Dates of Infection of CPs and DCs

The methodology described so far relies on the assumption that the infection status of all farms is known throughout the epidemic. Section 3 detailed how this information was arrived at for IPs. However, no such information is available for CP and DC farms since they could have been infected but culled before symptoms appeared. We consider the estimation of the proportion of these farms which were infected before culling, λC. The computational methodology used to do this is detailed in Section 9 in the supplementary material.

7. Parameter Estimates for the UK 2001 FMD Epidemic

7.1. Priors

When included in the model, b, the kernel power-law parameter, is informed by the tracing data. However, a fairly vague prior is used, (b) ~ (β̂, 10 × s.e.(β̂)²), where β̂ is the estimate of β as obtained by fitting the model shown in (5.8), and s.e.(β̂), its standard error. Recall from Section 5.4 that β̂ = −1.62 and s.e.(β̂)² = 0.000350. A small sensitivity analysis was carried out that appeared to show that increasing the variance of p(b) has little effect upon the mean posterior of b.

Positive half-normal priors with high variance (σ² = 10, 000) are assigned to the model parameters T_s, T_c, S_c, ψ_S,s, ψ_S,c, ψ_T,s and ψ_T,c. Parameter k₀ is assigned the same prior when included in the model. Normal priors with the same variance, but centered around high positive values (e.g., 1,000), produce very similar results to the half-normal priors, implying they are non-informative. A negative half-normal prior with variance σ² = 10, 000 is assigned to ∈. Finally δ₀, when included in the model, is assigned a uniform prior over the range [0, ${\delta }_0^{(\mathit{max})}$].

7.2. Results

Section 10 in the supplementary material details a comparison between the models used here, and that of Keeling et al. (2001). Section 11, in the on-line supplementary material, details a small simulation study used to ascertain that the estimation procedures employed in this paper are working correctly.

Parameter estimates for two versions of the model are given. Both models include a sparks term (∈) and allow for non-linear susceptibility and transmissibility. The first model, P_T, uses the tracing data kernel and the second, P_B, uses the change-point kernel. The full expression for P_T is

$$P_T(i,t)=1-exp\left(-\mathit{S}{\mathcal{L}}^2({\mathit{N}}_i^{{\psi }_S};{\psi }_S,{\varphi }_S)\left[\left\{\sum _{j\in \mathcal{I}(t)}\mathit{T}{\mathit{N}}_j^{{\psi }_T}{K}_T(d_{ij})\right\}-\epsilon \mid \mathcal{I}(t)\mid \right]\right),$$ (7.1)

and P_B is given in (5.3).

The estimation was carried out with a Metropolis Hastings MCMC algorithm using, in the main, random walk proposals to update parameters. When included in the model, parameters b, S_c, ∈, k₀, δ₀, ψ_S,s, and ψ_S,c were updated using single component normally distributed random walk proposals. Parameters T_s and ψ_T,s, and, T_c and ψ_T,c, were updated as two separate block updates to allow for correlation between each respective pair.

Marginal posterior density means and 95% HPDIs for both the P_T and P_B models are shown in Table 1. Of those parameters which are estimated in both models, Sc and the non-linearity parameters ψ_T,s, ψ_T,c, ψ_S,s, and ψ_S,s do not seem to differ significantly (e.g., there is overlap in the 95% HPDIs for these parameters).

Table 1.

Means (with 95% HPDIs) of marginal posterior densities for parameters for models fitted to the UK 2001 FMD epidemic data.

Parameter	Model PT	Model PB
b	n/a	−1.66 (−1.70, −1.62)
Ts	1.18 × 10−4 (0.21, 2.16) × 10−4	2.62 × 10−1 (0.64, 4.00) × 10−1
Tc	9.00 × 10−5 (2.40, 17.3) × 10−5	1.22 × 10−1 (0.23, 2.55) × 10−1
Ss	1.00	1.00
Sc	6.03 (4.38, 7.78)	7.14 (5.28, 9.07)
∈	−5.76 × 10−10 (−7.11, −4.40)×10−10	−2.45 × 10−10 (−3.16, −1.76) × 10−10
k0	n/a	1.85 × 10−5 (0.84, 2.93) × 10−5
δ0	n/a	719 (435, 1138)
ψT,s	0.113 (0.000, 0.249)	0.074 (0.000, 0.186)
ψT,c	0.304 (0.147, 0.471)	0.321 (0.139, 0.509)
ψS,s	0.908 (0.877, 0.941)	0.908 (0.879, 0.939)
ψS,c	0.887 (0.842, 0.934)	0.886 (0.844, 0.929)
λC	0.063 (0.053, 0.073)	0.035 (0.027, 0.043)

The transmissibility parameters, T_c and T_s, are not really comparable due to the difference in scale of the infection kernels used in each model and the fact that they are meaningless without consideration of ψ_T,s and ψ_T,c. In the case of ∈, the mean posterior value for the P_T model (5.76 × 10⁻¹⁰) is more than double that of the P_B model (2.45 × 10⁻¹⁰). The distance kernels obtained via the mean posterior distribution for each of the two models are shown in Figure 1. K_B is rescaled to take account of the difference in scale of transmissibility between P_B and P_T. We can see that the estimated kernel of P_B does indeed suggest (as mentioned in Section 4.1) that the tracing data kernel overestimates the risk of short-distance infection, and underestimates that of long-distance infections. The larger magnitude of ∈ in the P_T model is likely correcting for this, allowing for more long-range infections. It should also be noted that though the values of ∈ given are small for both models, this still accounts for a sizeable number of infections.

We can see that λ_C is larger for P_T (0.063) than for P_B (0.035); this difference may be due to the fact that the infection of CP culls, which tend to be close to IPs, are more likely under model P_T wherein the tracing data kernel is used.

Note that there is a small discontinuity at the change point for P_B, since no constraint is made that the lines on either side of the change point should meet. Intuitively, it would seem more natural for the lines to be forced to meet if describing a simple biological process. However, since the distance kernel is an approximation of a number of disparate infection mechanisms, we felt this constraint would be unreasonable, and allowed the kernel to be more empirically based.

The relationships between animal numbers and susceptibility, and animal numbers and transmissibility, given for the posterior mean, are shown in Figures 2 and 3. These plots show how the susceptibility (S_q N_i,q^ψSq, q ∈ {s, c}), and transmissibility (T_q N_i,q^ψT,q, q ∈ {s, c}), for each animal species under each model, P_T and P_B, vary as animal numbers vary.

Figure 2.

Mean posterior farm susceptibility (SNψS) against number of animals: (a) under model P_T; (b) under model P_B.

Figure 3.

Mean posterior farm transmissibility (T N^ψT) against number of animals: (a) under model P_T; (b) under model P_B.

We observe from these plots that the qualitative conclusions of Keeling et al. (2001), that each individual cow was more likely to transmit the disease, and also likely to be more susceptible to the disease than each individual sheep, are supported here. It would appear, however, that the linear assumption made in that paper was questionable in terms of transmissibility (a linear approximation looks more reasonable in the case of susceptibility).

Both in terms of susceptibility and transmissibility, the relationship with numbers of sheep, as compared with that of cattle, seems to be almost flat. More specifically, in terms of susceptibility, it would appear that an increase in sheep numbers on a farm has a unimportant effect, relative to a similar increase in cattle, on the risk of that farm being infected. In terms of transmissibility, it would appear that an increase in sheep numbers above a certain low threshold (around 20, dependent upon which model we consider), on a given infectious farm, has almost no effect on the risk of infection of susceptible farms.

It also appears that the relationship between susceptibility and animal numbers is very similar under both models P_T and P_B, with the susceptibility ratio between sheep and cattle being slightly lower when the tracing data kernel is used. This plot also suggests that the transmissibility ratio between sheep and cattle is higher when the tracing data kernel is used, and the magnitude of this ratio difference increases as animal numbers increase.

8. Discussion

We consider some work that might be carried out in the future. First, in the FMD example in this paper, we assumed a constant latent period. This latent period could, however, be allowed to vary, and thus be estimated. To do this, the ‘static’ ζ terms of Section 5 would need to be calculated and stored for different latent periods (i.e., an extra dimension added to the ζ variables). The techniques used to impute missing infection times in Section 6 could also be extended to allow for a variable infectious period. Similar techniques would be required to carry out reversible jump MCMC to incorporate model uncertainty into our inference problem and thus sample from the joint model and parameter posterior distribution. This would be useful to test, not only if various parameters should be included in the model, but also the structure of the model. For example, is it wise to multiply the sparks term by the susceptibility of farm i in (4.1) and (5.3), or should it be included without the susceptibility term? Due to the computational requirements of such a scheme, however, this would not be a trivial development.

Questions about the sensitivity of conclusions to the choice of variables, such as the Taylor series centre-points, will be addressed in future work that will also consider the related issue of model choice.

ILMs could be applied to a wide range of infectious diseases where data expressing spatial location, exposure, and removal time is available. There are obvious applications in other agricultural problems for both animals (e.g., avian flu in domestic poultry), or plants (e.g., citrus canker in trees) where individuals do not move. However, there appears to be no theoretical barrier to applying ILMs to situations where the individuals are mobile (e.g., human and wildlife diseases), as long as at least partial spatial location data are available over time. Neither does the infection kernel, κ(i, j), in (2.1) need to refer to a Euclidean distance kernel. As well as the possibility of using other distance metrics (e.g., road distance), some sort of contact measure could be used. For example, in a study of the transmission of a human epidemic around the globe, an infection kernel representing traffic flows between airports could be considered. This may have relevance to diseases such as SARS or influenza.

The vital issue of goodness-of-fit for infectious disease models, which does not fit as naturally into the Bayesian setting, is not addressed in this paper. However, it is a key area of research which the authors intend to address in future work.