Abstract
Anatomical brain networks change throughout life and with diseases. Genetic analysis of these networks may help identify processes giving rise to heritable brain disorders, but we do not yet know which network measures are promising for genetic analyses. Many factors affect the downstream results, such as the tractography algorithm used to define structural connectivity. We tested nine different tractography algorithms and four normalization methods to compute brain networks for 853 young healthy adults (twins and their siblings). We fitted genetic structural equation models to all nine network measures, after a normalization step to increase network consistency across tractography algorithms. Probabilistic tractography algorithms with global optimization (such as Probtrackx and Hough) yielded higher heritability statistics than “greedy” algorithms (such as FACT) which process small neighborhoods at each step. Some global network measures (probtrackx-derived GLOB and ST) showed significant genetic effects, making them attractive targets for genome-wide association studies.
Index Terms: diffusion MRI, Brain Network, Tractography, ICC, Normalization
1. INTRODUCTION
Diffusion-weighted MRI is a non-invasive technique sensitive to white matter microstructure. Using diffusion MRI, water diffusion in each voxel can be modeled using a tensor or an orientation distribution function (ODF). Dominant diffusion directions may be extracted from these diffusion models; by following neighboring voxels’ dominant diffusion directions, large-scale neuronal tracts may be reconstructed. Anatomical brain networks can be modeled by counting the proportion of detected fibers that intersect or interconnect pairs of regions of interest (ROIs), defined on anatomical MRI. These structural brain networks are symmetric by definition. Characterized using graph theory, some brain network properties are altered in certain disorders, such as bipolar illness [1, 2], body dysmorphic disorder [3], Alzheimer’s disease [4], and even HIV/AIDS [5]. Large population studies, such as ADNI [6] and ENIGMA [7], are increasingly prevalent as they offer increased power to evaluate risk factors and biomarkers for diseases and detect genetic associations with brain measures.
Some studies have identified genetic effects on brain networks [8–10]. Jahanshad et al. [8] used a genome-wide association scan (GWAS) to screen brain connectivity matrices suggesting that common variants in the SPON1 gene may influence anatomical networks. Candidate gene studies (e.g., [10]) have suggested lower global efficiency of the brain network in people carrying a variant in the Disrupted-in-Schizophrenia-1 (DISC1) gene, although these reports await replication.
However, dozens of tractography algorithms have been developed [11–17] yielding very different brain networks. We previously found no detectable differences in performance when classifying Alzheimer’s Disease based on brain networks computed from nine tractography algorithms [18], but the choice of tractography algorithm may well affect genetic studies. Prior to embarking on large-scale GWAS studies of brain networks, here we evaluated nine different tractography methods with four different normalization approaches. We computed brain networks using each tractography algorithm and normalized each network using each normalization method. 10 network measures were extracted from each normalized network based on graph theory analysis. We addressed two questions: (1) Which normalization method leads to the least variation (i.e., greatest consistency) among different tractography algorithms; and (2) which network measures show greatest heritability, to prioritize or rank them for future in-depth genetic analyses.
2. METHODS
2.1 Participant Demographics and Imaging
DTI data from 853 young healthy adults were analyzed (Table 1 shows their demographics). Each participant was scanned with 3D T1-weighted anatomical brain MRI and diffusion-weighted imaging (DWI) on a 4T Siemens Bruker Medspec MRI scanner. T1-weighted images were acquired with an inversion recovery rapid gradient echo sequence, with TI/TR/TE= 700/1500/3.35 ms; flip angle, 8°; slice thickness, 0.9 mm. Diffusion MRI was acquired using single-shot echo planar imaging with a twice-refocused spin echo sequence to reduce eddy-current induced distortions. Acquisition parameters were: 23 cm FOV, TE/TR 92.3/8250 ms. 105 images were acquired per subject: 11 with no diffusion sensitization (i.e., T2-weighted b0 images) and 94 diffusion-weighted (DW) images (b=1159 s/mm2) with gradient directions evenly distributed on the hemisphere. Total scan time was 14.5 minutes.
Table 1.
Cohort Demographics.
| N | Age | Sex | |
|---|---|---|---|
| Monozygotic twins (MZ) | 228 | 22.38±2.74 y | 72M |
| Dizygotic twins (DZ) | 320 | 22.22±2.55 y | 127M |
| Siblings | 305 | 23.56±2.99 y | 108M |
| Total | 853 | 22.74±2.83 y | 306M |
2.2 Data Preprocessing
Non-brain regions were automatically removed from each T1-weighted image, and from a b0 image from the DWI dataset, using the bet function in FSL (http://fsl.fmrib.ox.ac.uk). A neuroanatomical expert manually refined all brain extractions. We corrected eddy current distortion in DWI scans using FSL’s eddy_correct function. All T1-weighted scans were linearly aligned using FSL (with 9 DOF) to a common space. For each subject, the 11 eddy-corrected b0 images were averaged, linearly aligned to the corresponding T1 image and elastically registered to the structural scan using a mutual information cost function to compensate for EPI-induced susceptibility artifacts. The resultant deformation field was applied to the other DWIs. Based on the registered DWIs, we computed whole-brain tractography with a wide variety of deterministic and probabilistic tracking algorithms that used tensor or full ODF-based models of diffusion.
2.3 Whole Brain Tractography
Among the deterministic methods were four tensor-based deterministic algorithms: FACT [12], the 2nd-order Runge-Kutta (RK2) method [11], the tensorline (TL) [13] and interpolated streamline (SL) methods [14] and two deterministic tractography algorithms based on 4th order spherical harmonic derived orientation distribution functions (ODFs) - FACT and RK2. We also tested three probabilistic approaches: one was “ball-and-stick model based probabilistic tracking” (Probtrackx) from the FSL toolbox [15]; the other two were based on ODFs represented by 4th order spherical harmonic series: the Hough voting method [16] and the Probabilistic Index of Connectivity (PICo) method [17].
All deterministic tracking approaches were conducted with the Diffusion Toolkit (http://trackvis.org/dtk/). Fiber tracking was restricted to regions where fractional anisotropy (FA) ≥ 0.2 to avoid gray matter and cerebrospinal fluid; fiber paths were stopped if the fiber direction encountered a sharp turn (with a critical angle threshold ≥ 30°). Sharp “right-angle” turns may be biologically possible in some cases [19], but allowing right-angle turns in tractography would create large numbers of false positive pathways at fiber crossings.
Probtrackx was performed after Bedpostx was applied. Bedpostx stands for Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques [15]. In our study, up to 3 fibers were modeled per voxel. Once Bedpostx had been run, we chose all voxels with FA≥0.2 as the seeds. Following Bedpostx, Probtrackx was run on each individual seed voxel. Probtrackx repeatedly samples from the voxel-wise principal diffusion direction calculated in Bedpostx, creating a new streamline at each iteration. This builds a distribution on the likely tract location and path, given the data. A value of 1000 iterations was chosen to ensure convergence of the Markov chains, from which the posterior distributions of the local estimate of the fiber orientation distribution were sampled.
The Hough voting method was performed with code provided by the authors [16]. ODFs at each voxel were computed using the normalized and dimensionless constant solid angle ODF estimator, derived for Q-ball imaging (QBI) in [20]. Tractography was performed by probabilistically seeding voxels with a prior probability based on the FA value (FA≥0.2). All curves passing through a seed point receive a score estimating the probability of the existence of the fiber, computed from the ODFs. Then a Hough transform voting process was adopted to determine the best fitting curves through each point. Hough probabilistic tractography optimizes the fiber pathway globally, so there is no explicit upper limit on the number of detectable crossing fibers although the data angular resolution will limit this in practice.
PICo was conducted with Camino (http://cmic.cs.ucl.ac.uk/camino/). Seed points were chosen at those voxels with FA ≥ 0.2. ODFs were estimated using 4th order Spherical Harmonics and a maximum of 3 local ODF maxima (where fibers mix or cross) were set to be detected at each voxel. Then, a probability density function (PDF) profile can be produced from the derived local ODF maxima. Monte Carlo simulation was used to generate fibers emanating from seed points inside the entire brain. Streamline fiber tracking followed the voxel-wise PDF profile with the Euler interpolation method, for 10 iterations per each seed point. The maximum fiber turning angle was set to 30°/voxel. Tracing stopped at any voxel whose FA was less than 0.2. This approach generates many more fibers than other methods used in this study.
2.4 Brain Network Computing and Normalization
34 cortical regions of interest (ROI) per hemisphere, listed in [21], were automatically extracted from all aligned T1-weighted scans with FreeSurfer (http://surfer.nmr.mgh.harvard.edu). To ensure tracts would intersect cortical labeled boundaries, we dilated labels with an isotropic box kernel of size 5×5×5 voxels. For each ROI pair, the number of fibers connecting them was determined from the tractography. A fiber was considered to connect two ROIs if it intersected both ROIs. This process was repeated for all ROI pairs, to compute a 68×68 whole brain fiber connectivity matrix. This matrix (M0) is symmetric, by definition, and the diagonal elements represent the total number of fibers originating from each ROI. Since Probtrackx can output the brain network directly, the results from all other tractography algorithms except Probtrackx were analyzed using the above procedures to generate brain network. We then defined four ways to normalize these brain networks (Table 2).
Table 2.
Matrix Normalization Equation
| Equation | ||
|---|---|---|
| Raw | M1=M0 ◦ (1-E) | |
| MaxNorm | M2=M1◦(1/max(M1)) | |
| SumNorm | M3=M1◦(1/sum(M1)) | |
| IndNorm |
M0 is the initial computed matrix; E is the unit matrix; ◦ is the Hadamard product; max() is the maximum value of all matrix elements; sum() is summation of all matrix elements; (i,j) is the element (i,j) in the matrix. M1–M4 are four normalized matrices.
2.5. Network measures
After normalization, M1–M4 were analyzed using graph theory. Nine network global measures were calculated including Mean Clustering Coefficient (MCC), Transitivity (TS), Characteristic Path Length (CPL), Density (DS), Degree (DG), Global Efficiency (GLOB), Strength (ST), Diversity (DV) and Small-Worldness (SW), using the brain connectivity toolbox (BCT) [22]. We used weighted versions of these 9 measures. Definitions and mathematical equations may be found at the BCT toolbox website (https://sites.google.com/site/bctnet/).
2.6. Statistical Analysis
For each network measure listed in section 2.5, we used generalized linear regression (GLR) to remove statistical effects of age, sex and total brain volume (TBV). The resultant residue (RR) was used for the following two analyses.
Our first aim was to find which normalization technique would minimize the variations among different tractography algorithms, i.e. yield most consistent networks across methods. So we ran one-way ANOVA on four sets of normalized matrices using all 853 subjects. Each group consists of 853 values. We first computed each subject’s variability across the nine tractography algorithms, defined as Q=abs(SD/mean), in which abs is absolute value, SD is the standard deviation of RRi (i=1–9) and the mean is the mean value of RRi (i=1–9). RRi is the residual network corresponding to the i-th tractography algorithm. We repeated this process nine times for the nine network measures in section 2.5.
Second, based on the “optimal” normalization technique, we aimed to find which tractography algorithm and which network measures showed evidence of heritability (genetic influence). So for each network measure from 114 pairs of MZ and 160 pairs of DZ twins, we fitted a structural equation model (SEM) to estimate to what extent the variance in each measure was attributable to additive genetic, A, common environment, C, and unique environment/measurement error, E (please refer to [23] for model details). MZ twins raised in a family share 100% of their genes, as well as a shared environment. Any differences arising between them in these circumstances are random (unique). The correlation between identical twins provides an estimate of A + C. DZ twins also share C, but share on average only 50% of their genes: so the correlation between fraternal twins is a direct estimate of ½A+C. Therefore, the additive genetic component of variance, a2, is approximately twice the difference between identical and fraternal twin correlations: the additive genetic effect (Falconer's formula) [24]. Measures with lower a2 values tend to be less promising candidates for further genetic analysis.
3. RESULTS AND DISCUSSIONS
3.1 Normalization Effects
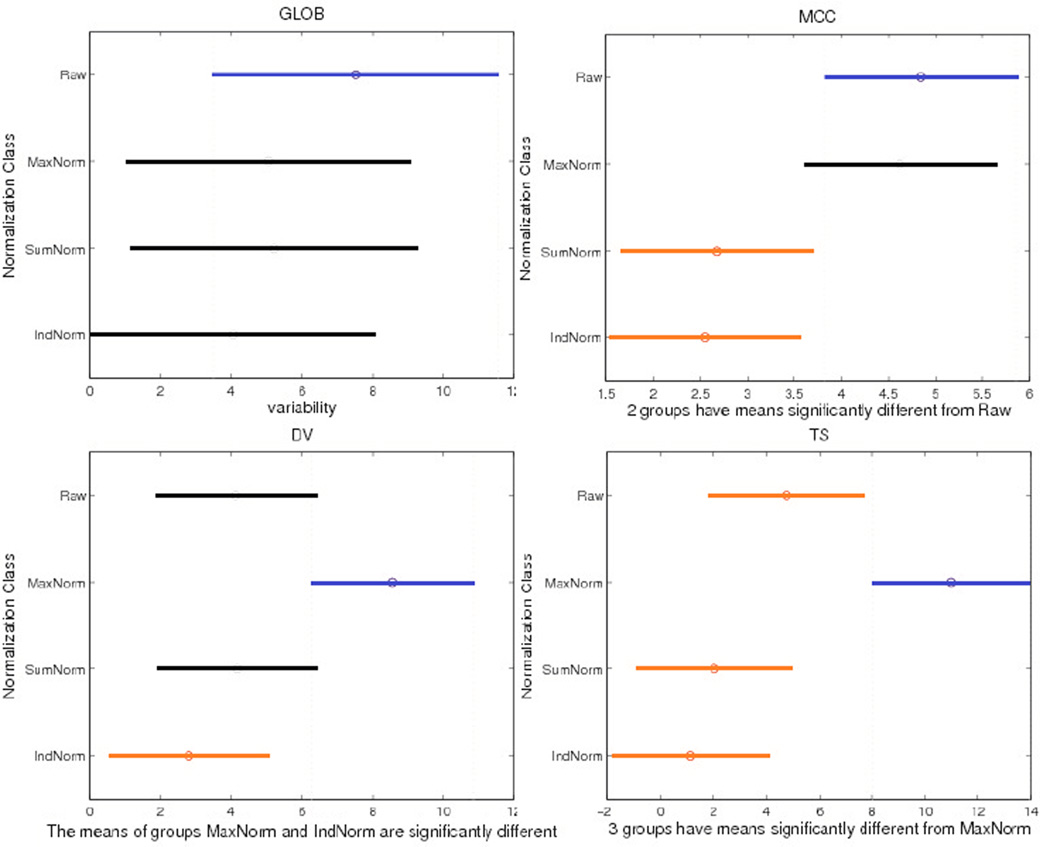
Figure 1 shows One-Way ANOVA results on variability (Q) for network measures in the four normalization groups across the cohort described in section 2.6. Only three measures (MCC, DV and TS) show significant differences in consistency that depends on the normalization method in One-Way ANOVA (P= P=2.5×10−3, 7.69×10−3 and 5.82×10−5 respectively). As only the IndNorm method gave consistently significant smaller mean variability (i.e., greater consistency) for these three network measures and there are no group differences in Q among four normalization methods for the other six network measures, we chose the IndNorm method for later analysis.
Figure 1.
One-Way ANOVA results for network measures. The y-axis shows the type of normalization used, and the x-axis is variability (Q) and its 95% confidence interval (CI) across the cohort described in Section 2.6. No CI overlap suggests significant differences between normalization methods. Different colors (blue and red) show pairs of methods with significant differences. We show GLOB as one example where there was no detectable difference in mean variability across the four normalization methods. For the network metrics MCC, DV and TS, there are significant differences among the four normalization methods - with P=2.5×10−3, 7.69×10−3 and 5.82×10−5 respectively in a one-way ANOVA.
3.2 Heritability statistic
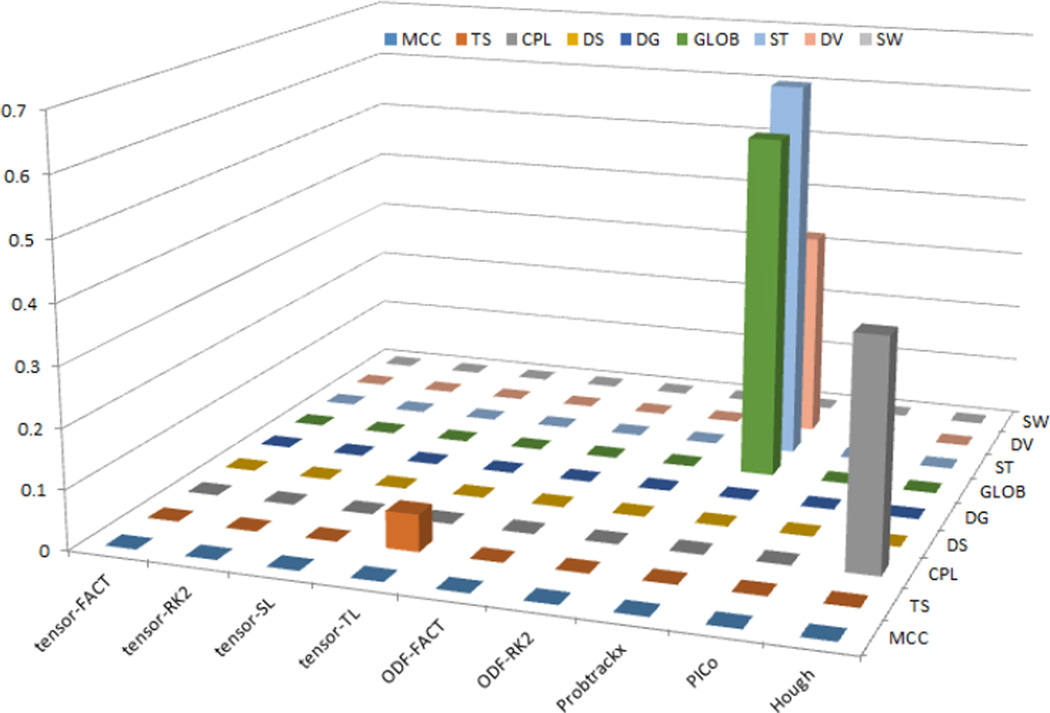
Based on the above results, we computed ACE-based heritability statistics for the IndNorm group only. Figure 2 shows the heritability statistic results (a2 values with P<0.05) for all network measures and for nine tractography algorithms. Our results indicated most A values do not differ detectably from zero, so those measures may not be suitable for further genetic studies. Five measures (including Tensor-TL derived TS, Probtrackx-derived GLOB, ST, DV and Hough-derived CPL) are highlighted in Figure 2. Table 3 summarizes the ACE outputs for these five measures.
Figure 2.
SEM heritability statistic results (a2 values) for all network measures and for all tractography algorithms, when using IndNorm as normalization method. Only Tensor-TL derived TS, Probtrackx-derived GLOB, ST, DV and Hough-derived CPL have a2 values significantly larger than 0 (with P value<0.05). Most of other measures have zero values.
Table 3.
Summary of ACE output for the five highlighted measures. 1: Tensor-TL derived TS; 2–4: Probtrackx-derived GLOB, ST and DV; 5: Hough-derived CPL. PACE represents how well the ACE model fits; the larger this value is, the better the ACE model fits. PA is the probability associated with the A term in ACE model.
| Index | PACE | PA | a2 (%) | c2 (%) | e2(%) |
|---|---|---|---|---|---|
| 1 | 0.60 | 8.51E-03 | 6.18 | 0 | 93.82 |
| 2 | 0.28 | 5.88E-05 | 58.11 | 0 | 41.89 |
| 3 | 0.11 | 1.13E-06 | 64.65 | 0 | 35.35 |
| 4 | 0.17 | 3.15E-02 | 35.18 | 0 | 64.82 |
| 5 | 0.99 | 4.6E-02 | 38.01 | 15.49 | 46.50 |
From Table 3, if Bonferroni correction is adopted to correct for multiple comparisons, our results still showed that Probtrackx-derived GLOB and ST have significant a2 values (PA less than 0.05/9/9≈6.2E-04). Probabilistic tractography algorithms with global optimization (such as Probtrackx and Hough) may yield higher heritability statistics for genetic studies than other “greedy” types of tractography algorithms (such as FACT) which process small neighborhoods at each step. Furthermore, probtrackx-derived GLOB and ST have significant (and large) a2 values (red colors in Table 3). For these measures, genetic factors may account for over 50% of the measured variance among individuals.
4. CONCLUSIONS
In our study, we the first used an IndNorm normalization technique to increase the consistent among network measures computed from 9 different tractography algorithms. Probabilistic tractography algorithms with global optimization generated measures in which a greater proportion of the variance was attributable to genetic differences among individuals. Probtrackx-derived GLOB and ST were two measures for which genetic factors explained over half of the overall variance across individuals. This suggests the value of further genetic association analysis, at least for these measures. Also in current study, we only investigated typical global network measures, which are averages computed from local network measures. Future work will also assess local network measures.
ACKNOWLEDGMENTS
This work was supported in part by NIH Big Data to Knowledge (BD2K) Center of Excellence grant U54 EB020403, funded by a cross-NIH consortium including NIBIB and NCI.
REFERENCES
- 1.Leow A, et al. Impaired Inter-Hemispheric Integration in Bipolar Disorder Revealed with Brain Network Analyses. Biological Psychiatry. 2013;73(2):183–193. doi: 10.1016/j.biopsych.2012.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.GadElkarim J, et al. A Framework for Quantifying Node-Level Community Structure Group Differences in Brain Connectivity Networks. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012. 2012:196–203. doi: 10.1007/978-3-642-33418-4_25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arienzo D, et al. Abnormal brain network organization in body dysmorphic disorder. Neuropsychopharmacology. 2013;38(6):1130–1139. doi: 10.1038/npp.2013.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nir T, et al. Small World Network Measures Predict White Matter Degeneration in Patients with Early-Stage Mild Cognitive Impairment. Proc IEEE Int Symp Biomed Imaging. 2012:1405–1408. doi: 10.1109/ISBI.2012.6235831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jahanshad N, et al. Disrupted brain networks in the aging HIV+ population. Brain Connect. 2012;2(6):335–344. doi: 10.1089/brain.2012.0105-Rev. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mueller SG, et al. Ways toward an early diagnosis in Alzheimer's disease: the Alzheimer's Disease Neuroimaging Initiative (ADNI) Alzheimers Dement. 2005;1(1):55–66. doi: 10.1016/j.jalz.2005.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stein JL, et al. Identification of common variants associated with human hippocampal and intracranial volumes. Nat Genet. 2012;44(5):552–561. doi: 10.1038/ng.2250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jahanshad N, et al. Genome-wide scan of healthy human connectome discovers SPON1 gene variant influencing dementia severity. Proc Natl Acad Sci U S A. 2013;110(12):4768–4773. doi: 10.1073/pnas.1216206110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thompson PM, et al. Genetics of the connectome. Neuroimage. 2013;80:475–488. doi: 10.1016/j.neuroimage.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li Y, et al. Less efficient information transfer in Cys-allele carriers of DISC1: a brain network study based on diffusion MRI. Cereb Cortex. 2013;23(7):1715–1723. doi: 10.1093/cercor/bhs167. [DOI] [PubMed] [Google Scholar]
- 11.Basser PJ, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44(4):625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 12.Mori S, et al. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45(2):265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 13.Lazar M, et al. White matter tractography using diffusion tensor deflection. Hum Brain Mapp. 2003;18(4):306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Conturo TE, et al. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci U S A. 1999;96(18):10422–10427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Behrens TE, et al. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aganj I, et al. A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography. Med Image Anal. 2011;15(4):414–425. doi: 10.1016/j.media.2011.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parker GJ, Haroon HA, Wheeler-Kingshott CA. A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J Magn Reson Imaging. 2003;18(2):242–254. doi: 10.1002/jmri.10350. [DOI] [PubMed] [Google Scholar]
- 18.Zhan L, et al. Comparison of 9 Tractography Algorithms for Detecting Abnormal Structural Brain Networks in Alzheimer's Disease. Submitted to PLOS ONE. 2014 doi: 10.3389/fnagi.2015.00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wedeen VJ, et al. The geometric structure of the brain fiber pathways. Science. 2012;335(6076):1628–1634. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Aganj I, et al. Reconstruction of the orientation distribution function in single- and multiple-shell q-ball imaging within constant solid angle. Magn Reson Med. 2010;64(2):554–566. doi: 10.1002/mrm.22365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Desikan RS, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31(3):968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- 22.Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 23.Neale M, Baker S, Xie G, Maes H. Mx: Statistical modeling. (6th ed.) 2002 [Google Scholar]
- 24.McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychological Methods. 1996;1(1):30–46. [Google Scholar]