A SPARSE REDUCED RANK FRAMEWORK FOR GROUP ANALYSIS OF FUNCTIONAL NEUROIMAGING DATA

Abstract

In spatial-temporal neuroimaging studies, there is an evolving literature on the analysis of functional imaging data in order to learn the intrinsic functional connectivity patterns among different brain regions. However, there are only few efficient approaches for integrating functional connectivity pattern across subjects, while accounting for spatial-temporal functional variation across multiple groups of subjects. The objective of this paper is to develop a new sparse reduced rank (SRR) modeling framework for carrying out functional connectivity analysis across multiple groups of subjects in the frequency domain. Our new framework not only can extract both frequency and spatial factors across subjects, but also imposes sparse constraints on the frequency factors. It thus leads to the identification of important frequencies with high power spectra. In addition, we propose two novel adaptive criteria for automatic selection of sparsity level and model rank. Using simulated data, we demonstrate that SRR outperforms several existing methods. Finally, we apply SRR to detect group differences between controls and two subtypes of attention deficit hyperactivity disorder (ADHD) patients, through analyzing the ADHD-200 data.

1. Introduction

The predominant functional imaging techniques, such as functional magnetic resonance imaging (fMRI), electroencephalography (EEG), and magnetoencephalography (MEG), have been widely used in behavioral and cognitive neuroscience to understand functional segregation and integration of different brain regions in a single subject and across different populations (Friston (2009)). Such statistical methods as principal component analysis (PCA), general linear models (GLM), and independent component analysis (ICA), have been developed to extract both spatial and temporal patterns of interest from functional signals, and to understand how different brain regions interact with each other. For instance, ICA has been widely used in single-subject fMRI/EEG studies to separate spatially or temporally independent components (McKeown et al. (1998); Beckmann and Smith (2004)). However, the extension of these methods to group inference is not straightforward due to striking neuroanatomic variations, and thus it remains an active research topic (Calhoun, Liu, and Adalı (2009)). The aim of this paper is to develop a sparse reduced rank (SRR) spatial-temporal modeling framework in the frequency domain for group analysis of functional imaging data across multiple groups.

Two strategies are typically adopted in group ICA of neuroimaging data. The first strategy is to perform ICA for each subject separately, and then to combine the outputs across subjects through, for example, clustering analysis and correlation analysis (Calhoun et al. (2001a); Esposito et al (2005)). These methods are sensitive to different source separations obtained from different subjects, making it diffcult to establish good correspondence among independent components across subjects. The second strategy is to concatenate functional imaging data either temporally or spatially, and then perform ICA on the concatenated data matrix. For instance, temporal concatenation, namely spatial ICA, implicitly assumes that neural activation is observed at the same locations across all subjects (Calhoun et al. (2001b); Guo and Pagnoni (2008)), whereas spatial concatenation, namely temporal ICA, assumes subject-specific spatial maps with a common temporal basis (Svensén, Kruggel, and Benali (2002)).

To avoid the assumption of spatial correspondence, a possible solution is to extend temporal ICA by addressing two major limitations: temporal inconsistency and noise sensitivity. In the time domain, assuming a common temporal basis across subjects can be unreasonable for functional neuroimaging data due to the large temporal variability in response latency, especially for resting-state data. Hence, performing data analysis in the frequency domain can be a remedy to achieve temporal consistency. Calhoun et al. (2003) performed group spatial ICA in the frequency domain. However, as in the other ICA methods, PCA is needed to reduce the number of time points. There are two potential solutions to noise sensitivity. The first is to increase the temporal sampling rate and improve data quality (Smith (2012)); the second is to use some advanced mathematical and statistical methods, such as compressed sensing theory and regularization methods (Tibshirani (1996); Donoho, Elad, and Temlyakov (2006)). There are a few recent developments on the use of sparse dictionary learning algorithms for neuroimaging data in the time domain (Aharon, Elad, and Bruckstein (2006); Lee et al. (2011a); Lee, Tak, and Ye (2011); Varoquaux et al. (2011)).

The objective of the current paper is to develop a sparse reduced rank (SRR) modeling framework in the frequency domain, with several novel developments in order to carry out group functional imaging analysis and comparison across multiple groups. We view SRR as a combination of temporal ICA and sparse dictionary learning algorithms. Our new developments include i) a group modeling framework in the frequency domain, ii) detection of common frequency basis functions, iii) sparsity of the frequency basis functions, iv) novel data-driven procedures to select sparsity level and model rank, and v) varying spatial functions across groups for group comparison and integration.

Different from many other methods, our proposal aims at finding “optimal” low-rank approximations to the power spectrum matrices of the original imaging data from multiple groups. The low-rank approximation assumes a set of common frequency factors, along with the subject-specific spatial maps which then enable group comparison and data integration across groups. Our modeling framework also imposes sparsity on the frequency factors, which is a natural consideration given the particular characteristics of power spectra of temporal functions. We propose an efficient alternating algorithm for estimating the frequency basis and spatial factors. We develop two Bayesian information criteria (BIC) for sparsity and rank selection, while accounting for dependence among observations at each distinct frequency. Simulation studies are performed to illustrate the nice performance of our method from a wide range of perspectives. Due to space limitations, we present the simulation results in the supplementary material. Through an analysis of the New York University (NYU) sub-sample of the ADHD-200 data, we demonstrate that our method can detect meaningful functional connectivity patterns across two ADHD subtypes and typically developing children (TDC), varying significantly across groups at some specific regions of interest.

The rest of the paper is organized as follows. In Section 2, we formulate our SRR model, and derive the alternating estimation algorithm, along with detailed discussions about the modified BICs. We report the analysis of the ADHD-200 data in Section 3, and compare functional connectivity patterns across one control and two patient groups. We conclude the paper with some discussion in Section 4. In Section S1 of the supplementary material, we report on the simulation studies that compare SRR with several existing methods.

2. Methods

2.1. Model formulation

It is well-known that most of functional imaging data show significant fluctuations at certain range of frequencies. For example, resting-state fMRI data focus on spontaneous low frequency fluctuations below 0.1 Hz in the BOLD signal (Biswal et al. (1995)). In addition, EEG data have revealed oscillatory activity in specific frequency bands, including delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (13–30 Hz), and gamma (30–70 Hz). As shown in Figure 1, we transform the standardized time courses from brain images to the frequency domain, and use the power spectra rather than the raw time courses. One advantage is that the power spectra matrices are much sparser, since strong power is believed to distribute in a specific range (e.g., below 0.1 Hz) of frequencies.

Figure 1.

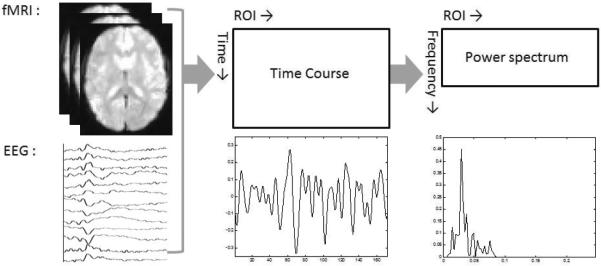
Illustration of data structures from time course measurements of brain activities to power spectra matrices.

Let T be the number of distinct frequencies and R be the number of regions (or voxels) of interest (ROI). Without loss of generality, we use ROI throughout the paper. We observe (or calculate) the T × R power spectra matrix ${\mathbf{Y}}_g^s$ of rank q = min(T, R) for each subject s of group g, where s = 1, …, N_g and g = 1, …, G. For example, the (i,j)th element of ${\mathbf{Y}}_g^s$ is the power spectrum of the jth ROI at the ith frequency for the sth subject of the gth group. Group g has N_g subjects, and the total number of subjects is $N={\sum }_{g=1}^G{N}_g$.

To integrate functional imaging data across subjects, we consider the following multi-group low-rank spatial-temporal model:

$${\mathbf{Y}}_g^s={\mathbf{UM}}_g^s+{\mathbf{E}}_g^s,$$ (2.1)

where U is the T × q frequency factor matrix common across groups, ${\mathbf{M}}_g^s$ is the corresponding q × R spatial factor matrix specific to each subject, and ${\mathbf{E}}_g^s$ is the subject-specific error matrix. A key assumption in Model (2.1) is that there is a set of common frequency basis functions for all subjects. This is a reasonable assumption for most functional neuroimaging studies. In fMRI studies, all subjects undergo the same set of experimental stimuli or conditions across time, and thus it is expected that frequency basis functions would be shared across subjects. For instance, Bai et al. (2008) have adopted the frequencies of stimuli used in the block design fMRI studies for their model formulation.

A schematic overview of our SRR framework is given in Figure 2. Using the data from multiple groups of subjects, SRR can extract the common frequency factors, while allowing the spatial factors to vary across subjects. We note that the common frequency factors do not mean that all subjects have the same dominating frequencies, but that we can use a common factor incorporating all the frequency information across subjects. Furthermore, Model (2.4) below enables follow-up hypothesis testing of spatial differences among groups.

Figure 2.

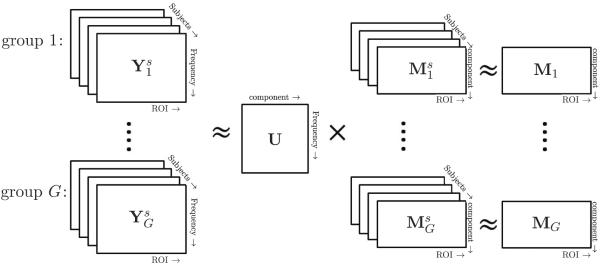
Illustration of the SRR model framework for incorporating multiple subjects across groups.

To estimate U and ${\mathbf{M}}_g^s$ in Model (2.1), we consider the squared loss function:

$$\sum _{g=1}^G\sum _{s=1}^{N_g}\Vert {\mathbf{Y}}_g^s-{\mathbf{UM}}_g^s{\Vert }_F^2\mathrm{s}.\mathrm{t}.{\mathbf{U}}^{\prime }\mathbf{U}=\mathbf{I},$$ (2.2)

where ∥ · ∥_F denotes the Frobenius norm. For model identifiability, we impose a set of orthogonality constraints on the frequency factors.

We further impose discontinuity and sparsity constraints on the frequency factors. It is common that the corresponding power spectra exhibit high-magnitude signals only in several dominating frequencies and nuisance noise elsewhere. To account for such characteristics in the frequency domain, we consider imposing sparsity on the frequency factor matrix which in turn leads to the identification of frequencies with large power spectra by shrinking small entries of U toward zero. One of the most popular approaches is to impose the L₁ (or lasso) penalty (Tibshirani (1996)). For model estimation, we thus consider minimizing the penalized loss function

$$\sum _{g=1}^G\sum _{s=1}^{N_g}\Vert {\mathbf{Y}}_g^s-{\mathbf{UM}}_g^s{\Vert }_F^2+\sum _{i=1}^q{\lambda }_i{\Vert {\mathbf{u}}_i\Vert }_1,$$ (2.3)

where ∥ · ∥₁ denotes the L₁ norm, u_i is the ith frequency factor, and λ_i ≥ 0 is the tuning parameter, to determine the degree of sparseness for u_i, which enables sparsity level to vary among factors.

After estimating ${\mathbf{M}}_g^s$, we can directly model ${\mathbf{M}}_g^s$ to make comparison and integration of functional imaging data across groups. For instance, if spatial correspondence is reasonable for a given data set, we can consider the spatial factor matrix as being group-specific:

$${\mathbf{M}}_g^s={\mathbf{M}}_g+{\mathbf{H}}_g^s,$$ (2.4)

where M_g represents the spatial factor matrix specific to the gth group and ${\mathbf{H}}_g^s$ is the corresponding error matrix assuming that vec($\text{vec}\left({\mathbf{H}}_g^s\right)$) have mean 0 and the qR × qR independent variance-covariance matrix.

Under Model (2.4), we can perform statistical tests of group differences, while preserving the inherent characteristics from each group. Furthermore, we can incorporate stimulus types or other individual characteristics, such as age or gender, to build a linear model as follows:

$${\left(\text{vec}\left({\mathbf{M}}_1^1\right),\dots ,\text{vec}\left({\mathbf{M}}_G^{N_G}\right)\right)}^{\prime }=\mathbf{XB}+{\left(\text{vec}\left({\mathbf{H}}_1^1\right),\dots ,\text{vec}\left({\mathbf{H}}_G^{N_G}\right)\right)}^{\prime },$$

where ${\left(\text{vec}\right({\mathbf{M}}_1^1),\dots ,\text{vec}({\mathbf{M}}_G^{N_G}\left)\right)}^{\prime }$ is an N × qR matrix, X is an N × p design matrix with p the number of covariates, B = (vec(B₁), ⋯, vec(B_p))′ is a p × qR coefficient matrix with B_k the q × R coefficient matrix for the kth covariate, and the error ${\left(\text{vec}\right({\mathbf{H}}_1^1),\dots ,\text{vec}({\mathbf{H}}_G^{N_G}\left)\right)}^{\prime }$ is an N × qR matrix.

2.2. Model estimation

The high-dimensionality of the problem makes it challenging to directly minimize the objective function in (2.3). To begin with, we horizontally concatenate the matrices ${\mathbf{Y}}_g^s$ and ${\mathbf{M}}_g^s$, respectively, for all subjects and denote the resulting matrices as Y and M. The concatenated matrix Y can be written by

$$\mathbf{Y}=({\mathbf{Y}}_1^1,{\mathbf{Y}}_1^2,\dots ,{\mathbf{Y}}_G^{N_G})\sum _{g=1}^G\sum _{s=1}^{N_g}{\mathbf{J}}_g^s\otimes {\mathbf{Y}}_g^s,$$

where ⊗ is the Kronecker product and ${\mathbf{J}}_g^s$ is a 1 × N vector of zeros, with the exception that the ($({\sum }_{i=0}^{g-1}{N}_i+s)$)-th element is 1, where N₀ = 0. Note that ${\sum }_{i=0}^{g-1}{N}_i+s$ corresponds to the location of the subject s within the group g when the N subjects are first ordered according to group and then within each group.

Similarly, we have $\mathbf{M}=({\mathbf{M}}_1^1,{\mathbf{M}}_1^2,\dots ,{\mathbf{M}}_G^{N_G})={\sum }_{g=1}^G{\sum }_{s=1}^{N_g}{\mathbf{J}}_g^s\otimes {\mathbf{M}}_g^s$. Instead of simultaneously minimizing the loss function (2.3) with respect to U and M, we describe below an iterative estimation algorithm that alternates the optimization with respect to U and M, while performing data-driven selection of the tuning parameters λ_i's as well as the underlying rank r.

2.2.1. Initial estimation

To initialize, we minimize the un-penalized loss function (2.2) that can be rewritten as

$$\Vert \mathbf{Y}-\mathbf{UM}{\Vert }_F^2\mathrm{s}.\mathrm{t}.{\mathbf{U}}^{\prime }\mathbf{U}=\mathbf{I},$$ (2.5)

where Y is the T × RN matrix and M is the q × RN matrix. Assuming that U is given, the minimizer is $\widehat{\mathbf{M}}={\mathbf{U}}^{\prime }\mathbf{Y}$ obtained by taking the derivative of (2.5) with respect to M. Plugging this into (2.5), we have

$$\underset{\mathbf{U}}{\min }\Vert \mathbf{Y}-U\widehat{M}{\Vert }_F^2=\underset{\mathbf{U}}{\min }\Vert \mathbf{Y}-{\mathbf{UU}}^{\prime }\mathbf{Y}{\Vert }_F^2=\underset{\mathbf{U}}{\max }\mathrm{tr}\left({\mathbf{U}}^{\prime }{\mathbf{YY}}^{\prime }\mathbf{U}\right),$$

where tr(A) denotes the trace of the matrix A. It suggests that the minimization of (2.5) with respect to U is equivalent to finding

$$\widehat{U}=\underset{\mathbf{U}}{\mathrm{argmax}}\mathrm{tr}\left({\mathbf{U}}^{\prime }{\mathbf{YY}}^{\prime }\mathbf{U}\right)\mathrm{s}.\mathrm{t}.{\mathbf{U}}^{\prime }\mathbf{U}=\mathbf{I}.$$ (2.6)

As shown in Jolliffe (2002, Chap. 2), the solution $\widehat{\mathbf{U}}$ in (2.6) is given by the first q eigenvectors of YY′. It then follows that $\widehat{\mathbf{M}}={\widehat{\mathbf{U}}}^{\prime }\mathbf{Y}$. We refer to $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{M}}$ as the initial estimators.

2.2.2. Sparse Estimation for U and M

We can further express (2.3) in a concatenated form as

$$\Vert \mathbf{Y}-\mathbf{UM}{\Vert }_F^2+\sum _{i=1}^q{\lambda }_i{\Vert {\mathbf{u}}_i\Vert }_1,\mathrm{s}.\mathrm{t}.{\mathbf{u}}_i\ge 0,i=1,\dots ,q.$$ (2.7)

We first present how to solve the above optimization problem without the non-negative constraints on the factors u_i then discuss ways of incorporating those constraints.

Given M, the optimization of (2.7) with respect to U is essentially a quadratic programming problem. However, direct minimization is computationally intensive given a large number of ROIs in neuroimaging data. We can rewrite (2.7) as a form of linear regression model: $\mid \mid \mathbf{y}-\mathbf{X}\beta \mid {\mid }_2^2+{\sum }_{i=1}^q{\lambda }_i\mid \mid {\beta }_i\mid {\mid }_1$, where y = vec(Y) is a TRN × 1 vector, X = M′ ⊗ I_T is a TRN × T² matrix, and β = (vec(u₁)′,…, vec(u_q)′)′ is a T² × 1 vector. For the ADHD-200 sample with R = 954, T = 24, and N = 178 in Section 3, the design matrix X has dimension 4, 075, 488 × 576, which requires a large amount of memory and tedious computation time. Therefore, we propose to sequentially estimate each component of U and M. The sequential extraction also makes it feasible to incorporate factor-specific sparsity through selecting a factor-specific tuning parameter. Simultaneous data-driven selection of multiple tuning parameters is computationally too costly.

For sequential estimation, we first express UM as the sum of q rank-one matrices given by $\mathbf{UM}={\sum }_{i=1}^q{\mathbf{u}}_i{\mathbf{m}}_i$, where u_i is the ith column vector of U and m_i is the ith row vector of M.

For the first rank-one term (i = 1), we consider minimizing

$$\Vert \mathbf{Y}-{\mathbf{u}}_1{\mathbf{m}}_1{\Vert }_F^2+{\lambda }_1{\Vert {\mathbf{u}}_1\Vert }_1.$$ (2.8)

Given the initial estimate ${\widehat{\mathbf{m}}}_1$ obtained in the initialization step, we estimate u₁ by minimizing

$$\Vert \mathbf{Y}-{\mathbf{u}}_1{\widehat{m}}_1{\Vert }_F^2+{\lambda }_1{\Vert {\mathbf{u}}_1\Vert }_1.$$ (2.9)

It can be shown that the minimizer ${\tilde{\mathbf{u}}}_1$ of (2.9) has the explicit form

$${\tilde{u}}_{j1}=\text{sgn}\left({\widehat{u}}_{j1}^{\mathit{OLS}}\right){\left(\mid {\widehat{u}}_{j1}^{\mathit{OLS}}\mid -\frac{{\lambda }_1}{2\Vert {\widehat{m}}_1{\Vert }_2^2}\right)}_{+}\text{for}j=1,\dots ,T.$$ (2.10)

Here sgn(·) is the sign function, the subscript “+” indicates the nonnegative part, and ${\widehat{u}}_{j1}^{\mathit{OLS}}=<{\mathbf{y}}_j,{\widehat{\mathbf{m}}}_1>∕\mid \mid {\widehat{\mathbf{m}}}_1\mid {\mid }_2^2$ is the ordinary least squares (OLS) estimate of u_j1 when setting λ₁ = 0 in (2.9), with < ·, · > denoting the inner product between two vectors, and y_j being the jth row of the matrix Y. The proof is given in Section S2 of the supplementary material.

Given the sparse estimate ${\tilde{\mathbf{u}}}_1$, m₁ can be updated by minimizing

$$\Vert \mathbf{Y}-{\tilde{\mathbf{u}}}_1{\mathbf{m}}_1{\Vert }_F^2,$$

which yields ${\tilde{\mathbf{m}}}_1={\left({\tilde{\mathbf{u}}}_1^{\prime }{\tilde{\mathbf{u}}}_1\right)}^{-1}{\tilde{\mathbf{u}}}_1^{\prime }\mathbf{Y}$. After estimating the first rank-one term as ${\tilde{\mathbf{u}}}_1{\tilde{\mathbf{m}}}_1$, we consider the residual matrix ${\mathbf{K}}_2=\mathbf{Y}-{\tilde{\mathbf{u}}}_1{\tilde{\mathbf{m}}}_1$. To find the second rank-one term, we modify the optimization criterion in (2.8) with

$$\Vert {\mathbf{K}}_2-{\mathbf{u}}_2{\mathbf{m}}_2{\Vert }_F^2+{\lambda }_2\Vert {\mathbf{u}}_2{\Vert }_1,$$

which can be minimized with respect to u₂ and m₂ in a similar alternating way. The rest of the rank-one terms, u_im_i, i = 3, …, q, can be obtained sequentially in a similar manner by using the residual matrices from the lower-rank approximations, denoted as ${\mathbf{K}}_i=\mathbf{Y}-{\sum }_{j=1}^{i-1}{\tilde{\mathbf{u}}}_j{\tilde{\mathbf{m}}}_j$, with K₁ = Y.

Thus, given the initial estimate ${\widehat{\mathbf{m}}}_i$, the minimization criterion for estimating u_i can be written as

$$\Vert {\mathbf{K}}_i-{\mathbf{u}}_i{\widehat{\mathbf{m}}}_i{\Vert }_F^2+{\lambda }_i\Vert {\mathbf{u}}_i{\Vert }_1\text{for}i=1,\dots ,q.$$ (2.11)

Setting λ_i = 0, the OLS estimator for u_i can be obtained as

$${\widehat{u}}_{ji}^{\mathit{OLS}}=\frac{<{\mathbf{k}}_{i,j},{\widehat{\mathbf{m}}}_i>}{\Vert {\widehat{\mathbf{m}}}_i{\Vert }_2^2},$$ (2.12)

where k_i,j is the jth row vector of the matrix K_i. Then the minimizer of (2.11) with respect to u_i can be explicitly given as

$${\tilde{u}}_{ji}=\text{sgn}\left({\widehat{u}}_{ji}^{\mathit{OLS}}\right){\left(\mid {\widehat{u}}_{ji}^{\mathit{OLS}}\mid -\frac{{\lambda }_i}{2\Vert {\widehat{\mathbf{m}}}_i{\Vert }_2^2}\right)}_{+}\text{for}j=1,\dots ,T.$$ (2.13)

The proof is given in Section S2 of the supplementary material.

Given the updated estimate ${\tilde{\mathbf{u}}}_i$, we minimize the objective function

$$\Vert {\mathbf{K}}_i-{\tilde{\mathbf{u}}}_i{\mathbf{m}}_i{\Vert }_F^2,$$ (2.14)

whose minimizer is ${\tilde{\mathbf{m}}}_i={\left({\tilde{\mathbf{u}}}_i^{\prime }{\tilde{\mathbf{u}}}_i\right)}^{-1}{\tilde{\mathbf{u}}}_i^{\prime }{\mathbf{K}}_i$. If ${\tilde{\mathbf{u}}}_i$ is a zero vector, we also set ${\tilde{\mathbf{m}}}_i$ to be a zero vector.

Finally, we comment that the estimated frequency basis functions ${\tilde{\mathbf{u}}}_i$ might be negative. Even though the proposed method has an explicit solution which reveals the dominating frequencies quite well, we can consider another approach that implicitly imposes the non-negativity constraints when estimating the frequency basis functions, in addition to the orthogonality or sparsity constraints. Each optimization can be solved via multiplicative iterative algorithm or alternating least squares algorithm for a semi-nonnegative matrix factorization problem (Cichocki et al. (2009)). However, such method is computationally extensive since the two estimation steps need to be iteratively updated. We leave this approach for future research.

2.2.3. Data-driven parameter selection

Our estimation algorithm involves a set of tuning parameters that needs to be selected in a data-driven fashion, including the sparsity tuning parameters λ_i, i = 1, …, q, and the model rank r. For tuning parameter selection, many criteria have been proposed and studied in the literature, such as the Akaike information criterion (Akaike (1973)), Bayesian information criterion (BIC) (Schwarz (1978)), and (generalized) cross-validation (Craven and Wahba (1979)). In linear model settings, it is well-known that BIC gives consistent model selection. We propose two BIC-type criteria for selecting the tuning parameters in our algorithm and illustrate the nice performance of the criteria in Section S1 of the supplementary material.

Following Lee et al. (2010), we are tempted to use a natural BIC for selecting the sparsity tuning parameter λ_i,

$$\frac{\Vert {\mathbf{K}}_i-{\tilde{\mathbf{u}}}_i{\widehat{\mathbf{m}}}_i{\Vert }_F^2}{\Vert {\mathbf{K}}_i-{\widehat{\mathbf{u}}}_i^{\mathit{OLS}}{\widehat{\mathbf{m}}}_i{\Vert }_F^2}+\frac{\log \left(\mathit{NTR}\right)}{\mathit{NTR}}\times df\text{for}i=1,\dots ,q,$$ (2.15)

where df is the number of nonzero elements in ${\tilde{\mathbf{u}}}_i$. However, this naive criterion failed to generate reasonable models in our study. For a large number of ROIs, this BIC imposes very small penalties on bigger models, and hence has the tendency to select the full model. Such a problem is caused by the intrinsic dependence in our data, suggesting that the effective sample size should be smaller than NTR used in the naive BIC (2.15).

To adjust for the dependence, we treat each frequency as a cluster because different frequencies illustrate different variabilities, and define the intra-cluster correlation coefficient (Killip, Mahfoud, and Pearce (2004); Faes et al. (2009)) as $\rho =V_b^2∕(V_b^2+V_w^2)$, where $V_b^2$ is the between-cluster variability and $V_w^2$ is the within-cluster variability. The setup is analogous to one-way analysis of variance (ANOVA), in which each frequency corresponds to one level of the factor, and the response variable is Y. We can then estimate the between-frequency and within-frequency variabilities using ANOVA. It follows that the effective sample size is

$$N_E=\frac{\mathit{NTR}}{1+\rho (NR-1)}.$$ (2.16)

If ρ = 0, the effective sample size remains NTR. As ρ increases, the effective sample size becomes closer and closer to T , the number of frequencies (i.e. clusters). Using the effective sample size, we revise the naive BIC as

$${\text{BIC}}_S\left({\lambda }_i\right)\frac{\Vert {\mathbf{K}}_i-{\tilde{\mathbf{u}}}_i{\widehat{\mathbf{m}}}_i{\Vert }_F^2}{\Vert {\mathbf{K}}_i-{\widehat{\mathbf{u}}}_i^{\mathit{OLS}}{\widehat{\mathbf{m}}}_i{\Vert }_F^2}+\frac{\log \left(N_E\right)}{N_E}\times d{f}_S,$$ (2.17)

where the subscript S indicates that this BIC is used for selecting the sparsity tuning parameter. For each component i = 1, …, q, we choose the optimal value of λ_i at which the minimum BIC_S is achieved.

Given the final estimates $\tilde{\mathbf{U}}$ and $\tilde{\mathbf{M}}$, we choose the “optimal” rank using the following BIC-type statistic. For r = 1, …, q,

$${\text{BIC}}_R\left(r\right)=\frac{\Vert \mathbf{Y}-\sum _{j=1}^r{\tilde{\mathbf{u}}}_j{\tilde{\mathbf{m}}}_j{\Vert }_F^2}{\Vert \mathbf{Y}-\sum _{j=1}^q{\tilde{\mathbf{u}}}_j{\tilde{\mathbf{m}}}_j{\Vert }_F^2}+\frac{\log \left(N_E\right)}{N_E}\times d{f}_R,$$ (2.18)

where df_R is the effective number of parameters in the rank-r approximation ${\sum }_{j=1}^r{\tilde{\mathbf{u}}}_j{\tilde{\mathbf{m}}}_j$. Under the independence assumption, the degrees of freedom in (2.18) should be (T + NR) × r for the rank-r model. Given the above discussion of intra-cluster-dependence, we adjust NR to NR/(1 + ρ(NR − 1)), where ρ is obtained from the ANOVA model with the response variable ${\sum }_{j=1}^r{\tilde{\mathbf{u}}}_j{\tilde{\mathbf{m}}}_j$. It then suggests that the effective degrees of freedom should be

$$d{f}_R=\left(T+\frac{N_E}{T}\right)\times r\text{for rank}r.$$

Algorithm 1 summarizes the key steps of the estimation procedure derived. We note that the resulting estimate $\tilde{\mathbf{U}}$ might not be orthogonal. Adding the

Algorithm 1 Estimation for U and M

Step 1: Initial Estimation for U and M

Minimize the un-penalized loss function in (2.5) to obtain the initial estimates $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{M}}$;

Step 2: Sparse Estimation for U and M:

For i = 1, …, q,

For each λi, obtain ${\tilde{\mathbf{u}}}_i$ by minimizing (2.11);

Then, select the optimal ${\widehat{\lambda }}_i$ that minimizes BICS(λi) in (2.17);

Given ${\tilde{\mathbf{u}}}_i$, obtain ${\tilde{\mathbf{m}}}_i$ by minimizing (2.14);

Step 3: Rank Determination:

For r = 1, …, q, compute BICR(r) in (2.18);

Then, choose the optimal rank $\widehat{r}$ that minimizes BICR(r);

Obtain the estimates $\tilde{\mathbf{U}}$ and $\tilde{\mathbf{M}}$ for the rank-$\widehat{r}$ model.

orthogonalization after Step 2 could make $\tilde{\mathbf{U}}$ lose sparsity. Even though we do not enforce orthogonality, our estimate is quite close to orthogonal in that ${\tilde{\mathbf{U}}}^{\prime }\tilde{\mathbf{U}}$ is close to an identity matrix and the off-diagonal elements are almost zero, based on our experience.

3. Application to the ADHD-200 Data

3.1. Data acquisition and preprocessing

We used the resting-state fMRI data from the ADHD-200 sample which is available from http://fcon_1000.projects.nitrc.org/indi/adhd200. The data were collected from eight sites of the ADHD-200 consortium. In this study, we only analyzed the data from NYU with the largest number of subjects. At NYU, a Siemens Allegra 3T scanner was used to acquire the 6-min resting-state fMRI scans. The scan parameters are the following: voxel size = 3 × 3 × 4 mm, slice thickness = 4 mm, number of slices=33, TR (repetition time) = 2 s, TE (echo time) = 15 ms, flip angle = 90°, and field of view = 240 mm. One or two resting-state fMRI scans were acquired for each subject in the NYU data. During acquisition, each subject was asked to be awake and not to think about anything under a black screen.

Table 1 shows the demographic information for the NYU sample. We excluded the ADHD hyperactive/impulsive subtype group which only has two subjects. Based on the quality control (QC) performance given in the phenotypic data, we deleted the scans showing artifacts and then chose one of the scans for each subject. If no scans passed QC, we removed the subject from our study. We also excluded subjects with the same values at all time points. In Table 1, the last column shows the number of subjects for each group used in our study.

Table 1.

Demographic information for the NYU sample of the ADHD-200 data. The number of females, males, and subjects with gender missing data are given in parentheses.

Diagnostic status	Frequency (female/male/missing)	Mean age (min/max)	No. used of subjects in our study
TDC	99 (52/47/0)	12.2 (7.2/18.0)	86 (44/42/0)
ADHD combined	77 (12/64/1)	10.7 (7.2/17.4)	61 (10/50/1)
ADHD hyperactive/impulsive	2 (0/2/0)	10.6 (9.2/11.9)	-
ADHD inattentive	44 (15/29/0)	12.0 (7.4/17.6)	31 (13/18/0)
Total	222 (79/142/1)	11.6 (7.2/18.0)	178 (67/110/1)

The ADHD-200 sample provides various types of time course data that were extracted using different atlases and pipelines. Among them, we used the `1,000 ROI extracted time courses' that were preprocessed by the Neuroimaging Analysis Kit (NIAK) (Lavoie-Courchesne et al. (2012)). To check the existence of frequency coherence, we examined the ROIs consisting of 30+ voxels, and computed the Moran's I statistic and its Z-score. Averaged across all subjects, 99.2% of ROIs had the Z-scores greater than 1.96, indicating that there exist frequency coherence within each ROI. Before analyzing the data, we standardized the time course data in order to have zero mean and unit variance. A band-pass filter is usually applied during preprocessing to eliminate some frequencies that are assumed to have nuisance noise, such as slow drift or physiological effects. Even though the NIAK applied a high-pass filter at 0.01 Hz to correct slow time drifts, some data still exhibit high power spectra below 0.01 Hz. Therefore, we additionally applied a band-pass Fourier filter (0.009–0.08 Hz) which is used in the Athena pipeline to remove frequencies not related to resting-state brain activity. We then focused on this frequency band, and thereby the number of distinct frequencies within this range is 24. Using the filtered data, we computed the power spectra matrices to be used for finding the group differences.

3.2. Results

Figure S8 in the supplementary material shows the BIC_R curve for selecting the model rank $\widehat{r}$. Note that the full rank is 24, the number of frequencies within the filtered frequency band. The minimum of BIC_R was achieved at $\widehat{r}=14$. For applying SRR, we thus used the first 14 components instead of the whole 24 components.

Figure S9 in the supplementary material displays the estimated U matrices as heat maps. The left panel displays the initial $\widehat{\mathbf{U}}$ matrix obtained from Step 1. The first column of each matrix tends to represent the average over all the frequencies. The first few elements at low frequencies are large and the rest are close to zero. We expect that the small noisy elements will be shrunken toward zero or become zero after penalization in Step 2. The right panel presents the sparse $\tilde{\mathbf{U}}$ matrix obtained from Step 2. As expected, only a few large elements remain and the rest are estimated to be zero after penalization. The red square shows the final $\tilde{\mathbf{U}}$ matrices after rank selection by BIC_R.

From Model (2.4), we tested whether there exist group differences in any specific ROI. We state a null hypothesis to test whether at least one group is different from the others. Specifically, for each i and j, we have

$$H_0:{\mathbf{M}}_1(i,j)={\mathbf{M}}_2(i,j)=\cdots ={\mathbf{M}}_G(i,j),$$ (3.1)

where M_g(i, j) is the (i, j)th element of M_g. To test this hypothesis, we considered a conditional inference procedure assuming ${\widehat{\mathbf{M}}}_g^s$ fixed, and then carried out an F-test under a linear regression setting. Unfortunately, we found no group differences in any ROIs under the significance level of 0.10 after the false discovery rate (FDR) correction (Benjamini and Hochberg (1995)). We also applied FastICA and K-SVD, which found no significant difference either.

Next we tested group differences between a pair of two groups. For groups g₁ and g₂, the null hypothesis is

$$H_0:{\mathbf{M}}_{g1}(i,j)={\mathbf{M}}_{g2}(i,j)\text{fot the}i\text{th component and the}j\text{th ROI}.$$ (3.2)

For each of the three pairwise comparisons, Table 2 lists the ROIs detected as significantly different between the groups, providing FDR-corrected p-values less than 0.10. Most of the ROIs were located in the frontal and temporal lobes. These findings are displayed in Figure S10 of the supplementary material, where – log₁₀(p-values) are superimposed on a brain anatomical image.

Table 2.

Comparison of spatial maps between two groups. The p-values are adjusted by FDR correction.

	Component	ROI ID (regions)	p-value
TDC vs ADHD combined	13	221 (R Transverse TG, Insula, Post- & Precentral G)	0.0906
	13	726 (R Superior TG, Insula, Transverse TG)	0.0906
	14	775 (L Middle TG)	0.0727
TDC vs ADHD inattentive	2	847 (R Tuber, Culmen, Fusiform G)	0.0050
	3	215 (L Insula)	0.0530
	12	116 (R Middle and Superior FG)	0.0706
	12	598 (L Inferior Parietal Lobule)	0.0319
ADHD combined vs ADHD inattentive	3	231 (L Medial FG)	0.0779
	3	257 (L Medial FG, Cingulate Gyrus)	0.0627
	3	300 (R Insula)	0.0627
	3	626 (R Postcentral G)	0.0779
	7	203 (R Middle and Inferior FG)	0.0789

L: left, R: right, G: gyrus, TG: temporal gyrus, FG: frontal gyrus

The top panel plots the ROIs showing the differences between TDC and ADHD combined subtype groups. The significant ROIs are included in the temporal lobe, right parietal lobe, right frontal lobe (precentral gyrus), and right insula. In the middle panel, we compared TDC with ADHD inattentive subtype group. We found significantly different activation in the left insula, right cerebellum, right temporal, right frontal and left parietal lobes. In the bottom panel, we compared two ADHD subtype groups and found different activations in the left and right frontal lobes, left limbic and right parietal lobes, and right insula.

The significant ROIs identified are consistent with existing clinical findings of ADHD patients. Both resting-state and task-based fMRI studies have been used for investigating brain activation patterns in ADHD patients (Teicher et al. (2000); Tian et al. (2008)). It is well known that the prefrontal cortex is an important brain region in ADHD studies. Moreover, it has been recently reported that ADHD patients show different activation pattern in the temporal lobe (Cherkasova and Hechtman (2009)). The temporal lobe is mainly associated with language and verbal memory. The cerebellum has been known to be responsible for motor control and cognitive functions. There are several papers which reported dysfunction in the cerebellum for ADHD patients (Toplak, Dockstader, and Tannock (2006)). In addition, the parietal lobe is related to attention, memory, and cognitive process. Different brain activations in the parietal lobe for ADHD patients have been reported in the literature (Tamm, Menon, and Reiss (2006)). Interestingly, functional relationship between the insula and cingulate gyrus has received a lot of attention in the literature (Taylor, Seminowicz, and Davis (2009); Medford and Critchley (2010)). The insula plays a role in consciousness related to emotions as well as perception, motor control, and self-awareness. The dysfunction in the insula has been observed in ADHD patients across a variety of task-related studies such as timing and error processing (Spinelli et al. (2011)). The cingulate gyrus is mainly associated with cognitive process that is linked to the signs of ADHD. There is growing evidence that suggests the anterior cingulate cortex dysfunctions in ADHD patients (Bush, Valera, and Seidman (2005)).

We present the boxplots to depict the groups showing different power spectra with the others in Figure S11 of the supplementary material. For each pair of groups, we display the boxplots of ${\tilde{\mathbf{u}}}_i{\tilde{\mathbf{m}}}_{ij}^{g,s}$ for the ith frequency component and the jth ROI, where significant group difference is detected, as shown in Table 2 and Figure S10 in the supplementary material. Due to sparsity on the $\tilde{\mathbf{U}}$, the ith frequency component has nonzero values at a few distinct frequencies. Therefore, ${\tilde{\mathbf{u}}}_i{\tilde{\mathbf{m}}}_{ij}^{g,s}$ has the same number of nonzero components. For simplicity, we only consider the frequency corresponding to the largest absolute value of ${\tilde{\mathbf{u}}}_i$. The corresponding frequencies are shown on the x-axis of each plot. Within each panel, the horizontal line is drawn at zero. These boxplots help us to interpret the results from our analysis. For example, on the top-left panel we can see that the ADHD combined subtype group shows higher power spectra than the control group at f = 0.043 in the 221st ROI (right transverse temporal gyrus, insula, postcentral and precentral gyri); on the other hand, the top-right panel shows that the ADHD combined subtype group has lower power spectra than the control group at f = 0.046 in the 775th ROI (left middle temporal gyrus).

For the purpose of comparison, we also analyzed the data using K-SVD and FastICA. (Note that GIFT cannot be used for ROI analysis.) First of all, both methods yielded very unstable results even for the same dataset. Therefore, we repeated the analysis 10 times for each method, and then examined the ROIs found to be significant in all repetitions. Since both methods assume a given model rank, we considered $\widehat{\mathbf{r}}=14$ as suggested by BIC_R. We tested the group difference by using the simultaneous test in (3.1) and pairwise tests in (3.2). As a result, both methods failed to find any significant difference.

4. Discussion

We have presented a novel sparse reduced rank modeling framework for group analysis of functional imaging data in the frequency domain. The key assumption of SRR is that the power spectra matrix of functional imaging data can be well approximated by a sparse representation of a set of common frequency factors. We have proposed a sequential penalization approach to learn the common frequency factors and the spatial factor matrix. Our method does not suffer from lack of memory or heavy computation even for a large number of ROIs. For testing the computation time of SRR algorithm, we have run the voxel-level whole brain images of ADHD-200 data with 48,472 voxels, and compared it with the ROI-based data used in Section 3. The computation times for the ROI- and voxel-based data were 51 seconds (0.01 hours) and 5113 seconds (1.42 hours), respectively. Considering a large number of subjects, it seems to run reasonably fast.

We have also proposed two novel BIC-type selection criteria for choosing the tuning parameters and for selecting the best model rank. We have demonstrated the promising performance of SRR using both the simulated data and ADHD-200 sample. In data application, we have performed F-tests based on the estimated spatial factors for group comparisons, and found significant group differences in some brain regions, such as the prefrontal cortex, temporal cortex, and cerebellum. These findings are consistent with existing clinical findings of ADHD studies.

The SRR framework in the frequency domain can be suitable for analyzing the resting-state neuroimaging data, as considered in this paper. However, it still has potential applicability for other fMRI studies with specific experimental designs. Bai et al. (2008) have applied the frequencies of stimuli used in the block design fMRI studies to the SVD model framework. In case of event-related design, it might be inappropriate to apply the frequency domain analysis. However, it would be possible to consider time domain analysis with smoothing penalty as a modified version of the SRR algorithm. We leave this extension for future research.