LIVER WHOLE SLIDE IMAGE ANALYSIS FOR 3D VESSEL RECONSTRUCTION

Abstract

The emergence of digital pathology has enabled numerous quantitative analyses of histopathology structures. However, most pathology image analyses are limited to two-dimensional datasets, resulting in substantial information loss and incomplete interpretation. To address this, we have developed a complete framework for three-dimensional whole slide image analysis and demonstrated its efficacy on 3D vessel structure analysis with liver tissue sections. The proposed workflow includes components on image registration, vessel segmentation, vessel cross-section association, object interpolation, and volumetric rendering. For 3D vessel reconstruction, a cost function is formulated based on shape descriptors, spatial similarity and trajectory smoothness by taking into account four vessel association scenarios. An efficient entropy-based Relaxed Integer Programming (eRIP) method is proposed to identify the optimal inter-frame vessel associations. The reconstructed 3D vessels are both quantitatively and qualitatively validated. Evaluation results demonstrate high efficiency and accuracy of the proposed method, suggesting its promise to support further 3D vessel analysis with whole slide images.

1. INTRODUCTION

Whole slide images scanned from high resolution digital scanners provide rich information about morphological and functional characteristics of biological systems. As a result, such image modality provides insights on the underlying mechanisms of disease onset and progression. Although numerous image analysis methods have been proposed to analyze microscopy images [1, 2], they mainly focus on 2D biological structure analysis with substantial information loss. This presents challenges to such applications involving 3D modeling and analysis. In liver disease diagnosis, for instance, 3D structural changes in liver vessels and their 3D spatial relationships are essential for better understanding disease pathological evolution and progression [3]. A large set of approaches on vessel structure analysis have been proposed, ranging from vessel segmentation [4], structure tracking [5], to 3D vasculature visualization [6]. However, these methods are developed for radiology image analysis. Applying them to whole slide images directly is not feasible, as pathology images have much higher resolutions and phenotypic variations.

In this paper, we present an automated framework for 3D vessel reconstruction with whole slide images of liver tissue sections. Due to the overwhelming number of vessels and large variations in vessel shapes, it is challenging to associate vessel cross-sections from different image slides in a biologically meaningful way. To address this, we formulate a cost function based on shape descriptors, spatial similarity and trajectory smoothness by taking into account four vessel association scenarios. Optimal vessel associations are achieved when the aggregated cost function is minimized by an entropy-based Relaxed Integer Programming (eRIP) algorithm that is efficient to converge to the global optimal solution. The proposed 3D vessel analysis framework is generic and can be readily applied to studies using other organ tissues.

2. METHODS

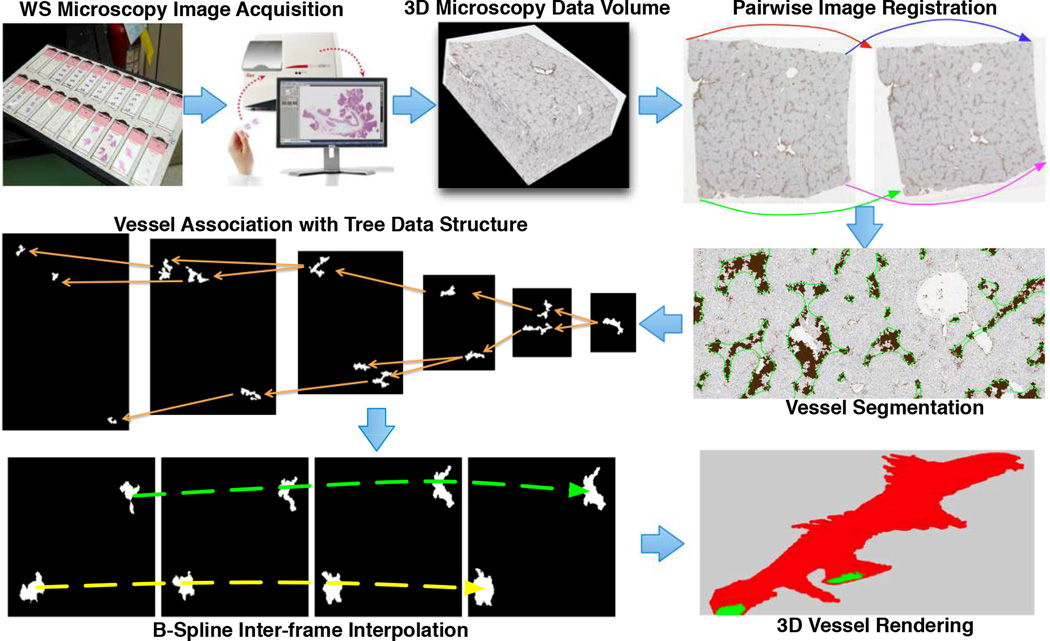
We illustrate in Figure 1 the overall working schema: image acquisition, registration, segmentation, vessel cross-section association, interpolation, and volumetric rendering. Our dataset includes 12 whole slide images of liver tissue sections [3] from the University of Leeds. Tissue sections are stained with dual chromogen Immunohistochemistry (IHC). Each whole-slide image has a typical resolution of 75k × 65k pixels, with the physical resolution 2.508e-1µm per pixel at the base level. Inter-slide physical resolution is 50 µm. We analyze images down-sampled from the base level by 64:1.

Fig. 1.

The overall workflow of 3D vessel analysis with whole slide imaging data.

2.1. Image registration

In order to accurately reconstruct and characterize vessels in 3D space, we first register sequential microscopy images into the same reference space. The registration process consists of rigid and non-rigid steps. For rigid registration, the scale, 2D rotation matrix, and translation vector are computed by phase correlation in a log polar coordinate system [3]. For non-rigid registration, the whole image is partitioned into a set of evenly spaced blocks that are aligned separately with a rigid block matching approach. A cubic B-Spline transformation [7] is estimated by a regularized least squared difference minimizing method [3] to approximate a set of point translations derived from the rigid block registration. In aggregate, non-rigid spatial changes at 8 × 8 = 64 knots are computed. This non-rigid transform is applied to the rigidly transformed image to compensate for the non-rigid residual. Given these 64 pairs of displacements {k(x(i),y(j)) = (k_x(x(i),y(j)),k_y(x(i),y(j))), i, j = 1,2, …,8} at locations of {(x(i),y(j))}, the non-rigid displacement at a given location (p,q) can be computed as $dx(p,q)=P^{T}S{K}_x^{(p,q)}{S}^{T}Q,dy(p,q)=P^{T}S{K}_y^{(p,q)}{S}^{T}Q$, where P = (p³ p² p 1)^T, Q = (q³ q² q 1)^T; S is a predefined 4 × 4 constant matrix [7].

For a given point (p,q), we construct two 4 × 4 matrices $K_x^{(p,q)}$ and $K_y^{(p,q)}$ where $K_x^{(p,q)}(m,n)=k_x(x(i^{*}-1+m),y(j^{*}-1+n)),K_y^{(p,q)}(m,n)=k_y(x(i^{*}-1+m),y(j^{*}-1+n)),m,n=\{1,2,3,4\}$, such that x(m = i*) < p ≤ x(m = i* + 1),y(n = j*) < q ≤ y(n = j* + 1).

The final displacement at location (p,q) is the summation of rigid and non-rigid displacement. Our results show the median and maximum absolute displacements in x-y pairs are (10.40,9.58) and (139.58,103.66) in pixels. We demonstrate the registration mappings of 12 images with deformed grids in Figure 2.

Fig. 2.

Registration results demonstrated by deformed grids.

2.2. Image segmentation

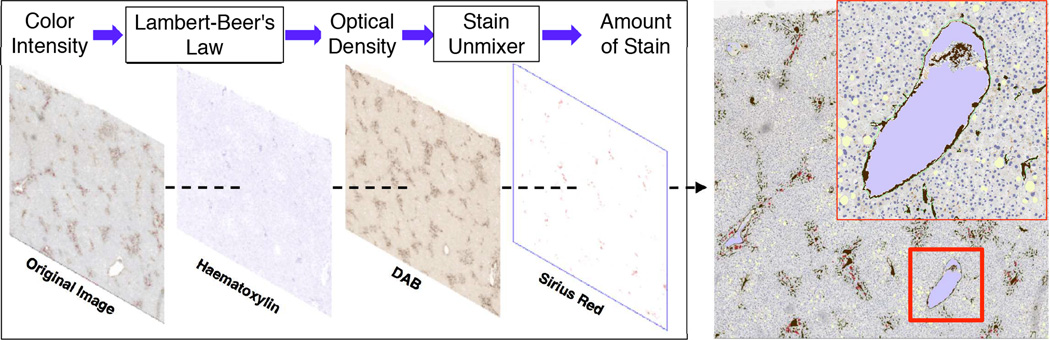
We next segment vessels in each registered image frame. First, we deconvolve each IHC stain component from the original color image. Color deconvolution [8] can be realized by Lambert-Beer’s law on the relationship between the intensity of light entering a specimen I_i and that through a specimen I_o as: I_o = I_ie^(−Ab) where A and b are the amount of stain and the absorption factor, respectively. The resulting Optical Density (OD) is defined as: OD = −log(I_o/I_i). We define the un-mixer $M\triangleq ({\overrightarrow{m}}_1⋮{\overrightarrow{m}}_2⋮{\overrightarrow{m}}_3)$ as a 3 × 3 matrix where its three columns have unit length and represent the OD values associated with the red, green, and blue channel for Hematoxylin, DAB, and Sirius Red. Given C(p,q) is a 3 × 1 vector representing three stain amounts at pixel (p,q), the OD levels for red, green, and blue channel Y would be Y = MC. As a result, an orthogonal representation of the stains can be written as C = M⁻¹Y. After stain components are deconvolved from RGB image, we start the segmentation process with fat and lumen detection. Hysteresis thresholding is applied to gray-scale image with shape and size constraints [9]. Next, vessels, nuclei, and bile ducts are identified with deconvolved DAB, Hematoxylin, and Sirius Red stain channels using a morphological reconstruction operation that locally “normalizes” image background [10]. Three deconvolved stains are presented in Figure 3 where brown, red, dark blue, light purple, and light yellow colors are used to represent vessels, bile ducts, nuclei, lumens, and fat in liver tissues, respectively. Additionally, the green vessel boundaries are superimposed on the original image.

Fig. 3.

Liver microscopy image segmentation. (Left): A color image deconvolved into three stain components; (Right): a close-up view of segmentation result.

2.3. Inter-frame vessel association

After blood vessel segmentation, inter-frame vessel grouping and filtering are performed. Vessel grouping is done by an image dilation operation [10] to make small vessel pieces cohesive to their source vessels. Candidates are then chosen among the grouped vessels by size for further analysis. We characterize the selected vessels by shape, spatial relationship and vessel trajectory smoothness. For our dataset, we consider four distinct vessel association cases: one-to-one (growing), one-to-two (bifurcating), one-to-none (disappearing) and none-to-one (appearing). The resulting cost functions are formulated as follows:

1. One-to-one (vessel extension to the next frame):

   $$\mathit{C}(v_i^t,v_j^{t+1})={\lambda }_1\mathit{g}(v_i^t,v_j^{t+1})+{\lambda }_2\mathit{d}(v_i^t,v_j^{t+1})+{\lambda }_3\mathit{b}(v_i^t,v_j^{t+1})$$
2. One-to-two (vessel bifurcation):

   $$\mathit{C}(v_i^t,v_{j_1}^{t+1},v_{j_2}^{t+1})={\lambda }_1\mathit{g}(v_i^t,v_{j_1}^{t+1}\cup v_{j_2}^{t+1})+{\lambda }_2\mathit{d}(v_i^t,v_{j_1}^{t+1}\cup v_{j_2}^{t+1})+{\lambda }_3\mathit{b}(v_i^t,v_{j_1}^{t+1}\cup v_{j_2}^{t+1})$$
3. One-to-none (vessel disappearance):

   $$\mathit{C}(v_i^t,v_{\varnothing }^{t+1})={\mathit{C}}_{\mathit{\text{const}}}^{\alpha }$$
4. None-to-one (new vessel emergence):

   $$\mathit{C}(v_{\varnothing }^{t-1},v_i^t)={\mathit{C}}_{\mathit{\text{const}}}^{\beta }$$

where $v_i^t$ is the i-th vessel object in image frame t; functions g(·), d (·), and b(·) denote similarity of vessel appearance by Fourier shape descriptors [12], distance of two vessel objects, and change in vessel trajectory orientations, respectively. ${\mathit{C}}_{\mathit{\text{const}}}^{\alpha }$ and ${\mathit{C}}_{\mathit{\text{const}}}^{\beta }$ are constant costs penalizing vessel disappearance and emergence; and {λ₁,λ₂,λ₃} s.t.λ₁+λ₂ + λ₃ =1 are constant weights to control the association smoothness.

Additionally, function g(·), d(·) and b(·) are defined as:

$$\mathit{g}(v_i^t,v_j^{t+1})=\mathit{\text{exp}}\left(\right(\Vert f(v_i^t)-f\left(v_j^{t+1}\right)\Vert )/{\sigma }_1^2)$$

$$\mathit{d}(v_i^t,v_j^{t+1})=\mathit{\text{exp}}\left(\right(\Vert o(v_i^t)-o\left(v_j^{t+1}\right)\Vert )/{\sigma }_2^2)$$

$$\mathit{b}(v_i^t,v_j^{t+1})=\mathit{\text{exp}}\left(\right(\Vert a(v_i^{t-1},v_i^t)-a(v_i^t,v_j^{t+1})\Vert )/{\sigma }_3^2)$$

where $f(v_i^t)$ is a vector of Fourier shape descriptors derived from vessel v_i at frame t; $o(v_i^t)$ denotes the centroid of $v_i^t$; and $a(v_i^t,v_j^{t+1})=\frac{\langle o(v_i^t),o\left(v_i^{t+1}\right)\rangle }{\Vert o(v_i^t)\Vert \Vert o\left(v_i^{t+1}\right)\Vert }$ indicates the orientation of the vessel vector from $v_i^t$ to $v_j^{t+1}$. Note that all these functions take the exponential form to force the resulting optimally associated vessels to have similar shape, low distance offset, and small orientation change in vessel trajectory.

We assume there are m₁ and m₂ vessel objects in frame t and t + 1 respectively, and r possible associations between these two frames. We solve the frame-by-frame vessel association problem by a Relaxed Integer Programming (RIP) framework [11]. The optimal vessel associations can be achieved as follows:

$$\text{Arg}\underset{\mathbf{x}}{\text{min}}{\mathbf{c}}^T\mathbf{x}\mathrm{s}.\mathrm{t}.{\left(M^T\mathbf{x}\right)}_i\le 1,A^T\mathbf{x}=\mathbf{1},0\le x_j\le 1$$

$$\text{for}i=1,\cdots ,m_1+m_2;j=1,\cdots ,r$$

where c is a r × 1 vector with each entry representing the cost of one vessel object association; M is a r × (m₁ + m₂) binary matrix with M_ij = 1 if and only if the i-th object association involves the j-th element from the union of m₁ vessel objects in frame t and m₂ in frame t + 1; (M^T x)_i is the i-th element of (M^Tx) and the constraint (M^Tx)i ≤ 1 guarantees that each vessel object in a given frame can be selected at most once in the result; A is a matrix composed with the first m₁ columns in M; 1 is a m₁ × 1 vector with all entries being 1s.This equality constraint guarantees that the sum of association probabilities for any given vessel object from frame t is one. The optimal solution x is a r × 1 binary vector where x_i = 1 indicates the i-th association is included in the optimal solution.

We propose an efficient entropy-based Relaxed Integer Programming (eRIP) mechanism to find the best vessel association with RIP as a building block (Algorithm 1). In eRIP, we first solve RIP for one possible solution x_RIP. If the entropy of x_RIP is sufficiently low, we take it as the final result. Otherwise, we switch to Integer Programming (IP) by replacing the constraint 0 ≤ x_j ≤ 1 in RIP with x_j ∈ {0,1}.

Algorithm 1.

Description of entropy-based Relaxed Integer Programming (eRIP) for Vessel Association

1	Solve the Relaxed Integer Programming (RIP) problem;
2	Compute the entropy ex of the solution xRIP from RIP;
3	if	ex ≤ e* then
		/* e* is a threshold (0 ≤ e* ≤ 1) */
4		x ← xRIP;
5	else
6		Replace the constraint of 0 ≤ xj ≤ 1 with xj ∈ {0,1};
7		Solve the corresponding Integer Programming (IP) problem for xIP with the updated constraint xj ∈ {0,1};
8		x ← xIP;
9	end
10	return x;

3. EXPERIMENTS AND RESULTS

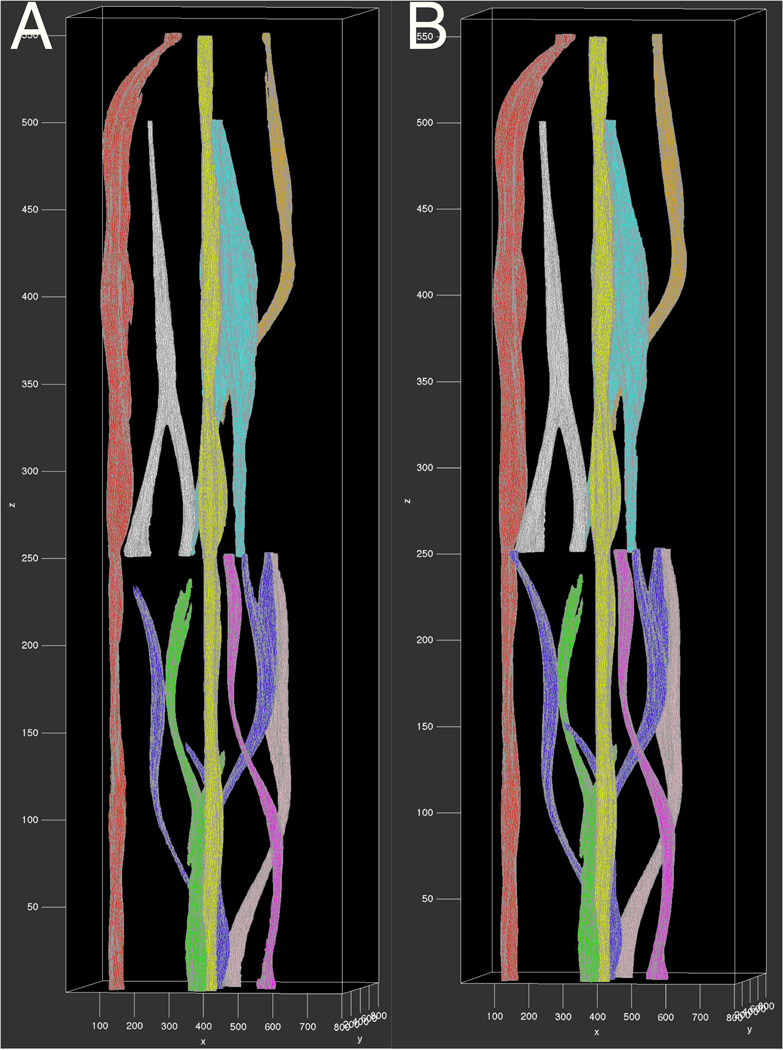
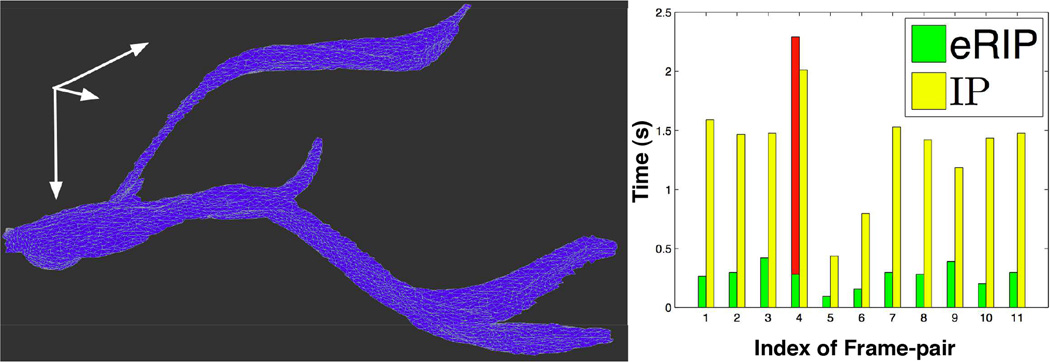
For vessel association, eRIP is proposed to identify the optimal vessel association between adjacent frames. We focus on the largest 25 vessel candidates by size on each slide. Of these candidates, the smallest vessel size is 304.25 ± 104.34 in pixels. At this stage, our working pipeline primarily deals with macro-vessels. The parameters are empirically set as λ₁ = 0.58, λ₂ = 0.33, ${\mathit{C}}_{\mathit{\text{const}}}^{\alpha }=0.35,{\mathit{C}}_{\mathit{\text{const}}}^{\beta }=0.38,{\sigma }_1^2=50000,{\sigma }_2^2=50$ and ${\sigma }_3^2=10$ . The median and maximum absolute displacements for these associated vessels in x-y pairs are (91.41,67.63) and (700.59,586.30) in pixels. Given the limited number of whole slide images in our dataset (n = 12), we perform B-Spline interpolation between associated vessel objects and volumetrically render 3D vessel structure with mesh representation [13]. In Figure 4 (Left), we present 3D visualization result of nine primary vessels from our dataset, with a close-up view of a representative vessel (blue) illustrated in Figure 5 (Left).

Fig. 4.

3D vessels reconstructed by (Left) our method; and (Right) human annotations.

Fig. 5.

(Left) A 3D close-up view of a representative vessel object; (Right) Time cost comparison between eRIP and IP.

We extensively evaluate our approach with human annotations quantitatively and qualitatively. Table 1 presents the validation results measured by Jaccard coefficient (Jac), precision (Pre), recall (Rec), F₁ score (F₁) and Hausdorff distance (Haus). The first column shows distinct vessels with their colors identically coded in Figure 4. The best performance assessed by each measure is in bold. Note Vessels in red and yellow are more regular in shape, leading to better agreement between the proposed method and human annotations. 3D vessel rendering results from human annotations in Figure 4 (Right) are used for qualitative assessments. By visual comparisons, 3D vessel structures in Figure 4 (Left) and (Right) are similar. Human annotated vessels are more regular and smooth in shape, whereas machine generated vessels tend to preserve more structural details. Overall, both quantitative measurements and qualitative comparisons suggest a satisfactory concordance between our method and human annotations.

Table 1.

Evaluation of the segmentation results (mean, Relative Standard Deviation%). The first column shows vessel color in Figure 4.

	Jac	Pre	Rec	F1	Haus
R	0.91,64.73	0.94,36.72	0.94,36.81	0.94,36.69	2.81,3.25
Y	0.92,60.40	0.92,37.41	0.92,37.53	0.92,37.41	2.72,3.02
G	0.80,125.13	0.86,41.10	0.86,41.06	0.86,40.91	4.10,5.88
B	0.80,109.28	0.85,41.90	0.85,41.69	0.85,41.62	4.10,5.81
P	0.84,79.79	0.84,39.95	0.84,39.82	0.84,39.75	4.10,5.78
M	0.81,86.55	0.81,40.58	0.81,40.45	0.81,40.35	4.09,6.00
W	0.87,57.26	0.88,35.40	0.88,35.52	0.88,35.35	3.81,3.96
C	0.81,81.88	0.82,37.69	0.82,37.80	0.82,37.69	4.22,3.13
O	0.86,61.80	0.85,37.22	0.86,37.33	0.86,37.21	3.92,3.11

In our tests, eRIP and IP produce identical vessel association results. We present the execution time for these two approaches in Figure 5 (Right). The green bars show eRIP execution time, with all values except the fourth less than 0.5 seconds and the majority around 0.3 seconds. By contrast, IP execution time is much longer, with majority around 1.5 seconds (yellow bars). Note that eRIP takes more time than IP for the fourth frame-pair (red bar), as entropy of the solution from RIP is greater than the threshold e* = 0.3. In this case, eRIP automatically switches to IP method. Most x_js from RIP are 0s or 1s in our tests, resulting in less execution time by eRIP overall.

4. CONCLUSIONS

In this paper, we present a framework for 3D vessel structure analysis on whole slide images of liver tissue sections. To identify vessel associations, we formulate a cost function with vessel shape descriptors, spatial similarity and trajectory smoothness for four vessel association scenarios. We also propose an eRIP optimization method to efficiently associate vessel objects between adjacent slides. Both quantitative and qualitative evaluation results demonstrate the effectiveness of our 3D vessel reconstruction framework and its promise as a platform for further 3D vessel analysis.