Pseudo-Rigid-Body Model and Kinematic Analysis of MRI-Actuated Catheters

Abstract

This paper presents a kinematic study of a pseudorigid-body model (PRBM) of MRI-compatible, magnetically actuated, steerable catheters. It includes a derivation of a mathematical model of the PRBM of the catheter, singularity studies of the model, and a new manipulability measure. While the forward kinematics of the model presented here is applicable to PRBMs for other applications, actuation method is unique to the particular design. Hence, a careful study of singularities and manipulability of the model is required. The singularities are studied from the underlying equations of motion with intuitive interpretations. The proposed manipulability measure is a generalization of the inverse condition number manipulability measure of robotic manipulators. While the PRBM is an approximation of the flexible catheter, kinematic studies of the PRBM still provide some insight into feasibility and limitations of the catheter, which is beneficial to the design and motion planning of the catheter.

I. Introduction

Recent advancements in robotic catheters for catheter ablation of atrial fibrillation have made the procedure more reliable [1], [2]. Magnetic Resonance Imaging (MRI) actuated catheters proposed in [3], [4], is a new robotic catheter concept which uses MRI’s superior soft tissue visualization for navigation and its strong magnetic field for remote steering.

In this new MRI compatible, magnetically actuated steerable catheter design, the catheter is actuated by three mutually orthogonal coils that deflect the catheter using the Lorentz force under MRI’s magnetic field. Since the orthogonal coils can only generate torques in the plane perpendicular to the magnetic field, the actuator effectively has only two degrees of freedom (DOF). However, the catheter, being a flexible mechanism, has a very high effective kinematic DOF. So, the catheter is underactuated because the actuation DOF is less than its actual kinematic DOF. On the other hand, the surface it operates on is two dimensional. Hence, the catheter is kinematically redundant from the task space point of view. Therefore, the kinematics of the proposed catheter system exhibits non-traditional characteristics. As such, the development of motion planning and control algorithms require a better characterization and understanding of the kinematics of the system which is the focus of this paper.

Specifically, this paper further investigates the feasibility of performing ablation with the actuation method. Using the pseudo-rigid-body model (PRBM) as an approximated model, singularities and manipulability of the catheter are studied. The definitions and relationships of different types of singularities are presented. Moreover, a new manipulability measure that takes the catheter’s elasticity into account is proposed.

The rest of the paper is organized as follows. First, a review of related work is given in Section II. The mathematical model of the PRBM is derived in Section III. Singularities are studied in Section IV. Manipulability and its measure are discussed in Section V. Finally, the conclusions are presented in Section VI

II. Related Work

Hansen Medical’s Sensei Robotic Navigation System and Stereotaxis’s Niobe Remote-Controlled Magnetic Navigation System are two commercial robotic catheter systems. Two steerable sheaths controlled by a pull-wire mechanism are used to steer Hansen Medical’s catheter while two external magnets are used to steer Stereotaxis’ catheter remotely [2].

Various robotic catheter technologies have been proposed in the literature. Catheters controlled via pull-wire mechanisms are described in [5]–[7]. An interleaved continuum-rigid manipulator is proposed in [8]. Modeling of a catheter equipped with a magnet in a magnetic field is presented in [9]. A continuum model of the MRI-actuated catheter is presented in [10].

The PRBM is an approximate model for compliant mechanisms which offers a trade-off between computational complexity and accuracy by reducing the dimensionality of the system while retaining its compliant characteristic. It consists of rigid links joined by revolute joints. The elasticity of the compliant mechanisms is modeled by torsional springs attached to the joints. Modeling of compliant mechanisms via the PRBM has been studied in [11]–[13]. The PRBMs have been used to model deflection of catheters in earlier studies (e.g., [7], [14]). In [7], a pull-wire ablation catheter is modeled using the PRBM. The paper presents a method of finding a set of parameters for the PRBM from a set of experimentation data.

Singularity and manipulability are well studied topics in robotics (e.g., [15]–[17]). Due to the catheter’s unique actuation method, the definition of singularity, manipulability, and manipulability measure have to be adapted for the specific application.

III. Mathematical Model

The derivation of the mathematical model of the catheter’s PRBM is presented in this section. First, a parameterization of joint rotations and the forward kinematics are introduced in Section III-A. Next, the angular velocity is discussed in Section III-B. Constrained equations of motion of the catheter performing ablation is presented in Section III-C. Finally, Actuation using the Lorentz force between the magnetic moment of the catheter and the MRI’s magnetic field is discussed in Section III-D.

A. Forward Kinematics

The PRBM consists of n rigid links connecting n spherical joints as shown in Fig. 1. The elasticity of the catheter is modeled as torsional springs attached to the joints. This paper assumes the torsional stiffness of the catheter to be much larger than bending stiffness so that torsional rotations can be neglected, and each joint can be modeled as a 2-DOF spherical joint with pure bending.

Fig. 1.

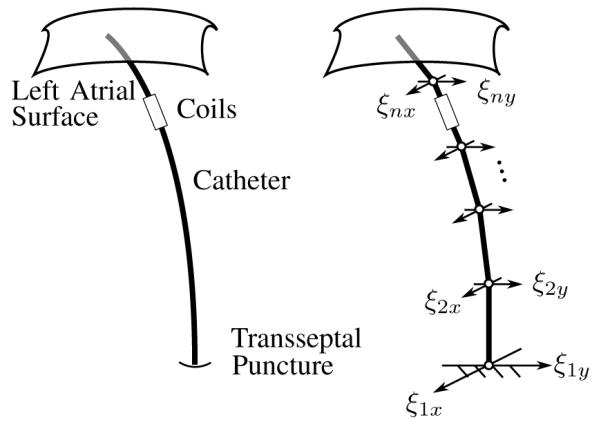
Continuum and pseudo-rigid-body model of the catheter. The rotation of the ith joint is expressed in terms of two orthogonal twists, denoted by ξ_ix and ξ_iy.

The rotation of each 2-DOF joint is parameterized by a linear combination of two orthogonal axes, i.e., for the i-th joint, ω_iθ_i = ω_ixθ_ix+ω_iyθ_iy, where ${\omega }_{\mathit{ix}},{\omega }_{\mathit{iy}}\in {\mathbb{R}}^3$ are the two orthogonal axes attached to the i-th joint, and θ_ix, ${\theta }_{\mathit{ix}},{\theta }_{\mathit{iy}}\in \mathbb{R}$ are the rotation angles around each axis respectively. The resulting rotation axis, ω_i, is a unit vector that specifies the direction of rotation, while the angle, θ_i, specifies magnitude of the rotation. The rotation of the i-th joint is illustrated in Fig. 2.

Fig. 2.

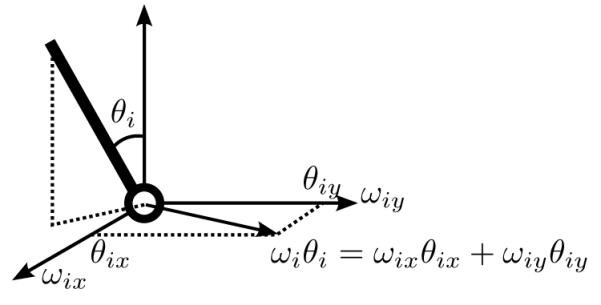
Rotation of the i-th joint. Since the rotation of one joint is considered in this case, the location of the joint, denoted by q_i with respect to the base frame can be neglect, and the rotation axis ω_i is used instead of the twist ξ_i.

The axes, ω_ix and ω_iy, at each joint are chosen to be mutually orthogonal among themselves and the initial direction of the next link. Hence, the bending angle at each joint can be described by a rotation around a vector lying in a plane orthogonal to the initial direction of the link. So the rotation obey Listing’s Law by construction [18].

Another benefit of using sum of orthogonal rotation axes is that joint torques are linear in the joint angles. This can be shown as follows. Consider the rotation of the i-th joint depicted in Fig. 2. The joint torque vector resulted from ω_iθ_i bending with stiffness k_i has the magnitude of k_iθ_i in the direction −ω_i, i.e., τ_i = −ω_i k_iθ_i = −k_iω_iθ_i = −k_i(ω_ixθ_ix+ω_iyθ_iy), which is linear in θ_ix and θ_iy.

With the parameterization of the 2-DOF rotation, the configuration of the catheter’s tip can be calculated using the product of exponentials formula as follows,

$$g_{\mathit{st}}\left(\theta \right)=e^{{\widehat{\xi }}_1{\theta }_1}{e}^{{\widehat{\xi }}_2{\theta }_y}\cdots e^{{\widehat{\xi }}_n{\theta }_n}{g}_{\mathit{st}}\left(0\right),$$ (1)

where g_st(θ) ∈ SE(3) is the configuration of the catheter’s tip for a given set of joint angles, $\theta =\left[{\theta }_{1x}{\theta }_{1y}\cdots {\theta }_{\mathit{nx}}{\theta }_{\mathit{ny}}\right]\in {\mathbb{R}}^{2n}$, g_st(0) is the initial configuration, and ${\widehat{\xi }}_i\in \mathit{se}\left(3\right)$ is the twists given by

$${\widehat{\xi }}_i=\left[\begin{array}{cc}\hfill {\widehat{\omega }}_i\hfill & \hfill -{\omega }_i\times q_i\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right].$$ (2)

with ${\widehat{\omega }}_i\in \mathit{so}\left(3\right)$ replaces ω_i × q_i with a matrix multiplication ${\widehat{\omega }}_i{q}_i$, and q_i is the initial location of the i-th joint. Note that while (1) has only n exponents, the catheter has 2n DOFs since each rotation has 2 DOFs.

B. Angular Velocities

In this section, the instantaneous spatial angular velocity, denoted by ω^s, of the 2-DOF joints is examined. The angular velocity is important because it is used in constructing the manipulator Jacobian, which is essential in studying the singularities of the catheter. There are two important results in this section. First, the angular velocity can be written as a linear combination of velocity axes, which are linearly independent under joint limits. Second, the velocity axes span a plane with the normal vector rotated halfway between the initial orientation and the rotated orientation of the attached link. Consequently, this plane will be referred to as the half-angle plane in this paper. These properties of the velocity axes are useful when studying the singularities of the PRBM because it reveals the relationship between the angular velocity and the joint angles.

Since the rotation of a single joint is considered in this section, for the sake of simplicity, the joint number will be dropped from the subscripts. So, the rotation of the 2-DOF joint is denoted by ω(t) = ω_xθ_x(t) + ω_yθ_y(t), where ω now contains both magnitude and direction of the rotation, and that the dependence of ω on t is made explicit. The rotation can be written as an element in the Lie algebra so(3) as follows,

$$\widehat{\omega }\left(t\right)=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill {\theta }_y\left(t\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\theta }_x\left(t\right)\hfill \\ \hfill -{\theta }_y\left(t\right)\hfill & \hfill {\theta }_x\left(t\right)\hfill & \hfill 0\hfill \end{array}\right].$$ (3)

The orientation of the link is given by the exponent of $\widehat{\omega }\left(t\right)$, i.e., $R\left(\theta \right(t\left)\right)=\exp \left(\widehat{\omega }\right(t\left)\right)$. The instantaneous spatial angular velocity in so(3) is defined as ${\widehat{\omega }}^s=\stackrel{.}{R}{R}^{-1}$ [15].

For a 1-DOF joint with a fixed rotation axis ω₀, the orientation is given by $R\left(t\right)=e^{{\widehat{\omega }}_0\theta \left(t\right)}$, and $\stackrel{.}{R}$ can be calculated from

$$\stackrel{.}{R}=\frac{d}{\mathit{dt}}{e}^{{\widehat{\omega }}_0\theta \left(t\right)}=\frac{\partial e^{{\widehat{\omega }}_0\theta }}{\partial \theta }\frac{d\theta }{\mathit{dt}}={\widehat{\omega }}_0{e}^{{\widehat{\omega }}_0\theta }\stackrel{.}{\theta }={\widehat{\omega }}_{0}R\stackrel{.}{\theta }.$$ (4)

In this case, ${\widehat{\omega }}^s=\stackrel{.}{R}{R}^{-1}={\widehat{\omega }}_0\stackrel{.}{\theta }$, so the angular velocity’s direction is ${\widehat{\omega }}_0$, which is the same of the rotation axis and it is independent of the rotation angle.

However, for the 2-DOF joints parameterized by θ_x and θ_y, the partial derivative ∂R/∂θ does not have a simple form such as in the 1-DOF case. This is because $\dot{\widehat{\omega }}$ does not commute with $\widehat{\omega }$. Fortunately, in [19], Hausdorff had shown that,

$$\left(\frac{d}{\mathit{dt}}{e}^{\widehat{\omega }}\right)e^{-\widehat{\omega }}=\dot{\widehat{\omega }}+\frac{1}{2!}\left[\widehat{\omega },\dot{\widehat{\omega }}\right]+\frac{1}{3!}\left[\widehat{\omega },\left[\widehat{\omega },\dot{\widehat{\omega }}\right]\right]+\cdots .$$ (5)

The right hand side of (5) is an element of the Lie algebra because it consists of sums of iterated commutators. Thus, ${\widehat{\omega }}^s$ is also an element of so(3). Let

$${\widehat{\omega }}^s=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -{\omega }_z^s\hfill & \hfill {\omega }_y^s\hfill \\ \hfill {\omega }_z^s\hfill & \hfill 0\hfill & \hfill -{\omega }_x^s\hfill \\ \hfill -{\omega }_y^s\hfill & \hfill {\omega }_x^s\hfill & \hfill 0\hfill \end{array}\right],$$ (6)

where the elements of ${\widehat{\omega }}^s$ are calculated from (5). After some simplification we arrive at

$${\omega }_x^s={\stackrel{.}{\theta }}_x+\frac{{\theta }_y}{{\theta }^2}(1-\frac{\sin \theta }{\theta })({\theta }_x{\stackrel{.}{\theta }}_y-{\theta }_y{\stackrel{.}{\theta }}_x),$$ (7a)

$${\omega }_y^s={\stackrel{.}{\theta }}_y-\frac{{\theta }_x}{{\theta }^2}(1-\frac{\sin \theta }{\theta })({\theta }_x{\stackrel{.}{\theta }}_y-{\theta }_y{\stackrel{.}{\theta }}_x),$$ (7b)

$${\omega }_z^s=\frac{1}{{\theta }^2}(1-\cos \theta )({\theta }_x{\stackrel{.}{\theta }}_y-{\theta }_y{\stackrel{.}{\theta }}_x),$$ (7c)

where $\theta ={({\theta }_x^2+{\theta }_y^2)}^{1∕2}$ denotes the magnitude of rotation. The angular velocity can be expressed in ${\mathbb{R}}^3$ as a linear combination of the velocity axes, denoted by w_x and w_y, ${\omega }^s=w_x{\stackrel{.}{\theta }}_x+w_y{\stackrel{.}{\theta }}_y$, as follows,

$${\omega }^s=\left[\begin{array}{c}\hfill 1-\frac{{\theta }_y^2}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill \frac{{\theta }_x{\theta }_y}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill -\frac{{\theta }_y}{{\theta }^2}(1-\cos \theta )\hfill \end{array}\right]{\stackrel{.}{\theta }}_x+\left[\begin{array}{c}\hfill \frac{{\theta }_x{\theta }_y}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill 1-\frac{{\theta }_x^2}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill \frac{{\theta }_x}{{\theta }^2}(1-\cos \theta )\hfill \end{array}\right]{\stackrel{.}{\theta }}_y.$$ (8)

With the closed form expression of ω^s, we can show that it is indeed contained in the “half-angle” plane.

Theorem 1

For ${({\theta }_x^2+{\theta }_y^2)}^{1∕s}\in [0,2\pi )$, (i) neither w_x nor w_y is identically zero, (ii) they are linearly independent and (iii) they are orthogonal to the half-angle vector,

$$v={\left[\frac{{\theta }_y}{\theta }\sin \frac{\theta }{2}-\frac{{\theta }_x}{\theta }\sin \frac{\theta }{2}\cos \frac{\theta }{2}\right]}^T$$

for $({\theta }_x,{\theta }_y)\in \left\{({\theta }_x,{\theta }_y):\sqrt{{\theta }_x^2+{\theta }_y^2}<\pi \right\}$

Proof

The proof of the first two parts can be found in Appendix B. While the third part can be proven using simple trigonometric identities

C. Equations of Motion

Equations of motion of the PRBM are presented in this section. Assuming the catheter moves with low acceleration and velocity, the inertial force is negligible. The catheter in contact with a surface is described by a constraint h(θ) = 0. The constrained equations of motion of the catheter is given by

$$C\left(\theta \right)\stackrel{.}{\theta }+K\theta +\nabla h\left(\theta \right)\lambda =\tau ,$$ (9)

where C(θ) is the viscous damping coefficient matrix, Kθ is the conservative force due to the springs, ▿h(θ)λ is the force exerted by the surface to keep the joint angles on the constraint surface, and τ is the joint torque vector. Friction and disturbances are not considered in singularity and manipulability studies, so the joint torque vector is the actuation torque vector. The term ▿h(θ) forms a basis for the constraint forces while λ specifies the relative magnitude of the forces. The magnitude of the constraint force is such that the joint velocity in the direction orthogonal to the constraint is zero, in other words, ${\stackrel{.}{\theta }}^T\nabla h\lambda =0$ [15].

The equations of motion of the catheter’s tip on the surface is derived next. First, let the position of the tip on the surface be denoted by x. The surface constraint, h(θ), can be written to explicitly include the tip position. Let’s denote it simply by h(θ, x). Then, the joint velocity can be decomposed into tip velocities and internal motion, denoted by $\stackrel{.}{x}$ and v_N respectively, as follows,

$$\stackrel{‒}{J}\stackrel{.}{\theta }={\stackrel{‒}{G}}^T\left[\begin{array}{c}\hfill \stackrel{.}{x}\hfill \\ \hfill v_N\hfill \end{array}\right],$$ (10)

where $\stackrel{‒}{J}$ and ${\stackrel{‒}{G}}^T$ are the extended Jacobian of the constraint h(θ, x) [14], [15]. The equations of motion in the task-space is obtained from (9) and (10),

$$\stackrel{‒}{C}\left(\theta \right)=\left[\begin{array}{c}\hfill \stackrel{.}{x}\hfill \\ \hfill v_N\hfill \end{array}\right]+\stackrel{‒}{N}\left(\theta \right)=F$$ (11)

where

$$\begin{array}{cc}\hfill \stackrel{‒}{C}& =\stackrel{‒}{G}{\stackrel{‒}{J}}^{-T}C{\stackrel{‒}{J}}^{-1}{\stackrel{‒}{G}}^T,\hfill \\ \hfill \stackrel{‒}{N}& =\stackrel{‒}{G}{\stackrel{‒}{J}}^{-T}K\theta ,\hfill \\ \hfill F& =\stackrel{‒}{G}{\stackrel{‒}{J}}^{-T}\tau .\hfill \end{array}$$

We have $\stackrel{‒}{G}{\stackrel{‒}{J}}^{-T}\nabla h\left(\theta \right)\lambda =0$, because $\stackrel{.}{\theta }$ that satisfies (10) do no work on the constraint surface. For the sake of simplicity for the subsequent sections, (11) shall be written as

$$\left[\begin{array}{c}\hfill \stackrel{.}{x}\hfill \\ \hfill v_N\hfill \end{array}\right]=f\left(\theta \right)+g\left(\theta \right)u=\left[\begin{array}{c}\hfill f_1\left(\theta \right)\hfill \\ \hfill f_2\left(\theta \right)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill g_1\left(\theta \right)\hfill \\ \hfill g_2\left(\theta \right)\hfill \end{array}\right]u$$ (13)

where $f\left(\theta \right)={\stackrel{‒}{C}}^{-1}\stackrel{‒}{N}\left(\theta \right)$ and $g\left(\theta \right)={\stackrel{‒}{C}}^{-1}\stackrel{‒}{G}{\stackrel{‒}{J}}^{-T}{J}_u^{T}B\left(\theta \right)$. The rows of f(θ) and g(θ) associated with $\stackrel{.}{x}$ are denoted by f₁(θ) and g₁(θ), while the rows associated with v_N are denoted by f₂(θ) and g₂(θ) respectively.

D. Actuation

The MRI-actuated catheter is actuated by the Lorentz force from the magnetic moment generated by the coils and the MRI’s magnetic field. The actuation wrench containing the Lorentz force is mapped into the joint torque vector through the body manipulator Jacobian as follows

$$\tau ={J_{\mathit{su}}^b}^T\left(\theta \right)\left[\begin{array}{c}\hfill 0_{3\times 1}\hfill \\ \hfill m\times b\hfill \end{array}\right],$$ (14)

where $\tau \in {\mathbb{R}}^{2n}$ is the joint torque vector, $J_{\mathit{su}}^b\in {\mathbb{R}}^{6\times 2n}$ is the body manipulator Jacobian, $m\in {\mathbb{R}}^3$ is the magnetic moment of the actuator, and $b\in {\mathbb{R}}^3$ is the MRI’s magnetic field. The actuation torque m×b can be simplified to exclude the direction of m that is aligned with b using the Singular Value Decomposition as follows,

$$m\times b=-\widehat{b}m=-U\Sigma V^{T}m=-U_0{\Sigma }_0{V}_0^{T}m=\mathit{Bu}.$$ (15)

In the equations above, $\widehat{b}=U\Sigma V^T$ is the SVD of $\widehat{b}$. The components associating with the zero singular value of Σ are dropped in $U_0{\Sigma }_0{V}_0^T$. Finally, define B = −U₀Σ₀ and $u=V_0^{T}m$. Henceforth, u is considered as the input to the system when performing calculations. The magnetic moment can be calculated from u using the right pseudo-inverse, i.e., $m=V_0{\left(V_0^T{V}_0\right)}^{-1}u$. The joint torque vector can now be written as

$$\tau =J_u^T\left(\theta \right)B\left(\theta \right)u,$$ (16)

where J_u is the bottom half of $J_{\mathit{su}}^b$. A detail calculation of J_u is provided in Appendix A. Note that the actuation torque vector is linear in u and B is full-rank by definition.

IV. Singularities

This section presents singularity studies of the PRBM catheter. Since the main application of the catheter is to perform ablation of atrial fibrillation, the task space is assumed to be a smooth surface. Using (9) and (16), one can show that the singular configurations of the PRBM catheter are of the Redundant Input/Impossible Output type according to [20]. There are multiple causes of such singularities. They are discussed in this section in a bottom-up fashion.

A. Singularities in The Joint Space

The input-output relationships between actuation and joint velocities are studied in this section. Joint torques due to joint springs are not considered here to separate the effect of joint springs from the geometrical properties of the catheter and the surface. Joint springs will be considered in Section V where manipulability is discussed. The equations of motion for singularity studies in the joint space is obtained by combining (9) and (16) and removing Kθ as follows,

$$C\left(\theta \right)\stackrel{.}{\theta }+\nabla h\left(\theta \right)\lambda =J_u^T\left(\theta \right)B\left(\theta \right)u.$$ (17)

First, A configuration is said to be actuation singular if there exists a nonzero actuation, u, that causes zero joint torques. This is made explicit in the definition below.

Definition 1

A configuration is said to be actuation singular if $J_u^T\left(\theta \right)B\left(\theta \right)u=0$ has u ≠ 0 as a solution.

Moreover, a configuration is called joint-space singular if there exists a nonzero actuation that results in zero joint velocities.

Definition 2

A configuration is said to be joint-space singular if there exists u ≠ 0 that satisfies (17) with $\stackrel{.}{\theta }=0$.

It is easy to see that actuation singularity implies joint-space singularity.

Before we proceed, some more definitions have to be made. The joints that are directly affected by the coils, i.e., the joints between the coils and the base, are called actuated joints, while the rest are called unactuated joints. The links that connect them are called actuated links and unactuated links respectively.

Two theorems that predict the singularity of a configuration is presented next. The first one deals with actuation singularity. It states that when the actuated joints are not bent in a specific pattern, then the actuator Jacobian, $J_u^T$, is full-rank and the configuration is not actuation singular.

Theorem 2

A configuration is not actuation singular if there exists a pair of the actuated joints with joint angles θ_ix ≠ −θ_(i+1)x and θ_iy ≠ −θ_(i+1)y.

Proof

A sketch of proof is as follows. The columns of $J_u^T$ are linearly independent if and only if there exists a pair of actuated joints with joint angles θ_ix ≠ −θ_(i+1)x and θ_iy ≠ −θ_(i+1)y. This is due to the dependency of the velocity axes on the joint angles as described in Section III-B. Since B is full-rank by construction, $J_u^{T}B$ is also full-rank. So, the only solution to $J_u^T\mathit{Bu}=0$ is u = 0. The complete proof is given in Appendix C

The next theorem states that if the unactuated links are not all perpendicular to the surface then the constraint force cannot annihilate actuation torques.

Theorem 3

Suppose a configuration is not actuation singular, it is not joint-space singular if there exists an unactuated link that is not perpendicular to the surface at the contact point.

Proof

Since Kθ is omitted in (17), the constraint force is given by $\lambda ={(\nabla h^T{C}^{-1}\nabla h)}^{-1}\nabla h^T{C}^{-1}{J}_u^T\mathit{Bu}$, so (17) can be written as

$$\begin{array}{cc}\hfill C\stackrel{.}{\theta }& =J_u^T\mathit{Bu}-\nabla h\lambda \hfill \\ \hfill & =[I-{(\nabla h^T{C}^{-1}\nabla h)}^{-1}\nabla h\nabla h^T{C}^{-1}]J_u^T\mathit{Bu}.\hfill \end{array}$$

Note that only ▿h is in the null space of [I – (▿h^TC⁻¹▿h)⁻¹▿h▿h^TC⁻¹]. If there exists an unactuated link that is not orthogonal to the surface then ▿h has nonzero components associated with the unactuated joints where the rows of $J_u^T$ are all zeros. Then ▿h cannot be in the range space of $J_u^T$. The complete proof is given in Appendix D.

The two theorems above tell us that the singularity is easily avoided if the actuated joints is bent with θ_ix ≠ −θ_(i+1)x and θ_iy ≠ −θ_(i+1)y, and the unactuated links are not perpendicular to the surface. Three examples of joint-space singularity are presented next. The first example is a trivial case of actuation singularity at θ = 0.

Example 1

Consider the catheter in Fig. 3(a) when all joint angles are zeros and the magnetic filed is along the x-axis. In this case J_u and B are

$$\begin{array}{cc}\hfill J_u& =\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill B& =\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill -1∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill \end{array}\right].\hfill \end{array}$$

$J_u^{T}B$ is rank-1 and $J_u^T\mathit{Bu}=0$ for $u={[1∕\sqrt{2}1∕\sqrt{2}]}^T$, or equivalently, m = [0 – 1 0]^T. Therefore, the configuration is actuation singular.

Fig. 3.

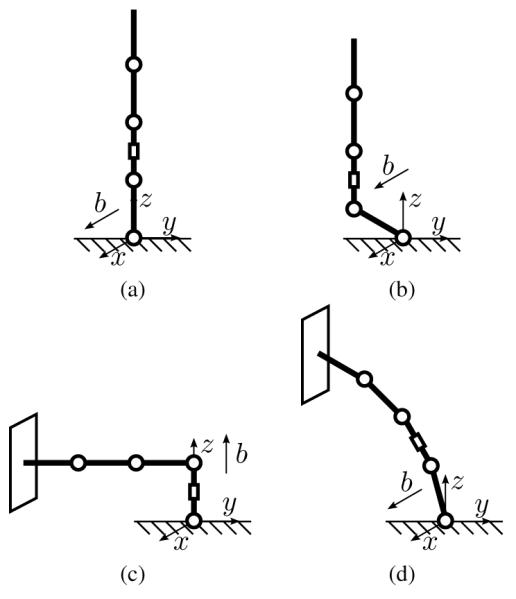
The PRBM of the catheter and the MRI’s magnetic field is different configurations. In (a) and (b), the catheter is actuation singular. In (c) it is joint-space singular and in (d) it is task-space singular.

Example 2

Consider the catheter in Fig. 3(b) when θ_1x = −θ_2x = π/4 while other joint angles are zeros and the magnetic filed is along the x-axis. In this case J_u and B are

$$\begin{array}{cc}\hfill J_u& =\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.9003\hfill & \hfill 0\hfill & \hfill 0.9003\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.3729\hfill & \hfill 0\hfill & \hfill 0.3729\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill B& =\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.9952\hfill & \hfill -0.0982\hfill \\ \hfill -0.0982\hfill & \hfill -0.9952\hfill \end{array}\right]\hfill \end{array}$$

$J_u^{T}B$ is rank-1 and $J_u^T\mathit{Bu}=0$ for u = [0.5348 1]^T, or equivalently, m = [0 1.0477 0.4340]^T. Therefore the configuration is actuation singular.

Example 3

Consider the catheter in Fig. 3(c) when θ_2x = π/2 while other joint angles are zeros and the magnetic filed is along the z-axis. Let surface contact configuration be

$$g_{\mathit{sc}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill -3\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

$J_u^{T}B$ and ▿h are given by

$$J_u^{T}B=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\nabla h=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \\ \hfill 0\hfill \end{array}\right]$$

$J_u^{T}B$ is full-rank, so there is no actuation singularity. However, $\stackrel{.}{\theta }=0$ is possible with u = [0 1]^T, and the configuration is joint-space singular

B. Singularities in The Task Space

Similar to the joint-space singularity study, the equations are obtained from (13) by omitting the spring torques. The equations used to study the singularity is simply

$$\left[\begin{array}{c}\hfill \stackrel{.}{x}\hfill \\ \hfill v_N\hfill \end{array}\right]=\left[\begin{array}{c}\hfill g_1\left(\theta \right)\hfill \\ \hfill g_2\left(\theta \right)\hfill \end{array}\right]u$$ (18)

Also similar to the joint space, a singular configuration in the task space is the configuration which there are nonzero u that causes no tip velocity.

Definition 3

A configuration is said to be task-space singular if there exists u ≠ 0 and v_N that satisfies (18) with $\stackrel{.}{x}=0$.

Note that joint-space singularity implies task-space singularity naturally, but the converse is not true. An example of a task-space singular configuration is presented next.

Example 4

Consider the catheter in Fig. 3(d) when θ_1x = θ_2x = θ_3x = θ_4x = π/12 while other joint angles are zeros. Let surface contact configuration be

$$g_{\mathit{sc}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill -2.3320\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 3.0391\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

$J_u^{T}B$ and ▿h are given by

$$J_u^{T}B=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill -0.6070\hfill & \hfill -0.7911\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill -0.7911\hfill & \hfill -0.6070\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\nabla h=\left[\begin{array}{c}\hfill 3.0391\hfill \\ \hfill 0\hfill \\ \hfill 2.0731\hfill \\ \hfill 0\hfill \\ \hfill 1.2071\hfill \\ \hfill 0\hfill \\ \hfill 0.5000\hfill \\ \hfill 0\hfill \end{array}\right]$$

$J_u^{T}B$ is full-rank, so there is no actuation singularity. Moreover, $J_u^{T}B$ and ▿h are linearly independent, so there is no joint space kinematics singularity. However,

$$g_1\left(\theta \right)=\left[\begin{array}{cc}\hfill -4.1447\hfill & \hfill -4.2564\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$

Hence, the configuration is task-space singular.

V. Manipulability Measure

The ability of the catheter to overcome its own stiffness is essential to the feasibility of the ablation procedure. In this section, the effect of joint springs on feasible tip velocities is studied. Even if the configuration is nonsingular, tip velocities in some directions may not be possible due to spring torques being larger than actuation limits. The ability to move in all directions is called manipulability and a configuration with such property is called a manipulable configuration. A formal definition is given below.

Definition 4

Let the set of all feasible actuation be denoted by U. A configuration is manipulable if $\{\stackrel{.}{x}:\stackrel{.}{x}=f_1(\theta )+g_1(\theta )u,\forall u\in U\}$ contains $\stackrel{.}{x}=0$ in its interior.

A Manipulability measure is a measurement of how easy it is for a manipulator to change the position or orientation of the end-effector at a given configuration. One common manipulability measure in robotic manipulation is the inverse condition number of the manipulator Jacobian, which is the ratio between the minimum and the maximum singular values of some Jacobian. This gives the ratio between the minimum and the maximum end-effector velocities under a unit joint velocity vector [15].

The manipulability measure presented in this paper is inspired by the inverse condition number manipulability measure. Some modifications are made to accommodate different characteristics of the catheter. First of all, joint velocities of traditional manipulators can be controlled directly and independently of one another. However, for the catheter, the joint torques can be controlled indirectly through the magnetic moments. Hence, the manipulability measure is calculated with the magnetic moments considered as the inputs instead of the joint velocities.

A consequence of taking joint spring torques into account when calculating manipulability measure is that instead of a unit joint velocity vector, a bound on u has to considered. This is because the relative size between actuation and spring torques is a major factor to the manipulability of the catheter. Heat dissipation during an ablation procedure is limited for safety reasons, so the currents are bounded by the maximum power. Hence, the set of feasible actuation is, denoted by U, is U = {u : u^TQu < P_max} where Q is a positive definite matrix.

The image of the boundary of U, denoted by ∂U, under g(θ) is an ellipse centered at the origin, and f(θ) shifts the ellipse from the origin. If the configuration is manipulable, then $\stackrel{.}{x}=0$ is contained in the shifted ellipse. The minimum and the maximum distance to the shifted ellipse are denoted by ${\stackrel{.}{x}}_{\text{min}}$ and ${\stackrel{.}{x}}_{\text{max}}$ respectively. The manipulability measure is given by

$$\mu =\frac{{\stackrel{.}{x}}_{\min }}{{\stackrel{.}{x}}_{\max }}\left(\theta \right)$$ (19)

where

$${\stackrel{.}{x}}_{\min }\left(\theta \right)=\underset{u\in \partial U}{\mathrm{minimize}}\mid \mid \stackrel{.}{x}\mid \mid$$ (20a)

$$\text{subject to}\stackrel{.}{x}=f_1\left(\theta \right)+g_1\left(\theta \right)u$$ (20b)

$${\stackrel{.}{x}}_{\max }\left(\theta \right)=\underset{u\in \partial U}{\mathrm{maximize}}\mid \mid \stackrel{.}{x}\mid \mid$$ (21a)

$$\text{subject to}\stackrel{.}{x}=f_1\left(\theta \right)+g_1\left(\theta \right)u$$ (21b)

Example 5

Consider the same case as in Example 4 with θ₁ = θ₃ = θ₅ = θ₇ = π/12 while other joint angles are zeros. The magnetic field is now b = [0 0 1]^T and the configuration is nonsingular. Each link has unit length and U is assumed to be a unit ball centered at the origin. For stiffnesses k = 1 for all joints, the corresponding manipulability measure is μ = 0.0284, but for stiffnesses k = 0.1, the manipulability measure is μ = 0.8274. Note that stiffer joint springs yield lower manipulability measure.

VI. Conclusions

In this paper, a mathematical model of the PRBM of MRI-actuated catheters is presented. Different types of singularities are defined. Two theorems on joint space singularities are presented. A manipulability measure for the catheter is introduced. Examples illustrating different singularities and manipulability are given. Future works include investigating the relationship between singularities and manipulability of the PRBM to the flexible catheter and their applications in planning and control, as well as in the design process, of the catheter.

Fig. 4.

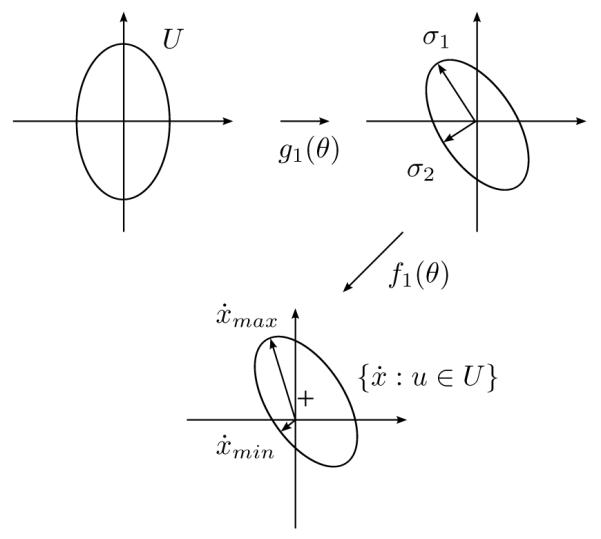
Illustration of how U is mapped into $\{\stackrel{.}{x}:u\in U\}$ via g₁ and f₁.

Appendix A. Actuator Jacobian Calculation

The calculation of J_u is presented next, starting from the calculation of $J_{\mathit{su}}^b$. Recall that the actuator is attached to the k-th link. The Manipulator Jacobian in the body frame is of the form

$$J_{\mathit{su}}^b\left(\theta \right)=\left[{\xi }_{1x}^{†}{\xi }_{1y}^{†}\cdots {\xi }_{\mathit{kx}}^{†}{\xi }_{\mathit{ky}}^{†}0\cdots 0,\right]$$

where for each i = 1, … , k,

$${\xi }_{\mathit{ix}}^{†}={\mathrm{Ad}}_{g_i\left(\theta \right)}^{-1}{\xi }_{\mathit{ix}}\text{and}{\xi }_{\mathit{iy}}^{†}={\text{Ad}}_{g_i\left(\theta \right)}^{-1}{\xi }_{\mathit{iy}},$$

and g_i(θ) is defined as

$$g_i\left(\theta \right)=e^{({\widehat{\xi }}_{\mathit{ix}}{\theta }_{\mathit{ix}}+{\widehat{\xi }}_{\mathit{iy}}{\theta }_{\mathit{iy}})}\cdots e^{({\widehat{\xi }}_{\mathit{kx}}{\theta }_{\mathit{kx}}+{\widehat{\xi }}_{\mathit{ky}}{\theta }_{\mathit{ky}})}{g}_{\mathit{su}}\left(0\right).$$

The last 2(n–k) columns of the Jacobian are zeros because the actuation does not effect the upper joints. Recall that for g ∈ SE(3), the inverse adjoint transformation can be calculated as follows,

$$g=\left[\begin{array}{cc}\hfill R\hfill & \hfill p\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\to {\mathrm{Ad}}_g^{-1}=\left[\begin{array}{cc}\hfill R^T\hfill & \hfill -R^T\widehat{p}\hfill \\ \hfill 0\hfill & \hfill R^T\hfill \end{array}\right].$$

So, for g_i = (R_i, p_i) defined above, the column vectors of the manipulator Jacobian are given by

$$\begin{array}{cc}\hfill {\xi }_{\mathit{ix}}^{†}& =\left[\begin{array}{cc}\hfill R_i^T\hfill & \hfill -R_i^T{\widehat{p}}_i\hfill \\ \hfill 0\hfill & \hfill R_i^T\hfill \end{array}\right]\left[\begin{array}{c}\hfill -w_{\mathit{ix}}\times q_{\mathit{ix}}\hfill \\ \hfill w_{\mathit{ix}}\hfill \end{array}\right],\hfill \\ \hfill {\xi }_{\mathit{iy}}^{†}& =\left[\begin{array}{cc}\hfill R_i^T\hfill & \hfill -R_i^T{\widehat{p}}_i\hfill \\ \hfill 0\hfill & \hfill R_i^T\hfill \end{array}\right]\left[\begin{array}{c}\hfill -w_{\mathit{iy}}\times q_{\mathit{iy}}\hfill \\ \hfill w_{\mathit{iy}}\hfill \end{array}\right],\hfill \end{array}$$

where w_ix and w_iy are the rotational velocity axes of joint i-th as in (8). So, the actuator Jacobian J_u, which is the bottom half of $J_{\mathit{su}}^b$, is given by

$$J_u=[R_1^T{w}_{1x}{R}_1^T{w}_{1y}\cdots R_k^T{w}_{\mathit{kx}}{R}_k^T{w}_{\mathit{ky}}0\cdots 0].$$

Appendix B. Proof of Velocity Axes Theorem

For simplicity, define a matrix with w_x and w_y as the first and the second column as follows,

$$W=\left[\begin{array}{cc}\hfill 1-\frac{{\theta }_y^2}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill & \hfill \frac{{\theta }_x{\theta }_y}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill \frac{{\theta }_x{\theta }_y}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill & \hfill 1-\frac{{\theta }_x^2}{{\theta }^2}(1-\frac{\sin \theta }{\theta })\hfill \\ \hfill -\frac{{\theta }_y}{{\theta }^2}(1-\cos \theta )\hfill & \hfill \frac{{\theta }_x}{{\theta }^2}(1-\cos \theta )\hfill \end{array}\right]$$

When θ_x = θ_y = 0, W is given by

$$W=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$

which is clearly nonsingular. When θ_x ≠ 0 but θ_y = 0,

$$W=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{\sin {\theta }_x}{{\theta }_x}\hfill \\ \hfill 0\hfill & \hfill \frac{1}{{\theta }_x}(1-\cos {\theta }_x)\hfill \end{array}\right].$$

The second column is linearly independent of the first column, and it is not identically zero for all 0 < ∣θ_x∣ < 2π. When θ_x = 0 with θ_y ≠ 0, we have

$$W=\left[\begin{array}{cc}\hfill \frac{\sin {\theta }_y}{{\theta }_y}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \\ \hfill -\frac{1}{{\theta }_y}(1-\cos {\theta }_y)\hfill & \hfill 0\hfill \end{array}\right].$$

The first column is linearly independent of the second column, and it is not identically zero for all 0 < ∣θ_y∣ < 2π.

Now consider the case when θ_x, θ_y ≠ 0 and $\theta ={({\theta }_x^2+{\theta }_y^2)}^{1∕2}<2\pi$. Suppose there exists θ_x and θ_y such that w_x and w_y are linearly dependent, then there exists $\alpha \in \mathbb{R}$ such that w_y = αw_x. Then from the third row of W we have

$$-\alpha \frac{{\theta }_y}{{\theta }^2}(1-\cos \theta )=\frac{{\theta }_x}{{\theta }^2}(1-\cos \theta )$$

which implies −αθ_y = θ_x. Substituting this into either the first or the second row of W leads to 1 = 0. Therefore, w_x and w_y are linearly independent. Moreover, neither of them is identically zero when θ ∈ (0, 2π). This can easily be seen in the third element of _wx and w_y.

Appendix C. Proof of The Actuation Singularity

The actuator Jacobian, derived in Appendix A is given by,

$$J_u=[R_1^T{w}_{1x}{R}_1^T{w}_{1y}\cdots R_k^T{w}_{\mathit{kx}}{R}_k^T{w}_{\mathit{ky}}0\cdots 0].$$

If J_u is full-rank then the configuration is not actuation singular. This is true if and only if there exists two plane spanned $R_{\mathit{ix}}^T{w}_{\mathit{ix}}$ and $R_{\mathit{iy}}^T{w}_{\mathit{iy}}$ for all actuated joints that are not coplanar. We will show that this is equivalent to θ_ix ≠ −θ_(i+1)x and θ_iy ≠ −θ_(i+1)y or equivalently, ω_iθ_i ≠ −ω_i+1θ_i+1. Without loss of generality, let i = 1 and the initial direction of link-1 be denoted by v. The normal vector of link-1 after the rotation is $v_1=\text{exp}({\widehat{\omega }}_1{\theta }_x∕2)$ and the normal vector of link-2 with ω₂θ₂ = −ω₁θ₁ is $v_2=\text{exp}(-{\widehat{\omega }}_1{\theta }_y∕2)\text{exp}\left({\widehat{\omega }}_1{\theta }_x\right)v=v_1$. So, the two plane spanned by (w_1x, w_1y) and (w_2x, w_2y) must be coplanar. The uniqueness of the joint angles is guaranteed by Listing’s Law.

Appendix D. Proof of Joint-Space Singularity Theorem

The constraint force can be written in terms of external force acting on the tip of the catheter,

$$\nabla h\lambda ={J_{\mathit{st}}^b}^T\left[\begin{array}{c}\hfill f\hfill \\ \hfill 0\hfill \end{array}\right],$$

with the manipulator Jacobian,

$$J_{\mathit{st}}^b=\left[{\xi }_{1x}^{†}{\xi }_{1x}^{†}\cdots {\xi }_{\mathit{nx}}^{†}{\xi }_{\mathit{nx}}^{†}\right].$$

The columns of $J_{\mathit{st}}^b$ are calculated as follows,

$${\xi }_{\mathit{ix}}^{†}={\mathrm{Ad}}_{\mathit{gi}\left(\theta \right)}^{-1}{\xi }_{\mathit{ix}}\text{and}{\xi }_{\mathit{iy}}^{†}={\mathrm{Ad}}_{\mathit{gi}\left(\theta \right)}^{-1}{\xi }_{\mathit{iy}},$$

with g_i(θ) given by

$$g_i\left(\theta \right)=e^{({\widehat{\xi }}_{\mathit{ix}}{\theta }_{\mathit{ix}}+{\widehat{\xi }}_{\mathit{iy}}{\theta }_{\mathit{iy}})}\cdots e^{({\widehat{\xi }}_{\mathit{nx}}{\theta }_{\mathit{nx}}+{\widehat{\xi }}_{\mathit{ny}}{\theta }_{\mathit{ny}})}{g}_{\mathit{st}}\left(0\right).$$

That is, g_i(θ) is the configuration of the tip frame given the joint angles from joint i to n. We can express it in a more meaningful way as g_i(θ) = (R_i, p_i) ∈ SE(3), where R_i and p_i are the orientation and the position of the tip written in the spatial frame. So, the columns of $J_{\mathit{st}}^b$ are given by

$$\begin{array}{cc}\hfill {\xi }_{\mathit{ix}}^{†}& =\left[\begin{array}{cc}\hfill R_i^T\hfill & \hfill -R_i^T{\widehat{p}}_i\hfill \\ \hfill 0\hfill & \hfill R_i^T\hfill \end{array}\right]\left[\begin{array}{c}\hfill -w_{\mathit{ix}}\times q_{\mathit{ix}}\hfill \\ \hfill w_{\mathit{ix}}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}\hfill R_i^T{w}_{\mathit{ix}}\times R_i^T(p_{\mathit{ix}}-q_{\mathit{ix}})\hfill \\ \hfill R_i^T{w}_{\mathit{ix}}\hfill \end{array}\right],\hfill \\ \hfill {\xi }_{\mathit{iy}}^{†}& =\left[\begin{array}{cc}\hfill R_i^T\hfill & \hfill -R_i^T{\widehat{p}}_i\hfill \\ \hfill 0\hfill & \hfill R_i^T\hfill \end{array}\right]\left[\begin{array}{c}\hfill -w_{\mathit{iy}}\times q_{\mathit{iy}}\hfill \\ \hfill w_{\mathit{iy}}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}\hfill R_i^T{w}_{\mathit{iy}}\times R_i^T(p_{\mathit{iy}}-q_{\mathit{iy}})\hfill \\ \hfill R_i^T{w}_{\mathit{iy}}\hfill \end{array}\right].\hfill \end{array}$$

Only the top part of $J_{\mathit{st}}^b$ (or more precisely, the left half of ${J_{\mathit{st}}^b}^T$) is multiplied to f. Using Jacobi identity, the joint torques of the i-th joint are then

$$\begin{array}{cc}\hfill {(\nabla h\lambda )}_{\mathit{ix}}& =\left[R_i^T{w}_{\mathit{ix}}\times R_i^T(p_{\mathit{ix}}-q_{\mathit{ix}})\right]\cdot f\hfill \\ \hfill & =\left[R_i^T(p_{\mathit{ix}}-q_{\mathit{ix}})\times f\right]\cdot R_i^T{w}_{\mathit{ix}},\hfill \\ \hfill {(\nabla h\lambda )}_{\mathit{iy}}& =\left[R_i^T{w}_{\mathit{iy}}\times R_i^T(p_{\mathit{iy}}-q_{\mathit{iy}})\right]\cdot f\hfill \\ \hfill & =\left[R_i^T(p_{\mathit{iy}}-q_{\mathit{iy}})\times f\right]\cdot R_i^T{w}_{\mathit{iy}}.\hfill \end{array}$$

Dot notation is used in the equation above to avoid using transposes. Jacobi identity is used to switch the order of operation. The terms $R_i^T(p_{\mathit{ix}}-q_{\mathit{ix}})$ and $R_i^T(p_{\mathit{iy}}-q_{\mathit{iy}})$ are the vectors from the tip to the i joint written in the tip frame, they will be referred to as the position vectors. Similarly, $R_i^T{w}_{\mathit{ix}}$ and $R_i^T{w}_{\mathit{iy}}$ are the rotation vectors of the i joint written in the tip frame. If the ith link is not perpendicular to the surface, then at least one of the cross products between the force and the position vectors is nonzero. The dot product is also nonzero because the force and the position vector cannot be simultaneously orthogonal to the half-angle vector, so the cross product between them cannot not orthogonal to the rotation vector. Therefore, the constraint force of the unactuated joints are not all zero.