Color constancy in a naturalistic, goal-directed task

Abstract

In daily life, we use color information to select objects that will best serve a particular goal (e.g., pick the best-tasting fruit or avoid spoiled food). This is challenging when judgments must be made across changes in illumination as the spectrum reflected from an object to the eye varies with the illumination. Color constancy mechanisms serve to partially stabilize object color appearance across illumination changes, but whether and to what degree constancy supports accurate cross-illumination object selection is not well understood. To get closer to understanding how constancy operates in real-life tasks, we developed a paradigm in which subjects engage in a goal-directed task for which color is instrumental. Specifically, in each trial, subjects re-created an arrangement of colored blocks (the model) across a change in illumination. By analyzing the re-creations, we were able to infer and quantify the degree of color constancy that mediated subjects' performance. In Experiments 1 and 2, we used our paradigm to characterize constancy for two different sets of block reflectances, two different illuminant changes, and two different groups of subjects. On average, constancy was good in our naturalistic task, but it varied considerably across subjects. In Experiment 3, we tested whether varying scene complexity and the validity of local contrast as a cue to the illumination change modulated constancy. Increasing complexity did not lead to improved constancy; silencing local contrast significantly reduced constancy. Our results establish a novel goal-directed task that enables us to approach color constancy as it emerges in real life.

Introduction

Color helps us to identify objects and learn about their current state; thus, in daily life, we frequently rely on color to select objects and decide how to interact with them. To serve as a reliable guide, color needs to support selection that is based on intrinsic object properties. Extracting information about surface reflectance, the physical correlate of perceived object color, from the spectrum of light reflected to the eye presents a challenging computational hurdle. This is because the light reflected from an object's surface entangles information about reflectance with the information about the incident illumination. Despite this, in daily life, we often use color to select objects across a wide range of illumination. For example, we rely on color to choose the ripest fruit both in the open-air farmers market and under fluorescent supermarket lights.

It is well known that color constancy mechanisms serve to partially stabilize object color appearance across illumination changes (Foster, 2011; Brainard & Radonjić, 2014). The question of how such stabilization supports accurate object selection, however, has not received much attention. In fact, color constancy has been rarely studied in the context of naturalistic selection tasks in which the subjects need to identify and select objects based on color across the illumination change (but see Robilotto & Zaidi, 2004, 2006; Zaidi & Bostic, 2008; also Bramwell & Hurlbert, 1996).

To study whether and to what degree color constancy supports accurate object selection across changes in illumination, we previously designed a task in which we asked subjects to select which of the two test objects presented under a test illumination matched a target object presented under a different illumination (Radonjić, Cottaris, & Brainard, 2015). Following the logic of maximum likelihood difference scaling (MLDS; Maloney & Yang, 2003; Knoblauch & Maloney, 2012), we developed a quantitative method that allowed us to use subjects' choices across a series of trials to infer a selection-based match—conceptually equivalent to the cross-illumination point of subjective equality—for a given target object and illumination change. We used these inferred matches to compute color constancy indices, which quantified the degree of color constancy that characterized subjects' performance. When we applied this elemental color selection task in a naturalistic stimulus context, we found that subjects demonstrated good constancy.

Here we extend our work by using the elemental color selection task as a building block to study performance in a more complex and naturalistic situation. We adapted the blocks-copying task used by Ballard and his collaborators, who introduced it to study eye movements and allocation of working memory (Ballard, Hayhoe, Li, & Whitehead, 1992; Ballard, Hayhoe, & Pelz, 1995). In this task, subjects copy arrangements of colored blocks.

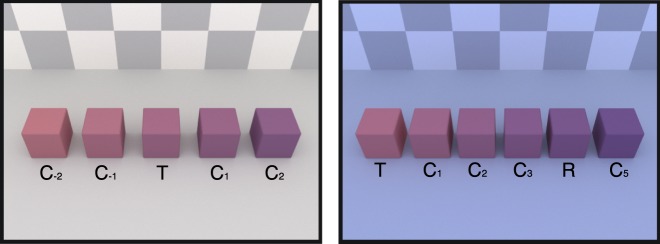
In our version of the blocks-copying task, subjects viewed three simulated rooms on a computer display (Figure 1), each room containing a set of blocks. The room on the left (the model) contained four colored blocks, which served as targets. The arrangement of these blocks (the target arrangement) varied from trial to trial. The room on the right (the source) contained eight blocks: a pair of potential matches for each target block. The middle room (the workspace) contained four black blocks. The subjects' task was to recreate the target arrangement as closely as possible by replacing the black blocks in the workspace with blocks they chose from the source. In illuminant-constant trials (Figure 1, top), all three rooms were rendered under the same simulated illumination (the standard illuminant, 6500 K). On illuminant-changed trials (Figure 1, bottom), only the model was rendered under the standard illuminant, and the source and workspace were rendered under a test illuminant. Thus, in illuminant-changed trials, subjects had to recreate the model across a change in illumination. Using the methods we developed previously for the elemental color selection task (Radonjić et al., 2015), we analyzed subjects' copies of the model to quantify color constancy.

Figure 1.

Stimuli in the blocks-copying task (Experiments 1 and 2, Set A). In each trial, subjects viewed three simulated rooms (the model, the workspace, and the source), each containing a set of blocks. Their task was to re-create the arrangement of blocks in the model as closely as possible by replacing the blocks in the workspace with blocks from the source. In illuminant-constant trials (top row), all three rooms were rendered under the same simulated illuminant (6500 K). In illuminant-changed trials (bottom row), the simulated illumination of the workspace and the source were changed to bluish (12,000 K), and the model remained under a 6500 K illuminant.

We report foundational experiments (Experiments 1 and 2) that show how our blocks-copying task may be used to quantify constancy and that establish baseline levels of performance. Across the two experiments, we measured constancy using two different sets of target reflectances and two different sets of simulated illuminants for two different groups of subjects. Experiment 3 used the blocks-copying task to investigate whether varying scene complexity and the local contrast—two stimulus characteristics thought to influence constancy in adjustment-based tasks—modulated constancy in our naturalistic, goal-directed task.

Experiment 1

Methods

Apparatus

Subjects viewed the stimuli on a calibrated 27-in. NEC MultiSync PA241W LCD color monitor driven at a pixel resolution of 1920 × 1080, a refresh rate of 60 Hz, and with eight-bit resolution for each RGB channel via a dual-port video card (NVIDIA GeForce GT120). The subject's head position was stabilized using a chin rest. The distance between the subject's eye and the center of the screen was 70 cm. The host computer was an Apple Macintosh with a Quad-core Intel Xeon processor. The experimental programs were written in Matlab and relied on routines from Psychtoolbox (Brainard, 1997; Pelli, 1997, http://psychtoolbox.org) and mgl (http://justingardner.net/doku.php/mgl/overview).

Stimulus

In each trial of the experiment, the subject viewed a stimulus consisting of three side-by-side images. We refer to these as the model, the workspace, and the source (Figure 1). Each image was a computer graphics rendering of a three-dimensional scene. Each scene consisted of a room containing a set of blocks. The rooms were identical in size and wall materials across the three scenes. The side walls, front wall, and ceiling were not visible in the image but affected it via mutual illumination. The side walls and ceiling were white with specified spectral reflectance equal to the white square in the Macbeth color checker chart (MCC; sample from row 4, column 1 of the chart; reflectances were obtained from http://www.babelcolor.com and provided as part of the RenderToolbox3 distribution, http://rendertoolbox.org, McCamy, Marcus, & Davidson, 1976). The front wall was located behind the camera position used for rendering and was blue (MCC sample from row 3, column 2). The floor was gray (MCC sample from row 4, column 2), and the back wall was covered with a white-and-gray checkerboard pattern using the MCC white and gray reflectances. All surfaces were matte.

The room displayed on the left (the model) contained four colored blocks. The same four block reflectances were used throughout a set of trials; their spatial arrangement was randomized in each trial. The middle room (the workspace) contained four blocks. At the beginning of each trial, the reflectance of these blocks was set to black (MCC sample from row 4, column 6). The room on the right of the stimulus (the source) contained eight blocks: a pair of potential matches for each of the target blocks. In each trial, these pairs of blocks were sampled from a competitor set, predefined for each target and illuminant condition (see below).

At the 70-cm viewing distance, each room subtended approximately 14.7° × 11.4° of visual angle (18 × 14 cm on the screen). In the target and workspace, each block subtended ∼2.5° (block height: 3 cm), and the size of the blocks in the source varied from ∼2.2° (2.7 cm) in the top row to ∼2.7° (3.3 cm) in the bottom row.

Illuminants

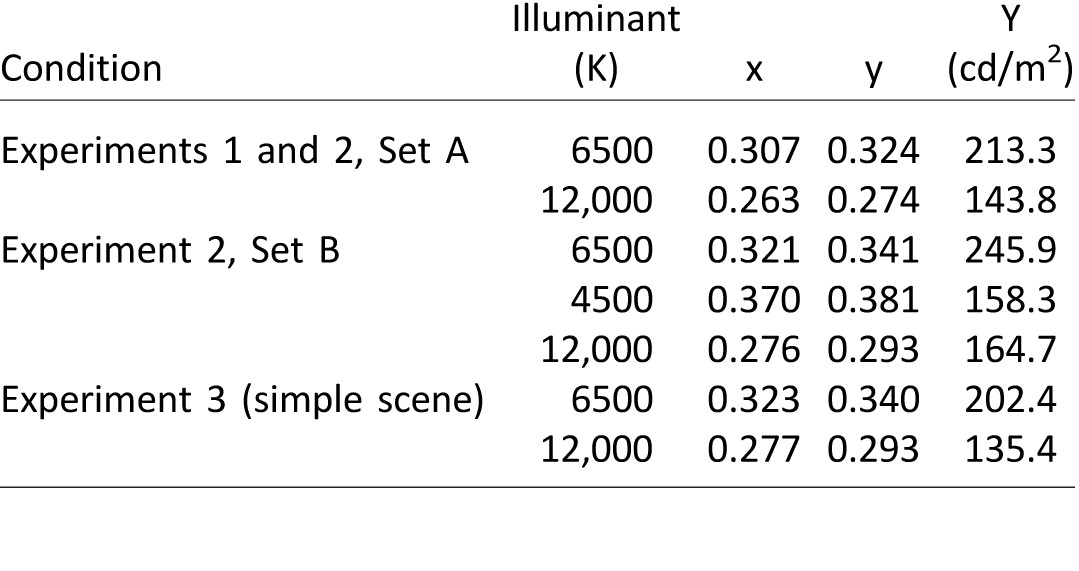
In illuminant-constant trials, all three scenes were rendered under the same standard illumination (CIE daylight; correlated color temperature 6500 K). In illuminant-changed trials, only the model was under the standard illuminant, and the simulated illumination of the workspace and the source were rendered under a test illuminant (CIE daylight: 12,000 K). Each room was illuminated by two area lights: one covering the entire surface of the ceiling and another covering the entire surface of the front wall. Secondary reflections off of the wall and ceiling surfaces were simulated by the rendering process. Table 1 provides illuminant specifications.

Table 1.

Chromaticity (xy) and intensity (Y; in cd/m²) of standard and test illuminants across experiments. Notes: The values were extracted from the image of a model in which the blocks were rendered as perfectly reflective surfaces. The values represent the mean xyY coordinates taken across pixels within a rectangular region inscribed at the top of each block and averaged across the four blocks.

Targets

Four colored blocks served as targets. Under the standard illuminant, all four blocks had essentially the same luminance. One of the blocks was achromatic (“gray”); the remaining three (“rose,” “teal,” and “green”) had roughly the same CIELAB chroma but varied in hue. Target surface reflectances were identical to those we used in a previous study in which we developed the elemental color-selection task that we here incorporate into the blocks-copying task (Radonjić et al., 2015). The spectral reflectances of the targets used to render the scenes are provided in the online supplement.

Competitor sets

We defined a set of competitors for each target block and illumination condition (Figure 2). In the illuminant-changed condition, the competitor set for each target block included six blocks: (a) the tristimulus match for the target block (denoted as T), whose reflectance was chosen so that under the test illuminant this block reflected a spectrum of light that had the same tristimulus coordinates as did the target block under the standard illuminant; (b) the reflectance match for the target (denoted as R), which had the same reflectance as the target but different tristimulus values when rendered under the test illuminant; (c–e) three color samples equally spaced between the tristimulus match and the reflectance match in CIELAB space (C₁, C₂, C₃); and (f) an overconstancy match. For a given target and test illuminant, we determined the nominal CIELAB values of competitors C₁, C₂, and C₃ by finding three equally spaced points on the line in three-dimensional CIELAB space connecting the tristimulus match and the reflectance match. The overconstancy match (C₅) was on the same line at equal distance from the reflectance match as competitor C₃ but displaced in the opposite direction in CIELAB space. Because the standard and the test illuminant differed in luminance (Table 1), the competitors also varied in luminance.

Figure 2.

Competitor set for one target block (“rose”). In the illuminant-changed condition (right), the competitor set consisted of six color samples: the tristimulus match (T) and the reflectance match (R) for the target, three blocks equally spaced between the tristimulus and the reflectance match in CIELAB space (C₁, C₂, C₃) and an overconstancy match (C₅). In the illuminant-constant condition (left), the competitor set consisted of five color samples: the tristimulus match (T), the two closest competitors from the illuminant-changed condition (C₁ and C₂) as well as two other competitors equally distant from the target but in the opposite direction along the same line in color space (C₋₁ and C₋₂).

In the illuminant-constant condition, each competitor set included five blocks. One of the blocks was a tristimulus match for the target (T), which in this condition was also the reflectance match for the target. Two competitors were the two closest competitors from the bluish illuminant-changed condition (C₁, C₂). The other two competitors were equally distant from the target as C₁ and C₂ but displaced in the opposite direction along the same line in the CIELAB color space (C₋₁ and C₋₂). For each competitor set, the table showing the distance between adjacent competitors (in CIELAB ΔE) is provided in the online supplement.

Reflectance functions for competitors were derived from their tristimulus values using a procedure we describe below.

In each trial, a pair of competitors for each target block was chosen randomly from its corresponding competitor set. This was done independently for each target. For example, in the illuminant-changed condition trial illustrated in Figure 1 (bottom row), the competitors for the rose target shown in the source were the tristimulus and the reflectance match (leftmost and rightmost block in the top row, respectively), but different pairs of competitors were used for the other target blocks (gray: C₁, C₂; teal: C₅, C₆; green: C₄, C₆). The location of each of the eight competitor blocks in the source was also assigned randomly in each trial. Across trials, each target block was paired with all pairwise combinations of its competitors.

Task

The subjects' task was to recreate the arrangement of blocks in the model as closely as possible by replacing the four black blocks in the workspace with four they chose from the source. They did so by using a mouse to move a cursor onto a block in the source, clicking, moving the cursor onto a block in the workspace, and clicking again. The chosen block was then rendered in the workspace, using a partitive mixture rerendering method that we have described previously (Griffin, 1999; Xiao & Brainard, 2008, see below). The subjects were allowed to choose and replace blocks in any order they wanted, and they could take as long as they needed to complete the task. In Experiment 1, they could only move a total of four blocks from the source into the workspace. It was possible for subjects to move a second block from the source and replace one that had already been set in the workspace. In this case, which occurred only in a small fraction of trials (for subject dlv: three, nit: four, kjf: four, ctg: nine trials out of 375), at least one block in the workspace remained black. In such cases, we did not obtain selection data for the corresponding target block in that trial but did use the data for the remaining targets.

Of note is that we did not explicitly instruct subjects to use color to guide their choices; this emerged naturally from the task structure. The experimental instructions are provided verbatim in the online supplement.

Procedure

At the beginning of the experiment, the subjects completed a brief training block, during which they listened to the experimental instructions and completed two trials (both from the illuminant-constant condition). They received no feedback about the quality of the arrangements they made.

Each subject then completed 15 experimental blocks of trials over four to five 1-hr sessions, each run on a different day. Each experimental block consisted of 25 trials (10 illuminant-constant and 15 illuminant-changed trials).

Subjects

Four subjects participated in Experiment 1 (all female; age 18–50). They all had normal or corrected-to-normal vision (20/40 or better as assessed by a Snellen chart) and normal color vision (Ishihara, 1977, no plates incorrect). One of the subjects (ctg) was a paid research assistant in the lab and familiar with the problem of color constancy in general but unaware of the logic and the goals of this experiment. The remaining three subjects were naive to the purpose of the experiment.

The research protocol has been approved by University of Pennsylvania Institutional Review Board and is in accordance with the World Medical Association Helsinki Declaration.

Stimulus geometry and rendering

The scene geometry of each room in the stimulus set was specified using the Blender modeling software (www.blender.org) and rendered using Mitsuba (http://www.mitsuba-renderer.org/), a physically based rendering program. Rendering was managed by RenderToolbox3 (Heasly, Cottaris, Lichtman, Xiao, & Brainard, 2014) routines, which enabled association of spectral surface reflectances with each object in the scene and spectral power distributions with each illuminant in the scene. Spectra were specified at 10-nm sampling intervals between 400 and 700 nm, and rendering was performed separately for each sample wavelength to produce hyperspectral image output. Rendering was done using Mitsuba's path tracer integrator, low discrepancy sampler, and a sample count of 320. Blender files describing the geometry of each room are available in the online supplement.

Rendering produced a 31-plane hyperspectral image of each scene. Each hyperspectral image was converted into a three-plane LMS representation by computing at each pixel the excitations that would be produced in the human L-, M-, and S-cones (via Stockman–Sharpe cone fundamentals; Stockman & Sharpe, 2000; CIE, 2007). The LMS images were then converted to RGB images for presentation using monitor calibration data that characterized both the spectral power distribution of the monitor's primaries and the nonlinear input–output relationship (gamma function) of each channel (Brainard, Pelli, & Robson, 2002). Monitor calibrations were made using a PhotoResearch PR-670 spectral radiometer.

Our calibration procedures did not include characterization of spatial inhomogeneities of the display. We instead measured the blocks in the model and the source at their screen locations for one stimulus set and found they were generally in good agreement with their expected values (see General discussion).

All data analysis was performed using nominal CIELAB stimulus values. As described above, we obtained nominal CIE XYZ tristimulus coordinates and CIELAB values for our stimuli from the underlying hyperspectral image data (see, for example, the next paragraph). Because the CIE XYZ color-matching functions are not an exact linear transformation of the Stockman–Sharpe cone fundamentals, the XYZ values we used differ slightly from those that would be obtained from direct measurement of the displayed stimuli even for a perfectly calibrated display. Rather, our nominal XYZ and CIELAB values are those that would be obtained from measurements of rendered stimuli for which the displayed stimuli are metamers when the metamers are computed with respect to the Stockman–Sharpe cone fundamentals.

In Experiment 1, target block reflectances were identical to those used in our previous study (Radonjić et al., 2015). The surface reflectance functions for each of the competitors were derived using the following procedure: To estimate the illuminant impinging on the surface of each of the target blocks, we rendered the target scene (one for each illuminant condition) in which the four blocks were specified as perfectly reflective surfaces (reflectance set to one at each sample wavelength). We then used these scenes to assess the uniformity of the illuminant across the target blocks (which was good: Across the tops of the four blocks, the luminance variation we measured was less than 1%, and chromaticity variation was less than 0.001 in x and y) and to estimate the illuminant spectra impinging on each of the target blocks. For one of the blocks (second from the left), we extracted the illuminant spectrum from the rendered hyperspectral images by averaging all pixels within a rectangular box inscribed on the top side of the block. We then used the target reflectance and this estimated illuminant spectrum to compute the XYZ coordinates of the tristimulus and the reflectance match in each condition (at this location). We converted these into CIELAB space (using the standard 6500 K illuminant's XYZ coordinates as the white point for the conversion) and then found the CIELAB values (as well as the corresponding XYZ values) for each competitor following the logic described above. These nominal CIELAB values were used in all further analyses. Note that, as would be the case with real objects, the CIELAB values for a block will change somewhat as its position in a rendered scene changes. We did not attempt to account for these changes.

We used standard colorimetric methods (Brainard & Stockman, 2010), together with a three-dimensional linear model for surface reflectance functions to compute the surface reflectance function for each competitor that would yield the requested XYZ values under the relevant illuminant. The linear model for surfaces that we used was derived from analysis of the spectra of Munsell papers (Nickerson, 1957) and is provided as part of the Psychophysics Toolbox distribution (http://psychtoolbox.org; first three columns of matrix B_nickerson).

Replacing the blocks in the workspace

It was not feasible to prerender each possible combination of blocks that the subject's choices would cause to appear in the workspace, nor could we rerender the entire workspace on the time scale of individual subject choices. To update the color of the four blocks in the workspace after each choice, we used a variant of the partitive mixture image synthesis method (Griffin, 1999). A previous paper from our lab (Xiao & Brainard, 2008) describes our implementation of this method in detail. In summary, for each illumination condition, we rendered a set of eight basis images of the workspace. The images were identical except for the rendered surface reflectance function of the four blocks. In each basis image, the surface reflectance function of all four blocks was identical and chosen across basis images so that the pixels at the top location of the blocks approximated each of the following monitor RGB values: {[0.8 0.8 0.8]; [0 0 0.8]; [0 0.8 0]; [0.8 0 0]; [0.2 0.2 0.2]; [0 0 0.2]; [0 0.2 0]; [0.2 0 0]}. In each basis image, we specified a separate region around each of the four blocks. Within each of these regions, we were able to independently recombine the eight basis images and synthesize these components into a single image that we displayed to a subject. In this way, we were able to manipulate the color of each of the four blocks independently and quickly produce the desired XYZ values for each block (which were found by combining the known surface reflectance function of the chosen block and the illuminant spectra impinging at the requested block location in the workspace). A Matlab class that supports this partitive mixing method is provided as part of the open source BrainardLabToolbox (http://github.com/DavidBrainard/BrainardLabToolbox; class PartitiveImageSynthesizer).

Online supplement

For all experiments, the online supplement (http://color.psych.upenn.edu/supplements/theblockstask/) provides instructions verbatim, detailed colorimetric specification of the stimuli (CIELAB, xyY and LMS values for each competitor set, and the white points used for CIELAB-XYZ conversion), and the spectral reflectances of targets and competitors as well as the illuminant spectra we used for rendering.

Inferring selection-based matches

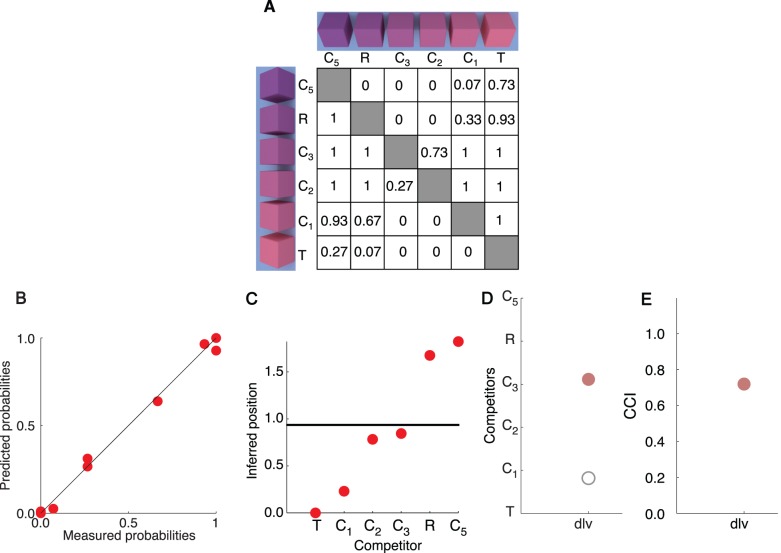
We analyzed each subject's performance in the blocks-copying task by summarizing the pattern of choices for each of the target blocks separately. Recall that within one experimental block, each target block was presented with all pairwise combinations of the competitors. For each target–competitor pair, we computed the proportion of trials in which one competitor in the pair was chosen relative to the other. The resulting pattern of choices for one target is shown as a choice matrix in Figure 3A. Each cell in the matrix gives the proportion of trials in which the block indicated by the row is chosen when paired with the block indicated by the column. For the matrix shown in the figure, for example, when the tristimulus match (T) is paired with the reflectance match (R), the tristimulus match is chosen 7% of the time.

Figure 3.

From subject's choices to color constancy indices. (A) The choice matrix for one subject (dlv) and target block (rose) in the illuminant-changed condition. For each pair of competitor blocks, the matrix indicates the proportion of trials in which the competitor from each row was chosen when paired with the competitor from each column. (B) The relationship between measured probabilities (shown in A) and those predicted based on the recovered positions of the target and the competitors. The log likelihood value corresponding to the solution shown was −15.7. For the illuminant change condition, the solution log likelihoods (across targets and subjects) ranged from −33.1 to −11.25 with a mean of −21.25. (C) Recovered positions of the target (horizontal black line) and competitors (red circles) corresponding to the solution in B. (D) The inferred match in the illuminant-changed condition is plotted as a filled circle (rose) relative to the space of competitors. The corresponding inferred match in the illuminant-constant condition is plotted as an open circle (gray). (E) The color constancy index corresponding to subjects' choices, computed from the inferred matches shown in D.

We analyzed the choice matrices to quantify the degree of color constancy, using the method we developed for the elemental color selection task (Radonjić et al., 2015). Our method relies on the observer model implemented in MLDS (Maloney & Yang, 2003; Knoblauch & Maloney, 2012), and it is described in detail in our previous paper. Briefly, we assume that each of the stimuli occupies a position in the subject's internal perceptual space and that this position varies from trial to trial because of perceptual noise. Thus, for each trial of our experiment, we can model the position each stimulus (the target and competitors) occupies in the perceptual space as a random draw from its own Gaussian distribution. We then assume that, in each trial, the subject chooses the competitor whose position in that trial is closest to that of the target.

The goal of our analysis is to infer the positions of the target and competitors in the perceptual space that best accounts for the subject's choices. To do this, we used a numerical search procedure. In each iteration, the search returns a set of candidate positions of the target and the competitors, which we then use to predict the probabilities in the choice matrix implied by that set of positions. Across iterations, the search procedure maximized the log likelihood of the measured choice matrix.

To constrain the search, we specified stimulus positions along a single dimension. Because the predictions of the underlying model are invariant with respect to shift of the origin and scaling of the space, we set the origin of the space (the position of the first competitor) at 0 and the scale, defined by the standard deviation of the noise, to 0.1. Note that, in our implementation, this noise was modeled as zero mean Gaussian noise and applied to the difference in target similarity (i.e., distance) to each of the two competitors (Maloney & Yang, 2003). We also required that the ordering of the mean positions of the competitors in the solution respected the ordinal nature of their specification and that the minimum distance between competitors in the solution was 0.025 (relative to the scale set by the standard deviation of 0.1). These analysis choices were developed in our earlier work (Radonjić et al., 2015.) and were not customized for the current data sets.

Figure 3B plots the relationship between the probabilities in the choice matrix of Figure 3A and the predicted probabilities based on the inferred stimulus positions. The agreement is very good, indicating that our underlying model accounts well for performance in this case. For each subject in each experiment, the choice matrices (in slightly different format) and plots that show the quality of the recovered solution (for each target and condition) are provided in the online supplement.

We refer to the recovered position of the target in the recovered perceptual space as the inferred selection-based match. Conceptually, the inferred match is equal to the selection-based point of subjective equality—it is the color sample that, when seen under the same illuminant as the competitors, the subject would choose most often when paired with any other competitor. As long as the recovered position of the inferred match falls within the range of the recovered positions of the competitors, we can obtain the physical stimulus coordinates for the inferred match by interpolating between the physical stimulus coordinates of the two competitors closest to it in the solution. The result of this procedure is illustrated in Figure 3D.

Across experiments, there were a few cases in which the recovered position of the inferred match for the illuminant-changed condition fell outside the range of the recovered positions of the competitors. In particular, in one condition of Experiment 3 (local-contrast-silenced condition with complex stimuli), subject mgo tended to choose the competitor closest to the tristimulus match to match one of the target blocks (“lettuce”). In this case, the position of the inferred match fell outside the range of the targets, and its exact position was not well constrained by the data. To handle this, we set the physical stimulus coordinates of the inferred match to be the CIELAB coordinates along the line between the tristimulus match and C₁, displaced from the tristimulus match away from C₁ by one tenth the CIELAB distance between T and C₁. This provides a quantification that is qualitatively consistent with the subjects' performance in such cases and allows us to compute corresponding constancy indices as described immediately below. We handled cases in which the inferred match fell outside of range on the opposite end of the competitor scale (beyond C₂ in the illuminant-constant or C₅ in the illuminant-changed condition) similarly. For subject iea in Experiment 2 and one target (set B, “lettuce”), this occurred in both the illuminant-constant and bluish illuminant change conditions. Here, the inferred match was assigned the physical stimulus coordinates along the line connecting the competitors in CIELAB space displaced from the last competitor by one tenth the CIELAB distance between R and C₅ (in the illuminant-changed condition) or C₁ and C₂ (in the illuminant-constant condition).

Computing color constancy indices

We used the inferred matches to compute a color constancy index (CCI) for each target and test illuminant:

In the formula, b denotes the Euclidian distance between the subjects' inferred match in the illuminant-changed condition and the reflectance match for the target (competitor R), computed in CIELAB space; a denotes the Euclidean distance between the inferred match in the illuminant-constant condition and the reflectance match for the target (Arend, Reeves, Schirillo, & Goldstein, 1991). In other words, the closer the subject's inferred match is to the reflectance match, the closer the CCI is to 1 (see Figure 4A and B). In computing the value of a for our main analyses, we chose to use the subjects' inferred match in the illuminant-constant condition rather than the values of the physical tristimulus match (T). We made this choice because using the subject's inferred matches in the illuminant-constant condition accounts for any bias observed in this condition (Burnham, Evans, & Newhall, 1957; Brainard, Brunt, & Speigle, 1997; Ling & Hurlbert, 2008). Indeed, across our experiments, the inferred matches for the illuminant-constant condition revealed small but consistent shifts away from the physical tristimulus match (T) toward the blue competitors. In secondary analyses, we also computed constancy indices with a computed with respect to the physical tristimulus match. In the results below, we note cases in which features of the data depend on which version of the constancy index is used.

Figure 4.

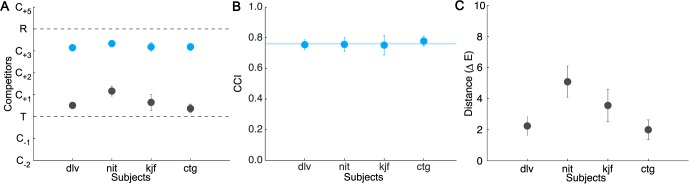
Results of Experiment 1. (A) Position of the inferred matches in the illuminant-constant condition (gray) and illuminant-changed condition (blue). Dashed lines indicate the tristimulus and reflectance matches. (B) CCIs, averaged across targets. Horizontal blue line indicates CCI averaged across subjects. (C) Distance between the inferred match in the illuminant-constant condition and the actual target block in ΔE_Lab units, averaged across targets. Error bars in all panels indicate ±1 SEM.

Results and discussion

For each of our four subjects, Figure 4 plots the position of the inferred match averaged across targets for the illuminant-constant condition (gray) and illuminant-changed condition (blue). The figure illustrates two main findings.

First, when the subjects copied the target arrangements with no change in illumination, they chose source blocks that matched the target blocks well; in the illuminant-constant condition, the difference between target blocks (T) and corresponding inferred matches was small for all subjects. We quantified the precision of subjects' matches in the illuminant-constant condition by computing the Euclidian distance (in CIELAB space) between each target and the inferred match. For most of our subjects, this difference was fairly small (mean across subjects: 3.22, ranging from 2.0 to 5.1, Figure 4C) and, for all but one subject (nit), smaller than the distance between the target and the nearest adjacent competitor (which ranged from 4.2 to 4.8 across targets; see online supplement). We found that precision varied significantly across subjects, F(3, 15) = 5.31, p < 0.05 (as shown by a repeated-measures ANOVA with subject as a random factor and target as a fixed factor).

Second, when the subjects copied block arrangements across an illumination change, the copied arrangements reflected a high degree of color constancy; the mean inferred matches in the illuminant-change condition were close to the reflectance matches (Figure 4A). Following the procedure described above, we computed constancy indices for each of the four target blocks (Figure 4B). On average, these indices were high for all four subjects (mean CCI = 0.76, range 0.75–0.78) and varied slightly across target blocks, F(3, 9) = 4.52, p < 0.05 (range across subjects: 0.68–0.82).

Experiment 2A

In Experiment 2A, we aimed (a) to replicate the findings from Experiment 1 with a different group of subjects and (b) to test a different, more naturalistic, set of block reflectances with a wider range of illumination changes. The subjects completed the blocks-copying task for two sets of stimuli. Stimulus Set A was identical to that from Experiment 1. Stimulus Set B (Figure 5) used different target block reflectances, different illuminant spectra, and competitor sets that did not include an overconstancy match.

Figure 5.

Stimuli for Experiment 2 (Set B). Target block reflectances were sampled from a set of natural reflectances provided by Vrhel et al. (1994). In illuminant-constant trials (top), all three rooms were rendered under the same simulated illuminant (6500 K). In illuminant-changed trials, the simulated illumination of the workspace and the source changed either to yellowish (4500 K, middle) or bluish (12,000 K, bottom). For illustration, we show examples of illuminant-changed trials in which for one target (Caucasian skin, leftmost block in the model for the illuminant-constant condition) the two competitors in the source are the tristimulus and the reflectance match. In the yellowish illuminant-change condition (middle row), the tristimulus and reflectance matches are the third and fourth blocks from the left in the top row, respectively. In the bluish illuminant-change condition (bottom row), the tristimulus match is the leftmost block in the top row, and the reflectance match is the rightmost block in the bottom row. In the illuminant-constant condition (top row), the tristimulus/reflectance match is the second block from the left in the bottom row.

Target reflectances for Set B were chosen from a database of surface reflectances measured for a set of natural and man-made objects (Vrhel, Gershon, & Iwan, 1994). We selected four samples of familiar natural reflectances for our target blocks labeled as corn, skin (Caucasian), lettuce, and bark (samples 132, 81, 141, and 128 in the database). Under each simulated illuminant, all target blocks differed considerably in chromaticity and luminance, and these differences were sufficiently large to make competitor samples for different target blocks clearly distinguishable from one another (see stimulus specification in the online supplement).

For Stimulus Set A, we used the same illuminations as in Experiment 1. For Stimulus Set B, we added a yellowish test illumination (4500 K daylight) in addition to the bluish test illuminant (12,000 K daylight). The standard and the bluish illuminants had the same correlated color temperature as in Experiment 1, but their overall intensity was reduced by ∼30%. In addition, the intensities of the yellowish and bluish test illuminants were roughly matched. The reflectance of the front wall for Stimulus Set B was changed to white (MCC sample from row 4, column 1). Due to modeling of secondary inter-reflections in the rendering process, this slightly changed the chromaticity of the illuminant spectra impinging on the blocks relative to those in Experiment 1 (the illuminant-constant and bluish illuminant-change condition; see Table 1).

In the illuminant-changed condition, the competitor sets for each target were constructed following the same methods as in Experiment 1 but did not include an overconstancy match. In the illuminant-constant condition, the competitor sets included the tristimulus (reflectance) match for the target (denoted as T) and the two closest competitors from the yellowish (C₋₁ and C₋₂) and bluish illuminant conditions (C₁ and C₂).

Unlike in Experiment 1, in Experiment 2 the number of blocks the subjects could move from the source into the workspace was not limited to four. Rather, the subjects were allowed to replace any of the blocks in the workspace with a block from the source as many times as they wished.

For Experiment 2, the host computer was upgraded to an Apple Macintosh Intel Core i7 (video card NVIDIA GeForce GTX 780M), which reduced the time needed to synthesize the workspace after each of the subject's choices.

A different group of six naive subjects participated in Experiment 2 (one male and five female; age 19–23). They all passed our initial acuity and color vision screening. Each subject completed 15 blocks of trials for each of the stimulus sets across six to seven experimental sessions (iea completed 16 blocks for Set A). For each subject, each session (typically lasting 60–90 min) was conducted on a different day. Within a session, blocks of trials using Stimulus Set A (10 illuminant-constant and 15 bluish illuminant-change trials) alternated with blocks using Stimulus Set B (10 illuminant-constant, 10 yellowish illuminant-change, and 10 bluish illuminant-change trials), and the order in which the two sets were presented was balanced across subjects (subjects ltd, iea, and hgc started with Set A).

Results and discussion

For each subject, Figure 6 plots the position of the inferred match averaged across targets for each stimulus set and illuminant condition. Inferred matches for Stimulus Set A are plotted in open circles and Stimulus Set B in filled circles; the illuminant-constant condition is plotted in gray, and the yellowish and bluish illuminant-changed conditions are plotted in orange and blue, respectively.

Figure 6.

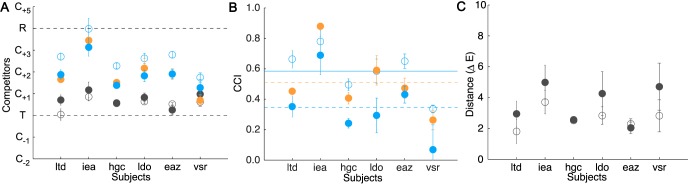
Results of Experiment 2A. Stimulus Set A is shown in open and Stimulus Set B in filled circles. The illuminant-constant condition is plotted in gray, bluish illuminant-change in blue, and yellowish illuminant-change in orange. The figure follows the same conventions as Figure 4. (A) Position of the inferred match across conditions. (B) CCIs averaged across targets. Horizontal lines indicate average CCI across subjects (solid blue line: Set A; dashed blue line: Set B bluish illuminant-change; dashed orange line: Set B yellowish illuminant-change). Error bars are symmetric and are truncated if the lower limb extends past the axis limit (0.0). (C) Distance between the inferred match (illuminant-constant condition) and the target block in ΔE_Lab units averaged across targets.

Consistent with the results of Experiment 1, the precision of subjects' matches in the illuminant-constant condition was good. The CIELAB ΔE distance between the inferred match and the target block was small and did not differ systematically across the two stimulus sets (Set A: M = 2.66, range: 1.80–3.70; Set B: M = 3.58, range: 2.03–4.98). For comparison, the distance between adjacent competitors for each competitor set is provided in the online supplement. Interestingly, the inferred matches in this condition showed slight but consistent blue bias: For both stimulus sets, the majority of inferred matches across all subjects were shifted toward the bluish competitors. If there had been no bias, we would expect the inferred matches to cluster around the tristimulus match and vary in both the bluish and yellowish directions. When we analyzed the inferred matches for individual targets across all subjects in this condition, we found that only three of 24 matches were shifted in the yellowish direction in Set A and only one out of 24 for Set B. We observed a similar bias in Experiment 1 (Figure 4A). There, only two out of 16 individual matches in the illuminant-constant condition was shifted in the yellowish direction. We hypothesized that the blue bias in the illuminant-constant condition emerged because the perceptual difference between the competitor samples T and C₁ was smaller than that between T and C₋₁. This, in and of itself, could lead to more choices of C₁ over T than of C₋₁ over T and thus lead to a small blue bias in the inferred match. However, we tested and rejected this hypothesis in Experiment 3 below.

Subjects' performance in the illuminant-changed condition revealed moderately high overall constancy for all conditions (Stimulus Set A: M = 0.58; Stimulus Set B, bluish illuminant change: M = 0.35; Stimulus Set B, yellowish illuminant change: M = 0.51). These constancy levels are lower than those we found in Experiment 1 (M = 0.76). In Experiment 2, we also see larger individual variability than we did in Experiment 1, and examination of Figure 6 reveals that this variation is systematic across stimulus sets and illuminant-change conditions. Although we found overall lower constancy in Experiment 2, the mean constancy index for one subject (iea) in Experiment 2 was within the range of those measured in Experiment 1, suggesting that one factor leading to the different constancy indices across the experiments may be real differences between the subjects who participated in the two experiments.

Further, constancy was significantly higher for the bluish illuminant-change condition for stimulus Set A than for Set B (matched pairs t test on mean constancy indices, t(5) = 7.37, p < 0.001). Although there was a small difference in the bluish illuminant used for the two stimulus sets, the primary difference was in the reflectances of the target blocks (the target blocks in Set A were more bluish than those in Set B).

Constancy was higher for the yellowish than for the bluish illuminant change condition for stimulus Set B, F(1, 15) = 21.43, p < 0.01. This “yellow advantage” is in the opposite direction from the blue–yellow asymmetry on constancy reported previously using achromatic adjustment (Delahunt & Brainard, 2004) and one that we found using asymmetric matching (Radonjić et al., 2015). Note, however, that the observed difference between blue and yellow illuminant disappeared in our secondary analysis in which constancy indices were computed using the physical tristimulus match as the referent. This is because a blue bias in the illuminant-constant matches reduces the constancy indices obtained for bluish illuminant changes and increases the constancy indices obtained for yellowish illuminant changes. Thus, in the absence of a good understanding of the cause of the small bias in illuminant-constant matches, we do not think any strong conclusions should be drawn from the finding that constancy was higher under the yellowish illuminant change we observed here.

Experiment 2B

In Experiment 2B, we explicitly tested the assumption underlying our analysis method that the inferred selection-based match we derived from subject's choices for a given target and illumination condition provided a good approximation of the subject's selection-based point of subjective equality. This assumption would be supported if, given the choice between a color sample corresponding to their selection-based match and any other sample from the competitor set, subjects predominantly choose their inferred match. To test this, for each of our subjects, we rendered two customized stimulus sets—one for Set A and one for Set B—based on a preliminary analysis of Experiment 2A.

For each stimulus set, the model and the workspace were designed following the same procedures as in Experiment 2A. As in Experiment 2A, the source contained a pair of potential matches for each target block, but these pairs were designed so that in each trial one of the blocks in the pair was close to the inferred selection-based match for that subject. For each target and illuminant condition, this block was paired with all other members of the original competitor set from Experiment 2A. Our stimulus construction was based on a preliminary analysis of the data in Experiment 2A, and the actual inferred matches in our final analysis differed slightly from the preliminary inferred matches that were presented. We account for this fact in our data analysis for Experiment 2B below.

Five subjects who participated in Experiment 2A took part in Experiment 2B (all but hgc). For each of the subjects, we rendered customized Stimulus Sets A and B that included samples corresponding to their preliminary selection-based match. The remaining competitors for each set were the same for all subjects and identical to those used in Experiment 2A. For each subject, we provide the coordinates of their inferred matches (both the preliminary and the final ones) in the online supplement.

Each subject completed the experiment (30 blocks of trials total, 15 per set) in three to four sessions, each run on a different day and typically consisting of 10 blocks of trials. Blocks of trials using customized Stimulus Set A alternated with those using customized Stimulus Set B blocks (but always started with Set A).

An experimental block for a customized Stimulus Set A consisted of 11 trials in which each of the competitors from the set was paired with the preliminary inferred match (five illuminant-constant trials and six illuminant-changed trials); blocks for customized Set B consisted of 15 such trials (five illuminant-constant trials, five yellowish illuminant-changed trials, and five bluish illuminant-changed trials).

Results and discussion

For each pair of presented test blocks (the preliminary inferred match and one of the competitors), we computed the proportion of trials across the 15 repetitions in which the subject chose the test block closer to his or her (final) inferred match from Experiment 2A. Generally, but not always, the test block closest to the final inferred match was the preliminary inferred match. For each target and condition, Figure 7 plots this proportion for each presented pair of blocks as a function of their relative distance to the inferred match in CIELAB space (ΔE_Lab units). Specifically, we computed the distances in CIELAB space between the inferred match and each of the two presented test blocks; the x-axis in Figure 7 shows the absolute difference between these two values.

Figure 7.

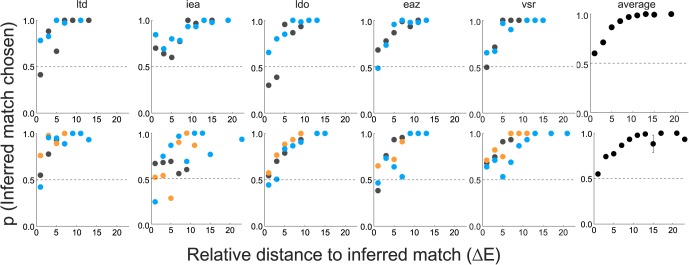
Results of Experiment 2B. Proportion of trials in which subjects chose the test block that was closer to their inferred matches (relative to another competitor) is plotted as a function of the relative distance to the inferred match (see text). These proportions are binned (bin size: two ΔE units), and the bin average is plotted at the center of each bin. Each subplot corresponds to one subject with data for sets A and B in the top and bottom rows, respectively. For each set, the illuminant-constant condition is plotted in gray, the bluish illuminant-change in blue, and the yellowish illuminant-change in orange. The subplots on the far right represent the average across all subjects and conditions for each set with error bars representing ±1 SEM.

Note that when the inferred match is equally distant from each of the test blocks presented in a trial, the probability of a subject choosing one sample in the pair relative to another should be near chance (0.5). When the difference between the inferred match and at least one of the samples is above threshold—if the logic of our MLDS analysis is correct—subjects should tend to choose the sample that is closer to their inferred match at greater than chance levels. The results are consistent with this prediction. For all levels of difference, subjects predominantly chose the test block closer to their inferred match with the average greater than 50% in all cases (right-hand panels of Figure 7). Further, as the distance between the inferred match and one of the test blocks increased relative to the other, the proportion of trials in which the subjects chose the block closer to the inferred match approached 1. These observations hold for both stimulus sets and all illumination conditions.

Experiment 3

In Experiment 3, we investigated whether the degree of color constancy that characterizes subject performance in our naturalistic task depended on stimulus characteristics, such as scene complexity and local contrast. Previous studies have shown that both of these factors can influence constancy when constancy is assessed using adjustment or match-to-palette methods. For example, increasing scene complexity (also referred to as “articulation”; Gilchrist & Annan, 2002) by increasing the number of contextual surfaces can sometimes, but not always, increase color and lightness constancy (Henneman, 1935; Gilchrist et al., 1999; Kraft, Maloney, & Brainard, 2002; Radonjić & Gilchrist, 2013). Further, studies that explore the role of local contrast information in maintaining color constancy have shown that when local contrast is “silenced”—so that the change in illumination conditions is not accompanied by a change in local contrast—constancy significantly decreases but is not fully abolished (Kraft & Brainard, 1999; Kraft et al., 2002; Delahunt & Brainard, 2004; Xiao, Hurst, MacIntyre, & Brainard, 2012).

In Experiment 3, we modified the wall and floor pattern across our three simulated rooms to vary scene complexity. In one condition (the simple scene condition), the walls and the floors were homogenous and assigned a single surface reflectance. In the other condition (the complex scene condition), the walls and the floors were divided into a number of separate “tiles” that were assigned a range of different surface reflectances. For each level of scene complexity, we also manipulated local contrast as we changed the illuminant. In one set of stimuli, information about the illuminant change carried by local contrast was preserved (i.e., the change in reflected light from the region of the floor that was retinally adjacent to the blocks was consistent with the illumination change as it was in the illuminant-changed conditions of Experiments 1 and 2). In a second set of stimuli, local contrast was silenced across the illuminant change (i.e., the average reflected light from the region immediately adjacent to the blocks was held constant across the illuminant change). This was done by changing the reflectance of the simulated surfaces adjacent to the blocks so as to counteract the effect of the illuminant change on the light reflected from this region of the scene.

Methods

We used the same block target reflectances as in Experiment 2B except for target T₁ (corn), which was replaced with the slightly darker sample from the Vhrel database that was similar in chromaticity (straw). We used the same spectra for the standard and the bluish test illuminant as in Experiment 2 (Table 1; the yellowish test illuminant was not used in this experiment). For each target block, the competitor set in the illuminant-changed condition was designed in the same manner as in the previous experiments. In the illuminant-constant condition, the competitor set was modified relative to our earlier design with the intention to overcome the subjects' bias toward selecting “bluish” competitors that was revealed for this condition in previous experiments. As discussed above, we hypothesized that this bias occurred because the perceptual difference between the target (T) and the nearest bluish competitor (C₁) was too small relative to the difference between the competitors T and C₋₁. We therefore increased the distance between the competitors T and C₁ in the illuminant-constant condition so that it was larger than the distance between samples T and C₁ in the illuminant-changed condition by a factor of 1.5. This change applied only to C₁ in the illuminant-constant condition. The placement of the other competitors in this condition was chosen according to the same logic as used for Experiment 1.

The simple and complex versions of the background were constructed in the following way: We first classified the set of reflectances in the Vhrel database into those that belong to natural versus man-made objects. Out of the 120 natural reflectances, we selected 48 samples that, when rendered under the standard illuminant, substantially differed from any of the target reflectances (by a minimal distance of 13 ΔE units in CIELAB space). These 48 samples constituted a set of surface reflectances that were used for tiling the rooms in our complex scene condition. We divided the visible surfaces of the back wall and the floor of each of the three rooms in the stimulus set into 62 distinct rectangular tiles (16 on the wall, 46 floor tiles, see Figure 8). On each rendering of each room, 24 surfaces were randomly selected from our stimulus set (without replacement) and assigned to different tiles in that room. No two adjacent tiles had identical reflectance. Manipulating the background in this way ensured that in each trial a random choice of surfaces would tile each room. Across rooms, surfaces could repeat because they were sampled from the same larger stimulus set. We choose to design our stimuli in this way rather than keeping the surfaces and their arrangement identical across the rooms because we wanted to model a situation in which the subject is recreating the target arrangement across different rooms, each having different wallpaper.

Figure 8.

Stimuli in the illuminant-changed condition of Experiment 3: simple (rows 1 and 2) and complex (rows 3 and 4) scenes. Examples of stimuli in which the local contrast is preserved when the illuminant in the workspace and the source changed to bluish are shown in the first and third rows. Stimuli for which the local contrast was silenced across the illumination change are shown in the second and fourth rows. For illustration, we show examples in which for one target (straw, shown as the rightmost block in the model in the top row) the two competitors shown in the source room are the tristimulus and reflectance match. From top to bottom rows of the figure, the tristimulus match is the fourth block in the top row (counting from left to right), third block in the bottom row, third block in the top row, and fourth block in the in the bottom row. The reflectance match is the first, second, first, and third block in the bottom row.

In the simple background condition, the visible portions of the wall and the floor across the rooms were homogenous and assigned the same surface reflectance, which was obtained by averaging the 48 reflectance samples from the tile set. Under the standard illuminant, at the location immediately surrounding the blocks the luminance and xy chromaticity of this surface were approximately 40 cd/m² and [0.41, 0.40]. As in Experiment 2, the ceiling and the walls that were not visible were all assigned the surface reflectance of the white MCC sample in all conditions.

To create the version of the background for which the local contrast was silenced, we first estimated the illuminant spectra impinging on the area immediately surrounding the target blocks by rendering 24 tiles in the center of the floor as perfectly reflective surfaces (reflectance of one). We then we used standard colorimetric methods (Brainard & Stockman, 2010) to find a “silenced” reflectance for each of the tiles from our set as well as for the mean surface reflectance used in the simple scene condition. Each “silenced” reflectance resulted in reflected light with the same tristimulus values (XYZ) under the bluish test illuminant as its generating reflectance would produce under the standard illuminant. Note that some of these “silenced” surfaces were not physically realizable. In performing this calculation, we used the same three-dimensional linear model for surfaces as we did for producing competitor reflectances with desired XYZ values under specified illuminants.

In the local-contrast-silenced condition, the “silenced” reflectances were used to tile the central area of the floor that immediately surrounded the blocks. In the complex scene condition, this area consisted of 24 central tiles (12 reflectance samples out of the initial 24 chosen to tile the room; see Figure 8). In the simple scene condition, the corresponding central area was covered with the “silenced” version of the surface that was covering the remaining parts of the wall and the floor. Thus, in this condition the spatial average of the light reflected from the central area surrounding the blocks was equivalent to the spatial average of the light reflected from the (nonsilenced) surfaces under the standard illumination. Note that in the complex scene condition the equivalence is only on average and not on a surface-by-surface basis because the draw of individual surfaces in this central area differed across the model, workspace, and source. The light reflected from the remaining surfaces was consistent with the bluish illumination change.

Occasionally, rendering some silenced reflectances in the workspace in the complex scene condition could cause image artifacts, which manifested as a golden glow at the points of contact between a block and the adjacent tile, particularly when both the chosen block and the tile had high luminance. To minimize these artifacts, we made the following adjustments to our method of creating the stimuli: (a) We excluded several of the most reflective Vhrel samples from the set of tiles, (b) we modified the first four images from the basis image set (used for synthesizing the block color in the workspace) so that each simulated block reflectance (at the top location) approximated the monitor RGB settings of {[0.55 0.55 0.55]; [0.55 0 0]; [0 0.55 0]; [0 0 0.55]}, (c) we replaced one of the targets (T₁) from the previous experiment (corn) with a darker sample (straw from the broom, sample 154), and (d) we doubled the rendering sampling rate (sample count 640). The combination of these steps eliminated any noticeable artifacts in the stimuli.

A new group of six naive subjects participated in the Experiment 3 (two male, four female; aged 19–21). They all passed our acuity and color vision screening tests. Each subject completed the experiment, which consisted of 32 blocks of trials total (16 simple and 16 complex) in eight sessions, each lasting approximately an hour. One additional subject (edh, female, age 19) was recruited but decided to stop participating in the experiment after the first session, and her data was not analyzed. Within a session, subjects typically completed four blocks of trials. Each block consisted of 30 trials. Within a block, the level of stimulus complexity was fixed (simple or complex), and the trials were presented in random order (10 illuminant-constant, 10 illuminant-changed with local contrast preserved, and 10 illuminant-changed trials with local contrast silenced). Within a session, blocks of trials using simple stimuli alternated with those using complex stimuli, and their order was balanced across subjects (subjects sed, nkj, and mgo started with simple stimulus set).

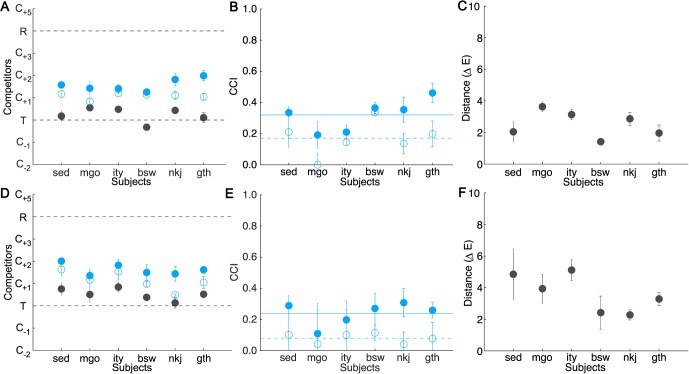
Results and discussion

Figure 9 plots the results for the simple scene (Figure 9A through C) and the complex scene conditions (Figure 9D through F).

Figure 9.

Results of Experiment 3. The simple scene condition is shown in the top and the complex scene in the bottom row. The illuminant-constant condition is plotted in gray; the illuminant-change conditions are plotted in blue (filled circles: local contrast preserved; open circles: local contrast silenced). The figure follows the same conventions as Figure 4. (A and D) Position of the inferred match across conditions. (B and E) CCIs averaged across targets. Horizontal lines indicate average CCI across subjects (solid line: local contrast preserved; dashed line: local contrast silenced). Error bars are symmetric and are truncated if the lower limb extends past the axis limit (0.0). (C and F) Distance between the inferred match (illuminant-constant condition) and the target block in ΔE_Lab units averaged across targets.

With respect to our primary experimental questions, we find (a) that increasing scene complexity did not improve constancy and (b) that silencing the change in local contrast across a change in overall scene illumination reduced constancy. Both of these findings replicate the results obtained in a preliminary study of similar design that we conducted in preparation for Experiment 3. A brief description of the stimuli, experimental design, and results of the preliminary study are available in the online supplement.

With respect to the effect of scene complexity, we observed a decrease in the mean constancy index between our simple and complex scene conditions. This change is in the direction opposite from the one we had expected. A three-way repeated-measures ANOVA (with scene complexity, local contrast, and target as within-subject factors) showed that this decrease was statistically significant (main effect of scene complexity, F(1, 15) = 11.83, p < 0.05). Nonetheless, we failed to replicate the finding that constancy decreases with increase in complexity when the ANOVA was repeated using constancy indices computed with respect to the physical tristimulus match for each target (rather than with respect to the corresponding inferred match from the illuminant-constant condition). The preliminary experiment also did not yield support for an increase in constancy with complexity with either analysis method (see online supplement). We are hesitant to conclude that our complexity manipulation decreased constancy because there was not a consistent effect across choice of analysis method in either the main or the preliminary experiment. What we can say with confidence is that our data provide no support for the hypothesis that increasing complexity by increasing the number of surfaces in the scene leads to improved constancy.

It is possible that the absence of an effect of scene complexity on constancy in our data is due to the particular way we chose to manipulate distribution of surfaces across our scenes. Recall that rather than keeping the surfaces fixed across rooms within a trial, we fixed the set of surfaces that could be used for tiling the scenes and randomly sampled a subset of these when rendering each scene. It may be that fixing the surfaces across scenes within a trial would provide more salient cues to the visual system about the change of illumination across scenes and hence increase constancy. Our design was motivated by the observation that, in real life, objects are often viewed against a different background across illumination changes.

Note also that particular stimuli we used in the complex scene condition have a visually jarring appearance—somewhat reminiscent of an image of an early 1970s discotheque—and that the presence of numerous colored tiles can make the target blocks more difficult to segment from the background. It is possible that this feature of the stimuli masks an underlying effect of complexity on constancy. Perhaps a more naturalistic way of increasing scene complexity, for example, by adding more contextual objects to the scene, would yield different results.

We found no effect of scene complexity on the precision of subjects' inferred matches in the illuminant-constant condition, F(1, 15) = 5.35, p = 0.07 (but see results of preliminary experiment). For both levels of scene complexity, the inferred matches for one of the targets (skin) were consistently more precise (main effect of target, F(3, 15) = 7.00, p < 0.01; based on the two-way repeated-measures ANOVA on the deviations from veridicality with the scene complexity and target as within-subject factors). Increasing competitor spacing failed to eliminate the blue bias: Analysis of the inferred matched for individual targets across all subjects revealed that the majority of matches in the illuminant-constant condition were shifted in the bluish direction (17 of 24 in the simple and 20 of 24 in the complex scene condition).

When the illumination in the source and in the workspace changes but the light signal from the background immediately surrounding the blocks remains, on average, the same as in the model, constancy is significantly reduced (main effect of local contrast, F(1, 15) = 32.15, p < 0.01). Silencing local contrast reduced overall constancy by 15% in the simple and by 16% in the complex scene conditions but did not fully abolish it: Both simple and complex condition t tests conducted on the mean constancy indices (averaged across targets) for each subject indicate that constancy is significantly different than zero (simple: t(5) = 3.80, p < 0.05; complex: t(5) = 6.15, p < 0.01). This finding is in agreement with a number of previous studies that also measured effects of silencing local contrast in fairly naturalistic scenes but used the method of achromatic adjustment (Kraft & Brainard, 1999; Kraft et al., 2002; Delahunt & Brainard, 2004; Xiao et al., 2012). Although silencing local contrast had a different effect for different target blocks, Local Contrast × Target interaction: F(3, 15) = 7.27 p < 0.01, the overall effect on constancy was comparable across the two levels of scene complexity (neither Scene Complexity × Local Contrast nor Scene Complexity × Local Contrast × Target interaction was significant).

General discussion

To approach understanding how color constancy operates in real life, we developed a goal-directed task in which we asked the subjects to re-create arrangements of colored blocks across a change of illumination. In Experiments 1 and 2, we demonstrated how this blocks-copying task could be used to quantify constancy. Across the two experiments, we used two different sets of block reflectances, two different sets of illuminant spectra, and two different groups of subjects. On average, the degree of color constancy mediating subjects' performance in the blocks-copying task was good in these experiments and slightly higher than that we found previously with the elemental color selection task (Radonjić et al., 2015). In the most comparable condition of that earlier study (bluish illuminant-change in Experiment 1), the mean constancy index (recomputed relative to the inferred match for the illuminant-constant condition) was 0.54 (ranging from 0.36 to 0.72), compared to 0.65 (ranging from 0.34 to 0.78) in Experiments 1 and 2A here. Given differences in design and subjects, we believe that the small overall difference in constancy and well-matched between-subject range across experiments suggest that our elemental color selection task and its more complex (blocks-copying) variant yield similar levels of constancy.

In Experiment 2, constancy was significantly higher for Stimulus Set A than for Stimulus Set B (bluish illuminant-change), which used different target reflectances but similar illuminant spectra. This difference held whether we computed constancy with respect to the inferred match in the illuminant-constant condition or with respect to the physical tristimulus match. On the other hand, within each experiment, we did not find a compelling effect of target reflectance on constancy. Although in some cases there was a significant main effect of target when constancy was computed with respect to one of the two ways of computing constancy indices, this effect was never significant for both analyses within a single experiment.

An important future goal is to develop a theory that predicts how an illuminant change affects performance for any target. There are several candidate theories available in the literature (Burnham et al., 1957; Stiles, 1978; Brainard & Wandell, 1992; Brainard et al., 1997), but evaluating these requires a data set with more target reflectances than we studied here. A number of these theories were developed in the context of studies that considered how early visual mechanisms adapt to low-level image properties (e.g., spatiotemporal means and variances of the cone responses and cone-opponent mechanisms) and are based on the data from parametric studies that employed simple and well-controlled retinal stimulation (e.g., spatially uniform spots presented on spatially uniform backgrounds). Although our results on the effect of silencing local contrast speak to the role of contrast mechanisms in constancy, obtaining a fuller understanding of the degree to which mechanisms of adaptation revealed by earlier studies can account for the effects we measure using our naturalistic stimuli and task remains an open question for future studies. Because subjects in our experiment freely fixate at different locations in the stimulus, making such links will require the use of eye tracking so that the detailed retinal image sequence may be derived and incorporated into a model.

Across experiments, we found that in the illuminant-constant conditions subjects consistently chose samples that led to an inferred match that was slightly bluer than the target. We do not have an explanation for this bias. As we noted earlier, we checked for spatial inhomogeneities in the display by measuring all stimuli in situ in the model and source images for one stimulus set (Experiment 2, Set B) and found minimal chromaticity differences with location. There were slight differences in luminance, but these seem unlikely a priori to produce the measured biases.

We also found that performance in the blocks-copying task could significantly vary across subjects. We reanalyzed the data from each experiment by modifying the ANOVAs so that they include subjects as a random factor in addition to the fixed within-subject factors. We found a significant effect of subject in Experiment 2 for both Set A, F(5, 23) = 10.35, p < 0.001, and Set B, F(5, 47) = 19.06, p < 0.05, but not in Experiments 1 and 3. Note also that the overall difference in constancy index between Experiment 1 (CCI = 0.76) and Experiment 2 Set A (CCI = 0.58) seems most likely to be caused by subject differences (as discussed above). Although the fact that subjects can significantly differ in their performance in color and lightness constancy tasks is well established (e.g., Ripamonti et al., 2004; Reeves, Amano, & Foster, 2008), we do not currently have a good understanding of what factors lead to the individual variability. One possibility is that differences in performance reflect different task strategies adopted by subjects. Alternatively, differences in constancy may be mediated by differences in perception, differences in cognitive processing (e.g., working memory; Allen, Beilock, & Shevell, 2012), or even individual artistic experience (for example, for painters and photographers conscious compensation for illuminant changes may be a result of artistic training).

Our findings further contribute to the literature showing the importance local contrast information plays in maintaining constancy: When the change in illumination was not followed by the corresponding change in local contrast, constancy was significantly reduced, but it was not fully abolished. Thus, additional mechanisms beyond local contrast also contribute to constancy. Our experiments were not designed to probe the nature of such mechanisms; indeed, our manipulation that silenced local contrast also affected other potential cues to the illuminant change (e.g., the change in the spatial average of the image). Our current finding is consistent with a number of previous studies that used adjustment methods (Kraft & Brainard, 1999; Kraft et al., 2002; Delahunt & Brainard, 2004; Xiao et al., 2012; see also Hansen, Walter, & Gegenfurtner, 2007, on the effect of reducing cues to the illuminant change in a color categorization paradigm), and it extends the general result to the more naturalistic task that we used here.

The fact that our scene complexity manipulation did not improve constancy is also consistent with findings from a number of earlier studies. For example, Amano, Foster, and Nascimento (2005) measured constancy using an asymmetric matching task and stimuli consisting of simulated square paper patches presented on a computer screen and found no significant change in constancy when the complexity of the pattern in which the test patch was embedded increased from two to 49 simulated surfaces (see also Valberg & Lange-Malecki, 1990). Similarly, Nascimento, de Almeida, Fiadeiro, and Foster (2005) studied subjects' ability to discriminate changes in illumination from changes in surface reflectance of a test object in real three-dimensional scenes and found that subjects performed equally well when the stimulus scene was sparse and when it contained 24 different colored objects. Finally, using a design similar to ours, Kraft et al. (2002) measured constancy via an achromatic adjustment method in real three-dimensional scenes while varying both complexity and local contrast information. Consistent with our results, they found that increasing complexity—by adding objects, such as Macbeth color chart and rectangular cuboids—had no effect on constancy when the local contrast information was preserved across a change of illumination. Unlike us, however, they found that increasing complexity significantly improved constancy when local contrast information was silenced.

Our interest in studying our complexity manipulation is that we would like, in general, to understand what aspects of scene variation influence constancy. Our choice to increase the number of distinct surfaces as an operationalization of complexity was motivated by theoretical work that suggests that having a larger set of surfaces to sample from increases the information available to the visual system for estimating the illuminant (Buchsbaum, 1980; Maloney & Wandell, 1986; Brainard & Freeman, 1997) as well as by the experimental studies cited above. We note that we do not have at present a precise technical definition of complexity nor precise ways of relating the concepts of scene complexity and scene naturalness.

One limitation of our current color selection task is that we restrict the position of the competitors to a line in color space connecting the tristimulus and reflectance matches. This choice then constrains the position of the inferred matches to lie along this line. Studies using asymmetric matching generally show that matches cluster in the vicinity of the line connecting tristimulus and reflectance matches (Brainard & Radonjić, 2014; Radonjić et al., 2015) so that this limitation is not likely to have a large distorting effect upon our results and conclusions. Nonetheless, it would be valuable to develop an adaptive version of our method that would allow subjects' inferred matches to fall anywhere in the three-dimensional color (see Jogan & Stocker, 2014).

In our previous paper (Radonjić et al., 2015) we explicitly compared the levels of constancy in our elemental color selection task with those measured using the asymmetric matching task and closely matched stimuli. For neutral instructions (“select the test that is closest in color to the target”; “adjust the test to match the target in color”), the two types of tasks are in good agreement. Carefully characterizing the relationship between matching and selection in our blocks-copying tasks is another important goal for future work. It is worth noting, however, that the overall levels of constancy in experiments we report here (mean CCI = 0.46; range: 0.24–0.76; averaged across experiments and conditions in which local contrast was preserved across a change in illumination) is comparable to those previously reported in the literature for studies that used simultaneous asymmetric matching (mean CCI = 0.52; range: 0.11–0.89; based on review by Foster, 2011). Also, the overall pattern of results in Experiment 3, which tested the specific mechanistic hypothesis about constancy, is in agreement with findings from previous studies that addressed similar issues using different methods. Although these comparisons are broad, they suggest that the classic literature on color constancy provides a useful foundation as we move toward studying constancy as it operates in natural tasks.

In summary, our blocks-copying task brings us closer to understanding constancy the way it operates in daily life. In common with many natural tasks, such as looking for the freshest and the most nutritious food, color in the blocks-copying task provides the key information required to achieve a goal. Further, although instrumental, the use of color is implicit in the task; in fact, the word “color” is never mentioned in the experimental instructions. This aspect of our task finesses many of the complexities of interpreting color matching data, where how subjects interpret sometimes complex instructions about what strategy they should adopt while making their matches can have a large impact on their performance (Arend & Reeves, 1986; Troost & de Weert, 1991; Bauml, 1999). In contrast, the task demands of blocks-copying set a well-defined goal for the subject, and the results thus speak directly to the main issue we want to understand: how subjects use color to achieve this goal.