Abstract
Purpose
An insulin-resistant rat model, induced by dexamethasone, was used to evaluate a Michaelis–Menten-based kinetic model using 6-deoxy-6-[18F]fluoro-D-glucose (6-[18F]FDG) to quantify glucose transport with PET.
Procedures
Seventeen, male, Sprague–Dawley rats were studied in three groups: control (Ctrl), control+insulin (Ctrl+I), and dexamethasone+insulin (Dex+I). PET scans were acquired for 2 h under euglycemic conditions in the Ctrl group and under hyperinsulinemic-euglycemic conditions in the Ctrl+I and Dex+I groups.
Results
Glucose transport, assessed according to the 6-[18F]FDG concentration, was highest in skeletal muscle in the Ctrl+I, intermediate in the Dex+I, and lowest in the Ctrl group, while that in the brain was similar among the groups. Modeling analysis applied to the skeletal muscle uptake curves yielded values of parameters related to glucose transport that were greatest in the Ctrl+I group and increased to a lesser degree in the Dex+I group, compared to the Ctrl group.
Conclusion
6-[18F]FDG and the Michaelis–Menten-based model can be used to measure insulin-stimulated glucose transport under basal and an insulin resistant state in vivo.
Keywords: PET, Glucose clamp, Kinetic modeling, Insulin resistant, Skeletal muscle
Introduction
Glucose transport across plasma membranes, and the control of glucose metabolism, continues to constitute areas of active research. The process of glucose transport in most types of tissue and cells is mediated by a family of facilitative, non-sodium-dependent transporters (GLUTs) that are expressed in a tissue-specific manner [1]. GLUT1 is a ubiquitous transporter that mediates much of the glucose transport under basal states, while glucose transport mediated by GLUT4 is stimulated in response to insulin [2, 3]. Control of GLUTs has an important role in various physiological and pathological conditions, including brain function [4], atherosclerosis [5], and type 2 diabetes [6]. However, measurement of the rate of glucose transport in vivo and the ability to resolve transport in an individual tissue remains challenging. The [13C]glucose NMR and MRS methods were proposed to assess glucose metabolism in vivo [7, 8]. However, as this approach requires a larger concentration of [13C]glucose than that of the tracer doses used in PET scanning, it may alter the physiological glycemic state. Using PET, 2-deoxy-2-[18F]fluoro-D-glucose ([18F]FDG) tracer is commonly used to monitor glucose uptake in the brain, myocardium, skeletal muscle, and other tissues [9–11]. The most common approach for measuring glucose metabolism is to estimate the values of the parameters of the “4K” model using the rate constants, k1 to k4, and use these with an assumed valueof the tissue-dependent “lumped constant” in order to obtain the metabolic rate of glucose [9]. However, the cellular metabolism of glucose and analogs such as [18F]FDG involves two distinct sequential steps which the 4K model does not resolve, namely glucose transport into cells and its phosphorylation catalyzed by hexokinase or glucokinase to [18F]FDG-6-phosphate. A “5K” model of glucose and [18F]FDG metabolism has been proposed by Bertoldo et al. in order to separately estimate the transport and phosphorylation rates [12]. Although this represents a great improvement over the standard 4K model, the increased number of parameters to estimate make separating glucose transport and phosphorylation quite challenging with [18F]FDG.
An alternative PET tracer, 3-O-[11C]methylglucose(3-[11C]-OMG), has been developed to monitor glucose transport. This is a 11C-labeled version of 3-OMG used to monitor glucose transport. In contrast to glucose and [18F]FDG, the 3-[11C]-OMG tracer is not phosphorylated upon entry into cells and thus can be used to estimate the activity of the glucose transport step, per se. However, due to the 11C label, the tracer has a shorter half-life, i.e., 20.4 min, than that of [18F]FDG which is 109.8 min. This reduces the PET image quality, limits its clinical utility, and reduces the duration over which physiological parameters can be assessed.
We have used 6-deoxy-6-[18F]fluoro-D-glucose (6-[18F]FDG), a novel 18F-labeled glucose tracer developed by Neal et al. [13], in several studies to measure the rate of glucose transport in vivo [14–16]. The advantage of this tracer is that it is transported by GLUTs, although by virtue of its being deoxy at C6, the tracer is not phosphorylated [15]. In these analyses, the lumped constant of the traditional [18F]FDG model is not used. Instead, we use rate constants with values that depend on the concentration of glucose according to the Michaelis–Menten model. Using the assumed values of the Michaelis–Menten constants (Kms) and Vmaxes calculated based on the steady-state model (see “Materials and Methods”), we are able to estimate the rates of the glucose transport and phosphorylation steps [17, 18]. This method directly models the dependence of the “rate constant” on the concentration of endogenous glucose. In previous studies, this tracer and the Michaelis–Menten-based 6-[18F]FDG model have been evaluated in euglycemic conditions and in hyperglycemic conditions in the controlled absence of insulin [17].
The purpose of our current study is to further evaluate the physiological behavior of 6-[18F]FDG as well as that of our Michaelis–Menten-based model in rats rendered mildly insulin-resistant following short-term treatment with dexamethasone, a glucocorticoid that induces insulin resistance in both humans and various mammals [19–25]. Although higher doses (1 mg/kg) and the more prolonged (1–2 weeks) use of dexamethasone leads to marked insulin resistance [20, 23, 25], we used a dose of 100 μg/kg per day for 2 days to induce a mild state of insulin resistance so that we could evaluate the sensitivity of our approach for detecting and assessing altered glucose transport. Using PET technology, we measured glucose transport in different physiological conditions in order to verify the expected presence of insulin resistance in the dexamethasone-treated rats.
Materials and Methods
Animals
Seventeen, male, Sprague–Dawley rats, 200 to 250 g, were assigned to one of three different groups, i.e., five normal rats for the control group (Ctrl), five normal rats that were administered insulin during the hyperinsulinemic-euglycemic clamp (Ctrl+I), and seven dexamethasone-treated rats administered insulin during the hyperinsulinemic-euglycemic clamp (Dex+I).
In preparation for these studies, catheters were placed in both the left carotid artery and the right jugular vein in the Mouse Metabolic Phenotyping Center of Case Western Reserve University [17]. A 500-U/ml heparin-glycerol “lock solution” (approximately 50 μL for each catheter) purchased from Braintree Scientific, Inc. (Braintree, MA), was used to preserve the catheter patency. Following catheter placement, the rats were maintained for at least 7 days prior to the experiments. On the day preceding the PET scanning, the glycerol lock solution was replaced with 100 U/ml of heparin in saline, and food withdrawn so that the rats would be in a fasted state for the scanning. The animal procedures were reviewed and approved by the Institutional Animal Care and Use Committee of Case Western Reserve University.
Dexamethasone-Induced, Insulin-Resistance Rat Model
Dexamethasone was used to create a model of insulin-resistance [19–21, 23, 25, 26]. Rats in the Dex+I group were subcutaneously injected with 100 μg/kg of dexamethasone under isoflurane anesthesia (1.5 % isoflurane in oxygen) each morning for the 2 days preceding the PET study. Control rats were similarly administered isoflurane anesthesia once a day for 2 days. Fasting plasma glucose (Pg) and the insulin concentrations were measured on the morning of the PET study (after an overnight fast) in order to verify the changes expected with dexamethasone treatment [27–29].
Experimental Protocol
The time line of the experimental protocol on the day of PET scanning is shown in Fig. 1. PET data were collected for 2 hours using an Inveon microPET scanner (Siemens, Knoxville, TN) [30]. Times are referenced relative to the bolus injection of 6-[18F]FDG, defined as time zero. Isoflurane was used for anesthesia. After allowing 30 min for stabilization, blood samples for basal glucose and insulin concentration determinations were taken. A 15-min, 57Co transmission scan was performed for attenuation correction in PET image reconstruction. After the transmission scan, the glucose clamp was started. For the insulin-stimulated groups (Crtl+I and Dex+I), insulin (NovoLog®) in sterile insulin diluent (Eli Lilly, Indianapolis, IN) was infused. For the untreated, control group (Ctrl), the diluent solution sans insulin was infused. A 25 % glucose solution was infused at a rate adjusted to maintain euglycemia (approximately 7.2 mM). The glucose infusion rate (GIR) was adjusted according to the plasma glucose concentration Pg, which was measured every 5 min using an ACCU-CHEK Aviva (Hoffmann-La Roche Ltd., Basel, Switzerland) glucometer and blood samples collected from the cut tail, i.e., approximately 1 μL/sample. For both the Ctrl+I and the Dex+I groups, the insulin solution was infused based on the weight of each subject in the amount of 50 mU/kg/min for the first 2 min and at 5 mU/kg/min, thereafter. Arterial blood, approximately 50 μL per sample, was collected for insulin concentration measurement at different time points, including a pre-procedure basal/fasting measurement and at 10 and 60 min after the 6-[18F]FDG injection. The insulin concentration was determined using an Ultra-Sensitive Rat Insulin ELISA Kit (Crystal Chem, Inc., Downers Grove, IL). After steady plasma glucose levels were achieved for 30 to 45 min, a 2-h, dynamic 6-[18F]FDG PET scan was started. The average GIR needed to maintain plasma glucose level during PET scanning was taken as the reference for insulin sensitivity [31].
Fig. 1.
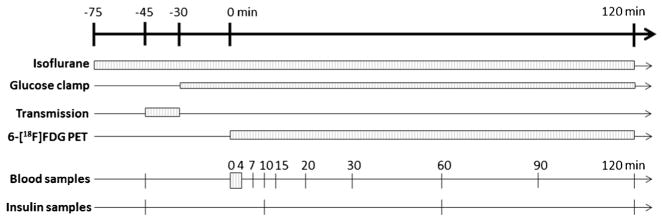
Time line of the experimental protocol. The top horizontal arrow indicates the time line of the entire experiment, including a 30-min stabilization period (from −75 to −45 min) followed by a 15-min transmission scan, a 30-min interval for clamp stabilization, and then 120 min for 6-[18F]FDG PET scanning. The boxes and lines are the durations or sampling time points for different procedures, as indicated.
Arterial blood was sampled from the carotid artery catheter in order to generate the input function used for the modeling analysis. To obtain high temporal resolution during the time when the blood radioactivity concentration was changing quickly, an automatic blood activity sampling machine was used [32]. Briefly, a syringe pump was used to draw the arterial blood for 4 min (0.2 ml/min) past a calibrated radiation detector and after which the blood activity count rate was recorded in 0.1-s bins [33]. These dynamic blood count data were corrected for sensitivity, delay, and dispersion in order to generate the early part of the input function [33–35]. Beginning at 4.5 min after the start of the scan, the blood drawn during the first 4 min was slowly injected back into the rat over a period of 30 s. Eight, arterial samples, all approximately 15 μL, were then manually obtained at 7, 10, 15, 20, 30, 60, 90, and 120 min.
Blood samples were also obtained from the cut tail in order to assay the plasma glucose concentration time course. Three other blood samples were taken using capillary tubes (approximately 9 μL/tube) and were then centrifuged in order to measure the hematocrit. One of these samples was obtained before the glucose clamp was performed so as to characterize the basal condition; the other two samples, i.e., duplicates, were taken at the end of the PET scans and were used to determine the radioactivity in the plasma and blood cells. Based on these values, the average ratio of plasma to blood activities and the average hematocrit were then used to transform the blood activity to plasma activity in order to yield the plasma input function [36].
To avoid excessive blood loss, a potentially confounding factor in rat studies, blood loss was kept at a minimum. Specifically, the total blood loss of each rat, including arterial- and venous-sampled blood, was approximately 0.5 ml, a value that is less than 4 % of the total blood volume of a 250-gram rat [37].
PET Imaging Data Analysis
List-mode data were processed using Fourier rebinning and were then histogrammed into 56 frames (5×2 s, 10×5 s, 12×30s, 8×60s, and 21×300 s). A two-dimensional, ordered-subset expectation maximization algorithm with 16 subsets and 12 iterations was used for reconstruction [38]. An image set with 128×128×159 voxels was reconstructed with 0.78×0.78×0.80 mm voxels. During reconstruction, data were corrected for randoms, dead time, scatter, and attenuation effects. The decay correction was applied for each reconstructed image in order to generate the final images used in this study.
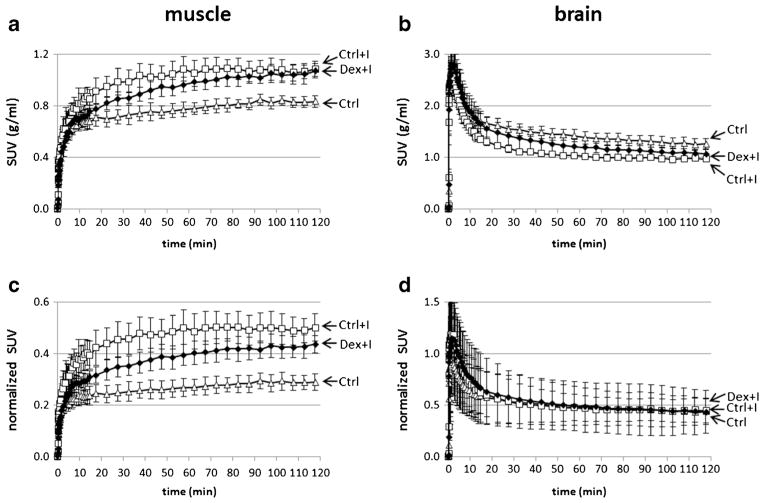
The time activity curves (TACs) for skeletal muscle and brain were obtained for each rat. Volumes of interest (VOIs) for different types of tissue were defined using the COMKAT Image Tool [39, 40]. Reconstructed transmission images were fused and were then used to define the skeletal muscle and brain VOIs across multiple planes, while excluding bone. The activity was converted to standardized uptake values (SUV) by dividing the tissue activity concentration by the injected activity per unit of body weight. We hypothesized that the difference in the uptake might be due to differences in 6-[18F]FDG concentration in plasma. To test this, we normalized the curves in Fig. 4a, b by dividing them by the average plasma 6-[18F]FDG concentration during PET scanning to obtain the curves shown in Fig. 4c, d. In addition, the model parameters of 6-[18F]FDG were estimated using the TAC of skeletal muscle. Details of this model are given in the following section.
Fig. 4.
Time-activity curves for the Ctrl (triangle), Ctrl+I (square), and Dex+I (solid diamond) groups in the skeletal muscle and the brain. Markers indicate means, and error bars indicate standard deviations. The tissue activity concentrations were divided by the injected activity dose per unit of body weight in order to obtain the standard uptake values (SUV). a muscle SUV vs. time curves. b brain SUV curves. To test if the differences in tissue 6-[18F]FDG concentration could be due to differences in plasma concentration of 6-[18F]FDG, the curves are further divided by the average of arterial plasma activities to generate c plasma-normalized muscle SUV (unitless) and d plasma-normalized brain SUV (unitless).
6-[18F]FDG Compartment Model
To characterize the physiological changes in skeletal muscle of rats due to dexamethasone treatment and insulin administration, a Michaelis–Menten-based kinetic model was used [17, 18]. In this model, glucose and 6-[18F]FDG passively diffuse from plasma to the interstitial space at a rate described by the rate-constant, k1 (1/min) and noting that the charge and molecular weights of glucose and 6-[18F]FDG are similar. Likewise, both may diffuse from the interstitial space to the blood according to the rate constant, k2 (1/min). As both glucose and 6-[18F]FDG would be carried by blood FLow and we assume that glucose and 6-[18F]FDG have both similar extraction fractions and distribution volumes, the ratio of k1/k2 would equal the ratio of (interstitial volume)/(total tissue volume), i.e., fIS. Once in the interstitial space of skeletal muscle, glucose and 6-[18F]FDG may be transported into a cell primarily via GLUT4. Assuming the Michaelis–Menten kinetics, as the transport rate depends on the concentration of the substrates, these transport “rate constants” are not actually constants. In fact, the “rate constants” account for the maximal transport capacity as well as the competition between glucose and its analogs, such as 6-[18F]FDG. Likewise, phosphorylation is modeled similarly to transport. These rate constants for glucose or a glucose analog are given as:
| (1) |
| (2) |
| (3) |
where ISg and ICg are interstitial and intracellular glucose concentrations (mM), and fIC is the volume fraction of the intracellular space and where x in the equation could be either g or a to indicate glucose or an analog of glucose such as 6-[18F]FDG. By substituting the Michaelis–Menten constant, KxG, in the equations with either KgG or K6FDGG, the rate constants (k3x, k4x, and k5g) of either glucose or 6-[18F]FDG can be obtained. k3x is a rate constant for transferring glucose or 6-[18F]FDG from the interstitial to the intracellular space (1/min); k4x is a rate constant for transferring glucose or 6-[18F]FDG from the intracellular to the interstitial space (1/min); k5g is a rate constant for glucose phosphorylation (1/min). Also, since the glucose and 6-[18F]FDG are transferred by the same type of glucose transporters, although with different afFInities, we assumed that the glucose transporters for glucose and 6-[18F]FDG had the same maximum transport rate, Vmax (VG), although with different Km (KgG and K6FDGG). Due to the fact that glucose, although not 6-[18F]FDG, would be phosphorylated, the Vmax and Km of hexokinase were only needed for glucose (VH and KgH). The Km of glucose transport, 6-[18F]FDG transport, and glucose phosphorylation (KgG, K6FDGG and KgH) were 3.5, 10, and 0.13 mM in this study, respectively [18, 41, 42].
The model output representing the prediction of the PET-measured activity during frame i of the dynamic imaging sequence, can be expressed as:
| (4) |
where SA denotes the (exponentially decaying) specific activity of 6-[18F]FDG, BIF denotes the blood input function expressed in terms of the radioactivity concentration, fv represents the blood fraction, tsi and tei are the start and end time points of frame i, and the integral calculates the value averaged over the time interval of frame i. COMKAT was used for the kinetic modeling in this study [39, 40]. Similar to the traditional kinetic model which uses an assumed value for the lumped constant in order to relate the behavior of glucose to that of [18F]FDG, our model entails assumptions as well. Specifically, the Michaelis–Menten-based 6-[18F]FDG model includes the rate constant, k1, two glucose concentrations, i.e., interstitial ISg and intracellular ICg,, and three volume fractions, i.e., fIS, fIC, and fv, all of which are estimated. We assume the k1, fIS, fIC, and fv for glucose and 6-[18F]FDG to be identical. We assign the fixed values noted above for Kms based on literature values and assume the values are independent of the metabolic state [43, 44]. Values for Vmaxes depend on the metabolic state, e.g., increase in response to insulin stimulation, and are determined from steady-state conditions according to Eqs. 5 and 6 [18].
| (5) |
| (6) |
Given the parameter values, cellular influx (CI), cellular efflux (CE), and the phosphorylation rate (PR) of glucose, can therefore, be determined as follows:
| (7) |
| (8) |
| (9) |
where k3g, k4g, and k5g can be calculated using Eqs. 1–3 using the Km of glucose. With the Michaelis–Menten-based model, the parameters, VG, VH, CI, CE, and PR, corresponding to the physiological components of glucose transport and metabolism, can be obtained and used to assess insulin resistance.
To robustly evaluate identifiability of the model parameters, we used Monte Carlo simulation. The mean values of the parameter estimates in each group were treated as the true values and used with the model to create what is considered to be noise-free data. For each such noise-free data set, 500 realizations of simulated noise, sampled from a normal distribution with zero mean and standard deviation [18] was added to the model output of frame i to produce simulated noisy data and where Mi is the model output representing noise-free data, and are the times of the start and end of the frame, and α is a scale factor that we determined by analysis of the residuals. The model was then fit to the resulting simulated noisy data using the same initial guess and convergence tolerances that were used to analyze the experimental data. The estimation error was determined by subtracting the true value from each estimate. Bias and precision were calculated as the mean and standard deviation, respectively, of the estimation error and expressed as a percentage of the true value (standard deviation as a percentage of the true value is equivalent to the coefficient of variation or CoV), and the matrix of correlation coefficients was calculated from the estimation errors.
Statistical Analyses
The results are expressed as the mean±standard deviation (SD) throughout. A two-tailed, Student’s t test assuming unequal variance was used for hypothesis testing (significance level=0.05). In special cases where prior knowledge suggested that the mean value of one group might be greater, although not less, than that of the other group, the one-tailed t test was used and is indicated in the text.
Results
Body weights and hematocrits of the rats are listed in Table 1. Body weights decreased post-surgery and returned to pre-surgery levels within 1 week. However, body weights decreased significantly (by 10.7 %, p<0.001) after 2 days of dexamethasone treatment. The changes in the hematocrit values before and after the experiments were less than 1 % in all of the studies. Compared to the Ctrl and Ctrl+I groups, dexamethasone treatment significantly increased the plasma glucose and insulin concentrations at baseline (p<0.05 for both; one-tailed t test) when measured immediately before the PET study (Fig. 2).
Table 1.
Study subject characteristics
| Ctrl (n=5) | Ctrl+I (n=5) | Dex+I (n=7) | |
|---|---|---|---|
|
|
|||
| Body weight before surgery (g) | 246.5±20.4 | 263.5±14.1 | 259.0±9.2 |
| Body weight at the time of PET scanning (g) | 242.6±18.3 | 269.4±11.5 | 244.0±14.7* |
| Hematocrit (%) during PET scans | 45.8±1.8 | 45.0±2.4 | 48.9±4.0 |
p<0.05 (denotes a significant difference between the body weight before surgery and the body weight at the time of the PET scanning (paired t test))
Fig. 2.
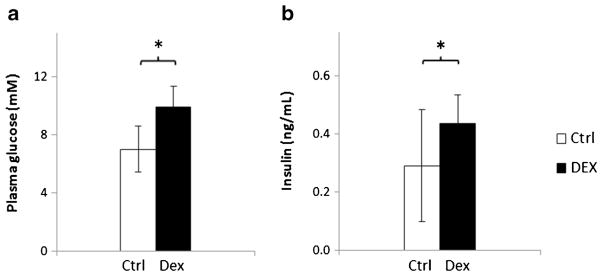
Plasma glucose and insulin concentrations in a fasting condition prior to PET scanning. a plasma glucose. b plasma insulin concentration. The empty and filled bars represent the results of the control (Ctrl) and the dexamethasone-treated rats, respectively. *p<0.05 using a one-tailed t test.
Glucose Clamp
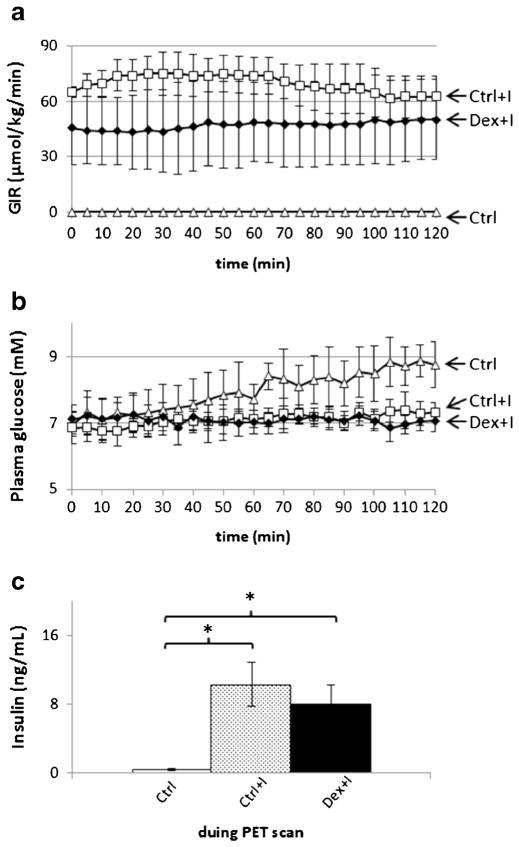
Figure 3 shows the means and standard deviations of the time courses of the glucose infusion rate (GIR) as well as the plasma glucose and insulin concentrations. In Fig. 3a, the time-averaged glucose infusion rates over the 120-min scanning interval (GIRavg) were 69.8±9.0 and 47.1±19.9 (μmol/kg/min) for the rats in the Ctrl+I and Dex+I groups, respectively. The difference in the rates between these groups was significant (p=0.026), and the values were significantly greater than zero which was the GIR for the Ctrl group. In the Ctrl group, the plasma glucose concentration of the Ctrl group tended to increase slowly over time, even though glucose was not infused. The GIRs in the Ctrl+ I group were reduced beginning at approximately 60 min in an effort to keep the plasma glucose concentration from increasing above the target concentration. In contrast, the GIR and plasma glucose concentrations were slightly more stable in the Dex+I group. In the blood samples collected during the PET scans, the mean plasma insulin concentration was the lowest in the Ctrl group rats into which no insulin had been infused. Compared to the Ctrl group, in the other two groups into which insulin had been administered, the plasma insulin concentrations were markedly increased, and the difference between the Ctrl+I and Dex+I groups not being significant.
Fig. 3.
Glucose clamp results during the scanning. a Group-mean glucose infusion rates (GIRs) versus time of PET scanning. The time-averaged GIR, GIRavg, between 0 and 120 min for Ctrl+I and Dex+I, are 69.8±9.0 and 47.1±19.9 μmol/kg/min (p<0.05). b Plasma glucose. Triangles, squares, and solid diamonds indicate the results for the Ctrl, Ctrl+I, and Dex+I groups, respectively. c Insulin concentration during PET scans. Bars from left to right show the results of Ctrl (empty), Ctrl+I (dotted), and Dex+I (filled) . The Ctrl+I and Dex+I groups are significantly different from control but not from each other. Error bars denote standard deviations.
Dynamic PET Data
The SUV time-course curves for skeletal muscle and brain, including correction for radioactive decay, are shown in Fig. 4. The animals were injected with 35.7±2.6 MBq 6-[18F]FDG. In all three groups, the SUVs in skeletal muscle increased during the entire scanning interval, whereas brain SUVs peaked early and then tended to decline toward a plateau. When comparing muscle SUVs, the 6-[18F]FDG radioactivity concentration was lowest in the Ctrl group compared to the two groups which were administered insulin. Considering these two, latter groups, the SUVs were higher in the Ctrl+I group than in the Dex+I group between 10 and 100 min after the beginning of the PET scanning, after which the SUVs tended to converge. The effect of insulin on the SUV was smaller in the brain and was even inverted, compared to that in skeletal muscle. To test the hypothesis that this smaller and inverted effect of insulin in the brain might be caused by a reduction of the plasma 6-[18F]FDG concentration due to the insulin action, the SUV curves in the skeletal muscle and the brain were normalized against plasma radioactivity by dividing the tissue SUV curves by the averaged plasma SUV during the PET scanning (Fig. 4c, d). With the normalization, the brain curves were essentially identical to each other, irrespective of the insulin state, whereas the skeletal muscle curves were further separated and no longer overlapped at the late time points.
6-[18F]FDG Model Parameters
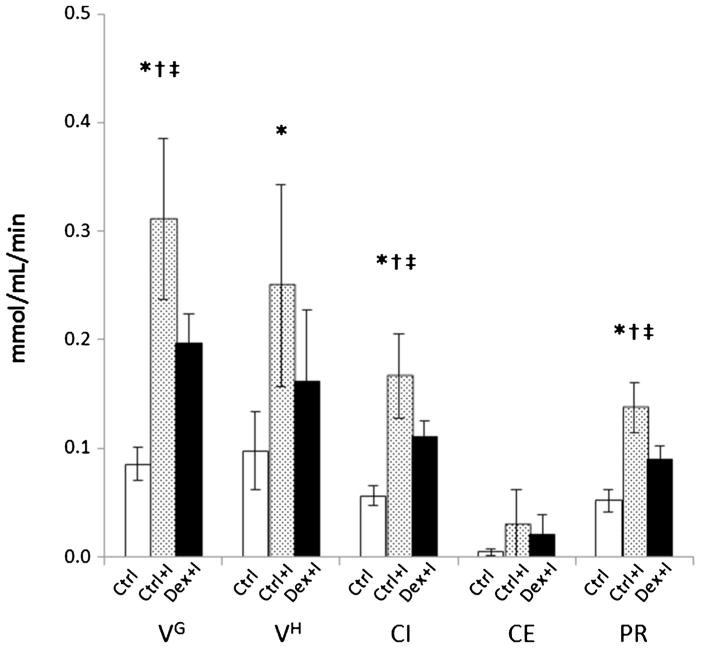
The time activity curves of skeletal muscle and modeling fits of those curves using the Michaelis–Menten-based model are shown in Fig. 5. The estimated values of the parameters, k1, fIS, fv, ISg, and ICg, are listed in Table 2. fIS increased and ISg decreased in the two, insulin-infused groups relative to the Ctrl, and with the effect being less in the Dex+I group than in the Ctrl+I group. Although the ICg was increased under the insulin stimulation condition, the difference between the ICg of the Ctrl+I and Dex+I groups was not clearly observed due to the large standard deviations of the ICg estimation. Table 3 shows a summary of the identifiability properties of the parameter estimates as obtained using Monte Carlo simulation. Analysis of residuals indicated that the value of the noise scaling factor α was 0.078. In considering the 30 parameters tabulated, 10 for each of the three groups, 28 were estimated with a bias of 10 % or less and 18 were estimated with a precision of 11.7 % or better. ICg and CE were estimated particularly poorly in the Ctrl group as the biases were approximately 50 % and the precision exceeded 100 %, although they were not so poorly estimated in the other groups. In addition, Table 4 also shows that the correlation among the parameters was highest between ISg and ICg. The high correlation between these two parameters is consistent with the difficulty in estimating ICg that is evident in Table 2. Figure 6 shows the Vmax for GLUT4 (VG), the Vmax for phosphorylation (hexokinase; VH), the glucose cellular influx (CI), the cellular efflux (CE), and the phosphorylation rate (PR). VG, indicating the maximum transport capacity of glucose, was increased 264 % in the hyperinsulinemic condition in the Ctrl+I group relative to the Ctrl group and was decreased by 36.6 % in the Dex+I group compared to that in the Ctrl+I group, and with the latter difference being statistically significant. Table 3 suggests the estimates of VG should be reliable, having low bias and good precision. The CI was 33.4 % lower in the Dex+I group compared to that in the Ctrl+I group. There was a similar tendency for VH, although the difference between the Ctrl+I and Dex+I groups did not attain statistical significance. The PR differed significantly among the groups, and it was 34.1 % lower in Dex+I than in Ctrl+I. All of the estimated parameters shown in Fig. 6 were increased in the insulin-stimulated groups compared to those seen in the Ctrl group, and with the increase being suppressed in the dexamethasone-treated group.
Fig. 5.
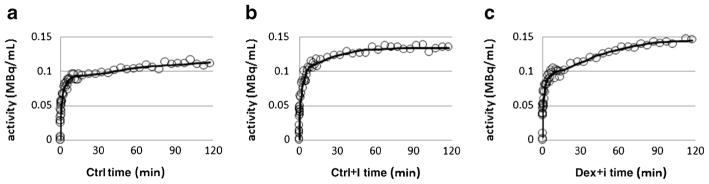
Time activity curves (circles) and model fits (solid line) for the Ctrl (a), Ctrl+I (b), and Dex+I (c) groups in the skeletal muscle.
Table 2.
Estimated values for the model parameters (mean±standard deviation)
| Ctrl (n=5) | Ctrl+I (n=5) | Dex+I (n=7) | |
|---|---|---|---|
|
|
|||
| k1 (1/min) | 0.049±0.003 | 0.047±0.009 | 0.040±0.011 |
| fIS (unitless) | 0.17±0.02 | 0.22±0.04* | 0.19±0.04 |
| fv (unitless) | 0.015±0.005 | 0.014±0.008 | 0.011±0.004 |
| ISg (mM) | 6.90±0.73 | 4.13±0.64* | 4.64±0.88* |
| ICg (mM) | 0.21±0.15 | 0.36±0.39 | 0.44±0.42 |
p<0.05 versus Ctrl
Table 3.
Monte Carlo simulation evaluation of bias and precision [bias (%) ±SD (%)]
| Ctrl | Ctrl+I | Dex+I | |
|---|---|---|---|
|
|
|||
| k1 | 0.4±6.7 | 1.0±8.3 | 0.9±7.5 |
| fIS | 0.7±2.6 | 0.3±7.2 | 0.3±4.7 |
| fv | −2.0±21.3 | −2.7±26.0 | −3.0±26.8 |
| ISg | 0.9±2.0 | 0.4±5.7 | 0.5±4.2 |
| ICg | 64.0±134.3 | 2.5±35.4 | 8.2±56.1 |
| VG | −1.4±4.8 | −0.2±8.1 | −0.2±5.9 |
| VH | 0.9±36.2 | 3.7±21.9 | 10.0±36.9 |
| CI | −1.1±4.5 | −0.1±8.3 | −0.1±5.6 |
| CE | 45.9±102.4 | 0.7±32.3 | 3.1±46.1 |
| PR | −5.0±11.7 | −0.3±9.9 | −0.8±11.7 |
Table 4.
Monte Carlo simulation evaluation of the correlation matrices of errors in parameter estimates
| State | |||||
|---|---|---|---|---|---|
| Ctrl | k1 | ISg | ICg | fIS | fv |
| k1 | 1.00 | – | – | – | – |
| ISg | 0.51 | 1.00 | – | – | – |
| ICg | 0.08 | 0.76 | 1.00 | – | – |
| fIS | −0.55 | 0.10 | 0.16 | 1.00 | – |
| fv | 0.13 | −0.24 | 0.12 | −0.64 | 1.00 |
| Ctrl+I | k1 | ISg | ICg | fIS | fv |
| k1 | 1.00 | – | – | – | – |
| ISg | 0.56 | 1.00 | – | – | – |
| ICg | 0.25 | 0.91 | 1.00 | – | – |
| fIS | 0.01 | −0.04 | −0.24 | 1.00 | – |
| fv | 0.07 | −0.47 | −0.56 | 0.28 | 1.00 |
| Dex+I | k1 | ISg | ICg | fIS | fv |
| k1 | 1.00 | – | – | – | – |
| ISg | 0.53 | 1.00 | – | – | – |
| ICg | 0.12 | 0.83 | 1.00 | – | – |
| fIS | 0.05 | 0.18 | 0.09 | 1.00 | – |
| fv | 0.08 | −0.42 | −0.23 | 0.02 | 1.00 |
Fig. 6.
Estimated values of the physiologic parameters of Vmax of glucose transporters and hexokinase (VG, VH, respectively). Glucose cellular influx, cellular efflux, and phosphorylation rates (CI, CE, and PR, respectively). The □,
 , and ■ bars are the results of the Ctrl, Ctrl+I, and Dex+I groups, respectively. *p<0.05 for Ctrl vs. Ctrl+I, Ctrl vs. Dex+I as †, and Ctrl+I vs. Dex+I as ‡.
, and ■ bars are the results of the Ctrl, Ctrl+I, and Dex+I groups, respectively. *p<0.05 for Ctrl vs. Ctrl+I, Ctrl vs. Dex+I as †, and Ctrl+I vs. Dex+I as ‡.
Discussion
Studying the control of the glucose transporter in both health and disease conditions is an important research topic. Monitoring the difference and change between health and disease conditions could be helpful for the research regarding disease progression and treatment efficiency. Nevertheless, in vivo measurement of the glucose transport step per se, i.e., without its phosphorylation or metabolism, has been challenging. Therefore, using PET to study glucose transport is important for monitoring physiological changes in vivo. In our study, 6-[18F]FDG and a Michaelis–Menten-based kinetic model were combined in order to evaluate whether this approach can measure changes in glucose transport in a mildly insulin-resistant state. We used two, daily, 100 μg/kg administrations of dexamethasone to produce a model of insulin resistance. After dexamethasone treatment, the small elevation of basal plasma glucose and of the insulin concentration (Fig. 2) and a lower GIR seen in the Dex+I group than that in the Ctrl+I group under a hyperinsulinemic-euglycemic condition demonstrates that the premise that a mildly insulin-resistant state was achieved. We purposely selected a small dose of dexamethasone and short treatment duration in order to elicit mild insulin resistance, assuming that a mild rather than overt insulin resistance offers a challenging test of our ability to detect insulin resistance using the novel tracer and the Michaelis–Menten model.
We used three groups of rats, Ctrl, Ctrl+I, and Dex+I, to study the efficacy of 6-[18F]FDG and used our kinetic model to estimate the rate of glucose transport in vivo. In the Ctrl group, the plasma glucose concentration slowly increased (Fig. 3b). The reason for the increasing plasma glucose concentration is unknown, although it might have resulted from the prolonged isoflurane anesthesia [45, 46].
The results clearly indicate that insulin greatly increased the rate of glucose transport in the skeletal muscle of the Ctrl+I group compared to the Ctrl group, while the rate of transport in brain remained unchanged. We also found that the GIR required to maintain euglycemia in the Dex+I group was significantly less than that required in the Ctrl+I group, despite markedly elevated insulin levels in both groups. These findings are consistent with the presence of an insulin resistant state following dexamethasone treatment. The induced insulin resistance was also reflected in the model parameter values. Unlike GIR which only provides a global measure of glucose uptake, the model parameters can provide localization and mechanistic insight into the details regarding the changes in glucose metabolism.
We attribute the differences in the radioactivity concentration time-courses in brain versus skeletal muscle to differential expression of the GLUT subtypes as well as to the low permeability of the blood–brain barrier to insulin. As GLUT1 is the predominant transporter of the blood–brain barrier, is very highly expressed in the cells, and is insensitive to insulin stimulation [2], the brain uptake curves of the Ctrl, Ctrl+I, and Dex+I groups would be expected to be similar to each other. This, indeed, was borne out in the data. The brain uptake of 6-[18F]FDG, especially with normalizing for the blood glucose concentration which differed according to the animal’s insulin sensitivity, was not different in the different groups, Fig 4d. This result also points out the importance of accounting for the plasma concentration, which is also the case with the tracer kinetic modeling, when a quantitative, mechanistic understanding is desired.
The Michaelis–Menten model, however, had difficulties with the brain data. In fact, we could fit the 6-[18F]FDG time-courses in the brain quite satisfactorily by a one-tissue-compartment model (not shown). This is not too surprising given that the blood flow, glucose transport, and glucose metabolism are much higher in the brain than in skeletal muscle. We speculate that a possible way to resolve the compartments would be to use sequential injections of 6-[18F]FDG and [18F]FDG. As [18F]FDG gets phosphorylated, it gets trapped intracellularly and builds up over time. This may allow compartments to be distinguished based on kinetics.
It has been reported that isoflurane anesthesia would result in an increase of blood flow in the brain and a decrease of the brain metabolic rate [47, 48]. However, the exchange between the spaces in the brain is too rapid in order to be resolved with PET data and our model. For this reason, the effect of anesthesia is inconclusive based on the brain curves obtained in this study.
Table 2 shows that fIS was greater in the insulin-infused groups than in the Ctrl group. This could be explained by an increase in the distribution volume for 6-[18F]FDG, due to the reported increase in interstitial space caused by insulin [49]. The fIS was significantly increased in the Ctrl+I group compared to the Ctrl group. This tendency is also found in the Dex+I results, although the increase of fIS was attenuated, presumably as dexamethasone decreased the insulin sensitivity. The results of the identifiability analysis presented in Table 3 show that ICg is estimated with poor precision and a high positive bias in the Ctrl group. Similar results have been shown in a previous study [18]. This finding is evidence that the data are relatively insensitive to ICg, and therefore difficult to estimate, when ICg is much less than the Km for glucose as there is little competition between 6-[18F]FDG and glucose under these conditions. Indeed, insulin stimulation is known to increase ICg and, as we would predict, the estimates are better in the Ctrl+I and Dex+I groups than in the Ctrl group. Taking together the computational results in Tables 3 and 4 suggest that the spread in the ICg estimates in the Ctrl group (Table 2) may be mainly attributed to identifiability issues rather than intersubject differences.
Estimates of the interstitial and intracellular glucose concentrations differ in the three groups in a way that is consistent with the expected physiological effects of insulin stimulation. Insulin would be expected to increase the translocation of GLUT4 to the plasma membrane, thereby increasing the rate of glucose transport into cells; this effect would be expected to be greatest in the Ctrl+I group and less so in the Dex+I group (relative to the Ctrl group). Increased glucose transport into cells would then shift the glucose balance to an increased intracellular concentration at the expense of a decreased interstitial concentration. The parameter estimates shown in Table 2 confirm this. Likewise, in the Ctrl+I group, compared to that in the Ctrl group, the ISg was significantly decreased and the ICg increased, although the difference in the ICg did not achieve statistical significance due to the large standard deviations in the ICg estimates. As further expected, the ISg in the Dex+I group were between the values obtained for the Crtl+I and the Ctrl groups, which is to be expected under the assumption that insulin had a smaller effect in the Dex+I group than in the Ctrl+I group.
The values of the physiological parameters, VG, VH, CI, CE, and PR, for both of the insulin-stimulated groups, were larger than those of the Ctrl group without insulin, and with the differences in the VG, CI, and PR being less in the Dex+I group than those in the Ctrl+I group. Therefore, not only the glucose transport but also the phosphorylation activity are reduced in Dex+I compared to those in Ctrl+I, and the difference can be clearly observed and used to portray the mild change in insulin sensitivity.
The Michaelis–Menten approach used in the present study has limitations. The model assumes that Kms of glucose transporter and hexokinase are not dependent on the metabolic state which is supported by the published literature reports [43, 44]. Nevertheless, if the assumed value for Km for glucose for transport or phosphorylation was incorrect or the assumed value for Km for 6-[18F]FDG transport was incorrect, then the estimates of Vmaxes and of glucose transport and phosphorylation would be biased.
Conclusion
The results of our study demonstrate that 6-[18F]FDG functions as a valid tracer for measuring glucose transport in vivo under control and hyperinsulinemic conditions, as well as with and without mild insulin resistance. Extension and usage of the 6-[18F]FDG methodology described above in normal and disease states in humans, would enable a better understanding of insulin-resistant states such as type 2 diabetes and obesity. A decrease in insulin-stimulated glucose transport is one of the major manifestations of the insulin resistant state. Unlike [18F]FDG, 6-[18F]FDG is not phosphorylated and thus enables the discrimination of the transport step from the phosphorylation step. Application of the model would provide insight into disease processes and will thus enable monitoring the progression of diseases and their response to pharmacological and non-pharmacological treatments.
Acknowledgments
We thank Dr. Chunying Wu for synthesizing the 6-[18F]FDG, Lan Wang for artery and vein catheterization, and Bonnie Hami, MA (USA) for her professional editing assistance. This study was supported by the National Institute of Diabetes and Digestive and Kidney Diseases, grant R01 DK082423. The artery and vein catheterization was performed at the Mouse Metabolic Phenotyping Center of Case Western Reserve University and was supported by grant U24 DK76169.
Footnotes
Conflict of Interest. The authors declare that they have no conflict of interest.
References
- 1.Wood IS, Trayhurn P. Glucose transporters (GLUT and SGLT): expanded families of sugar transport proteins. Br J Nutr. 2003;89:3–9. doi: 10.1079/BJN2002763. [DOI] [PubMed] [Google Scholar]
- 2.Hasselbalch SG, Knudsen GM, Videbaek C, et al. No effect of insulin on glucose blood–brain barrier transport and cerebral metabolism in humans. Diabetes. 1999;48:1915–1921. doi: 10.2337/diabetes.48.10.1915. [DOI] [PubMed] [Google Scholar]
- 3.Pardridge WM, Boado RJ, Farrell CR. Brain-type glucose transporter (GLUT-1) is selectively localized to the blood–brain barrier. Studies with quantitative western blotting and in situ hybridization. J Biol Chem. 1990;265:18035–18040. [PubMed] [Google Scholar]
- 4.Shah K, DeSilva S, Abbruscato T. The role of glucose transporters in brain disease: diabetes and Alzheimer’s disease. Int J Mol Sci. 2012;13:12629–12655. doi: 10.3390/ijms131012629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Libby P, DiCarli M, Weissleder R. The vascular biology of atherosclerosis and imaging targets. J Nucl Med. 2010;51:33S–37S. doi: 10.2967/jnumed.109.069633. [DOI] [PubMed] [Google Scholar]
- 6.Leto D, Saltiel AR. Regulation of glucose transport by insulin: traffic control of GLUT4. Nat Rev Mol Cell Biol. 2012;13:383–396. doi: 10.1038/nrm3351. [DOI] [PubMed] [Google Scholar]
- 7.Cline GW, Jucker BM, Trajanoski Z, et al. A novel 13C NMR method to assess intracellular glucose concentration in muscle, in vivo. Am J Physiol Endocrinol Metab. 1998;274:E381–E389. doi: 10.1152/ajpendo.1998.274.2.E381. [DOI] [PubMed] [Google Scholar]
- 8.Rivenzon-Segal D, Margalit R, Degani H. Glycolysis as a metabolic marker in orthotopic breast cancer, monitored by in vivo 13C MRS. Am J Physiol Endocrinol Metab. 2002;283:E623–E630. doi: 10.1152/ajpendo.00050.2002. [DOI] [PubMed] [Google Scholar]
- 9.Phelps M, Huang S, Hoffman E, et al. Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18) 2-fluoro-2-deoxy-D-glucose: validation of method. Ann Neurol. 1979;6:371–388. doi: 10.1002/ana.410060502. [DOI] [PubMed] [Google Scholar]
- 10.Kelley DE, Williams KV, Price JC. Insulin regulation of glucose transport and phosphorylation in skeletal muscle assessed by PET. Am J Physiol Endocrinol Metab. 1999;277:E361–E369. doi: 10.1152/ajpendo.1999.277.2.E361. [DOI] [PubMed] [Google Scholar]
- 11.Bengel FM, Higuchi T, Javadi MS, Lautamäki R. Cardiac positron emission tomography. J Am Coll Cardiol. 2009;54:1–15. doi: 10.1016/j.jacc.2009.02.065. [DOI] [PubMed] [Google Scholar]
- 12.Bertoldo A, Pencek RR, Azuma K, et al. Interactions between delivery, transport, and phosphorylation of glucose in governing uptake into human skeletal muscle. Diabetes. 2006;55:3028–3037. doi: 10.2337/db06-0762. [DOI] [PubMed] [Google Scholar]
- 13.Neal TR, Schumann WC, Berridge MS, Landau BR. Synthesis of [18F]-6-deoxy-6-fluoro-D-glucose ([18F] 6FDG), a potential tracer of glucose transport. J Labelled Compd Rad. 2005;48:845–854. [Google Scholar]
- 14.Landau BR, Spring-Robinson CL, Muzic RF, et al. 6-Fluoro-6-deoxy-D-glucose as a tracer of glucose transport. Am J Physiol Endocrinol Metab. 2007;293:E237–E245. doi: 10.1152/ajpendo.00022.2007. [DOI] [PubMed] [Google Scholar]
- 15.Muzic RF, Chandramouli V, Huang H-M, et al. Analysis of metabolism of 6FDG: a PET glucose transport tracer. Nucl Med Biol. 2011;38:667–674. doi: 10.1016/j.nucmedbio.2010.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Spring-Robinson C, Chandramouli V, Schumann WC, et al. Uptake of 18F-labeled 6-fluoro-6-deoxy-D-glucose by skeletal muscle is responsive to insulin stimulation. J Nucl Med. 2009;50:912–919. doi: 10.2967/jnumed.109.062687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang H-M, Chandramouli V, Ismail-Beigi F, Muzic RF., Jr Hyperglycemia-induced stimulation of glucose transport in skeletal muscle measured by PET-[18F] 6FDG and [18F] 2FDG. Physiol Meas. 2012;33:1661. doi: 10.1088/0967-3334/33/10/1661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huang H-M, Ismail-Beigi F, Muzic RF. A new Michaelis–Menten-based kinetic model for transport and phosphorylation of glucose and its analogs in skeletal muscle. Med Phys. 2011;38:4587. doi: 10.1118/1.3599034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Weinstein SP, Wilson CM, Pritsker A, Cushman SW. Dexamethasone inhibits insulin-stimulated recruitment of GLUT4 to the cell surface in rat skeletal muscle. Metabolism. 1998;47:3–6. doi: 10.1016/s0026-0495(98)90184-6. [DOI] [PubMed] [Google Scholar]
- 20.Sood A, Ismail-Beigi F. Effect of dexamethasone on insulin secretion: examination of underlying mechanisms. Endocr Pract. 2010;16:763–769. doi: 10.4158/EP09372.OR. [DOI] [PubMed] [Google Scholar]
- 21.Weinstein SP, Paquin T, Pritsker A, Haber RS. Glucocorticoid-induced insulin resistance: dexamethasone inhibits the activation of glucose transport in rat skeletal muscle by both insulin-and non-insulin-related stimuli. Diabetes. 1995;44:441–445. doi: 10.2337/diab.44.4.441. [DOI] [PubMed] [Google Scholar]
- 22.Folli F, Saad M, Kahn C. Insulin receptor/IRS-1/PI 3-kinase signaling system in corticosteroid-induced insulin resistance. Acta Diabetol. 1996;33:185–192. doi: 10.1007/BF02048541. [DOI] [PubMed] [Google Scholar]
- 23.Severino C, Brizzi P, Solinas A, et al. Low-dose dexamethasone in the rat: a model to study insulin resistance. Am J Physiol Endocrinol Metab. 2002;283:E367–E373. doi: 10.1152/ajpendo.00185.2001. [DOI] [PubMed] [Google Scholar]
- 24.Haber RS, Weinstein SP. Role of glucose transporters in glucocorticoid-induced insulin resistance: GLUT4 isoform in rat skeletal muscle is not decreased by dexamethasone. Diabetes. 1992;41:728–735. doi: 10.2337/diab.41.6.728. [DOI] [PubMed] [Google Scholar]
- 25.Qi D, Pulinilkunnil T, An D, et al. Single-dose dexamethasone induces whole-body insulin resistance and alters both cardiac fatty acid and carbohydrate metabolism. Diabetes. 2004;53:1790–1797. doi: 10.2337/diabetes.53.7.1790. [DOI] [PubMed] [Google Scholar]
- 26.Sakoda H, Ogihara T, Anai M, et al. Dexamethasone-induced insulin resistance in 3T3-L1 adipocytes is due to inhibition of glucose transport rather than insulin signal transduction. Diabetes. 2000;49:1700–1708. doi: 10.2337/diabetes.49.10.1700. [DOI] [PubMed] [Google Scholar]
- 27.Andrews RC, Walker BR. Glucocorticoids and insulin resistance: old hormones, new targets. Clin Sci. 1999;96:513–523. doi: 10.1042/cs0960513. [DOI] [PubMed] [Google Scholar]
- 28.Thompson MD, Gallagher WJ, Iaizzo PA, Lanier WL. The effect of chronic dexamethasone-induced hyperglycemia and its acute treatment with insulin on brain glucose and glycogen concentrations in rats. Anesthesiology. 2000;93:1279–1284. doi: 10.1097/00000542-200011000-00022. [DOI] [PubMed] [Google Scholar]
- 29.Venkatesan N, Lim J, Bouch C, Marciano D, Davidson MB. Dexamethasone-induced impairment in skeletal muscle glucose transport is not reversed by inhibition of free fatty acid oxidation. Metabolism. 1996;45:92–100. doi: 10.1016/s0026-0495(96)90205-x. [DOI] [PubMed] [Google Scholar]
- 30.Bao Q, Newport D, Chen M, Stout DB, Chatziioannou AF. Performance evaluation of the inveon dedicated PET preclinical tomograph based on the NEMA NU-4 standards. J Nucl Med. 2009;50:401–408. doi: 10.2967/jnumed.108.056374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nerpin E, Risérus U, Ingelsson E, et al. Insulin sensitivity measured with euglycemic clamp is independently associated with glomerular filtration rate in a community-based cohort. Diabetes Care. 2008;31:1550–1555. doi: 10.2337/dc08-0369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Salinas C, Pagel M, Muzic R., Jr Measurement of arterial input functions in rats [abstract] 2004 [Google Scholar]
- 33.Nelson A, Muzic R, Miraldi F, et al. Continuous arterial positron monitor for quantitation in PET imaging. Am J Physiol Imaging. 1989;5:84–88. [PubMed] [Google Scholar]
- 34.Muzic R, Jr, Nelson A, Miraldi F. Temporal alignment of tissue and arterial data and selection of integration start times for the H215O autoradiographic CBF model in PET. IEEE Trans Med Imaging. 1993;12:393–398. doi: 10.1109/42.241866. [DOI] [PubMed] [Google Scholar]
- 35.Nelson AD, Miraldi F, Muzic RF, et al. Noninvasive arterial monitor for quantitative oxygen-15-water blood flow studies. J Nucl Med. 1993;34:1000–1006. [PubMed] [Google Scholar]
- 36.Fang Y-HD, Muzic RF. Spillover and partial-volume correction for image-derived input functions for small-animal 18F-FDG PET studies. J Nucl Med. 2008;49:606–614. doi: 10.2967/jnumed.107.047613. [DOI] [PubMed] [Google Scholar]
- 37.Lee H, Blaufox M. Blood volume in the rat. J Nucl Med. 1985;26:72–76. [PubMed] [Google Scholar]
- 38.Hudson HM, Larkin RS. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans Med Imaging. 1994;13:601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- 39.Fang Y-HD, Asthana P, Salinas C, et al. Integrated software environment based on COMKAT for analyzing tracer pharmacokinetics with molecular imaging. J Nucl Med. 2010;51:77–84. doi: 10.2967/jnumed.109.064824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Muzic RF, Cornelius S. COMKAT: compartment model kinetic analysis tool. J Nucl Med. 2001;42:636–645. [PubMed] [Google Scholar]
- 41.Muzi M, Freeman SD, Burrows RC, et al. Kinetic characterization of hexokinase isoenzymes from glioma cells: implications for FDG imaging of human brain tumors. Nucl Med Biol. 2001;28:107–116. doi: 10.1016/s0969-8051(00)00201-8. [DOI] [PubMed] [Google Scholar]
- 42.Olson AL, Pessin JE. Structure, function, and regulation of the mammalian facilitative glucose transporter gene family. Annu Rev Nutr. 1996;16:235–256. doi: 10.1146/annurev.nu.16.070196.001315. [DOI] [PubMed] [Google Scholar]
- 43.Olefsky JM. Mechanisms of the ability of insulin to activate the glucose-transport system in rat adipocytes. Biochem J. 1978;172:137. doi: 10.1042/bj1720137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ciaraldi TP, Horuk R, Matthaei S. Biochemical and functional characterization of the rat liver glucose-transport system. Comparisons with the adipocyte glucose-transport system. Biochem J. 1986;240:115–123. doi: 10.1042/bj2400115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pomplun D, Möhlig M, Spranger J, et al. Elevation of blood glucose following anaesthetic treatment in C57BL/6 mice. Horm Metab Res. 2004;36:67–69. doi: 10.1055/s-2004-814104. [DOI] [PubMed] [Google Scholar]
- 46.Zuurbier CJ, Keijzers PJ, Koeman A, et al. Anesthesia’s effects on plasma glucose and insulin and cardiac hexokinase at similar hemodynamics and without major surgical stress in fed rats. Anesth Analg. 2008;106:135–142. doi: 10.1213/01.ane.0000297299.91527.74. [DOI] [PubMed] [Google Scholar]
- 47.Gelman S, Fowler KC, Smith LR. Regional blood flow during isoflurane and halothane anesthesia. Anesth Analg. 1984;63:557–565. [PubMed] [Google Scholar]
- 48.Maekawa T, Tommasino C, Shapiro HM, et al. Local cerebral blood flow and glucose utilization during isoflurane anesthesia in the rat. Anesthesiology. 1986;65:144–151. doi: 10.1097/00000542-198608000-00003. [DOI] [PubMed] [Google Scholar]
- 49.Thunhorst RL, Beltz TG, Johnson AK. Glucocorticoids increase salt appetite by promoting water and sodium excretion. Am J Physiol Regul Integr Comp Physiol. 2007;293:R1444–R1451. doi: 10.1152/ajpregu.00294.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]