Abstract
Dose selection for rifampin in the treatment of active pulmonary tuberculosis (TB) illustrates some of the challenges for dose optimization within multidrug therapies. Rifampin-based anti-TB regimens are often combined with antiretroviral therapies to treat human immunodeficiency virus (HIV) coinfection. The potent cytochrome P450 (CYP) enzyme inducing properties of rifampin give rise to significant drug-drug interactions, the minimization of which by limiting the dose, conflicts with the maximization of bacterial killing by increasing the dose. Such multiple and conflicting objectives lead to a set of trade-off optimal solutions for dose optimization rather than a single best solution. Here, we combine pharmacokinetic/pharmacodynamic (PK/PD) modeling with multiobjective optimization to quantitatively explore trade-offs between therapeutic and adverse effects of optimal dosing for the example of rifampin in TB-infected mice. The PK/PD model describes rifampin concentrations in plasma and liver following oral administration together with hepatic CYP enzyme induction and bacterial killing kinetics. We include optimization objectives descriptive of antimicrobial efficacy, CYP-mediated drug-drug interactions, and drug exposure-dependent toxicity. Results show non-conventional dosing scenarios that allow for increased efficacy relative to uniform dosing without increasing drug-drug interactions. Additionally, we find currently employed dosages for rifampin to be nearly optimal with respect to tradeoffs between efficacy and toxicity. While limited by the accuracy and applicability of the PK/PD model, these results provide an avenue for experimental investigation of complex dose optimization problems. This method can be extended to include additional drugs and optimization objectives, and may provide a useful tool for individualized medicine.
Keywords: Rifampin, PKPD, Multiobjective optimization, Tuberculosis, HIV, Modeling
Introduction
Rifampin is a rifamycin antibiotic with sterilizing activity against Mycobacterium tuberculosis and is an essential component of short-course treatment regimens for drug-susceptible pulmonary tuberculosis (TB) [1]. While the accepted 600 mg (10 mg/kg) daily dose of rifampin for TB treatment was established more than forty years ago [2, 3], analysis of various animal and clinical studies suggest that this dose may be suboptimal [4, 5]. Subsequently, multiple clinical trials to evaluate the safety and efficacy of high-dose rifampin for TB treatment were initiated and are currently underway or recently completed [6, 7, 8]. Our focus is on the trade-offs between therapeutic and adverse effects associated with higher than standard rifampin dosing in anti-TB combination regimens.
While the motivation for increasing rifampin dose amounts is to optimize antimicrobial efficacy, the frequent need to treat TB comorbidities [9] suggests that such dose optimization be considered in the context of potentially large and complex multidrug regimens. For example, first-line anti-TB therapy consists of a 2-month initial phase of rifampin, isoniazid, and pyrazinamide, with or without ethambutol, followed by a 4–7 month continuation phase of rifampin and isoniazid [1]; three or more antiretroviral drugs are often added to treat human immunodeficiency virus (HIV) co-infection [10], and combination therapies used to treat malaria or diabetes mellitus are commonly added as well [11, 12].
The potentially high number of drugs that may be co-administered with rifampin presents additional optimization objectives related to drug-drug interactions and toxicity that should be considered simultaneously with efficacy. With respect to drug-drug interactions; rifampin-mediated induction of cytochrome P450 (CYP) enzymes increases the rate of metabolism for many of the commonly co-administered antiretroviral, antidiabetic, and antimalarial drugs, which often requires their exclusion from the treatment regimen or their administration with increased doses [13, 14]. Regarding toxicity; drug-induced hepatotoxicity (DIH) is a serious adverse effect of anti-TB combination therapy with incidence reported in the range 2–28% [15]. While rifampin monotherapy is generally well tolerated, rifampin in combination with isoniazid, and rifampin in combination with pyrazinamide increases the risk of DIH compared to their separate administration [15]. Additionally, significant correlation between rifampin exposure and development of DIH during standard anti-TB therapy has been shown in a recent study by Satyaraddi et al. [16]. Overlapping and additive toxicities of rifampin and antiretroviral drugs, including hepatotoxicity, bone-marrow suppression, and skin rash [17] may also require consideration with increasing rifampin dosing. As drug exposure-dependent quantities, these optimization objectives of efficacy, toxicity, and drug-drug interactions, are conflicting in the sense that a dose regimen that results in minimum drug-drug interactions and toxicity (zero drug administered) will not generally be optimal with respect to efficacy. Optimization problems such as this, with multiple and possibly conflicting objectives, are common in engineering design and can be addressed using established methods of multiobjective optimization [18, 19].
A multiobjective optimization problem can be written as
| (1) |
where x is a vector of n ≥ 1 design (or decision) variables in a solution space X ⊂ IRn, and f(x) is a vector of k ≥ 2 objective functions which map X into an objective space IRk. The problem definition may also include a set of constraints which further define the structure and boundaries on X. In general, a solution, x, which minimizes one component of f will not be a minimum for another, and the objectives are said to be incommensurable or conflicting. In this case, no single x will be optimal in all objectives simultaneously, and optimal solutions are instead determined as a set of best possible trade-off solutions. The set of all such solutions is termed the Pareto set, and the image of the Pareto set in objective space is termed the Pareto front. A final selection of a single solution from the Pareto set can be made based on the relative value of each objective.
In the present work, we describe a pharmacokinetic/pharmacodynamic (PK/PD) model for rifampin treatment of TB-infected mice. The PK/PD model includes rifampin concentrations in plasma and liver following oral administration together with rifampin-mediated hepatic CYP enzyme induction and bacterial killing kinetics. We use this model to define a set of multiobjective optimization problems that are relevant to rifampin-based combination therapies. With a design space of dose regimens and an objective space associated with efficacy, toxicity, and drug-drug interactions, we use an evolutionary algorithm [20] to obtain approximate Pareto-optimized solutions for a wide range of the objective values. We choose individual regimens from each Pareto set that increase efficacy beyond that obtained with the current standard dosing, and we simulate the corresponding rifampin plasma concentrations and objective functions to illustrate predicted in vivo responses to these trade-off optimal regimens.
Materials and methods
Pharmacokinetic/pharmacodynamic model
The PK/PD model was constructed using the basic elements of a previously described compartmental model for in vivo rifampin-mediated CYP enzyme induction [21], combined with a term for bacterial population dynamics [22]. The full set of equations are
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where the model variables, each appearing as a derivative with respect to time, t, are functions of time only, and each of the parameters are constant.
Equations (2–4) describe rifampin pharmacokinetics, with AG, AH, and AP representing drug amounts in gut, liver, and plasma, respectively. Absorption and elimination are described as first-order processes with drug input to the liver from the gut. Drug concentrations were calculated in plasma as CP = AP/VP, and in liver as CH = AH/VH; where VP is plasma volume of distribution, and VH is physiological liver volume. The compartment volumes and volume flow rates were scaled to body weight, BW, as QH = BW · QHC, VH = BW · VHC, CLH = BW · CLHC, and VP = BW · VPC, where CLH is hepatic clearance, and QH is hepatic blood flow. The second term on the right-hand-side of equation (2) was included to describe repeated oral dosing as pulsed input with pulse-width Δ. Individual dose amounts, Dj, j = 0, …, nmax − 1, are administered at corresponding times tj, with nmax equal to the maximum number of doses within a specified treatment interval. θ(x) = 1(0) for x ≥ 0 (x < 0), is a step function. The initial conditions AG(t0), AH(t0), and AP(t0) were set to zero. Equations (5–8) describe the dynamics of CYP enzyme induction, where T1, T2, T3 represent transit compartments for CYP mRNA expression, with capacity limited stimulative effect and delay, and E denotes CYP enzyme activity (assumed proportional to CYP protein concentrations in [21]). The initial conditions T1,2,3(t0) = T0, and E(t0) = E0 represent basal CYP mRNA expression and enzyme activity, respectively. Equation (9) describes the bacterial population dynamics as capacity limited growth and sigmoidal killing, with N corresponding to the number of viable bacteria. The initial condition N(t0) = N0 is the number of bacteria at the start of drug treatment. All remaining parameters are described in Table 1.
Table 1.
PK/PD Model parameters.
| Parameter (units) | Value | Description |
|---|---|---|
| Rifampin pharmacokineticsa | ||
| Fa | 1.0 | Oral bioavailability |
| ka(h−1) | 0.69 | Oral absorption rate |
| CLHC(L/h/kg) | 0.0104 | Hepatic clearance |
| QHC(L/h/kg) | 5.4 | Hepatic blood flow |
| FH | 0.998 | Hepatic bioavailability |
| VHC(L/kg) | 0.065 | Liver volume |
| kP(h−1) | 26.4 | Plasma-to-liver transfer rate |
| VPC(L/kg) | 0.90 | Plasma volume of distribution |
| CYP3A11 enzyme kineticsa | ||
| τ(h) | 7.94 | Transit time |
| Smax(fold) | 7.86 | Maximum CYP enzyme mRNA expression |
| SC50(μM) | 6.2 | Half-maximum effect concentration |
| T0(fold) | 0.88 | Basal CYP mRNA expression |
| ksyn((nM/h/mg)/h) | 35.4 | CYP enzyme synthesis rate |
| kdeg(h−1) | 1.15 | CYP enzyme degradation rate |
| γ | 0.6 | mRNA amplification factor |
| E0(nM/h/mg) | 28.5 | Basal enzyme activity |
| Bacterial growth and killingb | ||
| μg(h−1) | 0.015 | Bacterial growth rate |
| Nmax(CFU) | 1.71×106 | Maximum CFU in untreated mice |
| kmax(h−1) | 0.049 | Maximum rate of antimicrobial killing |
| EC50(μM) | 4.72 | Half-maximum effect concentration |
| h | 0.60 | Hill coefficient |
| N0(CFU) | 7.98×105 | CFU at start of drug treatment |
Source: [21].
Source: Present study.
Parameter values
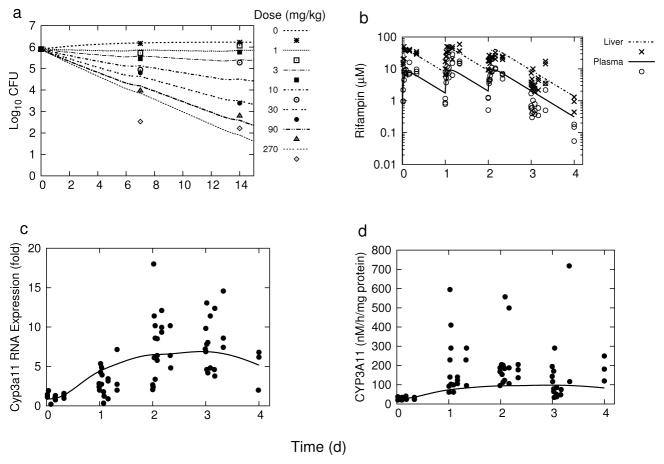
The parameter values for equations (2–9) were set using laboratory mouse data only. We set BW = 0.021 kg as representative of male and female 8–10 week-old BALB/c mice [23], and Δ = 0.001 h to approximate an oral bolus dose response. The rifampin pharmacokinetic and CYP enzyme induction parameters in equations (2–8) were set from the results in Raybon et al. [21] for steroid and xenobiotic X receptor (SXR) humanized mice and rifampin-mediated CYP3A11 enzyme induction. Parameter values in the bacterial dynamics equation (9) were determined in the present study by model calibration to rifampin time-kill data from M. tuberculosis-infected (H37Rv strain) BALB/c mice presented by Jayaram et al. [24].
The BALB/c mouse time-kill data [24] consisted of lung colony forming units (CFU) counts following aerosol infection (100 CFU/lung day 1 post-infection), with rifampin treatment beginning day 28 post-infection. The dosing was daily, 6 times/week, for one or two weeks with oral doses ranging from 0 to 270 mg/kg. Lung CFU counts were plotted for days 0, 7, and 14 of treatment (days 28, 35, and 42 post-infection, respectively); numerical values of the mean CFU’s were obtained from the published plot by digital extraction using g3data [25, 26]. We set N0 and Nmax equal to the mean CFU counts for the zero-dose group of mice at the beginning (day 0) and end of treatment (day 14), respectively. The values for the remaining parameters in equation (9) were set using a Bayesian calibration of the model to lung CFU data for the full-range of administered doses.
The model calibration included (i) the assignment of uniform prior probability distributions to each of the parameters; μg, kmax, EC50, and h, (ii) the specification of a likelihood, and (iii) sampling of the joint posterior distribution (product of the likelihood and priors) for the parameters conditioned on the mouse lung CFU counts for the full range of tested doses. The posterior sampling was performed using Markov chain Monte Carlo (MCMC) simulation [27]. The marginal posterior means for each parameter were used as the calibrated values. A prior mean for μg = 0.014h−1, was calculated from the day 1 and day 28 post-infection mouse CFU/lung counts. A rifampin dose-response curve which summarized an M. tuberculosis macrophage infection experiment in Jayaram et al. [24] was used to set the prior means; kmax = 0.05h−1, EC50 = 4.1μM, and h = 0.48. Preliminary simulations with these prior mean values (data not shown) indicated a close approximation to the mouse CFU data, and we subsequently set upper and lower bounds on the prior distributions to allow for a 50% deviation from the mean. All other model parameters were held fixed at their already specified values. We used a normal likelihood with a non-informative loguniform error distribution and log-transformed CFU counts.
Optimization problems
We defined objective functions for antimicrobial efficacy, drug-induced toxicity, and drug-drug interactions, on a treatment interval [t0 = 0, tfinal = T]. We used bacterial load, BT, for efficacy; plasma area under the concentration-time curve, AUCT, for toxicity; and time averaged enzyme induction ratio, MT, for drug-drug interactions; where
| (10) |
| (11) |
| (12) |
M(t) = E(t)/E0 is the ratio of CYP enzyme activity at time t divided by the basal activity [21]. The relation of MT to drug-drug interactions is through the use of M(t) as a multiplier of the plasma elimination rate for a CYP enzyme substrate drug as described in Raybon et al. [21]. Plasma AUCT serves as a surrogate for toxicity in the absence of specific mechanisms.
In the context of dose optimization, the objectives were defined to be minimized; maximizing efficacy in this case, is equivalent to minimizing bacterial load. We set the design variables to be independent dose amounts in a periodic schedule of administration, with a design vector (which defines a dosage regimen) denoted by D = (D0, D1, …, Dn−1); where n is the maximum number of doses administered in the dosing period.
We considered three optimization problems related to (i) maximizing efficacy and minimizing drug-drug interactions (P1), (ii) maximizing efficacy and minimizing toxicity (P2), and (iii) maximizing efficacy and minimizing drug-drug interactions and toxicity (P3). These three problems were defined as
-
P1
(13) -
P2
(14) -
P3
(15) where Dj,min(Dj,max) specify a lower (upper) bound for the jth dose.
Optimal dosing regimens were obtained for each problem, P1, P2, P3, as approximate Pareto optimal solutions using a multiobjective genetic algorithm [20, 28]. Plasma concentration-time profiles and the corresponding objective functions for selected individual optimal regimens were simulated to illustrate various aspects of the trade-offs between the different objectives.
Computational software
MCSim v5.5.0 [29] was used for PK/PD model simulations; it includes LSODES [30] as the differential equation solver, and Metropolis-within-Gibbs [27] sampling for MCMC simulation. NSGA II v1.1.6 [31] is a multiobjective genetic algorithm that was used to determine Pareto sets and fronts for each optimization problem. R v3.0.3 [32] was used for statistical calculations, including CODA [33] for analysis of the MCMC simulations.
Results
Parameter values
An initial MCMC simulation using the mean CFU counts from day 1 post-infection, and treatment days 0, 7, and 14, from the untreated (zero-dose) mice was run to establish a posterior mean value for μg. The posterior for μg was held fixed in a second MCMC simulation using the CFU counts for the drug-treated mice to determine posterior values for kmax, EC50, and h. For both simulations, the posterior parameter distribution was sampled using five independent Markov chains. Each chain was run for 50,000 iterations keeping every fifth iteration of the final 10,000. Convergence of the chains was assessed using the Gelman-Rubin R diagnostic [34], with R < 1.01 obtained for all parameters in our simulations. The aggregate of the five-chains was used to calculate the marginal posterior means reported in Table 1.
The experimental data that was used for model calibration (previously by Raybon et al. [21] for rifampin pharmacokinetics and CYP3A11 pharmacodynamics, and in the present study with the lung CFU counts from Jayaram et al. [24]) is shown in Figure 1 together with the corresponding model simulations using the parameter values in Table 1.
Fig. 1.
Model simulations and experimental data for: (a) pulmonary M. tuberculosis killing kinetics, (b) rifampin plasma and liver concentrations, (c) hepatic Cyp3a11 mRNA expression, and (d) hepatic CYP3A11 enzyme activity. The experimental data points in (a) were digitally extracted from Jayaram et al. [24], and those in (b), (c), and (d) were digitally extracted from Raybon et al. [21].
Optimization
For each of the optimization problems P1, P2, and P3, we considered two separate periodic schedules of administration as (i) 5 times per week (5x/wk) daily dosing, and (ii) 7 times per week (7x/wk) daily dosing. The 5x/wk schedule is common in a laboratory setting [35], while 7x/wk is common in a clinical setting [36]. We set a 14-day treatment interval [t0 = 0, T = 14 d], allowing for two complete weekly cycles of dosing. Individual daily doses were allowed to vary independently and continuously in the range [Dj,min = 0, Dj,max = 30](mg/kg), for j = 0, …, 6; except for D5 = D6 = 0 in the 5x/wk schedule. The upper limit of 30 mg/kg was chosen as triple the current accepted 10 mg/kg dose.
Approximate Pareto sets and fronts were obtained using NSGA II [31] with standard settings: crossover probability = 0.9, mutation probability = 0.1, distribution index for crossover = 15, distribution index for mutation = 20; for P1 and P2 we used population size = 200, and number of generations = 100; for P3 we used population size = 1000 and number of generations = 500.
The Pareto fronts in each problem became approximately stationary by 50 generations, with no significant change in shape or location throughout the remaining generations. The Pareto fronts for 5x/wk dosing for P1 and P2 are shown in Figure 2. Each front is well dispersed and uniform over the range of possible model outputs. The Pareto front for P3 (data not shown) is an approximately two-dimensional bounded surface resulting from the three-objective problem. Each point on the Pareto front corresponds to an optimal regimen. Uniform dosing regimens for 10 and 20 mg/kg dose amounts were used for baseline comparisons to the Pareto-optimized regimens; the 10 mg/kg being the current accepted dosing, and the 20 mg/kg dosing as a tested regimen in each of the current high-dose rifampin clinical studies [6, 7, 8]. The 10 mg/kg regimen is seen to be less than optimal for minimized efficacy and enzyme induction (P1), but is nearly optimal for minimized efficacy and toxicity (P2). The 20 mg/kg uniform dosing is more nearly optimal in both minimized efficacy and enzyme induction, and minimized efficacy and toxicity. The 7x/wk dosing results (not shown) were qualitatively similar to the corresponding 5x/wk plots.
Fig. 2.
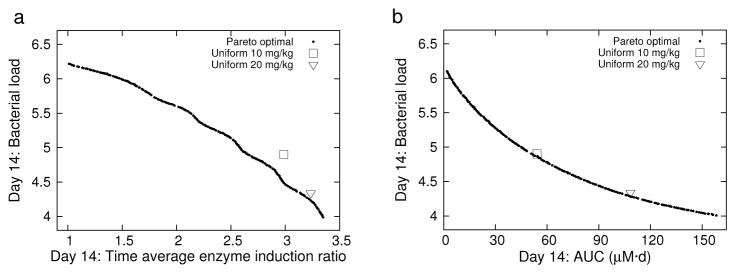
5x/wk dosing: Pareto fronts and uniform 10 and 20 mg/kg regimens for T = 14 d. (a) P1 and uniform 10 and 20 mg/kg regimens. (b) P2 and uniform 10 and 20 mg/kg regimens.
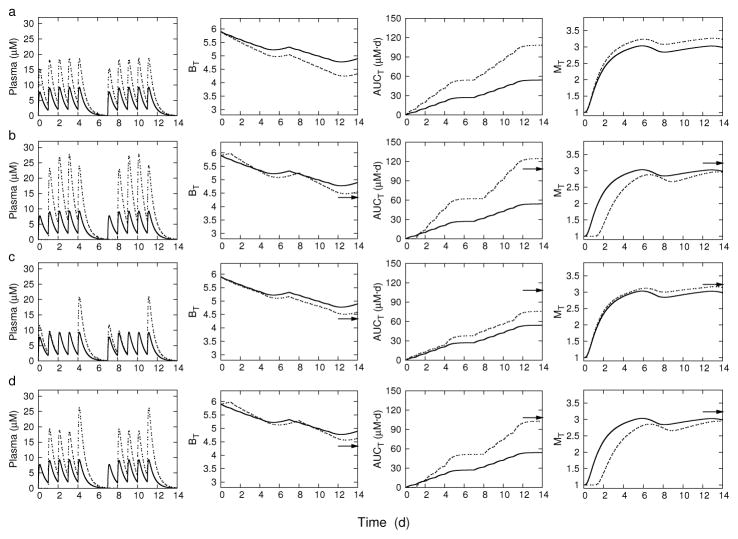
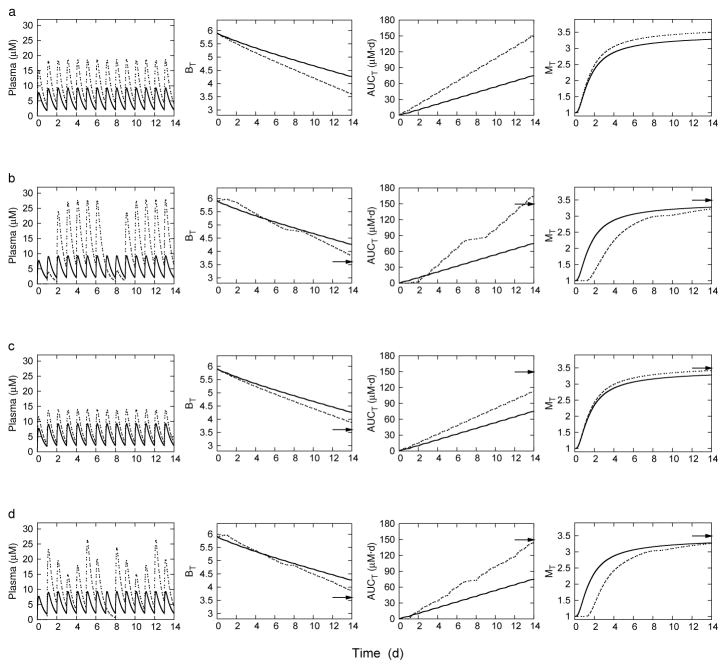
Tables 2 and 3 show the uniform 10 and 20 mg/kg dosage regimens and selected optimal regimens together with their corresponding objective function values at the end of the treatment interval, T = 14 d. The examples were chosen to illustrate optimal regimens that increased bacterial killing relative to the standard uniform 10 mg/kg dosing. Bacterial load is given as the change in log10 CFU over the 14-day interval. The objective functions were evaluated with the dosage regimens shown, which were rounded to the nearest 5 mg/kg from the NSGA II generated solutions as a more convenient dose amount for possible experimental testing.
Table 2.
Uniform and selected optimal dosing regimens for 5x/wk schedule of administration. Objective functions are evaluated at T = 14 d.
| Regimena | ΔBb | AUCT(mg · d/L) | MT |
|---|---|---|---|
| Uniform dosing | |||
| (10, 10, 10, 10, 10, 0, 0) | −1.01 | 54.15 | 2.99 |
| (20, 20, 20, 20, 20, 0, 0) | −1.57 | 108.29 | 3.23 |
| Optimized dosing | |||
| (0, 30, 30, 30, 25, 0, 0)c | −1.35 | 124.53 | 2.96 |
| (15, 10, 10, 10, 25, 0, 0)d | −1.32 | 75.78 | 3.14 |
| (0, 25, 20, 20, 30, 0, 0)e | −1.27 | 102.85 | 2.94 |
Weekly regimen (D0, D1, D2, D3, D4, D5, D6) (mg/kg).
ΔB = BT − B0, B0 = log10N0.
P1: Minimized (BT, MT).
P2: Minimized (BT, AUCT).
P3: Minimized (BT, AUCT, MT).
Table 3.
Uniform and selected optimal dosing regimens for 7x/wk schedule of administration. Objective functions are evaluated at T = 14 d.
| Regimen a | ΔBb | AUCT(mg · d/L) | MT |
|---|---|---|---|
| Uniform dosing | |||
| (10, 10, 10, 10, 10, 10, 10) | −1.64 | 74.75 | 3.28 |
| (20, 20, 20, 20, 20, 20, 20) | −2.29 | 149.49 | 3.49 |
| Optimized dosing | |||
| (0, 5, 30, 30, 30, 30, 30)c | −2.06 | 164.65 | 3.23 |
| (15, 15, 15, 15, 15, 15, 15)d | −2.02 | 112.12 | 3.41 |
| (0, 30, 20, 15, 20, 30, 20)e | −2.03 | 143.93 | 3.27 |
Weekly regimen (D0, D1, D2, D3, D4, D5, D6) (mg/kg).
ΔB = BT − B0, B0 = log10N0.
P1: Minimized (BT, MT).
P2: Minimized (BT, AUCT).
P3: Minimized (BT, AUCT, MT).
Figures 3 and 4 show simulation results for the dosage regimens in Tables 2 and 3, respectively. Each of the figures is arranged in rows, and displays the time course of rifampin plasma concentration and each objective function. The 10 mg/kg uniform dosing regimen is shown in each plot as a baseline comparison. The corresponding 20 mg/kg uniform dosing endpoint is also indicated by an arrow at time t = T = 14d for comparison. The dosing pattern for each regimen is reflected in the peak plasma concentrations. The uniform dosing regimens in the top row illustrates the conflicting characteristics of the objective functions; as bacterial load decreases, both cumulative drug exposure and enzyme induction increase. Enzyme activities can be kept at or below baseline while also increasing efficacy with dosing regimens that have short but high intervals of administration. However, such regimens increase toxicity with higher cumulative exposures. For 5x/wk dosing, efficacy can be increased while keeping exposure minimal with increased dose amounts at the end of the five-day treatment, however, enzyme activities are not kept low. Similarly, for 7x/wk dosing, uniform administration is optimal, but again, without the ability to keep enzyme induction at baseline. Optimizing against all three objectives identifies regimens that can keep enzyme induction at baseline, while increasing efficacy, and keeping exposure below a doubling of the 10 mg/kg uniform dose.
Fig. 3.
5x/week dosing: Rifampin plasma concentrations and corresponding objective functions on the treatment interval T. BT, bacterial load; MT, time averaged enzyme induction ratio; and AUCT, plasma area under the concentration-time curve. Row (a): Uniform dosing at 10 mg/kg (solid line) and 20 mg/kg (dashed line). Row (b): Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P1 (dashed line). Row (c) Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P2 (dashed line). Row (d): Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P3. The arrows point to the day 14 objective function values for uniform 20 mg/kg dosing.
Fig. 4.
7x/week dosing: Rifampin plasma concentrations and corresponding objective functions on the treatment interval T. BT, bacterial load; MT, time averaged enzyme induction ratio; and AUCT, plasma area under the concentration-time curve. Row (a): Uniform dosing at 10 mg/kg (solid line) and 20 mg/kg (dashed line). Row (b): Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P1 (dashed line). Row (c) Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P2 (dashed line). Row (d): Uniform dosing at 10 mg/kg (solid line) and optimized dosing for P3. The arrows point to the day 14 objective function values for uniform 20 mg/kg dosing.
Discussion
Dose optimization is inherently multiobjective with solutions obtained as trade-offs between therapeutic and adverse effects. However, current PK/PD methods for optimization of antimicrobial drugs are based on single objective exposure-response relationships [37], with trade-offs considered within a therapeutic window of superposed exposure-efficacy and exposure-toxicity relationships [38]. While such methods have proven useful for single-drug regimens [39], our purpose here was to apply multiobjective optimization to a basic example of the more complex dose optimization problems presented by combination therapies.
An application of multiobjective optimization to persistent bacterial infection [40] provided a motivating example for the present work. Additional examples of multiobjective optimization that are related to the present work can be found in applications to treatment of HIV [41], cancer [42], and a chemical engineering process of epoxy polymerization [43].
We used a PK/PD model that illustrated basic in vivo responses to rifampin, including a sigmoid effect for bacterial killing and time delay in CYP enzyme induction. The design space of dose regimens was chosen to loosen the constraint of uniform dosing while maintaining schedules of administration that are common in laboratory and clinical settings. Regarding the optimization objectives; bacterial load was treated as a direct measure of drug efficacy, while cumulative plasma drug exposure and time-averaged enzyme induction ratio were considered as surrogate measures for toxicity and drug-drug interactions, respectively. While CYP enzyme mediated drug-drug interactions are well characterized [13, 21], the use of rifampin exposure-dependent toxicity is not as clearly described in the literature [4]. Support for the use of rifampin AUC as a surrogate for possible exposure-dependent toxicity is found in the recent anti-TB DIH study by Satyaraddi et al. [16]. In this study, rifampin, pyrazinamide, and isoniazid peak plasma concentrations (Cmax) and AUC from 0 to 4 hours (AUC0–4h) were measured on days 1, 7, and 14 of standard anti-TB treatment, and compared in patients with and without subsequent DIH. The study included 110 patients, 15 of whom developed DIH with a median 22 day latency from start of treatment. Rifampin Cmax and AUC0–4h were found to significantly correlate with the development of DIH, while no such correlation was found with the corresponding measures for isoniazid and pyrazinamide. Further, the day 7 and day 14 exposure parameters better correlated with DIH than the day 1 measures, suggesting to the authors of the study that rifampin accumulation is responsible for the DIH.
Beyond the current focus on high-dose rifamycins [44], our choice of rifampin in mice as an example system for multiobjective optimization was based on the rich set of experimental data that supported the PK/PD model development [24, 21]. The model output in this case provides a quantitative baseline to guide further experimental investigation of the dose optimization results. The central results are a set of Pareto-optimized regimens that were chosen to illustrate the trade-offs between efficacy, toxicity, and drug-drug interactions associated with rifampin treatment of TB-infected mice. Uniform dosing is found to be nearly optimal with respect to trade-offs between efficacy and toxicity, with increased efficacy necessarily accompanied by increased toxicity. The difference between efficacy versus toxicity optimized regimens for the 5 days per week and 7 days per week schedules of administration appear as an increase of the fifth dose for the former. Dose regimens that concentrate higher doses in a shorter interval can increase efficacy with minimal or no increase in CYP enzyme induction. Interestingly, the current standard 10 mg/kg uniform dosing was found to be a nearly optimal solution with respect to trade-offs between efficacy and toxicity, but not between efficacy and enzyme induction. While doubling this standard dose to 20 mg/kg daily is a better optimized solution with respect to both efficacy versus toxicity and efficacy versus enzyme induction; the tradeoff for this better optimized solution is increased toxicity. These results (minding the mouse-based context) may be relevant to considerations regarding increased toxicity with high-dose rifampin regimens, and also rifampin-mediated interactions in anti-TB/HIV regimens which have established dose adjustments for the co-administered antiretroviral drugs [13]. Of note, there are additional considerations for adverse effects in humans, such as hypersensitivity reactions linked to dosing interval [45], that were not included in the optimization problems here.
As the genetic algorithm acts on the model predicted objective values, the primary source of uncertainty in the results is from limitations on the accuracy and applicability of the PK/PD model and calibration data. In this case, extension of the model beyond the two-week time frame becomes increasingly uncertain due to the lack of supporting experimental data and the relative simplicity of the model components. We do not include expressions to account for the biphasic killing kinetics of bacterial populations that include persisters [46]. We also do not include physiological changes that may occur with extended treatment duration, such as changing disease state and basal concentrations for enzyme activity, nor do we include an accounting for antimicrobial resistance. The parameter values were specific to rifampin PK and CYP3A11 enzyme activity in SXR-humanized mice, the H37Rv strain of M. tuberculosis, and the host-drug-bacteria interactions in the lungs of BALB/c mice. However, the structural elements of the PK/PD model are sufficiently general to allow for application of the optimization method to different strains of mice and bacteria through re-calibration to the appropriate experimental data. Application of the present single drug PK/PD model to combination therapies assumes an additive effect of increasing concentration of rifampin on bacterial load in combination with other antimicrobials. While such an assumption may not be valid in general, such additivity is seen with the standard anti-TB combination drugs in the results of a rifampin dose-ranging study by Rosenthal et al. [47]. This study showed a nearly proportional decrease in bacterial load in BALB/c mice with increasing rifampin dosing (in a range of 10–40 mg/kg) against a fixed background of standard isoniazid and pyrazinamide dosing. Application of the optimization procedure to more complex models, including additional drug targets, optimization objectives, and drug-dependent interactions, can be addressed similarly to the present example through the appropriate PK/PD model development.
Multiobjective optimization extends the use of PK/PD modeling beyond conventional dose-ranging simulations and the characterization of variability [48]. Using a PK/PD model to establish a relationship between a design space of dose regimens and objective functions for any of the model outputs, multiobjective optimization algorithms provide a method of screening to better focus experimental investigations on a targeted set of potentially optimal regimens, and in turn, provides an additional means to critically examine PK/PD model predictions. This approach provides a potentially useful tool to address some of the goals of individualized medicine [49]. For example, a design space could be defined as the individual doses of multiple separate drugs (possibly needed to treat multiple co-occurring diseases) constrained to a desired frequency of administration and duration of treatment. An appropriately detailed PK/PD model could be calibrated to a set of measurements that describe the physiological and disease state of an individual patient (e.g., body weight, kidney and liver function, and individual metabolomic profile). Pareto-optimized combination regimens could then be found that maximize efficacy, suppress resistance, and minimize adverse or unwanted effects for the specific individual; with a final choice of optimal regimen chosen based on clinical judgment. Such an example may be relevant to the complex treatment regimens involved with multidrug resistant TB and HIV co-infections [50], and provides additional motivation for the development of accurate and predictive PK/PD models.
Acknowledgments
The author thanks Mary Ann De Groote and Scott Irwin (Colorado State University (CSU)) for helpful discussions, Raymond Yang and Anne Lenaerts (CSU) for helpful suggestions and review of the manuscript, Ole Steuernagel and Daniel Polani (University of Hertfordshire) for helpful suggestions regarding NSGA II, and Kenneth “KJ” Sullivan for helpful discussions on genetic algorithms. This work was supported by National Institutes of Health Grant Number K25AI089945.
References
- 1.Centers for Disease Control and Prevention . Treatment of tuberculosis, American Thoracic Society, CDC, and Infectious Disease Society of America. MMWR Recomm Rep. 2003;52(RR-11):1–77. [PubMed] [Google Scholar]
- 2.Constans P, Baron A, Parrot R, Coury C. A study of 200 cases of active, recent pulmonary tuberculosis treated with rifampin-isoniazid. A follow-up history of one and one-half to three years. Chest. 1972;61(6):539–549. doi: 10.1378/chest.61.6_supplement.539. [DOI] [PubMed] [Google Scholar]
- 3.Raleigh JW. Rifampin: clinical experience with a new anti-tuberculosis drug. Trans Am Clin Climatol Assoc. 1972;83:104–112. [PMC free article] [PubMed] [Google Scholar]
- 4.van Ingen J, Aarnoutse RE, Donald PR, Diacon AH, Dawson R, Plemper van Balen G, Gillespie SH, Boeree MJ. Why Do We Use 600 mg of Rifampicin in Tuberculosis Treatment? Clin Infect Dis. 2011;52(9):e194–199. doi: 10.1093/cid/cir184. [DOI] [PubMed] [Google Scholar]
- 5.Steingart KR, Jotblad S, Robsky K, Deck D, Hopewell PC, Huang D, Nahid P. Higher-dose rifampin for the treatment of pulmonary tuberculosis: a systematic review. Int J Tuberc Lung Dis. 2011;15(3):305–316. [PubMed] [Google Scholar]
- 6.Harvard University Faculty of Medicine. ClinicalTrials.gov. Bethesda (MD): National Library of Medicine (US); 2014. Trial of High-Dose Rifampin in Patients With TB (HIRIF) [Internet] Available from:. http://clinicaltrials.gov/ct2/show/NCT01408914Z, nLM Identifier: NCT01408914. [Google Scholar]
- 7.Radboud University. ClinicalTrials.gov. Bethesda (MD): National Library of Medicine (US); 2013. Pharmacokinetics and Pharmacodynamics of High Versus Standard Dose Rifampicin in Patients With Pulmonary Tuberculosis (High RIF) [Internet] Available from:. http://clinicaltrials.gov/ct2/show/results/NCT00760149, nLM Identifier: NCT00760149. [Google Scholar]
- 8.Radboud University. ClinicalTrials.gov. Bethesda (MD): National Library of Medicine (US); 2014. Safety, Tolerability, Extended Early Bactericidal Activity and PK of Higher Doses Rifampicin in Adults With Pulmonary TB (HR1) [Internet] Available from:. http://clinicaltrials.gov/ct2/show/results/NCT00760149, nLM Identifier: NCT00760149. [Google Scholar]
- 9.Marais BJ, Lonnroth K, Lawn SD, Migliori GB, Mwaba P, Glaziou P, Bates M, Colagiuri R, Zijenah L, Swaminathan S, Memish ZA, Pletschette M, Hoelscher M, Abubakar I, Hasan R, Zafar A, Pantaleo G, Craig G, Kim P, Maeurer M, Schito M, Zumla A. Tuberculosis comorbidity with communicable and non-communicable diseases: integrating health services and control efforts. Lancet Infect Dis. 2013;13(5):436–448. doi: 10.1016/S1473-3099(13)70015-X. [DOI] [PubMed] [Google Scholar]
- 10.Dooley KE, Flexner C, Andrade AS. Drug interactions involving combination antiretroviral therapy and other anti-infective agents: repercussions for resource-limited countries. J Infect Dis. 2008;198(7):948–961. doi: 10.1086/591459. [DOI] [PubMed] [Google Scholar]
- 11.Dooley KE, Chaisson RE. Tuberculosis and diabetes mellitus: convergence of two epidemics. Lancet Infect Dis. 2009;9(12):737–746. doi: 10.1016/S1473-3099(09)70282-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sousa M, Pozniak A, Boffito M. Pharmacokinetics and pharmacodynamics of drug interactions involving rifampicin, rifabutin and antimalarial drugs. J Antimicrob Chemother. 2008;62(5):872–878. doi: 10.1093/jac/dkn330. [DOI] [PubMed] [Google Scholar]
- 13.Baciewicz AM, Chrisman CR, Finch CK, Self TH. Update on rifampin, rifabutin, and rifapentine drug interactions. Curr Med Res Opin. 2013;29(1):1–12. doi: 10.1185/03007995.2012.747952. [DOI] [PubMed] [Google Scholar]
- 14.Centers for Disease Control and Prevention. Managing Drug Interactions in the Treatment of HIV-Related Tuberculosis. 2013 [online] Available from www.cdc.gov/tb/TB_HIV_Drugs/default.htm.
- 15.Tostmann A, Boeree MJ, Aarnoutse RE, de Lange WC, van der Ven AJ, Dekhuijzen R. Antituberculosis drug-induced hepatotoxicity: concise up-to-date review. J Gastroenterol Hepatol. 2008;23(2):192–202. doi: 10.1111/j.1440-1746.2007.05207.x. [DOI] [PubMed] [Google Scholar]
- 16.Satyaraddi A, Velpandian T, Sharma SK, Vishnubhatla S, Sharma A, Sirohiwal A, Makharia GK, Sinha S, Biswas A, Singh S. Correlation of plasma anti-tuberculosis drug levels with subsequent development of hepatotoxicity. Int J Tuberc Lung Dis. 2014;18(2):188–195. doi: 10.5588/ijtld.13.0128. [DOI] [PubMed] [Google Scholar]
- 17.Kwara A, Flanigan TP, Carter EJ. Highly active antiretroviral therapy (HAART) in adults with tuberculosis: current status. Int J Tuberc Lung Dis. 2005;9(3):248–257. [PubMed] [Google Scholar]
- 18.Collette Y, Siarry P. Decision Engineering. Springer; 2003. Multiobjective Optimization: Principles and Case Studies. [Google Scholar]
- 19.Marler R, Arora J. Survey of multi-objective optimization methods for engineering. Struct Multidiscip Optim. 2004;26(6):369–395. [Google Scholar]
- 20.Deb K, et al. Multi-objective optimization using evolutionary algorithms. Vol. 2012. John Wiley & Sons; 2001. [Google Scholar]
- 21.Raybon JJ, Pray D, Morgan DG, Zoeckler M, Zheng M, Sinz M, Kim S. Pharmacokinetic-pharmacodynamic modeling of rifampicin-mediated Cyp3a11 induction in steroid and xenobiotic X receptor humanized mice. J Pharmacol Exp Ther. 2011;337(1):75–82. doi: 10.1124/jpet.110.176677. [DOI] [PubMed] [Google Scholar]
- 22.Vaddady PK, Lee RE, Meibohm B. In vitro pharmacokinetic/pharmacodynamic models in anti-infective drug development: focus on TB. Future Med Chem. 2010;2(8):1355–1369. doi: 10.4155/fmc.10.224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Charles River Laboratories Inc. Charles River Laboratories Research Models & Services; 2006. http://www.criver.com. [Google Scholar]
- 24.Jayaram R, Gaonkar S, Kaur P, Suresh BL, Mahesh BN, Jayashree R, Nandi V, Bharat S, Shandil RK, Kantharaj E, Balasubramanian V. Pharmacokinetics-pharmacodynamics of rifampin in an aerosol infection model of tuberculosis. Antimicrob Agents Chemother. 2003;47(7):2118–2124. doi: 10.1128/AAC.47.7.2118-2124.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bauer B, Reynolds M. Recovering data from scanned graphs: performance of Frantz’s g3data software. Behav Res Methods. 2008;40(3):858–868. doi: 10.3758/brm.40.3.858. [DOI] [PubMed] [Google Scholar]
- 26.Frantz J. G3data, Version 1.5.2, Software. 2012 Available from https://github.com/pn2200/g3data.git.
- 27.Gilks WR, Best N, Tan K. Adaptive rejection Metropolis sampling within Gibbs sampling. Applied Statistics. 1995:455–472. [Google Scholar]
- 28.Zitzler E, Laumanns M, Bleuler S. Metaheuristics for multiobjective optimisation. Springer; 2004. A tutorial on evolutionary multiobjective optimization; pp. 3–37. [Google Scholar]
- 29.Bois FY, Maszle DR. MCSim: A Monte Carlo Simulation Program. Journal of Statistical Software. 1997;2(i09):1–60. [Google Scholar]
- 30.Hindmarsh AC. In: ODEPACK, A Systematized Collection of ODE Solvers. Stepleman RS, et al., editors. Vol. 1. North-Holland; Amsterdam: 1983. pp. 55–64. [Google Scholar]; IMACS transactions on scientific computation. 1:55–64. [Google Scholar]
- 31.Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evolutionary Computation, IEEE Transactions on. 2002;6(2):182–197. [Google Scholar]
- 32.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2014. http://www.R-project.org/ [Google Scholar]
- 33.Plummer M, Best N, Cowles K, Vines K. CODA: Convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- 34.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. Chapman and Hall/CRC; Boca Raton, FL: 2003. [Google Scholar]
- 35.De Groote MA, Gilliland JC, Wells CL, Brooks EJ, Woolhiser LK, Gruppo V, Peloquin CA, Orme IM, Lenaerts AJ. Comparative studies evaluating mouse models used for efficacy testing of experimental drugs against Mycobacterium tuberculosis. Antimicrob Agents Chemother. 2011;55(3):1237–1247. doi: 10.1128/AAC.00595-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chang KC, Leung CC, Grosset J, Yew WW. Treatment of tuberculosis and optimal dosing schedules. Thorax. 2011;66(11):997–1007. doi: 10.1136/thx.2010.148585. [DOI] [PubMed] [Google Scholar]
- 37.Mouton JW, Ambrose PG, Canton R, Drusano GL, Harbarth S, MacGowan A, Theuretzbacher U, Turnidge J. Conserving antibiotics for the future: new ways to use old and new drugs from a pharmacokinetic and pharmacodynamic perspective. Drug Resist Updat. 2011;14(2):107–117. doi: 10.1016/j.drup.2011.02.005. [DOI] [PubMed] [Google Scholar]
- 38.Drusano GL, Ambrose PG, Bhavnani SM, Bertino JS, Nafziger AN, Louie A. Back to the future: using aminoglycosides again and how to dose them optimally. Clin Infect Dis. 2007;45(6):753–760. doi: 10.1086/520991. [DOI] [PubMed] [Google Scholar]
- 39.Ambrose PG, Bhavnani SM, Rubino CM, Louie A, Gumbo T, Forrest A, Drusano GL. Pharmacokinetics-pharmacodynamics of antimicrobial therapy: it’s not just for mice anymore. Clin Infect Dis. 2007;44(1):79–86. doi: 10.1086/510079. [DOI] [PubMed] [Google Scholar]
- 40.Steuernagel O, Polani D. Multiobjective optimization applied to the eradication of persistent pathogens. Evolutionary Computation, IEEE Transactions on. 2010;14(5):759–765. [Google Scholar]
- 41.Heris SMK, Khaloozadeh H. Open-and closed-loop multiobjective optimal strategies for HIV therapy using NSGA-II. Biomedical Engineering, IEEE Transactions on. 2011;58(6):1678–1685. doi: 10.1109/TBME.2011.2110651. [DOI] [PubMed] [Google Scholar]
- 42.Petrovski A, McCall J. Evolutionary multi-criterion optimization. Springer; 2001. Multi-objective optimisation of cancer chemotherapy using evolutionary algorithms; pp. 531–545. [Google Scholar]
- 43.Deb K, Mitra K, Dewri R, Majumdar S. Towards a better understanding of the epoxy-polymerization process using multi-objective evolutionary computation. Chemical engineering science. 2004;59(20):4261–4277. [Google Scholar]
- 44.Dooley KE, Nuermberger EL, Diacon AH. Pipeline of drugs for related diseases: tuberculosis. Curr Opin HIV AIDS. 2013;8(6):579–585. doi: 10.1097/COH.0000000000000009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Martínez E, Collazos J, Mayo J. Hypersensitivity reactions to rifampin: pathogenetic mechanisms, clinical manifestations, management strategies, and review of the anaphylactic-like reactions. Medicine. 1999;78(6):361–369. doi: 10.1097/00005792-199911000-00001. [DOI] [PubMed] [Google Scholar]
- 46.Zhang Y, Yew WW, Barer MR. Targeting persisters for tuberculosis control. Antimicrob Agents Chemother. 2012;56(5):2223–2230. doi: 10.1128/AAC.06288-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rosenthal IM, Tasneen R, Peloquin CA, Zhang M, Almeida D, Mdluli KE, Karakousis PC, Grosset JH, Nuermberger EL. Dose-ranging comparison of rifampin and rifapentine in two pathologically distinct murine models of tuberculosis. Antimicrob Agents Chemother. 2012;56(8):4331–4340. doi: 10.1128/AAC.00912-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Katsube T, Yano Y, Wajima T, Yamano Y, Takano M. Pharmacokinetic/pharmacodynamic modeling and simulation to determine effective dosage regimens for doripenem. J Pharm Sci. 2010;99(5):2483–2491. doi: 10.1002/jps.21997. [DOI] [PubMed] [Google Scholar]
- 49.Lesko LJ, Schmidt S. Individualization of drug therapy: history, present state, and opportunities for the future. Clin Pharmacol Ther. 2012;92(4):458–466. doi: 10.1038/clpt.2012.113. [DOI] [PubMed] [Google Scholar]
- 50.Zumla AI, Gillespie SH, Hoelscher M, Philips PP, Cole ST, Abubakar I, McHugh TD, Schito M, Maeurer M, Nunn AJ. New antituberculosis drugs, regimens, and adjunct therapies: needs, advances, and future prospects. Lancet Infect Dis. 2014;14(4):327–340. doi: 10.1016/S1473-3099(13)70328-1. [DOI] [PubMed] [Google Scholar]