Dynamical Binding of Hydrogen Bond Surrogate-Derived Bak Helices to Anti-apoptotic Protein Bcl-x_L

Abstract

A new peptide modification strategy was recently developed to replace the i to i+4 hydrogen bond of the main chain of an a-helix with a carbon-carbon covalent bond to afford highly stable constrained α-helices, termed Hydrogen Bond Surrogate (HBS) helices. HBS helices that mimic the Bak BH3 domains were experimentally demonstrated to target protein Bcl-x_L with high affinity. In this study, molecular dynamics (MD) simulation is used to understand how the covalent modification of the natural Bak sequence affects the binding to Bcl-x_L at molecular levels. The binding mechanism of HBS helix to Bcl-x_L and the effect of synthesized cyclic structures are analyzed by molecular dynamics and MM-PBSA calculations for comparison with the native binding of Bak-Bcl-x_L. The present MD result shows that the entropy of the HBS structure is considerably reduced and the presence of the N-terminal HBS macrocycle impacts residues at the C-terminus of the helix. But the conformation of the corresponding binding structures is not significantly changed. Our analysis shows that substitution of an aspartic acid residue – a helix breaker – with a hydrophobic residue not only enhances the helicity of the peptide but also stabilizes the structure of the binding complex. The present computational result is consistent with the experimental observation and provides explanations for the altered binding properties of the artificial Bak a-helix. Our study underscores the importance of dynamical effect in protein-peptide interaction in which entropic effect plays a major role.

1. Introduction

The α-helix is a ubiquitous structural motif in proteins and is frequently involved in protein-protein interactions that dominate many biological pathways. In theory, peptides that mimic the helical domains at protein interfaces are ideal ligands for selective targeting of proteins and modulation of their biological functions [1, 2]. However, short peptide domains do not remain structured when taken out from their original biological environments. The in vivo efficacy of peptides is compromised by their loss of secondary structure, susceptibility to proteolytic degradation, and difficulty in penetrating intact cell membranes.

Recently a hydrogen-bond surrogate (HBS) strategy was developed to stabilize peptide secondary structures, specifically α-helices (Figure 1a) [3]. In this approach, an N-terminal main-chain i to i+4 hydrogen bond is replaced by a carbon-carbon bond to nucleate the helical conformation [4-5]. In theory, constraining flexible molecules into conformations that mimic their bound structures is expected to lower the entropic cost of the binding processes. Anti-apoptotic protein Bcl-x_L and its natural peptide ligand Bak BH3 domain provide a good system to test the effectiveness of this method (Figure 1b). Arora and coworkers designed two HBS helices that mimic the Bak BH3 domains (Figure 1c-d). One of these helices, HBS 2a, is a direct mimic of the natural Bak BH3 sequence. HBS 2b was designed to further improve the helicity of the Bak helix. The Bak peptide 1 contains a GDD tripeptide residue (residues 582-584 in the Bak BH3 domain) in the middle of the Bak peptide sequence may limit the propagation of the helix and lower the overall helical content of 2a, since glycine is known to be a potent “helix breaker” and aspartic acid has been implicated as a helix stop signal. [6-8] Gly-582 and Asp-583 residues cannot be substituted with alanine without sacrificing binding affinity for the protein; however, Asp-584 may be replaced without any deleterious effects [9]. To test the effect of replacing Asp-84 on the helicity of Bak peptide, Arora et al. prepared HBS α-helix 2b in which Asp-584 is substituted with a side chain acetylated-lysine (Lys^Ac) (Figure 1d). [10] This single substitution provided a significant boost in α-helicity; HBS helix 2b is roughly 140% more helical than 2a. Binding assays showed that both HBS peptides bound Bcl-x_L with high affinities, with 2b binding with a higher affinity in agreement with its enhanced helicity.[11]. We were motivated to investigate the detailed binding mechanisms of these HBS peptides and evaluate their biological effects by using computational modeling techniques. In particular, we expect that dynamical effect such as entropic effect may play an important role in protein-peptide binding due to much increased flexibility of the peptide relative to rigid small molecular binders.

Figure 1.

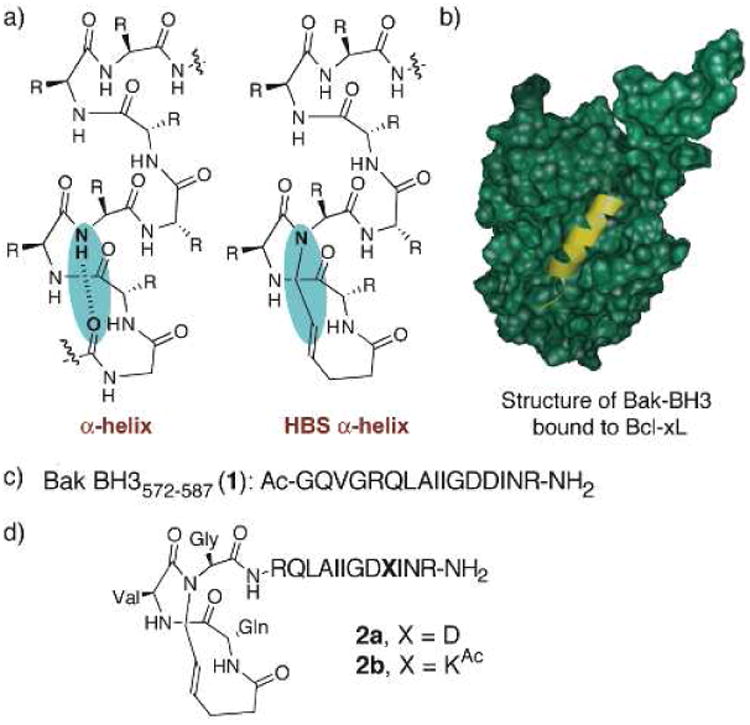
a) Formation of hydrogen-bond surrogate (HBS) derived α helices by replacement of a main-chain hydrogen bond with a carbon–carbon bond. b) HBS a helix and recognition of Bcl-xL (green) with Bak BH3 a helix (yellow); PDB code: 1BXL. c) Sequence of the unconstrained Bak BH3 peptide 1. d) Structures of HBS Bak a helices 2a and 2b.

In this paper, we present MD simulation studies for three peptide-Bcl-x_L systems. The binding free energies are calculated from the MD trajectories, and the roles of different interactions and their effects are analyzed. The results reveal that although the HBS macrocycle doesn't directly impact its binding configuration, it does have the influence on configurations of residues in distance; the hydrophobic side chain at the site of Asp584 not only stabilizes the helical structure of the peptide but also increases the hydrophobic interactions with the Bcl-x_L.

2. Computational Methods

The starting structure of the Bak-Bcl-x_L complex was obtained from the Protein Data Bank (PDB) [12] with PDB entry 1BXL (Figure 1b) [9]. The HBS helices and K^AC residue were constructed by InsightII, and optimized at the B3LYP/6-31G* level by Gaussian03 [13]. The partial charges of HBS helix and KAC were generated by using RESP [14] program, based on the ESP potentials generated by the ab initio calculation at the B3LYP/6-31G* level by Gausian03. AMBER9 [15] package was used to carry out molecular dynamics simulations with ff03 version of Amber force field [16]. Counterions were placed by Leap to neutralize the charges of three systems. A rectangular-shaped box of water was constructed using the TIP3P water model [17], with the buffering distance set to 10 Å. For each system, 500 steps of energy minimization constraining the solute were carried out, followed by 1000 steps of energy minimization without any constraints. After energy minimization, each system was heated to 300K by weak coupling algorithm in 50ps, and equilibrated in the following 2ns. 10ns of product MD calculations were carried out for each system under periodic boundary conditions. The cutoff was set to 8 Å. The long-range electrostatic interactions were calculated by the particle-mesh Ewald algorithm [18]. The time step of the MD simulations was set to 2.0fs, and the SHAKE algorithm was used to constrain hydrogen bond lengths at their equilibrium values. The system pressure was maintained at 1atm and coordinates were saved for analysis every 1ps.

Binding free energy of Bcl-x_L to each peptide was calculated by using the MM-PBSA protocol, 400 snapshots of each model were taken at the time intervals of 5 ps from the last 2 ns production runs. The dielectric constants inside and outside the molecule were set as 1.0 and 78.0 respectively. The solvent accessible surface area (SASA) was computed with the molsurf module in AMBER9, using a probe radius of 1.4 Å. The surface tension proportionality constant and the free energy of nonpolar solvation of a point solute were set to 0.00542 kcal/mol/Å and 0.92 kcal/mol, respectively [19], at this stage, the configurational entropies were calculated by nmode module in AMBER9. Single trajectory method was used in MM-PBSA binding free energy calculations. Although MM-PBSA is empirical in nature, when the sampling is appropriate and parameters are properly chosen, it can produce reasonably accurate results for biomolecular systems.

In order to investigate detailed differences of entropic changes in three peptide-protein systems, Schlitter's formula [20] was later used for the analysis of configurational entropy, which yields an upper bound to the true entropy S_true,

$$S_{\mathit{\text{true}}}<S=\frac{1}{2}{k}_{B}ln\text{det}[1+\frac{k_{B}T{e}^2}{{\hslash }^2}M\sigma ]$$ (1)

where k_B is the Boltzmann constant, T is the absolute temperature, e is Euler's number, ħ is the Plank's constant divided by 2π, M is the mass matrix that holds on the diagonal the masses belonging to the atomic Cartesian degrees of freedom, and σ is the covariance matrix of atom-positional fluctuations [20-22]. The elements of the covariance matrix are given by

$${\sigma }_{ij}=<(x_i-<x_i>)(x_j-<x_j>)>$$ (2)

where x_i are the Cartesian coordinates after least-square superposition of the trajectory configurations with respect to a particular subset of atoms by using Kabsch's algorithm [23]. In our simulation, all the backbone atoms are included for covariance matrix and entropy calculations.

The entropy change on receptor-peptide binding is given by

$$\mathrm{\Delta }{\mathrm{S}}_{\mathrm{C}}={\mathrm{S}}_{\mathrm{C}}-{\mathrm{S}}_{\mathrm{R}}-{\mathrm{S}}_{\mathrm{P}}$$ (3)

where S_C, S_R, and S_P is the entropy of the binding complex, receptor and the peptide, respectively. Similarly, we can evaluate the entropy change for each molecule (receptor and peptide) between bound and free states

$$\mathrm{\Delta }{\mathrm{S}}_{\mathrm{B}-\mathrm{F}}={\mathrm{S}}_{\mathrm{B}}-{\mathrm{S}}_{\mathrm{F}}$$ (4)

where S_B and S_F is, respectively, the entropy of the molecule after and before the binding.

Direct calculation of the absolute entropy of a molecule requires a complete sampling of all the translational and vibrational freedoms of the system. For complex systems such as proteins, this is not practical because the limitation in computational cost. Estimating configurational entropy from MD trajectory was first proposed by Karplus [21] by using the formula ΔS = 0.5k_B ln(det δ_a / det δ_b) where kB is the Boltzmann constant, δ_a and δ_b are covariance matrices of atomic positional fluctuations of configurations a and b. Later a heuristic formula based on Cartesian coordinates was introduced by Schlitter [20]. This formula computes an upper bound to the absolute entropy from a MD trajectory. Strictly speaking, the entropy calculated from this method is only approximate, yet it provides a practical and computationally feasible method in studying entropic effects in complex systems of many degrees of freedoms. Although decomposing the entropic contributions into subset of atoms neglects the correlation of motions between this subset and the rest of the system, nonetheless this method could be considered as a reasonable first order approximation of entropy for complex systems in which exact inclusion of all degrees of freedoms for entropy calculation is currently impossible. By this analysis we can quantitatively investigate the contributions of different subsets of the system to the overall entropy, which can provide additional insight information on dynamical properties of proteins.

3. Results and Analysis

a) RMSD of peptide-Bcl-x_L Complexes and unliganded Bcl-x_L

We carried out MD simulations for three binding complexes, the natural helix binding complex (Bak-Bcl-x_L), HBS1 binding complex (HBS2a-Bcl-x_L), and HBS2 binding complex (HBS2b-Bcl-x_L). Bak is a multidomain BH1-3 proapoptotic protein required for outer mitochondrial membrane permeabilization (OMMP) and apoptosis induced by many types of cell death stimulation. [24-25] Bcl-x_L, an antiapoptotic member of Bcl-2 family, inhibits Bak activation by binding to BH3 α helix domain of Bak protein [26-28]. BH3 α helix from Bak protein can bind to and antagonize Bcl-x_L and thus activate apoptosis [29-30]. BH3 α helix from Bak protein is used to construct HBS proteins, the first hydrogen bonding at the N terminal of Bak peptide is covalently connected by replacing the H-O hydrogen bond with a C-C covalent bond. Asp584 is replaced by an Acetyl-Lysine residue in order to increase the stability of the helix in HBS2b peptide [11]. The root mean square deviations (RMSD) of C_α atoms from the initial structures of each complex and free Bcl-x_L are shown in Fig. 2. The RMSD of each system is stabilized around 1 ns. The average RMSDs and corresponding standard deviations from 2 ns to 10 ns are: 1.66±0.38 Å (Bak-Bcl-x_L), 3.38±0.35 Å (HBS 2a-Bcl-x_L), 2.64±0.42Å (HBS ab-Bcl-x_L), 2.99±0.37Å (free Bcl-xL), respectively. These results suggest that there is no significant structural drift in each system during the MD simulations, and there is no significant structural change when Bcl-x_L is unliganded, which is in agreement with the crystal structure of Bcl-x_L [31].

Figure 2.

Time evolutions of the RMSD of C_a atoms during 10 ns MD simulations of three peptide-Bcl-x_L complexes and unliganded Bcl-x_L.

b) Binding free energies and comparison with experimental data

Table I shows the binding free energy components of three complexes from the MM-PBSA calculation. All three complexes have large negative enthalpies, large negative electrostatic energies and van der Waals energies. There are important interaction energy components in determining the binding affinities of peptide-Bcl-x_L system, indicating the binding processes are energetically favorable. HBS2b peptide overall has the lowest binding free energy, and the lowest van der Waals and electrostatic interaction energies. HBS2a peptide also shows more negative Van Der Waals interaction energy comparing with the natural peptide Bak (around 11.5 kcal/mol lower), this is probably due to the fact that both HBS peptides are more stable in bound states, thus results in better contacts with the Bcl-x_L. The electrostatic interaction energy of HBS2a is about 20 kcal/mol higher than Bak and HBS 2b peptides as shown in Table 1.

Table 1.

Components of binding free energy for three binding complexes (all the units are in kcal/mol). (The standard deviations of TΔS for three systems are 10.92 kcal/mol, 12.35 kcal/mol and 8.93 kcal/mol, respectively, ΔE_gas=ΔE_ele+ΔE_vdw)

	Bak-Bcl-xL	HBS2a-Bcl-xL	HBS2b-Bcl-xL
ΔEele	-152	-132	-153
ΔEvdw	-89	-100	-100
ΔEgas	-241	-232	-253
ΔGSA	-14	-14	-14
ΔGPB	190	166	187
ΔGEtot	-65	-80	-80
TΔS	-43	-72	-40
ΔΔGBinding	-22	-8	-40

In general, both HBS peptides exhibit more favorable enthalpy changes upon binding relative to the natural Bak peptide. However, when conformational entropic effects are included, the order of binding affinities could be changed. Considering the entropic changes from normal mode calculations, the dominant free energy increase comes from HBS2a system, which gives a large entropic change (TΔS=-72kcal/mol), and consequently, a relatively small binding free energy (-8kcal/mol). This suggests that HBS2a peptide is less effective in binding comparing with the natural Bak peptide and HBS2b and the system adopts a different binding mode in some sense. Combining the solvated free energies with entropic changes from normal mode calculations, the order of affinities from our calculation are in good agreement with the experimental affinity data [11].

c) Flexibilities of peptide helicities of free and bound peptides

The minimal region of Bak protein required to bind to Bcl-x_L is a 16-amino acid peptide derived from the BH3 region of Bak protein [29]. This peptide tends to form random coil in solution but again forms an α-helix when it binds to Bcl-x_L. The Ramachandran plots of the backbone distributions of the representative residues in free Bak peptide and corresponding residues in HBS peptides are shown in Fig. 3. There are two glycine residues inside Bak peptide, since glycine is known as one of the helix-breakers due to small size of its side chain, the flexibilities of glycine residues play influential roles in helix forming and breaking. The phi-psi distribution of Gly75 falls into regions mostly representing random coil and a small portion of left-handed helix, while Gly82 has some conformations falling into α-helix region. All of glycine residues show considerable flexibilities and there is only a small possibility that the phi-psi distribution falls into the α--helix region, that's probably the main reason that this peptide is largely random coil in solution.

Figure 3.

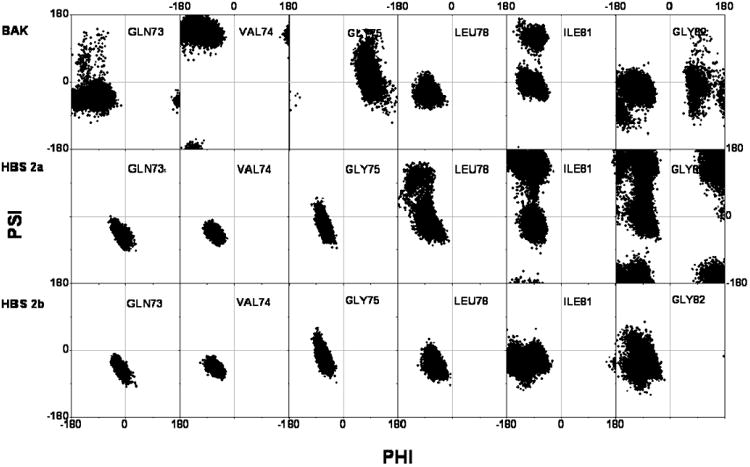
The Ramachandran plots of most flexible residues from Bak peptide and the comparisons with HBS peptides (Free states) A: Gln73, B: Val74, C: Gly75, D: Leu78, E: Ile81, F: Gly82.

Besides glycine residues, there are two other residues noteworthy to mention, Val74 and IIe81. Val74 takes the β-sheet backbone conformation in nearly all structures, and Ile81 also has considerable possibility to take the β-sheet backbone conformation.

When the Bak peptide is modified to HBS peptides, since the backbones of the residues which anticipate the formation of the HBS ring are covalently fixed, there is rarely possibility that they take the any other conformations but α--helix conformation. The Ramachandran plots of the backbones of these residues (Three are shown in Fig. 3) are not only inside the α-helix region but also restricted into very limited space, as expected.

Because of its rigidity and large spatial volume, the HBS ring has other impacts on the conformation of the peptide. The backbone distributions of Leu78, Ile81 and Gly82 are more diffused comparing with the natural Bak peptide. From the view of root-mean-square-fluctuation (RMSF) of each residue (Figure 5A), it is clear that the HBS ring induced consistently larger fluctuations.

Figure 5.

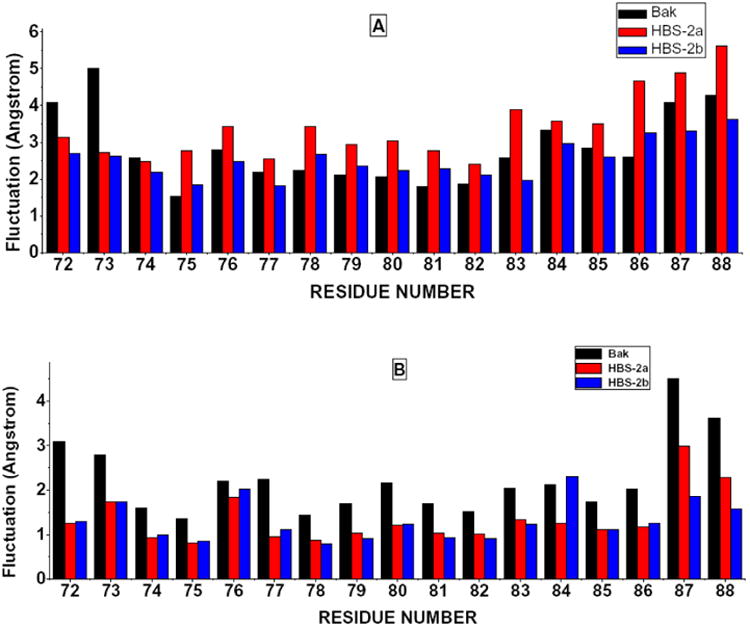
Residue Root Mean Square Fluctuation of Free and Bound States, A: Free States, B: Bound States.

The substitution of Asp84 by Lys^AC, however, provides additional side chain contacts with nearby residues and stabilized the secondary structure and minimized the fluctuations, because of the prolonged flexible hydrophobic side chain on K^AC. This is proved by the distributions of Ramachandran plots and RMSF values as shown in Figs. 3-4. Experimentally determined helicities of three peptides are: Bak ≈20%, HBS helix 2a ≈45%, HBS helix 2b ≈65% [11], which are qualitatively in good agreement with our simulations.

Figure 4.

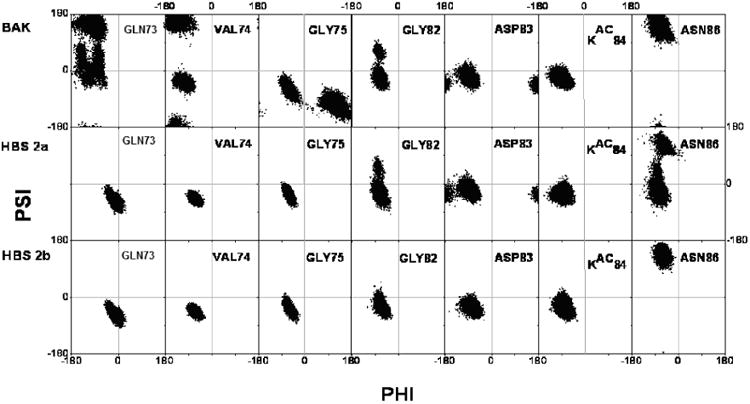
The Ramachandran plots of most flexible residues from Bak peptide and the comparisons with HBS peptides (Bound states).

After peptide-Bcl-x_L complex formation, it is expected that the flexibilities of some residues will be restricted, Ramachandran plots of two glycine residues (shown in Fig. 4) indicate the α--helix-forming trends have been largely improved comparing with free states. On the other hand, the different position of Asn86 in bound HBS helix 2a implies that the binding mode of HBS helix 2a is not identical to the natural Bak peptide and HBS helix 2b. The overall residual fluctuations of the bound states have been considerably reduced (Fig. 5B), however, the natural Bak peptide is still quite flexible in bound state. Roughly speaking, in free states, the HBS helix 2a shows the largest fluctuation, natural Bak peptide is the next; in bound states, the residual fluctuation of HBS helix 2a is dramatically lowered, and natural Bak peptide is more flexible in this case. Finally, HBS helix 2b is the least fluctuated peptide in both cases.

d) Analysis of conformational entropies

The conformational entropic changes of backbone atom sets of free peptides and Bcl-x_L and their complexes are shown in Fig. 6A. According to the recent protein-protein binding model proposed by Grunberg et al. [32], the protein-protein binding process follows a three-step mechanism of diffusion, free conformer selection, and refolding. The recognition step is an entropy loss process because only a subset of free conformations will be selected. After recognition, the complex is relaxed again, and it will regain some entropy. The entropies of three peptides begin to level off after ∼0.5 ns. For larger systems of Bcl-x_L and three complexes, it takes around 2ns to level off. All systems show satisfactory convergences within the 10ns simulation time. However, since the absolute values of entropies are nearly 100 fold than ΔS values, it can still cause convergence problems. Fortunately, the ΔS^{complex-receptor-peptide} values for three systems converge well within 10ns. All systems undergo drastically entropic drops at the beginning, then gradually get back and level off. This process takes around 3ns for three systems, and the general entopic change picture is in agreement with the model proposed by Grunberg et al. [32]. Bak-Bcl-x_L system has the lowest entropy loss, 99.09 cal/mol, the entropy loss of HBS helix 2b-Bcl-x_L is 140.94 cal/mol, while HBS helix 2a-Bcl-x_L system gives the largest entropy loss, 365.90 cal/mol, which is expected from the RMSFs of free and bound states.

Figure 6.

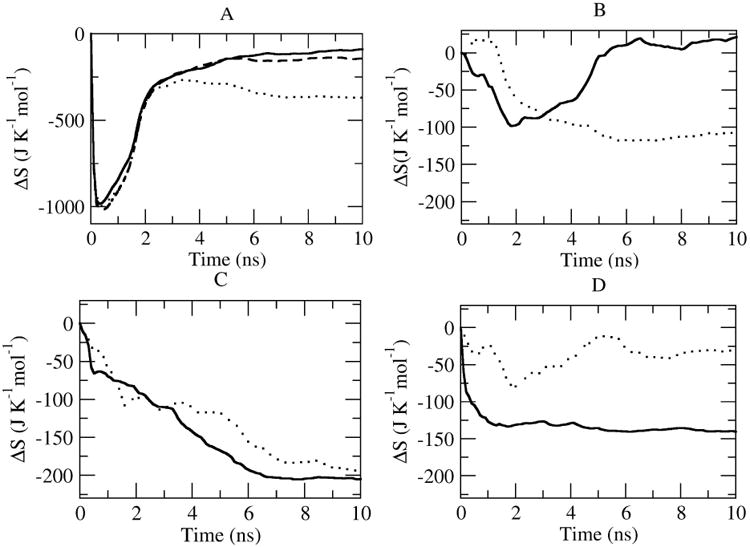
A) Entroy change ΔS^{complex-receptor-peptide} as a function of simulation time (solid line: Bak-Bcl-xL system; dots: HBS2a-Bcl-x_L system; dashed line: HBS2b-Bcl-x_L system;. B-D) Decompositions of entropy changes of inhibitory peptides and Bcl-x_L (B: Bak-Bcl-x_L, C: HBS helix 2a-Bcl-x_L, D: HBS helix 2b-Bcl-x_L (Solid line: Bcl-x_L dots: peptides). The entropy at each time point is derived from the covariance matrix calculated as a time average taken over configurations in the trajectories.

Although the entropic difference is a relatively small value comparing to the absolute value of the individual systems and the sampling may not be converged yet because of the computational limitations, the order of entropic changes calculated from the triple trajectory method by covariance matrix scheme coincides with the result of normal mode method, and confirms that HBS2a peptide brings significant entropic loss when bound to Bcl-x_L.

e) Decomposition of Entropic Changes by Peptides and Bcl-x_L

Changes in conformational entropy upon binding can also be estimated from the contributions of the peptides and the receptor. For this purpose, the atom-positional least-square fitting of trajectory structures was performed by using backbone atoms of the individual peptides or receptor in order to exclude the entropy contributions of collective motions. Figure 6 B-D shows the entropic differences by the peptides and Bcl-x_L, for the both cases of Bak and HBS helix 2b system, the entropic differences of peptides keep dropping and finally level off; on the other hand, the entropic differences of the Bcl-x_L are all of the similar feature that the entropic differences drop down around 2ns then go up, after some fluctuations and finally level off, indicating that the Bcl-x_L doesn't undergo large structural changes during the binding processes, which is in agreement with the structural determinations of free Bcl-x_L and Bak-Bcl-x_L complex. HBS helix 2a system, however, is different from Bak and HBS helix 2b systems. The entropic difference of Bcl-x_L, keeps dropping and only starts to level off after 8ns, further proves the binding process of HBS helix 2a to Bcl-x_L is in some sense different with Bak and HBS 2b, thus longer simulation time for entropic difference of Bcl-x_L is required. Specific entropic values from covariance matrix method are listed in Table 2.

Table 2. Average values of entropy change TΔS from covariance matrix method.

	TΔS
Bak-Bcl-xL c-l-r	-29.5 (0.9)
HBS 2a-Bcl-xLc-l-r	-109.1 (0.9)
HBS 2b-Bcl-xLc-l-r	-42.0 (0.8)
Bak in Bak-Bcl-xL b-f	-32.7 (0.6)
Bcl-xL in Bak-Bcl-xL b-f	4.5 (1.3)
HBS helix 2a in Bak-Bcl-xL b-f	-60.66 (0.21)
Bcl-xL in Bak-Bcl-xL b-f	-55.98 (1.45)
HBS helix 2b in Bak-Bcl-xL b-f	-38.33 (0.49)
Bcl-xL in Bak-Bcl-xL b-f	-9.40 (0.42)

(c: complex; l: ligand; r: receptor; b: bound state; f: free state all the units are kcal/mol, numbers in parentheses are standard deviations, all the values are averaged from the entropy values of last 2 ns of all trajectories)

f) Similarities and differences in three peptide-Bcl-x_L complex systems

The residues are considered as contacting if the distance of one atom pair from two residues is within 4Å. Contacts are counted if the interaction ratios are over 60% during simulations, Table 3 lists all these residues for three systems.

Table 3.

Detailed residue-residue contacts in binding of Bcl-x_L with Bak, HBS2a and HBS2b.

Bcl-xL	Bak	HBS 2a	HBS 2b
Gly572	-	Gln125, Gln129	Gln125, Val126, Glu129
Gln573	Gln111	Gln111	Gln111
Val574	Gln111, Leu112, Ser122, Gln125, Val126, Glu129, Phe146	Tyr101, Leu108, Gln111, Leu112, Val126, Phe146	Tyr101, Gln111, Leu112, Val126, Phe146
Gly575	Val126, Glu129,Leu130	Gln125, Val126, Glu129, Leu130	Val126, Glu129, Leu130
Arg576	Glu129	Glu129	Glu129
Gln577	Tyr101, Phe105	Tyr101, Phe105, Gln111	Tyr101, Phe105, Gln111
Leu578	Phe97, Tyr101, Leu108, Leu126, Leu130, Ala142, Phe146	Phe97, Tyr101, Leu108, Leu130, Ala142, Phe146	Phe97, Tyr101, Leu108, Leu126, Leu130, Ala142, Phe146
Ala579	Glu129, Leu130, Arg139	Glu129, Leu130, Arg139	Glu129, Leu130, Arg139
Ile580	-	Phe105	Phe105
Ile581	Phe97, Arg100, Tyr101	Phe97, Arg100, Tyr101, Ala104, Phe105	Phe97, Arg100, Tyr101, Ala104, Phe105
Gly582	Phe97, Gly138, Arg139 Ala142	Phe97, Leu130, Gly138, Arg139, Ala142	Phe97, Gly138, Arg139, Ala142
Asp583	Gly138, Arg139	Asn136, Arg139	Arg139, Arg204
Asp584 (KAC for HBS2b)	Arg100, Arg204	Arg100	Arg100, Ala104, Arg204, His215
Ile585	Ala93, Glu96, Phe97, Arg100, Gly138, Val141, Ala200	Ala93, Glu96, Phe97, Arg100, Gly138, Val141, Ala142, Tyr195	Glu96, Phe97, Arg100, Gly138, Val141, Ala142, Tyr195, Ala200
Asn586	Trp137, Gly138	Gly138, Leu194, Tyr195, Asn136, Trp137, Arg139	Gly138, Leu194, Tyr195, Ala200, Arg204
Arg587	Ser203	Leu194, His214, His215	Leu194, Tyr195, Gln207
NH2 terminal	Ala164, Ser167	Leu158, His178, His179	Tyr159, Ala164

According to the results of Alanine mutation experiments [9], the starting GQVGR sequence, Arg576, Leu578, Ile581, Asp583, Ile585 play important roles in stabilizing the complex, from Table 3 and Fig. 7, it is clear that the binding conformations of the peptides for the N-end to Asp583 in three systems are very close, shows that the synthesized cyclic structure does not interfere with peptide binding in this region significantly. However, this cyclic structure does have spatial impacts on binding structures of the region from Asp584 to the C-end. In the simulation of original Bak-Bcl-x_L complex, Asp584 forms salt bridges with two Arg residues; comparing with two synthesized peptides, two residues at the C-end of Bak are quite flexible, few residues of Bcl-x_L can form stable contacts with them. In HBS helix 2a system, Asp584 can only form salt bridge with Arg100, thus may largely weaken the binding affinity. In HBS helix 2b system, the extra long hydrophobic side chain of K^AC is firmly anchored in the hydrophobic pocket comprised by Arg100, Ala104, Arg204 and His215 as shown in Fig. 8, and the C-end residue Arg587 is pointing to the region of Leu194, Tyr195 and Gln207, which can hardly be reached by Bak and HBS helix 2a. The binding conformation of K^AC and the Asp to Ala mutation at this point both implies that although there are two Arg residues to form salt bridges with Asp584 of the peptide, the enhanced hydrophobic interactions are more effective in stabilizing the complex. This prediction is supported by the single residue modification of Asp584 to KAC at Bak peptide, which gives the highest binding affinity among the Bak and two HBS helix peptides (unpublished data).

Figure 7.

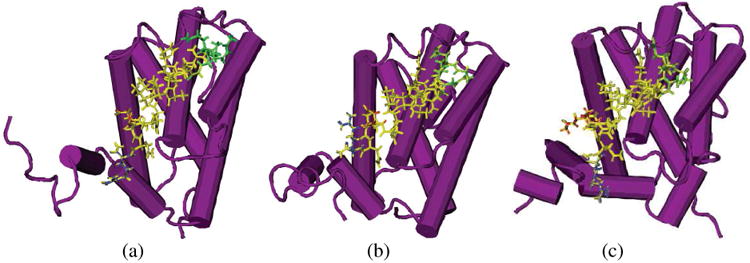
Structures of the Bcl-x_L with three peptides for simulations at t=10 ns. (A: Bak-Bcl-x_L system; B:HBS helix 2a-Bcl-x_L system; C: HBS helix 2b-Bcl-x_L system) Bcl-x_L structures are shown in purple, residues in Bak from Gly572 to Gly575 and the corresponding cyclic rings in HBS helix 2a and HBS helix 2b are shown in green; residue Asp584 (K^AC in HBS helix 2b) is shown in red, HBS helix 2b forms a Y shape and anchors at the hydrophobic surface of Bcl-x_L. The rest Parts of the three inhibitive peptides are shown in yellow.

Figure 8.

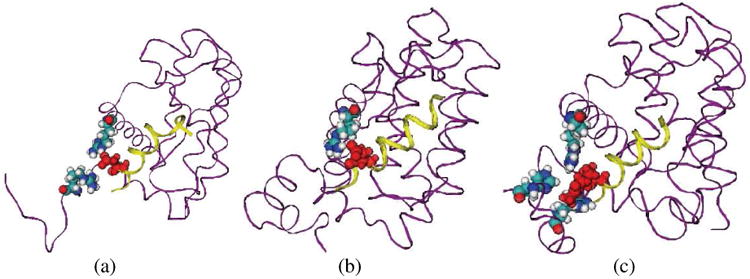
Detailed molecular interactions between Asp584 (K^AC in HBS helix 2b) and Bcl-x_L. (A. Bak-Bcl-x_L system, residue Arg100 and Arg204 at Bcl-x_L involved; B. HBS helix 2a-Bcl-x_L system, Arg100 at Bcl-x_L involved; C. HBS helix 2b-Bcl-x_L system, Arg100, Ala104, Arg185, His215 at Bcl-x_L involved) Bcl-x_L is represented in purple ribbon, while the peptides are in yellow ribbon; Asp584/K^AC584 residues are represented in red VDW form, and all residues interacting with Asp584/K^AC584 are represented in VDW form with atom type color representation.

Conclusions

In the present study, the binding mechanisms of HBS helix peptides with Bcl-x_L and the effects of macrocyclic regions within the synthetic helices are analyzed by molecular dynamics and MM-PBSA calculations for comparison with the native binding of Bak-Bcl-x_L. Based on our results, the HBS structure largely decreases the entropy of the system but does not significantly change the conformation of the corresponding binding structures. It indirectly impacts the binding conformation at the C-end of the peptides. Our simulation shows that substitution of a hydrophobic side chain at Asp584 not only enhances the helicity of the peptide but also stabilizes the structure of the binding complex.