Identification and Management of Nonsystematic Purchase-Task Data: Towards Best Practice

Abstract

Experimental assessments of demand allow the examination of economic phenomena relevant to the etiology, maintenance, and treatment of addiction and other pathologies (e.g., obesity). Although such assessments have historically been resource-intensive, development and use of purchase tasks—in which participants purchase one or more hypothetical or real commodities across a range of prices—have made data collection more practical and increased the rate of scientific discovery. However, extraneous sources of variability occasionally produce nonsystematic demand data, in which price exerts either no, or inconsistent, effects on purchasing of individual participants. Such data increase measurement error, can often not be interpreted in light of research aims, and likely obscure effects of the variable(s) under investigation. Using data from 494 participants, we introduce and evaluate an algorithm (derived from prior methods) for identifying nonsystematic demand data, wherein individual participants’ demand functions are judged against two general, empirically based assumptions: (1) global, price-dependent reduction in consumption, and (2) consistency in purchasing across prices. We also introduce guidelines for handling nonsystematic data, noting some conditions in which excluding such data from primary analyses may be appropriate and others in which doing so may bias conclusions. Adoption of the methods presented here may serve to unify the research literature and facilitate discovery.

In behavioral economics, examination of demand elasticity (sensitivity of consumption to increasing price) and demand intensity (level of consumption unconstrained by price) provides objective estimates of a commodity's value (see Hursh & Silberberg, 2008), wherein lower elasticity or higher intensity reflect greater valuation of the commodity under investigation. Assessment of these constructs has been particularly informative in the area of addiction, allowing examination of abuse liability of different drugs (e.g., Hursh & Winger, 1995; O'Connor et al., 2014; Rowlett, Rodefer, Spealman, 2002), effects of clinical treatment variables on drug demand (e.g., Bujarski, MacKillop, & Ray, 2013; Madden & Kalman, 2010), drug valuation as a risk factor for drug treatment failure (MacKillop & Murphy, 2007), and differences in drug valuation across populations (e.g., MacKillop & Tidey, 2011; Yurasek, Murphy, Clawson, Dennhardt, & MacKillop, 2013) or in the presence of potential substitutes (e.g., Lenoir & Ahmed, 2007; Shahan, Odum, & Bickel, 1999).

In traditional behavioral-economic assessments, price is defined as the behavioral output required to obtain one unit of a commodity (e.g., a self-administered cigarette puff or piece of nicotine gum; Shahan et al., 1999). Price is manipulated across several, lengthy sessions and its effects on consumption and behavioral output is measured. This method has provided fundamental knowledge of behavioral-economic principles and, in translation, their implications for public policy (for review, see Hursh & Roma, 2013). However, the time and additional resources this method requires can be prohibitive, limiting the number of prices that can be examined, the number of participants that contribute data, the demographic populations that can be examined (e.g., those able to participate in lengthy studies), and the number of researchers that can investigate behavioral-economic phenomena (e.g., those with access to operant self-administration equipment). Moreover, this method may compromise external validity, as the laboratory environment minimizes the influence of some variables known to impact drug consumption (e.g., social reinforcement or punishment).

In response to these limitations, some researchers have developed and refined variants of a drug purchase task, in which participants purchase a given drug (for use outside the laboratory) across a range of monetary prices. Consumption is typically constrained by asking participants to make purchases in line with a real-life or experimentally provided income, and to assume that purchases are to be used over a pre-defined period (e.g., 24 hours), cannot be saved or given away, and are unavailable from any other source. In most versions of the task, purchases are hypothetical (e.g., Jacobs & Bickel, 1999; MacKillop & Murphy, 2007); in others, purchases are either potentially real (i.e., participants receive the purchases from one randomly selected price), or entirely real (e.g., Amlung, Acker, Stojek, Murphy, & MacKillop, 2012; Koffarnus, Wilson, & Bickel, 2014). Research to date has shown within-subject correspondence between demand estimates from hypothetical and real tasks (Amlung et al., 2012). Moreover, purchase tasks demonstrate high test-retest reliability, inter-method reliability, and construct validity, with demand estimates agreeing across time, different step sizes in price, and with real-world drug consumption and markers of addiction (Few, Acker, Murphy, & MacKillop, 2011; Murphy, MacKillop, Skidmore, & Pederson, 2009; Reed, Kaplan, Roma, & Hursh, 2014; Murphy, MacKillop, Tidey, Brazil, & Colby, 2011). As such, purchase tasks represent an effective, flexible, and practical approach for examining demand under a broad set of conditions.

One barrier to interpreting findings, however, is the presence of demand functions that are not systematically affected by price (e.g., invariant, inconsistent, or no consumption across prices). Participants may contribute such data for a number of reasons, including inattention to the task, errors in response entry (e.g., typing 55 instead of 5), or failure to understand task directions. In these cases, experimenters should consider excluding such data from primary analyses in order to preserve the fidelity of the variable(s) under investigation. However, in other cases, the presence of nonsystematic data may reflect an important property of the study population (e.g., heavy vs. occasional smokers), the commodity under investigation (e.g., novel tobacco products), or the parameters of the task itself (e.g., restricted price range). In these cases, nonsystematic data should be retained and handled appropriately. However, the difference between data that do and do not merit exclusion may not always be apparent. The purpose of this paper is to introduce and evaluate a method and set of guidelines for identifying and handling nonsystematic purchase-task data, which, if adopted, would enhance accuracy of data reported in the literature and facilitate comparison of data obtained or analyzed across heterogeneous conditions (e.g., different laboratories, participant populations, etc.).

Identification of Nonsystematic Data

A Three-Criterion Algorithm

To identify potentially nonsystematic demand functions in individual participants, we refined and expanded upon an algorithm used in prior research on temporal discounting (Johnson & Bickel, 2008) and demand (Bruner & Johnson, 2014). This algorithm may be applied to any data set, regardless of the number and range of prices imposed, the commodity under investigation, the probability of that commodity's receipt (i.e., hypothetical, potentially real, or real), or the method used to analyze data (e.g., exponential or linear demand models; Hursh & Silberberg, 2008; Hursh, Raslear, Baumann, & Black, 1989; Killeen, 1995). The algorithm makes only two general assumptions, in no order of importance: (1) a global reduction in consumption from first price to last, and (2) consistency in the directional change in consumption across price increments. In the following section, we define three specific criteria an experimenter may use to detect whether data sets meet these general assumptions.

Criterion 1: Trend

Drawing from more than a century of economic research and theory, the law of demand describes a near-universal phenomenon in which, all else being equal, increases in the price of a commodity reduce consumption of that commodity (Stigler, 1954). Degree of reduction, of course, depends on a number of variables, including the necessity of the commodity, individual differences in commodity valuation, the availability of viable substitutes, and the range of prices imposed. In contrast, the conditions under which increases in a commodity's price instead produce increases in consumption, as in the case of Giffen goods (Marshall, 1895; e.g., Battalio, Kagel, & Kogut, 1991; DeGrandpre, Bickel, Rizvi, & Hughes 1993; Dougan, 1982), are rare. For these reasons, the Trend criterion assumes a non-negligible reduction in consumption from the first to last price imposed. The algorithm then flags data for further consideration when detecting negligible reductions, no change, or increases in consumption.

Formally, the algorithm calculates the log-unit reduction in consumption (base 10) from the first to last price. Log-unit reduction in consumption is then expressed relative to log-unit range in price in order to accommodate varying price ranges across tasks, wherein smaller changes in consumption should be expected with smaller ranges in price. Relative change scores can be calculated, as follows:

$$\Delta Q=\frac{\log Q_1-log{Q}_n}{log{P}_n-log{P}_1},$$ (1)

where ΔQ is relative change in the quantity purchased; Q₁ and Q_n are the quantities purchased at the first and last price, respectively; and P₁ and P_n are the first and last prices, respectively¹. The calculated value of ΔQ is then compared to a criterion detection limit, X, wherein values of ΔQ below X would be identified as nonsystematic. Here, we suggest setting X to a value of 0.025, indicating that the algorithm will identify demand functions as nonsystematic if it detects less than a 0.025 log-unit reduction in consumption per log-unit range in price. To illustrate, if an experimenter employs prices in a purchase task that span one log unit (e.g., $1.00-$10.00), a decrease from 100 to 94 units purchased (ΔQ = .027) would pass without detection. However, if price spans two log units (e.g., $1.00 to $100.00), an identical decrease (100 to 94 units; ΔQ = .014) would be detected and flagged for further consideration.

Note that the Trend criterion will detect the special case in which a participant makes zero purchases at all prices (but see footnote above). A participant may contribute such data for a number of reasons, including severe constraints on income or limited valuation of the commodity under investigation (as may occur with novel commodities or following treatment designed to reduce demand). In many cases, these “null” demand functions may represent important information and should be considered in subsequent analyses (see Handling of Nonsystematic Data, below).

Criterion 2: Bounce

The Trend criterion (above) assumes a global effect of price on consumption (i.e., a non-negligible reduction from first price to last). However, the present algorithm also assumes consistent local effects of price, wherein the majority of increments in price should produce a reduction (or at least no change) in consumption. In contrast, frequent price-to-price increases in consumption—even in the presence of global reduction—likely indicates inattention to the task or errors in response entry. In turn, such variability, or bounce, is likely to impact estimates of demand. However, an experimenter may tolerate some degree of variability, particularly in cases in which price order is randomized, as the local effects of small price changes are less robust than those for larger changes. For these reasons, the Bounce criterion assumes that either no, or relatively few, price increments contain local increases in consumption.

Formally, the algorithm calculates the number of price-to-price increases, or “jumps,” in consumption that exceed 25% of initial consumption at the lowest price. The number of these jumps is then expressed relative to the total number of price increments to accommodate varying numbers of prices used across tasks, wherein more prices would increase the opportunities for jumps to occur. Defined in this way, the algorithm calculates an index of bounce, B, by dividing the number of detected jumps by the number of price increments.² This value is then compared to a criterion detection limit, X. Here, we suggest a value for X of 0.10, indicating that the algorithm will identify demand functions as nonsystematic when detecting jumps at more than 10% of price increments. To illustrate, if an experimenter employs 25 prices in a task, then two detected jumps (B = .08) would pass without detection. However, if an experimenter employs only 10 prices, then the same number of jumps (B = .22) would be detected and flagged for further consideration.

Criterion 3: Reversals from Zero

Although the Bounce criterion addresses price-to-price variability in consumption, it does not explicitly address the special case in which a participant ceases consumption at a given price and resumes consumption at higher prices. We note that these reversals from zero may be observed in demand functions that the Bounce criterion otherwise identifies as systematic. These reversals reflect an economic inconsistency more severe than the typical price-to-price fluctuation described above, and should therefore be identified and handled distinctly. A price-dependent reduction to zero consumption is an explicit acknowledgement that the ratio of a commodity's price to the benefit that commodity may bestow has exceeded some critical value. Reflecting this distinction, the “breakpoint” often serves as an independent index of demand in operant assessments and purchase tasks (e.g., MacKillop & Murphy, 2007; Shahan, Bickel, Madden, & Badger, 1999), and is defined as the lowest price at which consumption or spending falls to zero (Hodos, 1961). Thus, all else being equal, any prices higher than this breakpoint should be equally incapable of sustaining consumption. However, as above, an experimenter may wish to tolerate brief reversals (i.e., at a single price), perhaps due to errors in response entry or in cases in which price is randomized. Formally, the algorithm identifies data as nonsystematic if it detects an instance of zero consumption at two or more consecutive prices followed by any non-zero consumption at higher prices. With the use of ascending prices in purchase tasks, however, we note that some experimenters use the first instance of zero consumption as a criterion to end the task, after which no additional prices are imposed. Such a method is reasonable, assuming that all participants are in contact with the programmed contingencies. However, given the present discussion and the data presented below, a more conservative method is to expose participants to all prices, regardless of their behavior.

Applying the Algorithm to Hypothetical Purchase Tasks

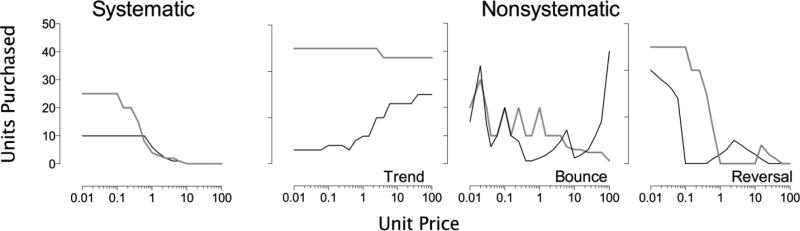
For illustrative purposes, Figure 1 depicts example demand functions that the algorithm identifies as either systematic (left panel) or nonsystematic for failing to meet either the Trend, Bounce, or Reversal criteria (right three panels). Note that in these examples, each nonsystematic demand function identified failed to meet only one criterion; however, in some cases, demand functions may fail to meet multiple criteria.

Figure 1.

Example demand functions that that the three-criterion algorithm identifies as systematic (left panel) or nonsystematic for failing to meet the Trend, Bounce, or Reversal criteria (right panels).

To test the algorithm, we analyzed data from four hypothetical cigarette purchase tasks from our lab, each chosen to provide heterogeneity in the number and range of prices examined. Participants (N = 494) smoked, on average, between 10 and 20 cigarettes per day (see Table 1 for additional details). The first three tasks featured 68 prices (range: $0.00-5.00), 22 prices (range: $0.00-100.00), and 9 prices (range: $0.00-1000) per individual cigarette. In these tasks, participants were asked to make purchases in line with their real-life budget and to purchase cigarettes for use over a 24-hr period. Price was imposed in an ascending order.

Table 1.

Study parameters, percent of demand functions identified as nonsystematic for any criterion (as well as individual criteria).

		Purchase Task
		68 prices: $0.00-5.00	22 prices: $0.00-100.00	9 prices: $0.00-1000.00	4 pricesa: $2.50-20.00
Study Parameters	Study Location	Lab	Lab	MTurk	MTurk
	Cigarette Units	1	1	1	20
	Price Order	Asc.	Asc.	Asc.	Rand.
	N	104	51	289	50
	% Female	49	45.1	53.7	44
	% Caucasian	59.6	56.9	80.6	86
	% Some College	37.6	29.4	82.4	86.0
	Age (SD)	38.9 (11.1)	39.6 (12.6)	35.8 (10.9)	31.0 (7.7)
	C/d (SD)	21.1 (9.2)	21.2 (8.0)	10-19b	15.7 (5.5)
	Any Criterion	10.6	21.6	5.9	26.0
Percent Nonsystematic	Trend	4.8	15.7	4.5	20.0
	Bounce	1.9	11.8	1.0	6.0
	Reversal	4.8	3.9	0.0	4.0

^aData taken from the Experimental Tobacco Marketplace

^bReflects the mode response from a range of ordinal options.

MTurk = Amazon Mechanical Turk; Asc. = ascending; Rand. = random; C/d = self-reported cigarettes/day. Note: Sum of functions failing to meet individual criteria may not equal total percent identified as nonsystematic, as data for some participants failed to meet multiple criteria.

The fourth task featured four prices (range: $2.50-20.00) per pack of cigarettes. In this task, participants made hypothetical cigarette purchases in an online Experimental Tobacco Marketplace, featuring a user interface similar to other online merchants (e.g., Amazon.com; for a detailed description of this method using real rewards, for a similar method used in obesity research, see Epstein, Dearing, Roba, & Finkelstein, 2010). Cigarette price was manipulated across conditions (order randomized) while the price of concurrently available e-cigarette products remained constant. Here, participants made purchases according to an experimentally provided account balance based on their real-world tobacco expenditure, and were asked to purchase products for use over the next seven days. We applied the algorithm only to cigarette demand functions from this task.

Table 1 presents the percentage of demand functions identified as nonsystematic in each purchase task. We considered a demand function nonsystematic if it failed to meet at least one of the three criteria described above. The algorithm identified 11 of 104 functions (10.6%) as nonsystematic in the 68-price task; 11 of 51 functions (21.6%) as nonsystematic in the 22-price task; 17 of 289 functions (5.9%) as nonsystematic in the 9-price task, and 13 of 50 functions (26.0%) as nonsystematic in the 4-price task.

Procedural differences (e.g., laboratory vs. online sampling, sample size; see Table 1) prohibit direct comparisons across tasks. However, general trends within tasks indicate that only a relatively small proportion of demand functions failed to meet the Bounce and Reversal criteria. In contrast, the majority of nonsystematic functions failed to meet the Trend criterion, with instances of increasing trend and no trend frequently observed. Half of all demand functions failing to meet this Trend criterion (18 of 36 Trend violations) were due to participants making zero purchases at all prices (for further discussion, see Handling of Nonsystematic Data).

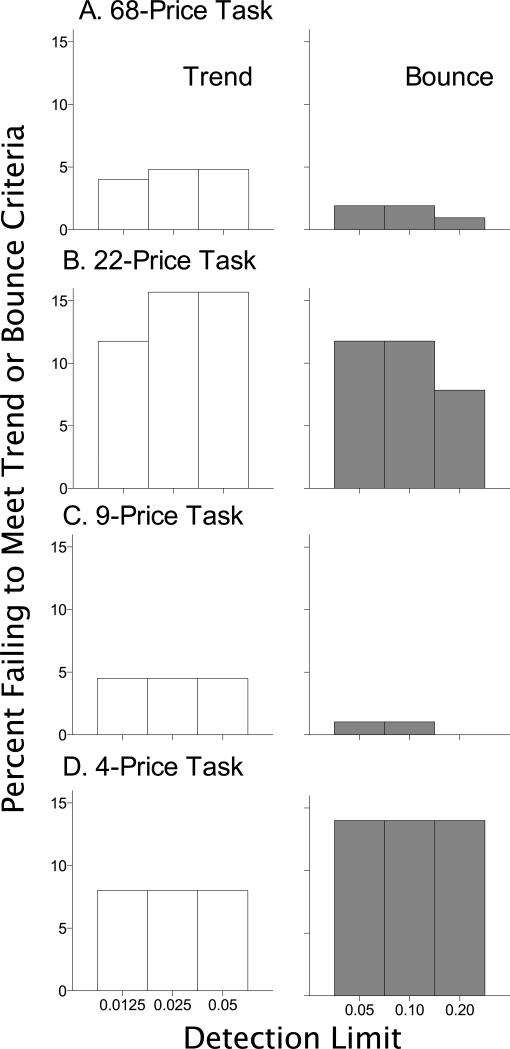
These observed proportions of systematic and nonsystematic data, however, may be highly dependent on the precise values of the detection limits used for the Trend (ΔQ = 0.025) and Bounce criteria (B = 0.10). Thus, we re-analyzed data from each task using a range of values (ΔQ = 0.0125 – 0.05; B = 0.05 – 0.20). Figure 2 depicts the results of this analysis. Generally, all values investigated produced similar levels of nonsystematic data, although the values used in the original analyses tended also to be the most stringent tested.

Figure 2.

Percent of demand functions that failed to meet the Trend (left panels) and Bounce (right panels) criteria when varying detection limits were used. See text for details.

To further test the algorithm, we sought to determine whether it would consistently differentiate between demand functions that were and were not consistently related to price. Using functions previously identified as systematic, we randomly shuffled purchases globally across all prices within each participant's function and then applied the algorithm to these shuffled data. Table 2 provides results of this analysis. Across all tasks, the majority of shuffled functions failed to meet the Bounce criterion. For the 68- and 22-price tasks, the algorithm identified 100% of the shuffled functions as nonsystematic for failing to meet at least one criterion. For the 9- and 4-price tasks, the algorithm identified 270 of 272 (99.26%) and 34 of 37 (91.89%) functions as nonsystematic, respectively. Although the algorithm identified fewer nonsystematic functions in these latter two tasks, such a decrement in performance can be attributed to the tasks themselves, as the probability of an orderly demand function emerging from random responding is inversely proportional to the number of prices imposed. For example, the three demand functions in the 4-price task that the algorithm failed to identify (i.e., were orderly by chance) consisted of (a) 5, 4, 1 and 1, (b) 5, 6, 0, and 0, and (c) 10, 7, 1, and 3 purchases across ascending prices.

Table 2.

Percent of randomly shuffled, formerly systematic demand functions that the algorithm identified as nonsystematic for failing to meet any criterion (as well as individual criteria) for each of four hypothetical purchase tasks.

		Purchase Task
		68 prices: $0.00-5.00	22 prices: $0.00-100.00	9 prices: $0.00-1000.00	4 prices: $2.50-20.00
Percent Nonsystematic	Any Criterion	100.00	100.00	99.26	91.89
	Trend	66.67	57.50	70.00	62.16
	Bounce	93.55	100.00	99.26	91.89
	Reversal	20.43	65.00	69.50	2.70

Prior Methods of Identifying Nonsystematic Data

A number of methods deserve note that have previously been used to identify nonsystematic demand data. The simplest of these relies on visual identification (e.g., Amlung et al., 2012; MacKillop & Tidey, 2011). Such a method, however, may be problematic (particularly when used to exclude data), as visual analyses are inherently imprecise and difficult for independent experimenters to replicate. Application of the quantitative criteria in the present paper avoids such imprecision and facilitates communication. However, we are not the first to propose such methods. In an empirical paper on cocaine demand, Bruner & Johnson (2014) used an algorithm adapted from one used previously in research on temporal discounting (Johnson & Bickel, 2008). In the context of demand, this algorithm identifies data as nonsystematic if at least one of two criteria are met: (1) less than a 10% reduction in consumption is observed from the lowest to the highest price (similar, in purpose, to the present algorithm's Trend criterion), and (2) consumption at any given price exceeds consumption at the previous price by 20% or more (similar to the present algorithm's Bounce criterion). Using this method, Bruner & Johnson (2014) reported that no demand functions failed to meet the first criterion; however, 8 of 86 (9.30%) demand functions contained at least one data point that failed to meet the second criterion. Demand functions that violated the second criterion more than once (i.e. at multiple prices) were excluded from subsequent analyses. Aside from these two criteria, four additional demand functions with exceedingly high, model-derived estimates of maximum spending at any price (O_max) were also excluded from analyses, as well as one demand function with limited variability in consumption.

Similarly, in a comparison between alcohol purchase tasks featuring either ascending or randomized price orders, Amlung and MacKillop (2012) quantified nonsystematic demand as the number increments in price that produced any increase in consumption (regardless of size). Such inconsistent consumption (comparable to the Bounce criterion in the present paper) was rare with use of ascending prices (0.5% of data), but significantly more common with randomized prices (5.0% of data). These authors made no specific quantitative analyses regarding trend

Despite similarities, the algorithm proposed here improves upon prior methods of identifying nonsystematic data. Specifically, as discussed previously, the present algorithm automatically accounts for varying price ranges across tasks in its application of the Trend criterion, as well as varying numbers of prices and individual differences in initial consumption in its application of the Bounce criterion. The resulting indices (ΔQ and B) may be reported in manuscripts to aid in evaluation of data analyses. In the absence of such proportionally defined criteria, previous methods are prone to differential detection of nonsystematic data as a function of task-specific parameters and, as a result, may be too stringent in some cases and too liberal in others.

Limitations

Although the algorithm consistently identified demand functions in line with its assumptions, at least one limitation deserves note. Specifically, the algorithm does not detect instances in which participants purchase unrealistically high quantities of a commodity under conditions of minimal price (e.g., 1000 cigarettes). Such high initial values are likely to produce spuriously high demand estimates and may arise from participants failing to understand task constraints (e.g., that the commodity should be purchased for use over a pre-defined period and cannot be saved or given away). An experimenter could, of course, establish a fourth criterion in which the algorithm identifies functions as nonsystematic if initial purchases exceed X units, where X is either constant for all participants or proportional to individual participants’ self-reported daily consumption. Alternatively, an experimenter may wish to cap purchases within the task itself (i.e., not allowing participants to purchase more than X cigarettes). However, we refrain from explicitly defining such a criterion, as appropriate values depend on specific properties of the commodity under investigation, including amounts that can be reasonably used within the pre-defined period (e.g., wherein cigarettes would differ from fuel) or that may be functionally aversive (e.g., due to nicotine overdose). A complementary approach, however, would be to ensure that the task itself minimizes the conditions under which participants produce such functions. Specifically, instructions could be verified with each participant prior to data collection through a brief questionnaire. Similarly, purchasing at the initial price (typically $0.00 or $0.01) could be established using a separate interface in which, following response entry, a participant must provide a confirmatory answer to the following:

You answered [participant's stated quantity] cigarettes. Could you smoke [participant's stated quantity] cigarettes in [the pre-defined purchase period], without saving any for a future date or giving any away?

If the participant answers “no,” additional instructions could be provided before continuing. Such a strategy would add confidence that outlying estimates of initial consumption, if observed, are subject to the intended constraints.

Handling of Nonsystematic Data

Once identified, nonsystematic demand functions may be handled using a number of methods, such as exclusion of nonsystematic data or use of alternate or supplemental analyses. Which method an experimenter chooses, however, may depend on a number of study-specific variables (e.g., the population or commodity under investigation) and which criteria demand functions failed to meet. In the following section, we highlight a number of relevant considerations.

Nonsystematic Data, in Context

Criterion 1: Trend

For reasons discussed above, the law of demand (i.e., an inverse relation between price and consumption) is a generalized phenomenon that is robust against varying commodities, methodologies, and conceptualizations of price. Thus, the assumption of the Trend criterion (i.e., a price-dependent reduction in consumption) is valid across a broad range of contexts. One option for handling demand functions that fail to meet this assumption is to exclude these data from primary analyses, as the behavior that produced such data was likely affected by one or more extraneous variables not germane to the investigation (e.g., inattention or failure to understand task constraints). Because inclusion of such data may impede discovery, exclusion is often warranted. However, an experimenter should first consider whether the presence of apparently nonsystematic data reflects an important property of the experimental arrangement or variable(s) under investigation.

First, the examination of a restricted price range combined with particularly inelastic commodities may produce flat (or perhaps slightly increasing, due to measurement error) demand functions in some participants. Although the minimum reduction in consumption that the Trend criterion allows is proportional to range in price (see Equation 1), some price ranges (e.g., those spanning less than one log unit and within a normally inelastic portion of the demand curve) may be insufficient to produce change in consumption. For example, a highly dependent smoker may defend cigarette consumption across a four-fold increase in price (e.g., $0.25-1.00 per cigarette), whereas this may not be the case if a ten-fold increase were used. In these cases, exclusion of functions that fail to meet the Trend criterion would preferentially ignore low (but otherwise valid) estimates of elasticity and produce spurious conclusions. As a remedy in these instances, experimenters may wish to relax the detection limit. For example, instead of a requisite 0.025 log-unit reduction in consumption per log-unit range in price, an experimenter may change this value to 0 (allowing flat functions) or some nominal negative value (allowing slightly increasing functions). Alternatively, except under conditions in which an experimenter explicitly wishes to investigate a range of prices that can be reasonably employed under prevailing political and social conditions (e.g., $2.50-$20.00 per pack of cigarettes), an experimenter could ensure that the range of imposed prices is sufficient to detect reductions in consumption in all but the most extreme cases.

Second, in our own experience, a number of conditions may produce the null demand functions described earlier (i.e., zero consumption at all prices), including the examination of novel commodities with which the participant has little or no experience (e.g., emerging tobacco/nicotine products) and commodities that a participant may find aversive (e.g., chewing tobacco). In addition, pre-post measures of cigarette demand in smoking cessation or reduction treatment, such as administration of bupropion, would likely contain a number of these null demand functions. In these cases, such data may be directly relevant to research aims, but would not be captured if one ignores these functions indiscriminately based on failure to meet the Trend criterion. Individual participants’ null functions, of course, cannot be analyzed using traditional quantitative curve-fitting models (e.g., Hursh & Silberberg, 2008) that assume variation in consumption; however, an experimenter may wish to include these data when fitting group average demand functions. Alternatively, these functions may be excluded when estimating elasticity, but included in supplemental analyses of raw consumption (i.e., in the absence of curve fitting) at individual prices. We caution, however, against universally assigning significance to these null demand functions. All else being equal, null functions from participants who normally consume and purchase the commodity under investigation (e.g., cigarettes for smokers, fuel for drivers) likely reflect one or more of the extraneous sources of variability mentioned previously and are thus not germane to primary research aims.

Finally, a number of environmental conditions, although rare, have been shown to produce upwardly sloping demand functions. Specifically, complex interactions between a commodity's price and variables such as social influence (as in the case of prestige and bandwagon goods; e.g., Leibenstein, 1950) or price-dependent income depletion (as in the case of Giffen goods; Marshall, 1895) could produce seemingly paradoxical, but otherwise rational, patterns of consumption. We note that these circumstances are atypical for the methodology described in this paper, but in some cases could be an unintended feature of a study's design. For example, imagine a scenario in which experimenters are interested in assessing demand for an inferior, generic brand of cigarettes (perhaps in order to inform public policy regarding such brands). These experimenters may design a task in which the inferior, inexpensive brand is available across a range of prices while a number of preferred, but more expensive, brands are available at constant prices. In a classic example of the Giffen effect, a participant may satisfy her habit at low prices by purchasing a large quantity of the inferior brand, but allow herself an indulgence by purchasing some smaller quantity of the preferred brands (e.g., DeGrandpre et al., 1993). However, at higher prices, spending on the inferior “staple” depletes this participant's resources sufficiently such that she can no longer afford the occasional indulgence and now has to purchase progressively more of the inferior brand to satisfy her habit. The result for the inferior good would be an upwardly sloping demand curve that experimenters ignore at their own peril.

Criteria 2 and 3: Bounce and Reversals from Zero

In contrast to the Trend criterion, instances in which demand functions fail to meet the Bounce or Reversal criteria are relatively straightforward. Assuming the absence of any of the conditions described above that may produce upwardly sloping demand functions, price-to-price increases in consumption likely reflect extraneous sources of variability that are not germane to primary research aims. Thus, an experimenter may wish to exclude these functions from primary analyses. However, an alternative to this method is to selectively exclude individual nonsystematic purchases, assuming these occur infrequently and the demand function is otherwise orderly (i.e., meets the Trend criterion). The remaining function may be left intact and subjected to analysis. We note, however, that this method works best for purchase tasks featuring a large number of prices (e.g., the 22- or 68-price tasks used here), as the impact on demand estimates of consumption at any single price is proportional to total number of prices. An experimenter should exercise caution with purchase tasks featuring fewer prices (e.g., the 4- or 9- price tasks used here).

Nonsystematic Data and Demographic Variables

We also examined whether the frequency of nonsystematic data differed as a function of demographic variables. Identification of demographic groups who contribute nonsystematic data more frequently than others would be important in the understanding and interpretation of findings, as either the presence of such data or its disproportionate exclusion may bias conclusions. For each purchase task, we coded demand functions as either systematic (0) or nonsystematic (1) and used logistic regression to examine the association between this classification and a range of demographic variables: sex, race, age, education, and smoking rate. Of these, sex and race were treated as dichotomous variables (male/female, Caucasian/Non-Caucasian). Age, education, and smoking rate were treated as continuous variables (years of age or education; cigarettes per day), with the following exceptions: only non-continuous, ordinal ranges were available for education in the 9- and 4-price tasks (e.g., high school graduate, some college, college graduate, etc.) and for smoking rate in the 9-price task (e.g., 10-19 cigarettes per day). All analyses were performed in SPSS (ver. 21, SPSS Inc., Chicago, IL).

Table 3 provides results of logistic regressions. In all tasks, sex, age, and smoking rate were unrelated to frequency of nonsystematic data. In contrast, both race and education uniquely predicted nonsystematic data in the 68-price task. Specifically, being non-Caucasian predicted greater odds of contributing nonsystematic data, Wald's χ² = 8.41, odds ratio = 6.73, p = .004, as did having been exposed to fewer years of education, Wald's χ² = 5.81, odds ratio = 0.50, p = .02. These same variables (race and education) were not significant predictors of nonsystematic data in any other task, although race was marginally significant in the 22-price task, Wald's χ² = 2.89, odds ratio = 4.93, p = .09.

Table 3.

Logistic regressions predicting nonsystematic data for each of four hypothetical purchase tasks.

		Purchase Task
Demographic Predictor	Regression parameter	68 prices: $0.00-5.00	22 prices: $0.00-100.00	9 prices: $0.00-1000.00	4 prices: $2.50-20.00
Sex	Wald's χ2	0.02	0.01	0.05	0.04
	OR (95% C.I.)	1.09 (0.35 – 3.38)	1.08 (0.22 – 5.28)	0.89 (0.32 – 2.49)	1.15 (0.30 – 4.41)
	p value	.88	.93	.82	.43
Race	Wald's χ2	8.41	2.89	0.00	0.62
	OR (95% C.I.)	6.73 (1.85 – 24.38)	4.93 (0.78 – 31.08)	0.98 (0.29 – 3.32)	2.08 (0.34 – 12.75)
	p value	.004	.09	.98	.43
Age	Wald's χ2	0.07	0.01	1.06	0.66
	OR (95% C.I.)	1.01 (0.96 – 1.05)	1.00 (0.94 – 1.07)	0.97 (0.92 – 1.03)	0.96 (0.86 – 1.06)
	p value	.80	.93	.30	.42
Education	Wald's χ2	5.81	2.24	1.74	0.39
	OR (95% C.I.)	0.50 (0.28 – 0.88)	0.56 (0.26 – 1.12)	1.56 (0.81 – 3.01)	0.73 (0.28 – 1.95)
	p value	.02	.14	.19	.53
C/d	Wald's χ2	0.06	0.52	1.75	0.85
	OR (95% C.I.)	0.99 (0.91 – 1.08)	0.47 (0.85 – 1.08)	0.65 (0.35 – 1.23)	1.06 (0.94 – 1.20)
	p value	.81	.47	.19	.36

Bolded values indicate statistical significance. C/d = self-reported cigarettes/day.

Although methodological differences between the four data sets prohibit straightforward comparisons, greater heterogeneity in race and education in the two laboratory-based tasks (68 and 22 prices), compared to the two online tasks (9 and 4 prices) may have facilitated relatively stronger associations between these demographic variables and nonsystematic data. At minimum, the present data highlight the importance of examining and reporting associations between demographic variables and nonsystematic demand data. Demographic differences, such as those reported here, may bias conclusions and restrict generality of findings if not handled appropriately, particularly if nonsystematic data are excluded prior to analysis.

Assessments of Cross-Price Elasticity of Demand

Under some conditions, changes in the price of a given commodity alter consumption of one or more additional commodities whose price remains constant. Study of this phenomenon, termed cross-price elasticity of demand (Hursh, 1980, 1984), reveals complex interactions that cannot be predicted from assessment of individual commodities in isolation (Bickel, DeGrandpre & Higgins, 1995). For example, increases in the price of cigarettes reduce cigarette consumption, but increase consumption of concurrently available, price-constant nicotine gum (Johnson, Bickel, & Kirschenbaum, 2004; Shahan et al., 2000) and electronic cigarettes (Grace, Kivell, & Laugesen, 2014), indicating the latter two commodities serve as substitutes for cigarettes. Conversely, increases in the price of alcohol reduce consumption of both alcohol and price-constant cigarettes (e.g., Cameron & Williams, 2001), indicating a complementary relation between these two commodities.

In preparations designed to assess cross-price elasticity, the assumptions of the algorithm presented in this paper remain largely valid when considering a commodity's own-price demand function (i.e., demand for the commodity being manipulated). Specifically, the presence of alternative commodities should not be expected to produce internally inconsistent own-price demand (see the Bounce and Reversal criteria). Nor should increases in a commodity's own price, regardless of the number or type of alternatives available, be expected to produce flat or upwardly sloping own-price demand functions (see the Trend criterion). However, one possible exception deserves note. That is, the presence of available substitutes often decreases consumption of the price-manipulated commodity (e.g., Grace et al., 2014; Johnson et al., 2004). In extreme cases, the presence of one or more highly preferred alternative commodities may siphon consumption away from the own-price demand function at all prices, thereby producing the null demand functions discussed earlier. Consideration of this possibility (and corroborating analyses) may prevent exclusion of meaningful data.

In cases in which the algorithm identifies own-price demand functions as nonsystematic and none of the extenuating conditions discussed previously are present, exclusion of these functions from primary analyses is likely justified. Exclusion of their associated cross-price functions (i.e., for concurrently available, price-constant alternative commodities) would also be justified, as these are dependent on the same extraneous variability that produced the own-price data. However, we do not advise that the present algorithm be applied directly to cross-price demand functions. Even robust economic relations between two or more commodities are defined in the aggregate, with the strength and even the direction of such relations heterogeneous across individual participants. Thus, for any given participant, the experimenter has no a priori knowledge from which to base assumptions on the direction or consistency of cross-price effects. As a result, exclusion of putatively nonsystematic cross-price demand functions would preferentially constrain the less frequently observed portion of the distribution (whether reflecting substitution, complementarity, or independence) and may artificially inflate observed relations. For this reason, we analyzed only own-price cigarette demand functions from the Experimental Tobacco Marketplace, in which concurrently available electronic cigarette products could also be purchased.

Summary and Conclusions

In research on temporal discounting, previous efforts to formalize criteria for identification of nonsystematic data have produced an algorithm used often in that area (Johnson & Bickel, 2008; cited 88 times in Google Scholar, to date). Here, we refined, expanded upon, and evaluated analogous criteria (Bruner & Johnson, 2014) for a growing research literature on behavioral-economic demand, in which much of the research and discussion in recent years has focused on purchase tasks (i.e., at least 80 papers published from 2009-2014³). We also proposed related guidelines for managing such data.

The methods proposed in this paper require only two general assumptions: (1) a global reduction in consumption across price, and (2) consistency in the directional change in consumption across individual price increments. We analyzed data from four hypothetical purchase tasks featuring heterogeneity in both the number and range of prices, with the algorithm identifying demand functions consistent with our assumptions in all tasks. In a separate analysis, we demonstrated that the algorithm differentiates between known orderly and randomized data. We also outlined a number of methods for handling nonsystematic demand data, noting several conditions in which excluding such data from primary analyses may be appropriate, and others in which doing so may bias conclusions. Even if all data are retained, however, experimenters should routinely report the frequency of nonsystematic data to allow for appropriate evaluation of analyses, as well as to allow possible differences between populations, commodities, or task variants to be detected in literature reviews.

Aside from the empirically based assumptions discussed earlier, the algorithm and related guidelines remain atheoretical, thus allowing a variety of analysis methods to be applied to the data (e.g., exponential or linear demand models; Hursh & Silberberg, 2008; Hursh, et al., 1989; Killeen, 1995). In addition, although we focused on hypothetical cigarette purchase tasks in our analyses, the methods presented in this paper can be generalized to other demand assessments—specifically, those featuring other drug and non-drug commodities (e.g., cocaine or fuel; Bruner & Johnson, 2014; Reed et al., 2014) and task types (e.g., operant methods in which price is defined as behavioral output; Shahan et al., 1999). The assumptions of the algorithm remain valid under any condition in which increases in price, broadly defined, are expected to reduce consumption. Experimenters may wish to remain flexible, however, regarding individual criteria under varying conditions. For example, assessment of consumption in operant tasks in which a single price is imposed per session may be prone to extraneous variability that cannot be experimentally controlled (e.g., daily variation in stress or other emotional states). This, in turn, may manifest as greater variability in consumption across days and can be accommodated by relaxing the Bounce or Reversal criteria.

The methods proposed in this paper may be used in future studies to enhance accuracy of demand estimates and facilitate cross-study comparisons, in which methodological differences in outlier exclusion may otherwise impede discovery. Alternatively, some experimenters may wish to include all data in analyses and instead use these methods solely for descriptive purposes. Appropriate identification and handling of nonsystematic data will likely enhance the resolution of demand instruments to detect effects of treatment or differences between commodity types (e.g., conventional vs. electronic cigarettes) or demographic populations (e.g., male vs. female). Moreover, use of this algorithm and reporting of its results in future research may help identify variants of the purchase task that minimize collection of nonsystematic data, thus improving procedure selection.