Abstract
Pulsatile release of cortisol from the adrenal glands is governed by pulsatile release of adrenocorticotropic hormone (ACTH) from the anterior pituitary. In return, cortisol has a negative feedback effect on ACTH release. Simultaneous recording of ACTH and cortisol is not typical, and determining the number, timing, and amplitudes of pulsatile events from simultaneously recorded data is challenging because of several factors: (I) stimulator ACTH pulse activity, (II) kinematics of ACTH and cortisol, (III) the sampling interval, and (IV) the measurement error. We model ACTH and cortisol secretion simultaneously using a linear differential equations model with Gaussian errors and sparse pulsatile events as inputs to the model. We propose a novel framework for recovering pulses and parameters underlying the interactions between ACTH and cortisol. We recover the timing and amplitudes of pulses using compressed sensing, and employ generalized cross validation for determining the number of pulses. We analyze serum ACTH and cortisol levels sampled at 10-minute intervals over 24 hours from 10 healthy women. We recover physiologically plausible timing and amplitudes for these pulses and model the feedback effect of cortisol. We recover 15 to 18 pulses over 24 hours, which is highly consistent with the results of another cortisol data analysis approach. Modeling the interactions between ACTH and cortisol allows for accurate quantification of pulsatile events, and normal and pathological states. This could lay the basis for a more physiologically-based approach for administering cortisol therapeutically. The proposed approach can be adapted to deconvolve other pairs of hormones with similar interactions.
I. Introduction
Secretion of some hormones is stimulated by a well-known sequence of pulsatile events governed by a natural control system. Neural interactions in the hypothalamus result in the release of hormone-releasing hormones (e.g. corticotropin releasing hormone (CRH)), which in turn induce the release of hormones from the pituitary (e.g. Adrenocorticotropic hormone (ACTH)); pituitary hormones then induce secretion of hormones from the target glands (e.g. cortisol). These hormones implement regulatory functions in the body and also have a feedback effect on the release of hormone-releasing hormones and pituitary hormones [15]. In the 1960s, endocrinologists realized that these hormones are not secreted in a continuous manner, and instead are secreted in pulsatile episodes [26] and cleared exponentially [14]. It is currently unethical to measure the hormone-releasing hormones of the hypothalamus (e.g. CRH) in human participants, and therefore it is crucial to infer these pulsatile episodes using serum measurements of only a subset of the hormones within these hierarchical hormone systems (e.g. ACTH and cortisol).
ACTH and cortisol are steroid hormones that influence multiple areas of mammalian physiology including metabolism, inflammation and stress [2]. ACTH and cortisol levels vary over a 24-hour period as a result of the ultradian modulation of the timing and circadian modulation of the amplitudes of the ACTH and cortisol secretory pulses [2]. In order to understand the physiology and psychophysiology, effects of drugs, and other interventions, there is a need for quantifying pulsatile episodes in ACTH and cortisol secretion. A question of interest is whether elevated cortisol levels observed in some medical conditions are caused by changes in the pulsatile episodes or by the increased sensitivity of the adrenal glands to ACTH [27]. One method for investigating whether a pathological condition related to cortisol has been initiated by the hypothalamus, the pituitary, or the adrenal glands, is to construct a model based on these interactions and develop an algorithm that can find both the pulsatile episodes of hormone release in the hypothalamus and the model parameters corresponding to each step of the cascade using data from individuals with and without the disorder. It is therefore advantageous to have a model and an estimation algorithm that can investigate the role of the amplitude and frequency of the pulses as well as the sensitivity of the target gland to the pituitary input. Moreover, a treatment could be designed to use an optimal dosage (amount and timing) by employing a model that predicts the dose-response. This requires a comprehensive model that includes the pulsatile secretion of hormones and the feedback effect in hormone release, so that hormone secretion and hormone concentration in the blood can be estimated.
As a first step in understanding endocrine systems quantitatively, we investigate concurrent release of ACTH and cortisol in the Hypothalamic-Pituitary-Adrenal (HPA) axis. Various models of the HPA axis and cortisol secretion have been proposed; for instance see [2], [6], [7], [12], [8], and [3]. These models describe cortisol synthesis in the adrenal glands based on the first-order kinetics of cortisol synthesis. Current mathematical models for concurrent ACTH and cortisol measurements include [21], [19], [23], [22], and [18]. Peters et al. modeled ACTH and cortisol levels as a function of exogenous CRH [21]. They intravenously injected CRH to the participants, collected ACTH and cortisol levels until 4 hours after injection, and estimated the model parameters given the injected CRH [21]. Another data-driven model of concurrent ACTH and cortisol levels was proposed by Lonnebo et al. where they assumed a surge-based nonlinear model with one morning surge and one afternoon surge [19]. Van Cauter proposed a method for recovering episodic hormone fluctuations [23], used it to analyze the 24-hour profile of concurrent ACTH and cortisol data and recovered the secretory events for each of the two hormone profiles [18], [22]. Then, by analyzing the timing of the detected ACTH and cortisol pulse peaks and the respective durations those pulses overlapped, they determined which detected ACTH and cortisol pulses were concomitant [18], [22].
Some data analysis methods for recovering hormone secretory events are developed for single hormone time series (e.g. only cortisol) and are mostly based on pulse detection algorithms [25] or assume that the timing of the secretory events belong to a certain class of stochastic processes [14]. We recently showed that hormone secretory events can be recovered using compressed sensing [5]. Compressed sensing allows for reconstruction of sparse signals (i.e., signals in which only a small number of coefficients are large and most coefficients are zero or close to zero) using fewer measurements than required by the Shannon/Nyquist sampling theorem [1].
Our goal in this study is to quantify the secretory events and the feedback control mechanisms that underly the HPA axis. To tackle this problem, we develop a model that calculates the first-order kinetics underlying the HPA axis and the infusion and clearance coefficients, given datasets that include concurrent measurements of ACTH and cortisol serum levels. We use a multi-rate state space representation of the system and by using a coordinate descent approach, we recover the model parameters and the secretory events. Based on the physiology, between 15 to 22 secretory events are expected for the ACTH-cortisol system over 24 hours [2], [24]. Considering that these secretory events are sparse (i.e., there are a small number of secretory events), we employ compressed sensing techniques to recover the secretory events. The exact number of secretory events for each participant is unknown; using generalized cross-validation, we find the number of pulses such that there is a balance between capturing the noise and the sparsity. Since cortisol, growth hormone, thyroid hormone, estrogen, and testosterone are synthesized and secreted using a similar feedback control mechanism, the proposed framework could potentially be applied to all these endocrine hormones.
II. Methods
A. Experiment
To test our model, we used serum ACTH and cortisol measurements collected simultaneously from an inpatient study of 10 healthy women. The participants were recruited via advertisements in local newspapers to serve as healthy controls for a study on women with fibromyalgia; participants with abnormal laboratory test results or current medical problems were excluded [5], [16]. None of the participants had received glucocorticoids or estrogen/progesterone within the year or 4 months before the study, respectively [5], [16]. Clinical characteristics of the participants are given in Table I. For 3 consecutive nights, at the General Clinical Research Center of the Brigham and Women's Hospital, participants had 8 hours of scheduled sleep in the dark at their habitual sleep-wake times and three meals and two snacks; on day 4, all participants started a constant routine protocol that was designed to minimize the effects of stress, posture changes, eating, and ambulatory temperature on the participants [5], [16]. Blood drawing for hormones analyzed in this study was performed during the third night of sleep and during the first 16 hours of the constant routine [5], [16]. Therefore, this dataset can be used to quantify ACTH and cortisol variations as a function of the circadian and the ultradian patterns. Blood was collected via an indwelling intravenous catheter every 10 minutes for 24 hours, was assayed for ACTH and cortisol in duplicate, and the immunoassay error for each time series was obtained. Plasma ACTH levels were determined using the Nichols Allegro HS-ACTH kit (Nichols Institute Diagnostics, San Juan Capistrano, CA). This assay has a lower limit of detection 0.2 pmol/L, interassay coefficient of variation 7-8%, and intraassay coefficient of variation 3%. Serum cortisol levels were measured using the chemiluminescence assay by Beckman Coulter, Inc., Chaska, MN, interassay coefficient of variation 6-10%, and intraassay coefficient of variation 2.6-6.5% [16]. This project has been reviewed and approved by the Brigham and Women's Hospital Institutional Review Board (IRB). During the review of this project, the IRB specifically considered (i) the risks and anticipated benefits, if any, to subjects; (ii) the selection of subjects; (iii) the procedures for securing and documenting informed consent; (iv) the safety of subjects; and (v) the privacy of subjects and confidentiality of the data.
TABLE I.
Clinical Characteristics of the Participants [5]
| AGE | BMI |
|---|---|
| 28 | 20.8 |
| 41 | 23.6 |
| 41 | 22.5 |
| 24 | 20.7 |
| 23 | 27.4 |
| 26 | 25.2 |
| 23 | 29.3 |
| 37 | 29.6 |
| 44 | 29.9 |
| 42 | 22.9 |
BMI refers to Body Mass Index. None of the participants had a current diagnosis of depression.
B. Modeling Formulation
We build our model based on the stochastic differential equation model of diurnal cortisol patterns in [2]. This model is based on the first-order kinetics for cortisol synthesis in the adrenal glands, cortisol infusion to the circulation, and cortisol clearance by the liver. It uses a doubly stochastic pulsatile input with gamma distributed interarrival times and a Gaussian circadian amplitude [2]. This input marks pulsatile cortisol synthesis in the adrenal glands.
We represent the secretory events of the anterior pituitary using an impulse train. This impulse train marks the timing and amplitude of the secretory events that result in ACTH synthesis in the anterior pituitary. We assume that there are between 15 to 22 secretory events that control the 24-hour serum cortisol level, based on [2], [24]. We also include the known cortisol negative feedback effect on ACTH secretion [2], [12], [17], [6], [7] in our model. Equations (1)-(3) model the HPA axis and cortisol and ACTH release:
| (1) |
| (2) |
| (3) |
where x1 is the serum ACTH concentration, x2 is the cortisol concentration in the adrenal glands, x3 is the serum cortisol concentration, and θ3 is the ACTH gain. θ1 and θ2 represent the infusion rate of ACTH from the anterior pituitary to the blood and the cortisol negative feedback gain, respectively. θ4 and θ5 represent the coefficients corresponding to infusion of cortisol into the circulation from the adrenal glands and clearance of cortisol by the liver, respectively. u(t) is an abstraction of the secretory events in the anterior pituitary that result in ACTH release and consequent cortisol release:
| (4) |
where qi denotes the amplitude of a secretory event initiated at time τi, and m denotes the number of the secretory events. Our goal is to estimate the model parameters (θj for j = 1, 2,..., 5), the number of the secretory events (m), and the amplitudes (qi for i = 1, 2,..., m) and timing (τi for i = 1, 2,..., m) of the secretory events using serum ACTH (x1) and cortisol (x3) levels collected in 10-minute intervals.
We start by putting the control feedback model of ACTH and cortisol secretion (equations (1)-(3)) in a state-space form, and writing the discrete analog of the system assuming that the input and the state remain constant over one-minute intervals. Since the data are collected every 10 minutes, we form the corresponding multi-rate system. Then, using the initial conditions of the serum ACTH and cortisol levels, we can represent the system as:
| (5) |
| (6) |
where yA represents serum ACTH levels, yC represents serum cortisol levels collected at 10-minute intervals, and z0 is a vector of the initial conditions of the serum ACTH concentration, the adrenal glands’ cortisol concentration, and the serum cortisol concentration. u represents the entire input over 24 hours. Elements of u take nonzero values qi at times τi for i = 1, 2,..., m when there is a secretory event, and are zero otherwise. FθA, FθA, DθA, and DθC are functions of θj for j = 1, 2,..., 5. νA and νC represent the ACTH and cortisol measurement errors, respectively. Complete details can be found in Supplementary Information.
C. Model Estimation
Between 15 to 22 secretory events are expected for the ACTH-cortisol system over 24 hours [2], [24], so we assume the minimum number of secretory events umin = 15 and the maximum number of secretory events umax = 22. Considering that a pulse can occur at any minute, we assume u contains umin to umax nonzero elements out of 1440 possibilities, and all these nonzero elements are nonnegative (umin ≤ ∥u∥0 ≤ umin, u ≥ 0). Since hormone gains, infusion, and clearance coefficients cannot be negative, we assume that θ ≥ 0. Furthermore, we follow [2] and assume that the infusion coefficient of cortisol from the adrenal glands to the circulation is at least four times the clearance coefficient of cortisol by the liver (4θ5 ≤ θ4). We can formulate this problem as an optimization problem:
| (7) |
s.t.
σA and σC represent the standard deviation of the ACTH and cortisol measurement errors, respectively. In this optimization problem, solving for u is a combinatorial problem, which is generally NP-hard, and is solved using greedy algorithms and ℓp-optimization algorithms. The greedy algorithms include Matching Pursuit (MP), Othogonal MP, Iterative Hard Thresholding, Hard Thresholding Pursuit, Gradient Descent with Sparsification, and Compressive Sampling Matching Pursuit [13]. In the ℓp-optimization algorithms, the ℓ0-norm is approximated by an ℓp-optimization problem where 0 < p < 2 [13]. ℓp-optimization algorithms are more accurate than greedy algorithms, but computationally more expensive [13]. It is possible to cast the above optimization problem as:
| (8) |
where the ℓp-norm is an approximation to the ℓ0-norm (0 < p ≤ 2) and λ is chosen such that the sparsity of u is between umin to umax. Then, using a coordinate descent approach, this optimization problem can be solved iteratively using the following steps until convergence is achieved:
-
1)
(9) -
2)
(10)
The optimization problem in (9) can be solved using the Focal Underdetermined System Solver (FOCUSS) algorithm [10]. The FOCUSS algorithm is based on the iteratively reweighted least squares algorithm, and enforces a certain degree of sparsity [28]. The sparsity is determined by λ (the sparsity of u increases with λ), and λ balances between sparsity and the residual error. We use an extension of the FOCUSS algorithm called GCV-FOCUSS+ [5]. The GCV-FOCUSS+ algorithm is based on FOCUSS+ [20] that solves for nonnegative u such that u has a certain maximum sparsity n (i.e., n = 22 for the HPA axis), and uses the generalized cross-validation (GCV) technique [9] for estimating the regularization parameter. In particular, GCV-FOCUSS+ is closely related to a version of the FOCUSS algorithm by Zdunek et al. [28], which uses the GCV technique for updating the regularization parameter λ. Choosing a λ value that balances between the noise and sparsity is important in detecting the sparsity level. If λ is too small, overfitting can occur and noise can be detected as signal; on the other hand, if λ is too large, it leads to underfitting the data, and as a result, the signal will not be constructed completely. The FOCUSS+ algorithm and the GCV-FOCUSS+ algorithm are described in more detail in Supplementary Information.
An important factor in estimating the model parameters and the input is the initialization of u and θ: this should be done systematically. It is possible to obtain a good initial estimate for the timing of the pulses that result in cortisol secretion by first deconvolving the cortisol data using the model and the algorithm in [5]. This algorithm detects the significant pulses that result in cortisol release. Some peaks might not appear to be significant given only cortisol measurements and the corresponding pulses might not be detected; however, when analyzing the ACTH and cortisol data together these pulses might now appear significant. Hence, we first find the peaks in the cortisol data, and then break the data into peak-to-peak segments, and then for the segments that no pulse is detected, we allow for the support (i.e., the timing of pulses) to occur any time over that segment. We use the findpeaks function in MATLAB R2011b to compare each cortisol data point to its neighboring values, and then, by finding the data points that take values higher than both of their neighbors, we detect the peaks in the cortisol data. This process gives a good initial condition for the possible support of u; θ can be initialized randomly in the first step. Using these initial conditions, we start the initialization algorithm that is provided in detail in Supplementary Information; the model parameters and the input that minimize Jλ (θ, u) in (8), denoted by and û0, respectively, are good initializers for the main estimation algorithm.
The following is the algorithm that we propose for estimation of concurrent measurements of cortisol and ACTH:
-
1)
Initialize the algorithm at and û0 using the initialization algorithm
-
2)
Set equal to ; using GCV-FOCUSS+, solve for ûk by initializing the optimization in (9) at ûk–1
-
3)
Set û equal to ûk, and using the Levenberg-Marquardt method, solve for by initializing the optimization in (10) at
-
4)
Iterate between steps (2) and (3) until convergence
-
5)
Repeat steps (1)-(4) for various initializations
-
6)
Set the estimated model parameters and û equal to the values that minimize Jλ (θ, u) in (8).
The optimization problem in (8) is non-convex and there are multiple local minima; the proposed algorithm selects the set of model parameters and the input that give the best goodness of fit. We have implemented the algorithm under the assumption that hormone pulses occur at integer minutes. The serum ACTH measurements are by 4 orders of magnitude smaller than serum cortisol measurements, and this leads to issues for numerical analysis due to the difference in the order of magnitude, the much smaller ACTH appears as noise. To handle numerical issues in running the estimation algorithm, we scaled up the ACTH measurements by a factor of 4 orders of magnitude. Then, we scaled down the estimated θ2 by 4 orders of magnitude and scaled up the estimated θ3 by 4 orders of magnitude to compensate for scaling up ACTH in the estimation. This step balances the units in the system of equations that describe the HPA axis. For evaluating the R2, we estimated the ACTH and cortisol levels using scaled θ values (reported in Table 1), and ACTH and cortisol initial conditions with units . Also, the impulse input had units so that all equations were balanced when evaluating the R2. In implementing the GCV-FOCUSS+ algorithm, we solve for u by letting p = 0.5. Data analysis, estimation, and simulations were performed in MATLAB R2011b.
III. Results
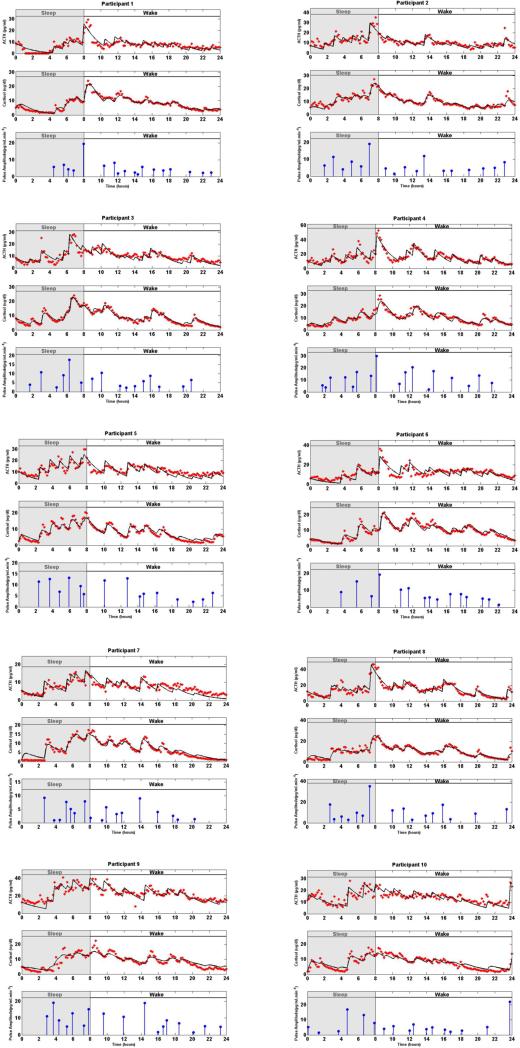
Figure 1 shows the model-predicted ACTH and cortisol estimates, and the estimated amplitudes and timing of hormone pulses for each participant. The timing and amplitudes of the detected hormone pulses vary over a 24-hour period across participants. The amplitudes of the recovered pulses have a circadian rhythm; for most participants, there are fewer recovered pulses at the beginning of the scheduled sleep, and there is a large pulse towards the end of the sleep period or beginning of the wake period. There are multiple small and medium sized pulses during the wake period.
Fig. 1. Estimated Deconvolution of the Experimental Twenty-Four-Hour Concurrent ACTH and Cortisol Levels in 10 Women.
In each panel, (i) the top sub-panel shows the measured 24-hour ACTH time series (red stars), and the estimated ACTH levels (black curve), (ii) the middle sub-panel shows the measured 24-hour cortisol time series (red stars), and the estimated cortisol levels (black curve), (iii) the bottom sub-panel shows the estimated pulse timing and amplitudes (blue vertical lines with dots) using concurrent measurements of ACTH and cortisol for the corresponding participant. The shaded gray area corresponds to sleep period and the white area corresponds to wake period. The estimated model parameters are given in Table 1.
The number of recovered pulses for all participants is within their corresponding physiologically plausible ranges [2], [24] and varies among participants. The squares of the multiple correlation coefficients (R2) are between 0.82 and 0.94 for cortisol time series and between 0.46 and 0.79 for ACTH time series using concurrent measurements of ACTH and cortisol time series (Table 2).
TABLE II.
The estimated model parameters for the fits to the experimental ACTH and Cortisol time series
| Participant | θ1 (min–1) | θ2 (min–1) | θ3 (min–1) | θ4 (min–1) | θ5 (min–1) |
|---|---|---|---|---|---|
| 1 | 0.0043 | 4.2×10–7 | 561 | 0.5044 | 0.0510 |
| 2 | 0.0046 | 2.4×10–7 | 530 | 0.6513 | 0.0549 |
| 3 | 0.0054 | 2.5×10–7 | 997 | 0.9162 | 0.1055 |
| 4 | 0.0082 | 1.6×10–7 | 335 | 0.9788 | 0.0506 |
| 5 | 0.0054 | 2.8×10–7 | 804 | 0.9959 | 0.1092 |
| 6 | 0.0062 | 1.9×10–7 | 792 | 0.9995 | 0.0914 |
| 7 | 0.0060 | 1.3×10–7 | 1161 | 0.4494 | 0.1122 |
| 8 | 0.0070 | 1.4×10–7 | 382 | 0.7089 | 0.0573 |
| 9 | 0.0045 | 1.1×10–7 | 205 | 0.1953 | 0.0488 |
| 10 | 0.0035 | 2.6×10–7 | 548 | 0.8185 | 0.0919 |
| Median | 0.0054 | 2.2×10–7 | 554 | 0.7637 | 0.0743 |
The parameter θ1 is the estimated infusion rate of ACTH from the anterior pituitary into the circulation; θ2 is the estimated cortisol negative feedback gain; θ3 is the estimated ACTH gain; θ4 is the estimated coefficient corresponding to infusion of cortisol into the circulation from the adrenal glands and θ5 is the estimated coefficient corresponding to clearance of cortisol by the liver.
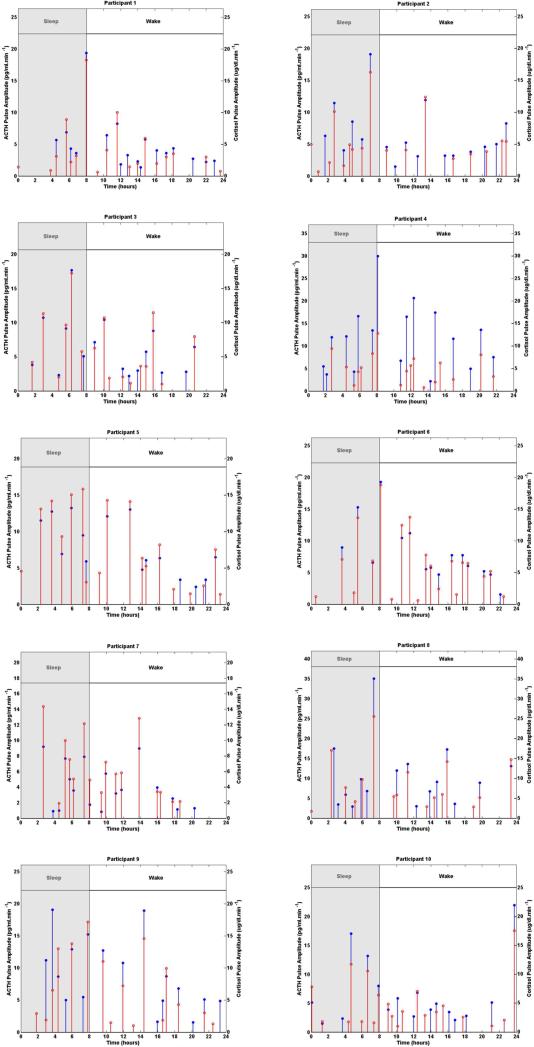
The number of pulses obtained using concurrent measurements of ACTH and cortisol range from 15 to 18 pulses; the number of pulses obtained only from cortisol measurements varies from 16 to 20 pulses. Figure 2 shows the estimated secretory events of the anterior pituitary recovered using concurrent ACTH and cortisol measurements as well as the estimated secretory events of the adrenal glands recovered using the cortisol measurements. The timing of most of the significant pulses recovered from concurrent measurements of ACTH and cortisol are in agreement with the timing of most significant pulses recovered only from cortisol measurements for most participants; however, some of the less significant pulses are not in agreement in terms of timing or have not been recovered when analyzing concurrent ACTH and cortisol data versus cortisol data alone. The mismatch between the detected ACTH secretory events and cortisol secretory events could be due to the noise that exists in the HPA axis during the secretion process as well as measurement noise or some nonlinearities in the HPA axis. These results suggest that using only cortisol serum measurements one can find the timing of most of the significant secretory events in the HPA axis (i.e. the timing of pulses that are crucial in both cortisol and ACTH profiles). By including ACTH serum measurements, either some of the pulses that were detected using only cortisol data are not detected anymore or some new pulses are captured that were not detected previously. Also, there can be small differences in the timing of the detected pulses depending on whether cortisol data was used alone or both ACTH and cortisol data were used. The amplitude of the recovered ACTH secretory events are by 4 orders of magnitude smaller than those of cortisol, which is expected as the amplitudes of the ACTH data are by 4 orders of magnitude smaller than those of the cortisol data.
Fig. 2. Comparison of Estimated Pulse Timing and Amplitudes Using the Experimental Twenty-Four-Hour Cortisol Levels Only with Estimates from Concurrent ACTH and Cortisol Levels in 10 Women.
Each panel shows the estimated pulse timing and amplitudes (blue vertical lines with dots) using concurrent measurements of ACTH and cortisol, and the estimated pulse timing and amplitudes (red vertical lines with dots) using only cortisol measurements for the corresponding participant. The shaded gray area corresponds to sleep period and the white area corresponds to wake period.
The parameters θ4 and θ5 are estimated coefficients corresponding to the infusion and clearance of cortisol, respectively. These coefficients are functions of the underlying infusion and clearance rates of cortisol, respectively, which we reported in [5]. Gains on ACTH are larger than the cortisol infusion and clearance coefficients by 4 orders of magnitude and negative feedback gains on cortisol are smaller by 4 orders of magnitude than the infusion rate of ACTH by the anterior pituitary. These differences in the orders of magnitudes are expected as ACTH serum levels are smaller than cortisol serum levels by 4 orders of magnitude. On average, after scaling up the ACTH measurements by a factor of 4 orders of magnitude and referring to the standard deviation of the scaled-up ACTH measurements as σA, we have .
IV. Discussion
Cortisol is released in pulses in response to pulses of ACTH, and in return, has a negative feedback effect on ACTH release. Typically, cortisol serum measurements are collected and analyzed, and simultaneous recording of ACTH and cortisol is not typical. In this study, we analyze simultaneously recorded serum ACTH and cortisol measurements from 10 healthy women.
Modeling the HPA axis and determining the number, timings, and amplitudes of pulsatile events using simultaneously recorded serum ACTH and cortisol measurements is a challenging problem. (i) Due to data collection costs, the sampling interval of 10 minutes is relatively large compared to the inter-pulse intervals, and secretion and clearance rates in the HPA axis. This large sampling interval makes it challenging to identify the potential consecutive pulses that occur over one sampling interval as well as the potential delays over one sampling interval. (ii) Since ACTH decays faster than cortisol, due to the low resolution of the data, the ACTH response to a small pulse might not be observed in the ACTH data while the cortisol response might be observed in the cortisol data. Distinguishing between such a small pulse and noise is challenging. (iii) The properties of noise in the HPA axis are not known. (iv) The HPA axis exhibits circadian rhythmicity in multiple parameters over 24 hours; therefore, the model parameters might be time-varying. (v) There is inter-individual variation, even among healthy individuals.
We model ACTH and cortisol secretion simultaneously using a third-order linear differential equations model with Gaussian measurement errors and sparse pulsatile events as inputs to the model. We propose a novel framework for recovering pulses and parameters underlying interactions between ACTH and cortisol. We recover the timing and amplitudes of pulses using compressed sensing, and employ generalized cross validation for determining the number of pulses. We analyze simultaneously recorded serum ACTH and cortisol levels sampled at 10-minute intervals over 24 hours from 10 healthy women. The 24 hours began with 8 hours of scheduled sleep followed by 16 hours of wake.
We recover physiologically plausible timings and amplitudes for these pulses and model the feedback effect of cortisol. We obtain 15 to 18 pulses over 24 hours. The amplitudes and frequencies of the obtained secretory events are consistent with the physiologically plausible amplitudes and pulse frequencies as a function of the time of the day, without including an explicit model for pulse amplitudes and inter-pulse intervals.
In [5], we modeled cortisol secretion using the first-order kinetics underlying cortisol secretion and recovered the secretory events that lead to cortisol release and the corresponding model parameters. The recovered pulses in this study are highly consistent with cortisol serum measurements analysis using a different model and estimation algorithm reported in [5]. Since our model herein includes both ACTH and cortisol, pulses that are detected using our approach are significant in both ACTH or cortisol data, and pulses that only appear in ACTH or cortisol data might be due to noise, and are not reported as significant. For cortisol data, the high R2 values (above 0.82 for all 10 participants) suggest that our proposed algorithm can successfully reveal physiologically plausible information regarding cortisol release in the HPA axis. Considering that the half-life of ACTH is less than that of cortisol and a sampling interval of 10 minutes can not capture all characteristics of the ACTH profile (e.g. the peak values), the current ACTH data is not as reliable as the current cortisol data; this may explain why the R2 values obtained for the ACTH data were lower than the R2 values found for the cortisol data. The variations in the hormone data also might be due to undersampling (when the sampling frequency is low), and experimental error that can be caused by assay variability and pipetting [11].
Our model enables analyzing the HPA axis as a whole and allows for accurate quantification of pulsatile events, and normal and pathological states relating the control of cortisol and ACTH secretion. This can potentially lead to a systematic approach for treating disorders related to cortisol and also for achieving normal cortisol secretion in an optimal manner. Modeling the interactions between ACTH and cortisol by including concurrent data from both hormones allows for understanding the input/output relationship between ACTH and cortisol. Currently, stimulation tests are used to diagnose hormonal disorders that are caused by a problem in the anterior pituitary or the adrenal glands. Using data from a large population of healthy human subjects, a model and a deconvolution algorithm that includes the ACTH gain and cortisol negative feedback like the model proposed in this study, we could find a range for model parameters for the healthy population. This could then be used to recognize the site of origin for some hormonal disorders of the HPA axis for specific patients. For example, if a patient has elevated cortisol levels, the model can distinguish whether the negative feedback effect of cortisol on ACTH is too low, or the gain on ACTH is too high, or the clearance rate of cortisol by the liver is too low. The algorithm provided in our study is a novel way of recovering the feedback gain, ACTH gain, and ACTH secretory events simultaneously.
The described approach to estimation of ACTH and cortisol measurements is a general approach that can similarly be applied to concurrent measurements of other hormones. In this work, we used a state space approach in estimation of the HPA axis. We formulated the problem in a way that allows for concurrent deconvolution of two hormone profiles, while considering one hormone (ACTH) as the input resulting in the release of the other hormone (cortisol). The proposed state space framework can be applied to other hierarchical endocrine hormone systems (e.g. thyroid-stimulating hormone and thyroid hormone).
The proposed approach is also beneficial for analyzing concurrent measurements when one of the observations is very noisy; using the proposed approach, one can fit the noisy data implicitly and reduce the effect of noise when performing estimation. By implicitly fitting the ACTH data, we reduced the effect of the high noise in the data, and compensated for the cases in which there is a pulse of ACTH without a cortisol response or vice versa.
While we used a deterministic approach for deconvolution of cortisol levels, it is possible to cast the parameter estimation problem as a Bayesian estimation problem by considering a Gaussian distribution for the ℓ2-norm and a Laplace distribution for the ℓ1-norm in the cost function in (8), and obtain confidence intervals for the model parameters and the pulses underlying cortisol secretion. Future directions of this research include developing a physiologically plausible optimal control formulation that can result in impulse control.
V. Conclusion
Cortisol is released in pulses (in response to pulses of ACTH), and in return, has a negative feedback effect on ACTH release. Simultaneous recording of ACTH and cortisol is not typical, and determining the number, timing, and amplitudes of pulsatile events from simultaneously recorded data is challenging. In this study, we analyzed simultaneously recorded serum ACTH and cortisol measurements from 10 healthy women. We modeled ACTH and cortisol secretion simultaneously using a linear differential equations model, with Gaussian errors and sparse pulsatile events as inputs to the model. We proposed a novel framework for recovering pulses and parameters underlying the interactions between ACTH and cortisol. We recovered the timing and amplitudes of pulses using compressed sensing, and employed generalized cross validation for determining the number of pulses. The amplitudes and frequencies of the obtained secretory events are consistent with physiologically plausible amplitudes and pulse frequencies as a function of the time of the day, without including an explicit model for pulse amplitudes and inter-pulse intervals. Our model enables analyzing the HPA axis as a whole and allows for accurate quantification of pulsatile events, and normal and pathological states relating the control of cortisol and ACTH secretion. This can potentially lead to a systematic approach for optimally treating disorders related to cortisol. The proposed state-space framework can be applied to other hierarchical endocrine hormone systems (e.g. growth hormone, thyroid hormone, and gonadal hormones).
Supplementary Material
TABLE III.
The estimated number of pulses and the squares of the multiple correlation coefficients (R2) for the fits to the experimental ACTH and cortisol time series
| participant | M | N | ||
|---|---|---|---|---|
| 1 | 18 | 18 | 0.94 | 0.74 |
| 2 | 17 | 17 | 0.88 | 0.65 |
| 3 | 16 | 16 | 0.94 | 0.66 |
| 4 | 17 | 17 | 0.88 | 0.73 |
| 5 | 18 | 15 | 0.89 | 0.52 |
| 6 | 20 | 15 | 0.92 | 0.58 |
| 7 | 16 | 17 | 0.91 | 0.51 |
| 8 | 16 | 16 | 0.89 | 0.79 |
| 9 | 16 | 17 | 0.83 | 0.67 |
| 10 | 20 | 17 | 0.82 | 0.46 |
| Median | 17 | 17 | 0.89 | 0.66 |
M is the estimated number of Cortisol pulses using only measurements of Cortisol levels, and N is the estimated number of ACTH pulses using concurrent measurements of ACTH and cortisol levels. and are the square of the multiple correlation coefficient for cortisol and ACTH time series, respectively.
Acknowledgments
Funding
RTF's work was supported in part by the NSF Graduate Research Fellowship. For this work, ENB is supported in part by NIH DP1 OD003646, and NSF 0836720, MAD is supported in part by EFRI-0735956, EBK is supported in part by NIH P01-AG09975, K24-HL105664, RC2-HL101340, R01-HL-11408, R01-64105018 and HFP01603 and HFP02802 from the National Space Biomedical Research Institute through NASA NCC 9-58 and GKA is supported in part by NIH K24 HL103845. Clinical studies were performed at the Brigham and Women's Hospital General Clinical Research Center. Grants supporting the original data collection include NIH R01AR43130 (GKA), M01RR20635 (BWH GCRC), K01AG00661 (EBK), R01GM 53559 (ENB), and NASA NCC9-58 with the NSBRI. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
A preliminary version of this work was presented in R.T. Faghih's Ph.D. thesis [4].
Author Contributions
EBK and GKA collected the data. RTF, MAD, and ENB developed the algorithms. RTF analyzed the data and wrote the paper. All authors edited the paper.
Competing Interests
EBK received an unrestricted gift to the Brigham and Women's Hospital from Sony Corporation in 2011. The rest of the authors have declared that no competing interests exist.
Contributor Information
Rose T. Faghih, Department of Electrical Engineering and Computer Science and the Laboratory for Information and Decision Systems, Massachusetts Institute of Technology.; Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, and Massachusetts General Hospital.
Munther A. Dahleh, Department of Electrical Engineering and Computer Science and the Laboratory for Information and Decision Systems, Massachusetts Institute of Technology.; Engineering Systems Division, Massachusetts Institute of Technology.
Gail K. Adler, Harvard Medical School. Division of Endocrinology, Diabetes and Hypertension, Brigham and Women's Hospital.
Elizabeth B. Klerman, Harvard Medical School. Division of Sleep and Circadian Disorders, Brigham and Women's Hospital.
Emery N. Brown, Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, and Massachusetts General Hospital.; Harvard Medical School. Institute for Medical Engineering and Science, Massachusetts Institute of Technology.
References
- 1.Boufounos P, et al. Sparse signal reconstruction from noisy compressive measurements using cross validation. IEEE Workshop on Statistical Signal Processing. :299–303, 2007. [Google Scholar]
- 2.Brown EN, et al. A stochastic differential equation model of diurnal cortisol patterns. American Journal of Physiology -Endocrinology And Metabolism. 2001;280(3):E450–E461. doi: 10.1152/ajpendo.2001.280.3.E450. [DOI] [PubMed] [Google Scholar]
- 3.Conrad M, et al. Modeling the hypothalamus pituitary adrenal system: homeostasis by interacting positive and negative feedback. Journal of Biological Physics. 2009;35(2):149–162. doi: 10.1007/s10867-009-9134-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Faghih RT. Ph.D. thesis. Massachusetts Institute of Technology; 2014. System Identification of Cortisol Secretion: Characterizing Pulsatile Dynamics. [Google Scholar]
- 5.Faghih RT, et al. Deconvolution of serum cortisol levels by using compressed sensing. PLOS ONE. 2014;9(1):e85204. doi: 10.1371/journal.pone.0085204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Faghih RT, et al. A feedback control model for cortisol secretion. Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2011;716 -719 doi: 10.1109/IEMBS.2011.6090162. [DOI] [PubMed] [Google Scholar]
- 7.Faghih RT. S.M. thesis. Massachusetts Institute of Technology; 2010. The FitzHugh-Nagumo model dynamics with an application to the hypothalamic pituitary adrenal axis. [Google Scholar]
- 8.Frank V, et al. The minimal model of the hypothalamic pituitary adrenal axis. Journal of Mathematical Biology. 2011;63(4):663–690. doi: 10.1007/s00285-010-0384-2. [DOI] [PubMed] [Google Scholar]
- 9.Golub GH, et al. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics. 1979;21(2):215–223. [Google Scholar]
- 10.Gorodnitsky IF, Rao BD. Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing. 1997;45(3):600–616. [Google Scholar]
- 11.Gudmundsson A, Carnes M. Pulsatile adrenocorticotropic hormone: An overview. iological Psychiatry. 1997;41(3):342–365. doi: 10.1016/s0006-3223(96)00005-4. [DOI] [PubMed] [Google Scholar]
- 12.Gupta S, et al. Inclusion of the glucocorticoid receptor in a hypothalamic pituitary adrenal axis model reveals bistability. Theoretical Biology and Medical Modelling. 2007;4(1):8. doi: 10.1186/1742-4682-4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.He Z, et al. On the convergence of FOCUSS algorithm for sparse representation. CoRR,abs/1202.5470, http://arxiv.org/abs/1202.5470, 2012.
- 14.Johnson TD. Bayesian deconvolution analysis of pulsatile hormone concentration profiles. Biometrics. 2003;59(3):650–660. doi: 10.1111/1541-0420.00075. [DOI] [PubMed] [Google Scholar]
- 15.Kettyle WM, Arky RA. Endocrine pathophysiology. Lippincott-Raven; Philadelphia: 1998. [Google Scholar]
- 16.Klerman EB, et al. Circadian rhythms of women with fibromyalgia. Journal of Clinical Endocrinology & Metabolism. 2001;86(3):1034–1039. doi: 10.1210/jcem.86.3.7293. [DOI] [PubMed] [Google Scholar]
- 17.Kyrylov V, et al. Modeling robust oscillatory behavior of the hypothalamic-pituitary-adrenal axis. IEEE Transactions on Biomedical Engineering. 2005;52(12):1977–1983. doi: 10.1109/TBME.2005.857671. [DOI] [PubMed] [Google Scholar]
- 18.Linkowski P, et al. The 24-Hour Profile of Adrenocorticotropin and Cortisol in Major Depressive Illness. The Journal of Clinical Endocrinology & Metabolism. 1985;61(3):429–438. doi: 10.1210/jcem-61-3-429. [DOI] [PubMed] [Google Scholar]
- 19.Lonnebo A, et al. An integrated model for the effect of budesonide on ACTH and cortisol in healthy volunteers. British Journal of Clinical Pharmacology. 2007;64(2):125132. doi: 10.1111/j.1365-2125.2007.02867.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murray JF. Ph.D. thesis. University of California; San Diego: 2005. Visual recognition, inference and coding using learned sparse overcomplete representations. [Google Scholar]
- 21.Peters A, et al. The principle of homeostasis in the hypothalamus-pituitary-adrenal system: new insight from positive feedback. Biometrics. American Journal Physiology Regulatory, Integrative and Comparative Physiology. 2007;59293(3)(1):650–660. R83–98. doi: 10.1152/ajpregu.00907.2006. [DOI] [PubMed] [Google Scholar]
- 22.Refetoff S, et al. The Effect of Dexamethasone on the 24-Hour Profiles of Adrenocorticotropin and Cortisol in Cushing's Syndrome*. The Journal of Clinical Endocrinology & Metabolism. 1985;60(3):527–535. doi: 10.1210/jcem-60-3-527. [DOI] [PubMed] [Google Scholar]
- 23.Van Cauter E. Human Pituitary Hormones. Springer; Netherlands: 1981. Quantitative methods for the analysis of circadian and episodic hormone fluctuations. pp. 1–28. [Google Scholar]
- 24.Veldhuis JD, et al. Amplitude modulation of a burstlike mode of cortisol secretion subserves the circadian glucocorticoid rhythm. American Journal of Physiology-Endocrinology And Metabolism. 1989;257:E6–E14. doi: 10.1152/ajpendo.1989.257.1.E6. [DOI] [PubMed] [Google Scholar]
- 25.Vidal A, et al. Dynpeak: An algorithm for pulse detection and frequency analysis in hormonal time series. PLOS ONE. 2012;7:e39001. doi: 10.1371/journal.pone.0039001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vis DJ, et al. Endocrine pulse identification using penalized methods and a minimum set of assumptions. American Journal of Physiology - Endocrinology And Metabolism. 2010;298(2):E146–E155. doi: 10.1152/ajpendo.00048.2009. [DOI] [PubMed] [Google Scholar]
- 27.Young EA, et al. Twenty-four-hour ACTH and cortisol pulsatility in depressed women. Neuropsychopharmacology. 2001;25:267–276. doi: 10.1016/S0893-133X(00)00236-0. [DOI] [PubMed] [Google Scholar]
- 28.Zdunek R, Cichocki A. Improved M-FOCUSS algorithm with overlapping blocks for locally smooth sparse signals. IEEE Trans. Signal Process. 2008;56(10):4752–4761. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.