Closed-Loop Multitarget Optimization for Discovery of New Emulsion Polymerization Recipes

Abstract

Self-optimization of chemical reactions enables faster optimization of reaction conditions or discovery of molecules with required target properties. The technology of self-optimization has been expanded to discovery of new process recipes for manufacture of complex functional products. A new machine-learning algorithm, specifically designed for multiobjective target optimization with an explicit aim to minimize the number of “expensive” experiments, guides the discovery process. This “black-box” approach assumes no a priori knowledge of chemical system and hence particularly suited to rapid development of processes to manufacture specialist low-volume, high-value products. The approach was demonstrated in discovery of process recipes for a semibatch emulsion copolymerization, targeting a specific particle size and full conversion.

Experimental platforms enabling automated search for optimal process conditions,¹⁻⁴ new chemical structures,⁵ or new bioactive compounds⁶ emerged very recently as a disruptive technology that has a potential to change the way chemical processes are developed across many areas of molecular sciences. The technology delivers increased throughput of a single investigator and provides a discovery platform for new entities through a directed search, as opposed to trial-and-error of high-throughput methods.

This technology was made possible through miniaturization of experiments both in batch and flow modes and the use of in-line and in situ analytics. The opportunities for directed discovery are created through coupling of automated experiments with the decision-making software.

Automated experiment systems were recently demonstrated for multistep organic syntheses^4,7−9 or discovery of unknown inorganic clusters⁵ in continuous flow microreactors. This type of chemical experiments naturally lends itself to automate the decision-making process through use of design of experiments (DoE) algorithms. To achieve this automation, real time chemical sensing must be available to the decision-making algorithm. First steps regarding decision-making algorithms were exemplified on heterogeneous catalytic reactions in combination with in line GC analysis.^2,3 These approaches were recently expanded to other chemical sensing techniques, such as MS, NMR, IR, and so forth.^2,10−16

Notably, in most published examples, simple optimization routines were successfully applied to automate the design of experiments. This is mainly due to fairly simple problems being explored thus far, with very few input variables, few measured variables, and, usually, a single optimization criteria/target. Simple optimization algorithms require large numbers of experiments to converge and thus restrict the approach to inexpensive experiments. They also do not allow to explore systems with complex multimodal output space.

We argue that without a significant advance in optimization and design of experiments algorithms the technology for self-optimization would be resigned to very simple tasks and would not allow exploration of the more interesting challenges of discovery within molecular sciences. Most real challenges are either experimentally expensive, have high dimensionality of input variable space, or/and have several desired features and hence require multiobjective optimization.

To exemplify this hypothesis, we turned to the problem of discovery of recipes in emulsion copolymerization. Although emulsion polymerization has been studied for many decades,¹⁷ the process is still not fully understood. It is a complex multiphase system consisting of monomer droplets, latex particles, and continuous aqueous phase and is strongly influenced by temperature, pH, surfactant, and inhibitor concentrations and types, ratio of monomers, and so forth. Closed loop control of emulsion polymerization industrial plants requires a fully predictive model.¹⁸⁻²³ However, many industrial plants are run on the basis of predetermined recipes mainly due to the absence of robust physical models. Inspired by the huge impact copolymerization of styrene and butyl acrylate has in industry and research,²⁴⁻³⁰ we studied this two-monomer system as an example of a complex process leading to a functional product.

The experimental optimization problem was designed to simulate the process of discovery of a completely new process. Any prior knowledge of the process was deliberately ignored, and only physical constraints were taken into account. This resulted in the problem including 14 input variables and two targets: full monomer conversion and a 100 nm product latex particle size. We formulated the problem of discovery as that of target optimization. An attractive strategy for target optimization in the case of multiple objectives and large number of input variables is to combine sequential experiments with a DoE algorithm that would take into account the outcomes of previous experiments to select the next experiment. One of the most prominent algorithms for such sequential optimization is the Efficient Global Optimization (EGO) algorithm.³¹ Wenzel et al., for instance, made use of the concepts of desirability³² and virtual observations³³ to construct an algorithm capable of identifying and, with each iteration, improving on a cluster of solutions that best associate with target values. Even though the algorithm undoubtedly explores globally throughout the search, it is not designed to actively search for solutions that would allow one to gain the most information about the underlying process (i.e., solutions optimal in terms of experimental design).

The implementation of machine learning algorithms in closed-loop systems for chemical reactions or process discovery has not been reported. However, various advanced optimization algorithms had been developed for different applications, such as automatic chromatographic separation of human serum and yeast fermentation,³⁴ tuning the transition time of polymer reactions³⁵ or optimization of polymerization under power failure conditions,³⁶ or developing predictive models of catalytic activity using nonlinear regression of statistical models based on data mining.³⁷ We must emphasize that conventional design-of-experiments approaches, such as factorial design, were frequently employed to investigate emulsion polymerization about 20–30 years ago. The technique allowed to sample experimental space and identify very roughly the regions of emulsion instability³⁸ but could not be used for automated discovery of recipes for two main reasons, apart from the poorer state of development in analytical methods, chemoinformatics, and computing power at the time: the highly nonlinear nature of the problem and its high dimensionality result in poor prediction of infeasible (unstable) experimental regions, which in turn result in large number of failed experiments. These are overcome, in part, by the machine learning approach, which is better suited to multidimensional problems. The issue of the lack of predicting power with respect of emulsion stability remains but is approached with the use of a nonlinear multidimensional classification algorithm, vide infra.

Recently we developed an algorithm that specifically addresses the challenge of experimental sequential optimization and discovery under the constraints of expensive experiments. The resulting multi objective active learner (MOAL) algorithm utilizes both Gaussian Processes surrogate models and evolutionary algorithms. It was shown to outperform other similar algorithms in silico.³⁹

We first adopted a physical model of emulsion copolymerization¹⁸ to perform in silico target optimization driven by the MOAL algorithm. This process was run for 84 virtual experiments and discovered 18 unique recipes satisfying the target of high conversion (≥99%) and particle diameter of ca. 100 nm (within 1%); see Figure 1. This indicates that the optimization problem is highly multimodal. Throughout the optimization, scattering around the target of particle size is more pronounced than that of the target of full conversion, which is consistent with theory of emulsion polymerization.⁴⁰ The particle size is affected by many factors: transport of monomer, free radicals and surfactant to the growing particles, and partition of these reagents among the continuous aqueous phase, emulsified monomer droplets (monomer reservoir), monomer-swollen polymer particles (primary reaction loci), and oil–water interface.

Figure 1.

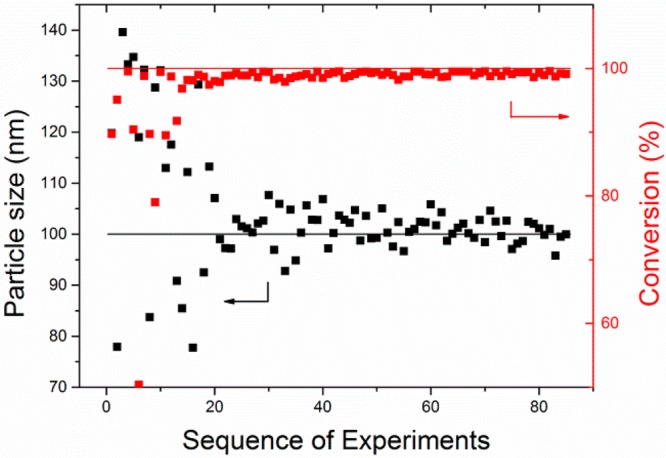
Results of in silico discovery of new copolymerization recipes. The two straight lines indicate the targets: particle size 100 nm and 100% conversion.

The first experiment that reached both targets was experiment number 27, excluding the 15 initial training experiments. This is quite remarkable, given the 14-dimensional input space of the problem. However, we should clarify that we cannot use this particular physical model to reliably define an optimal decision space size with respect of the overall decision space due to the validity of the model. Out of the 84 simulated recipes, only 18 reached both targets of full conversion and particle size diameter of 100 nm simultaneously. The list of the 84 simulated experiments is given in Supporting Information, Table S1, and results with respect of the optimization targets are shown in Table S2. The 84 simulated experiments do not include the 15 experiments of the initial training set.

Some of the 18 recipes were tested in the laboratory. Results of the validation experiments are shown in Supporting Information, Table S3. This revealed that the assumption of the monomer-starved emulsion polymerization was not satisfied in practice and the physical model of the process did not adequately represent the actual polymerization process. However, high conversion was obtained in three experimentally tested recipes. The second target, particle size of 100 nm in diameter, was not obtained in any recipe predicted by the in silico optimization. However, two recipes produced particle sizes of 135 and 178 nm, which where the closest values to the target.

To perform sequential discovery of new recipes without a priori process knowledge, we included a classification algorithm, which learns infeasible process conditions, in this case corresponding to reactor fouling due to coagulation and precipitation. The MOAL model was trained with only five experiments to explore the decision space. Two early experiments (Nos. 2 and 5) were infeasible due to reactor fouling. None of the initial five experiments reached the set targets. It was expected that, due to the low number of the initial set of experiments, the algorithm would require more iterations to discover successful recipes. Only one experiment failed during the optimization run. The failure was caused by too-high reaction temperature and the consecutive reactor fouling. However, small number of failed experiments suggests the successful implementation of the classification algorithm. Results of sequential process discovery are shown in Figure 2, and the complete set of obtained recipes is shown in Supporting Information, Table S4.

Figure 2.

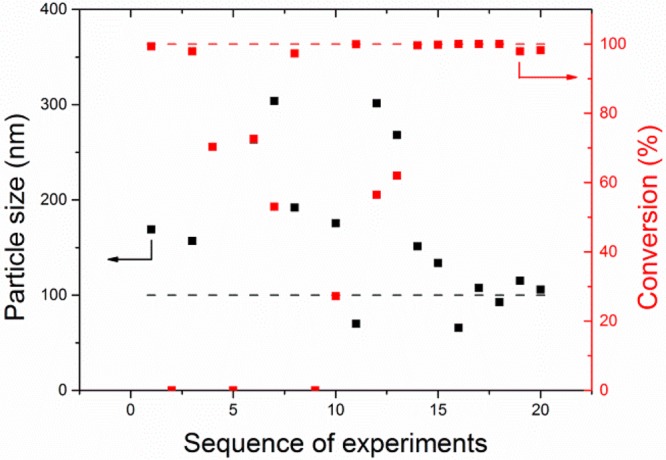
Results of the MOAL optimization of emulsion copolymerization carried out in the laboratory. The dotted lines indicate the targets to be reached.

The first experiment that reached both targets simultaneously was experiment 17 (including the five experiments from the initial training set). In this case we accepted 10% error in particle size and 5% error in conversion. As expected, following the results obtained from the simulations, the more difficult target to reach was the particle diameter. Despite the fact that obtaining particles with a certain size is a rather complex physical process, the sequential discovery processes reached both targets from iteration 17 onward. The optimization was stopped after 20 experiments.

One experiment reached only 27% conversion with the reaction time of 163 min. This is the lowest conversion achieved from all of the feasible experiments. The reason for the low conversion could be the high solid content (60% wt) and/or the low amount of the initiator solution (0.5 mL, 0.13 g mL^–1). The other five experiments with low conversion (x < 75%) had in general low amount of initiator fed into the reactor.

A high amount of solid content can lead to coagulation and fouling, so it was not surprising that the experiments which failed or did not reach the targets had high solid content.

Although in this discovery process all 14 input variables were treated as independent, it is known from polymerization theory that some of those must be correlated. However, in the experimental results obtained, no pairwise correlations between input variables were observed (see Supporting Information, Figures S4–S6). Most likely this is due to the very small number of experimental points and a highly multimodal nature of the problem.

Comparing the successful in silico recipes with the recipes performed in the experimental system the main differences are (i) lower temperature for the laboratory experiments, (ii) in general higher ratio of initiator to monomer in the in silico recipes and (iii) all in silico recipes were considered feasible.

The model copolymerization system is well-studied and is produced commercially.^24,29,41 Therefore, we can compare the known industrial recipe (Supporting Information) with those discovered through the sequential experimental optimization. A number of differences between the recipes can be highlighted. The total feeding time in the discovered recipes is much shorter than in the commercial one, but the total reaction times are similar. In the last four discovered recipes the amount of the initiator changed, but generally speaking, the discovered recipes still have a higher concentration of initiator than the recipe used in industry. Similarly, for the solid content, the solid content changed from 18% (Exp. 17) to 44% (Exp. 20). A higher solid content is preferential in industry. However, experiment 20 is close to the solid content used in the commercial recipe. There are also differences between the discovered recipes and the recipe used in the industry in the amount of surfactant and the ratio of initiator to monomer. The discovered recipes contained more surfactant and initiator. Consequently, the discovered recipes are likely to be more expensive than the recipe used in industry. This implies that the multitarget optimization should also include cost target.

Conclusion

In conclusion, we demonstrated for the first time the discovery of a new process, assuming little a priori knowledge of the chemical system. The developed approach is generic and allows multitarget optimization, automated learning of feasible process conditions, and minimizing the number of experiments. The approach is particularly suited to systems with large dimensionality of input variables and multimodal optimization surface. The approach was used to discover new recipes for the required targets of high conversion and particle diameter, without any prior knowledge of emulsion polymerization process. The system was capable to discover, after 27 experiments in silico and after 17 experiments in closed-loop experiments, a recipe to obtain a product with the desired property in a process with the required conversion.

Experimental Section

Materials

Styrene (ST, Aldrich, 98%), butyl acrylate (BA, Sigma-Aldrich, 99%), sodium dodecyl sulfate (SDBS, Sigma, 99%), tert-dodecylmercaptan (CTA, Sigma 98.5%), and sodium persulfate (NaPS, Aldrich) were all used as received. Super-Q water was used in all experiments. Polystyrene seed particles were produced in house.

Methods

The particle size was measured off line by dynamic light scattering (DLS, Malvern Zetasizer Nano-ZS). Conversion was monitored by GC-FID with an internal standard (toluene).

Reaction Setup

A reaction system, schematically shown in Figure S3 (Supporting Information) included a 0.5 L double-jacketed reactor with a four-blade turbine impeller, two syringe (Harvard PHD Ultra), and one metering (Eldex Optos) pumps. The pumps and the heating unit were controlled through a dedicated LabVIEW program. The information transfer, namely, the next recipe suggested by the MOAL algorithm, from MATLAB to LabVIEW was established via DataHub middleware.

MOAL Algorithm

A detailed description of the MOAL algorithm can be found elsewhere.^42,43 For this work the algorithm was adapted to the problem of target value optimization with unknown constrains to account for infeasible process conditions resulting in experimental failures. In the specific case of emulsion copolymerization stable and unstable solutions were labeled as feasible (1) and infeasible (−1), respectively. As a result, the next recipe to perform is chosen from the part/s of the decision space that are predicted (by the classification model) to consist of feasible recipes only. The highly dimensional decision space of 14 variables was chosen to allow the discovery of new recipes for the target of high conversion and particle size of 100 nm. The 14 variables were relaxed as much as possible to allow the discovery of new recipes with the MOAL algorithm. However, only physical constraints were made to obtain feasible recipes, as for the amount of surfactant and initiator the water solubility was taken into account, or in another example for the reaction temperature, the activation temperature of the initiator and the boiling point of water were taken into account. The algorithm was implemented in Matlab.

In Silico Optimization

A first-principles model of emulsion copolymerization of styrene and butyl acrylate in a semibatch processes¹⁸ was used for in silico optimization and discovery. Both models were implemented in Matlab.

Experimental Closed-Loop Optimization

Each experiment was carried out in a similar way. First, the four solutions were prepared: starting reactants, initiator solution (feed 1), surfactant solution (feed 2), and monomer solution (feed 3). The solutions were then degassed for an hour. After the starting reactants were heated up to the required reaction temperature, the feeding started. The stirrer speed was 400 rpm in all experiments. The statistical model was programmed in such a way that feeding rate of the initiator solution could be changed into feeding time 1.1 and feeding time 1.2, whereas feeding rate of the monomer and surfactant solutions where constant over the entire feeding time. The reaction was carried out under nitrogen atmosphere. Analysis of particle size and conversion was performed off line, and manual experimental setup and reactor cleaning were performed.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.oprd.5b00210.

• Definition of input variables and their constraints, a full list of in silico and experimental optimization recipes, graphs showing correlations between targets and some input variables, description of experimental setup and details of an industrial recipe which the obtained results are compared with. The published recipes provide all underlying research data to comply with EPSRC research data policy. (PDF)

The authors declare no competing financial interest.