Ca²⁺-dimethylphosphate complex formation: providing insight into Ca²⁺ mediated local dehydration and membrane fusion in cells

Abstract

Earlier studies using x-ray diffraction, light scattering, photon correlation spectroscopy, and atomic force microscopy, strongly suggest that SNARE-induced membrane fusion in cells proceed as a result of calcium bridging opposing bilayers. The bridging of phospholipid heads groups in the opposing bilayers by calcium leads to the release of water from hydrated Ca²⁺ ions as well as the loosely coordinated water at PO-lipid head groups. Local dehydration of phospholipid head-groups and the calcium, bridging opposing bilayers, then leads to destabilization of the lipid bilayers and membrane fusion. This hypothesis was tested in the current study by atomistic molecular dynamic simulations in the isobaric-isothermal ensemble using hydrated dimethylphosphate anions (DMP−) and calcium cations. Results from the study demonstrate, formation of DMP-Ca²⁺ complexes and the consequent removal of water, supporting the hypothesis. Our study further demonstrates that as a result of Ca2+-DMP self-assembly, the distance between anionic oxygens between the two DMP molecules is reduced to 2.92 Å, which is in close agreement with the 2.8 Å SNARE-induced apposition established between opposing bilayers, reported earlier from x-ray diffraction measurements.

1. Introduction

In cells, specialized proteins called SNAREs (t-SNAREs in the target membrane, and v-SNARE in the vesicle membrane) overcome repulsive forces to bring opposing membranes close to within a distance of ~ 2.8 Å, imparting specificity and regulation to membrane fusion (Jeremic et al., 2004a, 2004b). Studies using light scattering and x-ray diffraction measurements of SNARE-reconstituted liposomes demonstrate that fusion proceeds only when Ca²⁺ ions are available between the t- and v-SNARE-apposed membranes. Studies show that no fusion between vesicles occurs when t-SNARE-vesicles and v-SNARE-vesicles are first mixed, prior to the addition of calcium (Jeremic et al., 2004b). The result suggests that hydrated calcium [Ca(H₂O)₆]²⁺, measuring ~6 Å, is too large to fit between the ~ 2.8 Å t- and v-SNARE-apposed membranes space (Jeremic et al., 2004b), hence unable to bridge the opposing membrane bilayers.

Calcium ion is essential to a number of life processes and is present in every living cell. It participates in diverse cellular activities, such as metabolism, secretion, proliferation, muscle contraction, cell adhesion, learning, and memory. Although calcium is abundantly present within the cell, it is well sequestered and is available only on demand. Upon certain stimulus, Ca²⁺ concentrations in specific nano environments of the cell are elevated by several orders of magnitude within a brief period (<1ms). This prompt mobilization of Ca²⁺ is essential for numerous physiological functions, such as membrane fusion, leading to the release of neurotransmitters, enzymes, or hormones. Experimental evidence strongly suggests calcium bridging of opposing bilayers, leading to the release of water from hydrated Ca²⁺ ion as well as the loosely coordinated water at the PO-lipid head group. Local dehydration of phospholipid headgroups is expected to destabilize bilayers, leading to membrane fusion (Jeremic et al., 2004a, 2004b). This hypothesis was tested in the current study by atomistic molecular dynamics simulations in the isobaric-isothermal ensemble, using hydrated dimethylphosphate anions (DMP⁻) and calcium cations. Results from the study demonstrate formation of DMP-Ca²⁺ complexes and the consequent removal of water, supporting the hypothesis.

2. Methods

Simulation

NPT molecular dynamics simulations were performed at 298 K and 101.325 kPa on a system containing 2000 water molecules, 11 Ca⁺² cations and 22 dimethylphosphate anions (DMP⁻). Periodic boundary conditions and the minimum image convention were applied in all three dimensions. Electrostatic interactions were calculated using a particle mesh Ewald. Lennard-Jones interactions were truncated after 14 Å. The CHARMM force field version 27 was used to model all interactions between molecules, including water (Foloppe et al., 2000). Simulations were initiated from a random initial configuration created by Packmol (Martinez JM and Martinez L, 2003). NAMD version 2.6 was used for all simulations (Phillips et al., 2005), while visualization of molecular configurations and other data analyses were performed with VMD version 1.8.6 (Humphrey et al., 1996). Simulations were performed for 20 ns (16 ns equilibration, 4 ns production) using a 2 fs time step. The volume of the system reached its average value of 61.4 nm³ (r = 1.06 g/cm³) within 200 ps. Simulations were run for an additional 10 ns beyond the 20 ns reported in this work and no significant changes were observed in the Ca²⁺-O(water) RDF after a 16–20 ns period.

3. Results and discussion

Molecular dynamics simulations in the isobaric-isothermal ensemble at 298 K and 101.325 kPa was used to determine whether Ca²⁺ was capable of bridging opposing phospholipid head groups in the early stages of the membrane fusion process. As previously utilized in the study of nucleic acids (Guan et al., 1994, 1995; Schneider et al., 1996), DMP⁻ was chosen for the current study since it represented the smallest molecular fragment of typical membrane phospholipids that retained properties of the phopholipid head-group, while providing a significant reduction in the computational complexity, and hence enhance accuracy of the study. Furthermore, the strategy of using the DMP⁻, rather than full phospholipids, in these simulations facilitates the search for spontaneously formed Ca²⁺-phospholipid structures, which may bridge the head groups of opposing phospholipids bilayers. The DMP⁻ fragments can undergo free translational and rotational diffusion, as well as rapid internal conformation changes, so that structure formation with Ca²⁺ is explored rapidly and comprehensively, whereas full membrane phospholipids can exist only in self-assembled bilayers that restrain the motion of individual phospholipids molecules and greatly lengthen the time scale for structure formation. For example, in the phospholipids bilayer simulations of Bockmann and Grubmuller, 2004, sequential binding of Ca²⁺ to phospholipids carbonyl oxygens within a single bilayer was incomplete even after 150 ns of simulation time, and those simulations did not include mechanisms for Ca²⁺ bridging of opposing bilayers. However, we have to remain aware of the possibility that both the initiation of membrane fusion due to Ca²⁺ bridging of opposing bilayers and the entire membrane fusion reaction occur within different time frames and different kinetics. It is the initiation of membrane fusion of fusion via calcium and the organization of participating atoms in this process with which we have been concerned in this report.

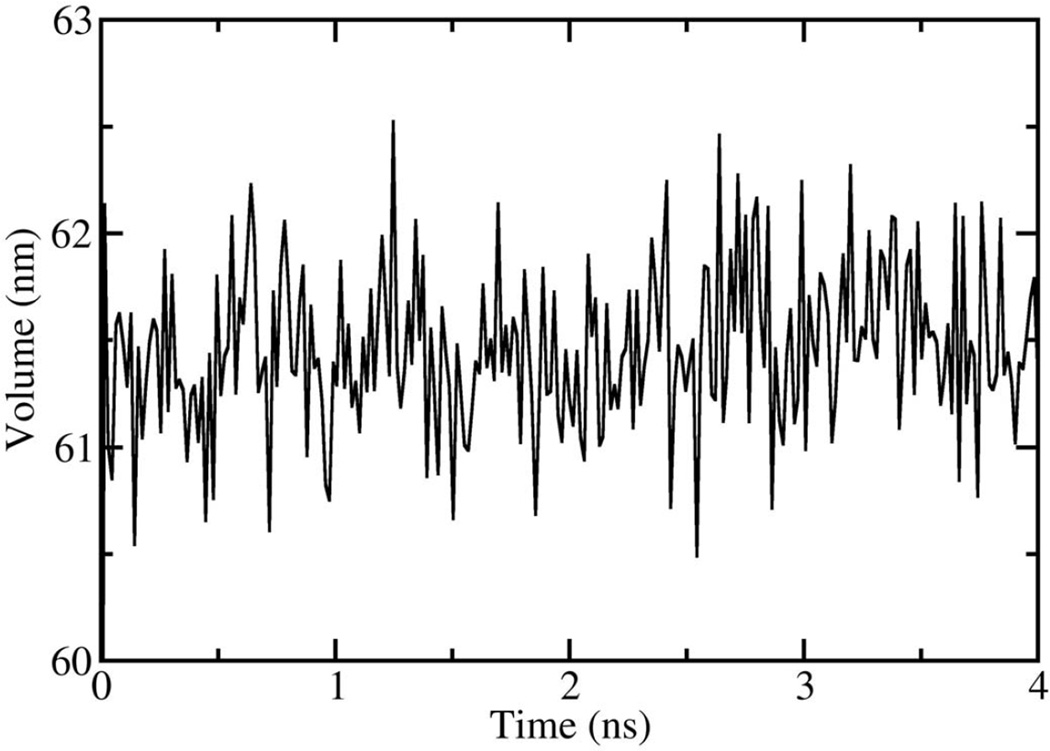
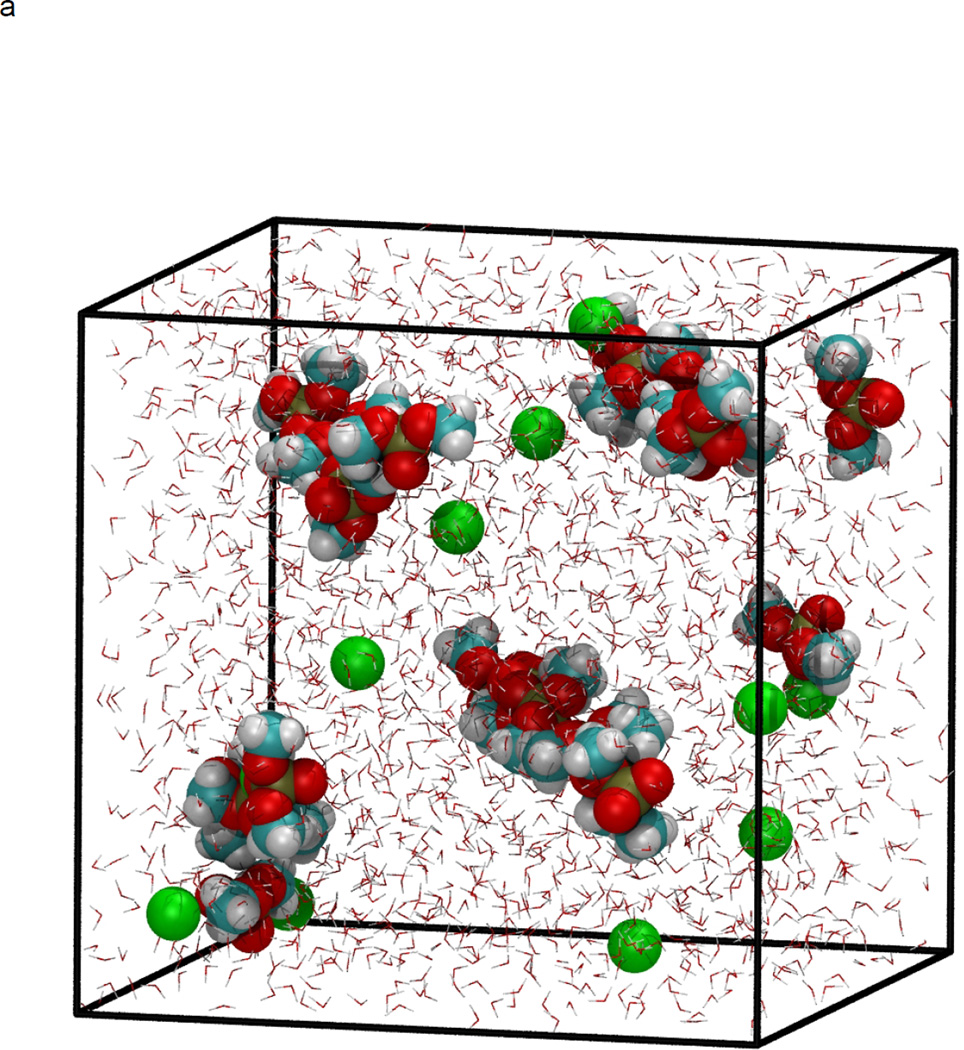
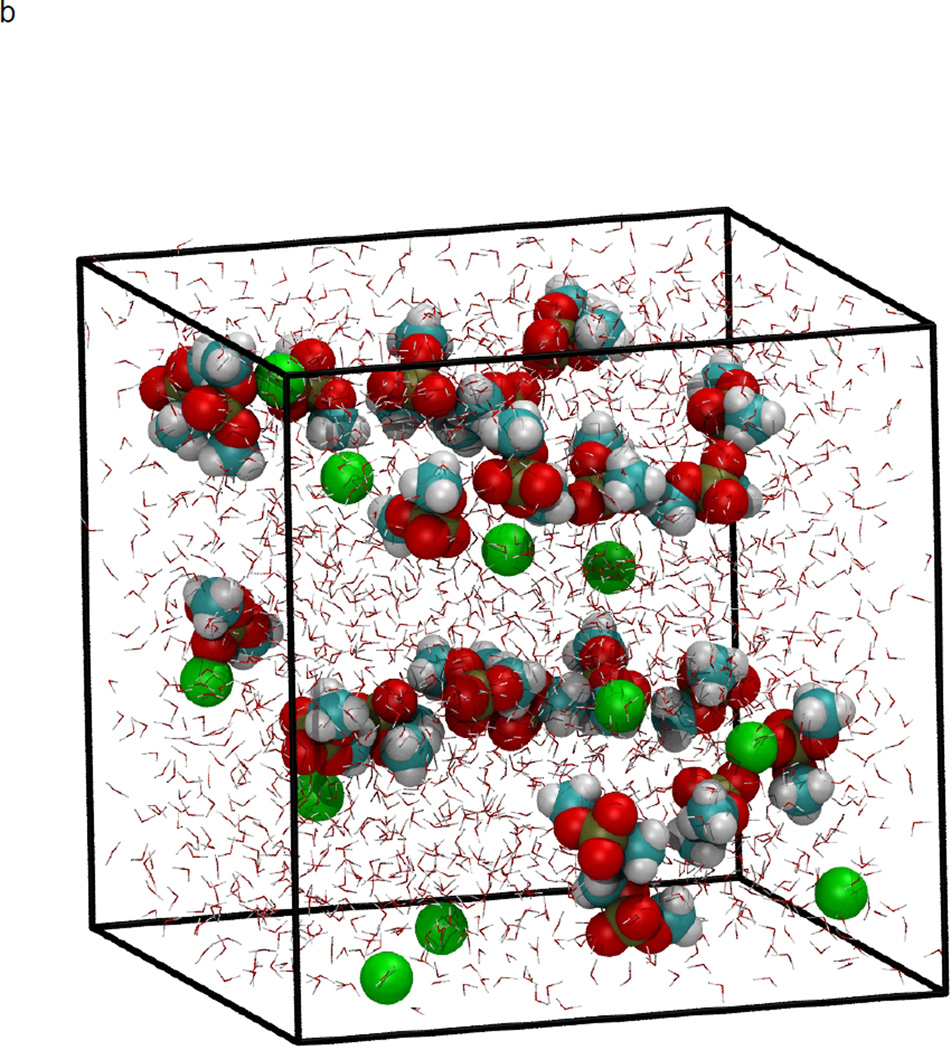
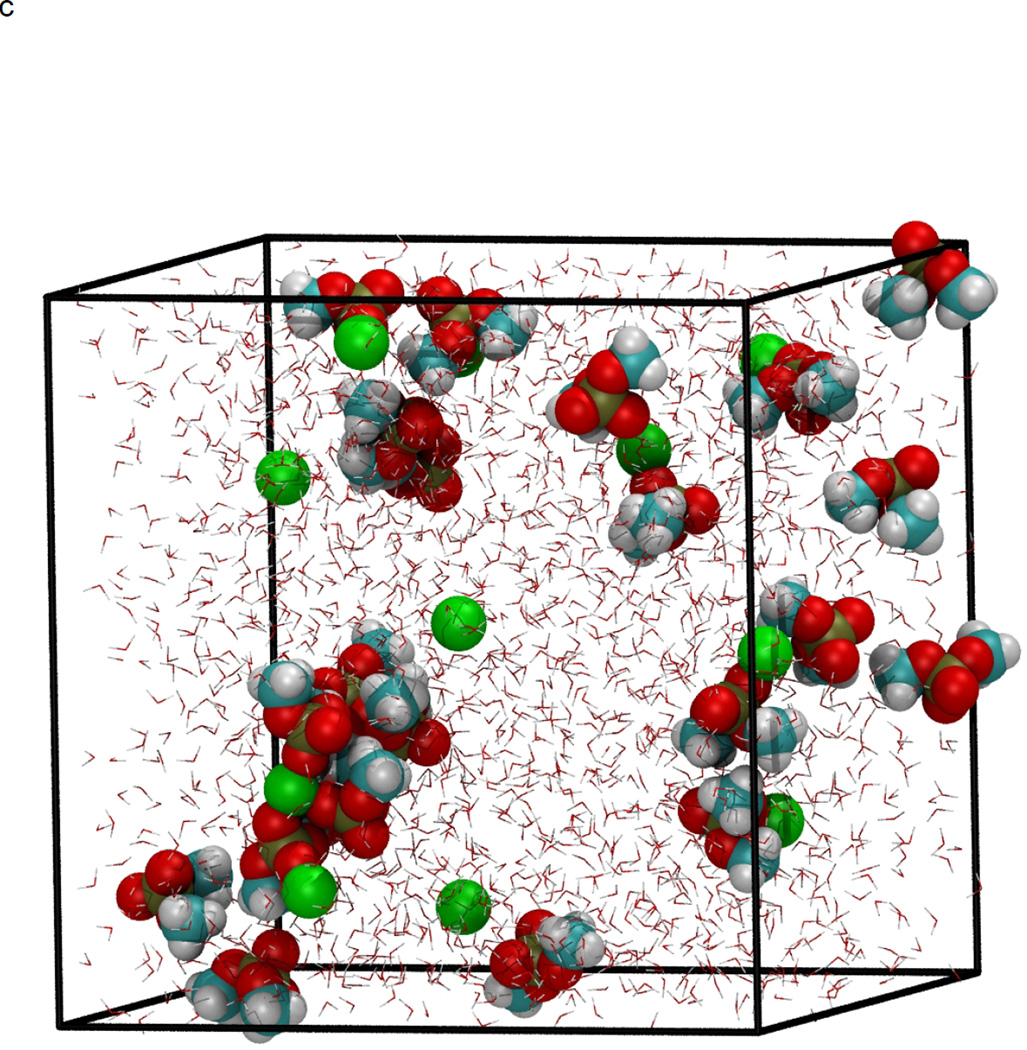
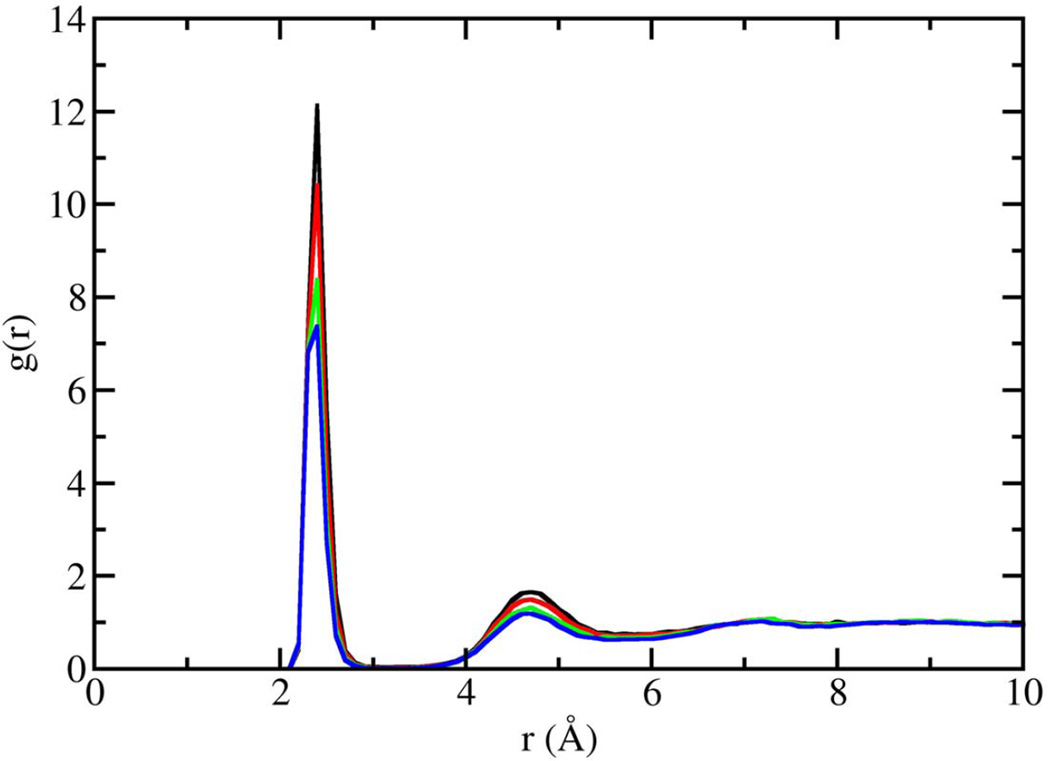
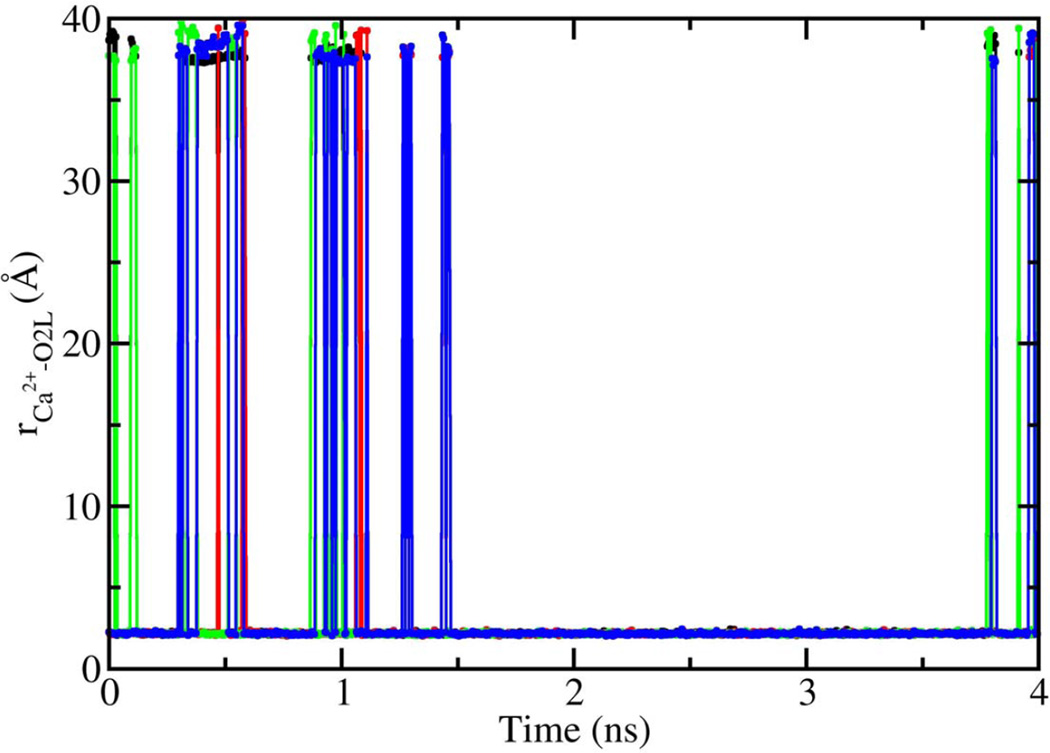
In figure 1, the volume fluctuations for the first 4 ns of simulations are presented, illustrating the rapid equilibration of the system with respect to density. While the volume of the system was stable after 200 ps, significant changes in the microstructure were observed between 0.2–8 ns following initiation of simulation (Fig. 2). Snapshots of molecular configurations observed during the course of the simulations are shown in figure 2. Radial distribution functions (RDF) were calculated at various points during the course of the simulation, to quantify the local order in the vicinity of Ca²⁺ and the anionic oxygens of DMP⁻. In figure 3, the radial distribution function for Ca²⁺ interacting with the oxygen of water is shown as a function of time step. In the early stages of the simulation, all calcium ions are found associated with water. However, as the simulation progresses, preferential association of Ca²⁺ with the anionic oxygen of DMP⁻ limits the number of water molecules that may associate with Ca²⁺. The result is a significant reduction in the height of the Ca²⁺-O(water) peak of the RDF over time. After 8 ns of simulation, the emergence ring structures involving two Ca²⁺ and two DMP⁻ were observed. An example of such a ring complex observed after 17 ns of simulation is shown in figure 4. The average distances between Ca²⁺ and the anionic oxygens of DMP⁻, and the resultant bond angles formed by O-Ca-O were determined by taking averages during the 2.25 ns when the ring complex was stable. This time period was determined through observation of the Ca²⁺-O(DMP⁻) interaction distances as a function of time step for the last 4 ns of the simulation, as shown in figure 5. These data show that while the ring complex is quite stable, it does dissociate and reform multiple times over the course of the simulation. These multiple dissociation-association events ensure that the molecular dynamics simulations have adequately sampled phase space and that the ring complex is not simply an artifact of the initial configuration used to start the simulation. Furthermore, radial distributions were calculated for various interactions of water with DMP- and Ca²⁺. The RDF for the interacting anionic DMP⁻ oxygens and Ca²⁺ are shown in figure 6. In the RDF’s, no distinction is made between Ca²⁺ bound to one or two DMP⁻ molecules, nonetheless, the RDF clearly illustrates how the binding of Ca²⁺ to DMP⁻ alters the local structure of water around the anionic oxygens of DMP⁻.

Figure 1.

Volume as a function of time, for NPT molecular dynamics simulations at 298 K and 101.3 kPa.

Figure 2.

NPT molecular dynamics simulation at 298 K and 101.3 kPa, demonstrating formation of DMP-Ca²⁺ complex. Initial configuration at time=0 (a), and after minimization and heating (b), four ns of simulation at 298 K and 101.3 kPa (c), and 8 ns (d). Atoms are color coded as: Carbon (cyan), hydrogen (white), oxygen (red), phosphorous (gold), and Ca²⁺ (green). Water molecules are represented as background red-white V’s for clarity.

Figure 3.

Radial distribution function for Ca²⁺-O(water) interactions as a function of timestep. Zero to 4 ns (black line), 4–8 ns (red line), 8–16 ns (green line), 16–20 ns (blue line).

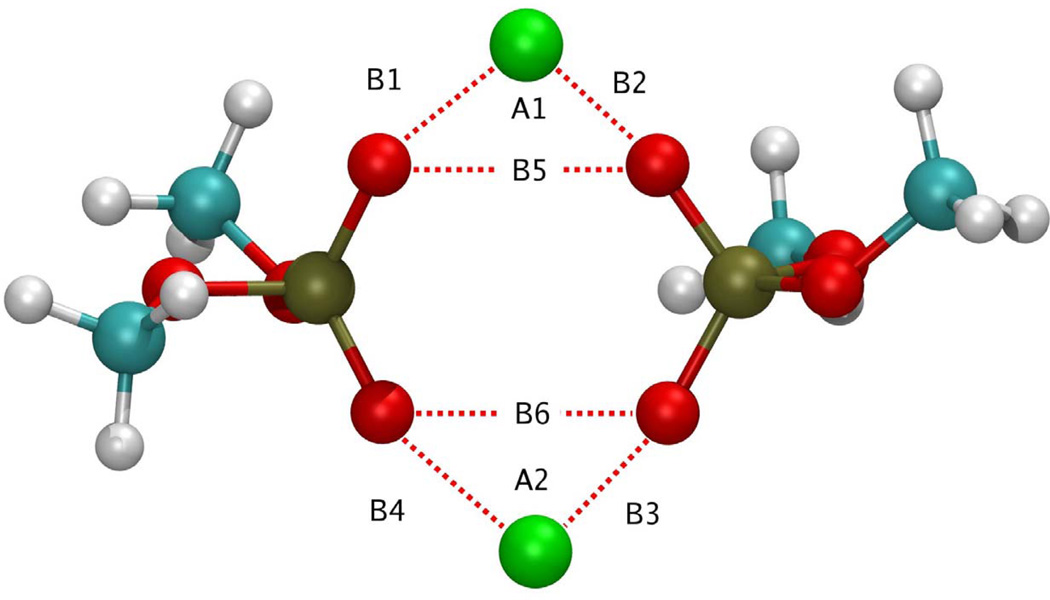
Figure 4.

Ca²⁺-DMP⁻ ring complex observed during molecular dynamics simulations. Atoms are colored as follows: Carbon (cyan), hydrogen (white), oxygen (red), phosphorous (gold), and Ca²⁺ (green). B1=2.146 Å, B2 = 2.145 Å, B3 = 2.140 Å, B4=2.145 Å, B5 = 2.92 Å, B6 = 2.92 Å, A1 = 85.79°, A2 = 85.07°.

Figure 5.

Ca²⁺-O(DMP⁻) interaction distances as a function of time step. Data correspond to the 16–20ns portion of the NPT molecular dynamics simulations. Distances correspond to labels in Figure S4; B1 (black line), B2 (red line), B3 (blue line), B4 (green line).

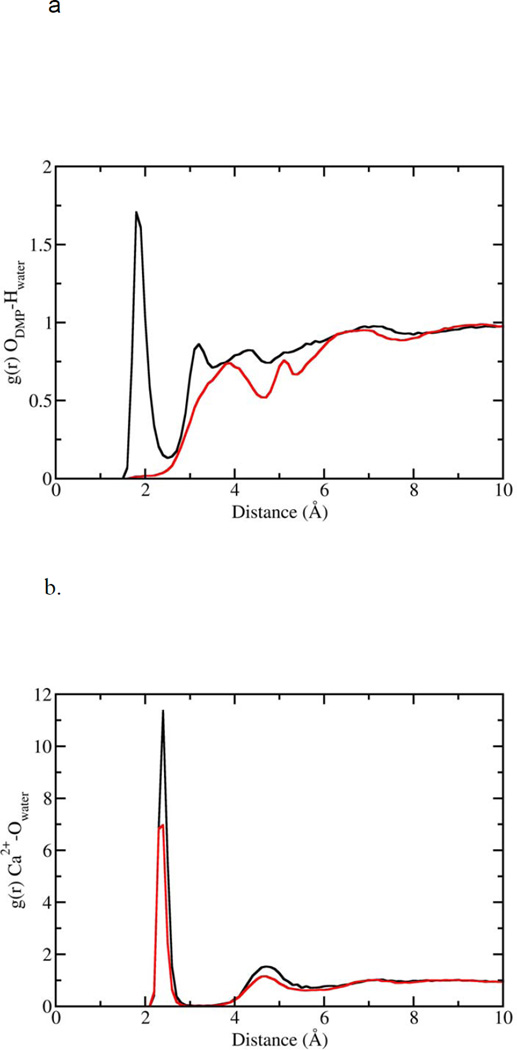
Figure 6.

Radial distribution functions for water interacting with the DMP⁻ and Ca²⁺. (a) Hydrogen atoms of water interacting with anionic DMP⁻ oxygens. Black curve corresponds to DMP− in free solution; red curve corresponds to DMP− bound to Ca²⁺. (b) Oxygen of water interacting with Ca²⁺. Black curve represents Ca²⁺ unbound to DMP−; red curve represents Ca²⁺ bound to DMP⁻.

Careful examination of molecular configurations obtained from the molecular dynamics simulations reveals the establishment of self-assembled Ca²⁺-DMP− complexes. As shown in figure 4, Ca²⁺ can bridge two opposing DMP⁻ molecules by binding to the anionic oxygens of the DMP molecule, resulting in the formation of a somewhat ring-like structure. In addition to this ring conformation, linear and bent aggregates are also established when a single Ca²⁺ cation bridges two DMP molecules. In figure 4, the co-ordinates of atoms established when such a single Ca²⁺ bridges two DMP molecules, is illustrated. In this illustration, the distance between the interacting atoms and the resulting bond angles formed is shown in angstrom and degrees. It was observed, that without Ca²⁺, DMP⁻ molecules fail to associate with each other. Formation of a single O-Ca²⁺-O bridge was frequently observed during the 16 ns equilibration period, and resulted in an O-Ca²⁺-O distance of 4.2 Å. However, as shown in figure 4, the inclusion of an additional Ca²⁺ results in the formation of a ring-like complex, which provides a means for mitigating the electrostatic repulsion between the two anionic oxygens in the DMP⁻ molecule. As a result of Ca²⁺-DMP self-assembly into such a ring complex, the distance between anionic oxygens is reduced to 2.92 Å, which is in close agreement with the 2.8 Å SNARE-induced apposition established between opposing bilayers, reported from x-ray diffraction studies (Jeremic et al., 2004a, 2004b). During the course of the simulation, it was seen that the complex assembled and disassembled a number of times. The bond length and bond angle data presented in figure 4 have been averaged over a 2.25 ns period where the ring conformation was stable. The four anionic oxygens participating in the ring complex reside in a planar arrangement, for the full lifespan of the structure, with only minor out-of-plane excursions as the ring structure flexed (Fig. 4). In the Ca²⁺-DMP⁻ complex, both Ca²⁺ ions reside above the plane formed by the oxygens, enabling the Ca²⁺ ions to retain interaction with limited water molecules.

A thorough analysis of the structure also revealed that Ca²⁺ binds only to the anionic oxygens. Furthermore, Ca²⁺ was never observed to bridge the anionic oxygens of a single DMP⁻ molecule. These observations are supported by a number of recent density functional calculations performed on [Ca(H₂O)₆]²⁺ and [Ca(H₂O₆]²⁺-DMP⁻ clusters (Petrov et al., 2005; Sundaresan et al., 2006; Pavlov et al., 1998; Katz et al., 1996). In case of DFT B3LYP/6-311+G(2d,2p), calculations on [Ca(H₂O)_n]²⁺ clusters and the H₂O-Ca²⁺ binding energies were found to decrease monotonically from −56.9 kcal/mol for one water bound to Ca²⁺ to −24.7 kcal/ol for the sixth water bound to Ca²⁺. It therefore becomes clear that the enthalpic penalty for removal of a water molecule from the [Ca(H₂O)_n]²⁺ complex progressively increases, with the removal of each additional water molecule. Binding energies for the hexahydrated Ca²⁺ with DMP⁻ in an implicit water solvent (CPCM) have also been determined by DFT calculations at the B3LYP/6-31g(d,p) level by Petrov, et al. The net interaction energies for [Ca(H₂O)₆]²⁺ losing a water molecule to become [Ca(H₂O)₅]²⁺ and binding to a single anionic oxygen (monodentate) for the gg and tg conformers were determined to be −10.17 and −10.74 kcal/mol, respectively. Conversely, net binding energies for [Ca(H₂O)₆]²⁺ losing two water molecules and bridging two anionic oxygens on the same DMP⁻ molecule (bidentate) for the gg and tg conformers were calculated to be 3.28 and 0.71 kcal/mol, respectively. These results, combined with the results of molecular dynamics simulations presented here, demonstrate the enthalpic loss due to water removal and entropic loss that results from Ca²⁺ bridging anionic oxygens on the same DMP⁻ molecule, cannot be overcome by the anionic oxygen-Ca²⁺ interaction. However results from the study show that the loss of a single water molecule from Ca²⁺ is favorably replaced by interactions with anionic oxygen.

Having demonstrated that Ca²⁺ is capable of bridging phospholipid head groups, we then focused on the second aspect of the hypothesis, e.g. that binding of Ca²⁺ to oxygens in the phospholipid head group results in an expulsion of water from the head group. Number integrals (Fig. 7) for the interaction of the anionic oxygens with water hydrogen atoms were calculated from our simulations for DMP⁻ that was unbound, as well as the DMP⁻ molecules that participated in the formation of Ca²⁺-DMP⁻ ring complex (Fig. 4). The number integrals (Fig. 7) show, that for unbound DMP⁻molecules, there are on average 2 water molecules associated with each anionic oxygen at a distance of 2.2 Å. On the contrary, when two DMP⁻ molecules combine with 2 Ca²⁺ cations to form the ring-like complex, there is a total expulsion of water from the anionic oxygens of DMP⁻. Additionally, calculations for DMP⁻ complexed with one Ca²⁺ show that water is completely expelled from the oxygen bound to Ca²⁺, but 2–3 water molecules remain associated with the oxygen not bound to Ca²⁺.

Figure 7.

Number integrals for the anionic oxygens of DMP⁻ interacting with the hydrogen atoms of water as determined from NPT molecular dynamics simulations at 298 K and 101.3 kPa. Red line corresponds to DMP⁻ that is not bound to Ca²⁺, while the black curve represents interactions of water with the same oxygens for the Ca²⁺-DMP⁻ ring complex.

In summary, we have shown using molecular dynamics simulations, that hydrated Ca²⁺ is capable of bridging phospholipid head groups, and that such bridging results in an expulsion of water from both the phospholipid head groups and calcium (Fig. 8). These results are, to our knowledge, the first evidence in support of the principle hypothesis that Ca²⁺ bridging of phospholipid head groups during SNARE-induced membrane fusion results in the release of water from hydrated Ca²⁺ ion and loosely coordinated water at the PO-lipid head groups, leading to bilayer destabilization and membrane fusion (Jeremic et al., 2004b).

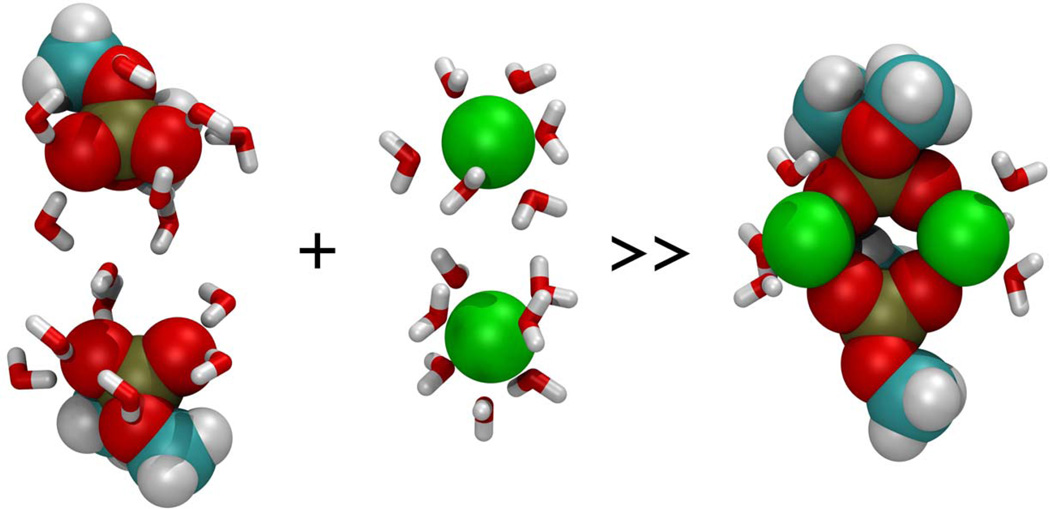
Figure 8.

Ca²⁺-DMP complex (extreme right) formed in NTP MD simulations at 298 K and 101.3 kPa. Hydrated calcium ions (center), and hydrated DPM molecules (extreme left), interact to form Ca²⁺-DMP complex (extreme right) having less associated water molecules. Color codes of atoms: Carbon (cyan), Hydrogen (white), Oxygen (red), Phosphorous (gold), Calcium (green), and water (red-white V’s).