The multiple facets of Peto's paradox: a life-history model for the evolution of cancer suppression

Abstract

Large animals should have higher lifetime probabilities of cancer than small animals because each cell division carries an attendant risk of mutating towards a tumour lineage. However, this is not observed—a (Peto's) paradox that suggests large and/or long-lived species have evolved effective cancer suppression mechanisms. Using the Euler–Lotka population model, we demonstrate the evolutionary value of cancer suppression as determined by the ‘cost’ (decreased fecundity) of suppression verses the ‘cost’ of cancer (reduced survivorship). Body size per se will not select for sufficient cancer suppression to explain the paradox. Rather, cancer suppression should be most extreme when the probability of non-cancer death decreases with age (e.g. alligators), maturation is delayed, fecundity rates are low and fecundity increases with age. Thus, the value of cancer suppression is predicted to be lowest in the vole (short lifespan, high fecundity) and highest in the naked mole rat (long lived with late female sexual maturity). The life history of pre-industrial humans likely selected for quite low levels of cancer suppression. In modern humans that live much longer, this level results in unusually high lifetime cancer risks. The model predicts a lifetime risk of 49% compared with the current empirical value of 43%.

1. Introduction

In its evolutionary arc, cancer emerges from a predictable and probably inevitable conflict in levels of selection between a metazoan and its constituent cells. Normally, a multicellular organism is the unit of natural selection, and each cell of its body is part of a whole-organism trait or strategy. That is, global cellular activities (e.g. division, differentiation and function) are entirely governed by host instructions that promote survival and reproduction of the whole organism. By contrast, a cancer cell becomes the unit of selection within a multicellular organism. Survival and proliferation of a transformed cell is independent of host instructions and instead governed by the cell's heritable properties, including both gene mutations and altered expression of normal genes.

Via Darwinian dynamics, tumour cells engage in a ‘struggle for existence’ among themselves and the outcome is dependent on the individual's ability to obtain space and substrate, and evade the predator-like effects of host responses such as the immune system. In some ways, the usual host-cell dynamic is reversed as the cancer cell typically uses components of the host (including circulating growth factors and blood vessels) to promote its own proliferation. Thus, carcinogenesis can be defined as a phase transition in which an individual cell becomes the unit of natural selection rather than one of an ensemble of cells that collectively forms the whole organism.

In effect, multicellular organisms must ‘play with evolutionary fire’ as their maintenance of fitness requires continuous turnover of their cellular populations. Unfortunately, each time the cells of a metazoan divide, mutations or other heritable changes may move the cell lineage towards the phase transition of a self-defined fitness function [1]. These transformed cells, in effect, become a single-celled, asexual protist.

If cancer initiation is governed by chance mutations, then the incidence of cancer within an animal species should correlate with the total number of cell divisions in its lifetime, which is the product of its total number of cells, the rate of cell division required for homeostasis and its typical longevity. In short, larger animals with more cells, or longer lived animals with more lifetime cell divisions should have higher cancer incidences. This expectation is supported by observations that within human organs, the risk of cancer is directly related to the lifetime number of stem cell divisions [2] as well as the tissue type [3]. However, observations seem contrary to this expectation. Larger animals do not seem to die from cancer more often than smaller organisms. This is Peto's paradox [4].

It is widely assumed that Peto's paradox arises from quantitative and qualitative differences in the cancer-suppression adaptations between animals [5]. Clearly, death from cancer can be a potentially strong selection force in multicellular organisms. In fact, cancer-suppression adaptations and genes appear to have arisen rapidly within the earliest of metazoans. Some oncogenes were present even in the Early Cambrian [6].

However, it is likely Peto's paradox has a number of facets beyond body size and longevity. If cancer suppression were cost-free, one would expect all organisms, big or small, short- or long-lived, to have the same suite of nearly flawless anti-cancer adaptations. As this does not seem to be the case, it is likely that, similarly to most survival enhancing adaptations, cancer suppression must come with a metabolic or efficiency cost, albeit a cost that should be minimized by natural selection. Thus, we expect there must be trade-offs between the degree of cancer-suppression adaptations and other aspects of whole-organism survival and fecundity.

Here, we use the Euler–Lotka equation from population ecology to model an organism's fitness and to develop this model into an evolutionary model of cancer suppression. We assume that cancer suppression can be approximated as a quantitative trait. This trait trades off the likelihood of age-specific mortality from cancer with age-specific fecundity—the greater the value of this trait, the lower the likelihood of dying from cancer, and the lower the animal's fecundity [7]. This contrasts somewhat with other models of life-history evolution where increased mortality (from parasites, for instance) selects for earlier maturation at the expense of fecundity [8]. By couching cancer suppression in the context of life-history evolution, we can reveal additional and potentially testable facets of Peto's paradox.

This allows us to address conventional questions that straightforwardly emerge from Peto's paradox such as: does the magnitude of cancer-suppression adaptations increase with the size of the organism, the organism's lifespan, the age at first reproduction and the age at last reproduction (senescence)? It also allows us to examine less obvious questions such as variations in the value of cancer suppression based on age-specific death rates. The optimal level of cancer suppression may depend on whether the death rate generally increases with age (Type I survivorship curve, like humans) or declines with age (Type III like sea turtles and alligators).

2. The Euler–Lotka equation as a model of the evolution of cancer suppression

An animal's fitness can be defined as its per capita growth rate. If fitness is constant, then a population either increases or decreases exponentially. Alternatively, fitness may be density-dependent. Usually, fitness and proliferation will decline with density as increasing intra-population competition for available space and resources limits growth. However, in some populations, fitness increases with density when, for example, individuals receive some benefit from the presence of others, such as protection from predators in herds, known as the Allee effect [9].

Here, we characterize populations in an age-specific manner where age is represented by x. For species with age-specific survivorship and age-specific fecundity, the Euler–Lotka equation [10,11] gives the expected per capita growth rate, r, of a population that has achieved its stable age-distribution:

2.1

where l_x is the probability of a newborn surviving until age x, m_x is the expected number of newborns produced by an individual of age x, and r is the per capita growth rate of such a population with these survivorship and fecundity terms. The integral is evaluated from age 0 until the age beyond which no individuals survive. When population growth and fecundity are limited by females, then survivorship refers to females, and offspring refer to daughters.

For our evolutionary model and analyses, we shall use the following discrete approximation for the Euler–Lotka equation [12]:

2.2

We assume that the ecology of the organism and its needs to acquire particular resources and withstand particular hazards largely determine the evolution of its life history described by the number of age classes, the survivorship curve (l_x) and fecundity schedule (m_x). Once l_x and m_x are specified, the value of r is determined. The equation is transcendental and cannot be solved analytically, but it does have an exact solution that can be approximated as closely as desired numerically [13]. (Alternatively, one can convert this equation into the form of a Leslie matrix and use the dominant eigenvalue as a measure of fitness [14].) Here, we choose to work directly from the Euler–Lotka equation as it lends itself to life tables and is computationally efficient.

We imagine that mortality from cancer reduces survivorship from that which the organism would otherwise experience from all other aspects of its ecology. Let q_x be the probability of NOT dying of cancer at age x. This can occur either because cancer has not yet evolved within the organism, or because the current cancer burden of the organism has not yet proved lethal. We can now adjust background survivorship l_x by the mortality consequences of cancer:

2.3

The adjusted survival probability to age x is the background survivorship multiplied by the need to survive cancer during each of the preceding age classes.

We assume that cancer development and progression is, itself, a Darwinian process that proceeds with varying evolutionary velocity as mutations leading to a cancerous cell lineage must accumulate over time. Hence, the likelihood of dying of cancer at age x increases with age. To represent this, we use the following functional form for q_x:

2.4

where 0 < Q < 1 represents the likelihood that a newborn will not die from cancer during its first year of life. Presumably, Q is very close to unity. The term a assesses how quickly the probability of not dying of cancer declines with age x. This term likely varies with the organism's taxonomic affiliation and may increase with the number of mutagens present in the organism's diet and environment, the size of the organism (number of cells), and the rate of cell division and turnover in the organism as a consequence of lifestyle or need for wound healing. Among humans and among breeds of domestic dogs, it likely varies with genetic predispositions for cancer [15].

We let u be the organism's cancer-suppression trait that can take on any value between zero and unity. We let u = 0 represent no cancer-suppression adaptations, and u = 1 as the maximum possible allocation of whole-organism effort to cancer suppression. As such, increasing u increases the likelihood of the organism not dying of cancer.

The functional relationship between u and q_x is intentionally nonlinear. In the absence of any suppression, as u goes to zero, the organism will die of cancer as it faces the full brunt of cancer via undefended mutations. This is consistent with suggestions that some cancer suppression is necessary for metazoans to exist at all [16,17]. As u increases towards unity, the likelihood of surviving cancer converges on a maximum: Q^ax. If Q is close to unity and a is small then maximum cancer suppression virtually ensures a cancer-free lifetime. Decreasing Q or increasing a increases the likelihood of dying from cancer for any given level of cancer suppression. Finally, with this functional form, there are diminishing returns to cancer suppression as u increases from zero to unity.

If cancer suppression u were cost-free, then the animal would evolve to have u = 1. But, we assume, like all other anti-predator adaptations, that there is a cost. We shall assess this cost through fecundity. Increasing u reduces m_x from what it would have been in the absence of cancer-suppression adaptations:

2.5

This is just one of many ways to build in a trade-off between cancer suppression and other aspects of survivorship and fecundity [18–20]; and it is a likely trade-off from some types of cancer-suppression mechanisms. For small values of b ≪ 1, the cost of cancer suppression is small and we might expect to see fairly large investments in cancer-suppression adaptations, while for large b, cancer suppression is costly.

By combining the effects of the organism's cancer-suppression strategy into the Euler–Lotka equation, we make per capita growth rate, r(u), a function of u.

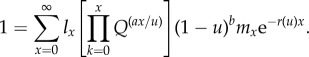2.6

We assume that natural selection will favour the level of anti-cancer suppression that maximizes r(u). The limitation of this approach is that we are not explicitly considering population size and density effects that might directly influence l_x and m_x. With density-dependence and limits to growth, we expect population size to equilibrate where per capita growth rate r = 0. For biological realism, we shall assume roughly steady-state populations near carrying capacity or at equilibrium population sizes. Thus we will work with life tables yielding r > 0 but close to zero.

The life-history parameters associated with the equilibrium population size will generate a net reproductive rate of R₀ = 1. The net reproductive rate is the number of daughters that a newborn female can expect to have over her lifetime:

2.7

Several other life-history metrics will be useful for evaluating the role of cancer within the animal's life. Given that an individual dies between age x − 1 and x, we can determine the probability that death was caused by cancer, c_x, rather than some other cause of death:

2.8

where (1 − q_x) is the probability of dying of cancer and (1 − (l_x/l_x−1)) is the probability of dying of something else. Given that a death occurs during the interval from (x − 1) to x, the likelihood of it being from cancer, c_x, is just the probability of dying of cancer over the age interval divided by the sum of both the probability of dying of something else and the probability of dying from cancer.

The fraction of total deaths in the population, f_x, that occur among individuals between the ages of x − 1 to x is

2.9

and hence the probability that a newborn dies of cancer over the course of her lifetime, C, is

2.10

3. Results

In our model, five sets of parameters determine the optimal level of cancer suppression, u*: the survivorship curve, l_x, the fecundity schedule, m_x, the baseline propensity for cancer survivorship, Q, the effect of age on cancer mortality, a, and the fecundity cost of cancer suppression, b. All of these parameters may govern Peto's paradox. Larger animals typically have: (1) greater longevity and hence higher values of l_x than smaller animals; (2) delayed reproduction so that m_x = 0 for a longer period of adolescence; (3) greater number of cells and cell divisions to achieve adulthood so that the baseline propensity for cancer survivorship, Q, may be smaller for larger than smaller animals; (4) increased size and longevity likely increase episodes of wound healing and general cell turnover resulting in more cell divisions than smaller animals and hence have a higher value for a. That said, actual life histories vary considerably so that species of the same size may have very different life expectancies and fecundity schedules.

An interesting parameter in our model is the fecundity cost of cancer suppression, b. While it is reasonable to assume that the value of b, like virtually all adaptive strategies, is not zero, it is unclear how the fecundity cost of cancer should vary with body size. Insofar as there is an economy of scale, b may decline with body size. However, b could also increase with body mass if cancer suppression operates less efficiently at larger than smaller size. More likely, the cost of cancer suppression varies in fascinating and yet unknown ways based on taxonomic group such as reptiles versus fish versus invertebrates, etc.

Our model identifies two methods for comparing cancer in organisms that vary in life history. The first is simply a measure of whether one species or another has a higher likelihood of surviving cancer from age x − 1 to age x, q_x. The second focuses on the likelihood that an animal, given its life history, dies of cancer or of something else, C. In what follows, we consider the effects of each set of parameters on the evolution of cancer suppression, and on mortality patterns. We will conclude with examination of the combined effects of parameters on cancer suppression and the likelihood of dying of cancer.

(a). Life-history tables

The life histories found among organisms in nature are staggeringly diverse. It is not our goal to investigate all of them. Rather, we aim to reveal general properties of life histories that may have predictable and testable effects on the degree of cancer suppression that we can expect to see when comparing animals with different life histories. As our point of comparison, we shall adopt a modified form of a published life-history table for the North American beaver [21]. These are large, long-lived rodents and thus represent a reasonable mid-point for subsequent examination of small (mouse) and large (elephant) organisms.

Using the beaver life-history data (table 1) for l_x and m_x; setting a = 0.01, b = 0.2 and Q = 0.97, and applying our model we obtain an optimal level of cancer suppression, u* = 0.101, a lifetime likelihood of C = 0.022 of dying from cancer, and the fraction of deaths from cancer by age shown in figure 1 (Type II survivorship curve). As there is no extant cancer data on beavers, the model predictions cannot be verified. However, as an illustration of the model and its output, we can make qualitative predictions regarding how changing life-history attributes will influence cancer mortality and selection for cancer-suppression adaptations.

Table 1.

The beaver life table that forms the baseline life table for our comparative analyses. We have adjusted the values of l_x from Payne's [21] actual life table upwards by assuming a death rate that is 90% of what Payne found. This adjusts survivorship in anticipation of the reduction from cancer mortality. The fecundity schedule is stylized to imagine average litter sizes that start with one pup at age 1 and increase to four pups by age 3. These are then halved to give the expected number of daughters to a female of age x.

X	lx	mx
1	0.4971	0.5
2	0.3129	1.5
3	0.2115	2
4	0.1259	2
5	0.096	2
6	0.0735	2
7	0.0614	2
8	0.0477	2
9	0.0439	2
10	0.0348	2
11	0.0215	2
12	0.0187	2
13	0.0115	2
14	0.01	2

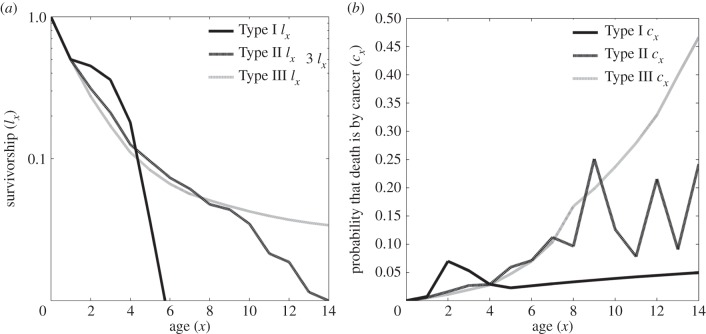
Figure 1.

The effect of survivorship curves (plots of age x versus ln(l_x)) on the likelihood that a death during age x is caused by cancer rather than some other mortality source, c_x. Figure 1a shows the three survivorship curves for the beaver model, where the Type II survivorship curve (relatively constant death rate with age) is our baseline model. The Type I (increasing death rate with age) and Type III curves (declining death rate with age) are modifications to the baseline where the values of l_x have been adjusted to keep life expectancy and net reproductive rates relatively constant. The Type III curve results in the highest optimal level of cancer suppression, u* = 0.111, and the lowest lifetime likelihood of dying of cancer, C = 0.0184; while the Type I is opposite (u* = 0.100, C = 0.0239). As shown in figure 1b, this is despite the fact that the age-specific cause of death from cancer rises most steeply for the Type III curve and least for the Type I. This is because with a Type III curve, the death rate from other causes declines with age, whereas the likelihood of dying from cancer always increases with age in our model regardless of survivorship curve. The gyrations in figure 1b for Type II survivorship are because we have used actual published data for beaver survivorship that has presumably stochastic variation in age-specific mortality from other causes with age—hence for age classes with unusually low death rates, a high proportion of those deaths shall be from cancer.

(b). Survivorship curves and cancer suppression

Two aspects of survivorship should influence the evolution of cancer suppression and cancer incidences. The first is the shape of the survivorship curve; the second is overall life expectancy. To examine this in our life-history model of beavers, we simply increase (or decrease) survivorship at all age classes by reducing (or increasing) the death rates of each age class. A 10% decrease or increase in death rates selects for an increase to u* = 0.111 or decrease to u* = 0.1, respectively. The increase (or decrease) in survivorship translates into a lower, C = 0.0184 (or higher, C = 0.0239), likelihood of death by cancer over the animal's lifetime. But the effect is limited because a longer lived organism, by not dying of some non-cancer cause at each age class, increases the chance of dying of cancer later in its life. As expected, all else being equal, a longer lived organism will evolve a greater level of cancer suppression, experience a lower age-specific cancer mortality rate and a slightly lower likelihood of dying from cancer than from something else.

The beaver life table exhibits a Type II survivorship curve in which age-specific death rates are relatively constant once adulthood is reached. We modified the survivorships, l_x, of the life table to reflect a Type I or a Type III survivorship curve while keeping the net reproductive rate, R₀, relatively constant as shown in figure 2. For the Type I, this means adjusting l_x up for small values of x and down for later age classes; and vice versa for the Type III survivorship curve. The Type I survivorship curve (typical of large mammals) results in less cancer suppression u* = 0.0808 than the Type III (typical of large fishes and reptiles) where u* = 0.1212. This is because the average age of a newborn's mother (generation time) is lower for the Type I than for the Type III survivorship curve. Cancer suppression will evolve to be more extreme as generation time increases and fecundity late in life becomes relatively more important.

Figure 2.

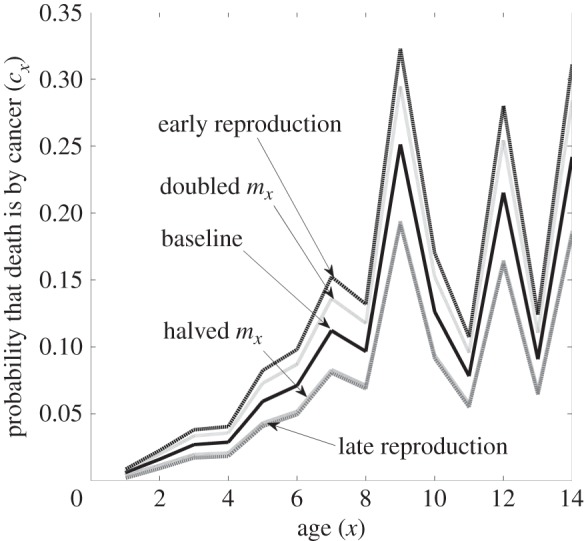
The effect of the fecundity schedule, m_x, on the likelihood that a death during age x is caused by cancer, c_x. We show the baseline beaver model (same line as the Type II in figure 1b) and four modifications where: (1) fecundity is halved for all age classes, (2) fecundity is doubled for all age classes, (3) fecundity has been front-loaded to earlier age classes while holding net reproductive rate, R₀, equal to the baseline and (4) fecundity has been back-loaded to later age classes while holding net reproductive rate equal to the baseline. Table 1 shows the effects of these scenarios on the optimal level of cancer suppression and the lifetime likelihood of dying from cancer. Early reproduction, while holding R₀ constant, results in the highest fraction of age-specific deaths occurring from cancer, followed by a halving of all values of m_x. Late reproduction, and doubling of the values of m_x results in the lowest values of c_x. Perhaps coincidentally, these last two scenarios resulted in the same curves because they select for the same optimal level of cancer suppression.

The shape of the survivorship curve has dramatic effects on the likelihood that an age-specific mortality event is from cancer or something else. While appearing counter-intuitive, the Type III curve has a very high likelihood of mortality from cancer later in life, while the Type I is the opposite (figure 1). Why? Paradoxically, for our beaver model, the probability of surviving cancer, q_x, is always higher with the Type III curve because of its higher level of cancer suppression. But, by virtue of declining death rates from other mortality sources (typical of Type III curves), the likelihood that a given death is from cancer actually increases with age!

(c). Fecundity schedule and cancer suppression

Age at first reproduction, age at last reproduction and changes in fecundity with age should all influence the evolutionary value of cancer suppression. For the beaver example, the value of cancer suppression increases with delayed reproduction. Thus, the optimal level of cancer suppression increases with generation time. Similarly, increasing (or decreasing) the number of offspring (m_x) results in a decrease (or increase) in the value of cancer suppression. Increasing m_x magnifies the cost of cancer suppression without any corresponding change in the survivorship benefits, thus tilting the cost–benefit ratio in favour of less cancer suppression.

In the beaver model, we can investigate changes in the fecundity schedule in four ways (table 2 and figure 1): (1) halving all of the m_x from our baseline model (this also halves the net reproductive rate, R₀), (2) doubling all of the m_x (this doubles the R₀), (3) shifting reproduction to earlier age classes while holding R₀ constant and (4) shifting reproduction to later age classes while holding R₀ constant. For early reproduction, we doubled the value of m_x at age x < 3 and halved later m_x (x > 2). This results in a lower generation time and a lower optimal level of cancer suppression. For later reproduction, we halved values of m_x for x < 4 and doubled m_x for x > 3. This results in a longer generation time and higher evolutionary values of cancer suppression (figure 2).

Table 2.

The effects of different fecundity schedules on the optimal level of cancer suppression, u*, fitness, r, net reproduction rate, R₀, and likelihood of dying from cancer over one's lifetime, C. Starting with the baseline life table for the beaver, entries show the effects of (1) halving all values of m_x, (2) doubling all values of m_x, (3) early reproduction where values of m_x are doubled for x < 3 and halved for x > 2 and (4) late reproduction where values of m_x are halved for x < 4 and doubled for x > 3. The early and late fecundity schedules were modified to keep the net reproduction rates similar to the baseline model.

	baseline beaver life table	halved mx	doubled mx	early reproduction	late reproduction
R0	2.0802	1.0446	4.1309	2.0773	2.5313
r	0.2046	0.0102	0.4691	0.3133	0.1858
u*	0.101	0.1414	0.0808	0.0707	0.1414
C	0.022	0.0161	0.0270	0.0305	0.0161

(d). Propensity for cancer survivorship

If Q (cancer survivorship) is essentially equal to unity and there is no propensity to die from cancer, the optimal level of cancer suppression is u* = 0. In our simulated beaver life table with values of a = 0.01 and b = 0.2, the optimal level of cancer suppression, u*, increases as Q declines (figure 3a). Mortality from cancer would increase rapidly with declining Q for a fixed level of cancer suppression. Allowing cancer suppression to evolve mitigates some of the adverse effects of a declining Q on age-specific and lifetime cancer mortality. Yet, age-specific mortality from cancer, c_x, and lifetime probability of dying from cancer, C, still increase with a lower propensity for cancer survivorship. Hence, lower cancer rates in larger bodied animals and Peto's paradox cannot be explained through cancer suppression in response to a lower Q. As expected from the structure of our model, the effect of Q on cancer is most pronounced in the older age classes.

Figure 3.

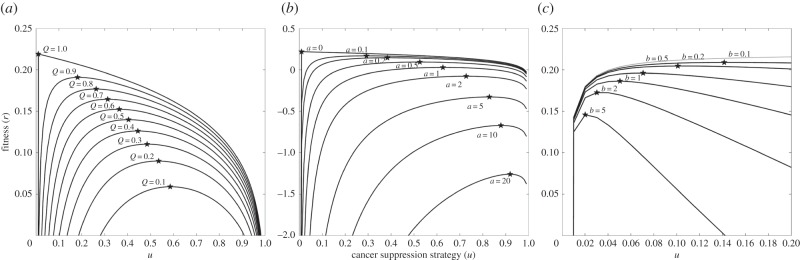
The effects of the propensity for dying of cancer, Q (a), effect of age on this propensity, a (b), and the cost of cancer suppression, b (c), on the optimal level of cancer suppression. The effects are shown as adaptive landscapes that plot fitness, r, as a function of the cancer-suppression trait, u. The different curves show different values for Q, a or b. The peaks of these curves show the optimal level of vigilance, u*, for a given set of parameter values. In going from curve to curve, one sees the effects of Q, a or b on fitness and the optimal level of vigilance. The shape of each curve shows the strength of selection for cancer suppression.

(e). Effect of age on cancer mortality

The effect of age on cancer mortality likely increases with the size of the animal, the rate of cell turnover and the taxonomic affiliation. For instance, the nematode, Caenorhabditis elegans, will have an expected value a ∼ 0 because, once adulthood (with about 1000 cells) is achieved, there is no additional cell division and no wound healing. On the other hand, a mammal with billions of cells, wound healing and regular cell turnover will have relatively high values for a (figure 3b). Genetic predispositions for cancer or environmental mutagens likely manifest as higher values for a. All else being equal, and for a fixed level of cancer suppression, age-specific survivorship from cancer, q_x, declines with a; and the probability of dying from cancer rather than from something else increases sharply with a. As a consequence, the adaptive level of cancer suppression increases with a. This mitigates somewhat, but does not reverse, the cancer mortality patterns associated with a stronger effect of age on cancer mortality. Again, higher cancer suppression for larger animals with a higher a is insufficient to explain Peto’s paradox

(f). Fecundity cost of cancer suppression

As expected, we find that cancer suppression is increasingly beneficial as the fecundity cost of cancer b decreases (figure 3c). Thus, if cancer suppression is evolutionarily inexpensive (i.e. little or no fecundity cost), we would expect near-perfect cancer suppression with virtually no incidence of malignant tumours in multicellular organisms. From this we can infer that the fecundity cost of cancer suppression is significant but as yet unknown empirically. It is also likely that this cost will vary across taxonomic groups such as cephalopods (squid and octopus), decapods (lobsters, crabs, etc.), reptiles, birds and mammals in ways that may explain different taxonomic-specific cancer rates.

(g). Peto's paradox and the combined effects of body size on cancer suppression and mortality

The three great life-history trade-offs, which optimize survivorship and fecundity, include: (1) offspring number versus offspring quality, (2) offspring now versus offspring later and (3) offspring versus parental survivorship [22,23]. It seems reasonable that death from cancer and the cost of cancer suppression must be components of these life-history trade-offs. To investigate this, we examine the expected dynamics of cancer and cancer suppression in organisms at the extremes of survivorship and fecundity including meadow voles (a very short lived and highly fecund meadow mouse), elephants, naked mole rats and humans (both primitive and modern), which are relatively long lived with low rates of fecundity. The life tables are given in the electronic supplementary material. The resulting population growth rate parameters (r and R₀), the optimal level of cancer suppression (u*) and the lifetime risk of dying from cancer (C) are shown in table 3. The vole exhibits little cancer suppression, whereas the elephant exhibits the highest level of cancer suppression. In rank order of u* we see: elephant > naked mole rat > primitive humans > beaver > vole; in terms of lifetime likelihood of dying from cancer: elephants > primitive humans > naked mole rats > beavers > voles. Size per se is not relevant to Peto's paradox.

Table 3.

The effects of different species' life tables on the optimal level of cancer suppression, u*, fitness, r, net reproduction rate, R₀, and likelihood of dying from cancer over one's lifetime, C. The life tables used for these analyses are given in the electronic supplementary material. For the life table for modern humans, we consider the effect of having the level of cancer suppression (i) optimal for primitive humans and (ii) the one that would be optimal for modern humans.

	baseline beaver	vole	elephant	naked mole rat	primitive human	modern human with primitive u*	modern human
R0	2.0802	1.2274	1.2715	1.0642	1.0304	0.8278	0.8438
r	0.2046	0.0576	0.0099	0.003	0.0032	−0.0125	−0.0111
u*	0.101	0.0606	0.5051	0.4545	0.3939	0.3939	0.5152
C	0.022	0.004	0.2156	0.054	0.0998	0.5856	0.4909

The vole, beaver and elephant all conform to expectations of their respective life histories. The vole is very short-lived and fecundity occurs within months of birth. Hence, the cost of cancer suppression is high in terms of reduced early fecundity, and the value of cancer suppression for survival into old age is meaningless. The elephant should have higher cancer suppression. It is long lived, has low fecundity (low values of m_x), delayed reproduction and continued fecundity into old age. Its larger size may also mean that it has a lower propensity for surviving cancer, Q, and this will select both for additional cancer suppression and higher likelihoods of dying of cancer late in life.

Empirically, the naked mole rat has already been identified as a mammal that seems to evade cancer and have an unusually high level of cancer-suppression genes or mechanisms [24–26]. It has been suggested that this results from their relative longevity, their novel social structure and relatively low activity levels [27]. In brief, naked mole rat colonies average approximately 75 individuals with just a single breeding female producing an annual litter of about 10 pups. A queen may remain so for over 10 years and individuals have been recorded to live as long as 30 years. Established and older females can reproduce only if they successfully compete to become sexually active when the queen dies. This creates a life table in which fecundity per female is very low (imagine a colony with 30 adult females for example), and the likelihood of being the queen increases with age (perhaps only to a point because of age and injuries).

Finally, it is instructive to examine variations in cancer-suppression dynamics in the vole (small, short lived, high fecundity), naked mole rat (small, long lived, low fecundity) and elephant (large, long lived, low fecundity). We find that there is little evolutionary value for cancer suppression in the vole. On the other hand, the naked mole rats should have a high level of cancer suppression—on par with an elephant. This somewhat counter-intuitive result emerges because naked mole rats have a Type II survivorship curve, low average fecundities per female (even lower than elephants), and the expected number of daughters per female actually increases with age. Elephants have a Type I survivorship curve (mortality increases with age), and fecundity decreases with age. These life-history differences combine to select for very high cancer suppression in this small rodent resulting in a remarkably low lifetime likelihood of dying from cancer.

(h). Humans and cancer

Humans present a novel analytic challenge because they have substantially increased their longevity during the recent history of the species. Thus, many extant human phenotypic traits evolved in response to selection forces that have, over the past 100 years, greatly changed. To examine the evolutionary dynamics of humans prior to the industrial revolution, we examine the life table for primitive humans [28]. When these data are used to parametrize our model, we predict that early humans would, relative to elephants and naked mole rats, have lower cancer suppression and less likelihood of dying from cancer relative to other sources of mortality. As adults, primitive humans had a Type II survivorship curve with a relatively low life expectancy and higher fecundity than elephants.

We can then take the u* = 0.3939 for primitive humans and hold it fixed for modern humans by adjusting the survivorship curve of Danish women in 2000. To this survivorship curve, we adapt a fecundity schedule as reported for British women [29]. The evolutionary mismatch between traits once adapted for earlier humans but no longer completely adaptive for modern humans is a crucial theme for evolutionary medicine (e.g. obesity, cholesterol, senescence, etc.). We can use our model to examine the consequence for cancer of mismatched cancer-suppression adaptations by seeing what natural selection would favour if we were adapted to our modern life table.

Thus, when the model's life-history parameters are changed from those of primitive to modern humans with the exception of the cancer-suppression term (u*), the lifetime risk of cancer increases from 10% to 59%, respectively. However, relative to primitive humans, the modern human life history would select for a much higher level of cancer suppression because of lower age-specific fecundities and longer life expectancies. If we allow evolution of cancer suppression in the modern era, we estimate a reduction of lifetime risk to 48%. By comparison, the estimated lifetime cancer risk in the US is 43% [19]. Our model predicts age- and lifetime-specific mortality risk from cancer. In reality, these mortality rates from cancer become beneficially distorted with cancer therapy and negatively distorted by factors such as obesity and carcinogens. Regardless, the model demonstrates that selection for cancer suppression has maximal population effects during childhood and young adulthood—consistent with observations that cancers in young people remain rare. However, age eventually mitigates the survival advantage of higher cancer suppression but the post-reproductive age classes exert no selection at all for additional cancer suppression [19]. Thus, older, non-reproducing human adults should not be under selection for cancer suppression.

4. Discussion

Peto's paradox juxtaposes logic with observation. Logically, large mammals with orders of magnitude more cells than small mammals (mice to humans to elephants to whales) should be more cancer prone as each cell division carries a finite risk of cancer-promoting mutations. Empirically, the incidence and mortality from cancer does not seem to rise with body size. We note that there are potential flaws in both components of Peto's paradox. The logic rests on an assumption of linearity—that cancer risk increases directly with total cell number. Within the conventional, genetic model of cancer this is reasonable. However, if somatic evolution is dependent on non-genetic intra- and extracellular components, some effects of size (a reduction in the metabolic rate, for example) may tend to reduce the cancer rate [30]. Similarly, the empirical data are limited as the true cancer rate of any non-human species is difficult to assess.

Nevertheless, if we accept the logic and the empirical observations as correct, the resolution of Peto's paradox likely lies in species to species and taxon to taxon differences in anti-cancer-suppression adaptations [31], but not because of body size itself, but rather other life-history attributes that correlate with body size. In our model, increasing body size, all else being equal, will select for greater cancer suppression but not sufficiently so to change the expectation that larger mammals should have higher cancer incidences (per age and per lifetime). This is because the model assumes diminishing returns to increased cancer suppression, and larger animals will have an inherently higher cancer incidence per ‘unit’ of cancer suppression. Rather, delayed reproduction, long reproductive lifespans and low annual birth rates likely explain Peto's paradox insofar as they correlate with body size.

We have modified and used actual life-history tables from various wildlife species, focusing specifically on the beaver as our reference point for drawing comparisons. For this species, our estimate of mortality from cancer is much less than 10%, and only reaches higher levels in our elephant and human models. But even for these examples, the per year rate of cancer mortality is small and only rises substantially in the older age classes. This suggests that cancer suppression is effective within the normal life history of wildlife species and that high incidences of cancer should only manifest in zoos (unusually long-lived individuals), inbred populations or certain polluted environments. Hence, low levels of cancer in wild populations do not mean that cancer or the threat of cancer has been evolutionarily or ecologically unimportant [32].

Prior mathematical models of Peto's paradox have generally accepted the assumption that cancer initiation results from a fixed number of critical mutations. In this context, the models demonstrate an accelerating and tight allometry between body size and cancer incidence [5]. A population genetics model considered two cancer-suppression traits, tumour suppressor genes and oncogenes, and demonstrated these ‘tools' could be used in often non-intuitive combinations to provide greater protection for larger animals [33]. Fig. 2 in [33] provides a conceptual framework for integrating multiple environmental, ecological and life-history features that may influence the evolution of cancer-suppression adaptations. In the spirit of this framework, we developed a life-history model based on the Euler–Lotka equation to evaluate the optimal level of cancer suppression.

As anticipated by Roche et al. [33], we find Peto's paradox has multiple facets. Some of the dynamics are expected. For example, we find the adaptive value of cancer suppression (and, of course, the likelihood of dying from cancer over one's lifetime) increases with the probability of death from cancer and the rate at which this propensity increases with age: parameters Q and a, respectively. These are the original parameters of Peto's paradox which proposes the reasonable assumption that, based on cell numbers, an elephant should have lower values of Q and higher values of a than a meadow vole.

An unknown but potentially important factor of Peto's paradox is the evolutionary trade-off between the cost and benefit of cancer suppression. If, for example, cancer suppression reduces fertility, then organisms must balance the likelihood of dying from cancer with the fecundity cost of cancer suppression (parameter b). This fecundity cost may vary primarily with taxonomic group, and we can speculate that this cost is higher for endotherms (birds and mammals—high metabolisms) than for ectotherms (molluscs, reptiles and fish—low metabolism).

In terms of life-history attributes, all else being equal, we find cancer-suppression adaptations should be of greater adaptive value for organisms with Type III than Type I survivorship curves. That is cancer-suppression adaptations should be most evident in large reptiles and fishes in which the probability of death decreases with age when compared with large mammals in which the probability of death increases with age. Similarly, delayed maturation, low fecundity rates and fecundities that increase with age should all select for higher cancer suppression and lower likelihoods of cancer mortality. Interestingly, this places naked mole rats, long-lived molluscs, large reptiles and large fishes into the most promising taxa for investigating novel and extreme cancer-suppressing adaptations.

Our model is intentionally agnostic on the actual cancer-suppression mechanism. We agree with Nunney [31] that cancer initiation and suppression are likely polygenic, highly variable among taxa, and may be best approximated as a quantitative trait. Furthermore, these adaptations are likely diverse and sometimes subtle. For instance, the separation of germ from somatic cell lines, the stem cell versus cell differentiation systems, telomere length and degradation, apoptosis, cell size and metabolism, and the Rube–Goldberg like design of mammalian immune systems may all be or have elements of cancer suppression [19,34]. These are in addition to the more familiar systems built around oncogenes and tumour-suppressor genes [35].

Like Roche et al. [33], we assumed that cancer-suppression traits represent a trade-off between survivorship from cancer and a loss in fecundity. But other trade-offs have been suggested including immunity from other diseases and pathogens [20], survival while young versus survival while aged [18,19], and starvation. Our model could be extended to consider a trade-off between age-specific survivorship from cancer versus survivorship from other mortality factors. Furthermore, our cancer-suppression strategy was assumed to be static and a fixed property of the organism. However, the anti-cancer strategy and the parameters of the model may themselves be age-dependent. For instance, in organisms with a Type III survivorship curve (large fishes and reptiles), cancer-suppression adaptation may be low early in life and increase with age, whereas the opposite might be adaptive for Type I survivorship (whales and elephants). The effect of age on the incidence of cancer (parameter a in our model) may be age-dependent and decline with old age as the number of cell divisions and wound healing decline, perhaps explaining the drop in cancer incidences in elderly humans.

What of humans? The model supports the idea that cancer will in general be a disease of old age. In humans, this may be exacerbated by an evolutionary mismatch between the adaptive level of cancer suppression in pre-industrial environments and the current life history of modern humans. Indeed, we present evidence from a life-history table for primitive humans that suggest Homo sapiens evolved a level of cancer suppression considerably smaller than that of elephants, whales and even naked mole rats. This would likely have been adaptive and sufficient to result in low incidences of cancer (less than 10%) given the life history of primitive humans. Thus, human cancer incidence is likely an inevitable consequence of life history, evolutionary mismatch and living far beyond the age of last reproduction (although inclusive fitness effects of grandparents throughout human evolution may produce effective fecundity well past actual fecundity [36]). Thus, our model predicts that the once-upon-a-time adaptive level of cancer suppression in humans is now insufficient to prevent, in the absence of medical intervention, a high lifetime risk of cancer in our modern world, a fact readily confirmed by the burgeoning cancer rate in the modern era.

As prospectus, our model points to a number of promising research avenues. In bio-prospecting for cancer-suppression adaptations, long-lived mammals with fecundity well into old age (elephants, bowfin whales and naked mole rats) remain excellent subjects. However, our models demonstrate that long-lived molluscs, large reptiles (crocodiles) and fishes (groupers) will also maintain extensive cancer-suppression adaptations by virtue of high life expectancies, Type III survivorship curves, and possible roles for ectothermy [37]. However, strategies for bio-prospecting should also be mindful of other dynamics as cancer-suppression adaptations may be age and/or organ specific and subject to diverse trade-offs with other life-history properties [3]. In conclusion, we hope for a lockstep between more complete mathematical treatments of the evolution of cancer suppression and empirical evidence to refute or inform these models.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Funding statement

Financial support came from grant no. 1U54CA143970-01 from the Moffitt Cancer Center PSOC, NIH/NCI and a grant from the McDonnell Foundation.

Authors' contributions

R.A.G., J.J.C. and J.S.B. designed the study. J.J.C. performed the computational experiments. R.A.G., J.J.C. and J.S.B. wrote the manuscript.

Competing interests

We have no competing interests.