Peto's paradox and human cancers

Abstract

Peto's paradox is the lack of the expected trend in cancer incidence as a function of body size and lifespan across species. The leading hypothesis to explain this pattern is natural selection for differential cancer prevention in larger, longer lived species. We evaluate whether a similar effect exists within species, specifically humans. We begin by reanalysing a recently published dataset to separate the effects of stem cell number and replication rate, and show that each has an independent effect on cancer risk. When considering the lifetime number of stem cell divisions in an extended dataset, and removing cases associated with other diseases or carcinogens, we find that lifetime cancer risk per tissue saturates at approximately 0.3–1.3% for the types considered. We further demonstrate that grouping by anatomical site explains most of the remaining variation. Our results indicate that cancer risk depends not only on the number of stem cell divisions but varies enormously (approx. 10 000 times) depending on anatomical site. We conclude that variation in risk of human cancer types is analogous to the paradoxical lack of variation in cancer incidence among animal species and may likewise be understood as a result of evolution by natural selection.

1. Introduction

All else being equal, the probability of obtaining at least a single invasive cancer over an organism's lifespan should scale with the number of ‘targets’—that is, cell number, cell lifespan and the number of cell divisions. Peto's paradox is the lack of such a relationship [1] and is good evidence that over the millions of generations of multicellular evolution, natural selection has provided species with levels of cancer protection that are proportional to their body masses and lifespans [2–5]. Several articles in this Special Issue present background and new results on some of the causes, protection mechanisms and emergent patterns. Far less studied is the extent to which this phenomenon is obtained within a species [6]. That is, do different cell lineages within an organism show differing levels of cancer protection based on their relative vulnerabilities (e.g. total stem cell number, stem cell division rate, mutagenic exposure) and associated cancer mortality risks for the whole organism? To the extent that cancer is a selective force on differential resistance between cell lineages, such resistance, being a priori costly to evolve, may also result in constraints on the evolution of body plans, an aspect of Peto's paradox that has rarely been investigated [7,8].

Here, we use the lens of evolution to re-evaluate and reinterpret the data and results of a recent study by Tomasetti & Vogelstein [9] (hereafter T&V), who explored possible sources of variation in risk between cancer types. We show that ca 50% of variation in cancer risk is due to tissue size, indicating that, independent of stem cell divisions, larger tissues are more likely to harbour cancers than smaller tissues. A simpler measure of T&V's extra cancer risk (a classification of cancers most likely to be caused by carcinogens) yields similar findings to these authors, with some notable differences. Moreover, when using the total number of stem cell divisions as a metric for cancers that are not typically the result of disease or carcinogenic exposure, and employing additional data sources, we find that lifetime cancer risk per tissue plateaus at approximately 0.3–1.3% for the cases in an augmented dataset. We further demonstrate that most of the remaining variation in cancer risk can be explained by grouping cancers by anatomical site (e.g. pancreas, bone and intestine) and that each site has a very different risk per stem cell division. Our study indicates new directions for research in showing how tissue characteristics may independently explain variation in cancer incidence. We hypothesize that evolution by natural selection has occurred on cancer prevention at different anatomical sites in humans as the underlying driver of overall pattern, analogous to variation in cancer incidence across species, i.e. Peto's paradox.

2. Results

Tomasetti & Vogelstein [9] found a correlation between cancer risk per tissue and the lifetime number of stem cell divisions (lscd) within the tissue for a set of 31 cancer types. They concluded that most of the variation in risk among cancer types could be explained by random ‘bad luck’ mutations. Furthermore, the authors assessed the remaining variation in cancer risk due to external environment and inherited factors, which they quantified with an extra risk score (ERS). Cancers with high ERS are indeed known to be associated with carcinogenic exposure (fig. 2 in [9]). Below, we reinterpret their results through new statistical analyses and then reanalyse their dataset with several new additions to assess signatures of natural selection for cancer prevention.

(a). Independent contributions of division rate and stem cell number

Tomasetti and Vogelstein calculated the total lscd as s(2 + d) − 2, where s is the size of the organ's stem cell population, and d is the lifetime number of divisions per stem cell. They then tested for a correlation between lscd and lifetime risk of cancer. One way in which their analysis could be extended is to differentiate the individual contributions of s and d to cancer risk [10,11]. For instance, a small stem cell population with many replications (e.g. oesophageal cells) may have the same lscd as a large stem cell population with few replications (e.g. lung cells, see electronic supplementary material, table S1, in [9]). However, in the former case, cancer risk may result mainly from replication errors, while the latter has a considerably larger number of cells potentially exposed to carcinogenic environments at any point in time.

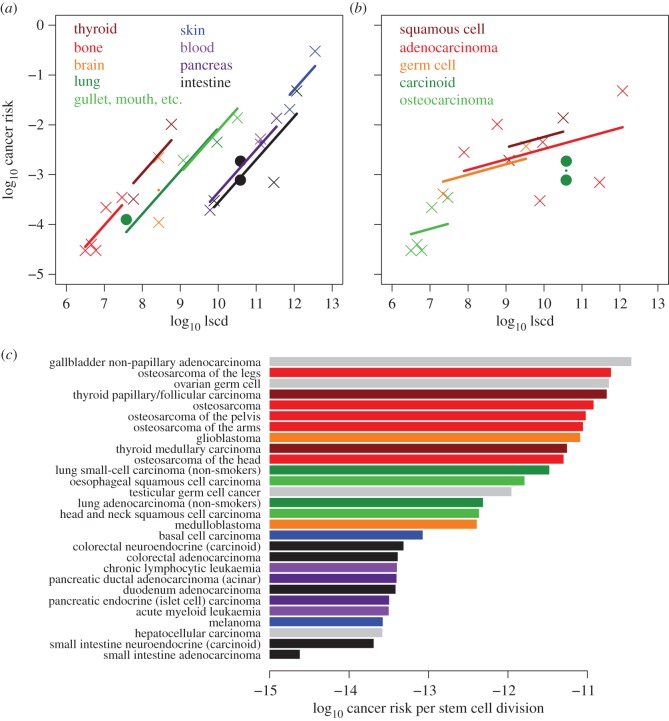
We conducted a multiple regression analysis with cancer risk as the response variable, and log(d + 1), log s and the interaction of log(d + 1) and log s as the explanatory variables. There was no significant correlation between the two explanatory variables (r = 0.16, n = 31, p > 0.3), indicating that variation in s is largely independent of variation in d. The multiple regression revealed significant positive effects of both log s and log(d + 1) on cancer risk (F_1,27 > 18, p < 0.0002); the interaction between log s and log(d + 1) was not significant (F_1,27 = 0.21, p > 0.6). Overall, as expected, the model explained 65% of the variation in cancer risk, which is identical to the estimate for the composite lscd in Tomasetti & Vogelstein [9]. To test the effect of stem cell number on cancer risk, independently of division rate, we first regressed cancer risk on s, and then performed a partial regression of residual cancer risk on d. The aim was to remove effects of stem cell number and so obtain the ‘pure’ effect of division rate. When correcting for effects of s in this way, stem cell division explains 40% of the variation in risk (figure 1a). This division rate effect is weaker than that found by T&V, because our analysis is based on replications per stem cell rather than over the population of stem cells. Conversely, tissue stem cell number explains 44% of the variation after correcting for stem cell division rate (figure 1b). Figure 1c depicts the combined positive effects of log(d + 1) and log s: cancer risk increases with both increasing stem cell number and replication in the organ.

Figure 1.

Relationships between the number of stem cells per tissue (s), the lifetime number of replications per stem cell in that tissue (d) and lifetime cancer risk, across 31 cancer types (data from electronic supplementary material, table S1, in [9]). (a) Relationship between stem cell replication (d) and cancer risk, after statistically correcting for the effect of stem cell number (s). This correction was done by regressing cancer risk on s, and then performing the partial regression of residual cancer risk on d. The r² value is the square of the partial regression coefficient and quantifies the amount of variation in residual cancer risk explained by stem cell division rate. (b) Relationship between stem cell number (s) and cancer risk, after statistically correcting for the effect of stem cell replication (d). The partial r² quantifies the variation in residual cancer risk explained by stem cell number. (c) Illustration of the combined positive effects of stem cell number (s) and stem cell replication (d) on predicted cancer risk. Predicted values were obtained from the multiple regression of cancer risk on d and s (see text). In 0.5 log-intervals, we assigned a colour gradient to the predicted values, ranging from light orange (low predicted risk) to dark red (high predicted risk). Thus, cancer risk increases with increasing values of both s and d. All analyses and figures use log-transformation of s, d and cancer risk. The black lines in (a,b) represent regression lines, and the shaded areas the 95% confidence intervals around the regression. Colour-coding of points based on fig. 2 in [9], denoting deterministic D-tumours (blue) and replicative R-tumours (green).

Based on our regression model, we propose a simple alternative evaluation of the replication-independent ERS. Whereas T&V calculate the ERS as the product of the logarithms of lifetime risk and total stem cell replications, we use the residual lifetime risk, describing the difference between observed and predicted values from the regression (figure 1c). Like the ERS, our more intuitive method identifies a subset of cancers that occur more often than we would expect from the lscd, including most of those that T&V classed as deterministic D-tumours (figure 2, blue bars). Of equal importance for understanding possible causation, the residual lifetime risk also quantifies the extent to which some cancer rates are lower than expected. Carcinomas of the small intestine, duodenum and pancreas are more than ten times less frequent than one would predict from the total number of stem cell divisions (figure 2, red bars), and these three cancer types appear as outliers in the residuals distribution and quantile–quantile plots (not shown). We note that very similar results can be obtained using the residuals from the regression of risk against lscd, as has been proposed by Tomasetti & Vogelstein [12] and Altenberg [10] since the publication of Tomasetti & Vogelstein's initial article [9].

Figure 2.

Residual lifetime risk of 31 cancer types, calculated as the difference between observed values and predictions of our multiple regression model (figure 1a,b). Most of the cancers that T&V classed as deterministic D-tumours (blue bars) also have high residual risks according to our alternative metric, compared to the cancers that T&V classed as replicative R-tumours (green and red bars). Many cancers with high residual risks are associated with known causative factors (oncoviruses, chemical carcinogens or inherited cancer susceptibility genes). The additional identification of cancers with very low residual lifetime risks (red bars) suggests that some tissue types may be differentially resistant to tumours.

(b). The saturation of cancer risk

The above analysis separating the effects of s and d revealed significant, independent effects of these variables in explaining variation in cancer risk in the T&V dataset. The relatively shallow gradients of the linear regression models present a challenge to the hypothesis that the variation in cancer risk is largely due to differences in lifetime numbers of stem cell divisions. We next consider in more detail the shape and interpretation of the relation between the composite index, lscd and cancer risk.

If the risk per cell division were the same for every tissue, then

2.1

where C is the risk per stem cell division. If C ≪ 1 and cancer risk ≪1 (which holds for almost all of the T&V data), then this relationship can be re-expressed (using the binomial approximation) as

2.2

Equivalently,

2.3

which means that the slope of the linear regression models should be approximately unity. As the gradient of the one-factor linear regression model of T&V is only 0.53, the risk per stem cell division cannot be the same for all tissues. Indeed, the risk per stem cell division decreases approximately linearly with lscd, as shown in figure 3. The unexpectedly shallow gradient of the correlation between cancer risk and lscd has been noted before [10,12] but has not, in our view, been sufficiently investigated.

Figure 3.

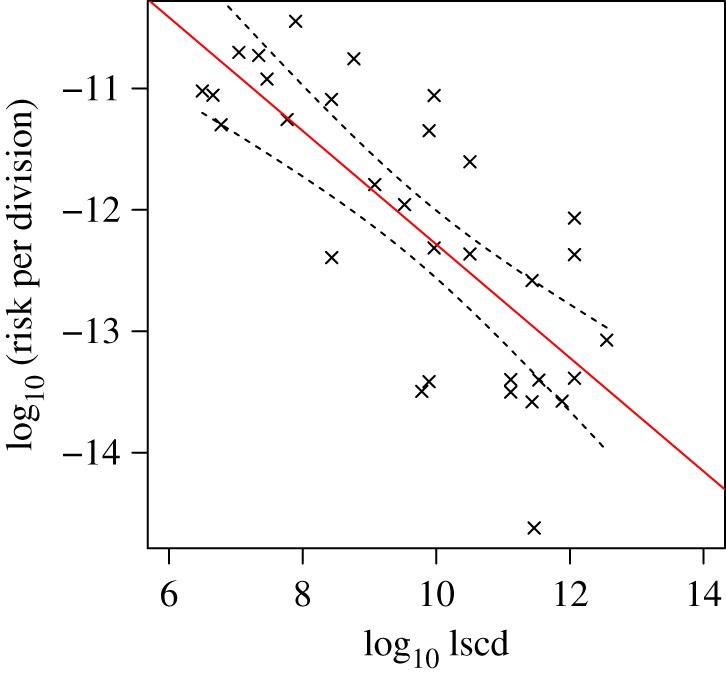
Relationship between cancer risk per stem cell division (risk/lscd) and lscd in 31 cancer types. The negative correlation contradicts the hypothesis that the cancer risk per stem cell division is the same for all tissues (in which case the line would be flat, with gradient zero). Dashed lines show 95% confidence intervals for the linear regression (R² = 0.58, p < 10⁻⁶). (Online version in colour.)

We propose that the observed relationship between cancer risk and number of stem cell divisions can be partly explained by the saturation of cancer risk at a maximum level substantially less than 100%. There are at least two (non-mutually exclusive) reasons to expect such a saturating effect. First, different causes of mortality (e.g. cancers, heart disease, cerebrovascular disease, accidents) each have a characteristic probability distribution as a function of age. Because of the primacy of mortality events, increases in the probability of a given mortality type will tend to be reflected as increased incidence as the age at which that event occurs decreases. Thus, all else being equal, a given source of mortality will not exceed approximately 1/N, where N is the total number of possible attributed, independent causes of mortality. Of course, all else is not equal, but nevertheless we would expect a saturation effect as the cancers in T&V's dataset tend to be life threatening at older ages (and therefore have less primacy). Second, tissues that are especially vulnerable to life-threatening cancers would be expected to evolve stronger means of protection [6]. That all tissues do not employ the same protection mechanisms would be suggestive of either a fitness cost of cancer protection to the organism (i.e. that the cost of added protection in terms of reductions in survival and reproduction outweighs the benefits of lowered risks of life-threatening cancer), or that the phylogenetic emergence of tissue-specific protection was somehow linked with tissue differentiation occurring during ontogeny. Therefore, for either or both hypotheses, we would expect the gradient of the correlation between risk and lscd to become shallower with increasing lscd, as illustrated in figure 4.

Figure 4.

A hypothetical one-factor, nonlinear model of the relationship between cancer risk and lscd. If each stem cell division has the same probability of causing cancer, then there should be a linear relationship between cancer risk and lscd with a gradient of unity. However, we argue that the risk cannot rise indefinitely, but must be bounded by a maximum limit, either due to the primacy of other causes of mortality and/or due to differential cancer prevention in tissues with larger total numbers of stem cell divisions. (Online version in colour.)

A simple model that is consistent with these assumptions is

2.4

where y is log(cancer risk) and x is log(lscd). For small x, this function approaches y = x + b (slope = 1), and for large x, it approaches y = −log a (slope = 0). We used a least-squares method to fit the nonlinear model to data (using the nls function in the R statistical language [13]).

Figure 5a shows the result of fitting the above model to the data for all 31 cancer types in the T&V dataset and three additional neuroendocrine cancers (small-cell lung carcinoma, and colorectal and small intestine carcinoids—see electronic supplementary material for data and sources). According to this model, most of the types with higher than expected risk belong to subpopulations exposed to carcinogens (hollow circles in figure 5a). These include lung cancer in smokers, intestinal cancer in those with certain inherited genetic alterations, liver and head and neck cancer in those infected with an oncovirus, and basal cell carcinoma, which is generally correlated with a combination of genetic factors and UV-light exposure, and which is very rarely fatal [14].

Figure 5.

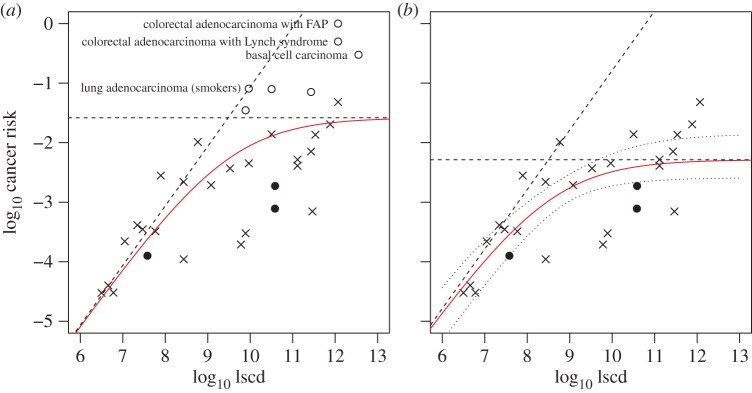
(a) Relationship between cancer risk and lscd in 34 cancer types, described by a model that assumes that the gradient of the correlation is unity for small lscd and is zero for large lscd. Data from T&V are shown as crosses or hollow circles; additional data are shown as filled circles. The model asymptotes are included as dashed lines. (b) The same model fitted to the set of 27 cancer types not associated with a high-risk subpopulation (the excluded data points are shown as hollow circles in (a)). Dotted lines indicate the approximate 95% confidence interval of the regression curve. (Online version in colour.)

When the risks related to specific subpopulations are omitted from the T&V dataset, as expected, the lifetime risk per cancer type saturates at a lower level. In the extended dataset with three additional cancer types, the saturation level is approximately 0.5% (95% CI: 0.3–1.3%, figure 5b). Moreover, the additional data points (filled circles in figure 5b) do not change the model fit. Therefore, all of the data appear to be consistent with a model in which the risk of life-threatening cancer increases with lscd with a slope of unity, until it is bounded by a threshold of ca 0.3–1.3%, i.e. well below the theoretical maximum of 100%. The fit of this model is statistically similar to that of the linear model (residual standard errors 0.59 and 0.58, respectively), and, as in the preceding analysis, s and d have independent, non-correlated statistical effects on variation in cancer risk in the alternative dataset (p < 0.005). However, the nonlinear model is more biologically plausible, and it may therefore reveal more about the multiple factors that determine cancer risk, including natural selection.

(c). Variation between tissues

We have shown that tissues with higher numbers of stem cell divisions generally have a lower risk of cancer per stem cell division. However, one would also expect cancer risk per stem cell division to be approximately constant within sets of related tissues, which are likely, though not certain, to have similar protection mechanisms. By splitting the data into subsets of similar cancer types, we should be able to divide the variation in risk into two parts (figure 6). If the members of each subset indeed have similar cancer risk per stem cell division then variation within subsets will be mostly due to lscd, whereas variation between subsets will be related to tissue type and/or environment (e.g. mutagens).

Figure 6.

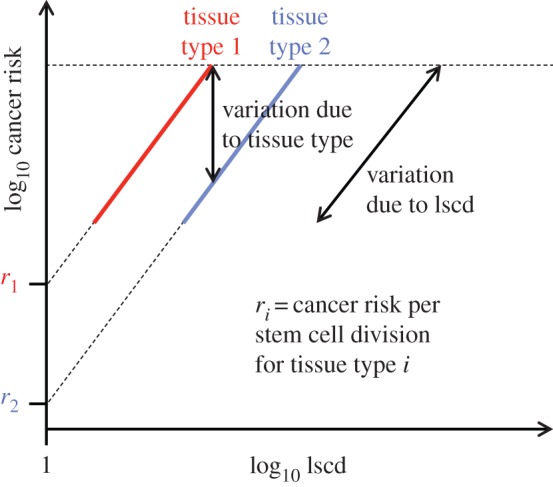
A two-factor, linear model of the relationship between cancer risk and lscd. In this case, the cancer types are divided into subsets according to tissue type. The subsetting partitions variation into within-subset variation (due to lscd) and between-subset variation (due to tissue type). The gradient of the correlation within subsets is expected to be close to unity. The dashed line indicates a hypothetical maximum risk threshold. For each tissue type, the cancer risk per stem cell division can be estimated by extrapolating the regression line to the point where lscd = 1 (i.e. log lscd = 0). (Online version in colour.)

In particular, if we assume that carcinogenesis requires a sequence of M mutations and C is the risk per stem cell division, then

2.5

as discussed by Nunney & Muir [15]. Thus,

2.6

If division rates d and numbers of mutations M are similar within each subset, then the ratio of risks for two cancer types is given by

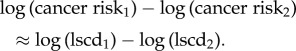2.7

Therefore, the slope of the regression line for each subset will be approximately unity, and the cancer risk per stem cell division (i.e. the risk of having acquired all necessary mutations, relative to lscd) will be approximately the value at which each regression line intercepts the vertical axis (i.e. log lscd = 0, figure 6).

We hypothesized that cancer risk per stem cell division might be associated with either anatomical site or the cell type of the transformed tissue. We first divided the cancer types by anatomical site (electronic supplementary material, table S1), according to the topographical codes in the International Classification of Diseases for Oncology (ICD-O) [16], which is widely used in clinical diagnosis. We included data for three neuroendocrine cancers not considered by T&V, but excluded six cancer types affecting particular groups (lung cancer in smokers, intestinal cancer in those with certain inherited genetic alterations, and liver and head and neck cancer in those infected with an oncovirus). We then fitted a two-factor regression model to the subsets containing at least two data points (nine subsets, 24 cancer types). According to this model, for each cancer type i,

2.8

where A is the gradient of the linear regression line (assumed to be the same for all subsets), and B is the intercept (which depends on the subset). Therefore, there are nine parameters to be estimated (one slope and eight subset-specific intercepts).

The two-factor regression model explains most of the variation in cancer risk not explained by the model of T&V. For the extended dataset, the model explains 89% of the variation in cancer risk among 24 cancer types (F_9,14 = 12.7, p < 3 × 10⁻⁵, figure 7a). Log lscd by itself explains 68% of the variation, similar to the figure for the set of 31 cancer types analysed by T&V, whereas the anatomical subset factor explains an additional 21% (subset effect: p = 0.02). Supporting this finding, the risks for three cancer types not considered by T&V (filled circles in figure 7a) are almost exactly as predicted. There is no significant interaction between the log lscd and subset factors (p = 0.37). Furthermore, the gradient within the subsets is 0.86, with standard error 0.14, and is therefore, as predicted, not significantly different from unity. An alternative model that assumes the gradient for each subset is exactly unity also explains 89% of the variation (F_8,15 = 15.9; subset effect: p < 10⁻⁵).

Figure 7.

(a) Relationship between cancer risk and lscd in nine topographically defined subsets of 24 cancer types (electronic supplementary material, table S1). The model assumes that the risk per stem cell division may differ between subsets but that the slope of the correlation is the same for each subset. Data from T&V are shown as crosses; additional data are shown as filled circles. (b) Relationship between cancer risk and lscd in five morphologically defined subsets of 17 cancer types (electronic supplementary material, table S2). (c) Cancer risk per stem cell division for 28 cancer types, calculated by dividing risk by lscd. This formula assumes that the correlation between risk and lscd has a gradient of unity for each tissue type, which is supported by the results of the regression model (equation (2.8)). Cancer types are coloured by topographic subset, according to the scheme shown in (a). Four types that belong to topographic subsets with only one member (and so excluded from the analysis shown in (a)) are shown in grey.

Note that we chose to include skin cancers in this analysis even though most of the skin cancer risk in the T&V dataset is associated with UV-light exposure [17]. As UV-light exposure is assumed to increase the mutation risk per stem cell, we would expect this environmental factor to shift the regression line for the skin cancer subset upwards, towards higher cancer risk, but we would still expect the slope to be approximately unity. Indeed, the model fit for skin cancer is similar to that for the other subsets (figure 7a).

Much of the remaining variation is due to the brain cancer subset, but it can be argued that this subset is poorly defined. Whereas glioblastoma typically develops in the mature brain, medulloblastoma is considered to originate in the different environment of the early embryo [18], and it is the only cancer in the T&V dataset that predominantly occurs during childhood (median age 9 years at diagnosis). When the brain cancer subset is excluded, the two-factor regression model explains 92% of the variation (F_8,13 = 18.8) and the subset factor has a more significant effect (p = 0.005).

Apart from brain cancers, there is only one cancer type that substantially deviates from the topographical subsets model: although colorectal and duodenum adenocarcinomas lie almost exactly on a line of slope unity (also grouping with pancreatic cancers), small intestine adenocarcinoma falls well below this line, being approximately ten times less common than predicted. Therefore, testable predictions of our model are that (i) small intestine adenocarcinoma differs in some important way from the four other intestinal cancers (colorectal and duodenum adenocarcinomas, and colorectal and small intestinal carcinoids); (ii) that these tissues have much greater than expected levels of cancer prevention; and (iii) that the estimated lscd or incidence for this cancer type is inaccurate.

We also divided the data according to ICD-O morphological code, which describes the cancer cell type. This resulted in five subsets containing at least two data points, which together included 17 cancer types (electronic supplementary material, table S2). In the two-factor regression model (equation (2.8)), the morphological subset factor is not significant (p = 0.32). Therefore, we found no evidence that cancer risk in this dataset is related to cell type, independently of anatomical site (figure 7b). Nevertheless, as topography and morphology are moderately correlated in the T&V dataset, our results do not rule out a combined effect.

Given that the gradient of the correlation between cancer risk and lscd appears to be close to unity for each topographical type, we can calculate

2.9

The estimated risks per stem cell division for each individual cancer type are shown in figure 7c. These estimated risks vary by nearly four orders of magnitude—from less than 10⁻¹⁴ for small intestine adenocarcinoma, to approximately 10⁻¹¹ for osteocarcinoma and thyroid cancers. An untested hypothesis to explain this variation is that the number of genetic or epigenetic alternations required to obtain cancers typical of different anatomical sites, differs in characteristic ways (see also Nunney & Muir [15]).

In sum, variation in cancer risk in the dataset of T&V can be explained by the total number of stem divisions (lscd; [9]), but can also be understood as variation explained by tissue size and by variation in cancer risk per stem cell division (this study). When using the composite quantity lscd and only considering cancers that are not linked to heredity, disease or mutagenic exposure, we find that anatomical site explains most of the residual variation.

3. Discussion

Despite limitations in the Tomasetti and Vogelstein dataset [9], it contains a wealth of information that goes beyond their initial analysis. We have made four new findings based on their dataset, and we have verified that these findings are consistent with additional data. First, the total number of stem cells and the lifetime number of divisions per stem cell each significantly, and independently of one another, explain variation in lifetime risk of cancer (figure 1). Indeed, our finding of a significant correlation of s with cancer risk is consistent with the prediction that cancer incidence increases with the standing population size of an organ [19,20]. One possible mechanism for the tissue size effect is mutations associated with the 2s cell divisions during ontogeny for certain tissues [21]. Second, our more intuitive measure of extra cancer risk yields results that largely concord with T&V, but also yield certain notable differences (figure 2). Third, when assessing a subset of 27 cancers that are not primarily linked to pathogens, disease or carcinogenic exposure, we find a saturating effect of total stem cell divisions on cancer risk, with a plateau at about 0.3–1.3% (figure 5). This could be explained either by the primacy of mortality events limiting maximal mortality for any single type of event and/or increased cancer prevention mechanisms in tissues with the most total stem cell replications. Fourth, when dividing a subset of 24 cancers by anatomical site, we find that each type shows the same slope of approximately unity, but is displaced over four orders of magnitude in risk per stem cell division, consistent with the hypothesis that different tissues have contrasting protection mechanisms against cancer. Data for three neuroendocrine cancers, which were not considered by T&V, closely fit the predictions of this model. Our findings are consistent with the hypothesis that natural selection has resulted in differential cancer prevention in different anatomical sites [6], and to the best of our knowledge is the first such analysis for any cellular disease. We briefly discuss the implications of these findings below.

Our analysis clarifies one of the main findings of Tomasetti & Vogelstein [9]: variation in cancer risk is statistically explained by the independent effects of stem cell division rate (d) and stem cell number (s). Our analyses indicate, both for the full T&V dataset and for a dataset of cases that are a priori least likely to be derived from mutagenic exposure, that both s and d significantly contribute to explaining most of the variation in cancer risk, and variation explained by s and d are approximately equal in the full T&V dataset. We hypothesize, however, different relative contributions of d and s to explain variation in risk of cancers significantly associated with mutagenic effects (e.g. certain cancers with high ERS). Specifically, mutagenic exposure may result in stem cell death and replacement by mutated daughter cells [22]. Thus, we predict that the incidence of mutagen-derived cancers should significantly correlate with the number of standing ‘targets’ (s), and little or not at all with differences in stem cell division rates (d) between anatomical sites. We were not able to test this hypothesis, not only because of the small number of cases in the T&V dataset, but also because mutagenic exposure is likely to vary considerably both within and between anatomical types.

We have further shown that when considering the total number of stem cell divisions as a single metric that explains most of the variation in cancer risk, the remaining variation can be significantly explained by anatomical site, corresponding to the biological setting in which cancer arises. The pattern is consistent with differential cancer risks per stem cell division, such that in anatomical sites that harbour a relatively large number of stem cell divisions, each division event entails a relatively low risk of contributing to carcinogenesis. Our results therefore suggest that variation in cancer risk across human tissues is analogous to Peto's paradox, which is the observed lack of variation in cancer risk across animal species with different body masses and/or lifespans [1–4]. However, the inter-tissue relationship is not flat as in the interspecific comparison, but appears to be an increasing, saturating function. Most of the hypotheses proposed to explain Peto's paradox invoke the evolution of stronger cellular or tissue-level cancer prevention in larger and longer lived animal species (reviewed in [3]). Likewise, our results are consistent with a related conjecture of Peto [1] that tissues with high levels of stem cell turnover, such as the lining of the small intestine, might have evolved especially powerful anti-cancer mechanisms. For example, a larger number of mutations might be necessary to initiate cancer in such tissues ([15]), or tissue architecture might act to contain precancerous growths [1]. Most of the cancer types in the dataset occur at older ages and, as has been argued previously (e.g. [4]), such cancers would be largely shielded from present-day natural selection. Natural selection for cancer prevention is consistent with observations of occurrence at post-reproductive ages, yet maintaining the evolved protection mechanisms that reduce incidences at younger ages [4,23]. Our analysis with an extended dataset confirms our preliminary findings for the T&V dataset [11] and tests more recent predictions [24].

We have shown how simple rules (effects of total number of stem cell divisions and anatomical site) can predict variation in cancer risk with high confidence, when looking across cancer types. By extension, we speculate that the same rules also hold across individuals: having more stem cell divisions in a given anatomical site would then put an individual at greater risk for cancer originating at that site. We have not investigated whether variation in the total number of stem cell divisions between individuals is predictive of cancer risk, but some studies are suggestive of this type of effect (e.g. [4,20,25,26]). Thus, to the extent that a given individual is potentially more prone to certain cancers based on more expected lifetime stem cell divisions, this can be regarded as a risk factor.

Future research should extend Tomasetti and Vogelstein's dataset to other tissue types and cancer types within tissues (most notably high incidence cancers of the breast and prostate). Moreover, we need to identify possible tissue-specific mechanisms of cancer prevention to test the hypothesis that natural selection has influenced not only age-related patterns in cancer incidence, but also tissue-specific adaptations and cancer as a possible evolutionary constraint on tissue size [7,8].

Competing Interests

We declare we have no competing interests.

Funding

This work was supported by grants from the Agence National de la Recherche (EvoCan ANR-13-BSV7-0003-01) and ITMO (‘Physique Cancer’ (CanEvolve PC201306) to M.E.H.