Patient-specific Modeling of Cardiovascular Mechanics

Abstract

Advances in numerical methods and three-dimensional imaging techniques have enabled the quantification of cardiovascular mechanics in subject-specific anatomic and physiologic models. Patient-specific models are being used to guide cell culture and animal experiments and test hypotheses related to the role of biomechanical factors in vascular diseases. Furthermore, biomechanical models based on noninvasive medical imaging could provide invaluable data on the in vivo service environment where cardiovascular devices are employed and the effect of the devices on physiologic function. Finally, the patient-specific modeling has enabled an entirely new application of cardiovascular mechanics, namely predicting outcomes of alternate therapeutic interventions for individual patients. We will review methods to create anatomic and physiologic models, obtain properties, assign boundary conditions, and solve the equations governing blood flow and vessel wall dynamics. Applications of patient-specific models of cardiovascular mechanics will be presented followed by a discussion of the challenges and opportunities that lie ahead.

INTRODUCTION

At every stage of the circulatory system, whether blood is swirling in the heart or streaming through the arterial tree, a range of mathematical models have been employed to quantify biomechanical conditions. These models, ranging from lumped parameter, one-dimensional wave propagation, and three-dimensional numerical methods, can all be used with effect to describe cardiovascular mechanics. Computational methods were first applied to compute velocity and pressure fields in idealized, generic models of vascular anatomy and physiology. With the development of modern three-dimensional imaging techniques, especially magnetic resonance and computed tomography imaging, it is now possible to quantify cardiovascular mechanics in subject-specific anatomic and physiologic models.

Development of image-based modeling technologies for simulating blood flow began in the late 1990s (1-3). Since that time, many groups have developed and utilized these techniques to investigate the pathogenesis of occlusive and aneurysmal disease in the carotid artery (4, 5), the coronary arteries (6), the aorta (7), and the cerebral circulation (8-10). Patient-specific modeling techniques have also been applied in solid mechanics analyses to predict rupture risk of aneurysms (11).

Furthermore, patient-specific models of cardiovascular mechanics can play an important role in the development of medical devices. The design and evaluation of medical devices necessitates gathering information on the clinical problem that needs to be solved and the intended function of the device, the dynamic, three-dimensional anatomy of the portion of the body where the device will be deployed and the anatomic variability between subjects, the forces the body exerts on the device under a range of physiologic conditions, the mechanical performance of the device when subject to repetitive in vivo forces, and the biological and mechanical impact of the device on the body. Biomechanical models based on noninvasive medical imaging could provide invaluable data on the in vivo service environment where devices are employed and the effect of the devices on physiologic function. At present, medical device manufacturers have little information on anatomic variations, arterial deformation and biomechanical forces in the vascular system needed for the design of stents for occlusive disease and stent grafts to isolate aneurysms.

Finally, the construction of subject-specific geometric models from medical imaging data has enabled an entirely new application of cardiovascular mechanics, namely predicting changes in blood flow resulting from possible therapeutic interventions for individual patients. Patient-specific modeling of cardiovascular mechanics requires methods to: (i) construct geometric models from three-dimensional magnetic resonance imaging (MRI), computed tomography (CT), ultrasound (US) data, (ii) extract preoperative physiologic data from cine phase contrast MRI, US or cardiac catheterization data (iii) modify the preoperative model to incorporate an operative plan, (iv) assign boundary conditions incorporating upstream heart models and downstream microcirculation models, (v) discretize geometric models using automatic mesh generators, (vi) solve the equations governing blood flow and vessel wall dynamics, and (vii) visualize and quantify resulting physiologic information. Recent progress in developing patient-specific models of cardiovascular mechanics for treatment planning will be presented followed by a discussion of the challenges and opportunities that lie ahead. In closing, sensitivity analysis, verification and experimental validation of patient-specific models of cardiovascular mechanics will be described.

METHODS OF PATIENT-SPECIFIC MODELING OF CARDIOVASCULAR MECHANICS

Acquisition of Patient-Specific Anatomic and Physiologic Data

Methods for quantifying vascular anatomy for patient-specific modeling of cardiovascular mechanics include noninvasive imaging techniques such as computed tomography (CT), magnetic resonance imaging (MRI), and three-dimensional ultrasound (3DUS) and an invasive method combining angiography and intravascular ultrasound (IVUS). Contrast-enhanced CT and MRI are particularly suited for generating high-resolution volumetric images of many parts of the vascular tree and will be briefly described below. Generally, iodinated contrast is used in CT angiography, and a gadolinium-based contrast agent is used in MR angiography. MRI has the additional advantages of being able to quantify physiologic parameters, including blood flow, wall motion, and blood oxygenation.

MRI is based on spatial localization of signals emitted by material (generally hydrogen nuclei for living organisms) exposed to radiofrequency (RF) magnetic field gradients (12). MR images are formed by applying magnetic field gradients in orthogonal directions to spatially encode the MR signal. A large number of "pulse sequence repetitions" are executed, each collecting a portion of the needed data. In 2D imaging, spins in a thin (e.g. 2-10 mm) slice are excited using selective excitation. In direct 3D acquisitions, thinner contiguous slices can be imaged, and better signal-to-noise ratios (SNR) can be obtained as compared to multiple 2D acquisitions at the possible cost of a longer scan time. Contrast-enhanced MR angiography (CE-MRA) generally utilizes direct 3D acquisitions, allowing for thin slices (~2-3 mm slice thickness) to be acquired with a sufficient signal-to-noise ratio (SNR). CE-MRA, based on fast gradient echo sequences, can be used to acquire a time-averaged volume of data in a single breath-hold. Of particular relevance to using MR data in patient-specific modeling is the need to correct for gradient nonlinearities arising during acquisition to avoid image distortion in the slice direction of the magnetic field, the so called "grad warping" phenomena (13).

CT images are created by acquiring projection x-ray images as the gantry rotates around an object, and then reconstructing cross sections depicting the density variation (attenuation coefficient) in the object. Modern clinical CT allows visualization of detail as small as 0.5 mm in-plane, with a slice thickness that is typically 0.75mm. Temporal resolution, the time required for the acquisition of projection data used to reconstruct an image, is most important for dynamic applications, especially coronary CT angiography. Independent of the reconstruction technique, the temporal resolution is proportional to the gantry rotation period, typically less than 0.5 sec for recent commercial scanners. In cardiac gated imaging, if the cardiac or vascular motion can be assumed to be fairly periodic, data from multiple rotations can be combined to achieve temporal resolution that is well shorter than the rotation period. Advanced reconstruction algorithms can achieve temporal resolutions of less than 100 ms (14), and up to 10 phases can be reconstructed through the cardiac cycle. Note that this technique relies upon quasi-periodicity of the motion.

Systemic and pulmonary blood flow has been measured in vivo extensively using invasive methods. These techniques include utilization of fluorescent microspheres, electromagnetic flowmeters, laser Doppler anemometry, scintigraphy, and catheterization. Unfortunately, fluorescent microspheres, electromagnetic flowmeters, and laser Doppler anemometry are highly invasive, and as a result are not currently used for blood flow measurement in patients. At present, the gold standard for cardiac output quantification uses invasive cardiac catheterization. While these methods enable quantification of average cardiac output, they cannot measure the three-dimensional, pulsatile characteristics of blood flow that are needed in patient-specific models of cardiovascular mechanics relevant to congenital and acquired cardiovascular diseases. The current techniques to measure blood flow non-invasively include Doppler ultrasound, and magnetic resonance imaging (MRI). Doppler ultrasonography can acquire time-resolved blood velocities, however, it cannot resolve a velocity map on an arbitrarily-oriented anatomic plane. Phase contrast MRI (PC-MRI) can non-invasively and concurrently acquire anatomic and 3-direction velocity maps of large vessel anatomy and blood flow, respectively (15-17). The data acquired at each pixel in an MR image represents the "transverse magnetization" and is a vector quantity, i.e., it has a magnitude and phase. Typically, only the magnitude information is used to create an MR image and the phase information is discarded, however, the phase can be used to quantitatively image motion (15-17). To encode flow in the x, y, or z direction, a bipolar gradient pulse can be added to the gradient waveform in that particular direction. To image velocity in a single direction, two phase images are obtained with different values of the gradient first moment in the desired direction. These images are subtracted to remove irrelevant phase effects to produce an image which is proportional to the change in first moment and the velocity. Sensitivity to velocity can be adjusted, and is parameterized by the velocity encoding that produces a phase shift of 180°. Three component vector velocities can be measured by making four measurements (15): one reference, and three where the first moment along x, y, or z are switched. For the high spatial resolution images needed for many applications, all the raw data needed to form the desired images cannot be obtained in a single cardiac cycle. Instead, a large number of pulse sequence repetitions are executed, each collecting a portion of all the needed data. Assuming periodicity, some form of gating or synchronization of these repetitions enables the resolution of motion as a function of time in the cardiac cycle. In the "cine" method, data are collected continuously throughout the cycle, and the data are retrospectively sorted and interpolated to produce a number of frames as a function of time in the cycle. Cine imaging can be combined with PC MRI to generate velocity images as a function of time in the cardiac cycle.

Image segmentation and Image-based geometric modeling

Image segmentation can be defined as the division of an image into meaningful regions. Low-level segmentation techniques, e.g. thresholding and region-growing methods, depend on per-pixel information such as image intensity, while high-level techniques such as split-and-merge, pattern-recognition and texture-based methods, depend on the spatial distribution of data, such as the distribution of image features (18). Geometric segmentation techniques, sometimes referred to as active contours or deformable models, synthesize both low-level and high-level image information and maintain the spatial relationships among image features (19). Geometric image segmentation techniques use deforming contours (curves and surfaces) to detect structures in images. Energy terms (typically one term indicative of the smoothness of the contour and another indicative of how near it lies to gradients in the image) are used to deform the contour while minimizing its energy (19, 20). This approach suffers from two primary drawbacks (21). First, the final segmentation result obtained can be a strong function of initialization. Second, if explicit boundary-tracking methods are used to describe a deforming contour, arbitrary changes in contour topology cannot be handled. Among the refinements developed to address the first drawback was the “balloon force” introduced in (22), which gives an inflationary behavior to the deforming contour. This can enable the contour to move past local minima, making it less sensitive to initialization. In order to address the issue of topological change, Malladi et al. (23) and Caselles et al. (24) successfully applied the “level set” method to the active contour approach. The level set method (see (25)) is an implicit boundary-tracking technique that eliminates many of the difficulties encountered when modeling evolving curves and surfaces with more traditional techniques. It embeds geometry into a scalar field such that the geometry’s evolution can be described with a partial differential equation. A particular strength of the level set method is that it handles arbitrary topological changes and that it can be extended with relative ease to higher dimensions. Several researchers have described the application of level set methods to 3D segmentation problems (23, 26, 27).

Typically, geometric solid models of blood vessels have been constructed by (i) extracting a set of points (a contour) approximating the inside boundary of a vessel on a series of 2D image slices, (ii) interpolating the contour with a curve, (iii) lofting a surface through the interpolated curves and (iv) joining the surfaces together to form a bounded volume. Wang et al. described methods for constructing subject-specific vascular models based on volumetric magnetic resonance angiography (MRA) and computed tomography (CT) images (28). This approach included image segmentation techniques based on the level set method for vascular profile extraction and model construction using surface lofting with axis-normal profiles. Figure 1 depicts a geometric model of an abdominal aorta created using this approach (7).

FIGURE 1.

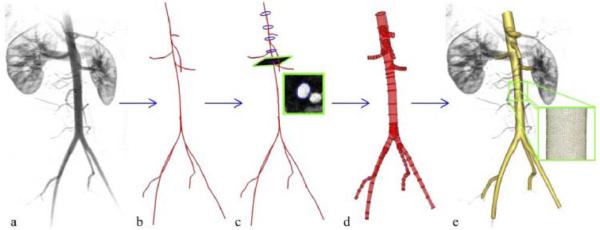
Schematic of solid model construction from imaging data. (a) Volume-rendered image of a contrast-enhanced magnetic resonance angiogram illustrating abdominal aortic anatomy. (b) Centerline paths were created along the vessels of interest. (c) Two-dimensional segmentations of vessel lumen were taken perpendicularly to the vessel path. Segmentations were found using a level set method. (d) Two-dimensional segmentations were lofted to form solid models for each vessel which were then joined to form a complete three-dimensional solid model of the aorta and its branches. (e) The solid model was discretized into a finite element mesh (gold) and is shown with the original volume-rendered magnetic resonance angiogram (7, 104).

A particular advantage of the 2-D segmentation and surface lofting approach is that complex geometries can be created even when there are regions of the volumetric image data with lower signal-to-noise ratio, as occurs in many if not most practical examples. As a result, very complex geometric models with numerous branch vessels can be created (see Figure 3, Figure 5-Figure 7 for examples of models created using this approach). However, this enhanced user control comes at the expense of user time. Specifically, a user must often manually identify the set of imaging slices needed to represent a feature, initialize and fine-tune the segmentation, and evaluate and refine the curve and surface interpolations. This is especially time-consuming at complicated anatomic regions such as vessel branches. The accuracy of current geometric models constructed using these methods can also be an issue since a 3D model is constructed using only local 2D information from the inherently 3D volumetric data.

FIGURE 3.

Simulation of blood flow in the pulmonary arteries of a 16-year-old male with repaired tetralogy of Fallot and left pulmonary arterial stenosis. Main, right, and left pulmonary arterial flow and pressure are shown for simulations performed with and without left pulmonary artery stenosis. Main pulmonary arterial flow and morphometry-based impedance outlet boundary conditions were prescribed. The predicted blood flow to the left lung is less than that to the right lung, and unaffected by removal of the stenosis (47).

FIGURE 5.

Volume rendering of velocity magnitude for patient-specific model of blood flow from aorta to cerebral arteries for a patient with a right middle cerebral aneurysm. Simulation results are visualized together with CT image data to provide anatomic context.

FIGURE 7.

Overview of simulation-based medical planning approach as applied to designing bypass surgery for patient with occlusive cardiovascular disease in aorta and iliac arteries. Shown from left are magnetic resonance angiography data, preoperative geometric solid model (red), operative plan (proposed aortofemoral bypass graft shown in yellow), and computed blood flow velocity in aorta and proximal end of bypass (103).

In the last several years, there has been an increased tendency to utilize 3D segmentation methods, extract triangulated surface meshes and then generate volumetric meshes (29-32). Bekkers and Taylor recently described an alternative method for the generation of image-based, three-dimensional, multi-scale vascular models (33). The method generates multi-scale surfaces based on either a linear triangulated or a globally smooth non-uniform rational b-spline (NURB) representation using sub-division surface techniques. A novel hierarchical global topology and feature analysis drives surface generation. The method is particularly suited for blood flow modeling of very large vascular models with a wide range in vessel sizes where adaptive mesh refinement based on flow features makes an underlying smooth surface representation desirable.

Automatic mesh generation

As noted by Prakash and Ethier (34), mesh refinement studies are rarely reported in the computational hemodynamics literature. Indeed, as mesh independence of solutions is not reported, it is likely that many of the reported solutions are under-resolved. Notably, complex recirculating flow features observed in many experimental fluid mechanics studies of blood flow are typically not seen in computational simulations (35, 36). Adaptive mesh generations techniques have recently been described for computational hemodynamics studies. Muller et al. (37) and Sahni et al. (38) described a method whereby a posteriori error estimators, based on the Hessian of the velocity magnitude (speed) field, provide necessary information to adaptively refine a finite element mesh. Directional information on the solution error can be used to generate anisotropic elements with greater refinement in the directions of steepest changes in velocity gradients, e.g. the radial direction. Furthermore, since resolution of wall shear stress is often of interest, boundary layer mesh generation techniques can be used to increase mesh density near the vessel wall (39). Figure 2 depicts an anisotropic, adapted boundary layer mesh for a healthy human abdominal aorta. Such mesh generation techniques will be necessary for obtaining mesh-independent solutions for patient-specific models of blood flow.

FIGURE 2.

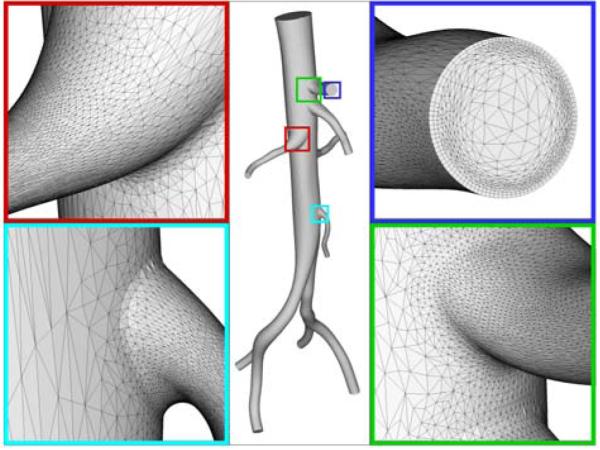
Anisotropic, adapted boundary layer mesh for a healthy human abdominal aorta. A boundary layer mesh is observed in the top right panel and anisotropic elements are highlighted in the bottom left panel (figure courtesy of Dr. Kenneth Jansen).

Patient-specific physiologic models & boundary conditions

Early three-dimensional simulations of blood flow in arteries focused on the velocity field and derived quantities like wall shear stress (1, 40, 41). Velocity profiles were prescribed at the inlet and outlets to achieve a desired flow distribution and a constant, generally zero, normal traction was prescribed at one or more outlets. As a result, blood pressure levels were not computed accurately and furthermore, simulations could not be performed where the flow distribution and pressure field were part of the desired solution. For example, this approach precluded models of wave propagation, resulted in unrealistic fluid-structure interaction simulations and negated the possibility of predicting outcomes of interventions. While one might be tempted to prescribe pressure waveforms at the inlet or outlets, this approach fails for multi-branched models or deformable models since pressure and flow wave amplitude, shape, and phase depend on the solution in the modeled domain and cannot be assigned a priori. In sum, the inability to model pressure wave propagation has led to a singular focus on wall shear stress as the primary hemodynamic factor contributing to atherogenesis, and aneurysm initiation, and enlargement.

An alternative to prescribing velocity profiles or pressure at inlet or outlet boundaries is to couple flow rate and pressure in the numerical domain to a reduced order model, i.e. a one-dimensional network or zero-dimensional (lumped) model (2, 42-45). This approach can be applied at the inlet or outlet boundaries of the patient-specific numerical model. The combined patient-specific and reduced-order model problem can be solved in an explicit, staggered manner or, preferably, by embedding the reduced-order model into the variational equations of the patient-specific model as is done in the Coupled Multidomain Method (44, 46). This latter, implicit-coupling, approach results in a stable, efficient formulation that, together with one-dimensional linear wave propagation theory can be used to couple distributed models with tens of millions of branches to numerical models (47). For the one-dimensional network models, branching patterns, length, diameter and material properties of vessel segments are assigned whereas for the lumped-parameter models, resistance, capacitance, inductance parameters and elastance functions (for lumped heart models) are set to achieve the desired hemodynamic characteristics of the upstream or downstream domain. Numerical optimization methods can be employed to tune the parameter values of the reduced-order models to match measured flow distribution or pressure values in the patient-specific model (48). Using this approach to boundary condition specification, flow distribution and pressure wave propagation arise naturally through the coupling between the patient-specific three-dimensional model and the reduced-order model (44, 49). Figure 3 depicts an application of this approach to modeling blood flow in the pulmonary arteries of a 16-year-old male with repaired tetralogy of Fallot and left pulmonary arterial stenosis. Main, right, and left pulmonary arterial flow and pressure are shown for simulations performed with and without left pulmonary artery stenosis. Main pulmonary arterial flow was prescribed at the inlet of the computational model and morphometry-based impedance boundary conditions were prescribed at each outlet (28). While, in this case, a one-dimensional nonlinear wave propagation model was used in the upstream domain, this example illustrates the importance of assigning realistic boundary conditions in patient-specific blood flow simulations.

A relatively new development in boundary condition specification has arisen due to difficulties in solving a class of problems where the patient-specific model is truncated in a region where flow is complex, recirculating or retrograde and a weakly enforced lumped-parameter or distributed reduced-order model is used to represent the downstream domain. Such numerical difficulties are inherent in problems related to modeling hemodynamics in the aorta or pulmonary arteries. Formaggia et al. (50) described a method, the total pressure boundary condition, to control the energy flux entering and exiting the computational domain, and stabilize problems with complex flows near boundaries. However, this approach requires an unconventional formulation of the Navier-Stokes equations and has not yet been proven to resolve boundary instability issues in complex hemodynamic simulations. An alternate solution to this problem proposed by Kim et al. (51) is to use the Augmented Lagrangian method to constrain the shape (but not the magnitude) of the velocity profile at inlet or outlet boundaries. This approach, applied to the same boundaries where a lumped-parameter or distributed network boundary condition is assigned, has the remarkable effect of stabilizing many problems with complex flows near outlet boundaries.

Numerical methods for FSI

Blood can be accurately represented as an incompressible fluid whose constitutive behavior is usually approximated by a Newtonian model. Arterial blood flow has been traditionally represented using the Incompressible Navier-Stokes equations in a fixed Eulerian frame of reference. However, blood velocity and pressure fields can be greatly influenced by the motion of external or internal vascular structures, such as the contracting cardiac muscle, moving heart valves, or deforming large arteries of the body. In these situations, one must characterize the mechanical behavior of the moving vascular structure (usually in a Lagrangian frame of reference), and its interactions with the blood flow. Modeling the interactions between an incompressible blood flow and a deforming vascular structure represents one of the major challenges in the field of cardiovascular mechanics.

Arbitrary Lagrangian-Eulerian formulations

One of the most well-known techniques used to describe Fluid-Structure Interactions (FSI) is the Arbitrary Lagrangian-Eulerian (ALE) formulation (52), (53). In this formulation, the Navier-Stokes equations are written in a moving reference frame that follows the motion of the vascular structure interface Γ_s (t) (see Figure 4). The evolution of this interface is determined by kinematic (continuity of velocities) and dynamic (continuity of forces) compatibility conditions between the blood flow and the vascular structure. In ALE formulations, the motion of the blood flow computational grid is arbitrary and defined by a grid velocity ${\stackrel{\rightharpoonup }{v}}_G\equiv (\partial \stackrel{\rightharpoonup }{x}∕\partial t){\mid }_{{\stackrel{\rightharpoonup }{x}}_0}$. This velocity is defined by the Lagrangian motion of the vascular structure at the fluid-solid interface Γ_s(t), but it needs to be generalized for the grid points of the flow domain not in contact with the vascular structure.

FIGURE 4.

Configurations of the blood and vascular structure domains.

In an ALE formulation, one must therefore solve the following three-field problem:

1. The Navier-Stokes equations of motion of a fluid in a moving domain Ω^f(t), to represent the blood motion.

   $$\begin{array}{cc}\hfill & {\nabla }_{\stackrel{\rightharpoonup }{x}}\cdot \stackrel{\rightharpoonup }{v}=0\hfill \\ \hfill & \rho \frac{\partial \stackrel{\rightharpoonup }{v}}{\partial t}{\mid }_{{\stackrel{\rightharpoonup }{x}}_0}+{\nabla }_{\stackrel{\rightharpoonup }{x}}\cdot (\rho \stackrel{\rightharpoonup }{v}\otimes (\stackrel{\rightharpoonup }{v}-{\stackrel{\rightharpoonup }{v}}_G))={\nabla }_{\stackrel{\rightharpoonup }{v}}\cdot \left(\underset{~}{\sigma }\right)+\stackrel{\rightharpoonup }{f}\mathrm{in}{\Omega }^f\left(t\right)\hfill \end{array}$$ (1)
2. The Elasto-dynamics equations of motion of the vascular structure Ω^s(t), usually written in a Lagrangian frame of reference with respect some initial configuration ${\Omega }_0^s$

   $${\rho }_0\frac{\partial \stackrel{\rightharpoonup }{v}}{\partial t}+{\nabla }_0\cdot \left(\underset{~}{\sigma }{F}^{-T}\right)={\stackrel{\rightharpoonup }{f}}_0\mathrm{in}{\Omega }_0^s$$ (2)
3. The motion of the computational grid for the blood flow over an interval I, defined by an arbitrary mapping Φ that matches the structure motion at the interface Γ_s(t).

   $$\begin{array}{cc}\hfill & \Phi :{\Omega }_0\times I\to \Omega \left(t\right)\hfill \\ \hfill & ({\stackrel{\rightharpoonup }{x}}_0,t)\to \stackrel{\rightharpoonup }{x}=\Phi ({\stackrel{\rightharpoonup }{x}}_0,t)\hfill \\ \hfill & \Phi ({\stackrel{\rightharpoonup }{x}}_0,t)\in {\Gamma }_s\left(t\right)\forall {\stackrel{\rightharpoonup }{x}}_0\in {\Gamma }_0^s\hfill \end{array}$$ (3)

The evolution of the ALE formulation is a boundary-fitting technique, where the fluid-solid interface is accurately captured due to continuous changes of the fluid grid. However, in situations where the motion of the vascular structure is large, ALE formulations may result in time-consuming computations. Currently, modular (also known as staggered) and non-modular (also known as monolithic) pre-conditioners for the solution of the coupled algebraic system resulting from the space-time discretization of the FSI problem represent an active area of research. Modular pre-conditioners allow for the use of independent, specialized fluid and structure solvers coupled via a relatively simple iterative scheme. However, these algorithms usually exhibit poor convergence behavior, especially in problems with large "added mass effect", where the density of the structure is comparable to the density of the fluid, as occurs in cardiovascular FSI problems. Alternatively, non-modular pre-conditioners require a more elaborate coupling between the fluid and solid solvers, but they usually result in faster, more stable algorithms. Geometric Conservation Laws that govern the evolution of geometric parameters, including grid positions and velocities, have been developed to avoid overly-diffusive grid motion strategies. A Geometric Conservation Law requires that motion of grid is computed in a way such that the numerical scheme is able to reproduce exactly a constant solution.

The use of ALE formulations in cardiovascular applications was pioneered by Perktold and collaborators (54, 55). More recently, Gerbeau and colleagues (56, 57), (58) have performed pressure wave propagation simulations in cerebral aneurysm and carotid bifurcation models; Hughes and colleagues (59),(60) have performed patient-specific FSI simulations using an isogeometric framework; Van de Vosse and colleagues (61) investigated a patient-specific abdominal aortic aneurysm model.

Immersed Boundary Method formulations

The Immersed Boundary Method, first introduced by Peskin (62), (63), is a non-boundary-fitting formulation that does not require any changes on the fluid computational grid. This formulation was first developed in the context of finite-difference approximations for the fluid domain, with a set of non-conforming, interconnected, elastic boundary points representing the structure. This structure interacts with the fluid via the introduction of body forces applied on the fluid domain at the position of the solid points. The Immersed Boundary Method has used in cardiovascular applications by Lemmon and Yoganathan (64) to examine left ventricular dysfunction; Watton et al. (65) to study prosthetic mitral valves; and Vigmond et al. (66) to develop a whole heart electro-mechano-fluidic computational framework. On the microscales, the Immersed Boundary Method has also been applied to modeling the interactions of red blood cells and plasma in the mesocirculation (67).

Fictitious Domain formulations

The Fictitious Domain method was first developed by Glowinski et al. (68). Although closely related to the Immersed Boundary Method, the Fictitious domain method was developed in a finite-element context, introducing Lagrange multipliers to constrain the motion of the fluid and the solid at the interface. Later, Baaijens (69) developed an extension of the method suitable for slender structures. The method has been successfully applied to FSI simulations of the aortic valve (70, 71). Van de Vosse and colleagues (72) proposed a combination of ALE and Fictitious Domain methods and applied it to the simulation of valve dynamics in a simple left ventricular flow models. More recently, Van Loon et al. (73) used a similar hybrid approach, and applied it to a heart valve dynamics problem.

Deforming Spatial Domain / Stabilized Space-Time method

In this formulation developed by Tezduyar et al. (74), the deforming spatial domain is handled by using space-time finite element spaces. Here, the motion of the unknown boundary is defined in terms of other variables, such as velocities or displacements of the interface. This formulation has been applied to study FSI in a patient-specific model of a cerebral aneursym (32).

Coupled-Momentum method

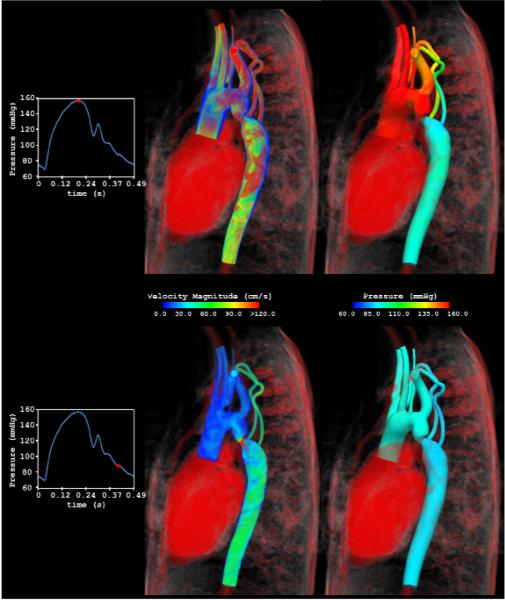
Figueroa, Taylor and colleagues (49) recently developed a Coupled-Momentum method to simulate blood flow and vessel deformation in arteries. This method embeds the elasto-dynamics equations into the variational form of the fluid via the definition of a fictitious body force that drives the motion of the vessel. By using a thin-wall assumption, this body force is related to the traction at the fluid-solid interface. The formulation results in a robust, monolithic scheme that is highly efficient for large scale fluid-structure interaction and wave propagation problems provided that the assumptions of small deformation and thin walls are reasonable. For example, Figure 5 shows results from a patient-specific model of blood flow from the aorta to the cerebral arteries for a patient with a right middle cerebral aneurysm. This computation included 3-element Windkessel outlet boundary conditions implemented using the Coupled Multidomain method (44), constraints on the shape of outlet velocity profiles (51) and fluid-structure interactions including spatially varying tissue properties modeled using the Coupled Momentum method (49). Figure 6 depicts the velocity magnitude and pressure fields at peak systole and mid-diastole for a patient-specific simulation of blood flow and vessel dynamics in the aorta of a 10 year old patient with aortic coarctation (75). In this simulation, the Coupled Multidomain method (44) and Augmented Lagrangian methods (51) are used to couple the three-dimensional patient-specific model to a lumped-parameter heart model at the inlet, and 3-element Windkessel models at the outlets and to constrain the shape of velocity profiles at inlet and outlet boundaries. The Coupled Momentum method (49) was used to solve the fluid-structure interaction problem on a finite element mesh with 2,647,619 elements, 475,866 nodes and a time step size of 0.025 ms.

FIGURE 6.

Velocity magnitude and pressure fields at peak systole and mid-diastole for a patient-specific simulation of blood flow and vessel dynamics in the aorta of a 10 year old patient with aortic coarctation.

Future challenges in FSI

New imaging techniques enable the characterization of the motion and thickness of vascular structures; however, it remains a challenge to incorporate this in vivo information into FSI formulations. A new class of "image-based FSI" problems will require the development of methods to assign tissue properties to the computer model from the medical image data, via the solution of an inverse problem.

APPLICATIONS

Disease research

Atherosclerosis

Atherosclerosis, the most prevalent of the acquired cardiovascular diseases, involves the accumulation of fatty material in the intima (inner layer) of arteries supplying the brain, heart, other vital organs, and lower extremities. However, while the biochemical stimuli for the development of atherosclerosis are diffuse throughout the body, the disease is very focal, localizing at branches and bends of the arterial tree. There is substantial and mounting evidence for the role of hemodynamic factors in the localization of atherosclerosis (76-78). Furthermore, atherosclerotic arteries continue to adapt in response to hemodynamic forces, in a mechanism known as compensatory remodeling (79). Patient-specific models have been widely used to quantify hemodynamic conditions in arteries for the purpose of understanding localization of atherosclerosis.

Due to the strong correlation between hemodynamics and atherosclerosis in the carotid bifurcation, it is not surprising that this vascular region has been widely studied. In particular, the Steinman group at the University of Western Ontario and the Ethier group at the University of Toronto have made important contributions to the field (5, 80-83). The group of Xu at Imperial College in London have also made significant contributions towards understanding hemodynamic conditions in the carotid artery (84, 85). Recently, Gimbrone’s lab at Harvard described phenotypic differences in endothelial cells exposed to different shear stress waveforms characterized using image-based modeling techniques in the carotid artery bifurcation (86).

The infrarenal abdominal aorta is another site prone to atherosclerosis likely due to unique hemodynamic conditions including low wall shear stress, high oscillatory shear and generally low flow, particularly for sedentary individuals (41, 87-91). Tang et al. reported the hemodynamic conditions under resting and exercise conditions in five patient-specific models of the abdominal aorta (7). When averaged over all subjects, wall shear stress significantly increased, whereas oscillatory shear index (OSI) decreased between rest and exercise at the supraceliac, infrarenal, and suprabifurcation levels, and significant differences in wall shear stress were found between anterior and posterior sections. Of note, in the atherosclerosis prone infrarenal aorta, wall shear stress increased six-fold between rest and exercise.

Finally, with the advent of small animal imaging techniques, image-based modeling techniques have been applied to quantify hemodynamic conditions in rodent models often used for disease research. For example, using small animal imaging and computational methods Greve et al. showed that shear stress varies across species in relation to their body mass according to the allometric law τ~M^−⅜ (92). Importantly, wall shear stress in the aorta of a mouse is more than 20-fold higher than that in humans. Feintuch et al. (93) and Suo et al. (94) confirmed these findings using image-based modeling to examine hemodynamic conditions in the mouse aortic arch.

Aneurysms

The recent review by Humphrey and Taylor (95) thoroughly discussed the role of computational mechanics in intracranial saccular and abdominal aortic aneurysm research. As noted in that review, image-based modeling techniques have been used in the last few years to conduct patient-specific investigations with the aim of determining whether biomechanical factors influence aneurysm initiation, growth and rupture (8-10, 96-101). In regards to hemodynamic forces, low wall shear stress, high wall shear stress and elevated dynamic pressure have been proposed to influence aneurysm growth. For example, Acevedo-Bolton et al. (2006) concluded that regions of basilar artery aneurysms that continued to enlarge experienced low wall shear stress. Very recently, using a longitudinal study of 7 patients with inoperable cerebral aneurysms, Boussel et al. provided compelling data to support the hypothesis that regions of low wall shear stress exhibited the greatest propensity for aneurysm growth (102). Undoubtedly, patient-specific computational methods will be used increasingly by investigators studying aneurysm growth and rupture.

Predictive Medicine

Interventional and surgical therapies used in the treatment of congenital and acquired cardiovascular diseases attempt to restore blood flow to compromised organs and tissues. Ideally, these therapies result in sufficient blood flow at appropriate physiologic pressures while avoiding adverse flow conditions such as flow recirculation and stasis that may lead to procedural failure and/or poor outcomes. Unfortunately, alternate treatments cannot be tested in the patients and physicians do not have the tools needed to evaluate the multiple options and design the optimal corrective procedures. Instead, the current paradigm for medical planning for the treatment of cardiovascular disease relies exclusively on diagnostic imaging data and physical measurements to define the present state of the patient, empirical data to evaluate the efficacy of prior treatments for similar patients, and the judgment and experience of the physician to decide on a preferred treatment. However, diagnostic imaging, physical measurements and empirical data are insufficient to predict the outcome of a given treatment for an individual patient due to anatomic and physiologic variations and system complexity.

In the new paradigm of “predictive medicine” a physician utilizes computational tools to construct and evaluate a combined image-based anatomic/physiologic model to predict the outcome of alternative treatment plans for an individual patient. For cardiovascular treatment planning, these simulation systems require an integrated set of software tools to model the effect of alternate treatments on blood flow. The key elements of such a system include a human-computer interface, image segmentation, geometric solid modeling, operative planning, discretization methods, fluid-structure interaction methods, and scientific visualization techniques. Simulation-based medical planning systems must be efficient and minimize user intervention so that results can be obtain in hours instead of days to weeks. These systems must also accurately describe the key hemodynamic variables, especially flow rate and pressure.

In 1998, Taylor and colleagues developed a prototype software system, Advanced Surgical Planning Interactive Research Environment (ASPIRE), for patient-specific cardiovascular surgery planning using computational methods for modeling blood flow. ASPIRE was demonstrated in the plenary research forum at the 1998 Society for Vascular Surgery (SVS) meeting and used successfully by four prominent vascular surgeons to evaluate alternate surgical plans for a case of lower extremity occlusive disease (2). Wilson et al. described the development of a new software system for image-based modeling and cardiovascular surgery planning, ASPIRE2 (103, 104). Modular software architecture was utilized to enable the use of best-in-class component technology and create a single application to go from medical imaging data to analysis results. Figure 7 provides an overview of the predictive medicine approach as applied to designing bypass surgery for patient with occlusive cardiovascular disease in aorta and iliac arteries (103).

In the last several years, a few groups have started to apply image-based modeling techniques to the assessment of surgical procedures for patients with congenital heart diseases. Notable amongst these efforts is the work of Yoganathan and colleagues (105, 106) and Migliavacca, Bove, de Leval and colleagues (42, 43, 107-109) to assess the hemodynamic efficiency of the total cavopulmonary connection. Marsden et al. recently used image-based modeling techniques to design a novel surgical repair to replace the existing Fontan procedures (110).

FUTURE ISSUES

Patient-specific tissue properties for FSI

With the advent of more powerful image acquisition and processing techniques, the accuracy and complexity of patient-specific cardiovascular geometric models has increased dramatically. However, the ever improving level of sophistication of computational formulations for blood flow and vascular structure interactions requires more information than just the mere definition of the vascular geometry: there is a pressing need to characterize the mechanical behavior of the vascular structure and the tissues around it. This behavior is represented by the stiffness, visco-elasticity, and mass of the tissues, but also by the tethering conditions that structures like bones and muscle impose on the vasculature. It is clear that given the large subject-to-subject variability of the cardiovascular system, the definition of the vascular and peri-vascular tissue properties must be made on a patient-specific basis. The definition of best-fit values of the material parameters characterizing tissue behavior in vivo is a challenging task. New methods such as MRI-based elastography (111) and data assimilation techniques (112) need to be developed to assign tissue properties to cardiovascular geometric models.

Predicting Long-term outcomes using FSG

Blood vessels exhibit a remarkable ability to adapt throughout life: We observe normal vascular adaptations in development and aging; adaptations to injury such as in wound healing and vasospasm; adaptations in disease, such as atherosclerosis and aneurysms; and lastly, adaptations to changes in the overall hemodynamic state of the subject, such as a chronic increase in flow in endurance training, or change in blood pressure as in hypertension or microgravity. These adaptations represent changes in both the shape and material properties of the vessel, and depend upon an array of factors such as gene pathways, complex biochemical processes in the vessel wall and, as many findings over the last few decades indicate, the mechanical environment of the vessel. Many observations at the sub-cellular, cellular and even cell matrix levels point to the existence of a "preferred" or "homeostatic" mechanical state across multiple space and time scales. Thus, it is thought that vascular growth and remodeling (G&R) happens in response to a significant alteration of the homeostatic state of a vessel (113).

Changes in the shape and mechanical properties of blood vessels are ultimately related to changes in its constituents: resident cells (smooth muscle and endothelial cells) and the extracellular matrix. The main remodeling agents in the vessel wall are the endothelial cells, vascular smooth muscle cells, and fibroblasts. Many studies have attempted to elucidate the role of each of these elements in arterial G&R. From a computational standpoint, two main methodologies have been proposed: the kinematic growth approach (114),(115), and the constrained mixture approach (116),(117),(118). The kinematic growth approach models the G&R without representing the underlying bio-chemo-mechanical mechanisms modulating growth. On the other hand, the constrained mixture framework incorporates the response of smooth muscle and collagen fibers to changes in mechanical loading, based on mass density production and removal functions. These responses can be characterized via the combination of adequate cell culture experiments and computational methods to model hemodynamic-induced loads on the vascular wall (113) such as cyclic stretch (or stress) and wall shear stress. For example, smooth muscle cells can increase their production of collagen in response to changes in intramural loading. Conversely, these cells can increase the production of Matrix Metalloproteinases (MMPs) responsible from selective degradation of collagen and elastin in response to the same mechanical stimulus (119). Furthermore, the endothelial layer can increase the production of nitric oxide (NO), a potent vasodilator, in response to local increases in wall shear stress levels. Conversely, endothelial cells can increase the production of endothelin-1 (ET-1), a potent vasoconstrictor, in response to decreases in wall shear stress. However, NO is also an inhibitor of both smooth muscle cell proliferation and its synthesis of collagen (120), whereas ET-1 is a promoter of smooth muscle proliferation and the synthesis of collagen (121). It becomes apparent that local changes in wall shear stress from baseline conditions play important roles in controlling smooth muscle contractility, they also contribute to the rate and extent of cell and matrix turnover within the wall.

Clearly, then, to understand hemodynamic-induced changes in vascular geometry, structure, and function, we must quantify the complexities of the flow field and the distribution of stress on and within the arterial wall on a patient-specific basis. Motivated by these and similar observations, Humphrey, Taylor and colleagues (122) have brought together for the first time a Fluid-Solid-Growth (FSG) computational framework for solving the full 3-D hemodynamics problem in patient-specific geometries and the wall mechanics G&R problem involving geometrically and materially nonlinear behaviors. The components of this multi-scale FSG framework are depicted in Figure 8. In this framework, the hemodynamic forces acting during the cardiac cycle provide the loads for the vascular G&R formulation, defined on a time scale of weeks to months, which in turn provides the updated geometry and material properties for the hemodynamic simulation.

FIGURE 8.

Iterative loop and information transferred in the coupling between the FSI and G&R parts of a FSG framework (122).

This framework is general enough to enable new data on stress-mediated growth and remodeling processes to be incorporated mathematically as they become available. For example, there is a pressing need for data on which to build more comprehensive constitutive models for mass production and removal as a function of the evolving state of stress (or strain). Once validated in well designed experiments, FSG modeling may become an essential tool in the understanding of diverse vascular pathologies, new clinical interventions (e.g., surgical planning), and the design of implantable medical devices.

Optimal treatment plans

Numerical optimization methods combined with simulations of blood flow and vessel dynamics represent an important direction for patient-specific modeling. Marsden et al described as shape optimization method for cardiovascular modeling based on a derivative-free approach using surrogates for increased efficiency together with mesh adaptive direct search to guarantee convergence to a local minimum (123). As noted by Marsden et al, the main challenges relate to employing physiologically accurate and validated methods, appropriate measures of performance (cost functions), implementing an optimization method appropriate for expensive, time-dependent, three-dimensional fluid mechanics problems, and tools should be developed for the efficient parameterization of patient-specific geometries. Ultimately, optimization methods coupled with fluid-solid-growth methods could ensure that individual patients get the best possible hemodynamic outcomes in the near and long term.

Device design and evaluation

Advances in biomaterials have enabled the development of various medical devices to treat cardiovascular disease. Computational mechanics principles have been used for the design and evaluation of many of these devices, such as stents, stent-grafts, mechanical heart valves, blood pumps and ventricular assisted devices (VAD).

Stents (bare-metal or drug-eluted) are structures used to alleviate diminished blood flow to organs beyond an obstruction or stenosis in order to maintain an adequate delivery of oxygenated blood. The placement of these mechanical structures changes the biomechanical environment of the artery. Migliavacca and colleagues have investigated different geometric and mechanical factors involved in stent deployment (124, 125); Holzapfel and colleagues have studied the interactions of vascular stents with human atherosclerotic lesions (126); LaDisa and colleagues have correlated stent design with alterations of wall shear stress and intima hyperplasia (127). Steiman (128) and Cebral (129) have investigated the altered hemodynamic conditions of flow in stented cerebral aneurysms.

Stent-grafts are stents covered with fabric that are primarily used to treat aortic aneurysms. These devices are usually delivered endovascularly. Stent-graft migration and endoleaks are the main complications associated with these devices. Morris and colleagues have performed a combined analytical and CFD study of the forces acting on AAA stent-grafts (130). Li and Kleinstreuer (131) have simulated the fluid-structure interactions in a stented abdominal aortic aneurysm (AAA) model.

Mechanical heart pumps and ventricular assisted devices (VAD) provide cardiac failure patients with supplemental circulatory support until a transplant becomes available (132). Originally intended to be a bridge therapy, continuous improvements in device design and lack of donors have shifted their use towards a destination therapy. The design of these devices presents important computational biomechanics challenges, such as models for blood damage and thrombosis, device optimization for hydrodynamic efficiency and durability, etc (133). Some of these issues are also shared by the design of mechanical heart valves (134).

In all instances presented here, it is paramount to have an understanding of the biomechanical environment experienced by the device in vivo, in order to secure its correct function and durability. However, the variability of this biomechanical environment from subject to subject is so large that the choice of device for the treatment of a particular patient should be made in a personalized manner.

Verification and Validation

In order for computational methods to be accepted into clinical practice for planning cardiovascular surgery, extensive verification and validation is needed. Verification of a numerical method is defined as the assessment of the numerical accuracy with which the method is implemented in a computer. This process usually relies on the existence of an analytical solution for the method. On the other hand, the validation of a computational method is a more complex process because it involves comparing the results of the method with those observed in the real world (135). It is clear that, when developing new methods for cardiovascular modeling, the verification should precede any attempt of validation. A succinct and clear distinction between verification and validation is given by Roache (136), where verification is described as "solving the equations right", whereas validation is described as "solving the right equations". Womersley’s solution for pulsatile flow in a straight semi-infinite circular deformable vessel (137) represents an excellent framework to understand some of the principles that govern wave propagation and fluid-structure interaction phenomena in the cardiovascular system and it is also a good tool to perform verification studies of mathematical models of blood flow in compliant arteries.

For more complex geometries in vitro experimental data has been used to validate numerical methods (3). Ku and colleagues (138) performed a validation study of CFD data with MRI data in an in vitro bypass graft model. Hoi et al. (139) developed a validation study of CFD data with particle image velocimetry data (PIV) in an in vitro model of a cerebral aneurysm.

However, validation of numerical methods is considerably more challenging in vivo, where experiments are difficult to control and measurement data is challenging to acquire. Ku et al. compared calculated flow rates to measured flow rates obtained using magnetic resonance imaging (MRI) techniques in thoraco-thoraco aortic bypass procedures in eight pigs (140). The predicted and measured waveforms had similar shapes and amplitudes, while predicted flow distribution was within approximately 10% of the experimental data. More recently, Saloner and colleagues performed a comparison of CFD results and in vivo MRI measurements of flow in cerebral aneurysms (141). While it appears that computational methods may be used effectively to predict flow distribution, experimental validation studies are very preliminary. In addition, it is likely that prediction of in vivo flow velocity profiles and pressure fields will present considerable challenges.