3D in vivo imaging of rat hearts by high frequency ultrasound and its application in myofiber orientation wrapping

Abstract

Cardiac ultrasound plays an important role in the imaging of hearts in basic cardiovascular research and clinical examinations. 3D ultrasound imaging can provide the geometry or motion information of the heart. Especially, the wrapping of cardiac fiber orientations to the ultrasound volume could supply useful information on the stress distributions and electric action spreading. However, how to acquire 3D ultrasound volumes of the heart of small animals in vivo for cardiac fiber wrapping is still a challenging problem. In this study, we provide an approach to acquire 3D ultrasound volumes of the rat hearts in vivo. The comparison between both in vivo and ex vivo geometries indicated 90.1% Dice similarity. In this preliminary study, the evaluations of the cardiac fiber orientation wrapping errors were 24.7° for the acute angle error and were 22.4° for the inclination angle error. This 3D ultrasound imaging and fiber orientation estimation technique have potential applications in cardiac imaging.

1. INTRODUCTION

Ultrasound imaging plays an important role in cardiovascular research and clinical examinations [1, 2]. The acquisition of cardiac image volumes can provide 3D geometry and comprehensive motion information of the heart. Moreover, as cardiac fiber orientations affect the cardiac anatomy, mechanical properties, and the electrophysiology inside the heart [3–5], the wrapping of cardiac fiber orientations to the ultrasound volume can supply useful information on stress distributions and electric action spreading. Currently, cardiac ultrasound imaging for the small animal hearts is generally in 2D, which only provides 2D images and requires geometric assumption for left ventricle calculations. It is still challenging to design a 3D ultrasound probe for small animal heart applications because of the high ultrasound frequency (>15 MHz).

For 3D ultrasound imaging of small animals, Dawson et al. developed a highly accurate, reconstructive 3D ultrasound imaging system for mouse hearts [6]. Further applications of 3D ultrasound imaging in small animal studies were summarized in [7]. However, there was no reliable method on 3D ultrasound imaging of rat hearts. In this study, we designed a 3D ultrasound volume acquisition approach for rat hearts in vivo. Especially for quantifying the right ventricular geometry or for the cases of severe heart remodeling, we tested the feasibility of in vivo imaging of a beating heart using an open-chest procedure. After image acquisition, the segmented cardiac myocardium is then reconstructed into 3D geometry.

For indirectly estimation of cardiac fiber orientation, the procedure of wrapping cardiac fiber orientations from DTI data of a template heart to the target heart has been applied to the MRI, CT and ultrasound modalities as reported by others and our group [5, 8, 9]. In this study, we further apply the procedure of mapping the cardiac fiber orientations to in vivo beating hearts. The accuracy of the cardiac fiber orientation wrapping method is quantitatively validated using magnetic resonance diffusion tensor imaging (MR-DTI). This is an important step to translate the ultrasound-based cardiac fiber estimation method from animals to humans.

2. METHODS

2.1 3D ultrasound imaging in vivo

The rat was settled on the imaging platform and was imaged by the Vevo 2100 ultrasound system (FUJIFILM VisualSonics, Inc., Toronto, Canada) with a 21 MHz transducer. B-mode ultrasound images of the hearts in the short-axis view were acquired slice by slice from base to apex at a 0.2 mm thickness. Each slice position was dynamically imaged as a serial of beating cycles. The pixel size in the B-mode image was 0.06 mm. During the image acquisition, both ECG and respiration signals were recorded. However, this method can have limitations in cases when the myocardial boundaries of the whole heart are required and when it is critical to accurately quantify the right ventricular geometry for severe heart remodeling. In order to image the 3D geometry of the remodeled geometry, the in vivo imaging procedure is performed on the beating heart after an open-chest surgical procedure. During imaging, the respiratory of the rat is kept by a respiratory machine and ECG signals are recorded.

2.2 Diffusion tensor imaging of rat hearts ex vivo

After in vivo ultrasound imaging, the rat heart was excised and then embedded in 2% agar phantoms for the MR imaging procedures. The phantoms were placed in a Biospec 7 T MRI system (Bruker Corporation, Massachusetts, USA). An RF coil with an inner diameter of 30 mm was used to transmit/receive the signals. Before diffusion tensor imaging, T1 anatomical images were acquired at a voxel resolution of 0.078 × 0.078 ×0.156 mm³. Then, the cardiac fiber orientations were imaged in 30 directions using a spin echo sequence at the 0.234 mm isotropic resolution. Total MRI time was 36 hours for each heart.

2.3 Mapping cardiac fiber orientation from diffusion tensor imaging to 3D ultrasound

Geometry and fiber orientation reconstruction

After data acquisition, the both ultrasound and MR images are processed. First, the end of systolic volume was selected from the ultrasound sequences based on the ECG signals and respiration signals. Both the ultrasound images and T1-weighted MR images were manually segmented using the Analyze software (AnalyzeDirect Inc., Overland Park, KS). The binary geometric volumes of the hearts were reconstructed. Based on the segmented heart mask from T1-MR images, the cardiac fiber orientations were reconstructed from the DTI data.

Cardiac fiber orientation wrapping

For warping of the cardiac fiber orientation from MR-DTI data, the 3D ultrasound images are registered with the T1-MRI data. Various imaging registration methods were developed in our group [15–23]. In this procedure, there are two steps to wrap cardiac fiber orientations from DTI to the target ultrasound geometries, which is illustrated in Figure 1.

Figure 1.

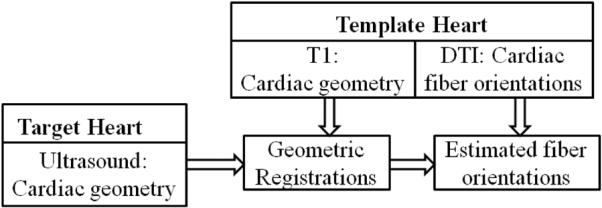
Flowchart of wrapping cardiac fiber orientation from DTI to 3D ultrasound in vivo.

The first step is to generate the deformation field between the ultrasound geometry of the target heart and the MRI geometry of the template heart. During the geometry registration step, the atlas geometry is first registered to target geometry by supervised affine transformations (translation, rotation, shear, and scaling) using Analyze software. After that, a diffeomorphic Demons registration method was applied to perform a deformable registration. In order to match two images I₀ and I₁ by a transformation s, the typical Demons registration requires a similarity criterion Sim(I₀, I₁, S) to measure the similarity between both images, and also a regularization energy Reg(s) to evaluate their transformation likelihood. They are defined as follows:

$$E\left(s\right)=\frac{1}{{\sigma }_i^2}\mathit{Sim}(I_0,I_1,S)+\frac{1}{{\sigma }_T^2}\mathit{Reg}\left(S\right),$$ (1)

where σ_i relates to the noise of the image and σ_T weighs the regularization effect. However, traditional Demons registration methods usually cannot supply the diffeomorphic transformations which are necessary for maintaining the topology of the cardiac anatomical structures and the invertible deformation field for the fiber reorientations of DTI data. Thus, Vercauteren et al. adapted the Demons as an optimization procedure on the entire space of displacement fields to a space of diffeomorphic transformations through the exponential. The modified energy function is described as followed

$$E_{diffeo}(I_0,I_1,s,u)=\mathit{Sim}(I_0,I_1,s°\exp (u\left)\right)+{\Vert u\Vert }^2,$$ (2)

where u is the velocity field and ∥u∥ is its norm. Its exponential exp(u) is a time stationary ordinary differential equation (ODE): ∂p(t) / ∂t = u(t) and p is the image position. Then, the transformation s is updated by exp(u) as the form of s °exp(u). Based on this improvement, the registration method can provide both efficient computations and invertible transformations between two geometries.

After the geometric registration, the next step is to relocate and reorient DTI fiber orientations of the template heart to the target heart as the final results based on the deformation field [24, 25].

2.4 Evaluations

Quantitative evaluation of the method is conducted by comparing the processed image with the corresponding reference image [12, 26–32]. The Dice similarity coefficient (DSC) is used as the performance assessment score of the similarity between both the reference and registered images [10–14,33]. Another evaluation method is the target registration error, which calculates the distance between corresponding markers in both images. We used the papillary muscles in the hearts as the anatomic markers for the calculation of the target errors. The distance between the mass centers in the corresponding markers was calculated for registration evaluation.

In order to evaluate the extracted cardiac fiber orientations from a template heart, the corresponding ex vivo DTI data of the same heart is utilized as the gold standard, which is mapped to the in vivo ultrasound geometry. Both estimated orientation and the gold standard from DTI at the same voxels are compared using two parameters: the acute angle error (AAE) and the inclination angle error (IAE). The acute angle is utilized to measure the angular separation between both orientations of the same fiber by inverting the absolute of their dot product in 3D into angles. But this angle is not sufficient enough for the evaluation because the cardiac fibers are arranged along the laminar sheets in myocardium rather than any direction. Thus, it will lead to more errors into the cardiac fiber estimations if only considering the acute angle. The inclination angle error serves as another parameter for the evaluation of fiber orientations [8].

3. RESULTS

3.1 Reconstruction of cardiac geometry from in vivo 3D ultrasound

First, the end of diastolic volume is reconstructed as shown in Figure 2(a) and its corresponding reconstructed 3D geometry of the heart after segmentation is shown in Figure 2(b).

Figure 2.

Reconstructed ultrasound volume and the segmented heart geometry. (a) Ultrasound volume in the end of the diastole phase. (b) Segmented and reconstructed 3D geometry of the heart.

Then, the cardiac geometries were compared between both in vivo ultrasound geometry and ex vivo MRI geometry of the same heart, shown in Figure 3. After deformable registration, the DSC between both geometries was 89.3%, which means that the geometry acquired from 3D ultrasound in vivo has a high similarity to that in the ex vivo, high-resolution MRI.

Figure 3.

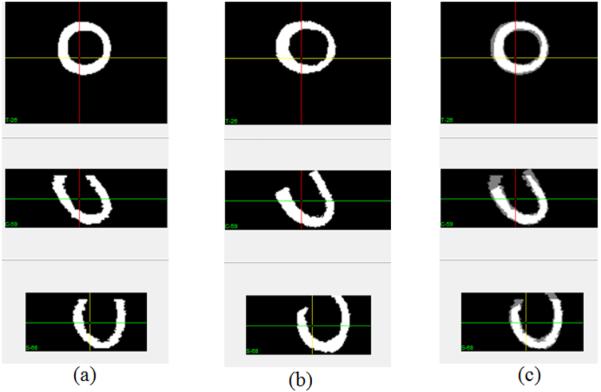
Comparison between in vivo geometry and ex vivo geometry of the same heart. (a) In vivo geometry from 3D ultrasound. (b) Ex vivo geometry from MRI. (c) Comparison after rigid registration.

3.2 Accuracy of wrapping cardiac fiber orientations to the cardiac geometry of the 3D ultrasound in vivo

After the geometry reconstruction of in vivo 3D ultrasound, the DTI fiber orientations from a template heart were wrapped to the in vivo ultrasound geometry following the procedure in Figure 1. The accuracy of the fiber orientation wrapping was validated by the cardiac fiber orientations of the target heart imaged by MR-DTI ex vivo.

As an illustration, cardiac fiber orientations were mapped from a template heart with MR-DTI data ex vivo to the geometry acquired from the in vivo 3D ultrasound images of another rat heart. The cardiac geometry in the diastole phase was segmented and reconstructed from the ultrasound volume. Finally, the fiber orientations were estimated by the proposed method, which used another ex vivo heart as the template. These results demonstrated the feasibility of estimating cardiac fiber orientations from the ultrasound images of the rat heart in vivo.

Moreover, the geometry registration accuracies between the target ultrasound geometry and the template MR-DTI geometry are listed in Table 1. Both AAE and IAE evaluations of the fiber wrapping accuracy are listed in the table.

Table 1.

Evaluation of the of the cardiac fiber orientations wrapping to the cardiac geometry of ultrasound in vivo

Target	Template	DSC (%)		AAE (degree)		IAE (degree)
		Affine	Deform	Affine	Deform	Affine	Deform
In vivo ultrasound	Ex vivo DTI	71.6	89.3	32.5	24.7	26.3	22.4

4. DISCUSSION AND CONCLUSION

An imaging approach is proposed to acquire 3D ultrasound image volumes of the rat hearts in vivo. After image acquisition, its segmented cardiac myocardium is reconstructed as 3D geometry. Based on the in vivo 3D geometry, the accuracy of the cardiac fiber orientation wrapping from a different heart is validated by the diffusion tensor imaging data of ex vivo hearts. Both geometry and wrapped fiber orientation comparisons between in vivo and ex vivo data indicated that this approach could be applied in the research of the cardiac fiber orientations. Moreover, we also tested the feasibility of imaging beating hearts in vivo after an open-chest surgical procedure. This could provide an alternative method to in vivo assess the 3D geometry of the heart in the small animals.