Imaging and sensing based on dual-pulse nonlinear photoacoustic contrast: a preliminary study on fatty liver

Abstract

The feasibility of diagnostic imaging and tissue characterization based on a new contrast realized by dual-pulse photoacoustic measurement was studied. Unlike current photoacoustic methods which are mostly focused on the measurement of tissue optical absorption, this contrast revealed by a dual-pulse laser excitation process takes advantage of the temperature dependence of Grüneisen parameter of tissue. The first laser pulse heats the sample and causes a temperature rise in the target tissue, which leads to the change of Grüneisen parameter and the amplitude of the photoacoustic signal from the second laser pulse. This new contrast is then quantified by percentile change in the second pulse signal as a result of the first laser pulse. Since the temperature-dependent Grüeneisen parameter is tissue specific and closely relevant to chemical and molecular properties of the sample, the dual-pulse photoacoustic measurement is able to differentiate various tissue types and conditions. The preliminary study on phantoms and a mouse model has suggested the capability of the proposed contrast in characterization of fatty livers and the potential for future clinical diagnosis of liver conditions.

Combining the high sensitivity of optical imaging and the excellent spatial resolution of ultrasonography in deep imaging, the emerging photoacoustic imaging (PAI) technique has drawn considerable attention in the last decade and has been explored extensively for its applications in biomedicine [1, 2]. Most of the current PAI procedures are aiming at the measurements of optical absorption coefficients of biological samples to realize noninvasive disease diagnosis and tissue characterization. To achieve this goal, nanosecond laser pulses are used to generate ultrasonic emission from biological tissues followed by detection via ultrasonic transducers to form images. To avoid thermal accumulation in the sample resulted from light illumination by a series of laser pulses, the intervals between laser pulses are fairly long (e.g. 0.1 second). In this case, the thermal accumulation in the sample as a result of photoacoustic laser illumination can be neglected.

Temperature is an important parameter of biological tissue and has a profound effect on many physical properties such as thermal conductivity, thermal expansion, speed of sound, and specific heat capacity [3]. All these temperature-dependent parameters are associated with the Grüneisen parameter of tissue, i.e. the coefficient in photoacoustic signal generation after pulsed light is absorbed by a biological sample. Therefore, PAI is intrinsically sensitive to not only tissue optical absorption but also temperature [2, 4–6]. In previous studies, by evaluating photoacoustic signal amplitude as a function of temperature, PAI has been adapted to monitor temperature change in biological sample during thermotherapy [5, 7–10]. Recently, Wang et al for the first time studied the nonlinear photoacoustic effect when two closely adjacent laser pulses are applied on the same biological tissue [11, 12]. The nonlinear photoacoustic effect reflected by a dual-pulse procedure was applied in photoacoustic microscopy to improve axial resolution [11] and wavefront shaping to achieve diffraction-limited optical focusing in optical scattering medium [12].

In this work, we explored the feasibility and technical challenges in achieving medical imaging and tissue characterization based on the new contrast reflected by the dual-pulse nonlinear photoacoustic technology. The dual-pulse nonlinear photoacoustic contrast (DPNPC) relies on different optical absorptions and thermal properties of chemical contents in biological tissue and its development is rather straightforward.

Assuming the tissue under investigation is a uniform mixture of several different chemical compositions and is sequentially illuminated by two laser pulses (namely the heating pulse and the detecting pulse) with a time interval of Δt, the effective absorption coefficient of the sample can be written as

$${\mu }_{\text{eff}}(\lambda )=\sum _i{f}_i{\mu }_i(\lambda ),$$ (1)

where ∑ f_i = 1, f_i and μ_i(λ) are the volume fraction and absorption coefficient of the ith chemical content at the wavelength λ, respectively. The photoacoustic signal of the heating laser received by transducer is

$$V_1=\eta \int {\int }_{\mathrm{\Sigma }}G(\xi ,\zeta )(\int \int {\int }_{S}f(x,y,z;\xi ,\zeta )·{\mathrm{\Gamma }}_{0i}{\mu }_{\text{eff}}({\lambda }_1){\mathrm{\Phi }}_1(x,y,z;{\lambda }_1;t_1)\mathrm{d}x\mathrm{d}y\mathrm{d}z)\mathrm{d}\xi \mathrm{d}\zeta =\eta \sum _i{\mathrm{\Gamma }}_{0i}{f}_i{\mu }_i({\lambda }_1)·\int {\int }_{\mathrm{\Sigma }}G(\xi ,\zeta )(\int \int {\int }_{S}f(x,y,z;\xi ,\zeta ){\mathrm{\Phi }}_1(x,y,z;{\lambda }_1;t_1)\mathrm{d}x\mathrm{d}y\mathrm{d}z)\mathrm{d}\xi \mathrm{d}\zeta =\eta \sum _i{\mathrm{\Gamma }}_{0i}{f}_i{\mu }_i({\lambda }_1)·F({\mathrm{\Phi }}_1),$$ (2)

where Φ₁ is fluence of the heating laser at time t₁, Γ_0i is the Grüneisen parameter of the ith chemical content at initial temperature T₀, η is a constant coefficient, G is the apodization function of the transducer, f is a propagating factor for acoustic wave from acoustic source S to transducer surface Σ, (x, y, z) and (ξ, ξ, z) are corresponding coordinates for S and Σ, respectively. Here we assume the Grüneisen parameter Γ is homogeneous throughout the sample.

As soon as the heating pulse evanesces, a temperature jump ΔT is established, which will cause changes in temperature-dependent physical properties of the tissue. One of the dominant is the thermal expansion coefficient β [13], which relates to the Grüneisen parameter via $\mathrm{\Gamma }=\beta {\nu }_{\mathrm{s}}^2/C_{\mathrm{p}}$, where ν_s is the speed of sound and C_p is the specific heat capacity at constant pressure. That is to say, the basic parameter Γ in the target tissue will change after the heating pulse and so is the photoacoustic signal from the detecting signal. Considering Γ changes linearly with temperature, its value at time t₂ becomes

$${\mathrm{\Gamma }}_i(T_0+\mathrm{\Delta }T;\mathrm{\Delta }t)={\mathrm{\Gamma }}_{0i}+{\mathrm{\Gamma }}_i^{\prime }·\mathrm{\Delta }T·{\tau }_i(\mathrm{\Delta }t),$$ (3)

where ${\mathrm{\Gamma }}_i^{\prime }$ is the change slope of Γ_i, τ_i is a decay function, and ΔT = f_iμ_i(λ₁)Φ₁(ξ, ξ; λ₁; t₁)/ ρ_iC_vi is the temperature rise due to the heating pulse, where ρ_i and C_vi are density and specific heat capacity at constant volume, respectively. Therefore, the photoacoustic signal of the detecting laser received by transducer with the heating pulse is

$$V_2^{\prime }=\eta \sum _i{\mathrm{\Gamma }}_{0i}{f}_i{\mu }_i({\lambda }_2)·F({\mathrm{\Phi }}_2)+\eta \sum _i\left\{\right[{\mathrm{\Gamma }}_i^{\prime }·\frac{f_i{\mu }_i({\lambda }_1)}{{\rho }_i{C}_{\mathrm{v}i}}·{\tau }_i(\mathrm{\Delta }t)]·f_i{\mu }_i({\lambda }_2)\}·F({\mathrm{\Phi }}_1{\mathrm{\Phi }}_2),$$ (4)

where Φ₂ is fluence of the detecting laser at time t₂. For comparison, the photoacoustic signal of the detecting laser without the heating pulse is

$$V_2=\eta \sum _i{\mathrm{\Gamma }}_{0i}{f}_i{\mu }_i({\lambda }_2)·F({\mathrm{\Phi }}_2).$$ (5)

The amplitude difference $\mathrm{\Delta }{V}_2=V_2^{\prime }-V_2$ changes nonlinearly with the change of the input laser fluence Φ₁ and Φ₂, as ΔV₂ ∝ Φ² when Φ₁ = Φ₂ = Φ. We define the nonlinear effect (or increase ratio) as

$$\alpha =\frac{\mathrm{\Delta }{V}_2}{V_2}=\frac{\sum _i[{\mathrm{\Gamma }}_i^{\prime }{f}_i^2{\mu }_i({\lambda }_1){\mu }_i({\lambda }_2)·{\tau }_i(\mathrm{\Delta }t)/{\rho }_i{C}_{\nu i}]}{\sum _i{\mathrm{\Gamma }}_{0i}{f}_i{\mu }_i({\lambda }_2)}·\frac{F({\mathrm{\Phi }}_1{\mathrm{\Phi }}_2)}{F({\mathrm{\Phi }}_2)}.$$ (6)

Equation (6) indicates the nonlinear effect α is determined by both the physical properties of the tissue (the first term) and the laser fluence (the second term). Regardless of the laser fluence issue, which can be calibrated in experiment, we are interested in how the first term contributes to the nonlinear effect α in different tissues. Considering μ_i, τ_i and f_i are tissue-dependent and Γ, ρ and C_v are both temperature- and tissue-dependent, the nonlinear effect α is tissue specific and renders a new contrast for differentiating various tissue types and conditions.

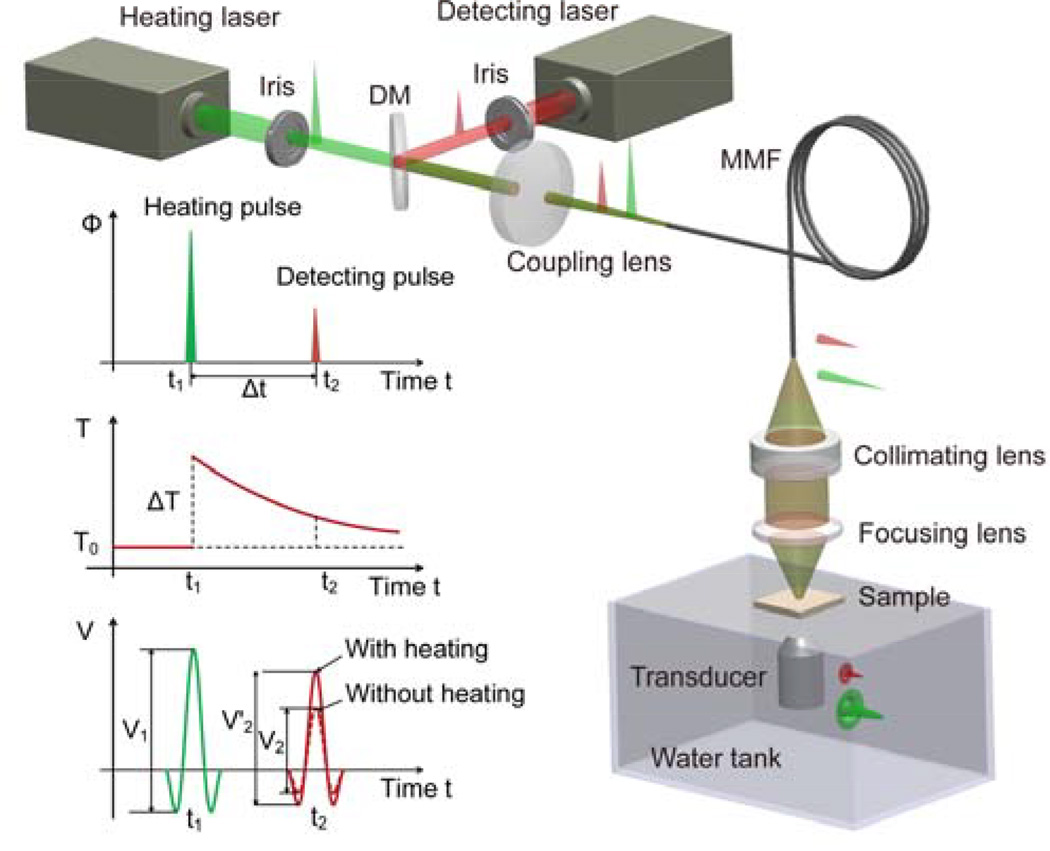
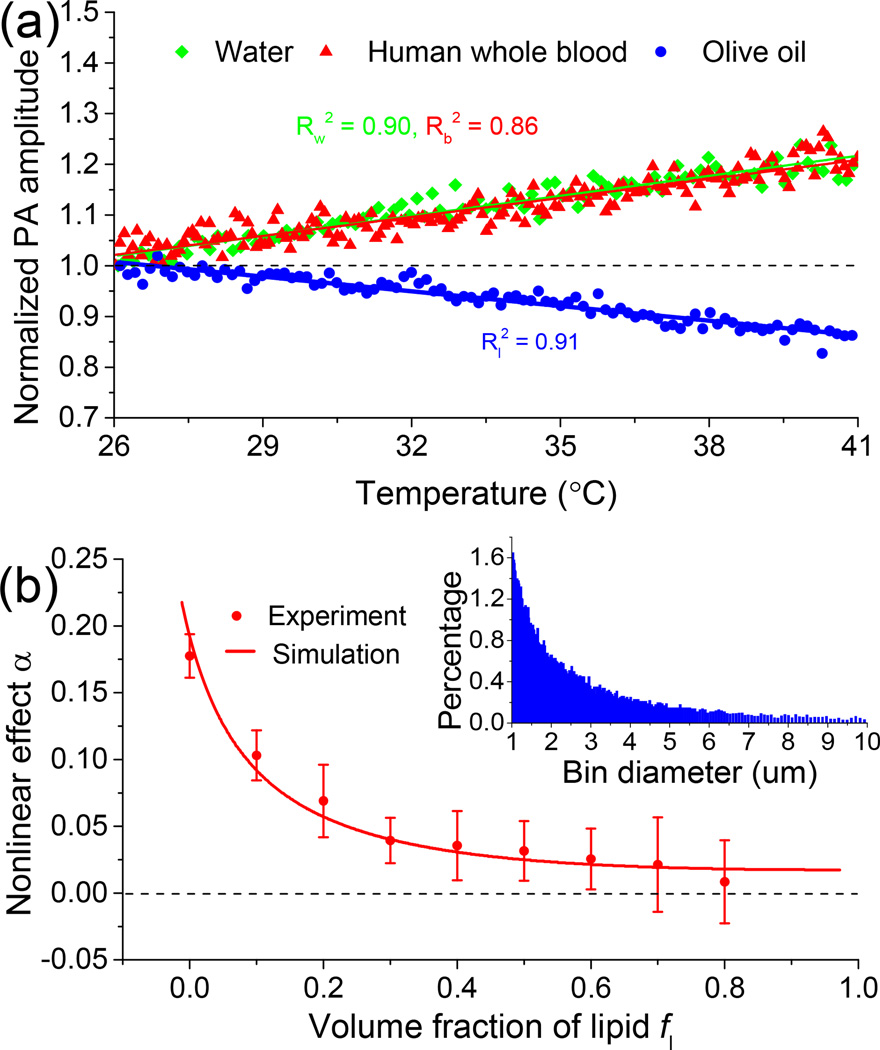
The DPNPC system (Fig. 1) employs two laser systems to create a pair of two short pulses. The heating laser is the second harmonic output (i.e., 532 nm) of a Nd:YAG laser (Powerlite DLS 8000, Continuum) with a pulse duration 6 ns and a repetition rate 10 Hz. The detecting laser is a tunable optical parametric oscillator (OPO) laser (Vibrant 532 I, Opotek Inc.) pumped by the second harmonic output of an Nd:YAG pulsed laser (Brilliant B, Quantel) with a pulse duration of 5 ns, and repetition rate of 10 Hz. The two lasers are sequentially triggered with a delay time Δt between them, which is precisely controlled by a delay generator (DG535, Standford Research Systems Inc.). The two laser beams are merged by a dichroic mirror (DMSP1000, Thorlabs) after passing the irises and then coupled into a multi-mode fiber (FG910LEC, Thorlabs; numerical aperture 0.22, core diameter 0.91 mm) by an aspheric lens (KPA031, Newport). The beams from the other port of the fiber are focused on the sample by a lens assembly consisting of a collimating lens (AC254-050-A, Thorlabs; focal length 50 mm) and a focusing lens (LB1757, Thorlabs; focal length 30 mm). The photoacoustic signals are received by a transducer (C323, Olympus NDT), amplified by a pulser and receiver (5072R, Olympus NDT) and finally digitized and recorded by an oscilloscope (TDS 540A, Tektronix). To validate that blood and lipid have different temperature-dependent Grüneisen parameters, photoacoustic signal amplitude versus temperature was measured for a whole blood specimen and an olive oil specimen, respectively. The sample temperature was adjusted precisely by using a temperature-controllable water bath. As shown in Fig. 2(a), the slopes of Grüneisen parameter of blood and lipid (i.e., ${\mathrm{\Gamma }}_b^{\prime }$ and ${\mathrm{\Gamma }}_l^{\prime }$) as functions of temperature rise are highly different. More specifically, Γ_b of blood increases with temperature rise, and shows a trend similar to that of water; while Γ_l of lipid decreases with temperature rise. The distinctive trends in photoacoustic signal amplitude verse temperature for different tissues lay foundation for possible diagnostic imaging and tissue characterization based on the DPNPC.

Fig. 1.

Schematic and principle of the DPNPC system. DM: dichroic mirror, MMF: multi-mode fiber.

Fig. 2.

(a) Photoacoustic signal amplitude as a function of temperature for water, human whole blood and olive oil. (b) Dual-pulse nonlinear photoacoustic effects of samples of blood and lipid mixtures with different lipid volume fractions. The inset shows the probability distribution of oil and water droplets with size.

We first studied the dual-pulse nonlinear photoacoustic effect in phantoms with different contents of lipid and blood, two major optical absorbers in liver tissues. To mimic the situation of different lipid contents for livers at various stages of steatosis, phantoms were made by mixing human whole blood and olive oil with different volume fractions. To mix blood and oil thoroughly, 1% Span 80 (S6760, Sigma-Alorich) and 1% Tween 80 (P8074, Sigma-Alorich) that make a blended surfactant with a hydrophile lipophile balance (HLB) value of ~10 were added to each sample. A grinder machine (Wig-L-Bug, Sigma-Alorich) was used to rapidly shake the solutions at a speed of 4800 rounds per minute (RPM) for 1 minute. The probability distribution of oil and water droplets with size after mixing is shown in the inset of Fig. 2(b). During the measurements, each sample was placed between two layers of clear plastic membranes, and then placed on the surface of the water. The heating laser works at λ₁ = 532 nm where hemoglobin has strong optical absorption; while the detecting laser works at λ₂ = 1210 nm which is an optical absorption peak of lipid. The delay time Δt between the two lasers is set to 30 µs. The scattered symbols in Fig. 2(b) show the experimental results from phantoms containing volume fractions of lipid f_l ranging from 0 to 0.8 with a constant interval 0.1. Each data point shows the average and the standard deviation of a number of 6 measurements each conducted with an average over 16 pairs of laser pulses. From Fig. 2(b), we can see that the nonlinear photoacoustic effect α of the mixtures first decreases rapidly with the increase of lipid content f_l and then stabilizes. To validate the photoacoustic measurements, simulations were also conducted based on the following parameters from the literatures [4, 14, 15]: μ_b(λ₁) = 234 cm⁻¹, μ_b(λ₂) = 1.0 cm⁻¹, μ_l(λ₁) = 0.01 cm⁻¹, μ_l(λ₂) = 1.6 cm⁻¹, Γ_0b = 0.12 at 22°C, ${\mathrm{\Gamma }}_b^{\prime }=0.005$, Γ_0l = 0.7 at 22°C and ${\mathrm{\Gamma }}_l^{\prime }=-0.015$. The simulation as shown by the solid curve in Fig. 2(b) has a good match with the experimental result, both suggesting that the DPNPC may contribute to the evaluation of chemical contents in biological tissues, e.g. increased lipid content in fatty livers.

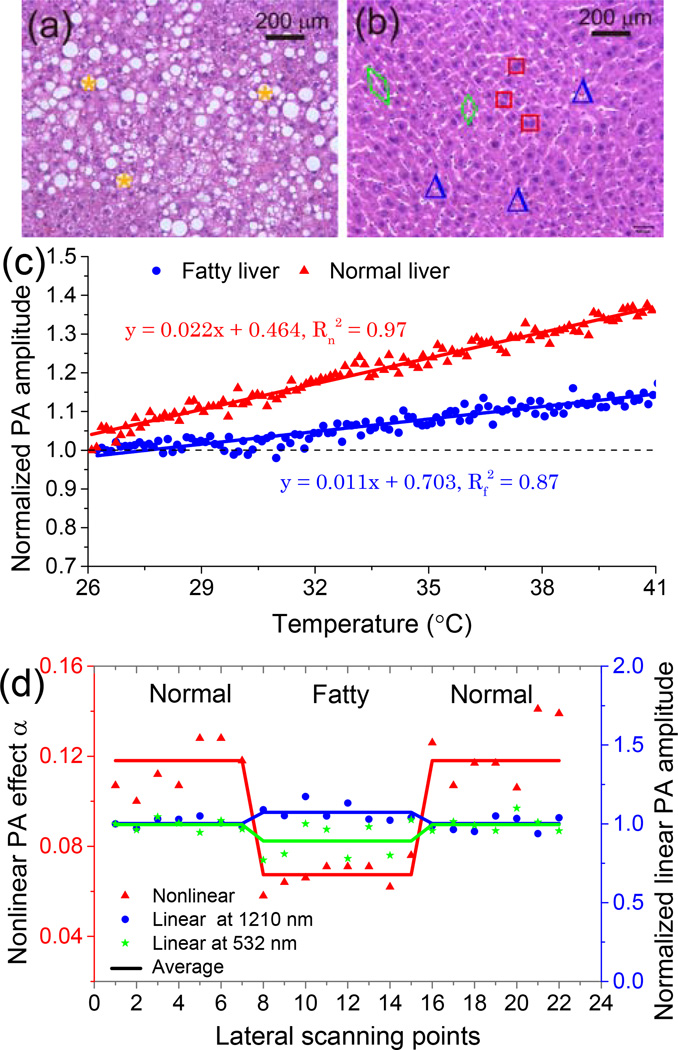
In normal livers, blood contributes to about 30% of the total liver weight; while the weight fraction of lipid is below 5% [16]. However, in fatty livers, fat accumulates significantly in hepatocytes; while the blood content in liver tissues decreases accordingly [16]. For severe cases, the lipid content may be more than 25% of the total liver weight [16]. To explore the sensitivity of the DPNPC to the change in lipid content in fatty liver, experiments were conducted on a well-established mouse model of liver steatosis. C57BL/6J wild type mice from Jackson laboratory were used. The obese group was fed with chow diet for the first 8 weeks, followed by 60% high-fat diet (Research diet, D12492) for the 12 weeks thereafter. The control group was fed with chow diet for 20 weeks. Both groups were sacrificed at the end of the 20th week. Then whole livers were harvested and kept fresh before photoacoustic measurements. As example histology photographs shown in Figs. 3(a) and 3(b), fatty livers in comparison with normal controls have a large number of lipid droplets in hepatocytes, as marked by yellow stars.

Fig. 3.

Characterization of fatty and normal mouse livers using the proposed DPNPC. (a) and (b) Example histology photographs of fatty and normal livers. *: lipid droplets, □: liver cell nuclei, △: blood cells, ◊: sinusoids. (c) Temperature-dependent photoacoustic signal amplitudes for a fatty liver and a normal control. (d) Dual-pulse nonlinear photoacoustic measurement (red triangles) and single-pulse linear photoacoustic measurements at 532 nm (green stars) and 1210 nm (blue circles) of fatty and normal livers.

We first conducted the temperature-dependent photoacoustic measurements on both fatty and normal livers at 1210 nm. Photoacoustic signals were collected from 26°C to 41°C with 64 averages at each temperature. As shown in Fig. 3(c), although the amplitude of photoacoustic signals from both the fatty and the normal livers increase with temperature, their trends are clearly different. The quantified slope of the fatty liver (0.011) is only about half of that of the normal control (0.022), which is a result of the tissue-specific temperature-dependent Grüneisen parameter.

The sample was prepared in such a way that a fatty liver was placed in the middle and two normal livers were on the two sides. Then dual-pulse nonlinear photoacoustic measurement was performed point-by-point across the sample surface. At each scanning point, the measurement was averaged over 36 pairs of laser pulses. The result scanned from the sample is shown in Fig. 3(d), where a distinct contrast exists between the fatty liver and the normal control. To quantify the contrast between them, the calculated contrast-to-noise ratio (CNR) is 14.2 dB. For comparison, we also performed single-pulse (i.e. linear) photoacoustic measurements of the fatty and the normal livers at 1210 nm and 532 nm, following the same sample preparing procedure and scanning geometry. The linear measurement results shown in Fig. 3(d) demonstrate weaker contrasts between the fatty and the normal livers with smaller CNRs of 3.7 dB for 1210 nm (blue circles) and 1.8 dB for 532 nm (green stars), respectively.

In conclusion, through the study on phantoms and a mouse model of fatty liver, we explored the feasibility of diagnostic imaging and tissue characterization based on a new contrast realized by dual-pulse photoacoustic measurement. Unlike conventional single-pulse photoacoustic measurement that maps tissue optical absorption, this DPNPC takes advantage of the temperature dependence of Grüneisen parameter of tissue, and presents additional diagnostic information for more comprehensive diagnosis. As demonstrated by the results on mouse livers, the nonlinear contrast can better differentiate fatty liver from normal control with a CNR larger than that of the linear contrast realized through the conventional single-pulse photoacoustic measurement. Based on the same contrast between lipid-rich and water-rich tissues, other potential applications in clinical settings include characterization of plaques in coronary arteries by evaluating the lipid contents in targeting plaques. Involving two lasers in the dual-pulse system leads to a higher cost, but this can be reduced by employing alternative heating mechanisms, such as high-intensity focused ultrasound (HIFU).

Since heating efficiency depends on the amount of absorbed laser energy, the dual-pulse nonlinear effect is sensitive to the heating laser wavelength and the laser fluence [Eq. (6)]. To maximize the nonlinear effect on livers, the heating and the detecting laser wavelengths should be optimized according to absorption peaks of both blood and lipid to achieve optimal temperature rise. In this preliminary study, to generate sufficient nonlinear effect, the estimated peak laser fluences for the heating and the detecting pulses were 900 mJ / cm² at 532 nm and 22 mJ / cm² at 1210 nm, respectively. Although the detecting pulse is safe, the heating laser fluence is much higher than the American National Standards Institute (ANSI) safety limit at 532 nm [17]. This value, however, is possible to be lowered by choosing proper heating laser wavelength, improving the sensitivity and stability of the system. In addition, considering the ANSI safety limit in the near-infrared range increases significantly (e.g. 1000 mJ / cm² at one optical absorption peak of lipid at 1720 nm [17]), the dual-pulse nonlinear measurement is possible to be realized in a noninvasive way. This was not considered in the prototype system because only one of the laser systems can cover the near-infrared spectrum.