Abstract
The field of vaccinology is increasingly moving toward the generation, analysis, and modeling of extremely large and complex high-dimensional datasets. We have used data such as these in the development and advancement of the field of vaccinomics to enable prediction of vaccine responses and to develop new vaccine candidates. However, the application of systems biology to what has been termed “big data,” or “high-dimensional data,” is not without significant challenges—chief among them a paucity of gold standard analysis and modeling paradigms with which to interpret the data. In this article, we relate some of the lessons we have learned over the last decade of working with high-dimensional, high-throughput data as applied to the field of vaccinomics. The value of such efforts, however, is ultimately to better understand the immune mechanisms by which protective and non-protective responses to vaccines are generated, and to use this information to support a personalized vaccinology approach in creating better, and safer, vaccines for the public health.
Introduction
Like personalized medicine, personalized vaccinology aims to provide the right vaccine, to the right patient, at the right time, to achieve protection from disease, while being safe (i.e., free from unintended side effects). The science through which such a vision can be realized is a field we have developed and termed “vaccinomics,” which is grounded within the immune response network theory[1-5]. The immune response network theory states that “the response to a vaccine is the cumulative result of interactions driven by a host of genes and their interactions, and is theoretically predictable.”[1] Further, the theory recognizes the impact of metagenomics, epigenetics, complementarity, epistasis, co-infections, and other factors including polymorphic plasticity. These factors, and others, explain the temporal, genetic, and immune responses that are deterministic and predictive of the immune response. In fact, we have published an initial equation describing this outcome.[4] Vaccinomics then uses this information to reverse engineer new vaccine candidates that overcome genetic or other barriers to the development of protective immunity.
Importantly, the above requires systems-level high-dimensional data in order to understand, at the whole-system level, the many perturbations a vaccine might induce in a host that result in immunity. Like any network, the immune response is composed of connected genetic features and networks of feedback loops. While exciting science, it makes application of systems biology to immune responses generated by vaccines in the individual challenging.
High-dimensional assays are generally resource intensive and typically used to perform an unbiased assessment of a biological system in order to generate hypotheses for further investigation. For example, measuring mRNA expression via next generation sequencing (NGS) allows one to screen approximately 20,000 genes for association with an outcome such as vaccine response. Although results from such screening studies must be replicated or functionally validated, it is nonetheless critical to avoid false-positive and false-negative findings by paying close attention to study design and analysis plans[6, 7]. Our goal herein is to convey some of the lessons we have learned over the last decade regarding sound principles of study design and analysis in experiments utilizing high-dimensional assays such as gene expression or genome wide SNP association studies, as applied to the field of vaccinology. While some of the points may appear simple and straightforward, which makes them easy to overlook, they require effort to implement in practice. We discuss study design, normalization, modeling, and determining statistical significance.
Study design
The relative abundance measures produced by most high-dimensional assays are susceptible to experimental artifacts such as batch effects[8]. Such artifacts add uninteresting, and often misleading, variation to the data. For example, in an mRNA Seq study we performed involving over 450 specimens, reagents were upgraded midway through the study, increasing the reads/lane by about 50% (Figures 1, 2). Usually, the causes of batch effects are less obvious than a reagent change. Thus, randomization, balance, and blocking are vital to ensure that biological effects and experimental artifacts can be distinguished from one another. Further information and detailed examples for how to implement these methods in practice are available[6, 9-12].
Figure 1.
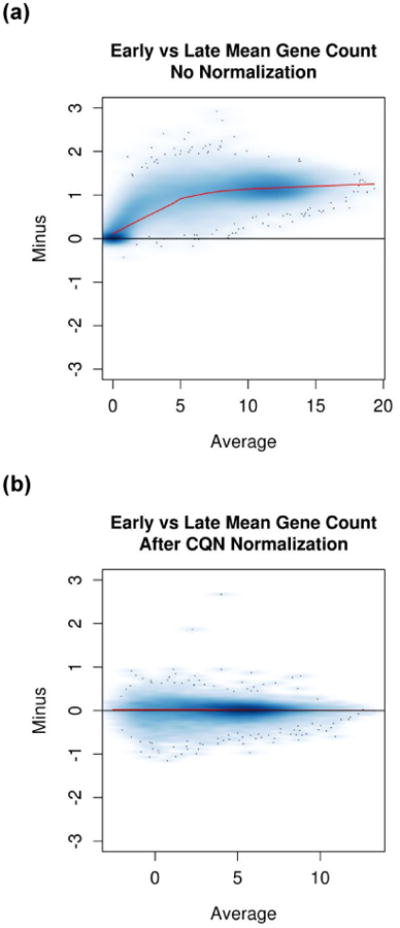
(a) Minus versus Average (MVA) plot demonstrating the effect of change in reagents and sequencing software. There is one data point for every feature measured on the assay. The x-axis is the average of each feature over all specimens in the study. Generally, the y-axis is the difference of each feature from the mean. Thus, if the observations are identical to the mean, all data points would lie on the y=0 line. Here, the y-axis is the difference between the before reagent change mean and the after reagent change mean. A reference line for y=0 as well as a loess smoother are included on the plot. If the smoother overlays the y-0 line, no normalization is needed. If the smoother is parallel to the y=0 line but shifted up or down, this indicates that between specimen biases are similar for all abundance levels and a linear normalization is needed. The nonlinear smoother demonstrates that nonlinear bias is present. (b). The same study shown after normalization and filtering out genes with median count <32. The fact that the smoother is now straight and lies on the y=0 line demonstrates that the bias has been removed.
Figure 2.
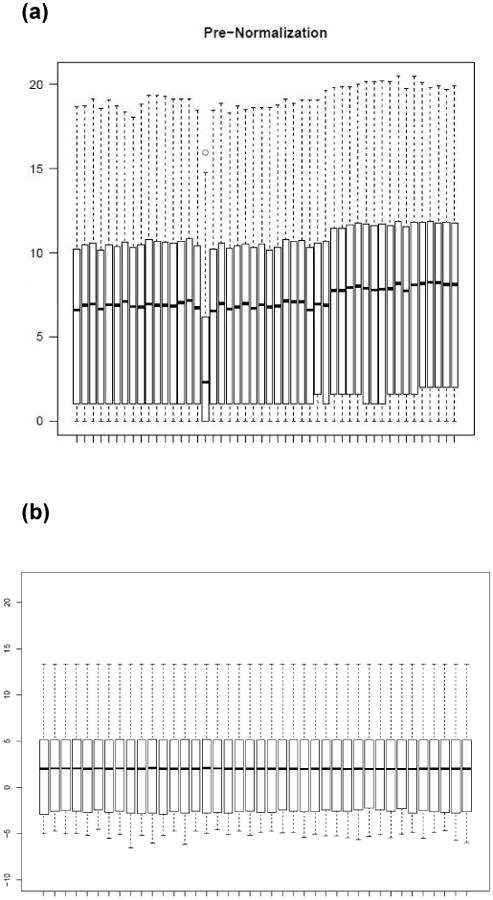
Box-and-whisker plots showing global distribution of per-gene counts on the log scale (y-axis) by lane (x-axis) sorted by assay order. Top, mid-line and bottom of boxes indicate 75th, 50th and 25th percentiles, respectively. (a) Pre-normalization. The total counts/lane increased from ∼150million to ∼200million after reagent and software upgrades. This is evident from the general shift up approximately two-thirds of the way across the plot. A failed specimen with median nearly half that of the neighboring specimens is evident about one-third of the way across the plot. The failed specimen was deleted in subsequent analyses. (b) Post-normalization. After normalization via Conditional Quantile Normalization (CQN)[82], the distributions of the specimens are aligned exactly at the maximum, 75th and 50th percentiles as expected. The lower counts are not exactly aligned since the smallest counts are not adjusted in CQN.
It is critical that study outcomes are appropriately defined. When studying vaccine response, known or established correlates of protection are typically used[13]. For example, an antibody level of at least 0.15ug/ml is considered protective against Haemophilus influenza type b. In other cases, commonly accepted levels of immunity are used as surrogates of protection (e.g., a hemagglutination inhibition antibody (HAI) titer of 1:40 for influenza or a neutralizing antibody titer of 1:32 for smallpox). These surrogates of protection represent a best guess at what level of immune response is sufficient to protect against overt disease at the population level.
Just as each pathogen and disease is different, so too are the immunologic responses critical for protection. Therefore, multiple immunologic endpoints may be tested in order to understand different components of the immune response. For example, for influenza one might consider an HAI titer of 1:40 to be protective, but define successful vaccine response as a four-fold increase in HAI titer. Alternatively, one might assess neutralizing antibody titer instead of, or in addition to, HAI titer. Also, for a fixed sample size, a dichotomous yes/no endpoint has approximately 30% less power than a continuous endpoint due to the information loss resulting from the categorization[14].
The proper timepoint(s) before and/or after vaccination must also be selected. For example, innate immune responses occur quite rapidly and monitoring after infection/vaccination might be hours (e.g., pattern recognition receptor pathway activation or IFNγ) or days (e.g., NK cell proliferation and activity). On the other hand, humoral immunity takes more time to develop, with IgM titers generally beginning to rise within 3-4 days and with plasmablasts being detectable between day 3 and 7, while IgG titers might peak at 2-4 weeks. Similarly, cellular immune responses might be best studied 2-3 weeks post-vaccination.
Another important consideration is the appropriate biological specimen for testing. Blood is an easily accessible biospecimen and yields both serum (antibody) and important leukocyte populations. A benefit of whole blood or peripheral blood mononuclear cell (PBMC) assays is that they require less manipulation and preserve cellular interactions among diverse cell subtypes. However, whole blood consists of multiple cell types, each with a unique response pattern that can be difficult to isolate or deconvolute from one another[15, 16]. Isolation of purified cell subtypes (e.g., by magnetic bead selection) allows one to obtain high-quality data on a single cell population without competing signals from less relevant cells. However, the purification process can be lengthy, with each manipulation provoking a stress response from the cells of interest. At the extreme single cell omics assays rapidly separate individual cells for study. Initial reports indicate that at the individual cell level, even phenotypically “identical” cells can differ dramatically[17]. Thus, at this point, the science is rapidly evolving and a gold-standard process is not yet apparent.
Assay quality control and normalization
Assessing data quality after assays are complete is important for both low and high-dimensional assays. An important step is normalization to remove systematic variation, such as variation in experimental conditions. We have extensively discussed the use of minus versus average (MVA) plots and box-and-whisker plots for this purpose elsewhere[12, 18]. These plots are useful for determining the appropriate normalization strategy for a given dataset as well. While normalization concepts are consistent across most high-dimensional assays, the precise strategies are assay dependent. The statistical model should describe all technical (normalization) effects and biological effects in the data. The general modeling framework is: observed value = experimental artifacts + biological effects +random error. In this regard, we briefly describe our experience in evaluating biases and normalization strategies for the Illumina DNA methylation 450K array. The complex assay design is described in full elsewhere[19]. In brief, there are two probe designs, each yielding an M and U intensity value (fluorescence intensity of methylated or un-methylated cells, respectively) that are mathematically combined to create an estimate of the percent methylation (β-value) in the specimen. We have observed nonlinear biases in both the M and U fluorescence intensities through the use of MVA plots (Figure 3a). However, it is not possible to model all effects due to confounding of technical and biological effects. We have observed, though, that these nonlinearities cancel out in the calculation of the β-value, and the between specimen biases on the β-value scale are linear (Figure 3b). A normalization strategy we have found to adequately address the technical artifacts without explicitly modeling each source of experimental noise is a variation on a strategy first proposed by Maribita et al. [20] as follows: 1) color-bias adjustment; 2) quantile normalization of intensity values between arrays, within probe design; 3) and beta-mixture quantile normalization (BMIQ)[21]. Box-and-whisker plots and MVA plots demonstrated that the assumption of only a few CpG sites being differentially methylated seemed to hold in our data.
Figure 3.
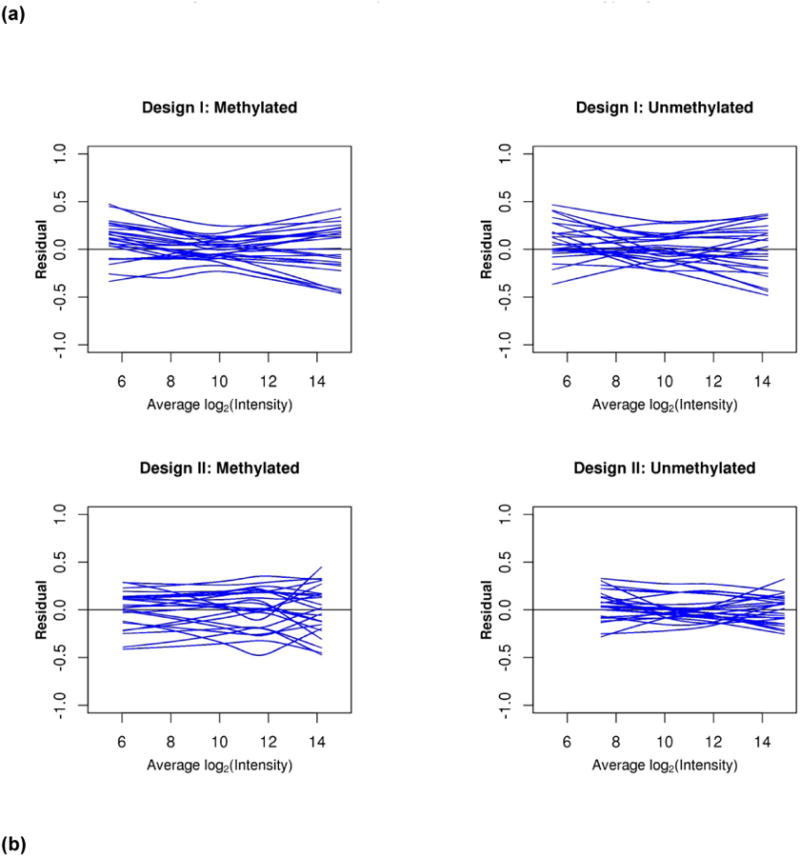
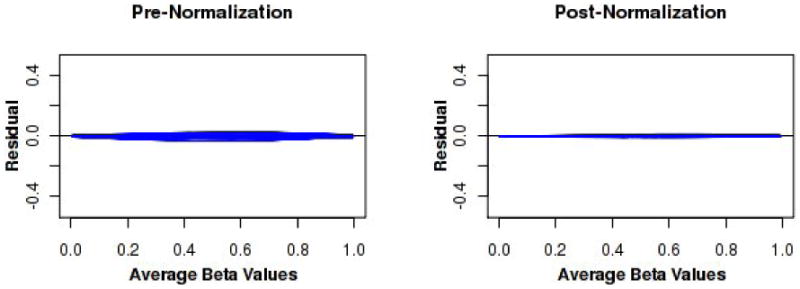
Over 450 PBMC specimens from healthy subjects aged 50-74 years old on were assayed on five bead array plates of the Illumina DNA methylation 450K assay. The assay utilizes two probe designs, each yielding an M and U intensity value (fluorescence intensity of methylated or un-methylated cells, respectively). These intensity values are mathematically combined to create an estimate of the percent methylation (β-value) in the specimen. (a) There is evidence of nonlinear between-specimen biases in the M and U expression intensities as demonstrated by these residual MVA plots. Each smoother represents one specimen. Nonlinearities are evident. (b) Between-specimen biases are near linear on the beta-value scale (left), are not large, and are essentially eliminated via this strategy (right).
Statistical Modeling
Appropriately applying analytical techniques to data is required to extract valid inferences from experimental data. Selecting an appropriate statistical approach requires knowledge of the properties of the phenotype, an understanding of the possible relationships between the explanatory variables and phenotype, and an evaluation of the ability of the method to detect meaningful associations. Correct application of statistical approaches can ensure the validity of the analytical results, and enhance the power to detect associations.
After quality control and normalization have been completed, it is essential that the distributional properties of the phenotype(s) are appropriate for analysis in a specific statistical approach. Because of the statistical power advantages of analyzing data on a continuous scale, it is often important that the distribution of the phenotype be reasonably well approximated by a normal distribution. If this assumption is not met, data transformations [e.g., setting y2 = log(y1)], can often be applied to approximate a normal distribution. For some outcomes it is often preferable to utilize models that are explicitly developed for the original source data. One example is the use of Poisson or negative binomial regression models for count data[22-24]. We and others have shown via use of MVA and Quantile-Quantile plots that the mean-variance relationship of mRNA Sequencing data agrees with negative binomial distributional assumptions[25].
Even when distributional assumptions are met, one must determine whether the modeling assumptions invoked to describe relationships between phenotype and explanatory variables are satisfied [26, 27]. The simplest relationship between explanatory and outcome variables is a linear one, which perfectly captures the relationship described by an explanatory variable with only two groups[26, 27]. Other relationships are often more appropriate. For example, it would not be appropriate to model a relationship that is expected to reflect exponential growth with a linear trend[26, 27]. Whether achieved through data transformations or by use of more sophisticated models [28], it is important to match statistical models to the expected behavior of the data.
Appropriately incorporating data measured in replicates into analyses can provide important benefits. Laboratory-based studies, where assay-to-assay variability is expected, are often performed in duplicate or triplicate[29-33]. A common analytical approach computes a summary measure and uses it as a single measured observation in analyses [34, 35]. However, it can be beneficial to utilize all observed values and test for associations while accounting for the repeated measurements. To quantify the benefit, we performed a simulation study of genetic associations between a SNP and a laboratory outcome, measured in triplicate in stimulated and unstimulated states. The results showed that statistical analyses that included and accounted for repeated measurements provided greater statistical power than analyses based on a single per-subject summary measure (see Figure 4), without inflating the false discovery rate. Additionally, when computing a summary measurement where subjects are evaluated in a control and an active state, one may be tempted to truncate the result and set the difference equal to a value of zero rather than allow a difference measure that is contrary to expected assay performance[36, 37]. However, the results from these simulations demonstrate that truncation to zero resulted in biased estimates of genetic effect size (Figure 5). This bias decreased when greater stimulatory effects were present for the assay, and where there was less measurement error, but these are situations with greatly reduced temptation for truncation.
Figure 4.
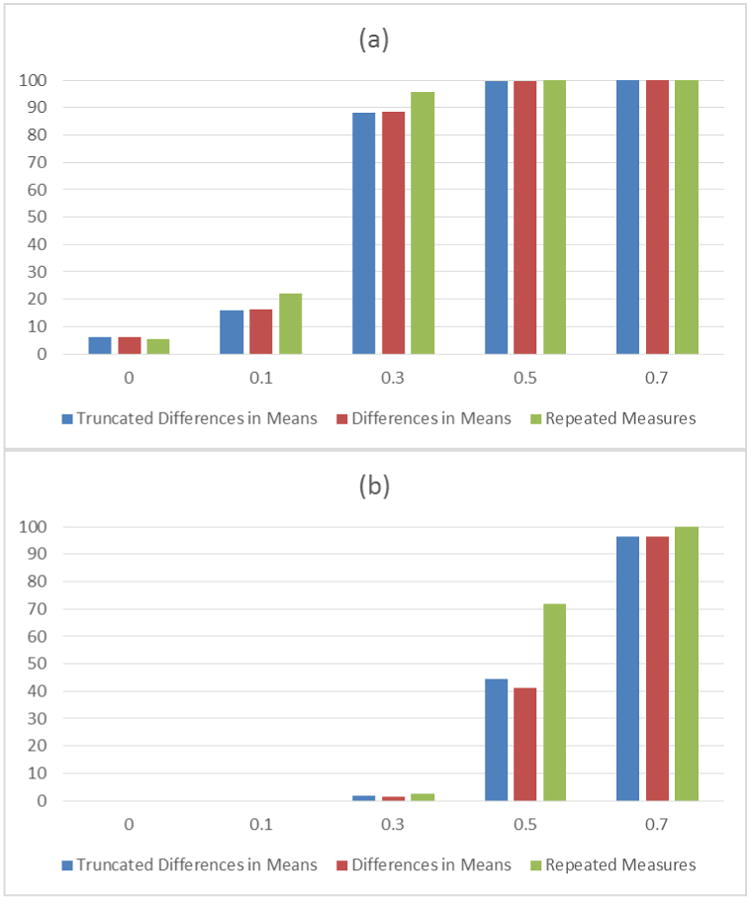
Power to detect genetic associations as a function of ordinal genotypic effect size for three different analyses, and with two different levels of significance. 1000 data sets were generated for each combination of parameters. Panel (a) shows statistical power for α=0.05 and panel (b) shows statistical power for a genome-wide significance threshold (α=5×10-8).
Figure 5.
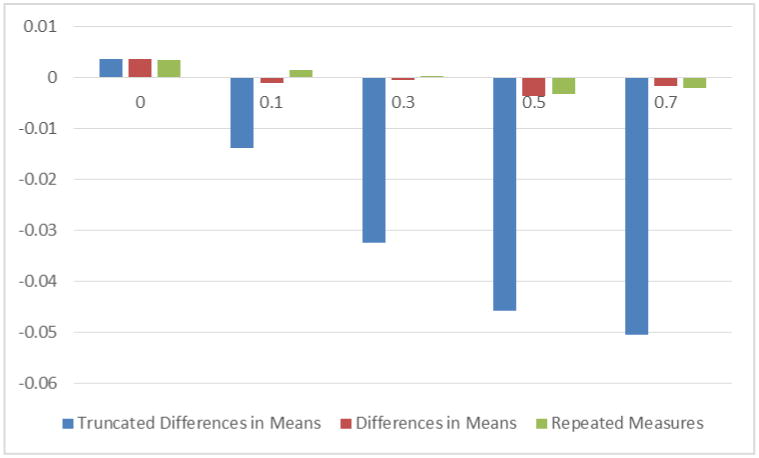
Bias in estimating an ordinal genotypic effect, as a function of the simulated ordinal genotypic effect size for three different analytical approaches.
Another aspect is whether baseline measurements should be used as an adjusting covariate when assessing change in response over time. There has been considerable debate [38-40] in the statistical literature on this topic because it is well known that different results—sometimes dramatic—can occur whether or not baseline is treated as an adjusting covariate. This has become known as Lord's Paradox[41] This paradox arises when the amount of change is associated with the baseline measurement. Without adjustment, the regression models evaluate whether change in response depends on covariates of interest, such as genetic markers. In contrast, adjustment for baseline gives a conditional change, conditional on groups having the same baseline. These two approaches answer different questions. Some advocate only adjusting for baseline when it is not associated with change (e.g., randomized studies)[38]. Perhaps the safest approach would be to perform both analyses to determine if adjustment for baseline leads to different results or unusual interpretations.
Declaring Statistical Significance
Exploratory analyses for high-dimensional data have great potential to discover new biologic mechanisms related to vaccine immunity and response, but come with the challenge of avoiding false-positive conclusions. Testing large numbers of hypotheses together with subgroup analyses make it necessary to attempt to control the number of false-positive results as well as assure adequate power. In traditional statistical testing, a result is declared statistically significant if the p-value is less than a threshold. When conducting a large number of statistical tests, the chance of at least one false positive result increases with the number of tests. Two commonly used approaches for controlling false discoveries are the Bonferroni correction and false-discovery rate (FDR). The two differ in the scope of tests considered. The Bonferroni correction controls the family-wise error rate (i.e., the chance of at least one false positive among all tests conducted), and is applied as the significance threshold divided by the total number of tests performed. FDR is a measure of the number of false discoveries, among those claimed to be significant, and is used to create an FDR-corrected p-value called a q-value[42]. If in truth there is at most one true effect out of the many statistical tests performed, then controlling the family-wise error rate is sensible, and the Bonferroni correction is the appropriate way to control false positives. In genome-wide association studies (GWAS), extremely small p-values, less than 5×10-8, have become standard for claiming statistical significance[43], with the benefit of producing reproducible results. Although this threshold is not solely based on the Bonferroni correction, but rather determined by empirical and simulation methods that capitalize on the linear structure of chromosomes and linkage disequilibrium among SNPs, it emphasizes the need for extremely small p-values when conducting hundreds of thousands to millions of statistical tests. In the field of gene-expression analyses, where there is prior biological evidence that many genes are often differentially expressed, the FDR and q-values have been the standard. Whether extreme p-values by Bonferroni correction, or less conservative FDR and q-values, are better depends on the number of underlying causal effects and whether the study is exploratory in nature versus being centered on planned hypotheses regarding an a priori list of genes. Another approach that focuses analysis on p-values is to evaluate whether small p-values tend to cluster in specified sets of genes (e.g., gene pathways). This sort of enrichment analysis, evaluating whether some genesets are more enriched for small p-values than other sets, has been widely popular for analyses of gene expression[44, 45], and to some extent for analysis of SNPs in GWAS[46, 47]. Given that most published findings are false[48], and p-values are not used as objectively and reliably as perceived[49], it is important to pay attention to the actual effect size, its confidence interval, and the sample size when interpreting results. In the end, reproducible results must be the gold standard[50].
An advantage of high-dimensional data is that one can examine the entire distribution of p-values to identify the existence of extreme p-values, and thereby make conclusions concerning statistical significance. When there is no true causal effect in a set of data, the p-values are expected to be uniformly distributed between 0 and 1. A skew of p-values toward 0 suggests that there is likely a mixture of true effects (with small p-values) and null effects (with p-values uniformly distributed 0-1). Although one could use a histogram to see if the p-values have a uniform distribution, a more refined way is a quantile-quantile (QQ) plot, which plots the observed versus null expected distributions. Any points deviating from the diagonal of the plot suggest departures from the null. In GWAS with few expected true effects, extremely small p-values are expected to depart the diagonal only at the end, where small p-values occur. Departure from the diagonal for many p-values, even those not extremely small, is a strong indicator of systematic bias, such as batch effects, or population stratification. Population stratification can arise in GWAS when the cases and controls are a heterogeneous mixture of different ancestral groups. A simple way to control for population stratification is to estimate the principal components of the SNP correlation matrix, and use those principal components that explain the most variation in the matrix as adjusting covariates[51]. Alternatively, in gene expression studies, many p-values are expected to deviate from the diagonal since many true effects are generally expected. Deviation indicating a skew toward non-significance could indicate presence of heavy between-gene correlation in the data, or that model assumptions are not satisfied. The principal component approach can be used for gene expression studies that have subtle batch effects to increase power, using principal components from the gene expression correlation matrix.
The importance of replicating a result found from an exploratory study cannot be over emphasized. But, replication can be a challenging and expensive task. Because of the importance of replication, and the challenges implementing it, the National Cancer Institute and National Human Genome Research Institute held a workshop on this topic for genotype-phenotype associations, resulting in published guidelines on evaluating and interpreting initial reports on genotype-phenotype associations, as well as criteria for replication (Table 1)[50]. Because replication is challenging, becoming more standard, and required by high-profile journals for publication, it is tempting to split a sample in half to use half for discovery and half for replication. This strategy, however, only works if both halves have sufficient power. Splitting a sample into two low-powered samples has lower power than a single sample analysis[52]. To emphasize, a low-powered discovery sample will likely miss important effects, never having the opportunity to replicate. Also, a low-powered replicate sample will likely fail to replicate an important discovery. It is better to analyze all the data for initial discovery, with optimal power, and find alternative ways to replicate (via collaborations) or to conduct functional studies.
Table 1. Summary of published guidelines for replication studies.
| • A strong rationale for what to replicate |
| • Sufficient sample size in replicate study |
| • Replication in independent data |
| • Similar replicate population as initial study |
| • Similar phenotype and biological assays |
| • Similar magnitude and direction of effect |
| • Statistical methods similar to the initial study |
| • Pre-specified statistical criteria for replicated significance |
Predicting vaccine immune response
One of the goals of high-dimensional analysis in vaccine studies is to use early changes in post vaccination gene expression to predict an individual's immune response. Early changes due to cellular activation and signaling induced by the vaccine are believed to set in motion steady-state immunogenicity and/or reactogenicity that may be predicted from the patterns of early expression change. For example, machine learning methods have been used for prediction of systemic adverse events in smallpox vaccine[53, 54] and high versus low HAI titer in yellow fever[55] and influenza[56].
There are numerous machine learning classifiers to choose from: tree-based (Random Forest, ADA Boost, etc.), Naïve Bayes, k-nearest neighbors, logistic regression, support vector machines (SVM), and discriminant analysis via mixed integer programming (DAMIP), etc.[57-60]. Most classifiers can yield competitive classification performance if sound internal model validation practices such as cross validation are utilized to provide honest estimates of model performance[14, 61]. K-fold cross validation is accomplished by leaving 1/k of the data out for validation and using the remainder to build a model. The process is repeated until all data has been left out for validation. Most classification methods have “tuning” parameters that must be estimated by using an inner cross validation loop called nested cross-validation[62, 63]. For gene expression data, sample size calculations for classifier development has been shown to rely primarily on the number of genes or features, maximum fold change, and the proportion of subjects in each group[64, 65].
Most algorithms are designed to predict dichotomous outcomes that can be used for outcomes such as ≥4-fold increase in HAI titer. However, one may wish to predict the continuous Day 28 HAI titer after adjusting for covariates like age and sex. The trivalent influenza vaccine also poses a challenge to defining outcome because there is an HAI outcome for each vaccine virus strain. A common solution is to use the maximum HAI from the three strains[56, 66]. For such continuous predictor and outcome data types, linear regression is a simple but powerful approach, and penalized regression has the added benefit of selecting important predictors, called feature selection[59].
Machine learning approaches typically use single-gene variable selection to select a set of genes for use in predicting response. However, immune response to vaccination is likely reflected in gene expression data by subtle variation distributed throughout functional gene networks. Analytical methods utilizing sets of genes believed to be functionally related, called genesets or modules, have been shown to have greater power than single-gene analyses, presumably due to the aggregation of multiple genes working in concert to achieve response to vaccination[67-69].
Immune-specific genesets and modules have been developed[70-73] and used for modeling vaccine response, and can be helpful in reducing the number of input variables[74, 75]. Modules and genesets have the potential to improve the predictive ability of machine learning classifiers since they are more likely to be rooted in biological function. Tan et al. successfully used single-sample GSEA (ssGSEA) scores[76] to summarize geneset activity as inputs into a classifier[72]. While use of previously defined modules reduces the risk of false positives, it has the risk of missing novel gene expression variation or interactions that may occur in a new vaccine, season or population. Data-driven module derivation should be included within a nested cross-validation procedure to avoid biased estimates of classification error rates.
Genes are generally included in a classifier that is based on single gene marginal associations with the outcome. However, additional information may reside in interactions among genes. Networks constructed from statistical gene-gene interactions have been able to detect gene hubs that influence smallpox vaccine response[77]. Relief-F is an algorithm that has been used to detect such interactions for microarray, RNA-Seq, and GWAS in measles and smallpox vaccine studies[78, 79]. Again, internal and external validation of findings is necessary.
Summary and Conclusions
The use of high-dimensional data in vaccinology has immense potential to advance the science and enable the creation of better and safer next-generation vaccines that protect the public health. Such scientific advances, however, are expensive since the generation, analysis, visualization, and interpretation of such data is extremely challenging. Rigorous attention to study design and the factors discussed above represent solutions to a number of the many challenges. The nature of understanding and predicting immune responses demands that large numbers of heterogeneous groups be studied under carefully controlled studies and processes. Discovery, replication, and validation of study findings require that consortia and “team” science be fully implemented in order to advance the science with alacrity. In turn, this requires the further development of increasingly more precise yet cheaper omics technologies, new analytic routines for visualization and interpretation of the data, and the collaboration of teams of scientists with content expertise in study design, bioinformatics, biostatistics, virology, immunology, and other disciplines. Particularly important is the need for large sample sizes, which can become prohibitively expensive; yet, without such sample sizes, the small to moderate size of genetic effects anticipated in immune response will likely go undetected. Large sample sizes are particularly important when studying rare vaccine phenomena such as adverse events – a field we have termed “adversomics”[4, 80, 81].
A nascent example of such consortia is the NIH-funded and sponsored Human Immunophenotype Consortium (HIPC, http://www.immuneprofiling.org/) within which the authors are contributing scientists. An advantage of such consortia is the ability to bring together teams of scientists working in different disciplines, centered on common scientific questions. Data generated from such studies are deposited into publically available databases for use by other scientists to further advance the science. Through participation in this Consortium, we have learned valuable lessons in the need for normalization, documentation, and standardization so that datasets can be productively shared with the larger research community. One important aspect is the development of transparent analysis pipelines that are robust and user-friendly for a broad user base. While we did not address this or analysis software here due to space constraints, the development of such pipelines in the absence of gold standard algorithms is not straightforward and requires immense communication.
The public health demands that new, better, and safer vaccines be developed – particularly against such threats a Ebola virus, hepatitis C, pandemic influenza viruses, malaria, TB, and a myriad of other hyper-variable viruses. In this regard, we believe that the use of vaccinomics and adversomics has the real potential to solve some of mankind's most pressing and vexing vaccine problems.
Acknowledgments
This research was supported by the U.S. Public Health Service, National Institutes of Health, contract grant number GM065450 (DJS), the National Institute of Allergy And Infectious Diseases of the National Institutes of Health, under award numbers U01AI089859 (ALO, GAP, BAM, RBK), U01IOFAI89859 (ALO, BAM), and N01AI40065 (ALO, DJS, GAP, BAM, VSP, RBK). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Conflicts of Interest: ALO, BAM, VSP, RBK and DJS declare no conflicts of interest. Dr. Poland is the chair of a Safety Evaluation Committee for novel investigational vaccine trials being conducted by Merck Research Laboratories. Dr. Poland offers consultative advice on vaccine development to Merck & Co. Inc., CSL Biotherapies, Avianax, Sanofi Pasteur, Dynavax, Novartis Vaccines and Therapeutics, PAXVAX Inc, Emergent Biosolutions, Adjuvance, and Vaxness. Dr. Poland holds two patents related to vaccinia and measles peptide research. These activities have been reviewed by the Mayo Clinic Conflict of Interest Review Board and are conducted in compliance with Mayo Clinic Conflict of Interest policies. This research has been reviewed by the Mayo Clinic Conflict of Interest Review Board and was conducted in compliance with Mayo Clinic Conflict of Interest policies.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Poland GA. Pharmacology, vaccinomics, and the second golden age of vaccinology. Clin Pharmacol Ther. 2007 Dec;82(6):623–6. doi: 10.1038/sj.clpt.6100379. [DOI] [PubMed] [Google Scholar]
- 2.Poland GA, Ovsyannikova IG, Jacobson RM. Personalized vaccines: the emerging field of vaccinomics. Expert Opin Biol Ther. 2008 Nov;8(11):1659–67. doi: 10.1517/14712598.8.11.1659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Poland GA, Oberg AL. Vaccinomics and bioinformatics: accelerants for the next golden age of vaccinology. Vaccine. 2010 Apr 30;28(20):3509–10. doi: 10.1016/j.vaccine.2010.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Poland GA, Kennedy RB, McKinney BA, Ovsyannikova IG, Lambert ND, Jacobson RM, et al. Vaccinomics, adversomics, and the immune response network theory: Individualized vaccinology in the 21st century. Semin Immunol. 2013 Jun 4; doi: 10.1016/j.smim.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Oberg AL, Kennedy RB, Li P, Ovsyannikova IG, Poland GA. Systems biology approaches to new vaccine development. Curr Opin Immunol. 2011 May 11; doi: 10.1016/j.coi.2011.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ransohoff DF. How to improve reliability and efficiency of research about molecular markers: roles of phases, guidelines, and study design. Journal of clinical epidemiology. 2007 Dec;60(12):1205–19. doi: 10.1016/j.jclinepi.2007.04.020. [DOI] [PubMed] [Google Scholar]
- 7.Ransohoff DF. Bias as a Threat to the Validity of Cancer Molecular-Marker Research. Nature Reviews Cancer. 2005;5:142–9. doi: 10.1038/nrc1550. [DOI] [PubMed] [Google Scholar]
- 8.Leek JT, Scharpf RB, Bravo HC, Simcha D, Langmead B, Johnson WE, et al. Tackling the widespread and critical impact of batch effects in high-throughput data. Nature reviews. 2010 Oct 11;11(10):733–9. doi: 10.1038/nrg2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ransohoff DF. Lessons from controversy: ovarian cancer screening and serum proteomics. J Natl Cancer Inst. 2005 Feb 16;97(4):315–9. doi: 10.1093/jnci/dji054. [DOI] [PubMed] [Google Scholar]
- 10.Croswell JM, Ransohoff DF, Kramer BS. Principles of cancer screening: lessons from history and study design issues. Seminars in oncology. Jun;37(3):202–15. doi: 10.1053/j.seminoncol.2010.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Oberg AL, Vitek O. Statistical design of quantitative mass spectrometry-based proteomic experiments. J Proteome Res. 2009 May;8(5):2144–56. doi: 10.1021/pr8010099. [DOI] [PubMed] [Google Scholar]
- 12.Oberg AL, Mahoney DW. Statistical methods for quantitative mass spectrometry proteomic experiments with labeling. BMC bioinformatics. 2012;13(Suppl 16):S7. doi: 10.1186/1471-2105-13-S16-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Plotkin SA. Correlates of protection induced by vaccination. Clinical and vaccine immunology : CVI. 2010 Jul;17(7):1055–65. doi: 10.1128/CVI.00131-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Harrell FE. Regression modeling strategies: with applications to linear models, logistic regression, and survival analysis. Springer; 2001. [Google Scholar]
- 15.Zhao Y, Simon R. Gene expression deconvolution in clinical samples. Genome Med. 2010;2(12):93. doi: 10.1186/gm214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shen-Orr SS, Tibshirani R, Khatri P, Bodian DL, Staedtler F, Perry NM, et al. Cell type-specific gene expression differences in complex tissues. Nature methods. 2010 Apr;7(4):287–9. doi: 10.1038/nmeth.1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shalek AK, Satija R, Adiconis X, Gertner RS, Gaublomme JT, Raychowdhury R, et al. Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells. Nature. 2013 Jun 13;498(7453):236–40. doi: 10.1038/nature12172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cunningham JM, Oberg AL, Borralho PM, Kren BT, French AJ, Wang L, et al. Evaluation of a new high-dimensional miRNA profiling platform. BMC medical genomics. 2009;2:57. doi: 10.1186/1755-8794-2-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bibikova M, Barnes B, Tsan C, Ho V, Klotzle B, Le JM, et al. High density DNA methylation array with single CpG site resolution. Genomics. 2011 Oct;98(4):288–95. doi: 10.1016/j.ygeno.2011.07.007. [DOI] [PubMed] [Google Scholar]
- 20.Marabita F, Almgren M, Lindholm ME, Ruhrmann S, Fagerstrom-Billai F, Jagodic M, et al. An evaluation of analysis pipelines for DNA methylation profiling using the Illumina Human Methylation 450 BeadChip platform. Epigenetics. 2013 Mar 1;8(3):333–46. doi: 10.4161/epi.24008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Teschendorff AE, Marabita F, Lechner M, Bartlett T, Tegner J, Gomez-Cabrero D, et al. A beta-mixture quantile normalization method for correcting probe design bias in Illumina Infinium 450 k DNA methylation data. Bioinformatics. 2013 Jan 15;29(2):189–96. doi: 10.1093/bioinformatics/bts680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Robinson MD, Smyth GK. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics. 2007 Nov 1;23(21):2881–7. doi: 10.1093/bioinformatics/btm453. [DOI] [PubMed] [Google Scholar]
- 23.Robinson MD, Smyth GK. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics. 2008 Apr;9(2):321–32. doi: 10.1093/biostatistics/kxm030. [DOI] [PubMed] [Google Scholar]
- 24.Robinson MD, McCarthy DJ, Smyth GK. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010 Nov 11;26(1):139–40. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Oberg AL, Bot BM, Grill DE, Poland GA, Therneau TM. Technical and biological variance structure in mRNA-Seq data: life in the real world. BMC genomics. 2012;13:304. doi: 10.1186/1471-2164-13-304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Draper N, Smith H. Applied Regression Analysis. Third. John Wiley & Sons, Inc.; 1998. [Google Scholar]
- 27.Kutner MH, Nachtsheim CJ, Netter J, Li W. Applied linear models. 2005 [Google Scholar]
- 28.Durrleman S, Simon R. Flexible regression models with cubic splines. Statistics in medicine. 1989 May;8(5):551–61. doi: 10.1002/sim.4780080504. [DOI] [PubMed] [Google Scholar]
- 29.van Meerloo J, Kaspers GJ, Cloos J. Cell sensitivity assays: the MTT assay. Methods Mol Biol. 2011;731:237–45. doi: 10.1007/978-1-61779-080-5_20. [DOI] [PubMed] [Google Scholar]
- 30.Musselli C, Ragupathi G, Gilewski T, Panageas KS, Spinat Y, Livingston PO. Reevaluation of the cellular immune response in breast cancer patients vaccinated with MUC1. Int J Cancer. 2002 Feb 10;97(5):660–7. doi: 10.1002/ijc.10081. [DOI] [PubMed] [Google Scholar]
- 31.Kennedy RB, Ovsyannikova IG, Pankratz VS, Vierkant RA, Jacobson RM, Ryan MA, et al. Gender effects on humoral immune responses to smallpox vaccine. Vaccine. 2009 May 26;27(25-26):3319–23. doi: 10.1016/j.vaccine.2009.01.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lambert ND, Haralambieva IH, Ovsyannikova IG, Larrabee BR, Pankratz VS, Poland GA. Characterization of humoral and cellular immunity to rubella vaccine in four distinct cohorts. Immunol Res. 2014 Jan;58(1):1–8. doi: 10.1007/s12026-013-8475-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kennedy RB, Ovsyannikova IG, Haralambieva IH, Lambert ND, Pankratz VS, Poland GA. Genome-wide SNP associations with rubella-specific cytokine responses in measles-mumps-rubella vaccine recipients. Immunogenetics. 2014 Aug;66(7-8):493–9. doi: 10.1007/s00251-014-0776-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Poland GA, Ovsyannikova IG, Jacobson RM, Vierkant RA, Jacobsen SJ, Pankratz VS, et al. Identification of an association between HLA class II alleles and low antibody levels after measles immunization. Vaccine. 2001 Nov 12;20(3-4):430–8. doi: 10.1016/s0264-410x(01)00346-2. [DOI] [PubMed] [Google Scholar]
- 35.Ovsyannikova IG, Jacobson RM, Vierkant RA, Jacobsen SJ, Pankratz VS, Poland GA. The contribution of HLA class I antigens in immune status following two doses of rubella vaccination. Human immunology. 2004 Dec;65(12):1506–15. doi: 10.1016/j.humimm.2004.07.001. [DOI] [PubMed] [Google Scholar]
- 36.Schumann A, Fiedler M, Dahmen U, Grosse-Wilde H, Roggendorf M, Lindemann M. Cellular and humoral immune response to a third generation hepatitis B vaccine. J Viral Hepat. 2007 Aug;14(8):592–8. doi: 10.1111/j.1365-2893.2007.00848.x. [DOI] [PubMed] [Google Scholar]
- 37.Roponen M, Yerkovich ST, Hollams E, Sly PD, Holt PG, Upham JW. Toll-like receptor 7 function is reduced in adolescents with asthma. Eur Respir J. 2010 Jan;35(1):64–71. doi: 10.1183/09031936.00172008. [DOI] [PubMed] [Google Scholar]
- 38.Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. 2nd. Hoboken, NJ: John Wiley & Sons, Inc.; 2011. [Google Scholar]
- 39.Norman GR. Issues in the use of change scores in randomized trials. Journal of clinical epidemiology. 1989;42(11):1097–105. doi: 10.1016/0895-4356(89)90051-6. [DOI] [PubMed] [Google Scholar]
- 40.Oakes JM, Feldman HA. Statistical power for nonequivalent pretest-posttest designs. The impact of change-score versus ANCOVA models. Eval Rev. 2001 Feb;25(1):3–28. doi: 10.1177/0193841X0102500101. [DOI] [PubMed] [Google Scholar]
- 41.Lord FM. A paradox in the interpretation of group comparisons. Psychological bulletin. 1967 Nov;68(5):304–5. doi: 10.1037/h0025105. [DOI] [PubMed] [Google Scholar]
- 42.Storey JD, Tibshirani R. Statistical significance for genomewide studies. PNAS. 2003;100(16):9440–5. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Frazer KA, Ballinger DG, Cox DR, Hinds DA, Stuve LL, Gibbs RA, et al. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007 Oct 18;449(7164):851–61. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Goeman JJ, Buhlmann P. Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics. 2007 Apr 15;23(8):980–7. doi: 10.1093/bioinformatics/btm051. [DOI] [PubMed] [Google Scholar]
- 45.Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA. 2005 Oct 25;102(43):15545–50. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schaid DJ, Sinnwell JP, Jenkins GD, McDonnell SK, Ingle JN, Kubo M, et al. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genetic Epidem. 2012 Dec 7;36:3–16. doi: 10.1002/gepi.20632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang L, Jia P, Wolfinger RD, Chen X, Zhao Z. Gene set analysis of genome-wide association studies: Methodological issues and perspectives. Genomics. 2011 Apr 30; doi: 10.1016/j.ygeno.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ioannidis JP. Why most published research findings are false. PLoS medicine. 2005 Aug;2(8):e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nuzzo R. Scientific method: statistical errors. Nature. 2014 Feb 13;506(7487):150–2. doi: 10.1038/506150a. [DOI] [PubMed] [Google Scholar]
- 50.Chanock SJ, Manolio T, Boehnke M, Boerwinkle E, Hunter DJ, Thomas G, et al. Replicating genotype-phenotype associations. Nature. 2007 Jun 7;447(7145):655–60. doi: 10.1038/447655a. [DOI] [PubMed] [Google Scholar]
- 51.Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature genetics. 2006 Aug;38(8):904–9. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 52.Skol AD, Scott LJ, Abecasis GR, Boehnke M. Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nature Genet. 2006;38(2):209–13. doi: 10.1038/ng1706. [DOI] [PubMed] [Google Scholar]
- 53.McKinney BA, Reif DM, Rock MT, Edwards KM, Kingsmore SF, Moore JH, et al. Cytokine expression patterns associated with systemic adverse events following smallpox immunization. The Journal of infectious diseases. 2006 Aug 15;194(4):444–53. doi: 10.1086/505503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Reif DM, Motsinger-Reif AA, McKinney BA, Rock MT, Crowe JE, Jr, Moore JH. Integrated analysis of genetic and proteomic data identifies biomarkers associated with adverse events following smallpox vaccination. Genes and immunity. 2009 Mar;10(2):112–9. doi: 10.1038/gene.2008.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Querec TD, Akondy RS, Lee EK, Cao W, Nakaya HI, Teuwen D, et al. Systems biology approach predicts immunogenicity of the yellow fever vaccine in humans. Nat Immunol. 2009 Jan;10(1):116–25. doi: 10.1038/ni.1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nakaya HI, Wrammert J, Lee EK, Racioppi L, Marie-Kunze S, Haining WN, et al. Systems biology of vaccination for seasonal influenza in humans. Nat Immunol. 2011 Aug;12(8):786–95. doi: 10.1038/ni.2067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gallagher RJ, Lee EK, Patterson DA. Constrained discriminant analysis via 0/1 mixed integer programming. Annals of Operations Research. 1997;74(0):65–88. [Google Scholar]
- 58.Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- 59.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second. Springer; Feb 09, 2009. (Springer Series in Statistics). 2009. [Google Scholar]
- 60.James G, Witten D, Hastie T, Tibshirani R. An Introduction to Statistical Learning: with Applications in R. New York: Springer; 2013. [Google Scholar]
- 61.Shi L, Campbell G, Jones WD, Campagne F, Wen Z, Walker SJ, et al. The MicroArray Quality Control (MAQC)-II study of common practices for the development and validation of microarray-based predictive models. Nat Biotechnol. 2010 Aug;28(8):827–38. doi: 10.1038/nbt.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Varma S, Simon R. Bias in error estimation when using cross-validation for model selection. BMC bioinformatics. 2006;7:91. doi: 10.1186/1471-2105-7-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Simon R, Radmacher MD, Dobbin K, McShane LM. Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification. Journal of the National Cancer Institute 2003. 2003 Jan 1;95(1):14–8. doi: 10.1093/jnci/95.1.14. [DOI] [PubMed] [Google Scholar]
- 64.Dobbin KK, Simon RM. Sample size planning for developing classifiers using high-dimensional DNA microarray data. Biostatistics. 2007;8(1):101–17. doi: 10.1093/biostatistics/kxj036. [DOI] [PubMed] [Google Scholar]
- 65.Dobbin KK, Zhao Y, Simon RM. How large a training set is needed to develop a classifier for microarray data? Clinical Cancer Research. 2008;14(1):108–14. doi: 10.1158/1078-0432.CCR-07-0443. [DOI] [PubMed] [Google Scholar]
- 66.Tsang JS, Schwartzberg PL, Kotliarov Y, Biancotto A, Xie Z, Germain RN, et al. Global analyses of human immune variation reveal baseline predictors of postvaccination responses. Cell. 2014 Apr 10;157(2):499–513. doi: 10.1016/j.cell.2014.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Newton MA, Quintana FA, Den Boon JA, Sengupta S, Ahlquist P. Random-set methods identify distinct aspects of the enrichment signal in gene-set analysis. The Annals of Applied Statistics. 2007;1(1):85–106. [Google Scholar]
- 68.Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci U S A. 2005 Oct 25;102(43):15545–50. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Efron B, Tibshirani R. On testing the significance of sets of genes. The Annals of Applied Statistics. 2007;1(1):107–29. [Google Scholar]
- 70.Chaussabel D, Quinn C, Shen J, Patel P, Glaser C, Baldwin N, et al. A modular analysis framework for blood genomics studies: application to systemic lupus erythematosus. Immunity. 2008 Jul 18;29(1):150–64. doi: 10.1016/j.immuni.2008.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Segal E, Shapira M, Regev A, Pe'er D, Botstein D, Koller D, et al. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nature genetics. 2003 Jun;34(2):166–76. doi: 10.1038/ng1165. [DOI] [PubMed] [Google Scholar]
- 72.Tan Y, Tamayo P, Nakaya H, Pulendran B, Mesirov JP, Haining WN. Gene signatures related to B-cell proliferation predict influenza vaccine-induced antibody response. Eur J Immunol. 2014 Jan;44(1):285–95. doi: 10.1002/eji.201343657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Li S, Rouphael N, Duraisingham S, Romero-Steiner S, Presnell S, Davis C, et al. Molecular signatures of antibody responses derived from a systems biology study of five human vaccines. Nat Immunol. 2014 Feb;15(2):195–204. doi: 10.1038/ni.2789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Furman D, Hejblum BP, Simon N, Jojic V, Dekker CL, Thiebaut R, et al. Systems analysis of sex differences reveals an immunosuppressive role for testosterone in the response to influenza vaccination. Proceedings of the National Academy of Sciences of the United States of America. 2014 Jan 14;111(2):869–74. doi: 10.1073/pnas.1321060111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Furman D, Jojic V, Kidd B, Shen-Orr S, Price J, Jarrell J, et al. Apoptosis and other immune biomarkers predict influenza vaccine responsiveness. Mol Syst Biol. 2013;9:659. doi: 10.1038/msb.2013.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Barbie DA, Tamayo P, Boehm JS, Kim SY, Moody SE, Dunn IF, et al. Systematic RNA interference reveals that oncogenic KRAS-driven cancers require TBK1. Nature. 2009 Nov 5;462(7269):108–12. doi: 10.1038/nature08460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Davis NA, Crowe JE, Jr, Pajewski NM, McKinney BA. Surfing a genetic association interaction network to identify modulators of antibody response to smallpox vaccine. Genes and immunity. 2010 Jul 8;11(8):630–6. doi: 10.1038/gene.2010.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.McKinney BA, White BC, Grill DE, Li PW, Kennedy RB, Poland GA, et al. ReliefSeq: a gene-wise adaptive-K nearest-neighbor feature selection tool for finding gene-gene interactions and main effects in mRNA-Seq gene expression data. PloS one. 2013;8(12):e81527. doi: 10.1371/journal.pone.0081527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.McKinney BA, Crowe JE, Guo J, Tian D. Capturing the spectrum of interaction effects in genetic association studies by simulated evaporative cooling network analysis. PLoS genetics. 2009 Mar;5(3):e1000432. doi: 10.1371/journal.pgen.1000432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Poland GA, Ovsyannikova IG, Jacobson RM. Adversomics: the emerging field of vaccine adverse event immunogenetics. Pediatr Infect Dis J. 2009 May;28(5):431–2. doi: 10.1097/INF.0b013e3181a6a511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Poland GA. Vaccidents and adversomics. Vaccine. 2010 Sep 14;28(40):6549–50. doi: 10.1016/j.vaccine.2010.08.032. [DOI] [PubMed] [Google Scholar]
- 82.Hansen KD, Irizarry RA, Wu Z. Removing technical variability in RNA-seq data using conditional quantile normalization. Biostatistics. 2012 Apr;13(2):204–16. doi: 10.1093/biostatistics/kxr054. [DOI] [PMC free article] [PubMed] [Google Scholar]


