Peptide Bond Formation Mechanism Catalyzed by Ribosome

Abstract

In this paper we present a study of the peptide bond formation reaction catalyzed by ribosome. Different mechanistic proposals have been explored by means of Free Energy Perturbation methods within hybrid QM/MM potentials, where the chemical system has been described by the M06-2X functional and the environment by means of the AMBER force field. According to our results, the most favourable mechanism in the ribosome would proceed through an eight-membered ring transition state, involving a proton shuttle mechanism through the hydroxyl group of the sugar and a water molecule. This transition state is similar to that described for the reaction in solution (J. Am. Chem. Soc. 2013, 135, 8708–8719) but the reaction mechanisms are noticeable different. Our simulations reproduce the experimentally determined catalytic effect of ribosome that can be explained by the different behaviour of the two environments. While the solvent reorganizes during the chemical process involving an entropic penalty, the ribosome is preorganized in the formation of the Michaelis complex and does not suffer important changes along the reaction, dampening the charge redistribution of the chemical system.

INTRODUCTION

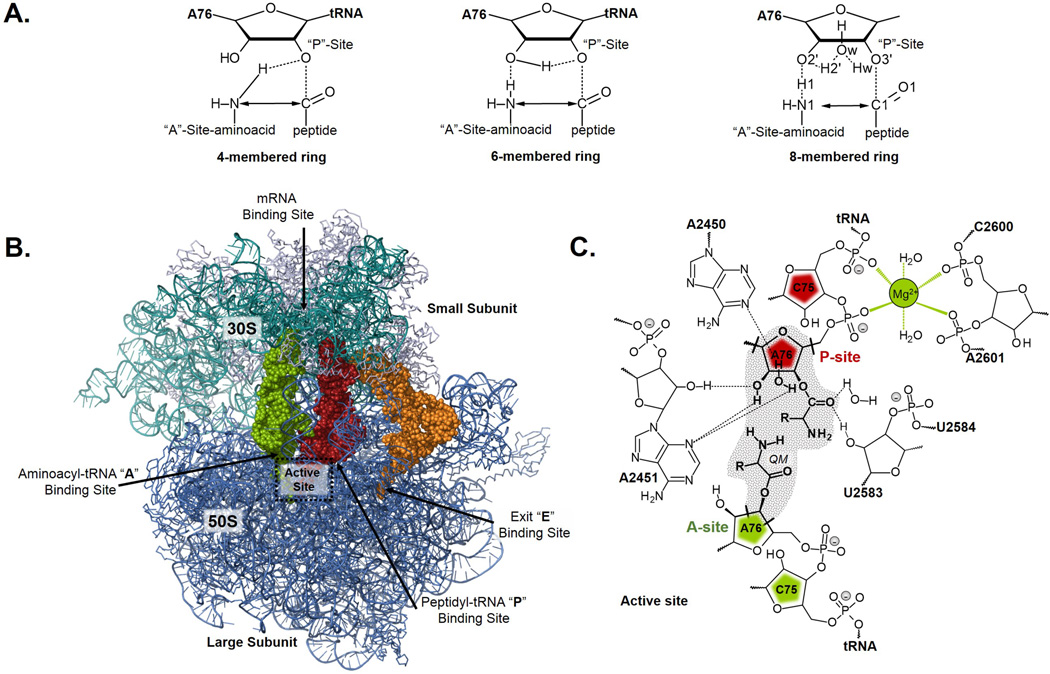
Ribosomes are considered as ancient enzymes, ribozymes, responsible of the flow of the genetic information encoded within genes into proteins in living organisms.^1,2 The ribosome catalyzes the peptide bond formation by the nucleophilic attack of an aminoacyl-tRNA in the A-site on ester carbon of the peptidyl-tRNA in the P-site. Despite the amount of research focused in studying ribosome, from experimental and theoretical tools, and the great progress in the study of the ribosome function in elongation step based on structural analysis of X-ray diffraction studies,^3,4,5,6,7 the mechanism of this process and the origin of the catalytic power of this ancient enzyme are still an unsolved puzzle. In particular, the large ribosomal subunit complexed with different analogues representing either intermediates or transition states (transition state analogues, TSA), in which a phosphate diester mimics the tetrahedral transition state, TS, that occurs during the peptide bond formation, were crystalized and their analysis suggested that the reaction proceeds through a tetrahedral intermediate with S chirality.⁸ Based on these X-ray diffraction studies, the initial mechanism proposed by Steitz and co-workers is described by formation of a zwitterion intermediate, which breaks down to deacylated tRNA and elongated peptidyl-tRNA. A key role is given to the 2’ hydroxyl of the P site substrate, A76, of the peptidyl-tRNA in the decomposition of the zwitterion intermediate, by serving as a proton shuttle. It would act as a general base that would abstract the proton from the α-amino group and would donate a proton to the deacylated 3’ hydroxyl. This mechanism would imply the formation of a six-membered ring TS. Alternatively, a water molecule detected in this site, interacting with the mentioned 2’ and 3’ hydroxyls of A76, could assist the proton transfer. In this case, the reaction would proceed through an eight-membered TS. A schematic representation of these possible TSs is shown in Figure 1A. Experimental studies that support the mechanism through an eight-membered TS were performed by Rodnina and co-workers based on inventory kinetic isotope effects (KIEs).⁹ Recently, Polikanov, Steitz and Innis have presented an alternative mechanism based on new X-ray diffraction studies of the Thermus thermophiles 70S ribosome at ~2.6 Å resolution.¹⁰ In this structure, apart from the water molecule located in the oxyanion hole and the water that can be the bridge between the 2’ and 3’ hydroxyls of A76, a new water molecule is located that could be part of a proton wire, along which three proton transfers would take place in a concerted, rate-limiting formation of a tetrahedral intermediate. In this proton wire, the proton from NH₂ is transferred to the O2’ hydroxyl of A76, from this O2’ a proton jumps to the hydroxyl of A2451, and from this hydroxyl the proton is transferred to the new water molecule that is activated by a phosphate group and a terminal NH₂ group of an alanine residue of L27. The tetrahedral intermediate presents a negative charge since the proton has been lost through the described proton network. Interestingly, this new mechanism is also in agreement with the inventory KIEs measured by Rodnina and coworkers.⁹

Figure 1.

Representation of 4-, 6- and 8-membered ring TS structures (A), ribosome structure (B) and schematic representation of the A and P site of Ribosome (C). Atoms included in the QM region are in shaded region.

Trobro and Åqvist combined available structural data to construct a model of the peptidyl transfer reaction center with bound substrates. In particular, molecular dynamics and free energy perturbation simulations in combination with an empirical valence bond (EVB)¹¹ description of the reaction energy surface were carried out to examine possible catalytic mechanisms.^12,13 Due to the use of a two-states model associated to the employed EVB potential, a two steps mechanism through the zwitterionic intermediate was explored in solution and in the ribosome environment. According to their results, catalysis by ribosome would be mainly achieved through a stable network of hydrogen bonds to the reactants that reduces the reorganization energy and the activation entropy of the reaction. Xiang and co-workers, based on B3LYP/MM calculations,¹⁴ studied the possible mechanism through a six and eight membered ring TS, concluding that the later was more favourable. On the other side, most of the attempts to study the peptide bond formation in the ribosome by means of quantum mechanics methods with reduced models in gas phase have proposed a concerted mechanism without the presence of the zwitterionic intermediate.^{15,16,17,18,19} Alternatively, other quantum mechanics calculations with cluster models have suggested a two steps mechanism but through a neutral intermediate where the proton of the α-amino group was already transferred to the carbonyl oxygen atom, O1.^19,20,21,22 All these contradictory results keep open the debate about the mechanism of the peptide bond formation in the ribosome and the existence and role of a zwitterion intermediate. The noncatalyzed peptide bond formation reaction in solution has been studied with reduced molecular models, treating the solvent with continuum and explicit solvent methods.^19,23,24,25 In all cases, the zwitterionic species were detected as stable or pseudostable state in the initial stage of the reaction but without a kinetic relevance. Nevertheless, this finding does not necessary imply that the reaction in the ribosome proceeds by formation of this addition complex.

Some experimental studies suggest differences in the mechanisms taking place in solution and in the ribosome. Thus, kinetic studies showed that, in contrast with most protein enzymes, the enthalpy of activation is slightly less favourable in the ribosome than in solution which would imply that the rate enhancement produced by the ribosome would be achieved entirely by lowering the entropy of activation.^26,27,28,29 This means that the ribosome acts as an “entropic trap”,³⁰ as first suggested by Sievers et al.²⁶ Studies based on Brønsted linear free energy relationships show slopes close to zero for the proton transfer reaction from the α-amino nucleophile with a series of puromycin derivatives indicating that, in the ribosome-catalyzed reaction, the nucleophile is neutral at the TS, in contrast to the substantial positive charge reported for typical noncatalyzed aminolysis reactions.^31,32 This suggests that the ribosomal TS involves deprotonation to a degree commensurate with nitrogen−carbon bond formation. Finally, KIEs studies render pH independent normal effect for ¹⁵N substitution of the incoming nucleophile.³³ This, together with studies of substitutions in other key atoms that potentially undergo changes during the noncatalyzed³⁴ and catalyzed reactions³⁵ suggests that the nitrogen atom is being deprotonated simultaneously to the formation of the C−N bond in the later, indicating that the ribosome promotes peptide bond formation by a mechanism that differs in its details from the noncatalyzed aminolysis reaction in solution. The possible differences between the catalyzed and noncatalyzed reactions supports the necessity of studying the reaction in the ribosome with a more accurate and realistic model.

The goal of the present paper is to study the reaction mechanisms of the peptide bond formation catalyzed by ribosome. A deep insight into the geometrical and electronic features of the reaction system and the response of the different environments will be carried out within fully explicit model of the ribosome. Special attention is paid to the existence of a zwitterionic species along the reaction path and its possible role. Comparison of results obtained in the catalyzed and noncatalyzed reaction will allow understanding the origin of catalysis in this complex and unsolved system.

COMPUTATIONAL METHODS

In order to study the mechanism of the peptide bond formation in condensed media, two different computational statistical strategies have been traditionally employed: the calculation of the free energy surface (FES) by means of umbrella sampling (US) in terms of a potential of mean force (PMF),^14,25 or by means of free energy perturbation (FEP) methods.²⁵ The former is based on the selection of a reduced number of coordinates (usually one or two) to define an approximate reaction coordiante. Then, if the real reaction coordinate of the chemical process under study can be properly described with this limited number of coordinates the method renders a realistic FES. Otherwise, this strategy presents serious limitations. Moreover, simulations for every displacement in the distinguished reaction coordinate is required to sample the conformations of the system by means of molecular dynamics (MD). This frequently implies the use of semiempirical methods when performing hybrid QM/MM MD simulations. The selection of ab initio or DFT Hamiltonians obliges to reduce the sampling, otherwise this method becomes computationally prohibitive. The second strategy, FEP methods, implies the sampling of the environment (usually the MM region) along a previously traced IRC from a TS located at QM/MM level. Thus, the method becomes cheaper and higher level Hamiltonians can be used to describe the chemical system (the QM region). Moreover, keeping in mind that the sampling is performed along the IRC, the free energy profile is obtained along a more realistic reaction coordinate. Nevertheless, since there is no sampling on the chemical system, the result could be biased by the fact that just one TS structure is used.

The mechanism of the aminolysis of an ester in solution through a four membered ring TS, mimicking the peptide bond formation step that takes place in the ribosome, was studied in our laboratory by means of FEP and PMF methods. In this case, the results based on a semiempirical method to describe the QM region showed that both strategies rendered equivalent results.²⁵ This encouraging findings support the use of FEP strategies with high level treatment of the chemical system to study mechanisms with more complex reaction coordinates, such as those taking place through six- and eight-membered ring TSs.

In the present study, the substrate, as depicted in Figure 1C, has been treated by means of the M06-2X hybrid funtional developed by Truhlar’s group^36,37 with the standard 6–31+G(d,p) basis set, that includes diffuse functions. The rest of the system (RNA, proteins, water molecules and counterions) was described using the AMBER³⁸ and TIP3P³⁹ force fields, as implemented in the fDYNAMO library.^40,41 Thus, the QM wave-function is polarized by the charges of the MM sub-set of atoms. The coordinates of the initial structure of the ribosome were chosen from the X-ray structures deposited in the PDB with code 2WDL and 2WDK.⁷ This X-ray structure, that did not contain any water molecule and not all the counterions required to electrostatically balance the system, mimics the pre-peptidyl-transfer structure with a nitrogen atom on the O3’ position. All tr-RNA and r-RNA atoms were included in our model but m-RNA was removed since it was far away from the peptidyl transferase center (PTC). Also, any protein more than 40 Å away from the PTC was deleted. The coordinates of the hydrogen atoms were added using the fDYNAMO library, considering the standard pKa values of the proteins titratable residues. The system, after properly modified, was placed in a pre-equilibrated sphere of water molecules of a radius of 40 Å centered in the PTC. Water molecules with an oxygen atom lying within 2.8 Å of any heavy atom of the RNA or protein were removed. The resulting QM/MM system consisted of 44 atoms in the QM region and 186374 atoms in the MM region.

To saturate the valence of the QM/MM frontier atoms, link atoms were placed between the A76 sugar ring of P-site and the subsequent phosphate group, between the same sugar ring and the adenine, and in the A76 sugar ring of A-site (see Figure 1C). Cut-offs for nonbonding interactions were applied using a switching-force scheme, within a range radius from 14.5 to 16 Å. All atoms included in a radius of 20 Å from active center were free to move during optimizations and dynamics (6870 atoms). Atoms located between 20 and 25 Å from the active center were constrained with a harmonic force (5151 atoms) while those atoms 25 Å away from active center were kept fixed (174347 atoms). After thermalization, a QM/MM MD simulation of the system in the NVT ensemble was ran during 500 ps at a temperature of 300 K using the Langevin-Verlet algorithm and a time step of 1 fs. Optimization of the TSs structures for the reaction mechanisms that take place through the four-, six- and eight-membered ring TSs (TS-4, TS-6 and TS-8, respectively) have been done at the M06-2X/MM level using as starting guess geometries of the chemical system those obtained for the counterpart mechanisms in aqueous solution,²⁵ and following an iterative micro-macro procedure.⁴² The configurations for which the free energy differences were estimated along the FEPs correspond to those structures obtained along the IRC calculation and are thus characterized by a single coordinate, s:

$$s_i=s_{i-1}+{\left[\sum _{j\in QM}{m}_j\right({(x_{j,i}-x_{j,i-1})}^2+{(y_{j,i}-y_{j,i-1})}^2+{(z_{j,i}-z_{j,i-1})}^2\left)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$ (1)

where x_ji, y_ji, and z_ji are the coordinates of the structure i belonging to the IRC traced from the transition state structure (x_j0, y_j0, z_j0 coordinates) and m_j are the masses of the atoms. Within this treatment the free energy relative to the reactant can be expressed as a function of the s coordinate as:

$$\mathrm{\Delta }{G}_{FEP}(s^R\to s^j)=\mathrm{\Delta }{E}_{QM}^{0,R\to j}+\mathrm{\Delta }{G}_{QM/MM}^{R\to j}==\left(E_{QM}^0\right(s^j)-E_{QM}^0(S^R\left)\right)-k_{B}T\sum _{i=R}^{i=j-1}\text{ln}{\langle \text{exp}\beta \left(E_{QM/MM}\right(S^{i+1})-E_{QM/MM}(S^i\left)\right)\rangle }_{MM,i}$$ (2)

where E⁰_QM is the gas-phase energy of the QM subsystem computed at M06-2X level, k_B is the Boltzmann constant, T is the temperature, and β = 1/k_BT. The QM/MM interaction contribution to the free energy difference between two different values of s is obtained by averaging the QM/MM interaction energy (including the polarization energy) over all the MM coordinates of the system obtained for a particular value of the s coordinate. The FEPs were performed at 300 K, using the NVT ensemble. Ten picoseconds of relaxation and 20 ps of production, with a time step of 0.5 fs, were run in each window. Depending on the mechanism, the number of windows required to generate the full free energy path was between 50 and 70.

The contribution of the vibrations of the QM subsystem to the free energy has been obtained, considering the quantum nature of its motions, under the harmonic approximation using the following expression:

$$G_{QM,\mathit{\text{vib}}}=\sum _{i=1}^m\frac{1}{2}h{\nu }_i+\sum _{i=1}^{m}RT\text{ln}(1-e^{\frac{-h{\nu }_i}{k_{B}T}})=ZPE+G_{QM,\mathit{\text{vib}}}^{\text{'}}(T)$$ (3)

where m is the number of vibrational modes to be considered and ν_i the fundamental frequency associated with each one of these modes. The first term is the well-known zero-point energy, while the second one contains the thermal contribution of the vibrations to the molecular free energy. In equation (3), since the six lowest frequency modes of the transition state and the reactant structures correspond to very low frequency librational motions,⁴³ the quantum correction is expected to be small and consequently, we omit these modes. Then, the correction is calculated over the 3N - 6 (in the reactant state) or 3N - 7 (in the transition state) frequency modes, with N being the number of atoms in the QM subsystems.

RESULTS

Energy profiles

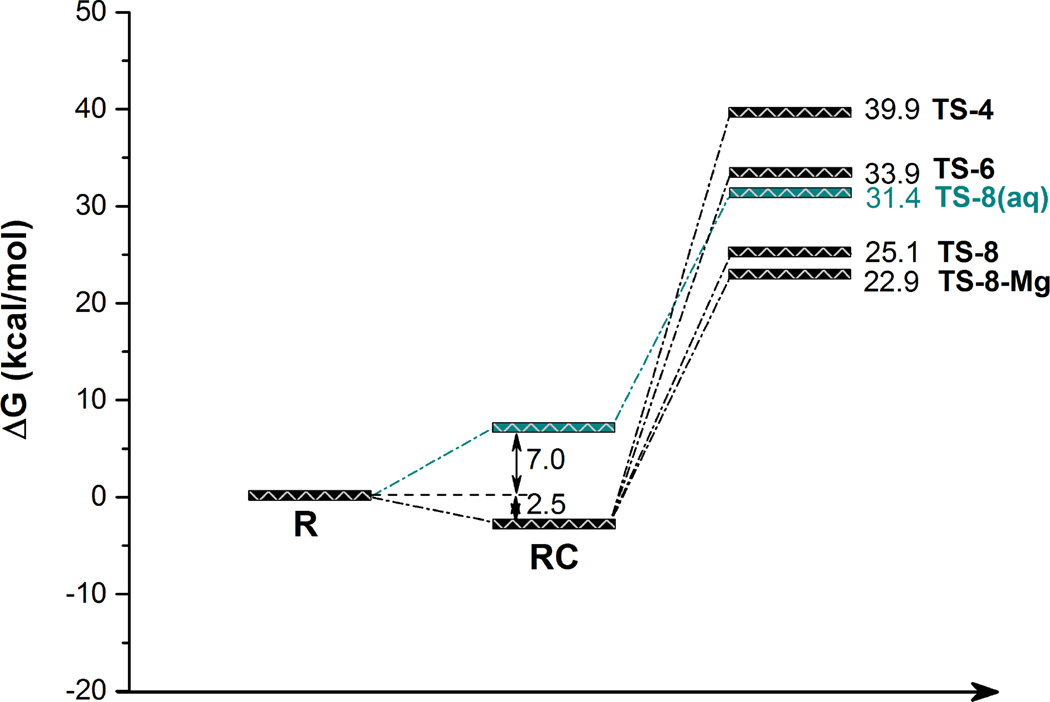
Free energy profiles for the peptide bond formation in the ribosome and in aqueous solution are schematically depicted in Figure 2 (all the computational values include Zero Point Vibrational Energy, ZPVE, corrections). The IRC path in solution, computed in our previous study,²⁵ leaded to a reactant complex that was estimated to be about 7 kcal·mol⁻¹ over the solvent separated species.^19,25 In the ribosome, the IRC leads to the Michaelis complex that has been experimentally estimated to be 2.5 kcal·mol⁻¹ below the reactants in solution.²⁶

Figure 2.

Schematic representation of the M06-2X/MM free energy profiles for the peptide bond formation catalyzed by ribosome through four- (TS-4), six- (TS-6) and eight-membered (TS-8) ring TSs in ribosome models. Line labelled as TS-8-Mg corresponds to the free energy profile obtained with two Mg²⁺ in the P-site (see text for details). The energy of the eight-membered ring TS in aqueous solution (TS-8(aq), blue line) is obtained from ref. 25 (26.8 kcal·mol⁻¹), after adding the energy required to form the RC from solvent separated species (7 kcal·mol⁻¹) and the ZPVE correction (−2.4 kcal·mol⁻¹). The free energy of formation of the RC in the ribosome (Michaelis complex) is taken from ref. 26. Energies of TSs in the ribosome models also include ZPVE corrections.

As observed in Figure 2, the mechanism through the four- and six- membered ring TSs present free energy barriers significantly higher than the one taking place through an eight membered ring. Moreover, the values are even higher than the counterpart reaction in solution (through an 8-membered ring TS). Thus, these two first mechanisms do not appear to present any kinetic advantage with respect to the noncatalyzed process. The fact that the six-membered ring mechanism in ribosome presents a barrier quite close to that observed in solution suggests that this proton shuttle mechanism, without participation of an additional water molecule as initially proposed by Weinger et al.,⁴⁴ is unreliable. In fact, the mechanism proposed by Weinger et al. was already questioned by measurements of Huang and Sprinzl^45,46 and by Green and co-workers.⁴⁷ According to our results, it seems that the reaction in the ribosome takes place through the eight-membered ring TS, with a free energy barrier below the reference reaction in solution, 25.1 kcal·mol⁻¹ versus 31.4 kcal·mol⁻¹. As later analyzed, this TS-8 implies the transfer of a proton of the α-amino group through the 2’-OH group and a water molecule, as initially proposed by Steitz, Strobel and co-workers.⁸ Geometries of the 8-membered ring TSs obtained in the ribosome and in solution are shown in Figure 3, while the four and six-membered ring TSs are shown in Figure S1 of Supporting Information.

Figure 3.

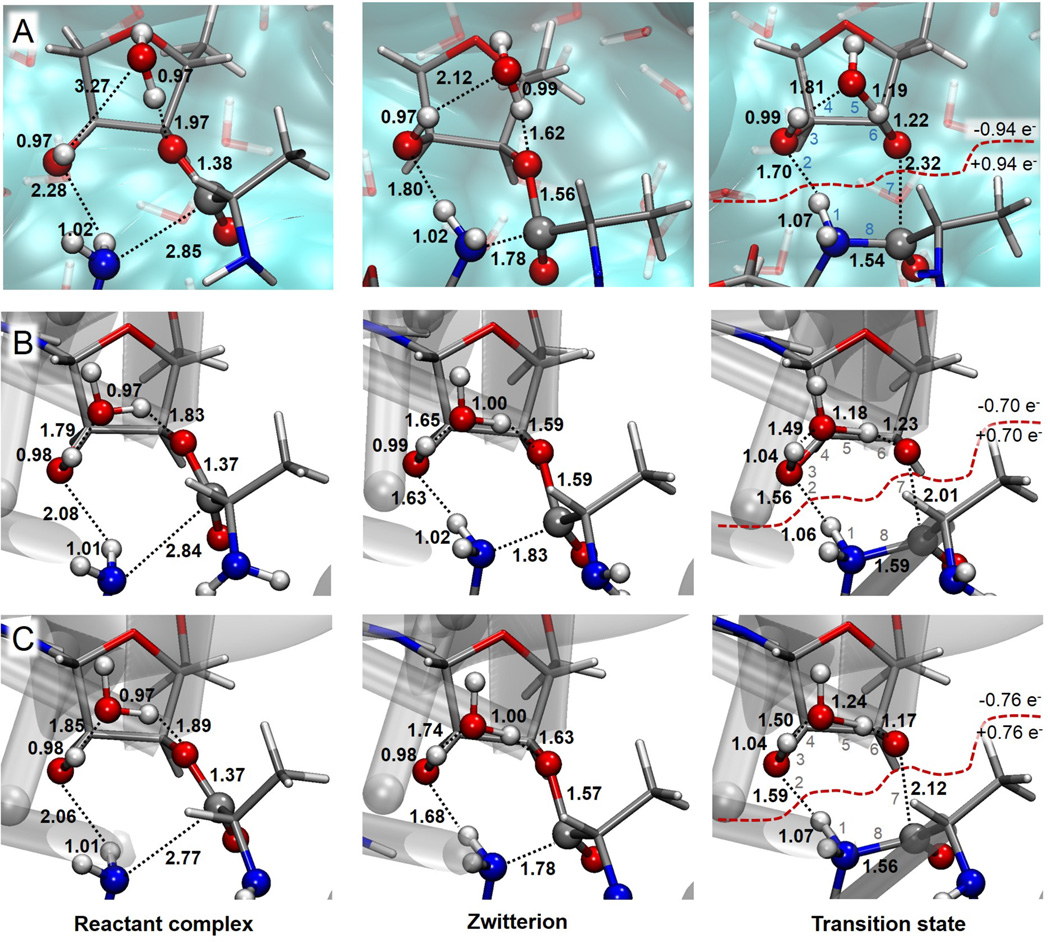
Geometries of the RC, ZW and the eight-membered ring TSs obtained for the peptide bond formation in water (A) and catalyzed by ribosome without additional Mg²⁺ ion (B) and with an additional Mg²⁺ ion (C), computed at M06-2X/MM level. Distances are reported in Å and charges of the two fragments in a.u.

Our estimation of the free energy barriers obtained through the eight-membered ring TSs in solution and in the ribosome, 31.4 and 25.1 kcal·mol⁻¹, are both overestimated with respect to the experimental values deduced by Sievers et al,²⁶ which were 22.2 kcal·mol⁻¹ in solution (derived from noncatalyzed rate constant between solvent separated species and TS: “k_non”) and 14 kcal·mol⁻¹ in the ribosome (derived from the kinetic constant associated to the transfer from the Michaelis complex to the TS, and the equilibrium constant between the separated species and the Michaelis complex: k_cat/K_M). Nevertheless, and more importantly, the experimentally determined catalytic effect, obtained from the difference in the activation free energies for the noncatalyzed and catalyzed processes, is 8.2 kcal·mol⁻¹ while our results predict a slightly smaller effect of 6.3 kcal·mol⁻¹. One possible source of error could be associated to the limitations of the DFT Hamiltonian employed to describe the quantum region of the system. As shown in a comparative study by Wallin and Åqvist, a reduction of activation enthalpies of 8 kcal·mol⁻¹ was obtained when going from B3LYP to MP2 level in cluster model calculations on the eight-membered TS mechanism.¹⁸ Nevertheless, such dramatic effect is not expected in our case since the DFT functional employed in the present study is the improved M06-2X. MP2/MM single point energy calculations on reactant complex and TS-8 structures obtained at M06-2X/MM level render a reduction in the barrier by 3.2 kcal·mol⁻¹, which is also in agreement with a modest decrease of the barrier of 3.5 kcal·mol⁻¹ observed when comparing calculations with M06-2X and MP2 in reduced models.¹⁹ Anyway, we must keep in mind that the MP2 method can underestimate reaction barriers (as the first order correction to the overestimated HF barriers) and thus, our predicted barriers could be even more accurate than expected from this comparison between DFT and MP2 methods.

Another possible source of error in our simulations could be due to the ribosome model. As explained in the Methods section, the X-ray coordinates used as starting point in our work⁷ did not contain any water molecule and not all counterions required to electrostatically balance the system. This absent information is particularly important in our system since, as stated by Steitz and co-workers, bound metal ions are abundant in the region surrounding the PTC.⁴⁸ Freisinger and Sigel already stressed in a review of 2007⁴⁹ the lack of Mg²⁺ cations in the crystal structure of the 50S subunit of H. marismortui.⁴⁸ This structure comprises 3045 nucleotides and then an equal number of negative charges originated from the phosphate groups need to be compensated by metal ions. However, only 10.6% of the phosphodiester-bridge charges are compensated by metal ions in the structure resolved by Steitz and co-workers (116 Mg²⁺ and 88 Na⁺/K⁺ ions were identified in the structure, resulting in a total of 320 positive charges). Thus the metal ions identified in the structure represent only a small fraction of the total number of ions that may be found tightly bound to the structure in solution.⁴⁹

Regarding the recent X-ray structure of Polikanov, Steitz and Innis,¹⁰ it is also worth mention that the problem of identified cations is not solved yet, despite the higher resolution obtain in their diffraction studies and the improvement in this regard. Thus, ca 45% of the phosphodiester-bridge charges are compensated by metal ions (2077 Mg²⁺, 2 K⁺ ions and 12 Zn²⁺ were identified in the structure in this new resolved structure).

A potential problem in classifying and surveying Mg²⁺ binding sites in RNA structures is the misidentification of this ion.⁵⁰ The misinterpretation of small molecules and ions, including Mg²⁺, has been reported in many macromolecule structures. Mg²⁺ has the same number of electrons as water and Na⁺, which cannot be distinguished from Mg²⁺ by difference electron density maps alone.⁵⁰

Because the electrostatic effects are expected to play a decisive role in the energetics of this reaction,^25,51 we have performed a deeper insight into this problem. In particular, analysis of the surroundings of active site reveals the presence of phosphate groups in close contact (see Figure S2 in Supporting Information). In our fist attempt, during the in silico solvation of the X-ray structure, a new solvent water molecule was placed between these two phosphate groups (TS-8 ribosomal model) that present a cavity large enough to accommodate this additional water molecule. Keeping in mind the large negative charge that is concentrated in this small region of the ribosome, and the limitations of the available X-ray diffraction structures in this regard, we decided to model the system changing this water molecule to a magnesium cation, Mg²⁺. Interatomic distances defining the coordination sphere of Mg²⁺ ions are listed in Table S1 of Supporting Information. After relaxing the system by means of QM/MM MD simulations, the procedure was repeated and a new 8-membered ring TS (TS-8-Mg in Figure 2) was localized. The resulting structure is shown in Figure 3. The free energy barrier obtained with an additional Mg²⁺ cation in the P-site is 22.9 kcal·mol⁻¹, 2.2 kcal·mol⁻¹ lower than the previously obtained TS-8 for the same reaction mechanism. More interestingly, the catalytic effect that can be derived from the best of our free energy barriers obtained in the ribosome with respect to the free energy in solution is now 8.5 kcal·mol⁻¹, in excellent agreement with the experimental value of 8.2 kcal·mol⁻¹ deduced from the second order rate constants measured by Sievers et al.²⁶ Thus, in spite of possible sources of systematic errors affecting the absolute values of the barrier in solution and in the enzyme, our analysis would indicate that the catalyzed reaction takes place through an 8-membered ring TS. According to our results, the presence of divalent cations in the surroundings of the active site can have not only structural effects on the ribosome⁵² but also catalytic effects. We thus analyzed in detail this reaction mechanism in solution and in the two models of ribosome (with and without an additional Mg²⁺ cation) in order to unravel their similarities and differences, and to rationalize the origin of the catalytic efficiency of the ribosome.

Molecular Mechanism

A first insight into the reaction mechanisms can be obtained from the comparison of the RC and TS structures (provided in Figure 3). Overall, the structures found in different environments are similar, although there are some relevant differences between the structures found in solution and in the two ribosomal models. The RC structures show that the oxygen atom of the hydroxyl group of the P-site, O2’, is closer to the nucleophilic amine group of the A-site in the ribosome than in solution, which should assist the proton transfer (see O2’-H1 distances in Figure 3). In addition, the water molecule is better placed to accept a proton transfer from this hydroxyl group in the ribosome than in solution (see H2’-Ow distances in Figure 3). In fact, while a hydrogen bond interaction is detected in the RC of ribosome environment (H2’-Ow distance in the ribosome without and with additional Mg²⁺ is 1.79 and 1.85 Å, respectively) this hydrogen bond does not exist in aqueous environment (H2’-Ow distance is 3.27 Å). Correct positioning of these reacting fragments in the ribosome is assisted by intermolecular hydrogen bonds with basis A2450 and A2451 (see Figure 1, Figure S3 and Table S2 of Supporting Information). At the TSs, the distances O2’-H1 and H2’-Ow are also shorter in the ribosome than in solution, indicating that these two proton transfers are more advanced in the former environment. The last hydrogen transfer, from water molecule to O3’, is more advanced in the TS-8 in the ribosome with an additional Mg²⁺ than without this cation or in water (see Ow-Hw and Hw-O3 distances in Figure 3, as defined in Figure 1). This proton transfer is obviously associated to the C1-O3’ heterolytic breaking bond, which is slightly more advanced in the ribosome with an additional Mg²⁺ than in the original ribosome model. The scenario in solution is different, the TS structure is more dissociative, with almost two separated fragments distinguished by a dashed-line in Figure 3. The C1-N1 forming bond (bond length of 1.54 Å) and the C1-O3’ breaking bond (bond length of 2.32 Å) are quite advanced in solution. Instead, the proton transfer from N1 to O2’ is in an early stage of the process (O2’-H1 bond length of 1.70 Å). This, together with a significant larger C1-O3’ distance in the TS in solution than in the ribosome, results in a large charge separation between the fragments. The aqueous environment stabilizes an ion pair character TS. In both ribosome models, the distance observed for the dissociating C1-O3’ bond is shorter than in solution and the proton transfer from N1 to O2’ is slightly more advanced (as reflected in the shorter O2’-H distance). All these differences observed in the geometrical description of the TSs are related with the charge distribution. The potential-derived charges for key atoms of the QM subsystem (averaged over a fluctuating MM environment), as well as the modulus of the dipole moment, are provided in Table 1. The main differences associated to the atomic charges when comparing aqueous solution with the ribosome can be explained by analysing the charge evolution of some key atoms. Thus, when going from RC to TS, the sum of electronic charges on H1 plus N1 is decreasing by 0.45 a.u. in solution while in the ribosome models this change account just to 0.02 and 0.16 a.u. without and with the additional Mg²⁺, respectively. The sum of electronic negative charges on the oxygen atoms involved in the 8-membered ring (O2’, Ow and O3´) increase by 0.64, 0.51 and 0.36 a.u. in solution and in the ribosome model without and with an additional Mg²⁺, respectively. The charge separation between the two fragments indicated above (see Figure 3) can be explained by combining these results. The ion pair character of the TS in solution is significantly less evident in the ribosome (the charges of the fragments change from ±0.94 a.u, in solution to ±0.70 a.u and ±0.76 a.u in the ribosome without and with the additional Mg²⁺, respectively). This result suggests some differences in the mechanism for the reaction in solution and in the ribosome. The atomic charges of the QM subsystem polarized by the electric field of the different environments create different dipole moments (see Table 1). As observed, the highest dipole moment is created at the TS obtained in solution (11.8 a.u.). The dipole moment at the RC is significantly smaller (7.8 a.u.). Despite noticeable lower values, this scenario is similar to the one observed in the ribosome with the additional Mg²⁺, but different from the results observed in the ribosome without Mg²⁺, where dipole moment is higher in RC than in the TS.

Table 1.

Averaged atomic charges of the QM subsystem polarized by the different environments computed at M06-2X/MM level. Dipole moments of the chemical system under the effect of the environment, μ, and gas phase dipole moments, μ₀, computed with the geometries obtained in solution and in the ribosome.

Charges (a.u.)	Aqueous solution			Ribosome			Ribosome+Mg2+
	RC	ZW	TS	RC	ZW	TS	RC	ZW	TS
H1	0.352 ± 0.025	0.347 ± 0.036	0.515 ± 0.039	0.380 ± 0.020	0.461 ± 0.033	0.600 ± 0.040	0.418 ± 0.019	0.480 ± 0.026	0.578 ± 0.032
N1	−0.869 ± 0.041	−0.447 ± 0.109	−0.583 ± 0.089	−0.892 ± 0.024	−0.860 ± 0.095	−1.095 ± 0.079	−0.956 ± 0.026	−0.833 ± 0.077	−0.958 ± 0.064
C1	0.665 ± 0.043	0.936 ± 0.083	0.753 ± 0.056	0.659 ± 0.032	1.010 ± 0.051	1.106 ± 0.045	0.601 ± 0.040	0.747 ± 0.063	0.789 ± 0.049
O3'	−0.470 ± 0.039	−0.555 ± 0.051	−0.715 ± 0.048	−0.247 ± 0.017	−0.356 ± 0.022	−0.425 ± 0.029	−0.283 ± 0.026	−0.352 ± 0.031	−0.453 ± 0.028
Hw	0.378 ± 0.029	0.295 ± 0.036	0.402 ± 0.051	0.309 ± 0.018	0.302 ± 0.014	0.349 ± 0.024	0.342 ± 0.015	0.275 ± 0.024	0.372 ± 0.033
Ow	−0.940 ± 0.025	−0.944 ± 0.036	−1.214 ± 0.043	−0.879 ± 0.015	−0.915 ± 0.014	−1.095 ± 0.019	−0.893 ± 0.017	−0.877 ± 0.020	−1.109 ± 0.020
H2'	0.430 ± 0.023	0.497 ± 0.027	0.524 ± 0.038	0.466 ± 0.011	0.448 ± 0.011	0.471 ± 0.013	0.494 ± 0.017	0.452 ± 0.012	0.470 ± 0.013
O2'	−0.745 ± 0.041	−0.792 ± 0.035	−0.876 ± 0.054	−0.761 ± 0.022	−0.813 ± 0.055	−0.872 ± 0.073	−0.851 ± 0.072	−0.794 ± 0.046	−0.821 ± 0.073
O1	−0.598 ± 0.050	−0.863 ± 0.065	−0.549 ± 0.044	−0.565 ± 0.023	−0.718 ± 0.021	−0.646 ± 0.026	−0.509 ± 0.022	−0.705 ± 0.035	−0.521 ± 0.022
Dipole moments (Debyes)
μ	7.79	7.06	11.79	7.12	4.58	5.96	3.58	5.55	8.96
μ0	5.47	4.20	8.47	4.18	1.32	3.60	2.05	3.42	6.77

In order to get a deeper insight into the role of the environment, dipole moments have been also computed in gas phase with the geometries obtained in solution and in the ribosome. The results listed in Table 1 show a larger electronic polarization in solution than in both ribosome models.

All these differences on geometries and electronic charges can be attributed to the effect of environment. In aqueous solution water molecules are able to stabilize the ion pair formed at the TS better than the ribosome does, but at the cost of a significant reorganization from RC to the TS. This change of the mechanism from aqueous solution to the ribosome can be discussed by performing a deeper insight in the evolution of the system along the reaction path.

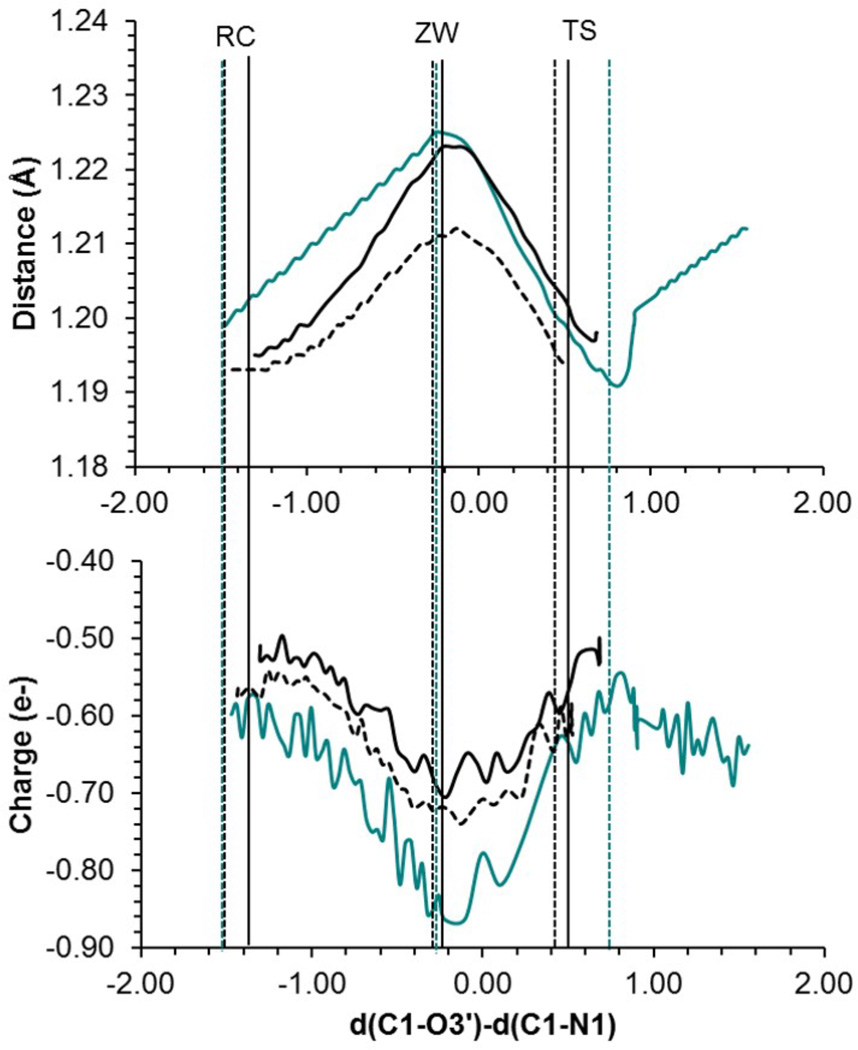
Figure 4 shows the evolution of the C1-O1 distance and the evolution of charge associated to the O1 atom along the minimum energy reaction paths in aqueous solution and in the two ribosomal models. The qualitative trends are similar demonstrating that the microscopic characteristics of the 8-ring membered mechanisms are similar in different environments. During the first stages of the nucleophilic attack of the A-site amino group to the P-site carboxylic carbon atom (C1) the C1-O1 bond length is elongated concertedly with an accumulation of negative charge on O1. As observed in Figure 4, a maximum value of the C1-O1 distance and negative charge on O1 is reached in between the RC and the TS. This structure presents a zwitterionic-like character where the positive charge is formally located on the attacking nitrogen atom (N1) and the negative charge on the O1 atom. It is important to point out that this structure does not correspond to a stationary point on the free energy profiles for the reaction obtained in solution or in the ribosome. As previously described, the formation of this transient zwitterionic structure in solution was associated with a shoulder on the free energy profile,^24,25 which has not been observed in the case of the ribosome. Geometries of these zwitterionic structures, ZW, are shown in Figure 3, while atomic charges on key atoms are listed in Table 1. As deduced from the values reported in Table 1, when the system evolved from RC to the ZW, a larger decrease of negative charge in N1 atom is obtained in solution (0.42 a.u.) than in both ribosome models (0.03 and 0.12 in the ribosome without and with additional Mg²⁺, respectively), together with a larger increase of the negative charge on O1 in solution (0.27 a.u.) than in the ribosome models (0.15 and 0.20 a.u. in the ribosome without and with additional Mg²⁺, respectively). This charge is stabilized by intermolecular hydrogen bonds with water molecules when reaction takes places in aqueous solution²⁵ and by interactions with the hydroxyl group of the sugar of U2583 in the ribosome (see Figure S3 and Table S2 of Supporting Information). This stage of the process can be described as an S_N2 mechanism where the nucleophilic attacking group would be the N1 atom and the O1 would correspond to the leaving group.

Figure 4.

Evolution of the C1O1 bond length (a) and the atomic charge on oxygen O1 (b) for the 8-membered ring mechanism in water (cyan line), Ribosome (dashed black line) and Ribosome with additional Mg²⁺ ion (solid black line). Vertical lines indicate the position of RC, ZW and TS in the different environments.

When approaching the TS region the zwitterionic character vanishes as reflected in the evolution of the C1-O1 bond length and the charge on the O1 atom in Figure 4. The C1-O1 bond distance is reduced to values corresponding to a double bond while the charge on O1 is restored to values similar to the ones obtained in RC. The negative charge that O1 is loosing is transferred, basically to the oxygen atoms of the upper fragment: O3´, Ow and O2´. This effect is more dramatic in solution (O1 atom is loosing 0.31 a.u.) than in the ribosome (0.07 and 0.18 a.u. in the ribosome without and with additional Mg²⁺, respectively). The TSs can be described as an ion pair with the negative charge located preferentially on the O2’, O3’ and Ow atoms rather than on the O1 atom. This stage of the process could be also described as an S_N2 mechanism, being the attacking group the O1 atom, and the O3’ atom the leaving group. Aqueous solution seems to stabilize more efficiently the charge flow taking place during the reaction (neutral reactant complex → zwitterion-like complex → ion pair TS) than the ribosome. Aqueous solution accommodates to the changes in the solute charge distribution amplifying them, while ribosome structure seems to slightly damp these changes. Finally, once crossing the TS, the last stage of the reaction can be described as a proton transfer between the two fragments (H1 atom from N1 to O2’) and the proton shuttle through the hydrogen bonds network until protonation of the O3´ atom. As deduced from the analysis of the TSs shown in Figure 3, this last stage is more advanced in the ribosome than in solution.

Role of the environment

In previous section, it has been shown how catalyzed and noncatalyzed peptide bond formation reactions follow similar molecular mechanism. Nevertheless, from analysis of interatomic distances and charges, significant differences can be underlined. Obviously, the origin of these differences comes from the different behaviour of the two environments. In aqueous solution, the charge separation developed on the reacting system induces a reaction field in the solvent, which is oriented to enhance the ion-pair solute dipole moment. In contrast, the ribosome is more rigid than water molecules in solution and then, there is a permanent electric field that would favour the reaction to proceed.

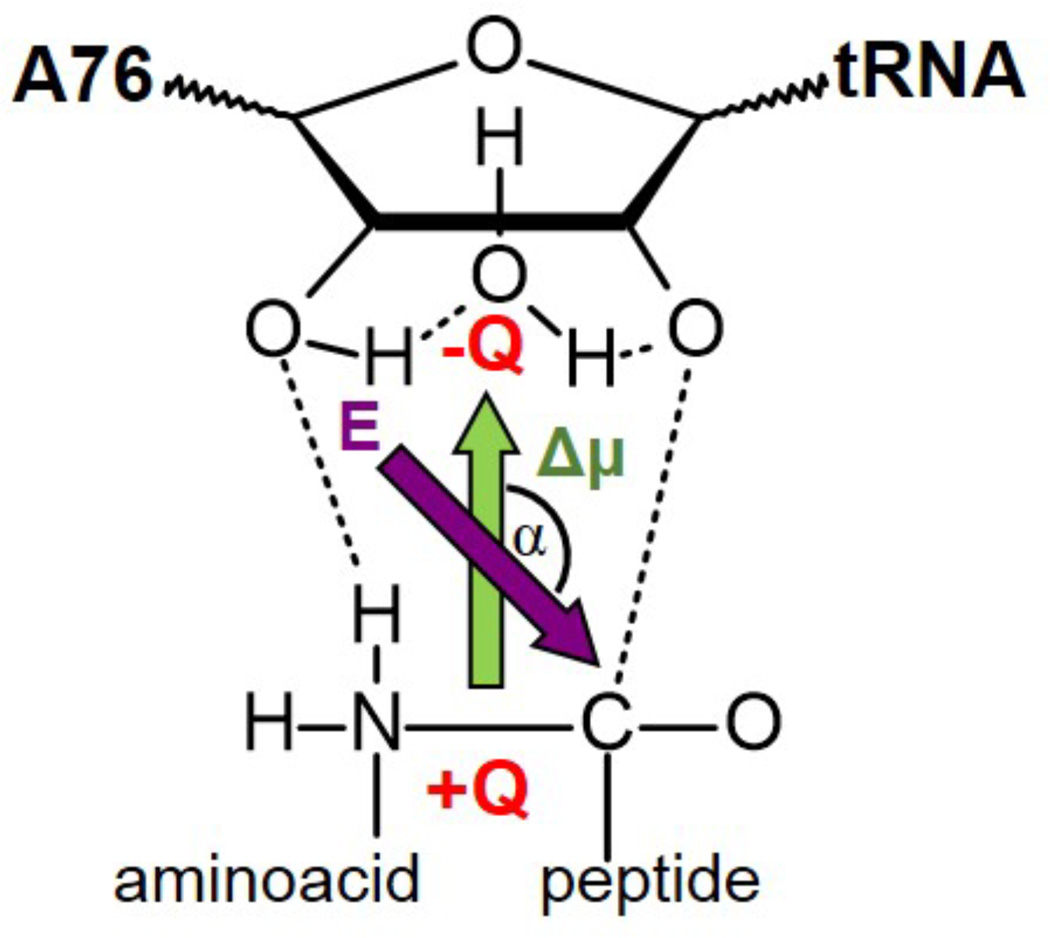
In order to get a deeper insight into the differences between the aqueous solution environment and the ribosome we have monitored the electrostatic coupling between the chemical subsystem and the surroundings. As explained above, the reaction mechanism takes place from two neutral species to the formation of an ion pair-like TS, with an important charge separation. The dipole moment on the TS of the reacting subsystem can be stabilized by a properly oriented electric field created by the environment. The modulus of the electric field created by the environment in the center of the eight-membered ring and the angle defined between this vector and the variation of the dipole associated to the substrate, from RC to TS, is schematically shown in Figure 5. A representation of the dipole moments of the reacting system in RC and TS is provided in Figure S4 of Supporting Information. As observed in Table 2, the change of the modulus of the electric field created by the environment is much larger in solution (0.45 ×10⁻² a.u.) than in the two models of the ribosome (−0.04 ×10⁻² and 0.26 ×10⁻² a.u. in the ribosome without and with the additional Mg²⁺, respectively). Moreover, the electric field in solution is not oriented along the dipole axis in RC (with an angle close to 90 degrees), since the solute does not present charge separation at this state. At the TS, the surrounding solvent water molecules are oriented to stabilize the ion-pair and, consequently, the angle with the ion-pair dipole moment is close to 180 degrees. In contrast, the orientation of the environment electric field in both models of the ribosome is not such well oriented at the TS. As observed by comparing with the RCs, the environment electric field reorientation is much smaller than in solution. Furthermore, the magnitude of the modulus of the electric field created by the environment in the TS is higher in solution (1.17×10⁻² a.u.) than in the ribosome (0.72 ×10⁻² and 0.75 ×10⁻² a.u. in the ribosome without and with the additional Mg²⁺, respectively). The TS will be more stabilized in solution than in the ribosome. The change in the modulus of the electric field and its orientation, from RC to the TS, is more dramatic in solution than in the ribosome, thus indicating a more important reorganization of the environment in solution.

Figure 5.

Schematic representation of the modulus of the electric field created by the environment in the center of the eight-membered ring, E, (purple arrow) and the angle α defined between this vector and the dipole associated to the substrate ion-pair formation, Δµ (green arrow).

Table 2.

Modulus (in a. u.) of the electric field created by the environment on the center of the eigth-membered cycle of the substrate and angle (in degrees) with respect to the solute dipole associate to the charge separation observed at the TS.

	Aqueous solution		Ribosome		Ribosome-Mg2+
	|E| ×102 (au)	α (deg)	|E| ×102 (au)	α (deg)	|E| ×102 (au)	α (deg)
Reactant Complex	0.72 ± 0.24	97 ± 22	0.76 ± 0.11	59 ± 6	0.49 ± 0.16	117 ± 15
Transition State	1.17 ± 0.14	167 ± 7	0.72 ± 0.15	81 ± 9	0.75 ± 0.12	125 ± 9

DISCUSSION

Free energy profiles presented in Figure 2 show how the reaction mechanism of peptide bond formation in the ribosome would proceed through an eight-membered ring TS. TS-4 is 6 kcal·mol⁻¹ higher in energy than TS-6, and this is higher in energy than TS-8 and TS-8-Mg by 8.8 and 11 kcal·mol⁻¹, respectively. This result is in agreement with the 10 kcal·mol⁻¹ difference obtained by Xiang and co-workers from exploration of two-dimensional PMFs.¹⁴ The antisymmetric combination of the C1-N1 and C1-O3’ distances reported by Xiang and co-workers for both TSs, which is one of the two distinguished reaction coordinates employed to generate the 2D-PMF describe a slightly more advanced TSs than the ones reported in the present study. As these authors comment in the text, their TS structures should be considered as “quasi-transition state”, since the position if the transferring protons may change when the degrees of freedom corresponding to the other proton transfers were considered in the reaction coordinate.¹⁴ In fact, when comparing the TS-6 geometries, the proton transfer from O2’ to O3’ is more advanced in their TS-6 than in our corresponding TS-6. Differences are also observed in the TS-8 geometries: the proton transfer from the water molecule to O3’ is also more advanced than in our TS-8, with and without the additional Mg²⁺, while the other two proton transfers (from N1 to O2’ and from O2’ to the water molecule) are less advanced in their TS-8 than in our two TS-8 structures. Dramatic differences are also detected in the RCs. While their RC for the mechanism through the TS-8 was found at a value of the antisymmetric combination of the C1-N1 and C1-O3’ distances of −0.4 Å, our RC structures are localized at −1.47 and −1.40 Å, for our TS-8 and TS-8-Mg models, respectively. Anyway, both studies suggest that the most favourable reaction mechanism for the peptide bond formation catalyzed by the ribosome proceed through an eight-membered ring TS, as initially proposed by Steitz⁸ and in agreement with previous quantum cluster models studies performed by Wallin and Aqvist¹⁸, and by one of us.¹⁹ Experimental studies by Rodnina and co-workers based on inventory KIEs,⁹ as stressed by the authors, are also consistent with a concerted eight membered TS. The prediction of the catalytic effect of ribosome, derived from the comparison between the free energy barrier of the reaction in solution and catalyzed by ribosome, is 6.3 and 8.8 kcal·mol⁻¹, for the mechanism through the TS-8 and TS-8-Mg, respectively. These results are in good agreement with the barrier difference of 7 kcal·mol⁻¹ derived from EVB calculations of Trobo and Aqvist,¹² and with the experimental measurements of Sievers et al., who reported a value of 8.2 kcal·mol⁻¹.²⁶ As discussed in previous section, the presence of divalent cations in the vicinity of the active center can have important effects in geometries and catalysis. In this system, the inclusion of an additional Mg²⁺ based on the geometrical analysis of the charge-unbalanced X-ray initial structure, has allowed obtaining results that are in better agreement with experimental data. This computational hypothesis opens the door for the evaluation of effects derived from the position and dynamics of divalent cations in biological catalysts.

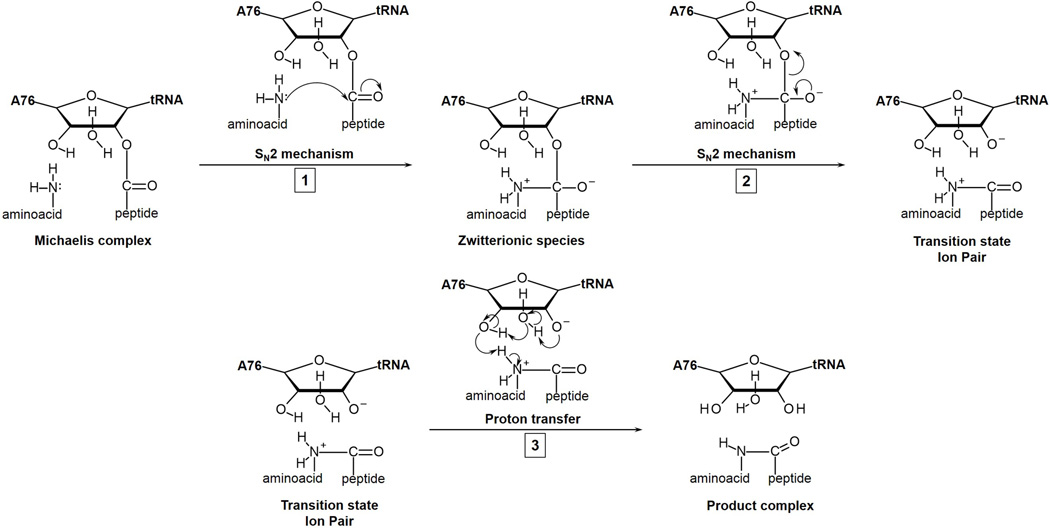
From the analysis of the evolution of the system along the reaction coordinate we have determined that the full mechanism can be decomposed in three stages schematically depicted in Figure 6. This can be confirmed by the variation of bond Wiberg indexes,⁵³ reported in Table 3. It can be observed how the smallest value of the bond Wiberg index of C1-O1 is always attained at the ZW while the value of N1-C1 index has substantially increased at this stage. In the second stage of the process, from the ZW to the TS, the C1-O1 index increases concertedly with the decrease of the C1-O3’ bond index. At the TS, the indexes of the forming bonds associated to the proton shuttle are small, except for the bond between the water molecule and the O3’, which is partially formed. The value of the Hw-O3’ indicates that the negative charge developed on O3’ atom is the driving force for the proton transfer. This analysis supports the three stages proposal shown in Figure 6. However, it must be considered that in our model these three stages take place in a single concerted step and they slightly overlap during the evolution of the system along the reaction path. Finally, mechanistic variations can be explained based on this scheme. For example, an hypothetical stabilization of the ZW structure could give rise to a step-wise mechanism as proposed by Steitz and coworkers.⁸ Alternatively, the mechanism proposed by Polikanov, Steitz and Innis¹⁰ can be also explained starting from the ZW structure, considering the activation of the O2’ hydroxyl atom after a proton transfer to the hydroxyl of A2451 and the subsequent abstraction of a proton from the nucleophilic NH2 group by the O2’ atom. This would result in the anionic tetrahedral intermediate suggested in the recent proposal.¹⁰

Figure 6.

Schematic representation of the different stages that can be identified in the peptide bond formation catalyzed by the ribosome.

Table 3.

Wiberg bond indexes computed at M06-2X/6-31G+(d,p) level.

	Water			Ribosome			Ribosome + Mg2+
	RC	ZW	TS	RC	ZW	TS	RC	ZW	TS
N1-H1	0.793	0.679	0.556	0.781	0.664	0.572	0.790	0.667	0.559
H1-O2’	0.012	0.065	0.125	0.021	0.091	0.143	0.017	0.083	0.147
O2’-H2’	0.713	0.666	0.588	0.649	0.599	0.517	0.653	0.619	0.511
H2’-Ow	0.001	0.034	0.090	0.048	0.090	0.166	0.043	0.070	0.169
Ow-Hw	0.727	0.643	0.402	0.679	0.599	0.387	0.690	0.619	0.340
Hw-O3’	0.020	0.082	0.308	0.034	0.102	0.305	0.028	0.088	0.353
O3’-C1	0.944	0.694	0.110	0.955	0.673	0.279	0.956	0.695	0.212
C1-N1	0.015	0.517	0.780	0.007	0.496	0.746	0.015	0.521	0.778
C1-O1	1.781	1.592	1.842	1.785	1.637	1.756	1.785	1.593	1.775

The evolution of the chemical system from RC to ZW and TS, is coupled to changes in the intermolecular interactions with the environment. As deduced from the evolution of some key intermolecular distances (reported in Table S2 of Supporting Information), in the first stage of the process, the negatively charged O1 leaving group is stabilized by interactions with a water molecule and/or the hydroxyl group of U2583 in the ribosome, reflected in the shortening of the respective distances. In contrast, in the second stage of the process, the O1 attacking group is desolvated, as indicated by the elongation of these distances. These changes illustrate how a more complete reaction coordinate could be defined including the environment.

From the comparison of the bimolecular reaction in solution and in the ribosome, Sievers et al.,²⁶ showed that while the former is favoured from the enthalpic point of view, the entropic contribution (−T·ΔS^‡) to the free energy barrier is smaller in the ribosome. This experimental observation was interpreted as an entropy trap, in the sense that the ribosome enhances the rate of the peptide bond formation positioning the substrates and/or excluding waters from the active site.²⁶

According to Figure 2, the activation free energy of the full bimolecular processes can be decomposed in two terms: the formation of RC (Michaelis complex in the ribosome) and from this RC to the TS. As shown in this figure, the free energy change from RC to TS is almost equivalent in solution (24.4 kcal·mol⁻¹) and in the ribosome (25.4 kcal·mol⁻¹). However, the entropic and enthalpic contributions are not the same in both media. In fact, as presented in the role of the environment section, our simulations indicate that the reorganization of the environment is much larger in solution than in the ribosome. At the TS, solvent dipoles reorganize around the solute giving rise to a larger and better oriented electrostatic field in solution that would explain the experimentally observed smaller enthalpic barrier. This larger reorganization implies a larger entropic penalty and then a larger entropic contribution to the free energy barrier in solution. Instead, the electrostatic response in the ribosome is quite different. As discussed above, the electric field doesn’t suffer a substantial reorientation from Michaelis complex to the formation of the ion-pair TS. A preorganized ribosomal structure avoids the entropic cost associated to the alignment of the environmental electric field from RC to TS. Experimentally, the entropic contribution (T·ΔS_‡) to the free energy barrier determined from the Michaelis complex has been experimentally estimated to be favourable by 0.7 kcal·mol⁻¹.²⁶

Figure 2 shows that all the catalytic effect is already attained in the first term of the total free energy barrier, from solvent separated reactants to the RC (Michaelis complex in the ribosome). In solution, formation of a RC involves the reorganization of a large number of water molecules and reorientation of the reactant fragments, which implies a considerable free energy cost. In the ribosome, this reorganization is already embedded in the binding process that becomes favourable by 2.5 kcal·mol⁻¹.²⁶

It is important to note that our simulations suggest a scenario compatible with the entropic trap proposal.²⁶ However, it must be emphasized that in our case the entropic cost in solution is not only associated to the rearrangement of the reacting subsystem (the solute) but to the reorganization of the environment (the solvent water molecules). The structure of the ribosome, preorganized at the Michaelis complex, provides adequate interactions to the substrate without needing a large reorganization of the environment (in this case the RNA and proteins structures).

CONCLUSIONS

In this paper, we present a study of the peptide bond formation reaction catalyzed by ribosome. Different mechanisms have been explored by means of FEP methods within hybrid QM/MM potentials, which have allowed exploring molecular mechanism with complex reaction coordinates. According to our results, the most favourable mechanism in the ribosome would proceed through an eight membered ring TS. When comparing with the reaction in solution,²⁵ our simulations reproduce the experimentally determined catalytic effect of ribosome, especially when an additional Mg²⁺ ion is included in the surroundings of the active center. This improvement achieved with the additional ion emphasizes the role of counterions in biological catalysis, opening an avenue for future research.

A deep insight into the reaction mechanism, through the analysis of the evolution of the system from RC to the TS, reveals that the full process can be described in three stages: i) an SN2 nucleophilic attack of the A-site amino group with the elongation of the carbonilic bond giving place to a transient zwitterionic species; ii) an SN2 reaction in wich the carboninic group recovers the double bond character and the C-O3’ bond is broken, leaving to an ion-pair TS; and iii) a proton transfer from the positively charged A-site fragment to the negatively charged O3’ through a shuttle mechanism involving the O2’ hydroxyl group and a water molecule. Nevertheless, the full process is concerted taking place in a single kinetic step.

Comparing the mechanism in solution and in the ribosome, differences are detected regarding the evolution of the chemical system that can be attributed to the different behaviour of both environments. The large charge separation of the solute that takes place during the reaction can be stabilized, and amplified, in solution but paying an entropic penalty. In contrast, the ribosome saves this entropic cost offering a more rigid environment that is preorganized at the Michaelis complex. As a consequence, the charge separation of the solute during the reaction is dampened in the ribosome, becoming less polar. This observation is in agreement with the enthalpic and entropic differences experimentally measured. An intriguing aspect of the ribosome, by comparison with protein enzymes, is that the full catalytic effect seems to be already attained at the Michaelis complex.