Abstract
Objective
Models of excitable cells consider the membrane specific capacitance as a ubiquitous and constant parameter. However, experimental measurements show that the membrane capacitance declines with increasing frequency, i.e., exhibits dispersion. We quantified the effects of frequency-dependent membrane capacitance, c(f), on the excitability of cells and nerve fibers across the frequency range from dc to hundreds of kilohertz.
Approach
We implemented a model of c(f) using linear circuit elements, and incorporated it into several models of neurons with different channel kinetics: the Hodgkin-Huxley (HH) model of an unmyelinated axon, the McIntyre-Richardson-Grill (MRG) of a mammalian myelinated axon, and a model of a cortical neuron from prefrontal cortex. We calculated thresholds for excitation and kHz frequency conduction block, the conduction velocity, recovery cycle, strength-distance relationship and firing rate.
Main results
The impact of c(f) on activation thresholds depended on the stimulation waveform and channel kinetics. We observed no effect using rectangular pulse stimulation, and a reduction for frequencies of 10 kHz and above using sinusoidal signals only for the MRG model. c(f) had minimal impact on the recovery cycle and the strength-distance relationship, whereas the conduction velocity increased by up to 7.9% and 1.7% for myelinated and unmyelinated fibers, respectively. Block thresholds declined moderately when incorporating c(f), the effect was greater at higher frequencies, and the maximum reduction was 11.5%. Finally, c(f) marginally altered the firing pattern of a model of a prefrontal cortex cell, reducing the median interspike interval by less than 2%.
Significance
This is the first comprehensive analysis of the effects of dispersive capacitance on neural excitability, and as the interest on stimulation with kHz signals gains more attention, it defines the regions over which frequency-dependent membrane capacitance, c(f), should be considered.
Keywords: electrical stimulation, frequency-dependence, capacitance, dispersion
1. Introduction
The lipid bilayer of the cell membrane is a dielectric that creates a capacitance by separating charge inside and outside the cell. Such capacitive behavior is represented in electrical equivalent circuit models of the cell membrane with an electrical capacitor element (McNeal, 1976). The membrane specific capacitance is considered constant and ubiquitous, with a value of 1-2 μF/cm2 (Gentet et al., 2000). Accordingly, myriad models of excitable cells and axons incorporate a constant membrane capacitance (McIntyre et al., 2002, Rattay, 1989, Sweeney et al., 1987). However, the dielectric properties of living tissues exhibit frequency-dependent behavior (Gabriel et al., 1996a, Gabriel et al., 1996b, Grimnes and Martinsen, 2010). The objective of the present study was to quantify the effects of frequency-dependent membrane capacitance on neuronal excitation and determine whether it is important to represent this feature in electrical models of single neurons.
The permittivity of biological materials decreases monotonically with frequency, with three major dispersion regions: alpha, beta and gamma, in the ranges of kHz, hundreds of kHz and MHz, respectively (Foster and Schwan, 1989). The cell membrane exhibits similar frequency-dependent behavior. For example, several relaxation processes for the membrane capacitance of frog skin epithelium were identified in the audio frequency range (i.e., alpha dispersion) (Awayda et al., 1999), and the specific capacitance of the squid giant axon membrane, which declines by half from dc to 100 kHz (Haydon and Urban, 1985), was fitted by a single relaxation between dc to 3 kHz (Fernández et al., 1983). Such behavior may influence excitability and it may be necessary to incorporate frequency-dependent membrane capacitance into models of excitable cells, particularly if the frequency of stimulation extends into the tens of kHz, for example to achieve conduction block (Kilgore and Bhadra, 2014) or with waveforms intended to penetrate more deeply into tissue (Medina and Grill, 2014).
In this study we introduce a model of a frequency-dependent membrane capacitance using a mathematical description of a relaxation process, and we incorporate this formulation into several models of excitable cells and axons to quantify the effect of the dispersive capacitance on excitability. The only previous study in which dispersion of the membrane capacitance was taken into account (Haeffele and Butera, 2007) considered the effects on conduction block in a Hodgkin and Huxley model of an unmyelinated fiber, and observed a decline in thresholds that did not accurately predict the non-monotonic relationship observed experimentally at frequencies > 10 kHz. We conducted a comprehensive analysis of the effect of the dispersive capacitance on the excitability of single compartment models of excitable cells, distributed cable models of myelinated and unmyelinated axons, and a distributed cable model of a cortical neuron. The results show that dispersive capacitance reduced activation thresholds for sinusoidal signals only for certain models, reduced block thresholds with kHz frequency signals, increased conduction velocity, and had minimal impact on the recovery cycle and the strength-distance relationship.
2. Methods
2.1. Electrical representation of a frequency-dependent capacitance
We modeled a frequency-dependent capacitance, c(s), using the following expression:
| (1) |
| (2) |
| (3) |
where, cdc is the specific membrane capacitance (F/m2) at ω = 0; c∞ is the membrane capacitance at ω = ∞; τ is the relaxation time (s); and ω = 2πf is the angular frequency (rad/s).
The impedance of c(s) (in Ω/m2) is given by Equation 4, and Equation 5 is the ordinary differential equation (ODE) that describes the relationship between the capacitive current density (ic in A/m2 and the transmembrane voltage (Vm) across the capacitor.
| (4) |
| (5) |
The prime symbol denotes the derivative with respect to time; and a0 = 1, a1 = τ, b0 = cdc, and b1 = τc∞ are constant coefficients determined with Equation 1. We reduced Equation 5 to a system of first order ODEs. However, preliminary analysis showed that this system of ODEs was moderately stiff (see Appendix) and thereby presented issues for numerical solution.
We therefore used a combination of linear circuit elements to model the frequency dependent capacitance, c(f) (Figure 1). The circuit representing c(f) consisted of a capacitance (c∞) in parallel with the series combination of a conductance (gΔ in S/m2) and capacitance (cΔ), and had an impedance equal to that of Equation 4. The ODEs describing the relationship between Vm and ic are given in the Appendix.
Figure 1.
Equivalent electrical circuit representations of the neural membrane. (a) The membrane was modeled using a nonlinear sodium conductance (gNa in S/m2), a nonlinear potassium conductance (gK), a linear leakage conductance (gL), and a frequency-dependent capacitance (dashed box). The frequency-dependent membrane capacitance consisted of a capacitance (c∞) in parallel with the series combination of a conductance (gΔ) and capacitance (cΔ). E and Vm denote the reversal and transmembrane voltages, respectively. (b) An analytic expression for Vm was obtained by replacing gNa, gK, and gL with a single linear constant membrane conductance (gm). Vrest is the resting voltage of the membrane. Expressions for the circuit elements are given in the Appendix.
2.2. Single-compartment models of neurons
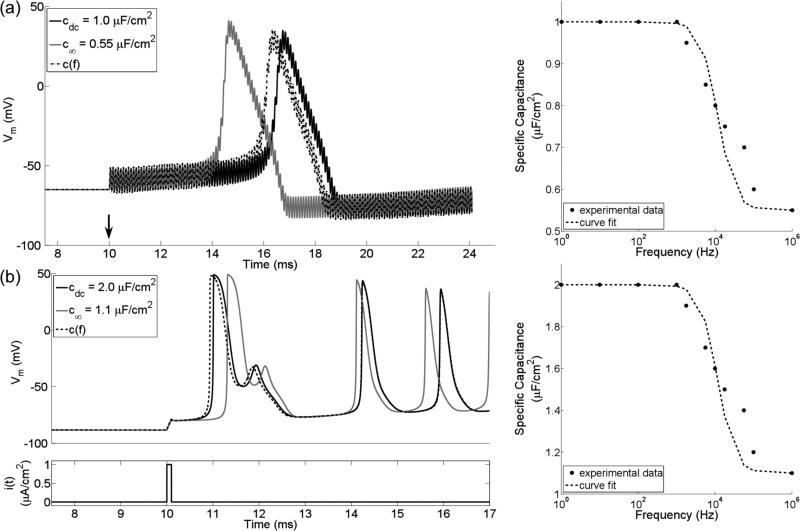
We implemented two single-compartment lumped models (SCMs) of neurons in MATLAB (v2014a, Mathworks, Natick, MA). The first, HH SCM, included Hodgkin-Huxley (HH) ion channels (Hodgkin and Huxley, 1952) and either a constant membrane capacitance or c(f). The constant membrane capacitance was set to either cdc = 1 μF/cm2 or c∞ = 0.55 μF/cm2, while c(f) declined from cdc to c∞ with τ = (2π104)−1 s (Figure 2a). We selected values for cdc, c∞, and τ based on measurements from a squid giant axon (Takashima and Schwan, 1974).
Figure 2.
Action potentials (left) in single-compartment lumped models (SCMs) of neurons with constant or frequency-dependent membrane capacitance (right). (a) 10 kHz sinusoidal stimulation of a SCM with HH ion channels and a membrane capacitance that was either constant (i.e., cdc or c∞) or declined with increasing frequency (right). Vm is the transmembrane voltage, and the arrow indicates the onset of stimulation. (b) Intracellular monophasic pulse stimulation (i) of a SCM with MRG ion channels found in the node of Ranvier of a myelinated axon. The pulse was 100 μs in duration. Note that the repetitive action potentials following a single stimulus are the result of implementing in a single compartment model membrane dynamics that were originally parameterized to represent a node of Ranvier in a multi-compartment cable model. The experimental data are from (Takashima and Schwan, 1974).
The second, MRG SCM, included ion channels representative of mammalian nerve fibers (McIntyre et al., 2002) and either a constant membrane capacitance or c(f). We set cdc = 2 μF/cm2 (Frankenhaeuser and Huxley, 1964), as there are no studies that analyze how the membrane capacitance varies with frequency in mammalian axons. c∞ was set to 1.1 μF/cm2, and τ was kept at (2π104)−1 s.
A more detailed description of the ODEs and parameters of the HH and MRG SCMs is given in the Appendix.
2.2.1. Lumped model validation, and implementation, and analysis
We used a linear circuit representation of the neural membrane (Figure 1b) to validate the numerical solutions of the SCMs. The solution was approximated using the stiff ordinary different equation solver, ode15s, in MATLAB, and we verified that the root mean square error between the numerical and analytical solutions was < 5×10−4 % (see Appendix).
We used three different types of intracellular current waveforms (A/m2) to stimulate the SCMs: a monophasic rectangular pulse, a train of monophasic rectangular pulses, and a sine wave (Figure 3). The pulse widths (PWs) of monophasic rectangular pulses ranged from 50 μs to 10 ms, as this range encompasses the range of possible PWs used in electrical stimulation devices.
Figure 3.
The effect of a frequency-dependent membrane capacitance on stimulation thresholds. A single rectangular pulse (a), a sinusoid (b), or a train of 100 μs rectangular pulses at fstim (c) was used to stimulate a single-compartment model with MRG ion channels. i is the applied intracellular current density. The membrane capacitance that was either constant (cdc = 2 μF/cm2) or frequency-dependent, c(f). The middle plots show the spectra of the stimulation signals pulse, and the bottom plots show the percent difference in the stimulation thresholds (ith) between the c(f) and cdc cases (i.e., [c(f) – cdc]/ cdc).
For stimulation with a train of pulses, PW was set to 100 μs, a typical PW used in deep brain stimulation (Kuncel and Grill, 2004), and the frequency of the pulse train ranged from 100 Hz to 10 kHz. Below 100 Hz, the stimulation thresholds were identical to the stimulation thresholds with a single pulse, and at and above 10 kHz, the pulses fused to produce direct-current stimulation. Therefore, only stimulation thresholds within the above range were analyzed.
For sinusoidal stimulation currents, frequencies ranged between 100 Hz and 100 kHz. The lower bound of this range was chosen because we assumed that no dispersion occurred at frequencies below 100 Hz (see Section 4.3), and the upper bound was chosen so that it encompassed the frequencies used in vivo for studying conduction block (Bhadra and Kilgore, 2005; Joseph and Butera, 2009).
The nonlinear SCMs (Figure 1a) were solved using ode15s. For stimulation with rectangular pulses, we used a variable time-step with a maximum step of 10 μs for PWs ≥ 100 μs, and 5 μs for PWs < 100 μs; and for sinusoidal stimulation, we used a variable time-step with a maximum of 10 ns for frequencies below 10 kHz and 0.5 ns for frequencies above 10 kHz. In all simulations, reducing the maximum time-steps by half altered the stimulation thresholds by < 1 %. Further, we imposed a 10 ms delay to ensure the model had reached steady-state before stimulation, and all simulations were run for 30 ms.
Thresholds to generate an action potential were calculated using a bisection algorithm (relative error < 1 %), and traces of Vm were inspected post hoc to ensure that at least one action potential was evoked at the calculated value (Figure 2).
2.3. Cable models of axons
We implemented two distributed models of axons in NEURON (v7.3) (Carnevale and Hines, 1997): a HH model of an unmyelinated axon with the same ion channels used in the HH SCM and an MRG model of a myelinated axon, which, at the nodes of Ranvier, contained the same ion channels used in the MRG SCM. The values that defined the membrane capacitance in the HH axon and MRG axon were the same as those used in the HH SCM and MRG SCM, respectively (see Section 2.2). For the unmyelinated fiber model, we used a 40 mm long axon segmented in 0.5 mm long cylinders (Tai et al., 2005), and the axons had diameters ranging from 50 to 800 μm to represent the squid giant axon (Matsumoto and Tasaki, 1977), and from 0.4 to 2 μm to represent mammalian unmyelinated axons. The myelinated axons were at least 10 mm in length and had diameters (including the myelin) ranging from 5.7 μm to 16 μm. The geometric and electric parameters of the myelin and intermodal regions were taken from a validated model of a mammalian myelinated axon (McIntyre et al., 2002). Both the myelinated and unmyelinated axons were long enough to avoid activation at the terminations of the axons, and we confirmed that in all of our simulations no action potentials were generated at the ends.
2.3.2. Distributed model implementation and analysis
A number of analyses were conducted to assess the effects of c(f) on neural excitability: (1) stimulation thresholds (see Section 2.2.2); (2) the recovery cycle, which is the change in stimulation thresholds following a supra-threshold conditioning stimulus; (3) the strength-distance relationship, which is the relationship between the stimulation thresholds and the axon-to-electrode distance; (4) the firing rate of the axon during repetitive pulse stimulation; (5) thresholds for conduction block; and (6) conduction velocity.
Stimuli were extracellular currents delivered in an infinite medium with homogeneous and anisotropic conductivity. The longitudinal (σz) and transverse (σxy) conductivity were 1/3 and 1/12 S/m, respectively (McIntyre et al., 2002). We calculated the extracellular potentials using the following function (Li and Uren, 1998):
| (6) |
where, Is is the amplitude of a point source current (in A), which was located at the origin; and x, y, and z are the coordinates of a point on an axon. We calculated the extracellular potentials in MATLAB and used the “extracellular” mechanism in NEURON to apply extracellular stimulation to the model axons. We implemented c(f) in NEURON by setting the membrane capacitance equal to zero and using the “LinearMechanism” class to define the corresponding ODEs (see Appendix). The axon models were solved using an implicit (trapezoidal) integration method with a fixed time step of 1 μs. Halving the time step altered the stimulation thresholds by < 1 %. Unless stated otherwise, there was a 1 ms delay before the onset of stimulation, and all simulation were run for a total of 10 ms.
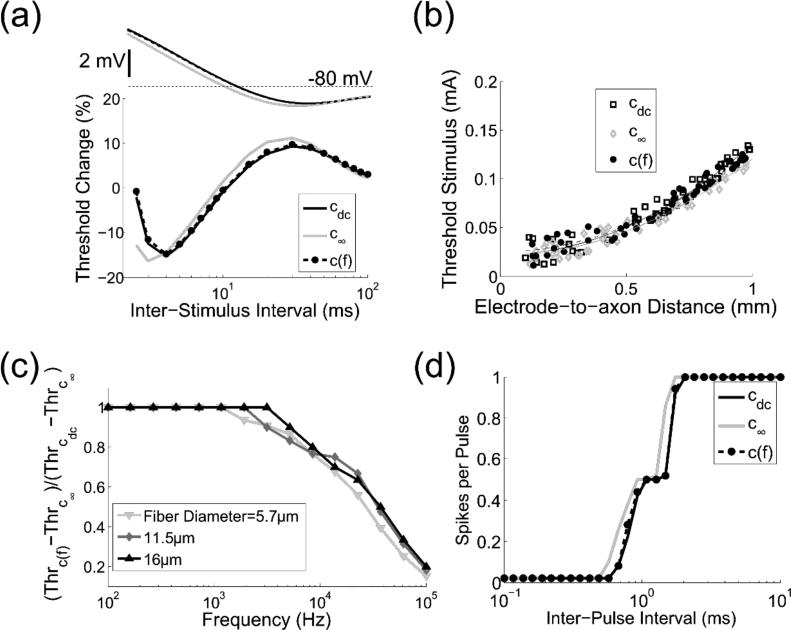
To analyze the recovery cycle, we stimulated a 5.7 μm diameter axon at an electrode-to-axon distance of 0.6 mm. The point source electrode was positioned over the middle node of Ranvier. The output metric was the percent difference in the stimulation threshold between two 1 ms rectangular pulses over inter-pulse intervals between 2.5 and 100 ms, as axons fully recover excitability after 100 ms (Kiernan et al., 1996).
In the strength-distance analysis, we stimulated a population of fifty myelinated axons with diameters of 5.7 μm, and each simulation was independent of each other, i.e., there were no axon-axon interactions. The axons were randomly placed in the medium so that the electrode-to-axon distances (r) were uniformly distributed between 0.1 mm and 1 mm - a range in which thresholds have been measured experimentally (BeMent & Ranck, 1969) - and the central node of Ranvier was laterally displaced by between −0.5 and +0.5 inter-nodal lengths from the point source electrode. We used least-squares regression to fit the stimulation thresholds (Ith) to the function: Ith = k1 + k2r2, where k1 and k2 are constant coefficients. The output metric in this analysis was k2.
To quantify the response of the distributed fiber models to repetitive pulse stimulation, we applied a train of 50 rectangular pulses of 100 μs duration and amplitude 10 % larger than the threshold for a single pulse. The time between the pulses ranged from 0.1 to 10 ms (i.e., frequencies of 100 Hz to 10 kHz), and the duration of the simulation was set to deliver 50 pulses. We counted the number of action potentials to obtain the spikes per pulse, which was the output metric in this analysis.
To quantify thresholds to achieve block of action potential conduction, we followed the approach of (Bhadra et al., 2007). Using an extracellular point source electrode located 1 mm above the middle of the fiber, we delivered a sinusoidal signal (3 – 40 kHz). 40 ms after the onset of the sinusoidal signal, we applied an intracellular test stimulus to one end of the fiber and determined whether the evoked action potential propagated to the other end. We used a bisection algorithm (1 μA resolution) to determine the minimum amplitude of the extracellular sinusoidal signal that blocked the conduction of the test action potential.
Finally, the conduction velocity was calculated by applying a suprathreshold 250 μs rectangular stimulus to a 101-node fiber and averaging local conduction velocities from node to node for the myelinated fiber and in segments of 0.5 mm for the unmyelinated fiber. Displacements from the location where the action potential was initiated to the location where the action potential was recorded were positive; therefore, by definition, all velocities were positive.
2.4 Model of a cortical neuron
We quantified the effect of c(f) on the firing rate of a model of a pyramidal neuron from prefrontal cortex (PFC). We used the “intrinsic bursting” cell type of (Sidiropoulou and Poirazi, 2012), and the NEURON implementation as available in the modelDB database (https://senselab.med.yale.edu/modeldb/ShowModel.asp?model=144089). The model comprises a large variety of membrane mechanisms distributed in one axon, one soma and 43 dendrites, and includes an artificial current with Poisson characteristics to simulate the ion channel noise observed in vitro. We inserted c(f) in all compartments as described in Section 2.3.2. We applied intracellular 500 ms constant current stimulation to the soma and quantified the number of action potentials. We calculated the input-output response function, i.e., the f-I curve, defined as the average firing rate as a function of stimulus amplitude in the range from 0.1 to 1.6 nA. Next, we applied natural patterns of synaptic stimulation as described in detail in (Sidiropoulou and Poirazi, 2012). Briefly, the dendrites were stimulated with 200 randomly distributed excitatory synapses that were activated 10 times at 20 Hz, and the soma was stimulated with 5 inhibitory synapses at 50 Hz. In this test, we increased the conductance of the Ca++-activated non-selective cation (CAN) current to 106 μS/cm2 to induce persistent activity and calculated the inter-spike interval (ISI) distribution for 25 five s duration simulations that differed in the randomly selected location of the excitatory synapses.
3. Results
We implemented single compartments models of neurons, distributed cable models of axons, and a distributed cable model of a cortical neuron and used these models to quantify the effects of frequency-dependent capacitance on neural excitability.
3.1. The effects of c(f) on thresholds for activation and conduction block
The effects of c(f) on thresholds for stimulation and block depended on the ion-channel kinetics and stimulation waveform. c(f) had a negligible effect on the stimulation thresholds of SCM neurons with HH ion channels: across all cases, stimulation thresholds were altered by at most 6.3 % (median = 1.4 %). In contrast, c(f) had a marked effect on the stimulation thresholds of the MRG SCM but only for sinusoidal waveforms (Figure 3). In the MRG SCM, incorporation of c(f) decreased the stimulation thresholds of sinusoidal waveforms by up to 48 % at f > 8 kHz. However, changing from cdc to c(f) had negligible impact on the stimulation thresholds with a train of 100 μs pulses at frequencies between 100 Hz and 10 kHz.
Similar results were observed in the distributed axons models, and the effect was slightly more accentuated in smaller diameter fibers (Figure 4c). The activation thresholds using sinusoidal stimulation declined by up to 19.3%, 14% and 11.5% for MRG axons with fiber diameters of 5.7, 11.5 and 16 μm, respectively. For unmyelinated axons, the activation thresholds varied less than 5.6% (median = 0.2%). The fidelity of the fiber response to repetitive pulsatile stimulation, which deteriorated at shorter inter-pulse intervals, was not affected by c(f) (Figure 4d).
Figure 4.
The effect of frequency-dependent membrane capacitance on (a) recovery cycle, (b) strength-distance relationship, (c) thresholds for fiber activation with sinusoidal stimulation, and (d) firing rate during repetitive pulse stimulation of the MRG fiber model. (a) A 1 ms suprathreshold pulse stimulus was followed by a 1 ms test stimulus, and the threshold for activation was determined as a function of the inter-pulse interval. The transmembrane voltage at the node of excitation after a supra-threshold stimulus (afterpotential) is plotted on the same time scale. (b) Activation threshold as a function of electrode-to-axon distance. (c) Ratio of the activation threshold (Thr) difference between c(f) and c∞ to the threshold difference between cdc and c∞ using sinusoidal stimulation. (d) Number of action potentials (spikes) per pulse for repetitive pulsatile stimulation of varying inter-pulse interval. The stimulus train was composed of fifty 100 μs duration pulses.
c(f) had negligible effects on both the recovery cycle and strength-distance relationship of the axon models (Figure 4). Switching from cdc to c(f) altered the recovery cycle by at most 1.4 % (median = 0.4 %) and k2 by 7.9 %. In the strength-distance relationship, the lateral displacements of the nodes relative to the electrode affected the thresholds, and this effect was greater for shorter electrode-to-axon distances. The thresholds were more widely scattered for electrode-to-axon distances smaller than 0.5 mm, and the subset of axons laterally displaced by less than 0.1 inter-nodal lengths had thresholds ~60% lower than those displaced more than 0.3 inter-nodal lengths (Figure 4b). On the other hand, this difference decreased to ~10% for electrode-to-axon distances greater than 0.5 mm. This was expected because fiber excitation with monopolar point-source electrodes is more affected by the distance from the electrode to the closest node than the perpendicular distance to the fiber (Rattay, 1989).
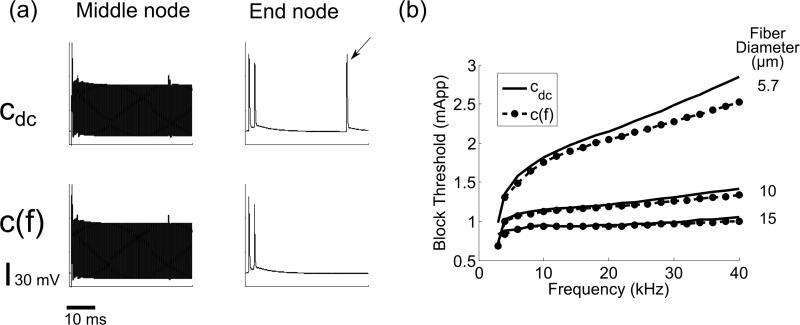
3.1.2. Thresholds for conduction block with sinusoidal signals
The threshold amplitudes of a sinusoidal signal to achieve block of action potential conduction were reduced by c(f), and the effect was more pronounced for smaller diameter fibers and higher signal frequencies (Figure 5). The maximum reductions in block threshold were 11.5 % (median 5.7%), 5.9 % (median 3 %) and 5.5 % (median 1.8%) for fiber diameters of 5.7, 10 and 15 μm, respectively.
Figure 5.
Conduction block thresholds. (a) Transmembrane voltage at the middle node (i.e., just below the electrode) and the end node opposite to the application of the test stimulus, for constant, cdc, and frequency dependent, c(f), membrane capacitance. The block signal was a 2.4 mA peak-to-peak 30 kHz sine wave, and the test stimulus was applied at 40 ms. The arrow indicates that the test action potential propagated, i.e., conduction block was not achieved. (b) Threshold to achieve conduction block of the test stimulus as a function of the sinusoidal blocking signal frequency for three fiber diameters.
3.2. The effects of c(f) on conduction velocity
The action potential conduction velocity was increased by the incorporation of c(f), and the effect was greater for the myelinated fiber (Figure 6). The maximum increase in conduction velocity was 7.9% (median 7.1%) and 1.7 % (median 1.3 %) for the myelinated and unmyelinated fibers, respectively.
Figure 6.
Effect of c(f) on action potential conduction velocity. (a) Transmembrane voltage (Vm) of a 10 μm myelinated fiber (MRG) and a 2 μm unmyelinated fiber (HH) that had either constant (cdc = 2 μF/cm2 or c∞ = 1.1 μF/cm2 for the myelinated fiber, and cdc = 1 μF/cm2 or c∞ = 0.55 μF/cm2 for the unmyelinated fiber) or frequency-dependent, c(f), capacitance. Vm was recorded at two different locations along each fiber as indicated in the insets (arrow: recording position, black dot: electrode position). The bottom plot shows the applied extracellular stimulus (−250 μA and −100 μA for the myelinated and unmyelinated fiber, respectively). (b) Conduction velocity as a function of fiber diameter for the myelinated (top) and unmyelinated (bottom) fiber models.
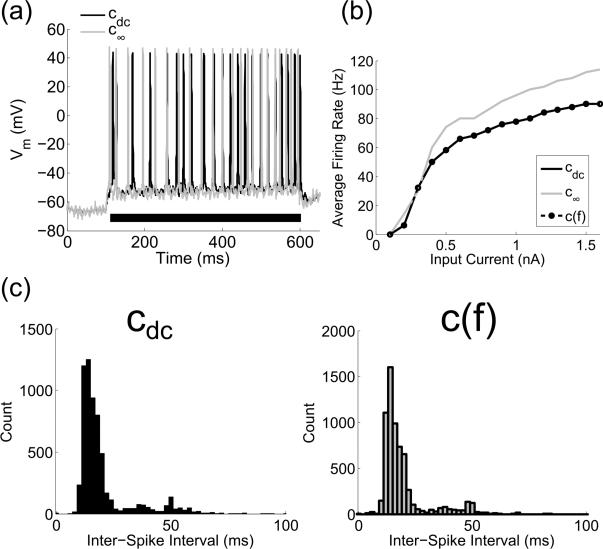
3.3 Effect of c(f) on the excitability of a cortical neuron
The incorporation of c(f) had a minimal effect on the firing properties of the model of a PFC neuron. Although reducing the (constant) capacitance to c∞ increased the firing rate by up to 25%, the f-I curve with c(f) overlapped with that with cdc (Figure 7b). With the simulated natural patterns of excitation, the model neuron fired persistently for both the cdc and the c(f) cases, but fired slightly more rapidly in the latter case, as reflected in the inter-spike interval (ISI) histogram (Figure 7c). The median ISI for cdc and c(f) was 15.9 ms (min = 0.2, max = 106.2) and 15.7 ms (min = 0.2, max = 84.2), respectively, across 25 simulations.
Figure 7.
Effect of c(f) on the firing properties of a distributed multi-compartment cable model of a cortical neuron. (a) Transmembrane voltage, Vm, of the soma upon application of a 500 ms (black bar) intracellular constant current step of 300 pA. Vm for c(f), which overlapped with Vm for cdc, is not shown for clarity. (b) Average firing rate as a function of the amplitude of a 500 ms intracellular current step. (c) Histogram of the inter-spike intervals for the cell in a state of persistent activity induced by natural patterns of excitation as described in (Sidiropoulou and Poirazi, 2012).
4. Discussion
We developed computational models of neural elements that included the dependence of the membrane capacitance on frequency, c(f), that arises from dielectric dispersion, and we used these models to quantify the effects of c(f) on neural excitability. The results revealed that substantial effects were restricted to changes in stimulation and block thresholds for sinusoidal signals at frequencies above 10 kHz. In addition, dielectric dispersion affected the conduction velocity of the action potential, but had a negligible effect on firing rate. Therefore, one should consider the effects of c(f) on neural excitation, particularly when studying the response of neural elements to stimulus waveforms with spectral content ≥ 10 kHz.
The results of our study may be of interest for applications in which kilohertz frequency signals are used to either stimulate or block nerve fibers. Since the impedance of the skin declines with increasing frequency, transcutaneous electrical stimulation (TES) may be optimized using kHz frequency signals (Medina and Grill, 2014). Examples of TES applications employing these signals are interferential currents, in which the paths of two kHz currents cross to produce an amplitude modulated signal (Ward, 2009), and the transdermal amplitude modulated signal (TAMS), in which a high-frequency sinusoidal carrier is modulated by rectangular pulses (Shen et al., 2011). Further, kHz frequency signals can produce transient conduction block of peripheral nerve fibers (Ackermann et al., 2011), and this principle was used for amputee pain relief by the application of a 10-20 kHz waveform to the sciatic nerve proximal to a distal neuroma (Soin, 2012). Finally, rectangular pulses delivered at rates of 5 or 10 kHz are used in clinical applications of spinal cord stimulation (Tiede et al., 2013) and vagus nerve stimulation (Sarr et al., 2012) for the treatment of pain and obesity, respectively.
4.1. Modeling dielectric dispersion
The decrease in the membrane capacitance with increasing frequency, or dielectric dispersion, can be modeled as an n-step relaxation process (Awayda et al., 1999):
| (7) |
| (8) |
where, for the ith relaxation step, cΔ,i is the change in the membrane capacitance, τi is the relaxation time, and γi is the Cole-Cole power-law factor, which is between 0 and 1 (Cole and Cole, 1941, Cole and Cole, 1942). In our analyses, we approximated dielectric dispersion using one relaxation step (i.e., n = 1), and we assumed γ1 = γ = 1 so that c(f) could be modeled using linear circuit elements.
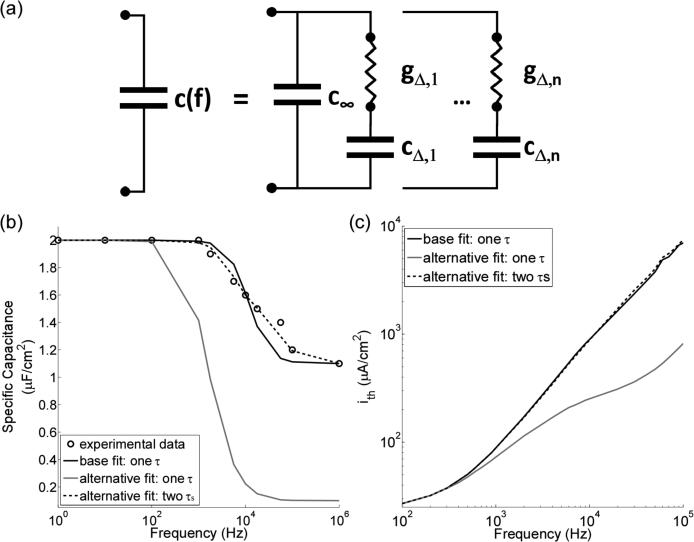
Dielectric dispersion at frequencies below 100 kHz is typically referred to as α dispersion and is associated with ionic diffusion processes at the cell membrane (Foster and Schwan, 1989). Because the relaxation event occurring at the neural membrane is not a first order process (Chew and Sen, 1982), one τ may not be suitable to describe α dispersion. The representation of c(f) can be improved by using n + 1 capacitances and n conductances to model n relaxation steps (Figure 8a). For example, using two relaxation steps better approximated the experimental values of c(f) (Figure 8b), but despite the better fit to the data, the stimulation thresholds only changed by at most 8.3 % (median = 2.0 %) compared to n = 1 (Figure 8c). Therefore, one τ was a reasonable approximation for α dispersion.
Figure 8.
Sensitivity of the stimulation thresholds to changes in the representation of the frequency-dependent membrane capacitance, c(f). (a) Dielectric dispersion, or c(f), can be modeled with a single capacitance (c∞) in parallel with n different series combinations of a conductance and capacitance (see Equation 7). (b) Three curves of c(f) for the MRG SCM: the baseline fit (black line), where, n = 1, cdc = 2 μF/cm2, c∞ = 1.1 μF/cm2, and τ = (2π104)−1 s (see Section 2.2); an alternative fit similar to the baseline, except c∞ = 0.1 μF/cm2 (grey line); and a second alternative fit (dashed line), where n = 2, c∞ = 1.1 μF/cm2, cΔ,1 = 0.5 μF/cm2, cΔ,2 = 0.4 μF/cm2, τ1 = (2π4.9×103)−1 s, and τ2 = (2π5.0×104)−1 s. Experimental data from (Takashima and Schwan, 1974). (c) The stimulation thresholds of the MRG SCM for each of the three different representations of c(f) in part b. The stimulus was an intracellular sinusoidal current density (i).
Alternatively, the assumption that all τi are all well separated (i.e., τ1 << τ2 << ... << τn) can be relaxed, which means some γi ≠ 1(Foster and Schwan, 1989). For many biological tissues, γi ≠ 1 (Gabriel et al., 1996c); therefore, the γi that describe dispersion in the neural membrane are likely not equal to one. For n = 1, changing γ from 1 to 0.7 reduced the relative percent difference between c(f) and the experimental data (Figure 2a) from between −19 % and +7.3 % (Figure 2a) to between −10 % and +4.3 % at frequencies between 1 kHz 100 kHz (not shown). However, relaxing the assumption that all γi = 1 is not trivial because this leads to a relationship between Vm and ic that involves fractional derivatives (Biswas et al., 2006). Solving a system of ODEs with fractional derivatives is not as straightforward as solving a system of ODEs with integer-valued derivatives (Diethelm et al., 2005). Therefore, it may be more practical to use a larger n with all γi = 1 than a smaller number of n with 0 < γi < 1, as the former may be more computationally tractable.
4.2. Basis for the effects of c(f) on neural excitability
4.2.1. The effects on stimulation thresholds
To understand why c(f) had an effect in some instances but not in others, we must first understand how changing a constant membrane capacitance (cm) affects Vm. For a constant cm, , and
| (9) |
As positive and negative charge builds up on the inner and outer surfaces of the neural membrane, respectively, the membrane is depolarized, and Vm increases more for a membrane with a smaller cm. In other words, when cm is smaller, it takes less charge to reach the threshold for excitation. This explains why decreasing cm from cdc to c∞ decreased stimulation thresholds (Figure 3).
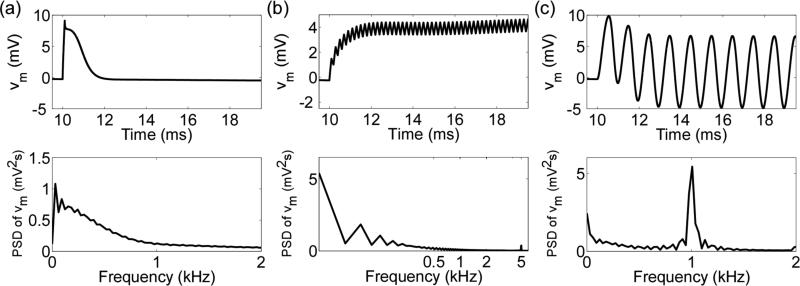
Next, we consider how the spectrum of Vm affects c(f). Below the threshold for excitation, the response of the neural membrane to a rectangular pulse of intracellular current resembles the response of the parallel combination of a resistor and capacitor (Figure 9a). Since the majority of the signal power in this exponential response is in the frequency band below 1 kHz (Figure 9a), and since c(f) ≈ cdc for frequencies <1 kHz, one expects that pulse stimulation thresholds will not be markedly different between the c(f) and cdc cases (Figures 3a and 3c).
Figure 9.
The subthreshold response of the neural membrane in the MRG SCM. Reduced transmembrane voltage (vm = Vm – Vrest) in response to subthreshold stimulation and the power-spectral density (PSD) of vm (bottom) with (a) a 100 μs rectangular pulse, (b) a train of 100 μs pulses at 5 kHz, and (c) a 1 kHz sinusoid.
With a train of rectangular pulses, the majority of the power in Vm is also in the frequency band below 1 kHz, even if the pulses are delivered at frequencies greater than 1 kHz. For example, consider a train of 100 μs pulses delivered at 5 kHz. One expects that Vm will have spectral content at 5 kHz because the power-spectral density of a 5 kHz train of pulses is maximal at the stimulation frequency. Indeed, during subthreshold stimulation, Vm appears to oscillate at 5 kHz but about a dynamic baseline that resembles the response of the parallel combination of a resistor and capacitor to a direct-current stimulus (Figure 9b). This occurs because as the frequency of the train approaches its fusion frequency (10 kHz, in this example), more power is concentrated near 0 Hz (Figure 9b), explaining why the stimulation thresholds did not differ markedly between the c(f) and cdc cases.
Unlike the pulsed rectangular stimulation, Vm followed the frequency of stimulation during subthreshold sinusoidal stimulation, and the majority of the power in the membrane response was concentrated near the stimulation frequency (Figure 9c). Therefore, at stimulation frequencies where c(f) was substantially less than cdc, one expects a reduction in the stimulation thresholds, which is what was observed (Figure 3b).
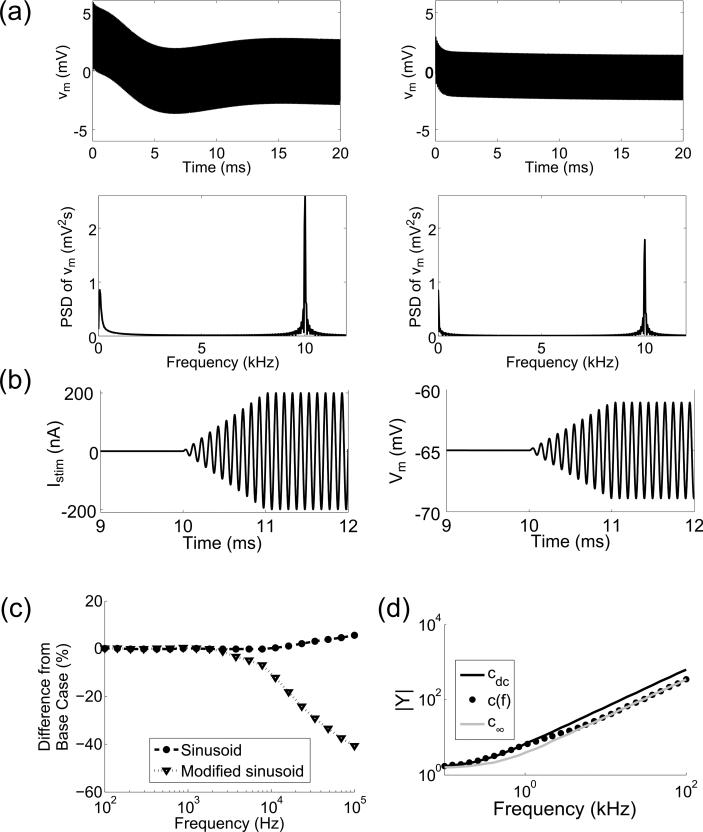
Examination of Vm also explained why c(f) had an effect on the MRG model thresholds but not on the HH model thresholds. At the onset of the sinusoidal stimulus, Vm oscillated at the stimulation frequency about a transiently changing baseline, which is known as the natural or characteristic response of the system. The time constant of the natural response (τnat) is equal to cm/gm, which is approximately equal to cm/gL for sub-threshold stimulation. Because gL in the HH model was more than 10 times larger than gL in the MRG model (see Appendix), the natural response was significantly longer in the HH model (Figure 10a). In the HH models, the natural response exhibited a marked amount of signal power in the frequency band below 1 kHz (Figure 10a), which, we hypothesized, caused c(f) to behave more like cdc.
Figure 10.
The effect of the natural response on stimulation thresholds. (a) Reduced transmembrane voltage (vm = Vm – Vrest, top) and the PSD of vm (bottom) in the HH axon model (left) and the MRG axon model (right) in response to subthreshold stimulation with an intracellular 10 kHz sinusoidal current. (b) The transmembrane voltage (Vm, right) of the HH model axon in response to an intracellular sinusoidal current (left) with a peak-to-peak amplitude that increases linearly from 0 to its maximum value over 1 ms. (c) Differences in the stimulation thresholds between the cdc and c(f) cases for the HH axon model using a sinusoid and the ramped sinusoid described in (b). (d) Magnitude of the admittance, |Y|, of the equivalent circuit of the linearized HH cell with the small-signal approximation of (Sabah and Leibovic, 1969).
If the natural response was the reason that c(f) had a negligible effect on sinusoidal stimulation thresholds in the HH models, then reducing the magnitude of the natural response should alter the results. We tested this prediction using a modified sinusoidal stimulus: the peak-to-peak amplitude of the sinusoid increased linearly from 0 to its maximum value over the course of 1 ms (Figure 10b), and this substantially reduced the magnitude of the natural response. With the ramped sinusoid, stimulation thresholds decreased appreciably for frequencies > 10 kHz (Figure 10c), which is what was observed in the MRG model (Figure 3b).
Moreover, we calculated the frequency response of the equivalent circuit proposed by (Sabah and Leibovic, 1969) for small-signal approximation of an HH cell (Figure 10d). The admittance, Y, of this circuit quantifies the steady-state transmembrane voltage for a sub-threshold sinusoidal current stimulus. The magnitude of Y increased with increasing frequency similarly to the threshold for sinusoidal stimulation, and upon incorporation of c(f), Y deviated for frequencies > 1 kHz. This further supports the effect of the natural response on the HH cell, since the admittance does not account for the transient cell response. Therefore, the natural response could explain the qualitative differences in the sensitivity of the HH and MRG models to the representation of the membrane capacitance.
4.2.2. The effects on the thresholds for conduction block
Thresholds for conduction block increased with increasing frequency, and larger fiber diameters exhibited lower block thresholds, consistent with experimental measurements (Bhadra et al., 2007). c(f) reduced thresholds for all cases, and the effect was more pronounced as the frequency of the block signal increased. As the frequency increases, more current flows through the capacitive component of the membrane. However, c(f) reduces the capacitance at higher frequencies and therefore more current is available for the ionic conductance. Thus, it is likely that c(f) acted by causing slightly larger oscillations of the transmembrane voltage at higher frequencies thereby reducing the current needed to block the fiber. For example, in Figure 5, we applied the same block stimulus of 2.4 mA to both cases, cdc and c(f). After the onset activity, the membrane voltage at the middle node, i.e., the node where block occurred, oscillated with an amplitude of 75.9 mV and 81.7 mV for the cdc and c(f) cases, respectively. Our results are in agreement with those of (Haeffele and Butera, 2007), who observed a reduction of block thresholds by incorporating a different implementation of a frequency-dependent capacitance into a model of an unmyelinated fiber with HH channels. As in our study, dispersive capacitance could not explain the experimental observations in sea-slug unmyelinated fibers that block threshold varied non-monotonically with frequency (Joseph and Butera, 2009), and therefore further investigation is needed to determine the basis for these findings.
4.2.3. The effects on conduction velocity
The incorporation of c(f) increased the conduction velocity in both myelinated and unmyelinated fibers, and this effect was more pronounced in myelinated fibers (Figure 6). Saltatory conduction in the myelinated fiber occurs through the passive charge and discharge of the internodal axolemma. Therefore, if the axolemma capacitance declines, then the time constant of the internodal segment drops and the speed increases, which we observed when we reduced the (constant) membrane capacitance to c∞. In turn, our formulation of c(f) incorporated linear circuit elements that increased the order of the circuit representation, and the internodal axolemma may have charged more rapidly due to the multiple time constants. Accordingly, we observed an increase in the conduction velocity with c(f). On the other hand, the propagation of an action potential along an unmyelinated fiber requires the activation of ionic channels along the entire length of the axon, and this continuous active conduction may be less dependent on passive membrane properties. Consequently, we observed a more modest impact of c(f) on the conduction velocity of the unmyelinated fiber. Notwithstanding, the reduced (constant) capacitance affected conduction velocity, suggesting that under continuous active propagation the charge and discharge of the axolemma still plays a role. Further, the calculations of (Matsumoto and Tasaki, 1977) suggest that the conduction velocity of unmyelinated fibers is inversely proportional to the membrane capacitance. Accordingly, we found that in the unmyelinated fiber model a 45% reduction in membrane capacitance increased the conduction velocity by 53% on average.
4.2.4 The effects on firing rate
Our results showed a minimal effect of c(f) on the firing rate of a cortical neuron model (Figure 7). The motivation to quantify the impact of c(f) on the firing rate of a pyramidal cell came from the findings of (Wang et al., 2012), who in a two compartment model of a pyramidal cell, observed great variation in the firing patterns of the cell by altering the (constant) capacitance of one or both compartments. In their model they defined quiescent, spiking, and bursting activity, and by introducing an imbalance between somatic and dendritic capacitance, the firing pattern transitioned between these states. Furthermore, reducing the membrane capacitance of any compartment increased the firing activity, as we observed in the f-I curve for the c∞ case. For example, simultaneously halving the capacitance of both compartments, approximately halved the inter-burst interval. Similarly, introducing c(f) to all compartments of the PFC model neuron reduced the average ISI by 4% as compared to the model with cdc. Since an artificial current with Poisson characteristics was injected in the soma, the net effect of c(f) can be a interpreted as a reduction of the capacitance due to broad band input.
4.3. Limitations and remaining questions
We limited our analysis to three basic waveforms: a monophasic rectangular pulse, a train of monophasic rectangular pulses, and a sinusoid. Simplifying the stimuli allowed us to develop a fundamental understanding of how c(f) affected neural excitability. However, in practice, the waveforms used for electrical stimulation are more complex. For example, the rectangular waveforms used in electrical stimulation therapies typically have two phases; the first (stimulation) phase is used to elicit the physiological response, and the second (opposite polarity charge-balancing) phase is used to reverse electrochemical reactions that may damage the electrode and/or tissue (Merrill et al., 2005).
To determine if a charge-balancing phase would alter the conclusions, we used a biphasic rectangular pulse to stimulate the MRG SCM. At all the PWs considered in this study (i.e., 50 μs to 10 ms), the addition of a symmetric charge-balancing phase of equal duration altered the stimulation thresholds by at most 7.9 % (median = 0 %) when the membrane capacitance was changed from cdc to c(f). The charge-balancing phase in many electrical stimulation therapies, however, is not symmetric but asymmetric. Similar results were observed when the charge-balancing phase was 9 times the duration and 1/9 times the amplitude of the stimulation phase. Therefore, we predict that the trends observed in this study will not be greatly impacted by the addition of a subsequent charge-balancing phase.
However, there are other aspects of electrical stimulation that may also play a role in altering the shape of the stimulation waveform. For example, the charge transduction process that occurs at the electrode-tissue interface (ETI) (Butson and McIntyre, 2005, Cantrell et al., 2008, Howell et al., 2014) and dielectric dispersion in the nervous tissue (Bossetti et al., 2008, Medina and Grill, 2014) can both alter the time course (shape) of the voltages appearing in the tissue. We observed that modification to the stimulus waveform could alter the response of the neural membrane and thereby the effects c(f) on neural excitation (Figure 10). Therefore, when studying the effects of c(f) in specific applications of electrical stimulation, the charging of the ETI and dielectric dispersion in the tissue should also be considered.
The parameterization of c(f) in this study was based on data from a limited number of studies on squid giant axons (Haydon et al., 1980, Haydon and Urban, 1985, Takashima and Schwan, 1974). These studies all indicate that the membrane capacitance is approximately constant from 100 Hz to 1 kHz and declines by approximately 50 % between 1 kHz and 100 kHz. Because none of these studies provided data for frequencies below 100 Hz, we assumed the low frequency membrane capacitance was constant. We also assumed that the membrane capacitances of mammalian and squid axons would exhibit similar frequency dependence. These were reasonable assumptions given the goal of this study was to develop an understanding of how c(f) impacted neural excitability.
5. Conclusions
We developed a versatile approach for incorporating dielectric dispersion (i.e., the dependence of membrane capacitance on frequency) into models of the neural membrane, and we used these models to assess the effect of a frequency-dependent capacitance on neural excitability. Dielectric dispersion had negligible effects on the stimulation and blocking thresholds for pulsatile stimulation but markedly reduced the stimulation and blocking thresholds for sinusoidal stimulation. The effect of dielectric dispersion on the sinusoidal stimulation thresholds depended on the electrical properties of the neural membrane. Moreover, dielectric dispersion increased action potential conduction velocity. Therefore, one should consider the impact of a frequency-dependent capacitance when studying the response properties of neural elements at frequencies of tens of kilohertz and above.
Table 1.
Symbols and Abbreviations
| Symbol/abbreviation | Description/definition | SI units |
|---|---|---|
| c | Specific capacitance | F/m2 |
| g | Specific conductance | S/m2 |
| V | Voltage | V |
| i | Current density | A/m2 |
| I | Current | A |
| τ | Relaxation time | s |
| MRG | McIntyre, Richardson, and Grill | none |
| HH | Hodgkin and Huxley | none |
| SCM | Single Compartment Model | none |
Acknowledgments
This work was supported by a Ruth L. Kirschstein F31 NS079105 Individual Predoctoral Fellowship, by Grant R01 NS040894 from the National Institute of Neurological Disorders and Stroke of the National Institutes of Health, and by a Fulbright-CONICYT Fellowship from Comisión Nacional de Investigación Científica y Tecnológica.
Appendix: Model Development and Validation
Validation of Frequency-Dependent Capacitance
We modeled a lumped single-compartment (SCM) neuron with linear circuit elements representing the neural membrane (Figure 1b). The membrane conductance (gm in S/m2) was constant and the membrane capacitance varied with frequency. The following system of ordinary differential equations (ODEs) model the response of the SCM neuron to a single monophasic rectangular pulse:
| (A.1) |
| (A.2) |
| (A.3) |
| (A.4) |
The frequency-dependent membrane capacitance consisted of a capacitance (c∞) in parallel with the series combination of a conductance (gΔ) and capacitance (cΔ). Vm and Vrest denote the transmembrane and rest voltages, respectively; VcΔ is the voltage drop across cΔ; is(t) is the waveform of the applied stimulus (in A/m2); the bar denotes a vector quantity; and T is the transpose operator.
When is(t) is a single monophasic rectangular pulse, the solution of Equations A.1-A.4 takes the following form:
| (A.5) |
| (A.6) |
| (A.7) |
| (A.8) |
| (A.9) |
λ1/2 are the eigenvalues of A.3, and Vo is the initial value of Vm. We compared the analytical solution (i.e., A.5-A.9) to the numerical solution (see Section 2.1.1). The root mean square error (RMSE) between the numerical and analytical solutions was < 5×10−4 %.
When is(t) is a sinusoid, the solution of Equations A.1-A.4 takes the following form:
| (A.10) |
| (A.11) |
| (A.12) |
| (A.13) |
| (A.14) |
For sinusoidal stimulation, the RMSE between the numerical and analytical solutions (A.10-A.14) was < 5×10−4 %.
Numerical Implementation
We used the ratio of the largest eigenvalue to the smallest eigenvalue, known as the stiffness ratio (LeVeque, 2007),
| (A.15) |
, to assess the numerical stability of the ODEs describing c(f). ∥ denotes the absolute value or magnitude of the eigenvalues. If a system of ODEs is stiff, S is typically >> 1, which means small to moderate perturbations in the system can lead to large fluctuations in some variables that force the numerical method to have large errors or become unstable (Spijker, 1996). For A.3, S ≈ 230.
When c(f) was modeled using Equation 5, achieving an RMSE of < 5×10−4 between the analytical and numerical solution required time step sizes of < 0.5 μs. To compare, when c(f) was modeled using Equations A.1-A.4, achieving the same degree of accuracy required time step sizes of < 0.1 ms. Compared to the other variables, the values of (see Equation 5) were disproportionately large, which could explain the large errors that resulted when modeling c(f) with Equation 5. Therefore, the stiffness of the ODEs consider in this work was only an issue when dealing with higher order terms (e.g., ).
Hodgkin-Huxley Model
We used the equations from the seminal work of Hodgkin and Huxley to model three current densities in a SCM of a HH neuron (Hodgkin and Huxley, 1952).
| (A.16) |
| (A.17) |
| (A.18) |
The sodium current density (iNa) had a maximum conductance (gNa,max), an activation gate (m), and an inactivation gate (h). The potassium current density (iK) had a maximum conductance (gK,max) and an activation gate (n). The leakage current density (iL) had a constant conductance (gL,max). The reversal voltages for iNa, iK, and iL were ENa, Ek, and EL, respectively.
The ODE describing the rate of change of the gate variables (ϕ = m, h, or n) with respect to time took the following form:
| (A.19) |
| (A.20) |
Where, q10 is a scaling factor that accounts for the effect of temperature (T in C°) on the rate constants (in s−1), α and β, for each gating variable. The equations describing the relationship between the rate constants and Vm can be found in (Abbott and Kepler, 1990).
The ODEs describing the response of the HH SCM neuron to an arbitrary stimulus, is, are given by the following:
| (A.21) |
| (A.22) |
The parameters of the HH SCM neuron are summarized in Table A.1 (Abbott and Kepler, 1990). Note that the system of ODEs described in (Abbott and Kepler, 1990) is a modified form of the original HH equations (Hodgkin and Huxley, 1952). In the original HH equations, Vrest = 0 mV, whereas in the modified HH equations, Vrest = −65 mV.
McIntyre-Richardson-Grill (MRG) Model
We implemented a validated model of a mammalian myelinated axon (McIntyre et al., 2002), and we used the equations describing the ion current densities and Vm to build a SCM neuron with faster ion channel kinetics. The transient sodium current density (iNa,t) and iL had the same form as Equations A.16 and A.18., respectively. The persistent sodium current density (iNa,p) and iK were described by the following equations:
| (A.23) |
| (A.24) |
Where, mp is the activation gate of iNa,p, and s is the activation gate of iK.
Note, in the work by McIntyre et al., q10 is implicit in the ODEs describing ϕ’. That is, the αs and βs of the gating variables have already been multiplied by their corresponding q10 values at T = 37 C°:
| (A.25) |
Where, mt and ht are the activation and inactivation gates of iNa,t, respectively.
The response of Vm to is is given by the following ODE:
| (A.26) |
VcΔ has the same form as A.22.
Table A1.
Electrical Properties of the HH Model*
| Parameter | Description | Unit(s) | Value |
|---|---|---|---|
| gNa, max | Maximum sodium conductance | mS/cm2 | 120. |
| gK, max | Maximum potassium conductance | mS/cm2 | 36.0 |
| gL, max | Maximum leakage conductance | mS/cm2 | 0.30 |
| ENa | Sodium reversal voltage | mV | 50.0 |
| EK | Potassium reversal voltage | mV | −77.0 |
| EL | Leakage reversal voltage | mV | −54.4 |
| Vrest | Membrane resting voltage | mV | −65.0 |
| T | Temperature | C° | 6.30 |
The parameters are summarized in (Abbott and Kepler, 1990).
Table A2.
Electrical Properties of the MRG Modela
| Parameter | Description | Unit(s) | Value |
|---|---|---|---|
| gNa, t, max | Maximum transient sodium conductance | mS/cm2 | 3.00×103 |
| gNa, p, max | Maximum persistent sodium conductance | mS/cm2 | 10.0 |
| gK, max | Maximum potassium conductance | mS/cm2 | 80.0 |
| gL, max | Maximum leakage conductance | mS/cm2 | 7.00 |
| ENab | Sodium reversal voltage | mV | 50.0 |
| EK | Potassium reversal voltage | mV | −90.0 |
| EL | Leakage reversal voltage | mV | −90.0 |
| Vrest | Membrane resting voltage | mV | −80.0 |
| T | Temperature | C° | 37.0 |
The parameters are summarized in (McIntyre et al., 2002)
The transient and persistent sodium channels have the same reversal voltage
References
- Abbott L, Kepler TB. Statistical mechanics of neural networks. Springer; 1990. Model neurons: From hodgkin-huxley to hopfield. [Google Scholar]
- Ackermann DM, Bhadra N, Gerges M, Thomas PJ. Dynamics and sensitivity analysis of high-frequency conduction block. Journal of Neural Engineering. 2011;8:065007. doi: 10.1088/1741-2560/8/6/065007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Kaisy A, Van Buyten J-P, Smet I, Palmisani S, Pang D, Smith T. Sustained effectiveness of 10 kHz high-frequency spinal cord stimulation for patients with chronic, low back pain: 24-month results of a prospective multicenter study. Pain Medicine (Malden, Mass.) 2014;15:347–54. doi: 10.1111/pme.12294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awayda MS, Van Driessche W, Helman SI. Frequency-dependent capacitance of the apical membrane of frog skin: dielectric relaxation processes. Biophysical Journal. 1999;76:219–232. doi: 10.1016/S0006-3495(99)77191-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BeMent S, Ranck J. A quantitative study of electrical stimulation of central myelinated fibers. Experimental Neurology. 1969;24:147–170. doi: 10.1016/0014-4886(69)90012-0. [DOI] [PubMed] [Google Scholar]
- Bhadra N, Kilgore K. High-frequency electrical conduction block of mammalian peripheral motor nerve. Muscle & Nerve. 2005;32:782–790. doi: 10.1002/mus.20428. [DOI] [PubMed] [Google Scholar]
- Bhadra N, Lahowetz E, Foldes S, Kilgore K. Simulation of high-frequency sinusoidal electrical block of mammalian myelinated axons. Journal of Computational Neuroscience. 2007;22:313–326. doi: 10.1007/s10827-006-0015-5. [DOI] [PubMed] [Google Scholar]
- Biswas K, Sen S, Dutta PK. Realization of a constant phase element and its performance study in a differentiator circuit. IEEE Transactions on Circuits and Systems. 2006;53:802. [Google Scholar]
- Bossetti CA, Birdno MJ, Grill WM. Analysis of the quasi-static approximation for calculating potentials generated by neural stimulation. J Neural Eng. 2008;5:44–53. doi: 10.1088/1741-2560/5/1/005. [DOI] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clin Neurophysiol. 2005;116:2490–500. doi: 10.1016/j.clinph.2005.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantrell DR, Inayat S, Taflove A, Ruoff RS, Troy JB. Incorporation of the electrode-electrolyte interface into finite-element models of metal microelectrodes. J Neural Eng. 2008;5:54–67. doi: 10.1088/1741-2560/5/1/006. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON Book. Cambridge University Press; Cambridge: 1997. [Google Scholar]
- Chew WC, Sen PN. Dielectric enhancement due to electrochemical double layer: Thin double layer approximation. The Journal of Chemical Physics. 1982;77:4683–4693. [Google Scholar]
- Cole KS, Cole RH. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. The Journal of Chemical Physics. 1941;9:341–351. [Google Scholar]
- Cole KS, Cole RH. Dispersion and Absorption in Dielectrics II. Direct Current Characteristics. The Journal of Chemical Physics. 1942;10:98–105. [Google Scholar]
- Diethelm K, Ford NJ, Freed AD, Luchko Y. Algorithms for the fractional calculus: A selection of numerical methods. Computer Methods in Applied Mechanics and Engineering. 2005;194:743–773. [Google Scholar]
- Fernández JM, Taylor RE, Bezanilla F. Induced capacitance in the squid giant axon. Lipophilic ion displacement currents. The Journal of General Physiology. 1983;82:331–46. doi: 10.1085/jgp.82.3.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster KR, Schwan HP. Dielectric properties of tissues and biological materials: a critical review. Critical reviews in biomedical engineering. 1989;17:25–104. [PubMed] [Google Scholar]
- Frankenhaeuser B, Huxley AF. The action potential in the myelinated nerve fibre of Xenopus laevis as computed on the basis of voltage clamp data. The Journal of Physiology. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues: I. Literature survey. Physics in Medicine and Biology. 1996a;41:2231–2249. doi: 10.1088/0031-9155/41/11/001. [DOI] [PubMed] [Google Scholar]
- Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Physics in Medicine and Biology. 1996b;41:2251–2269. doi: 10.1088/0031-9155/41/11/002. [DOI] [PubMed] [Google Scholar]
- Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dieletric spectrum of tissues. Physics in Medicine and Biology. 1996c;41:2271–2293. doi: 10.1088/0031-9155/41/11/003. [DOI] [PubMed] [Google Scholar]
- Gentet LJ, Stuart GJ, Clements JD. Direct Measurement of Specific Membrane Capacitance in Neurons. Biophysical Journal. 2000;79:314–320. doi: 10.1016/S0006-3495(00)76293-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimnes S, Martinsen ØG. Journal of Physics: Conference Series. IOP Publishing; 2010. Alpha-dispersion in human tissue. p. 012073. [Google Scholar]
- Haeffele BD, Butera RJ. Modifying the Hodgkin-Huxley Model for High Frequency AC Stimulation.. Neural Engineering; CNE '07. 3rd International IEEE/EMBS Conference on; 2-5 May 2007; 2007. pp. 550–552. 2007. [Google Scholar]
- Haydon DA, Requena J, Urban BW. Some effects of aliphatic hydrocarbons on the electrical capacity and ionic currents of the squid giant axon membrane. The Journal of Physiology. 1980;309:229–245. doi: 10.1113/jphysiol.1980.sp013506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haydon DA, Urban BW. The admittance of the squid giant axon at radio frequencies and its relation to membrane structure. The Journal of Physiology. 1985;360:275–291. doi: 10.1113/jphysiol.1985.sp015617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B, Naik S, Grill WM. Influences of interpolation error, electrode geometry, and the electrode-tissue interface on models of electric fields produced by deep brain stimulation. IEEE Transactions on Biomedical Engineering. 2014;61:297–307. doi: 10.1109/TBME.2013.2292025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph L, Butera RJ. Unmyelinated Nerves Exhibit a Nonmonotonic Blocking Response to High-Frequency Stimulation. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2009;17:537–544. doi: 10.1109/TNSRE.2009.2029490. [DOI] [PubMed] [Google Scholar]
- Kiernan M, Mogyoros I, Burke D. Differences in the recovery of excitability in sensory and motor axons of human median nerve. Brain. 1996;119:1099–1105. doi: 10.1093/brain/119.4.1099. [DOI] [PubMed] [Google Scholar]
- Kilgore KL, Bhadra N. Reversible Nerve Conduction Block Using Kilohertz Frequency Alternating Current. Neuromodulation: Technology at the Neural Interface. 2014;17:242–255. doi: 10.1111/ner.12100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuncel AM, Grill WM. Selection of stimulus parameters for deep bran stimulation. Clinical Neurophysiology. 2004;115:2431–2441. doi: 10.1016/j.clinph.2004.05.031. [DOI] [PubMed] [Google Scholar]
- LeVeque RJ. Finite difference methods for ordinary and partial differential equations: steady-state and time-dependent problems. Siam. 2007 [Google Scholar]
- Li P, Uren NF. Analytical solution for the electric potential due to a point source in an arbitrarily anisotropic half-space. Journal of Engineering Mathematics. 1998;33:129–140. [Google Scholar]
- Matsumoto G, Tasaki I. A study of conduction velocity in nonmyelinated nerve fibers. Biophysical Journal. 1977;20:1. doi: 10.1016/S0006-3495(77)85532-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. Journal of Neurophysiology. 2002;87:995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng. 1976;23:329–37. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- Medina EL, Grill MW. Volume conductor model of transcutaneous electrical stimulation with kilohertz signals. Journal of Neural Engineering. 2014;11:066012. doi: 10.1088/1741-2560/11/6/066012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrill DR, Bikson M, Jefferys JG. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Methods. 2005;141:171–98. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- Rattay F. Analysis of models for extracellular fiber stimulation. Biomedical Engineering, IEEE Transactions on. 1989;36:676–682. doi: 10.1109/10.32099. [DOI] [PubMed] [Google Scholar]
- Sabah NH, Leibovic KN. Subthreshold Oscillatory Responses of the Hodgkin-Huxley Cable Model for the Squid Giant Axon. Biophysical Journal. 1969;9:1206–1222. doi: 10.1016/S0006-3495(69)86446-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarr MG, Billington CJ, Brancatisano R, Brancatisano A, et al. The EMPOWER study: randomized, prospective, double-blind, multicenter trial of vagal blockade to induce weight loss in morbid obesity. Obesity Surgery. 2012;22:1771–1782. doi: 10.1007/s11695-012-0751-8. [DOI] [PubMed] [Google Scholar]
- Shen B, Roppolo JR, Subbaroyan J, Diubaldi A, Wahlgren S, de Groat W, Tai C. Neuromodulation of bladder activity by stimulation of feline pudendal nerve using a transdermal amplitude modulated signal (TAMS). Neurourology and Urodynamics. 2011;30:1686–1694. doi: 10.1002/nau.21084. [DOI] [PubMed] [Google Scholar]
- Sidiropoulou K, Poirazi P. Predictive Features of Persistent Activity Emergence in Regular Spiking and Intrinsic Bursting Model Neurons. PLoS Comput Biol. 2012;8:e1002489. doi: 10.1371/journal.pcbi.1002489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soin A. Long-term human testing of high-frequency nerve block for amputation pain.. 16th Annual Meeting North American Neuromodulation Society; Las Vegas,NV, USA. December 6 to 9, 2012. [Google Scholar]
- Spijker MN. Stiffness in numerical initial-value problems. Journal of Computational and Applied Mathematics. 1996;72:393–406. [Google Scholar]
- Sweeney J, Mortimer J, Durand D. Modeling of mammalian myelinated nerve for functional neuromuscular stimulation. IEEE 9th Annual Conference of the Engineering in Medicine and Biology Society. 1987:1577–1578. [Google Scholar]
- Tai C, de Groat WC, Roppolo JR. Simulation Analysis of Conduction Block in Unmyelinated Axons Induced by High Frequency Biphasic Electrical Currents. IEEE transactions on bio-medical engineering. 2005;52:1323. doi: 10.1109/tbme.2005.847561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takashima S, Schwan H. Passive electrical properties of squid axon membrane. The Journal of Membrane Biology. 1974;17:51–68. doi: 10.1007/BF01870172. [DOI] [PubMed] [Google Scholar]
- Wang L, Liu S, Zhang J, Zeng Y. Burst firing transitions in two-compartment pyramidal neuron induced by the perturbation of membrane capacitance. Neurological Sciences. 2012;33:595–604. doi: 10.1007/s10072-011-0819-6. [DOI] [PubMed] [Google Scholar]
- Ward AR. Electrical stimulation using kilohertz-frequency alternating current. Physical Therapy. 2009;89:181–190. doi: 10.2522/ptj.20080060. [DOI] [PubMed] [Google Scholar]