Task-Based Evaluation of a 4D MAP-RBI-EM Image Reconstruction Method for Gated Myocardial Perfusion SPECT using a Human Observer Study

Abstract

We evaluated the performance of a new 4D image reconstruction method for improved 4D gated myocardial perfusion (MP) SPECT using a task-based human observer study. We used a realistic 4D NURBS-based Cardiac-Torso (NCAT) phantom that models cardiac beating motion. Half of the population was normal; the other half had a regional hypokinetic wall motion abnormality. Noise-free and noisy projection data with 16 gates/cardiac cycle were generated using an analytical projector that included the effects of attenuation, collimator-detector response, and scatter (ADS), and were reconstructed using the 3D FBP without and 3D OS-EM with ADS corrections followed by different cut-off frequencies of a 4D linear post-filter. A 4D iterative maximum a posteriori rescaled-block (MAP-RBI)-EM image reconstruction method with ADS corrections was also used to reconstruct the projection data using various values of the weighting factor for its prior. The trade-offs between bias and noise were represented by the normalized mean squared error (NMSE) and averaged normalized standard deviation (NSD_av), respectively. They were used to select reasonable ranges of the reconstructed images for use in a human observer study. The observers were trained with the simulated cine images and were instructed to rate their confidence on the absence or presence of a motion defect on a continuous scale. We then applied receiver operating characteristic (ROC) analysis and used the area under the ROC curve (AUC) index. The results showed that significant differences in detection performance among the different NMSE-NSD_av combinations were found and the optimal trade-off from optimized reconstruction parameters corresponded to a maximum AUC value. The 4D MAP-RBI-EM with ADS correction, which had the best trade-off among the tested reconstruction methods, also had the highest AUC value, resulting in significantly better human observer detection performance when detecting regional myocardial wall motion abnormality. We concluded that the NMSE-NSD_av trade-off was shown to agree with observer performance for the detection task of the regional motion abnormality, and the optimized 4D MAP-RBI-EM method with ADS corrections provides significant improvement compared to 3D FBP and 3D OS-EM with ADS corrections in detecting regional myocardial wall motion abnormali in 4D gated MP SPECT.

Today, electrocardiograph (ECG) based gated myocardial perfusion (MP) SPECT studies (Mannting and Morgan-Mannting, 1993) are routinely used clinical procedures to obtain diagnostic information on both MP and left ventricular (LV) functions in a single study, and more than 90% of all MP studies in the U.S. are performed as gated SPECT (Abidov et al., 2006).

Estimation of parameters that are used to represent cardiac functional properties such as ejection fraction (Najm et al., 1989), and assessment of abnormal wall motion from animated 4D gated images (Levine et al., 1999) are two primary clinical tasks for which gated MP SPECT is used. Cardiac cycles can be more accurately described with a larger number of gating samplings within a cardiac cycle (Manrique et al., 2000; Kumita et al., 2001; Nakajima et al., 2001). However, since the images suffer from increased noise as the number of gates is increased, the individual frames are generally smoothed heavily for viewing, resulting in loss of details and diagnostic information.

Previously, various 4D image reconstruction methods that exploit the temporal correlation among the gated frames have been developed to improve image quality in gated MP SPECT to achieve better perfusion defect detectability and functional assessment (Narayanan et al., 2000; Gilland et al., 2002; Brankov et al., 2005; Gravier et al., 2006; Jin et al., 2009; Niu et al., 2011). A 4D maximum a posteriori rescaled-block iterative (MAP-RBI)-EM algorithm with Gibbs priors (Lalush and Tsui, 1998) was developed to take advantage of the MAP statistical model (Shepp and Vardi, 1982), which has been applied to projection data in emission tomography (Levitan and Herman, 1987), and the algorithm also utilizes the RBI-EM image reconstruction algorithm (Byrne, 1996). In a preliminary studies (Lee and Tsui, 2009; Lee et al., 2005a; Lee and Tsui, 2006), the 4D MAP-RBI-EM reconstruction algorithm with optimized parameters and with compensation of image degradation effects including attenuation, collimator-detector response and scatter (ADS) provided a significantly improved trade-off between normalized mean squared error (NMSE) and normalized standard deviation (NSD) of the 4D gated MP SPECT images when compared to conventional image reconstruction methods. The algorithm potentially allows for more temporal samplings per cardiac cycle for better detection of wall motion abnormalities. However, determination of the exact trade-off location for maximum performance of a given detection task requires an observer performance study. While there are many examples of observer study methodologies applied to static images, there are relatively few involving applications to cine images (Lalush et al., 2005; Eckstein et al., 1996; Wilson et al., 1999; Wilson and Manjeshwar, 1999).

In this study, we investigate the use of a human observer with receiver operating characteristic (ROC) analysis (Metz, 1978, 1986) to evaluate the effect of the 4D MAP-RBI-EM image reconstruction method with respect to the task of detecting a regional motion abnormality in simulated gated MP SPECT images. Based on our preliminary results and visual observations, the hypothesis is that the 4D MAP-RBI-EM, with correction of image degrading factors, will result in detectability that is as good as or better than the other image reconstruction methods for 4D gated MP SPECT images. Such reconstruction methods include 3D filtered-back projection (FBP) and 3D OS-EM followed by 4D post-filtering with various cut-off frequencies.

MATERIALS AND METHODS

Generation of Realistic 4D NCAT Phantom and Projection Data

Using a 4D NURBS-based CArdiac-Torso (NCAT) (Segars, 2001) (Fig. 1a) that can model realistic cardiac motion and defects in the LV wall, we generated a time series of 3D NCAT phantoms in a 256 × 256 × 256 array with a voxel size of 0.156 cm in x, y, and z to represent the radioactivity distribution of Tc-99m sestamibi over 384 time intervals per cardiac cycle. The sets can be regrouped to represent 8, 16, 24, and 32 gated time frames per cardiac cycle. For this study, we used 16 regrouped time frames.

FIGURE 1.

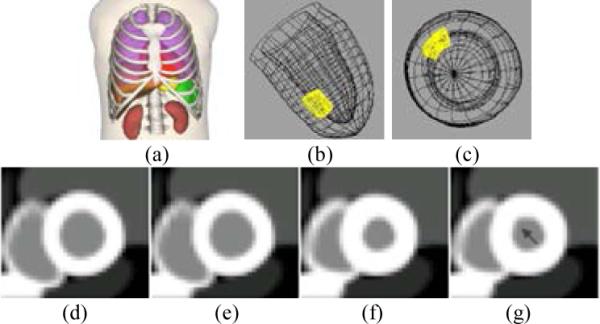
4D NCAT model with a beating heart. (Anterior view of the 4D NCAT phantom (a), LV with an anteroseptal hypokinetic area highlighted in long-axis view (b), short-axis view (c), short-axis view of ED frame for normal (d) and defective (e) heart. Short-axis view of ES frame for normal (f) and defective (g) which shows motion defect in the anteroseptal wall as indicated by the arrow).

Since coronary artery anatomy is highly variable from patient to patient and regional MP defects due to arterial blocks can occur anywhere in the arteries, these defects can occur in different locations and in different shapes and sizes (Svane et al., 1989; Segall and Davis, 1989). In this study, the center of the MP defect was placed in the anteroseptal area, about 4 cm from the apex, as one of the clinically possible conditions (Fig. 1b, 1c). The shape of the defect was modeled with smooth edges perpendicular to the short and long axes of the LV. The length of the defect was 2 cm in the long axis dimension, and the width was 40° in circumferential dimension.

The defect extended from the endocardial wall to 50% of the normal myocardium thickness, and its edges were smoothly tapered to the adjacent normal myocardium. The spatial extent of the simulated hypokinetic wall motion defect matched that of the myocardial defect with the decreased wall motion magnitude proportional to the defect magnitude. Thus, there was a 50% reduction in motion of the myocardium at the center of the defect and this reduced smoothly to normal motion at the edges of the defect. In our preliminary study, detecting hypokinetic motion was found to be relatively more difficult than detecting akinetic motion that is due to a transmural defect given the same defect size and location. Using the 50% hypokinetic motion defect model, the AUC values of our proposed method, i.e., 4D MAP-RBI-EM with ADS correction, ranged from 72 – 84%, compared to 57 – 64% for the 3D FBP method, resulting in a good separation of detectability (Metz, 1978) of the motion abnormality between the two methods.

Figure 1 (d)-(g) shows the short axis views of the phantom models in end-diastolic (ED) and end-systolic (ES) phases. Since unreasonable activity levels of background – blood-pool in this case – can affect detection performance, the activity level of blood-pool was adjusted to be 40% of the normal myocardium activity in this hypokinetic anteroseptal LV model, and an experienced nuclear cardiologist confirmed that this was a reasonably realistic model of a subtle motion defect.

Although the 4D NCAT phantom can model different anatomical properties of the body and organs, only one anatomical type was generated so that no beneficial nor confounding factors based on the anatomical features was introduced. Further, since the change of image intensity due to MP defect can be a cue for detecting motion defect, no change in image intensity within the motion defect with respect to its surrounding was simulated in this study, where the given task is to detect motion abnormality of the myocardium. Thus, the activity of the defect simulated in this study was the same as that of normal myocardium.

Projection data were generated using an analytical projector that includes the effects of nonuniform attenuation, collimator-detector response, and scatter (ADS) of a parallel-hole low-energy high-resolution (LEHR) collimator (Frey and Tsui, 1994; Frey and Tsui, 1996). Noise-free 2D projection data were generated for 64 angular views equally spaced over the typical 180° cardiac arc. A 256 × 256 projection matrix with 0.156 cm bins was used for each view. After the 256 × 256 noise-free projection data were collapsed to 128 × 128, they were scaled to the total count of 200,000 in an image slice 0.31 cm thickness through the center of the heart (Qi et al., 2004). Then the 95 Poisson noise realizations of a single noise-free normal heart and 95 noise realizations of a single noise-free myocardium with the motion defect were generated. Table 1 summarizes how the total 190 (95 normal, 95 abnormal) noise realizations were used in this study. Finally, they were reconstructed using three different image reconstruction methods for the use of human observer study, as shown in Tables 4 and 5.

Table 1.

Number of Poisson noise realization generated in this study

Large Training	Overall Training for Day 2	Training	Testing	Training	Testing	Total
30 (15 + 15)*	24 (12 + 12)*	20 (10 + 10)*	48 (24 + 24)*	20 (10 + 10)*	48 (24 + 24)*	190 (95 + 95)*

^*(normal + abnormal)

Table 4.

Example Procedure for Large Training of Day 1

	Large Training (15 blocks = 3 methods × 5 data points)
	FBP_1*	OS-EM_1	MAP_1	OS-EM_3	FBP_3	FBP_5	MAP_3	OS-EM_5	FBP_2	OS-EM_2	MAP_5	OS-EM_4	MAP_2	FBP_4	MAP_4	Total
Number of Images**	30	30	30	30	30	30	30	30	30	30	30	30	30	30	30	450
Observation Time (min.)	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	5.5	83

^*“method_datapoint” (example : FBP_1 = images reconstructed with FBP method at data-point #1)

Table 5.

Example Procedure for Day 2

Obs. #	Training	Training / Testing	Training / Testing	Training / Testing	Training / Testing	Training / Testing	Training / Testing	Total
1	FBP_1 / OS-EM_3 / MAP_2	FBP_1-1*	OS-EM_3-1	MAP_2-1	OS-EM_3-2	FBP_1-2	MAP_2-2
2	OS-EM_5 / MAP_4 / FBP_3	OS-EM_5-1	MAP_4-1	FBP_3-1	MAP_4-2	FBP_3-2	OS-EM_5-2
3	MAP_1 / FBP_5 / OS- EM_1	MAP_1-1	FBP_5-1	OS-EM_1-1	MAP_1-2	OS-EM_1-2	FBP_5-2
4	FBP_2 / MAP_3 / OS- EM_2	FBP_2-2	MAP_3-2	OS-EM_2-2	FBP_2-1	OS-EM_2-1	MAP_3-1
5	OS-EM_4 / FBP_4 / MAP_5	OS-EM_4-2	FBP_4-2	MAP_5-2	FBP_4-1	MAP_5-1	OS-EM_4-1
Number of Images	24 / 24 / 24	20 / 48	20 / 48	20 / 48	20 / 48	20 / 48	20 / 48	480
Observation Time (min.)	4.4 / 4.4 / 4.4	3.7 / 8.8	3.7 / 8.8	3.7 / 8.8	3.7 / 8.8	3.7 / 8.8	3.7 / 8.8	88

^*“method datapoint-group” (example : FBP_2-1 = group 2 images reconstructed with FBP method at data-point #1)

Image Reconstruction Methods for Gated Myocardial Perfusion SPECT

The noise-free and noise-added projection data were reconstructed using the conventional 3D FBP without correction and 3D OS-EM with ADS correction methods both followed by 3D spatial + 1D temporal Butterworth filtering with various cut-off frequencies. They were also reconstructed using 4D MAP-RBI-EM with ADS correction with different parameter values. Eight subsets with 8 projections per subset were used in both 3D OS-EM and 4D MAP-RBI-EM iterative reconstruction methods.

The 4D MAP-RBI-EM image reconstruction algorithm uses a 4D space-time smoothing Gibbs prior, which defines the relationship between a given image voxel and its neighboring voxels (Geman and Geman, 1984). It assumes that SPECT emissions are relatively uniform and continuous within regions of similar physiology but differs significantly between regions of dissimilar physiology. This has the effect of discouraging individual voxels from differing from all of their neighbors, thus smoothing noise while still permitting the formation of sharp boundaries between regions of different activities. The degree of the similarity or smoothness among a ‘clique,’ or a set of neighboring voxels, depends on a potential function. We used 18 nearest neighbors for the spatial domain clique and 7 for the time domain clique (Lalush and Tsui, 1998). Generalized potential function (GPF) was developed to increase the flexibility of the potential function (Lalush and Tsui, 1993). Its parameters δ, α, and γ define the smoothing constraints, and thus the choices of these parameter values have important effects on the quality of the reconstructed images (Lalush and Tsui, 1992; Lee et al., 2005b).

Guideline for selecting images for observer study

In 4D gated MP SPECT imaging, ‘best image quality’ refers to images that provide the best clinical diagnosis for a given specific task, such as the detection of a regional myocardial wall motion defect in this study. Although the determination of maximum detectability requires an observer performance study (Metz, 1986), it is expensive to test the entire parameter space with either human or model observers. Especially for the human observer study, it is certainly necessary to limit the experimental conditions since it involves human observers with a series of images and complex experimental procedures. Thus, we employed a ‘trade-off’ relationship between bias and noise to provide such a limited but reasonable range of images with different degrees of bias-noise combinations for the observer study, with the hope that the optimal trade-off could be found within the range by the human observer. Since bias and noise usually work against each other in the description of image characteristics, they are frequently used in the quantitative evaluation of image quality. Many studies have suggested that either extremely smoothed or extremely noisy images are not optimal for detecting low contrast myocardial perfusion defects in two-dimensional (Gilland et al., 1988; Wollenweber et al., 1998; Wells et al., 1999; Gifford et al., 1999; Gifford et al., 2000) and three-dimensional (Sankaran et al., 2002; Frey et al., 2002) SPECT images. They have also found that the optimal detectability would lie between these two extremes in human and mathematical observer studies.

NMSE represents how much the reconstructed image deviates from the ‘truth’ – in our case, the corresponding phantom image. It is based on the difference between the voxel intensity within a 3D cubical region-of-interest that encompasses the entire heart in the noise-free reconstructed image and the ROI's corresponding phantom frames (truth). During the calculation of the NMSE, the reconstructed and phantom images were normalized individually by dividing the voxel intensities by their mean so that differently scaled images could be compared. The NMSE is defined as follows:

$$NMSE=\frac{1}{nN}\sum _{i=1}^N\sum _{j\in RO{I}_{heart}}{\left(\frac{x_{i,t}}{{\overline{x}}_i}-\frac{{\lambda }_{i,t}}{{\overline{\lambda }}_i}\right)}^2$$ (1)

where x_i,t is the ith pixel value of the tth gate of the reconstructed image, λ_i,t is the ith pixel value of the tth gate of the phantom slice, x̄_i is the mean of ROI_heart of the tth gate of the reconstructed image, ${\overline{\lambda }}_i$ is the mean of ROI_heart of the tth gate of phantom slice, n is the number of pixels in the ROI_heart, and N is the number of gates in the gating scheme.

The averaged NSD (NSD_av) was used to evaluate the image noise level. It was computed for image voxels in a ROI_LV, i.e., a mid-myocardial region over the LV wall where the voxel intensity is relatively uniform, across all the frames. The NSD_av is given by

$$NS{D}_{av}\left(X\right)=\frac{1}{N}\sum _1^N\left[\frac{1}{n}\sum _{i\in RO{I}_{LV}}\frac{\sqrt{\frac{1}{m-1}\sum _{j=1}^m{(x_i^j-{\overline{x}}_i)}^2}}{{\overline{x}}_i}\right]$$ (2)

For NSD_av, $x_i^j$ is the ith pixel value of the jth noise realization, x̄_i is the ensemble mean value of pixel i, m is the number of noise realizations, n is the number of voxels in the ROI_LV, and N is the number of gates per cardiac cycle.

Generation of Reconstructed Image using NMSE-NSD_av Trade-off for Human Observer Study

In the preparation of images for the human observer study, it was important to include regions of the NMSE vs. NSD_av curve where the optimal trade-off between NMSE and NSD_av was most likely to occur. So we used the lowest combination of bias and noise level as a starting point and explored more combinations of data points around this in order to find more exact optimal trade-off combinations for human observers. As shown in Table 2, various cut-off frequencies of the smoothing filter were applied to the images reconstructed from 3D FBP without and 3D OS-EM with ADS correction methods. In using the 4D space-time Gibbs priors for 4D MAP-RBI-EM, we determined the values for each parameter in the GPF that possibly minimize both NMSE and NSD_av based on our previous study (Lee and Tsui, 2009). Then, a reasonable range of β, the weighting factor of the Gibbs priors that controls the overall smoothing of the reconstructed image, was chosen for the above selection of the δ, α, and γ combination so that the images with a wide range of the NMSE-NSD_av trade-offs could be included in the observer study. The compensation of ADS was also applied to the reconstruction method. We determined the range of iteration numbers for the human observer study to encompass the ‘heel’ region of the NMSE vs. NSD_av curve, within which the optimum trade-off between ‘bias’ and ‘noise’ and the maximum detectability was likely to occur (Lee et al., 2005b).

Table 2.

List of post-filtering parameters for 3D FBP and 3D OS-EM, and the weight of Gibbs prior for 4D MAP-RBI-EM

3D FBP without correction (3D cycle/cm + 1D cycle/sec)	3D OS-EM with ADS correction (3D cycle/cm + 1D cycle/sec)	4D MAP-RBI-EM with ADS correction (δ=0.5, α=3 and γ=0.5)
F1: 0.6 c/c + 3 c/s	O1: 0.6 c/c + 3 c/s	M1: β = 0.007
F2: 0.5 c/c + 2 c/s	O2: 0.5 c/c + 2 c/s	M2: β = 0.01
F3: 0.4 c/c + 1 c/s	O3: 0.4 c/c + 1 c/s	M3: β = 0.015
F4: 0.3 c/c + 0.9 c/s	O4: 0.35 c/c + 0.9 c/s	M4: β = 0.03
F5: 0.2 c/c + 0.8 c/s	O5: 0.3 c/c + 0.8 c/s	M5: β = 0.05

Develop an Interactive Application for Human Observer Studies of Cine Images

We developed tools and procedures to perform a human observer study since the software for static image observer studies may not be suitable for displaying cine images.

The display application for the cine images was developed using Microsoft^® Visual C++ to permit use of general Windows^®-compatible PC and accustomed computing environments for users. Figure 2 shows the display screen used in our observer studies. The display includes multiple image slices and views of the beating heart, including horizontal long-axis (HLA) images and vertical long-axis (VLA) images, as well as short-axis (SA) images with the appropriate frame rate.

FIGURE 2.

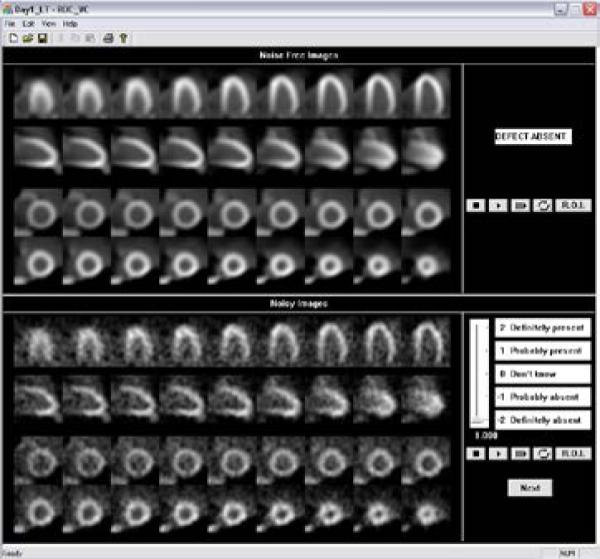
The display application for the human observer study of cine images.

The application runs in training and testing modes. In the training mode, the observer is presented with a series of noisy animations, and plays each animation as many cycles as desired. The animation loops repeatedly or frame by frame or over one cardiac cycle only. The ‘R.O.I.’ (region-of-interest) button moves a cross hair to the possible defective area on which the observer will focus. The observer is then asked to provide a rating using a continuous 5-point scale bar as to the likelihood of a motion defect being present. Afterwards, the corresponding noise-free images are shown in the upper panel of the application window and the observer is given the correct answer. The display of the testing mode is similar, except that the ratings are stored in an output file and the true result in the upper panel is not revealed to the observer.

Design of the Procedure for Human Observer Study

The pixel intensities of the images were remapped using a similar process as that used in the clinic. The pixel value of zero was selected as the minimum, and the maximum value of the remapped image was determined for each group of images. A group was defined to be a set of reoriented images with selected multiple image slices produced by the same noise realization and the same image reconstruction and processing technique. The maximum pixel value of a group was selected to be the 10th percentile of the maximum pixel intensities of that group; thus, 90% of the images of a group had a maximum pixel value higher than the selected maximum. This was close to the maximum of noise-free images in each group of images.

Pixel values of the remapped image were then linearly mapped to 8 bits of displayed intensity range. Pixel values greater than the maximum of the image group were set to the maximum of the displayed intensity range. This method reduced the effect of noisy pixels as in the clinic, and produced images without noticeable saturation effects. Finally, the displayed images were enlarged two times to a size useful for display. Images were displayed using a HP^® computer with NEC^® color LCD monitor. HLA and VLA images contained 9 image slices in a row whereas SA contained 18 image slices in two rows as shown in Figure 2.

The simulated images were presented in blocks of ‘training’ and ‘testing’ image sets. Each block contained images from only one of the methods. Training blocks were implemented to reset and stabilize the observer's internal decision criteria to the context of the particular reconstruction method being tested. Generally, it is desirable to have a large number of training image sets for better stabilization. However, observer fatigue and practical time constraints on the length of an observer study limit the maximum number of images. In our preliminary study, observers spent at least 60 minutes but less than 80 minutes for 480 images from all different cases. That meant observers spent 10 to 13 seconds per one 16-frame cine image, and from a preliminary study it was found that 11 to 12 seconds was as an average observation time per image displayed frame. We limited the study length for about 90 minutes without a break, expecting stable observation performance and minimal observer fatigue.

The required minimum number of images depends on how small a difference in the ROC curves one wants to measure relative to the uncertainty in the curves. In our preliminary study conducted using 54 testing images from each state per ROC curve, statistically significant difference (p<0.05) were found among the different reconstruction methods, as well as within a single method. However, statistical difference among the different post-processing methods within one reconstruction method (cf. 3D FBP without correction) was found only at the p<0.1 level. Considering the practical limit on observation time, we decided to have 48 images per state, which still showed statistically significant difference (p<0.05) among the different post-processing methods within one reconstruction method.

Based on the study design constraints such as observation time and number of images, the overall study procedure and total observation time for each observer were determined as shown in Table 3. The entire study required 6 days to complete for each observer. Unlike the study from Day 2 to Day 6 in which both testing and training blocks are included, Day 1 only comprises introduction to the study and training blocks, which gives observers an overall idea about the whole dataset to observe. Table 4 shows a sample procedure of the large training blocks of Day 1. A total of 15 blocks of images from 5 different data points, i.e., 5 different NMSE-NSD_av trade-offs, for each of the 3 different 3D & 4D image reconstruction methods, were randomly presented to each observer without informing them of the reconstruction methods for both training and testing sessions.

Table 3.

Overall Study Procedure and Total Observation Time for Each Observer

	Day 1		Day 2	Day 3	Day 4	Day 5	Day 6	Total
	Introduction	Large Training
Number of Images	N/A	450	480	480	480	480	480	2850
Observation Time (min.)	10	83	88	88	88	88	88	533

From Day 2 to Day 6, 160 sets of multi-sliced 16-frame noisy images for each cardiac axis for each tested method were presented to each observer. It was composed of two sets of 80 noisy images with and without motion defect, respectively. From the two sets of 80 noisy images, each observer viewed 48 pairs of testing images and 32 pairs of training images for each method per day, in addition to 30 pairs of training images of Day 1. Thus, observers viewed the large training blocks first from all 3 different methods and then viewed the 6 testing blocks, each preceded by a small training block with the same method, as shown in Table 5.

To avoid reading order effects (Metz, 1986; Metz, 1989), image order within the blocks was randomized. The ordering of the presentation of the blocks was also randomized. While all observers ultimately viewed all of the same training and testing images, each observer viewed totally different sets of images from each other during each day from Day 2 to Day 6. Corresponding noise-free images were also presented in the training sessions.

The observers consisted of two M.D./Ph.D. Nuclear Medicine physicians specialized in nuclear cardiology, one Ph.D. and two graduate students in the Division of Medical Imaging Physics, Department of Radiology at Johns Hopkins Hospital. The LABROC4 code (Metz et al., 1998) was used to estimate individual ROC curves for each reconstruction method. Each ROC curve was fitted using the nonlinear maximum likelihood curve fitting techniques based on a bi-normal model (Metz, 1978). Average AUC values were also calculated by MRMC (Multi-Reader-Multi-Case) software from University of Chicago (Roe and Metz, 1997; Dorfman et al., 1992). The software allows the conclusions drawn from a study to be generalized to both a population of readers and a population of cases.

The environmental conditions of the observation study such as brightness and contrast settings of the image display monitor or darkness of the observation room were strictly maintained during the study.

RESULTS AND DISCUSSIONS

NMSE-NSD_av Trade-off

The 3D FBP without compensation followed by 3D spatial + 1D post-temporal filtering was found to have the highest level of image error in terms of NMSE-NSD_av trade-off. However, the 3D OS-EM with ADS corrections followed by 3D spatial + 1D post-temporal filtering and 4D MAP-RBI-EM with ADS corrections were found to significantly reduce both image bias and noise of the test images, as shown in Figures 3 and 4. Although application of the post filter lowered the noise level in both 3D FBP and 3D OS-EM reconstructed images, it also caused NMSE to increase due to its non-selective smoothing property.

FIGURE 3.

Effect of different cutoff frequencies of 3D spatial and 1D temporal Butterworth filtering on 3D FBP and 3D OS-EM with ADS correction reconstructed images. (Images in the circles were selected for the human observer study.)

FIGURE 4.

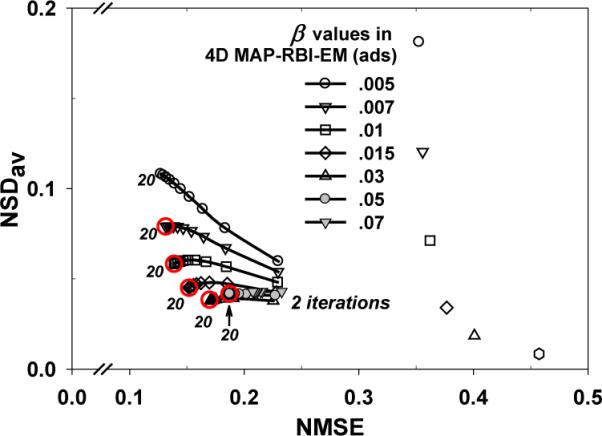
Effect of β for different iteration numbers with 16 frames in 4D MAP-RBI-EM with attenuation, CDR, and scatter (ADS) compensation. (δ = 0.5, α = 3, and γ = 0.5 for both spatial and time domains). (Images in the circles at 20^th iteration were selected for the human observer study.)

To select the candidates of the trade-off relationships for the human observer study, a total of 15 different trade-off points (5 for each of the 3 methods) were chosen so that they cover up a reasonable range in their trade-off relationships, as shown in the circles in Figures 3 and 4. Including various NMSE-NSD_av trade-offs is necessary because the optimal trade-off region in which the maximum performance of the task of detecting the regional motion abnormality was not known. However, the images from trade-off points outside the selected range were considered to be too noisy or too smoothed and were not considered in the study.

For the 3D FBP method without compensation, reconstructed images with 3D post-spatial filtering with cut-off frequencies of 0.2 – 0.6 cycle/cm and 1D post-temporal filtering with 0.8 – 3 cycle/sec were chosen for the human observer study. For 3D OS-EM method with ADS correction, reconstructed images with 3D post-spatial filtering with cut-off frequencies of 0.3 – 0.4 cycle/cm and 1D post-temporal filtering with cut-off frequencies of 0.8 – 1 cycle/sec at the 20^th iteration were chosen for the observer study. For the 3D OS-EM images with higher cut-off frequencies; i.e., 0.5 – 0.6 cycle/cm for 3D post-spatial filtering and 2 – 3 cycle/sec for 1D post-temporal filtering, reconstructed and filtered images at the 10^th iteration were chosen for the observer study. Preliminary studies showed that maximum AUC values from those with less-filtered images occurred at a fewer number of iterations, such as 10 compared to 20, because an additional iteration of the algorithm causes an increase in noise level. For 4D MAP-RBI-EM with ADS correction, reconstructed images at the 20^th iteration were chosen since the quality of the images did not change much beyond that as shown in Figure 4.

Figure 5 compares sample displayed images using the different image reconstruction methods with post filtering at various cut-off frequencies.

FIGURE 5.

The end diastole of the short axis reconstructed images of the heart.

Top Row: 3D FBP followed by 3D spatial + 1D post-temporal filtering (Method (a) F1, (b) F2, (c) F3, (d) F4, (e) F5 as in Table 2)

Middle Row: 3D OS-EM with ADS correction followed by 3D spatial + 1D post-temporal filtering (Method (f) O1, (g) O2, (h) O3, (i) O4, (j) O5 as in Table 2)

Bottom Row: 4D MAP-RBI-EM with ADS correction for different β (Method (k) M1, (l) M2, (m) M3, (n) M4, (o) M5 as in Table 2)

Human Observer ROC Study

Table 6 shows the result of the human observer ROC study from each of the 5 observers, and Figure 6 shows their average AUC values. Figure 7 shows the corresponding ROC curves. Method (F1) through Method (M5) in Table 6 and Figures 6 and 7 are the same as those in Table 2. For 3D FBP without correction and with post-filtering, the maximum AUC value from (F3), i.e. 3D spatial 0.4 cycle/cm + 1D post-temporal 1 cycle/sec, was significantly higher (p<0.05) than that of other methods such as Methods (F1), (F4), and (F5). For 3D OS-EM with ADS correction with post-filtering, the maximum AUC value from Method (O3), i.e. 3D spatial 0.4 cycle/cm + 1D post-temporal 1 cycle/sec, was significantly higher (p<0.05) than that of others such as Method (O1), (O4), and (O5). The maximum AUC values of Method (M3), i.e. β = 0.015 from 4D MAP-RBI-EM with ADS correction were significantly higher (p<0.05) than the values of others such as Method (M1) and (M5). These results showed that higher detection of regional wall motion abnormality occurs in the region that is close to the optimal NMSE-NSD_av trade-off.

Table 6.

Result of human observer ROC study (AUC value and its standard error)

Methods	3D FBP followed by 3D + 1D temporal filtering					3D OS-EM with ADS corrections followed by 3D + 1D temporal filtering					4D MAP-RBI-EM with ADS correction
Observers	(F1)*	(F2)	(F3)	(F4)	(F5)	(O1)	(O2)	(O3)	(O4)	(O5)	(M1)	(M2)	(M3)	(M4)	(M5)
1	0.66 (0.054)	0.70 (0.052)	0.74 (0.050)	0.68 (0.053)	0.60 (0.057)	0.65 (0.055)	0.75 (0.049)	0.76 (0.048)	0.66 (0.055)	0.61 (0.056)	0.79 (0.045)	0.86 (0.037)	0.91 (0.030)	0.77 (0.048)	0.71 (0.051)
2	0.64 (0.055)	0.65 (0.055)	0.67 (0.054)	0.60 (0.057)	0.59 (0.057)	0.60 (0.056)	0.67 (0.054)	0.71 (0.052)	0.62 (0.56)	0.52 (0.058)	0.73 (0.050)	0.78 (0.046)	0.86 (0.037)	0.80 (0.044)	0.71 (0.052)
3	0.68 (0.053)	0.76 (0.048)	0.76 (0.048)	0.65 (0.056)	0.64 (0.056)	0.71 (0.052)	0.75 (0.049)	0.76 (0.049)	0.72 (0.053)	0.66 (0.055)	0.82 (0.042)	0.83 (0.041)	0.83 (0.041)	0.88 (0.035)	0.76 (0.048)
4	0.58 (0.058)	0.59 (0.057)	0.65 (0.055)	0.61 (0.056)	0.53 (0.058)	0.62 (0.057)	0.65 (0.055)	0.71 (0.052)	0.62 (0.056)	0.54 (0.058)	0.76 (0.048)	0.84 (0.040)	0.86 (0.038)	0.82 (0.043)	0.76 (0.048)
5	0.55 (0.057)	0.58 (0.057)	0.61 (0.056)	0.57 (0.058)	0.51 (0.058)	0.54 (0.058)	0.61 (0.056)	0.64 (0.055)	0.60 (0.057)	0.51 (0.058)	0.75 (0.049)	0.80 (0.044)	0.83 (0.042)	0.74 (0.050)	0.70 (0.052)

^*The legends (F1) through (M5) are the same to those in Table 2.

FIGURE 6.

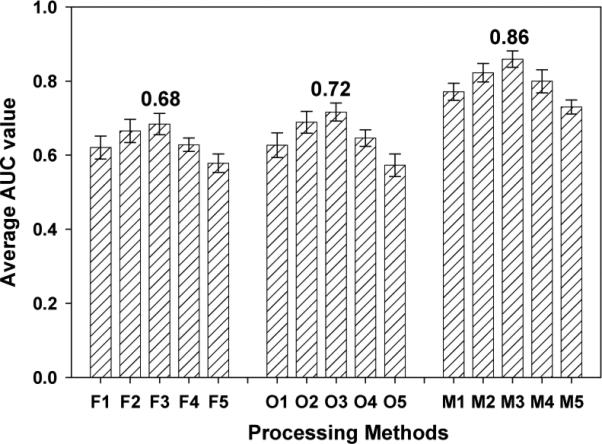
Average AUC values from 5 observers. The legends (F1) through (M5) are the same to those in Table 2.

FIGURE 7.

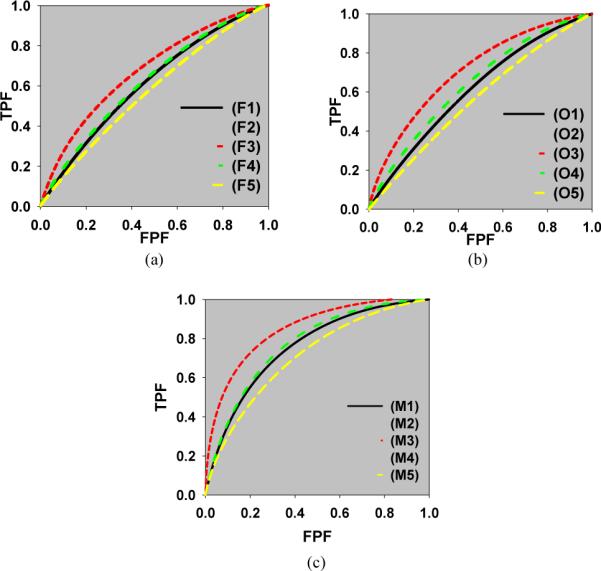
Averaged ROC curves for each method. ((a) 3D FBP followed by 3D spatial + 1D post-temporal filtering, (b) 3D OS-EM with ADS correction followed by 3D spatial + 1D post-temporal filtering, (c) 4D MAP-RBI-EM with ADS correction. (The legends (F1) through (M5) are the same to those in Table 2)

Figure 6 shows comparison of the average maximum AUC values from the different image reconstruction and post-filtering methods. Method (M3), i.e. β = 0.015 of 4D MAP-RBI-EM with ADS correction, shows a maximum AUC value of 0.86 which is significantly higher (p<0.0001) than those from 3D FBP without correction (F3), i.e. 0.68, and 3D OS-EM with correction (O3), i.e. 0.72. The AUC value of 3D OS-EM with ADS correction and post-filtering has a maximum AUC value of 0.72, which is slightly higher (p=0.12) than 0.68 from the 3D FBP without correction and with post-filtering. The results demonstrated that with the selection of optimal parameters, the 4D MAP-RBI-EM with ADS corrections provided better human observer detection performance compared to that of the other image reconstruction and post-filtering methods. The result also confirmed that the optimal β value occurs within the range of optimal NMSE-NSD_av trade-off obtained from the theoretical calculations.

DISCUSSION

We investigated the use of a task-based human observer ROC study to evaluate a new 4D MAP-RBI-EM method for improved 4D gated MP SPECT as compared to conventional methods, such as 3D FBP without correction and 3D OS-EM with corrections of image degrading factors.

One of the goals of this study was to test the hypothesis that the trade-off between bias and noise of the 4D SPECT images can be used as a general guide for the image evaluation study. The bias and noise trade-off is particularly important in the preparation of observer studies, since it can serve as a guide in selecting the range of tested images that have higher probabilities of being optimal, rather than doing so by a random search of the test images. Thus, we hypothesized that the optimal trade-off between NMSE and NSD_av and the difference among the trade-offs are related to human observer performance. We also hypothesized that the optimal trade-off will likely occur within the ‘heel’ region of the NMSE vs. NSD_av curve. The results indicated that the differences between the three 3D & 4D image reconstruction methods predicted by the NMSE vs. NSD_av curves were compatible with the results of the human observer study. In fact, either extremely noisy or extremely smoothed cases showed the lowest or the second lowest AUC values in our study. We also found that the optimal human observer performance occurred within the ‘heel’ region of the NMSE vs. NSD_av curve where there is relatively lower noise and lower bias, though the exact optimal trade-off point remains unknown. Hence, the results suggest that the trade-off between NMSE and NSD_av can be a useful guide for general image quality in detection task in 4D MP SPECT, and this study was the first to determine the optimal trade-off region for the task using a human observer study. For a different ‘task,’ we will need to conduct a separate human observer study to seek the location of the optimal trade-off.

The ROC study was designed to evaluate solely the quality of the image itself obtained from using different image reconstruction algorithms in terms of detectability without any beneficial or confounding factors (such as additional information like pre-test results or anatomical variations in the cardiac model) that might affect the outcome of the evaluation task. In this study, the nuclear medicine physicians showed higher AUC values and smaller standard deviations than those of other observers for all the tested methods. However, the ranking of data points in AUC values for each method was clearly the same for all the observers regardless of reader experience, as shown in Table 6. This suggests that a difference in image quality in terms of detectability does exist among the tested images, and that reader experience contributes to observer performance. The consistent rank among intra- and inter-observers in detection accuracy indicates that our findings should hold true for readers at various levels of experience.

In the comparison study of the performance of the new 4D MAP-RBI-EM and other conventional image reconstruction methods, the results indicated that the application of non-selective smoothing technique lowered the noise level, but NMSE increased concurrently. However, the 4D MAP-RBI-EM method with ADS corrections and with optimal selection of parameters for the Gibbs prior offers a much better trade-off between noise smoothing and preservation of important motion features, which results in higher performance in the human observer study for the detection task when compared to the other image reconstruction methods. This also suggests that the 4D MAP-RBI-EM can be effectively applied to 4D gated MP SPECT with lower injected doses for the same image quality or an increased number of frames per cardiac cycle for better visualizations of the 4D cardiac motion and detection of regional wall motion abnormality.

Based on our previous studies (Sankaran et al., 2002; Frey et al., 2002; He et al., 2004), we found that the main advantage with having anatomical variability in a mathematical observer study was observer sensitivity, e.g., the absolute AUC value from a CHO study was closely matched to that of a human observer study viewing the same test images. That is, a single anatomy would give much higher AUC values in a CHO study compared to that in a human observer study. However, the trends of the evaluation studies, including the maximum values of the AUC, are very similar. In this study, our main goal was to see if there is a difference among the three image reconstruction methods under the study and their orders in terms of detectability of regional myocardial wall motion abnormality, but not their ‘absolute’ performances such as the AUC values. We chose not to use anatomical variations so as to mask any differences, which could be potentially small, among the three image reconstruction methods. The task also involved a known motion abnormality in a specified location. As a result, the interpretation of the results of our study is limited with the considerations involved. However, we believe that the design of our human observer study will provide useful information about the performances of the image reconstruction methods for the specific detection task.

In our study design, we carefully selected a single phantom model and adjusted the difficulty level by adjusting contrast of the regional myocardial motion abnormality and the noise magnitude of the test images so that the detectability of the abnormality was neither too easy nor too difficult. This was to ensure a good separation of detectability among the image reconstruction methods and to achieve statistical power at average AUC values of around 0.75 – 0.80 (Metz, 1978, 1986). For example, a large severe motion defect located at the lateral wall (where larger wall motion occurs) was easily detected compared to a smaller and less severe motion defect located close to the septal wall (where minimal wall motion occurs). On the other hand, Chi et al. (Liu et al., 2006) reported that when conducting CHO studies to compare different imaging methods, including defects and too many anatomical variations in the phantom will reduce the differences in detectability among the various imaging methods. In order to provide sufficient statistical power to corroborate the small difference, an increasing number of tests will be required. These are important considerations in the design of an observer study using simulated test images.

We have used the 8-bit grayscale to display the test images. Traditionally, nuclear medicine specialists have used the grayscale for reading scans in the clinic since it keeps linearity for human eyes (Xu et al., 2009), and especially because it displays very dim objects better than the color scale (Christian and Waterstram-Rich, 2013). Thus, grayscale images have become widely accepted as a standard format for the specialists in making diagnostic decisions in human and mathematical observer studies in cardiac SPECT imaging. On the other hand, the color scale is becoming popular in commercial software as perfusion images are typically presented in a color display to emphasize the findings in images or in fusion images from different imaging modalities. However, the color scale is considered to be ‘semi-quantitative’ as opposed to the fully-quantitative grayscale because it assigns different colors according to relative grayscales (Kaul et al., 1997). The color scale can also produce contours, such as apparently sharp changes in pixel values, where none actually exist (Cherry et al., 2012), and its spectrum can become completely different by changing the color table (Christian and Waterstram-Rich, 2013). Thus, the images should always be scaled and displayed in a reproducible and standardized manner, and a proper scale should be carefully chosen with the consideration of the observers’ experience.

Despite its difficulties, human observer studies are widely accepted as the best means to evaluate medical images. So far most of the methodologies developed for the observer studies were for 2D or 3D static images. In this study, we extended the observer study procedures to include 4D cine images. Thus, we developed tools such as an application that can display multiple slices and orientations of cardiac motion images as seen in the clinic, and we established procedures for performing studies of this kind. We also used a continuous scale ROC design that was previously employed in SPECT on static images to estimate the ROC curves. Overall, our study demonstrates the possibility of a task-based evaluation study that uses both human observers and 4D cine images.

CONCLUSION

We conclude that the 4D MAP-RBI-EM image reconstruction method with ADS corrections and optimal selection of parameters for the Gibbs prior improves the detection of regional myocardial wall motion abnormality in 4D gated MP SPECT images under the given experimental conditions. We also found that the image evaluation and optimization study based on the trade-off between bias and noise level can be used as a guide in choosing a reasonable range of image reconstruction methods and associated parameter values in human observer studies to pinpoint the exact trade-off for a specific detection task. Although the conclusion of our study is limited to a single anatomy and a single motion defect location, our study provides an important comparison between image quality based on simple image quality indices and actual human observer performances, which is lacking in the field. We plan future studies on real human data for further evaluation and validation of the performance of the methods in clinical environments.