Use of Pooled Samples from the National Health and Nutrition Examination Survey

SUMMARY

The National Centers for Disease Control and Prevention (CDC) provides an ongoing assessment of the U.S. population’s exposure to environmental chemicals by using biomonitoring in conjunction with CDC’s National Health and Nutrition Examination Survey (NHANES). Characterizing the distributions of concentrations of environmental compounds or their metabolites in the U.S. population is a primary objective of CDC’s biomonitoring program. Historically, this characterization has been based on individual measurements of these compounds in body fluid or tissue from representative samples of the population. Pooling samples before making analytical measurements can reduce the costs of biomonitoring by reducing the number of analyses. For the first time in NHANES 2005–2006, a weighted pooled-sample design was implemented to facilitate pooling samples before making analytical measurements. This paper describes this design and the estimation method being developed in the National Center for Environmental Health, Division of Laboratory Sciences (NCEH/DLS) to characterize concentrations of polychlorinated and polybrominated compounds. I present percentile estimates for 2,2’,4,4’,5,5’-Hexachlorobiphenyl (PCB153) in specific subpopulations of the U.S. based on the NHANES 2005–2006 pooled-sample design. I also compare estimates based on individual samples from NHANES 2003–2004 with estimates based on artificially created pools from NHANES 2003–2004 using a pooled-sample design similar to the one used for NHANES 2005–2006. For NHANES 2005–2006 the number of analyses required to characterize the levels of 61 polychlorinated and 13 polybrominated compounds in the U.S. population was reduced from 2201 to 228. At a cost of $1400 per analytical measurement, this represents a savings of approximately $2.78 million.

INTRODUCTION

Recently Caudill [1] demonstrated how the distributions of concentrations of environmental compounds or their metabolites in a population can be characterized based on pooled-samples. A potential problem with estimates based on pooled-samples, however, has to do with the fact that the measured value for a pooled-sample is comparable to an arithmetic average of levels in the individual samples making up the pool. Thus, using pooled-samples to estimate the mean and variance of underlying data that is log normal will lead to biased estimates. To correct for this bias Caudill et al [2] presented a bias-correction method for pooled-sample estimates from samples with a log-normal distribution. This bias-correction method uses the variability among replicate pools within demographic groups to estimate the variance among individual samples. Pooling samples has been attempted in previous NHANES [3, 4], but NHANES 2005–2006 is the first survey in which a weighted pooled-sample design was implemented to facilitate pooling samples before making analytical measurements. Here I demonstrate the pooled-sample design and estimation method being developed to characterize the concentrations of polychlorinated and polybrominated compounds in the U.S. population based on NHANES 2005–2006. I present estimates of various percentiles for PCB153 in the U.S. population based on pooled-samples from NHANES 2005–2006. Then using artificially created pools from NHANES 2003–2004 and a pooled-sample design similar to the one used with the 2005–2006 data, I also compare pooled-sample estimates with estimates based on individual samples.

METHODS

The sampling scheme for NHANES 2005–2006 is a complex multistage, probability sampling design that selects participants who are representative of the civilian, non-institutionalized U.S. population. Over-sampling of certain population subgroups is done to increase the reliability and precision of health status indicator estimates for those groups. Because each sample person does not have an equal probability of selection, sample weighting is needed to produce correct population estimates of means, percentiles, and other descriptive statistics. Also, because of the use of stratified multistage selection, incorporation of the sampling design is needed to calculate sampling variances [5]. These variances can be related to variances based on simple random sampling via the design effects [6]. For polychlorinated and polybrominated compounds measured as part of CDC’s biomonitoring program, instead of using the full NHANES sample, a random one-third subsample of NHANES participants was used. Curtin et al [7] provide documentation of the construction of sampling weights for this one-third subsample. After collection, serum specimens are divided into aliquots, transferred to clean cryovials, frozen, shipped on dry ice to CDC’s National Center for Environmental Health, and stored at −70 °C.

In order to implement a pooled-sample design for NHANES 2005–2006 each aliquot was identified as belonging to one of 24 demographic groups based on race/ethnicity (non-Hispanic white: NHW, non-Hispanic black: NHB, Mexican American: MA), gender (Male: M, Female: F), and age group (12–19, 20–39, 40–59, and 60 years of age and older). For this analysis a pooled-sample design consisting of 24 demographic groups and 8 samples per pool was chosen based on the results of simulation experiments presented in Caudill [1]. The number of pools created for each of the 24 demographic groups varied depending on the total number of individual aliquots available. In the one-third subset of 2201 individual samples/aliquots, there were 2041 samples available from NHW, NHB, and MA subjects. Because the pooled-sample design requires that all samples be of sufficient volume and that there be the same number of samples in each pool, only 1824 samples were available to create 228 pools with 8 samples per pool.

In order to incorporate sample weighting into a pooled-sample design it is necessary to use a different volume of material from each sample contributing to a pool. The volume chosen for each sample in a pool depends on the ratio of its sampling weight to the sum of the sampling weights of all samples in the pool. To physically accomplish this pooling in the laboratory requires that the ratio of the largest to the smallest sampling weight of samples in the same pool be no larger than about 4 or 5. Based on examination of several sources of variation in data from previous surveys, NCHS statisticians concluded that it is very advantageous to form pools from samples with comparable sampling weights [personal communication]. Thus, the individual samples were sorted/stratified by sampling weight and pools were formed using samples with sampling weights adjacent to one another in the sorted list.

The number of samples available and the number of pools formed in each demographic group are presented in Table 1. Once the pools were created, summed sampling weights were further adjusted to account for the unused samples. Because samples were pooled across the design cells of the original NHANES sampling design, direct calculation of design effects may not be possible. So in accordance with previous pooled-sample studies based on NHANES data [3, 4], I present unadjusted confidence limits assuming simple random sampling along with adjusted confidence limits assuming specified design effects. Of course, there is no guarantee that the design effects chosen are applicable to the corresponding estimates, so further work needs to be done to determine whether and how design effects can be estimated for pooled-sample designs.

Table 1.

Number of individual serum samples available (number of pools formed) from NHANES 2005–2006 participants per demographic group

Race or Ethnicity	Gender	Number of Samples per Subpopulation (# of Pools)
		12–19 years	20–39 years	40–59 years	60+ years
		Non-Hispanic White	Male	76(9)	108 (13)	110 (13)	137 (17)
Female	85 (10)		136 (17)	111 (13)	146 (18)
Non-Hispanic Black	Male	114 (14)	57(7)	51(6)	52(6)
	Female	117 (14)	66(8)	62(7)	48(6)
Mexican American	Male	96 (12)	84 (10)	43(5)	38(4)
	Female	133 (16)	84 (10)	50(6)	37(4)

Measurements of polychlorinated and polybrominated compounds in samples from individuals tend to have a log-normal distribution, so I used the pooled-sample estimation method described by Caudill [1] to correct for the bias inherent in measurements from pooled-samples. I assume there are d demographic groups, p_i pools in the i^th demographic group and that each pool consists of s samples. For a log-normal distribution with mean and variance of the natural logarithm of individual values (i.e., y_ijk = ln(x_ijk);i = 1,2,…d; j = 1,2,…p_i;k = 1,2,…,s) equal to μ_yij and ${\sigma }_{y_{ij}}^2$, respectively, the single measured value of a pool (x̄_ij․) is comparable to a weighted average of log-normal values [${\overline{x}}_{ij․}=\sum _{k=1}^s{w}_{ijk}{x}_{ijk}/w_{ij․}$], if the volume of the k^th sample is given by v_ijk = w_ijk/w_ij․, where w_ijk is the sampling weight of the k^th sample in the j^th pool in the i^th demographic group and w_ij․ is the sum of the s sampling weights in the j^th pool in the i^th demographic group. Thus, the expected value of each (x̄_ij․) is equal to $\text{exp}\{{\mu }_{y_{ij}}+\frac{{\sigma }_{y_{ij}}^2}{2}\}$.

Letting $C_{V{\overline{x}}_{ij}}^2$ represent the square of the coefficient of variation of x̄_ij․ for pool j in demographic group i, the variance of y_ijk[= ln(x_ijk)] can be calculated as follows:

$${\sigma }_{y_{ij}}^2=\text{ln}\{w_{ij․}^2{C}_{V{\overline{x}}_{ij}}^2/\sum _{k=1}^s{w}_{ijk}^2+1\}$$ (1)

where w_ijk and w_ij․ are defined as above. Thus, the geometric mean of the j^th pool in the i^th demographic group can be estimated by:

$$G{\hat{\mu }}_{y_{ij}}=\text{exp}\{\text{ln}({\overline{x}}_{ij․})-\frac{{\sigma }_{y_{ij}}^2}{2}\}$$ (2)

The geometric mean of the i^th demographic group can be estimated by:

$$G{\hat{\mu }}_{y_i}=\text{exp}\{\sum _{j=1}^{p_i}{w}_{ij․}[\text{ln}({\overline{x}}_{ij․})-\frac{{\sigma }_{y_{ij}}^2}{2}]/w_{i‥}\}$$ (3)

A 100P^th percentile for the i^th demographic group can be estimated by:

$$G{\hat{U}}_{Pi}=\text{exp}\{\text{ln}(G{\hat{\mu }}_{y_i})+f_p{\hat{\sigma }}_{y_i}^{*})\},$$ (4)

where Gμ̂_yi is defined in Equation 3, f_P is the P^th critical value of the standard normal distribution, and ${{\hat{\sigma }}_{y_i}^{*}}^2$ is an estimate of the total (i.e., within-pool and among-pool) variance associated with the logarithm of the unmeasured individual samples. The within-pool component of variance for demographic group i is estimated using a weighted mean of the ${\hat{\sigma }}_{y_{ij}}^2$ values calculated as follows:

$${\hat{\sigma }}_{y_{i_{\mathit{\text{within}}}}}^2=\sum _{j=1}^{p_i}{w}_{ij}^{*}{\hat{\sigma }}_{y_{ij}}^2/[\sum _{j=1}^{p_i}{w}_{ij}^{*}]$$ (5)

where the $w_{ij}^{*}[=p_i{w}_{ij․}/w_{i‥}]$ are scaled to sum to the number of pools in demographic group i. The among-pool component of variance for demographic group i is estimated using a weighted variance of the ${\overline{y}}_{ij}[=(\text{ln}({\overline{x}}_{ij․})-{\hat{\sigma }}_{y_{ij}}^2/2)]$ values as follows:

$${\hat{\sigma }}_{y_{i_{\mathit{\text{among}}}}}^2=\sum _{j=1}^{p_i}{w}_{ij}^{*}{[{\overline{y}}_{ij}-{\overline{\overline{y}}}_{w_i}]}^2/(p_i-1)$$ (6)

where $w_{ij}^{*}$ is defined as before and y̿_wi is the weighted mean of the ȳ_ij values in demographic group i.

To obtain 95^th percentile estimates for a particular compound, the bias correction (i.e., ${\sigma }_{y_{ij}}^2/2$) needed when estimating the geometric mean (Gμ̂_yij) must be estimated for each pooled-sample estimate. Because only a few pooled-sample replicates are measured in each demographic group, it is not advisable [1, 2] to use the actual $C_{V{\overline{x}}_{ij}}^2$ estimates in equation 1. Instead the logarithms of the 24σ̂_x̄i estimates are modeled versus the natural logarithms of the 24 demographic group medians of pool measurements, where σ̂_x̄i represents the standard deviation of the x̄_ij․ values (i.e., the p_i pool measurements) from demographic group i. Weighted least squares is used to determine the relationship, where in this case the weights are based on the squares of the numbers of pooled-samples per demographic group. Thus the $C_{V{\overline{x}}_{ij}}^2$ estimates used in equation 1 are obtained by dividing the predicted ${\hat{\sigma }}_{{\overline{x}}_{iu}}$ values obtained from the weighted least squares model by the corresponding pool measured values (x̄_ij․).

Using the estimates of ${\sigma }_{y_{ij}}^2$ from equation 1, where $C_{V{\overline{x}}_{ij}}^2$ is estimated as described in the previous paragraph, ${\hat{\sigma }}_{y_i}^{*}$ is calculated as the sum of ${\hat{\sigma }}_{y_{i_{\mathit{\text{within}}}}}^2$ and ${\hat{\sigma }}_{y_{i_{\mathit{\text{among}}}}}^2$ for each demographic group. Even though ${\hat{\sigma }}_{y_{i_{\mathit{\text{among}}}}}^2$ theoretically includes a fraction of ${\hat{\sigma }}_{y_{i_{\mathit{\text{within}}}}}^2$, simulation results suggest that ${\hat{\sigma }}_{y_i}^{*}$ as calculated here provides a less biased estimate of this variance. But because the estimates of ${\hat{\sigma }}_{y_i}^{*}$ can fluctuate due to the varying sample sizes and the resulting estimated degrees of freedom, the $\text{ln}({\hat{\sigma }}_{y_i}^{*})$ values are modeled versus the natural logarithm of the bias-corrected geometric means [ln(Gμ̂_yi)] for the 24 demographic groups. Weighted least squares is used to determine the relationship, again using weights based on the squares of the numbers of pooled-samples per demographic group. Thus, the ${\hat{\sigma }}_{y_i}^{*}$ values used in equation 4 are obtained from the weighted least squares model corresponding to the values of ln(Gμ̂_yi).

To illustrate the estimation method, I present 95^th percentile estimates for PCB153 for each of the 24 demographic groups using equation 4 and include 95% confidence limit estimates using the method described by Caudill [1]. Previously, Caudill [1, 8] and Caudill et al [2] used simulation experiments to evaluate the accuracy and precision of pooled-sample estimates. It would also be instructive to be able to compare weighted estimates based on pooled-samples with weighted estimates based on individual samples using actual NHANES data. No individual-sample data was available, however, from NHANES 2005–2006. But individual-sample data was available from NHANES 2003–2004, so to make the comparison, I artificially created pools from NHANES 2003–2004 using a weighted pooled-sample design similar to the one used with the 2005–2006 data. I then compared weighted estimates based on NHANES 2003–2004 individual samples with weighted pooled-sample estimates from the artificial pools.

RESULTS

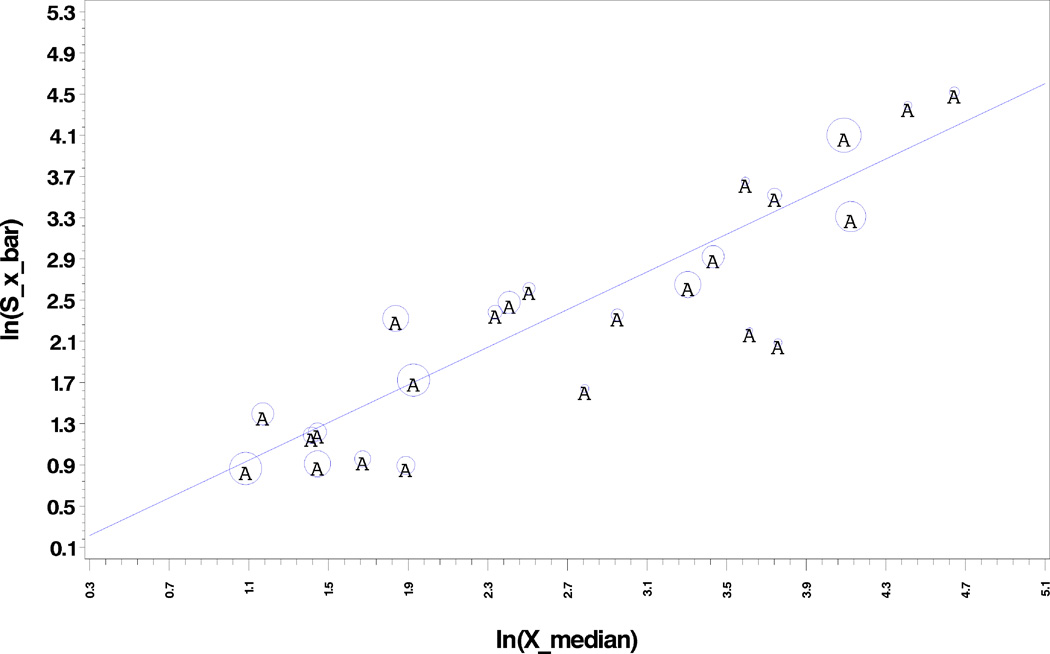
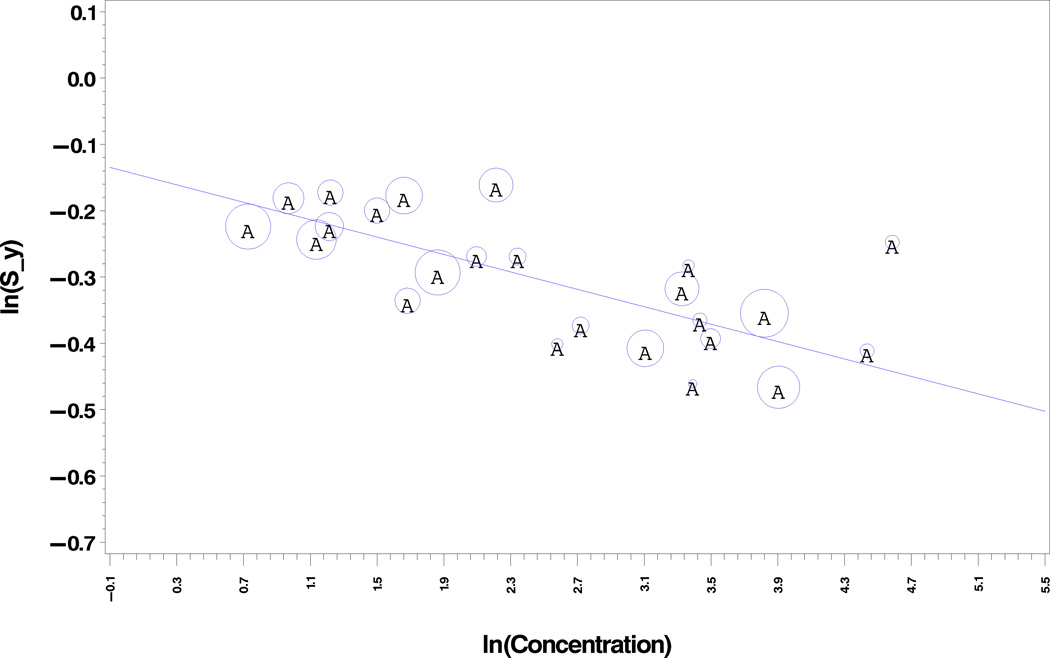
To obtain 95^th percentile estimates for PCB153, I first estimated the bias correction $({\sigma }_{y_{ij}}^2/2)$ by modeling the relationship between the logarithms of the 24σ̂_x̄i estimates versus the natural logarithms of the 24 demographic group medians of pool measurements, where the weights are based on the squares of the numbers of pooled-samples per demographic group. This relationship was approximately linear as shown in Figure 1 which displays a plot of ln(S_x_bar) versus ln(X_median), where S_x_bar on the abscissa represents σ̂_x̄i. The circle around each point indicates its relative weight in the weighted least squares modeling and the line indicates the weighted least squares fit. I used these model results to compute the $C_{V{\overline{x}}_{ij}}^2$ estimates used in equation 1. I then used the estimates of ${\sigma }_{y_{ij}}^2$ from equation 1, to calculate ${\hat{\sigma }}_{y_i}^{*}$ as the sum of ${\widehat{\sigma }}_{y_{i_{\mathit{\text{within}}}}}^2$ and ${\hat{\sigma }}_{y_{i_{\mathit{\text{among}}}}}^2$ for each demographic group. Finally, I used weighted least squares to determine the relationship between the $\text{ln}({\hat{\sigma }}_{y_i}^{*})$ values and the natural logarithm of the bias-corrected geometric means [ln(Gμ̂_yi)] for the 24 demographic groups, with weights again based on the squares of the numbers of pooled-samples per demographic group. I obtained the ${\hat{\sigma }}_{y_i}^{*}$ values used in equation 4 from the weighted least squares model corresponding to the values of ln(Gμ̂_yi). Figure 2 displays a plot ln(S_y) versus ln(Concentration), where S_y on the abscissa represents ${\hat{\sigma }}_{y_i}^{*}$ and ln(Concentration) on the ordinate axis represents ln(Gμ̂_yi). The circle around each point indicates its relative weight in the weighted least squares modeling and the line indicates the weighted least squares fit.

Figure 1.

Figure 2.

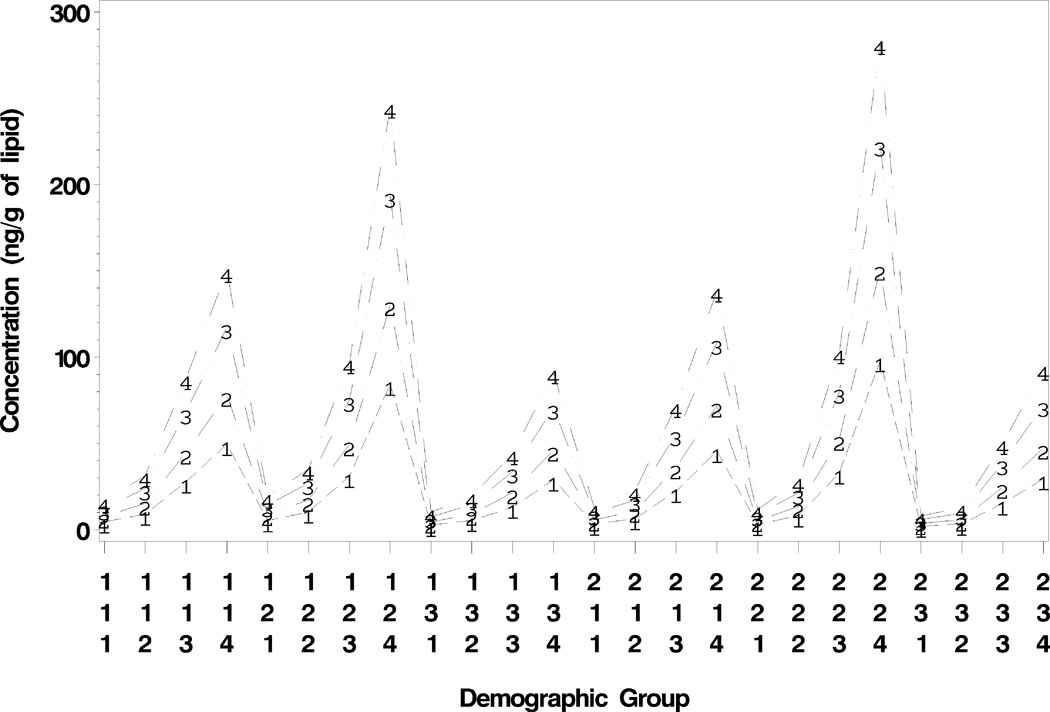
Figure 3 displays a plot of the 50^th, 75^th, 90^th, and 95^th percentile estimates of PCB153 for the 24 demographic groups denoted by XYZ, (where X = 1, 2 for male and female; Y = 1, 2, 3 for NHW, NHB, MA; and Z = 1, 2, 3, 4 for 12–19, 20–39, 40–59, and 60+ years of age). The 50^th, 75^th, 90^th, and 95^th percentile estimates are labeled with the numbers 1, 2, 3, and 4, respectively, and connected by dashed lines. This figure gives an idea of how the various percentiles differ across demographic groups but does not convey the uncertainty associated with the estimates, so I have also provided Table 1 which displays 95^th percentile estimates along with their 95% confidence limits for PCB153 for each of the 24 demographic groups. The degrees of freedom estimates used to compute the 95% confidence limits (described in Caudill [1]) are based on a modification of the Satterthwaite approximation presented by Mee and Owen [9] for obtaining factors for tolerance limits when the ratio of the variance between groups (pools) to the variance within groups (pools) is unknown. The modification involves using the variance estimates from equations 5 and 6 in the Methods section above, whereas the within-group and among-group variances of Mee and Owen are derived from a balanced one-way analysis of variance random model. The confidence limits in columns 7 and 8 are based on an assumption of simple random sampling, which is not the case for NHANES data. Therefore, to account for the potential under or over estimation of variance associated with the analyses, I also computed adjusted confidence limits by using the design effects for PCB153 estimates associated with NHANES 2003–2004 individual samples. Of course, there is no guarantee that the design effects from one survey are applicable to another survey, so further work needs to be done to determine whether and how design effects can be estimated for pooled-sample designs. In a few cases the estimated degrees of freedom were quite small (e.g., for Male Mexican Americans 60+ years of age the degrees of freedom is equal to 6.3) resulting in rather wide 95% confidence limit estimates.

Figure 3.

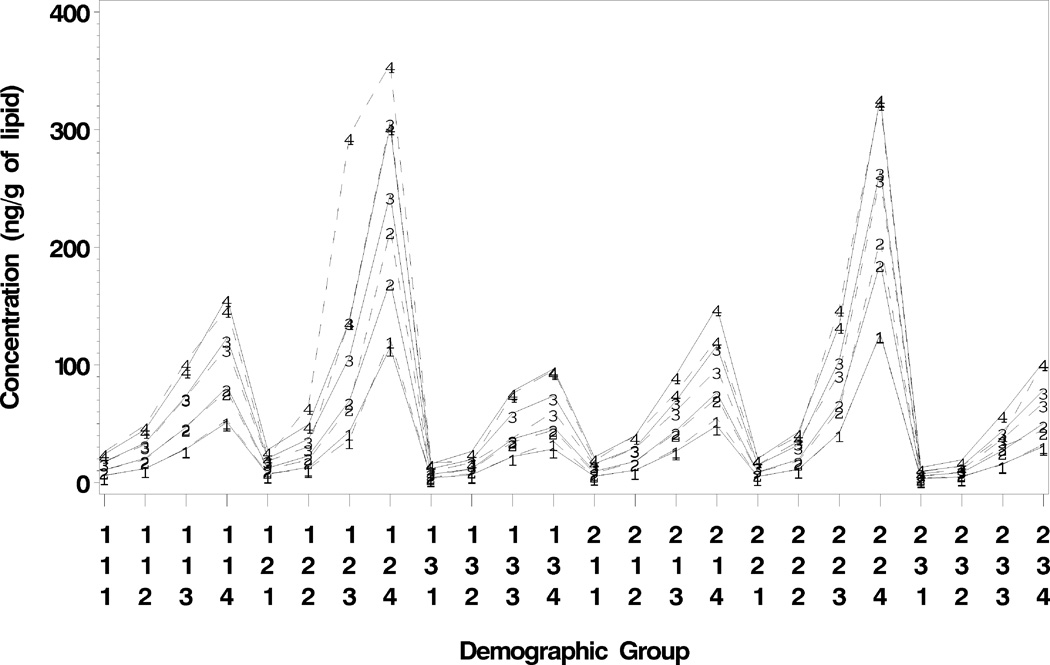
No individual-sample data from NHANES 2005–2006 was available to compare the pooled-sample estimates in Figure 3 with estimates based on individual samples. Individual-sample data was available, however, from NHANES 2003–2004. To compare weighted pooled-sample estimates with weighted estimates based on NHANES 2003–2004 individual samples, I artificially created pools from NHANES 2003–2004 using a weighted pooled-sample design similar to the one used with the 2005–2006 data. The results of this comparison for the 50^th, 75^th, 90^th, and 95^th percentile estimates are displayed in Figure 4 and are labeled with the numbers 1, 2, 3, and 4, respectively. The estimates based on individual samples are connected by dashed lines and those based on pooled-samples are connected by solid lines. Table 3 displays 95^th percentile estimates along with their 95% confidence limits. The individual sample and pooled-sample 50^th and 75^th percentile estimates in Figure 4 agree very well even though the pooled-sample estimates were based on fewer samples (i.e., N = 1774 for individual-sample estimates as opposed to N = 1672 [209 pools×8 samples/pool] for pooled-sample estimates). There are several estimates of 90^th and 95^th percentiles that differ substantially by the two methods of estimation (i.e., using individual sample estimation versus pooled-sample estimation). For example, the individual-sample based 95^th percentile estimate for demographic group 123 (Male NHB 40–59 years of age) is 295 ng/g of lipid whereas the pooled-sample estimate is 137.7 ng/g of lipid (see Table 3). It turns out that the individual-sample based 95^th percentile estimate and its upper 95% confidence limit correspond to the maximum value for the 44 persons in that demographic group because the sampling weight for this individual sample was more than 2 times larger than the average sampling weight of all 44 samples in this demographic group. The next 4 lower individual sample values were 173, 143, 138, and 103 ng/g of lipid which are more in line with the pooled-sample 95^th percentile estimate of 137.7 ng/g of lipid.

Figure 4.

Table 3.

95^thPercentile Estimates for PCB153

NHANES 2003–2004 Individual Samples versus Pooled-Samples

Gender	Race	Age	Individual Samples		Pooled Samples
			NI1	95th Percentile (L95I – U95I)2	NP3	95th Percentile (L95P – U95P)4
Male	NHW	12–19	77	26.1 (14.9 – 34.4)	9	24.1 (17.4 – 38.4)
		20–39	102	48.8 (31.5 – 111.0)	12	45.1 (33.54 – 69.7)
		40–59	106	103.0 (60.2 – 123.0)	13	96.4 (73.2 – 137.8)
		60+	153	148.0 (115.0 – 154.0)	19	157.4 (134.0 – 190.6)
	NHB	12–19	124	21.7 (17.6 – 39.4)	15	27.7 (23.9 – 33.1)
		20–39	39	65.4 (16.6 – 92.9)	4	49.4 (28.1 – 210.3)
		40–59	44	295.0 (60.0 – 295.0)	5	137.7 (82.0 – 402.2)
		60+	30	356.0 (215.0 – 546.0)	3	303.2 (212.6 – 1052.3)
	MA	12–19	98	17.0 (9.0 – 22.8)	12	15.9 (12.6 – 21.5)
		20–39	44	17.7 (11.4 – 27.3)	5	26.4 (19.9 – 40.6)
		40–59	30	75.8 (16.7 – 99.2)	3	77.7 (43.9 – 395.8)
		60+	37	95.3 (44.3 – 97.1)	4	96.5 (75.6 – 157.6)
Female	NHW	12–19	76	18.4 (8.5 – 24.0)	9	21.7 (16.5 – 30.5)
		20–39	128	40.0 (22.2 – 63.0)	16	39.9 (28.8 – 60.0)
		40–59	101	76.5 (56.4 – 91.9)	12	91.6 (75.2 – 116.3)
		60+	142	122.0 (94.5 – 146.0)	17	149.2 (127.5 – 181.0)
	NHB	12–19	106	20.7 (11.8 – 23.7)	13	20.2 (16.6 –25.7)
		20–39	46	39.5 (15.3 – 53.5)	5	43.0 (25.2 – 132.0)
		40–59	44	149.0 (64.2 – 189.0)	5	134.3 (96.9 – 251.3)
		60+	31	324.0 (126.0 – 345.0)	3	327.3 (230.0 – 897.7)
	MA	12–19	85	9.2 (5.9 – 15.9)	10	12.8 (9.7 – 18.1)
		20–39	54	13.8 (9.6 – 23.5)	6	19.2 (14.8 – 27.9)
		40–59	32	39.7 (30.6 – 195.0)	4	58.7 (36.4 – 425.9)
		60+	45	103.0 (33.1 – 137.0)	5	102.6 (62.6 – 247.8)

¹N_I is the number of samples in the indicated demographic group.

²L95_I and U95_I are the lower and upper 95% confidence limits, respectively, around the 95^th percentile estimate based on individual samples.

³N_Pis the number of replicate pools in the indicated demographic group.

⁴L95_P and U95_P are the lower and upper 95% confidence limits, respectively, around the 95^th percentile estimate based on pooled-samples adjusted for design effects obtained from individual samples.

DISCUSSION

Several aspects of the methods used in this paper for correcting the bias associated with pooled-sample measurements from log-normally distributed samples have been described in previous publications [1, 2, and 8]. Those publications used simulation experiments to demonstrate the accuracy and precision of estimates based on pooled-samples. In this paper I have focused more on presenting an actual example using NHANES 2005–2006 weighted pooled-sample data. For the example, I chose PCB 153 which is in a family of polychlorinated biphenyls that have been classified as probable human carcinogens by the International Agency for Research on Cancer and the National Toxicology Program [10]. The percentile estimates in Table 2 tend to increase with increasing age regardless of gender and race/ethnicity, as is typical for polychlorinated biphenyls due to age-related accumulation.

Table 2.

95^thPercentile Estimates for PCB153

Using NHANES 2005–2006 Pooled-Samples

Gender	Race	Age	N1	DF2	95th Percentile	Lower 95% CL3	Upper 95% CL3	Lower 95% CL4	Upper 95% CL4
Male	NHW	12–19	9	38.3	16.3	12.2	25.2	12.0	26.0
		20–39	12	35.1	31.4	23.3	49.1	23.8	47.6
		40–59	12	56.4	87.7	69.3	120.8	66.7	127.3
		60+	15	163.5	149.8	128.8	179.2	130.6	176.3
	NHB	12–19	13	51.7	19.0	14.4	27.6	15.8	24.4
		20–39	6	21.0	35.4	25.5	63.0	23.7	71.8
		40–59	5	17.4	96.8	70.3	176.8	60.6	233.9
		60+	5	14.1	245.0	177.8	471.8	181.8	451.0
	MA	12–19	11	59.0	10.1	7.7	14.5	7.9	14.0
		20–39	9	101.9	19.3	15.8	24.9	16.1	24.3
		40–59	4	19.7	44.0	32.0	78.7	29.4	91.8
		60+	4	6.3	91.0	59.0	352.4	67.7	228.8
Female	NHW	12–19	10	67.4	12.6	9.8	17.5	9.3	18.7
		20–39	16	151.3	22.8	19.0	28.3	17.7	30.8
		40–59	13	147.5	71.6	60.7	87.2	59.9	88.6
		60+	17	89.0	138.5	112.9	178.9	118.1	169.0
	NHB	12–19	14	132.4	11.7	9.6	14.9	9.9	14.5
		20–39	7	32.8	28.2	21.1	44.2	19.4	50.3
		40–59	7	46.7	102.7	81.3	143.6	81.7	142.4
		60+	5	6.9	282.0	190.1	891.1	187.8	923.9
	MA	12–19	16	157.0	8.1	6.7	10.2	6.3	10.8
		20–39	9	35.7	12.7	9.3	20.1	9.6	19.2
		40–59	6	53.2	50.1	39.8	69.2	40.9	66.4
		60+	3	7.4	93.1	61.9	296.9	50.2	540.7

¹N is the number of replicate pools in the indicated demographic group.

²DF is the estimated degrees of freedom associated with the corresponding 95^th percentile estimate.

³Confidence limits assuming simple random sampling.

⁴Confidence limits assuming design effects obtained in NHANES 2003–2004.

In addition to presenting weighted percentile estimates for PCB153 from NHANES 2005–2006, I also compared weighted estimates based on artificially created pooled-samples with weighted estimates based on individual samples. The individual samples and artificial pools for this comparison were obtained from NHANES 2003–2004. The individual-sample and pooled-sample results agree fairly well except for a few demographic groups (e.g., the 95th percentile estimate for male non-Hispanic blacks 40–59 years of age). Actually, the pooled-sample 95^th percentile estimate appeared to be more in line with expectations based on the pattern seen for other demographic groups as age increases and based on the fact that the 50^th and 75^th percentile estimates were very similar for this demographic group whether individual samples or pooled-samples were used for estimation (see Figure 4). The individual-sample based 95^th percentile estimate was 295 ng/g of lipid and corresponded to the maximum value for the 44 persons in that demographic group. Of course, small sample size along with a large range in sampling weights is one problem with using individual samples to estimate an extreme percentile. The pooled-sample estimates, on the other hand, benefit from the variance information in the entire set of pooled-samples through the use of models to relate variance estimates to concentration levels. Because samples are pooled across the design cells of the original NHANES sampling design, however, confidence limits on pooled-sample estimates need to be adjusted to reflect the design effects of the survey.

For NHANES 2005–2006 the number of analyses required to characterize the levels of 61 polychlorinated compounds and 13 polybrominated compounds was reduced from 2201 individual samples to 228 pooled-samples for a cost of about $320,000, as opposed to a cost of $3.1 million to measure the 2201 individual samples.

Future areas of research into the use of pooled-samples from surveys, such as NHANES, will likely include consideration of alternative variance estimation and modeling methods, exploration of the effects of left censoring (i.e., left censoring in individual samples may or may not lead to left censoring in pooled-samples), investigation of methods for estimating design effects associated with pooled-sample estimates from complex sample designs, and determination of the extent to which association studies and longitudinal studies based on pooled-samples might be possible.