Abstract
Oxygen is an important element in most biologically significant molecules and experimental solid-state 17O NMR studies have provided numerous useful structural probes to study these systems. However, computational predictions of solid-state 17O NMR chemical shift tensor properties are still challenging in many cases and in particular each of the prior computational work is basically limited to one type of oxygen-containing systems. This work provides the first systematic study of the effects of geometry refinement, method and basis sets for metal and non-metal elements in both geometry optimization and NMR property calculations of some biologically relevant oxygen-containing compounds with a good variety of XO bonding groups, X= H, C, N, P, and metal. The experimental range studied is of 1455 ppm, a major part of the reported 17O NMR chemical shifts in organic and organometallic compounds. A number of computational factors towards relatively general and accurate predictions of 17O NMR chemical shifts were studied to provide helpful and detailed suggestions for future work. For the studied various kinds of oxygen-containing compounds, the best computational approach results in a theory-versus-experiment correlation coefficient R2 of 0.9880 and mean absolute deviation of 13 ppm (1.9% of the experimental range) for isotropic NMR shifts and R2 of 0.9926 for all shift tensor properties. These results shall facilitate future computational studies of 17O NMR chemical shifts in many biologically relevant systems, and the high accuracy may also help refinement and determination of active-site structures of some oxygen-containing substrate bound proteins.
Introduction
Oxygen is an important element found in most biologically significant molecules such as proteins, nucleic acids, carbohydrates, and phospholipids. It is also at the center of numerous biological processes. Among the four most common biological elements: oxygen, hydrogen, carbon and nitrogen, oxygen is the element that only has a quadrupolar NMR-active stable isotope, 17O. This isotope is unique because its spin state is 5/2 as opposed to the 1/2 spin state seen in most frequently used isotopes of the other three elements. 17O has a natural abundance of only 0.037%,1-4 which makes solid-state 17O NMR studies rather challenging. However, recent experimental techniques have dramatically advanced this field and a number of types of oxygen-containing systems have been experimentally investigated,1-4 including various kinds of biologically relevant systems, such as those with CO,5, 6 NO,7, 8 and PO9 groups, amino acids,10-13 nucleic acid bases,14 pharmaceutical compounds,15 and large protein-ligand complexes.16 More recently, the solid-state 17O NMR studies have even been extended to some paramagnetic metal complexes with organic ligands.17
To help understand experimental solid-state 17O NMR results, a number of theoretical investigations have been reported, such as those on the calculated 17O NMR shifts of amides5, nucleic acid bases14, 18-20, amino acids11-13, carboxylic compounds21-23, peptides24 as well as a few metal containing compounds7, 8, 17, 25. For the diamagnetic systems, regarding the two major types of solid-state 17O NMR properties, the 17O NMR chemical shielding/shift tensor and electric field gradient tensor (or related quadrupole coupling constant), previous results show that quantum chemical predictions of the latter one are in most cases satisfactory with errors <10%, while the accurate predictions of the former one are relatively more challenging. For instance, in the case of amide compounds, previous work show that the mean percentage deviation (MPD) of the predicted 17O NMR isotropic chemical shifts (δiso’s) is about twice of the MPD of the calculated 17O quadrupole coupling constants.5 The predictions of δiso’s though in some cases can achieve an accuracy of <10-15% error, but also frequently have errors well above 20-30%, especially for metal-containing systems.5, 7-9, 11-14, 17-25
Clearly more studies are needed in order to make more accurate predictions of 17O NMR chemical shifts in diamagnetic oxygen-containing systems, which can also help future investigations of the diamagnetic contributions of the 17O NMR chemical shifts in paramagnetic oxygen-containing species. In addition, each of the published computational studies of 17O NMR chemical shifts is basically focused on one type of chemical systems. Therefore, this work aims to provide a relatively general computational approach towards accurate predictions of 17O NMR chemical shifts in a good variety of biologically relevant diamagnetic oxygen-containing systems, including HO, CO, NO, PO, and MO (M = metal) bonding groups. In addition, this work provides a systematic investigation of the computational factors on 17O NMR chemical shift predictions, including geometry, method of choice, basis scheme for both non-metal and metal elements, which points out some useful factors for future computational work of other oxygen-containing species. Results show that the overall calculated 17O NMR chemical shift tensor principal elements (δ11’s, δ22’s, δ33’s) in an experimental range of 1455 ppm have an excellent theory-versus-experiment correlation coefficient R2=0.9926, and the mean absolute deviation (MAD) of the predicted δiso’s is 13 ppm, with 5.7% MPD. These results shall help future computational studies of 17O NMR chemical shifts, which may also help structure refinement of some substrate bound proteins16 as done previously by using quantum chemical studies of other NMR chemical shifts.26, 27
Computational Details
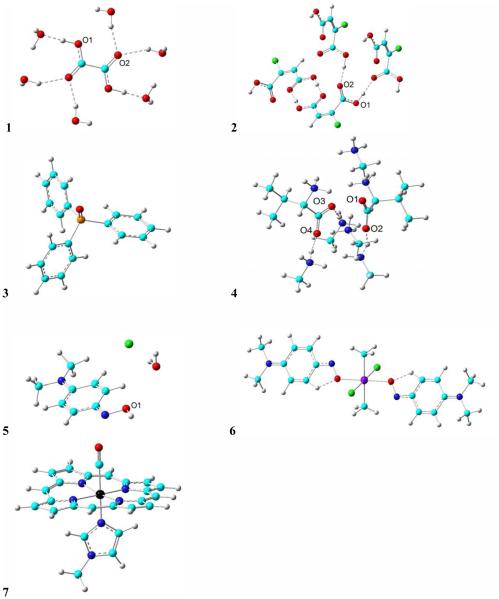
The structures studied in this work are shown in Figure 1: (1) oxalic acid23, (2) chloromaleic acid21, (3) triphenylphosphine oxide28, (4) L-valine13, (5) p-nitrosodimethylaniline (NODMA) hydrochloride hydrate8, 29 , (6) SnCl2(CH3)2(NODMA)28 and (7) Fe(TPP)(1-methylimidazole)(CO)25, TPP = tetraphenylporphyrinato (here the phenyl substituent is replaced by hydrogen). These molecules contain a good variety of bonding groups ‘XO’ where X= H, C, N, P, and Sn. A number of factors that could affect the accuracy of 17O NMR chemical shift predictions were studied, including geometry, method of choice, basis schemes for both non-metal and metal elements. All calculations were done using Gaussian 09.30
Figure 1.
Structures of the molecules (1-7) investigated in this work. Atom color scheme: Cl – green; O – red; P – orange; C – cyan; H – gray; N – blue; Fe – black; Tin – violet. Single dashed lines indicate hydrogen bonds. Where there are multiple oxygens, the labeled ones are with NMR properties studied.
Regarding geometry, both the original X-ray crystal structures of these molecules and partial geometry optimization with ~60 density functional theory (DFT) methods and basis set combinations were investigated, see details in the next section. Since previous work has repeatedly highlighted the importance of the inclusion of hydrogen bonding partners in 17O NMR chemical shift predictions,6, 11, 14 here by default, the hydrogen bonding partners are included in the calculations for compounds 1, 2, 4, as shown in Figure 1. In this work, only the first shell of hydrogen bonding partners of the nuclei of interest were studied since our goal is to develop an efficient computational approach for future studies of large biologically relevant molecules and the current results have already been of excellent theory-versus-experiment correlations with systematic errors that can be reduced by using predictions from regression results (vide infra).
Regarding NMR chemical shielding calculations, the gauge independent atomic orbital (GIAO) algorithm used in previous computational studies5-8, 14, 25 was also employed here. Both the pure DFT method OP8631, 32 and the hybrid DFT method B3LYP33 together with Pople-type basis 6-311++G(d,p) and 6-311++G(2d,2p), and Dunning type basis D95(d,p)34 and aug-cc-PVDZ35 for non-metal elements and the effective core potential basis LanL2DZ36 for metals were studied. Based on our recent work on some oxygen-containing systems17 and more studies in the Supporting Information, the LanL2DZ basis yields the best NMR shift predictions among a number of metal bases studied. Although the state-of-the-art CCSD(T) calculations shall provide better predictions of absolute NMR shift values than DFT methods,37 their uses are basically limited to small molecules. Therefore, to help develop a computational approach to study biologically relevant large molecules, we focused on the investigation of DFT calculations here.
The calculated chemical shielding tensor elements (σij) were then converted to the chemical shifts tensor elements (δij) using the standard 17O reference H2O. The formula δ = 287.5 − σ was used in order to obtain calculated chemical shift results, in which 287.5 ppm is the experimental absolute chemical shielding for liquid water,38 which is also similar to a more recent determination from high resolution rotational spectroscopy,39 289.2 ppm.
Results and Discussion
In this first work to have a systematic investigation of the effects of the used geometry, method, basis sets of both non-metal and metal elements towards a relatively general computational approach for accurate predictions of 17O NMR chemical shifts in some biologically relevant systems, a number of oxygen-containing compounds as shown in Figure 1 were chosen as a representative date set for those with HO, CO, NO, PO, and MO bonding patterns. Their experimental 17O NMR chemical shift tensor principal elements or isotropic shifts are listed in Table 1, which contain 22 independent data points covering an experimental range of 1455 ppm, a major part of the reported 17O NMR chemical shifts in organic and organometallic compounds.1
Table 1.
Experimental 17O NMR chemical shifts (unit: ppm)
| System | Atom | Value | Reference | |
|---|---|---|---|---|
| 1 | O1 | δ 11 | 351 | 23 |
| δ 22 | 142 | |||
| δ 33 | 55 | |||
| δ iso | 183 | |||
| O2 | δ 11 | 476 | ||
| δ 22 | 413 | |||
| δ 33 | 14 | |||
| δ iso | 301 | |||
| 2 | O1 | δ iso | 175 | 21 |
| O2 | δ iso | 329 | ||
| 3 | O | δ 11 | 130 | 28 |
| δ 22 | 11 | |||
| δ 33 | −5 | |||
| δ iso | 45 | |||
| 4 | O1 | δ iso | 313 | 13 |
| O2 | δ iso | 280 | ||
| O3 | δ iso | 264 | ||
| O4 | δ iso | 287 | ||
| 5 | O1 | δ 11 | 450 | 8, 29 |
| δ 22 | 260 | |||
| δ 33 | 100 | |||
| δ iso | 270 | |||
| 6 | O | δ 11 | 1450 | 8 |
| δ 22 | 600 | |||
| δ 33 | 100 | |||
| δ iso | 717 | |||
| 7 | O | δ iso | 372 | 25 |
Oxalic acid was the first model investigated here. As shown in Figure 1, based on the X-ray crystal structure,23 each oxalic acid molecule is surrounded by six hydrogen bonded water molecules. Since previous work has repeatedly highlighted the importance of the inclusion of hydrogen bonding partners in 17O NMR chemical shift predictions,6, 11, 14 this model with all six surrounding water molecules was used, which was previously found to have only 3.7% deviation regarding the largest and most affected tensor element from the use of a much more sophisticated and time-consuming model of 11 oxalic acid and 29 water molecules.23 We first tested the use of the X-ray structure without any geometry optimization. Although previously the quantum chemical methods at both the Hartree-Fock and DFT levels5, 7-9, 11, 13-17, 19, 21, 23-25, 28 were used for NMR chemical shielding calculations, here we focused on evaluating DFT methods, since eventually we will also investigate metal-containing systems. Both the pure DFT method OP8631, 32 and the hybrid DFT method B3LYP33 were studied here based on their previous good performance in predicting 17O NMR chemical shifts in some limited sets of oxygen-containing compounds.8, 13, 17, 19, 21, 23, 24 Regarding the basis sets, the relatively large Dunning type basis D95(d,p)34 and aug-cc-PVDZ35 and Pople-type basis 6-311++G(d,p) were investigated based on previous studies.8, 13, 19, 21-25 The calculated 17O NMR chemical shift tensor principal elements and isotropic shifts are shown in Table 2, along with the linear correlation coefficients and slopes for the regression of the calculated 17O NMR chemical shift tensor principal elements vs. experimental values. As shown in Table 2, both OP86 and B3LYP for each basis set tested have excellent predictions since R2 are all basically larger than 0.990, which is consistent with their excellent performance reported previously.8, 13, 17, 19, 21, 23, 24 OP86 results here have slightly better R2 than B3LYP data for all the studied basis sets. The average deviation of the slopes from ideal values is 6.7% for B3LYP calculations and 2.6% for OP86 calculations, again showing slightly better performance of OP86. For each method, the differences in R2 from using a different basis set are also small (<0.0025). However, the differences in slopes are a little bit larger. Based on the results in Table 2, the method combination of OP86/6-311++G(d,p) has the best R2 (0.9943) and slope (1.0187) values.
Table 2.
Calculated 17O NMR Data from using the X-Ray Structure of 1 (unit: ppm)
| Method | Basis Set | δ 11 | δ 22 | δ 33 | δ iso | R2 | Slope | |
|---|---|---|---|---|---|---|---|---|
| B3LYP | aug-cc-pVDZ | O1 | 309 | 126 | 59 | 165 | 0.9895 | 1.0261 |
| O2 | 493 | 421 | −1 | 304 | ||||
| 6-311++G(d,p) | O1 | 345 | 144 | 75 | 188 | 0.9911 | 1.0925 | |
| O2 | 535 | 458 | 10 | 334 | ||||
| D95(d,p) | O1 | 328 | 135 | 57 | 173 | 0.9919 | 1.0825 | |
| O2 | 509 | 447 | −6 | 317 | ||||
| OP86 | aug-cc-pVDZ | O1 | 303 | 133 | 59 | 165 | 0.9920 | 0.9748 |
| O2 | 466 | 408 | −1 | 292 | ||||
| 6-311++G(d,p) | O1 | 334 | 148 | 73 | 185 | 0.9943 | 1.0187 | |
| O2 | 497 | 434 | 10 | 314 | ||||
| D95(d,p) | O1 | 324 | 145 | 56 | 175 | 0.9932 | 1.0339 | |
| O2 | 483 | 435 | −6 | 304 |
Next, partial geometry optimization calculations were run on the same X-ray structure for 1 with only the hydrogen atoms being optimized. Here we focused on the evaluation of the effect of the hydrogen positions, since they are basically uncertain in conventional X-ray structures, and the above calculations using the X-ray structure have already yielded excellent results, which do not necessitate the use of more extensive geometry refinement. Due to the excellent performance of OP86 method in the above study, it was also examined as a method for geometry optimization, along with a modest size basis set 6-31G(d), which may be applied to relatively large systems to help future work on biologically relevant systems. Interestingly, as shown in Table 3, the geometry optimization on hydrogen positions indeed results in improvement in both R2 and slope, and this improvement occurs for both NMR calculations methods OP86 and B3LYP. Here, the use of a larger basis set of 6-311++G(2d,2p) compared to 6-311++G(d,p) yields almost the same R2 values and <1% difference in slopes. The best NMR computational method combination appears again to be OP86/6-311++G(d,p), with R2=0.9967 and slope=1.0059. In addition, another geometry optimization method based on the studies on metal-containing systems (vide infra), mPWP86/6-311G(d), was also investigated here. Results in Table 3 show that this method also generates similarly excellent calculations, with R2’s and slopes slightly inferior to those obtained using the OP86/6-31G(d) optimized structure.
Table 3.
Calculated 17O NMR Data for the Partially Optimized Structure of 1 (unit: ppm)
| Optimization | NMR | δ 11 | δ 22 | δ 33 | δ iso | R2 | Slope | |
|---|---|---|---|---|---|---|---|---|
| OP86/ 6-31G(d) |
B3LYP/ 6-311++G(d,p) |
O1 | 362 | 156 | 77 | 198 | 0.9965 | 1.0783 |
| O2 | 521 | 454 | 6 | 327 | ||||
| B3LYP/ 6-311++G(2d,2p) |
O1 | 360 | 156 | 76 | 197 | 0.9964 | 1.0762 | |
| O2 | 522 | 451 | 7 | 327 | ||||
| OP86/ 6-311++G(d,p) |
O1 | 349 | 160 | 74 | 194 | 0.9967 | 1.0059 | |
| O2 | 484 | 431 | 6 | 307 | ||||
| OP86/ 6-311++G(2d,2p) |
O1 | 347 | 160 | 73 | 194 | 0.9967 | 1.0070 | |
| O2 | 486 | 429 | 6 | 307 | ||||
| mPWP86/ 6-311G(d) |
B3LYP/ 6-311++G(d,p) |
O1 | 354 | 155 | 77 | 195 | 0.9938 | 1.0933 |
| O2 | 532 | 460 | 6 | 332 | ||||
| B3LYP/ 6-311++G(2d,2p) |
O1 | 353 | 155 | 76 | 195 | 0.9937 | 1.0889 | |
| O2 | 532 | 456 | 6 | 331 | ||||
| OP86/ 6-311++G(d,p) |
O1 | 342 | 159 | 74 | 192 | 0.9951 | 1.0189 | |
| O2 | 494 | 435 | 5 | 311 | ||||
| OP86/ 6-311++G(2d,2p) |
O1 | 341 | 160 | 74 | 192 | 0.9951 | 1.0177 | |
| O2 | 495 | 433 | 6 | 311 |
Overall, these results show that both the pure DFT and hybrid DFT methods can yield excellent predictions of the 17O NMR chemical shift tensor properties for this relatively simple system. In addition, data here also support the use of refined geometries, consistent with many prior reports which employed partial refinement of hydrogen positions,6, 14 and in some more difficult cases the refinement of other key group (e.g. MNO)7, and the whole crystal structure experimentally8 or computationally.9, 15 Therefore, the partial geometry optimization with only hydrogen positions refined was used in subsequent calculations.
Three more molecules (2-4) were then examined in order to see the excellent accuracy in the calculated 17O NMR chemical shifts for 1 could be extended to a few more organic molecules with either a different XO bonding group (PO in 3) or different intermolecular interactions and substituents around CO groups (2, 4), see Figure 1. The computed 17O NMR properties are shown in Table 4. As seen from Table 5 regarding the associated statistical analysis data for compounds 1-4, the overall accuracy is still excellent since R2 values are all above 0.984. With more data included in the regression analysis, now the computed 17O NMR properties from using B3LYP are of slightly better correlation with experiment than those from using OP86, though the slopes of B3LYP NMR calculations are still of larger deviations from the ideal value. The larger slopes results in slightly increased MAD’s by 2-3 ppm in the case of using OP86/6-31G(d) optimized structures. Regarding the basis set effect, now results from using 6-311++(2d,2p) are of marginally better correlations and better slopes, see Table 5. The use of another geometry optimization method mPWP86/6-311G(d) again results in similar and marginally less accurate data compared to the geometry optimization method OP86/6-31(d), with R2 values decreased by ≤ 0.0018. Here, the best MAD is only 3.1% of the experimental shift range (481 ppm) for compounds 1-4.
Table 4.
Calculated 17O NMR Data for the Partially Optimized Structures of 2-7 (unit: ppm)
| Optimization | Compound | Property | NMR: OP86 6-311++G(d,p) |
6-311++G(2d,2p) | NMR: B3LYP 6-311++G(d,p) |
6-311++G(2d,2p) |
|---|---|---|---|---|---|---|
| OP86/6-31G(d) | 2 | O1 δiso | 187 | 186 | 189 | 188 |
| O2 δiso | 319 | 319 | 336 | 335 | ||
| 3 | O1 δ11 | 166 | 166 | 157 | 156 | |
| O1 δ22 | 9 | 14 | 7 | 16 | ||
| O1 δ33 | −20 | −20 | −22 | −16 | ||
| 4 | O1 δiso | 280 | 279 | 293 | 293 | |
| O2 δiso | 280 | 280 | 294 | 293 | ||
| O3 δiso | 260 | 260 | 271 | 271 | ||
| O4 δiso | 320 | 319 | 337 | 335 | ||
| 5 | O1 δ11 | 734 | 705 | 551 | 545 | |
| O1 δ22 | 222 | 223 | 213 | 214 | ||
| O1 δ33 | 109 | 107 | 114 | 112 | ||
| 6 | O δ11 | 1743 | 1761 | 1735 | 1743 | |
| O δ22 | 632 | 635 | 692 | 695 | ||
| O δ33 | 40 | 40 | 41 | 41 | ||
| 7 | O δiso | 336 | 335 | 374 | 374 | |
| mPWP86/6-311G(d) | 2 | O1 δiso | 187 | 179 | 181 | 189 |
| O2 δiso | 319 | 349 | 372 | 335 | ||
| 3 | O1 δ11 | 166 | 166 | 157 | 156 | |
| O1 δ22 | 9 | 14 | 7 | 16 | ||
| O1 δ33 | −21 | −20 | −22 | −16 | ||
| 4 | O1 δiso | 279 | 279 | 293 | 292 | |
| O2 δiso | 286 | 286 | 300 | 299 | ||
| O3 δiso | 261 | 261 | 272 | 272 | ||
| O4 δiso | 320 | 318 | 336 | 335 | ||
| 5 | O1 δ11 | 734 | 706 | 554 | 548 | |
| O1 δ22 | 220 | 221 | 211 | 211 | ||
| O1 δ33 | 112 | 110 | 117 | 115 | ||
| 6 | O δ11 | 1632 | 1650 | 1634 | 1644 | |
| O δ22 | 614 | 617 | 672 | 676 | ||
| O δ33 | 39 | 37 | 39 | 39 | ||
| 7 | O δiso | 336 | 335 | 374 | 374 |
Table 5.
Statistical Analysis Results for 17O NMR Chemical Shift Tensor Properties
| Compounds | Optimization | NMR | R2 | Slope | MAD |
|---|---|---|---|---|---|
| 1-4 | OP86/6-31G(d) | OP86/6-311++G(d,p) | 0.9857 | 1.0021 | 15 |
| OP86/6-311++G(2d,2p) | 0.9860 | 0.9982 | 15 | ||
| B3LYP/6-311++G(d,p) | 0.9883 | 1.0718 | 18 | ||
| B3LYP/6-311++G(2d,2p) | 0.9885 | 1.0597 | 17 | ||
| mPWP86/6-311G(d) | OP86/6-311++G(d,p) | 0.9848 | 1.0111 | 16 | |
| OP86/6-311++G(2d,2p) | 0.9859 | 1.0171 | 16 | ||
| B3LYP/6-311++G(d,p) | 0.9870 | 1.0954 | 22 | ||
| B3LYP/6-311++G(2d,2p) | 0.9867 | 1.0687 | 18 | ||
| 1-7 | OP86/6-31G(d) | OP86/6-311++G(d,p) | 0.9705 | 1.2011 | 44 |
| OP86/6-311++G(2d,2p) | 0.9745 | 1.2094 | 44 | ||
| B3LYP/6-311++G(d,p) | 0.9924 | 1.1985 | 41 | ||
| B3LYP/6-311++G(2d,2p) | 0.9921 | 1.2012 | 40 | ||
| mPWP86/6-311G(d) | OP86/6-311++G(d,p) | 0.9683 | 1.1340 | 40 | |
| OP86/6-311++G(2d,2p) | 0.9737 | 1.1433 | 39 | ||
| B3LYP/6-311++G(d,p) | 0.9926 | 1.1386 | 38 | ||
| B3LYP/6-311++G(2d,2p) | 0.9926 | 1.1412 | 36 |
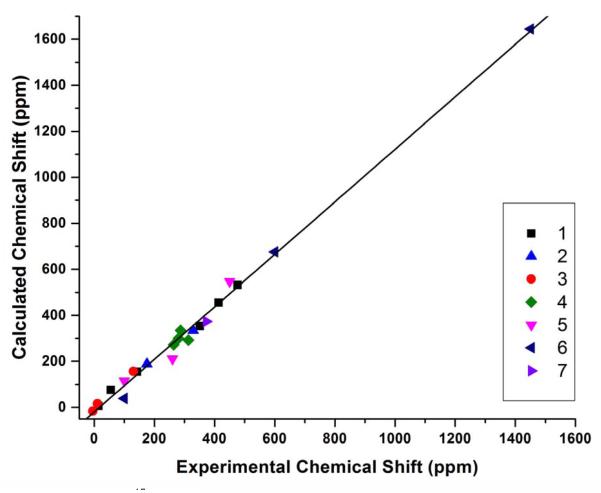
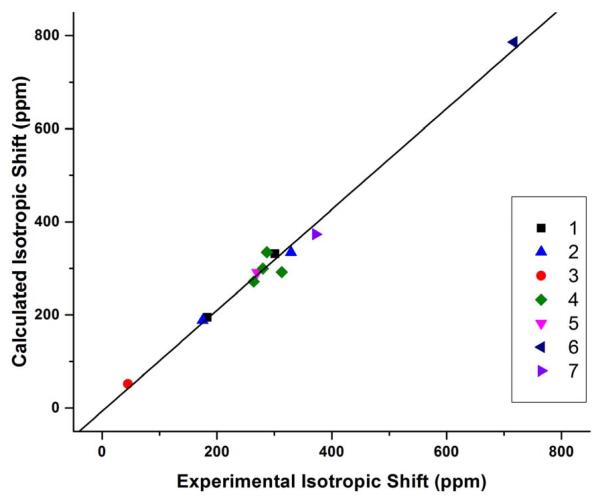
After obtaining accurate results for above organic molecules we then investigated the relatively more challenging NO-containing molecules and metal complexes 5-7.7, 8 For instance, in the case of 6 containing both NO and metal, the initial calculations using the X-ray structure have errors in δiso of 171-192 ppm (24-27%), which is similar to the errors of 202-218 ppm (28-30%) reported in the previous work.8 Therefore, a detailed methodogical study on geometry optimization method and basis sets for both non-metal and metal elements as well as NMR property calculation method and basis sets for both non-metal and metal elements using ~60 different method combinations was performed (see details in Supporting Information). The best calculated isotropic shift has an error dramatically descreased to 45 ppm or 6.3%. As shown in Table 5, after the data of compouds 5-7 are included in the statisitical analysis, the R2’s for NMR calculation method OP86 have been slightly reduced from ~0.98 to ~0.97, and the slopes have clear deterioration (~10-20% worse), indicating that these compounds are more challenging for computational studies. However, the R2’s for NMR calculation method B3LYP are slightly increased to be above 0.992 along with a more moderate deterioration in slopes. These results clearly indicate that 1) the effects of the geometry refinement and the method and basis set choices for metal elements in both geometry optimization and NMR calculations are significant; 2) the hybrid DFT method B3LYP appears to be better than the pure DFT method OP86 in 17O NMR chemical shift tensor property calculations when more challenging compounds are included; 3) the geometry optimization methods OP86/6-31G(d) and mPWP86/6-311G(d) are of similar performance with the latter one having slightly better R2’s, slopes, and MAD’s. Overall, considering R2, slope, and MAD, the best method combination here is to use mPWP86 with QZVP for metals and 6-311G(d) for non-metals in geometry optimization and use B3LYP with LanL2DZ for metals and 6-311++G(2d,2p) for non-metals in NMR calculation. It has an MAD of 36 ppm for all 17O NMR chemical shift tensor properties studied here, which is only 2.5% of the toal experimental range of 1455 ppm. As illustrated in Figure 2, the calculated chemical shift properties not only have an excellent overall correlation with R2 of 0.9926, but also basically evenly distributed around the regress line. In addition, as shown in Table 6 for the statistical results for isotropic 17O NMR chemical shifts in all compounds 1-7, the slope and MAD data are all better than those for the 17O NMR chemical shift tensor property calculations. The best method combination for the isotropic shift calculation is the same as for the tensor property calculations, with R2 of 0.988 and MAD of 23 ppm, or 3.4% of the experimental isotropic shift range of 672 ppm, see Table 1. The theory-versus-experiment correlation can be seen in Figure 3, again having all data points well distributed around the regress line to indicate the overall excellent accuracy. Since its slope still has ca. 8% deviation from the ideal value, we further evaluated the use of regression line information to predict isotropic shifts as follows:
The data are listed in Table 7 for the best method combination here. Because the shifts predicted using the regression line have ideal slope (1.0000) and intercept (0 ppm) compared to experimental data, the MAD was further reduced to be only 13 ppm, which is just 1.9% of the experimental shift range. The MPD of 5.7% is also excellent.
Figure 2.
Calculated 17O NMR chemical shift tensor properties from using the mPWP86/6-311G(d) geometry optimization and B3LYP/6-311++G(2d,2p) NMR calculation vs. experimental data for compounds 1-7.
Table 6.
Statistical Analysis Results for 17O NMR Isotropic Shifts in Compounds 1-7
| Optimization | NMR | R2 | Slope | MAD |
|---|---|---|---|---|
| OP86/6-31G(d) | OP86/6-311++G(d,p) | 0.9590 | 1.0977 | 26 |
| OP86/6-311++G(2d,2p) | 0.9619 | 1.1076 | 26 | |
| B3LYP/6-311++G(d,p) | 0.9855 | 1.1424 | 26 | |
| B3LYP/6-311++G(2d,2p) | 0.9846 | 1.1448 | 26 | |
| mPWP86/6-311G(d) | OP86/6-311++G(d,p) | 0.9616 | 1.0316 | 23 |
| OP86/6-311++G(2d,2p) | 0.9674 | 1.0482 | 23 | |
| B3LYP/6-311++G(d,p) | 0.9880 | 1.0892 | 26 | |
| B3LYP/6-311++G(2d,2p) | 0.9880 | 1.0838 | 23 |
Figure 3.
Calculated 17O NMR isotropic chemical shifts from using the mPWP86/6-311G(d) geometry optimization and B3LYP/6-311++G(2d,2p) NMR calculation vs. experimental data for compounds 1-7.
Table 7.
Predicted 17O NMR Isotropic Shifts from Using the Best Approach
| Compound | Atom | δ pred | |Δδpred| a) | |Δδpred| % |
|---|---|---|---|---|
| 1 | O1 | 186 | 3 | 1.7% |
| O2 | 312 | 11 | 3.7% | |
| 2 | O1 | 180 | 5 | 3.0% |
| O2 | 315 | 14 | 4.3% | |
| 3 | O | 54 | 9 | 20.6% |
| 4 | O1 | 276 | 37 | 11.9% |
| O2 | 283 | 3 | 0.9% | |
| O3 | 257 | 7 | 2.7% | |
| O4 | 315 | 28 | 9.8% | |
| 5 | O1 | 275 | 5 | 1.9% |
| 6 | O | 732 | 15 | 2.0% |
| 7 | O | 351 | 21 | 5.7% |
| Average | 13 | 5.7% |
This is the absolute deviation from experiment.
Conclusions
This work provides the first systematic study of the effects of geometry refinement, method and basis sets for metal and non-metal elements in both geometry optimization and NMR property calculations of some biologically relevant oxygen-containing compounds with a good variety of XO bonding groups, X= H, C, N, P, and M. Results suggest a number of important factors towards relatively general and accurate predictions of 17O NMR chemical shifts.
Geometry optimization is highly recommended, in particular for those containing metal or other special groups (such as NO). The partial geometry optimization involving just hydrogen atoms is essential as they are basically uncertain in conventional X-ray structures, and in more difficult cases, partial geometry optimization of local groups or full crystal structure refinements may be needed to help achieve reasonable accuracy as reported previously.7-9, 15 The pure DFT methods used here are good for geometry optimization, with mPWP86/6-311(d) being slightly better. For future work on other systems particularly containing other metal centers, the major attention is suggested to be on metal basis selection during the geometry optimization, as this was found out to be most influential on accuracy (e.g. up to ~350 ppm or ~50% error in δiso of 6).
Regarding 17O NMR chemical shift tensor property calculations, both the hybrid DFT method B3LYP and the pure DFT method OP86 were found to be good for organic molecules, but when more challenging metal- and NO-containing compounds are included, B3LYP is better. The basis set of 6-311++G(d,p) in this step is sufficient to produce excellent results, with a larger basis set of 6-311++G(2d,2p) having slightly better performance.
Overall, the best method combination based on above systematic investigation of a number of different types of biologically relevant oxygen-containing chemical systems is to use mPWP86 with the QZVP basis for metals and 6-311G(d) basis for non-metals in geometry optimization and use B3LYP with LanL2DZ for metals and 6-311++G(2d,2p) for non-metals in NMR calculation. It has an excellent R2 of 0.9926, with an MAD of 36 ppm for all 17O NMR chemical shift tensor properties studied here, being only 2.5% of the toal experimental range of 1455 ppm. The predictions of the isotropic NMR shifts are also excellent, with R2 of 0.988 and MAD of only 13 ppm, which is just 1.9% of the experimental shift range. These results shall facilitate future computational studies of 17O NMR chemical shifts in various biologically relevant systems, and the high accuracy may also help structure refinement and determination of some substrate bound proteins as done previously.26, 27
Supplementary Material
Acknowledgement
This work was supported by an NIH grant GM085774 to YZ.
Footnotes
Supporting Information Available
The methodological studies of ~60 method combinations for the 17O NMR chemical shift tensor properties of compound 6 are available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Wu G. Solid-state 17O NMR Studies of Organic and Biological Molecules. Prog. Nucl. Magn. Res. Spectr. 2008;52:118–169. doi: 10.1016/j.pnmrs.2019.06.002. [DOI] [PubMed] [Google Scholar]
- (2).Lemaitre V, Smith ME, Watts A. A Review of Oxygen-17 Solid-State NMR of Organic Materials--Towards Biological Applications. Solid State Nucl. Magn. Reson. 2004;26:215–235. doi: 10.1016/j.ssnmr.2004.04.004. [DOI] [PubMed] [Google Scholar]
- (3).Gerothanassis IP. Oxygen-17 NMR Spectroscopy: Basic Principles and Applications (Part II) Prog. Nucl. Magn. Reson. Spectr. 2010;57:1–110. doi: 10.1016/j.pnmrs.2009.12.001. [DOI] [PubMed] [Google Scholar]
- (4).Gerothanassis IP. Oxygen-17 NMR Spectroscopy: Basic Principles and Applications (Part I) Prog. Nucl. Magn. Reson. Spectr. 2010;56:95–197. doi: 10.1016/j.pnmrs.2009.09.002. [DOI] [PubMed] [Google Scholar]
- (5).Yamada K, Dong S, Wu G. Solid-state O-17 NMR Investigation of the Carbonyl Oxygen Electric-Field-Gradient Tensor and Chemical Shielding Tensor in Amides. J. Am. Chem. Soc. 2000;122:11602–11609. [Google Scholar]
- (6).Dong S, Ida R, Wu G. A Combined Experimental and Theoretical 17O NMR Study of Crystalline Urea: An Example of Large Hydrogen-bonding Effects. J. Phys. Chem. A. 2000;104:11194–11202. [Google Scholar]
- (7).Godbout N, Sanders LK, Salzmann R, Havlin RH, Wojdelski M, Oldfield E. Solid-state NMR, Mossbauer, Crystallographic, and Density Functional Theory Investigation of Fe-O-2 and Fe-O-2 Analogue Metalloporphyrins and Metalloproteins. J. Am. Chem. Soc. 1999;121:3829–3844. [Google Scholar]
- (8).Wu G, Zhu J, Mo X, Wang R, Terskikh V. Solid-state (17)O NMR and Computational Studies of C-nitrosoarene Compounds. J. Am. Chem. Soc. 2010;132:5143–5155. doi: 10.1021/ja909656w. [DOI] [PubMed] [Google Scholar]
- (9).Gervais C, Profeta M, Lafond V, Bonhomme C, Azais T, Mutin H, Pickard CJ, Mauri F, Babonneau F. Combined Ab initio Ccomputational and Experimental Multinuclear Solid-state Magnetic Resonance Study of Phenylphosphonic Acid. Magn. Reson. Chem. 2004, 42, 445–452. doi: 10.1002/mrc.1360. [DOI] [PubMed] [Google Scholar]
- (10).Pike KJ, Lwmaitre V, Kukol A, Anupold T, Samson A, Howes AP, Watts A, Smith ME, Dupree R. Solid-State 17O NMR of Amino Acids. J. Phys. Chem. B. 2004;108:9256–9263. [Google Scholar]
- (11).Gervais C, Dupree R, Pike KJ, Bonhomme C, Profeta M, Pickard CJ, Mauri F. Combined First-Principles Computational and Experimental Multinuclear Solid-State NMR Investigation of Amino Acids. J. Phys. Chem. A. 2005;109:6960–6969. doi: 10.1021/jp0513925. [DOI] [PubMed] [Google Scholar]
- (12).Yamada K, Honda H, Yamazaki T, Yoshida M. Solid-state 17O NMR Study of the Electric-Field-Gradient and Chemical Shielding Tensors in Polycrystalline Gamma-Glycine. Solid State Nucl. Magn. Reson. 2006;30:162–170. doi: 10.1016/j.ssnmr.2006.09.001. [DOI] [PubMed] [Google Scholar]
- (13).Yamada K, Nemoto T, Asanuma M, Honda H, Yamazaki T, Hirota H. Both Experimental and Theoretical Investigations of Solid-state 17O NMR for L-valine and L-isoleucine. Solid State Nucl. Magn. Reson. 2006;30:182–191. doi: 10.1016/j.ssnmr.2006.09.003. [DOI] [PubMed] [Google Scholar]
- (14).Wu G, Dong S, Ida R, Reen N. A Solid-State O-17 Nuclear Magnetic Resonance Study of Nucleic Acid Bases. J. Am. Chem. Soc. 2002;124:1768–1777. doi: 10.1021/ja011625f. [DOI] [PubMed] [Google Scholar]
- (15).Kong X, Shan M, Terskikh V, Hung I, Gan Z, Wu G. Solid-State 17O NMR of Pharmaceutical Compounds: Salicylic Acid and Aspirin. J. Phys. Chem. B. 2013;117:9643–9654. doi: 10.1021/jp405233f. [DOI] [PubMed] [Google Scholar]
- (16).Zhu JF, Ye E, Terskikh V, Wu G. Solid-state 17O NMR Spectroscopy of Large Protein-Ligand Complexes. Angew. Chem.-Int. Edit. 2010;49:8399–8402. doi: 10.1002/anie.201002041. [DOI] [PubMed] [Google Scholar]
- (17).Kong X, Terskikh V, Khade RL, Yang L, Rorick A, Zhang Y, He P, Huang Y, Wu G. Solid-State 17O NMR Spectroscopy of Paramagnetic Coordination Compounds. Angew. Chem.-Int. Ed. 2015;54:4753–4757. doi: 10.1002/anie.201409888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Ida R, De Clerk M, Wu G. Influence of N-H…O and C-H…O Hydrogen Bonds on the 17O NMR Tensors in Crystalline Uracil: Computational Study. J. Phys. Chem. A. 2006;110:1065–1071. doi: 10.1021/jp0554947. [DOI] [PubMed] [Google Scholar]
- (19).Amini SK, Shaghaghi H, Bain AD, Chabok A, Tafazzoli M. Magnetic Resonance Tensors In Uracil: Calculation of 13C, 15N, 17O NMR Chemical Shifts, 17O and 14N Electric Field Gradients and Measurement of 13C and 15N Chemical Shifts. Solid State Nucl. Magn. Reson. 2010;37:13–20. doi: 10.1016/j.ssnmr.2009.12.001. [DOI] [PubMed] [Google Scholar]
- (20).Kwan IC, Mo X, Wu G. Probing Hydrogen Bonding and Ion-Carbonyl Interactions by Solid-state 17O NMR Spectroscopy: G-ribbon and G-quartet. J. Am. Chem. Soc. 2007;129:2398–407. doi: 10.1021/ja067991m. [DOI] [PubMed] [Google Scholar]
- (21).Wong A, Pike KJ, Jenkins R, Clarkson GJ, Anupold T, Howes AP, Crout DH, Samoson A, Dupree R, Smith ME. Experimental and Theoretical 17O NMR Study of the Influence of Hydrogen-bonding on C=O and O-H Oxygens in Carboxylic Solids. J. Phys. Chem. A. 2006;110:1824–1835. doi: 10.1021/jp055807y. [DOI] [PubMed] [Google Scholar]
- (22).Wu G, Yamada K. Determination of the 17O NMR Tensors in Potassium Hydrogen Dibenzoate: A Salt Containing a Short O…H…O Hydrogen Bond. Solid State Nucl. Magn. Reson. 2003;24:196–208. doi: 10.1016/s0926-2040(03)00046-8. [DOI] [PubMed] [Google Scholar]
- (23).Zhang Q, Chekmenev EY, Wittebort RJ. 17O Quadrupole Coupling and Chemical Shielding Tensors in an H-Bonded Carboxyl Group: Alpha-Oxalic Acid. J. Am. Chem. Soc. 2003;125:9140–9146. doi: 10.1021/ja034495e. [DOI] [PubMed] [Google Scholar]
- (24).Chekmenev EY, Waddell KW, Hu J, Gan Z, Wittebort RJ, Cross TA. Ion-Binding Study by 17O Solid-State NMR Spectroscopy in the Model Peptide Gly-Gly-Gly at 19.6 T. J. Am. Chem. Soc. 2006;128:9849–9855. doi: 10.1021/ja060191r. [DOI] [PubMed] [Google Scholar]
- (25).Salzmann R, Ziegler CJ, Godbout N, McMahon MT, Suslick KS, Oldfield E. Carbonyl Complexes of Iron(II), Ruthenium(II), and Osmium(II) 5,10,15,20-Tetraphenylporphyrinates: A Comparative Investigation by X-Ray Crystallography, Solid-State NMR Spectroscopy, and Density Functional Theory. J. Am. Chem. Soc. 1998;120:11323–11334. [Google Scholar]
- (26).Mao JH, Mukherjee S, Zhang Y, Cao R, Sanders JM, Song YC, Zhang YH, Meints GA, Gao YG, Mukkamala D, Hudock MP, Oldfield E. Solid-State NMR, Crystallographic, and Computational Investigation of Bisphosphonates and Farnesyl Diphosphate Synthase-Bisphosphonate Complexes. J. Am. Chem. Soc. 2006;128:14485–14497. doi: 10.1021/ja061737c. [DOI] [PubMed] [Google Scholar]
- (27).Yang L, Ling Y, Zhang Y. HNO Binding in a Heme Protein: Structures, Spectroscopic Properties, and Stabilities. J. Am. Chem. Soc. 2011;133:13814–13817. doi: 10.1021/ja204072j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Bryce DL, Eichele K, Wasylishen RE. An 17O NMR and Quantum Chemical Study of Monoclinic and Orthorhombic Polymorphs of Triphenylphosphine Oxide. Inorg. Chem. 2003;42:5085–96. doi: 10.1021/ic020706p. [DOI] [PubMed] [Google Scholar]
- (29).Drangfelt O, Romming C. Crystal Structure of N,N-Dimethyl-p-nitrosoaniline Hydrochloride Hydrate. Acta Chem. Scand. 1974;28:1101–1105. [Google Scholar]
- (30).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, et al. Gaussian, Inc.; Wallingford CT: 2010. Gaussian 09, Revision B.01. [Google Scholar]
- (31).Hoe W-M, Cohen A, Handy NC. Assessment of a New Local Exchange Functional OPTX. Chem. Phys. Lett. 2001;341:319–328. [Google Scholar]
- (32).Perdew JP. Density-functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- (33).Becke AD. Density-Functional Thermochemistry .3. the Role of Exact Exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- (34).Dunning TH., Jr . In: In Modern Theoretical Chemistry. Schaefer HF III, editor. Vol. 3. Plenum; New York: 1977. pp. 1–28. [Google Scholar]
- (35).Davidson ER. Comment on ‘Comment on Dunning's correlation-consistent basis sets’. Chem. Phys. Lett. 1996;260:541–518. [Google Scholar]
- (36).Hay PJ, Wadt WR. Ab initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Scandium to Mercury. J. Chem. Phys. 1985;82:270–283. [Google Scholar]
- (37).Teale AM, Lutnas OB, Helgaker T, Tozer DJ, Gauss J. Benchmarking Density-functional Theory Calculations of NMR Shielding Constants and Spin–Rotation Constants Using Accurate Coupled-Cluster Calculations. J. Chem. Phys. 2013;138:024111. doi: 10.1063/1.4773016. [DOI] [PubMed] [Google Scholar]
- (38).Wasylishen RE, Bryce DL. A Revised Experimental Absolute Magnetic Shielding Scale for Oxygen. J. Chem. Phys. 2002;117:10061–10066. [Google Scholar]
- (39).Puzzarini C, Cazzoli G, Harding ME, Vázquez J, Gauss J. A New Experimental Absolute Nuclear Magnetic Shielding Scale for Oxygen Based on the Rotational Hyperfine Structure of H2O17. J. Chem. Phys. 2009;131:234304. doi: 10.1063/1.3274062. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.