Technical Note: Characterization and correction of gradient nonlinearity induced distortion on a 1.0 T open bore MR-SIM

Abstract

Purpose:

Distortions in magnetic resonance imaging (MRI) compromise spatial fidelity, potentially impacting delineation and dose calculation. We characterized 2D and 3D large field of view (FOV), sequence-independent distortion at various positions in a 1.0 T high-field open MR simulator (MR-SIM) to implement correction maps for MRI treatment planning.

Methods:

A 36 × 43 × 2 cm³ phantom with 255 known landmarks (∼1 mm³) was scanned using 1.0 T high-field open MR-SIM at isocenter in the transverse, sagittal, and coronal axes, and a 465 × 350 × 168 mm³ 3D phantom was scanned by stepping in the superior-inferior direction in three overlapping positions to achieve a total 465 × 350 × 400 mm³ sampled FOV yielding >13 800 landmarks (3D Gradient-Echo, TE/TR/α = 5.54 ms/30 ms/28°, voxel size = 1 × 1 × 2 mm³). A binary template (reference) was generated from a phantom schematic. An automated program converted MR images to binary via masking, thresholding, and testing for connectivity to identify landmarks. Distortion maps were generated by centroid mapping. Images were corrected via warping with inverse distortion maps, and temporal stability was assessed.

Results:

Over the sampled FOV, non-negligible residual gradient distortions existed as close as 9.5 cm from isocenter, with a maximum distortion of 7.4 mm as close as 23 cm from isocenter. Over six months, average gradient distortions were −0.07 ± 1.10 mm and 0.10 ± 1.10 mm in the x and y directions for the transverse plane, 0.03 ± 0.64 and −0.09 ± 0.70 mm in the sagittal plane, and 0.4 ± 1.16 and 0.04 ± 0.40 mm in the coronal plane. After implementing 3D correction maps, distortions were reduced to <1 pixel width (1 mm) for all voxels up to 25 cm from magnet isocenter.

Conclusions:

Inherent distortion due to gradient nonlinearity was found to be non-negligible even with vendor corrections applied, and further corrections are required to obtain 1 mm accuracy for large FOVs. Statistical analysis of temporal stability shows that sequence independent distortion maps are consistent within six months of characterization.

1. INTRODUCTION

Due to its superior soft tissue contrast, using magnetic resonance imaging (MRI) can result in more accurate structure delineation than computed tomography (CT).^1,2 Typically, MRI is used to define the target and organs at risk (OARs) and contours are transferred to the CT via image registration, which is then used for treatment planning and dose calculations. However, this workflow increases the clinical workload, while co-registration of MR and CT images may introduce additional systematic uncertainties that can be detrimental to target and OAR localization.^3–5 Therefore, implementing MR as a stand-alone simulation modality for radiation therapy treatment planning (RTP) is advantageous.

Implementation of MRI for single modality simulation is limited by the lack of electron density information for dose calculation, as well as both patient-induced and system-level distortions that significantly degrade treatment planning accuracy.^6,7 To support MR-only simulation, we⁸ and others^9–12 have demonstrated the feasibility of generating synthetic CTs or implementing bulk density overrides for dose calculation and DRR generation. Patient-induced distortions from susceptibility and chemical shift have shown a dependence on field strength and can be considered clinically negligible for low field systems,^13,14 such as our 1.0 T MR simulator (MR-SIM). System-level distortions arise from the inhomogeneities in the B₀ field and nonlinearities in the spatial encoding gradients. We have previously reported on our magnet’s B₀ field inhomogeneity and found that it was within American College of Radiology guidelines.¹⁵ This technical note focuses on the technical characterization of gradient nonlinearity (GNL) for large fields of view (FOVs), develops and evaluates a correction scheme, and then quantifies the temporal stability of the measurements for a clinically available MR-SIM system. GNL is the focus of this work, because it is one of the dominant sources of image distortion^16,17 and is insensitive to the acquisition sequence.¹⁸ In this manner, clinical recommendations regarding the frequency of measurement and robustness of results for ongoing quality assurance (QA) can be ascertained to support MR-simulation for single modality RTP.

2. METHODS AND MATERIALS

2.A. Large field of view distortion phantoms

For routine temporal GNL measurements, a 36 × 43 × 2 cm³ distortion phantom (Philips Medical Systems, Cleveland, OH) consisting of 255 capsule-shaped landmarks with ∼4 mm radius and 25 mm centroid-to-centroid spacing was used. The phantom can be oriented in cardinal directions (axial, sagittal, and coronal), allowing a 2D distortion map to be obtained in all three planes as shown in Fig. 1 (top row). For 3D distortion characterization, a 465 × 350 × 168 mm³ phantom with over 4600 control points and 1.6 mm centroid-to-centroid spacing was used.

FIG. 1.

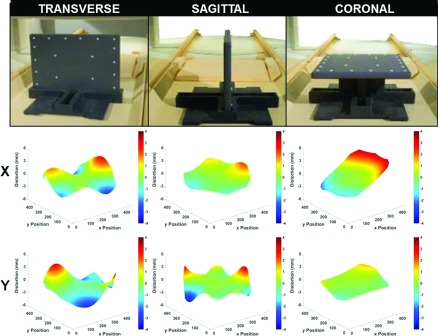
(Top row) Setup of 2D distortion phantom. (Middle row) Corresponding x-axis distortion map (mm) vs image pixel location. (Bottom row) Corresponding y-axis distortion map (mm) vs image pixel location.

2.B. Image acquisition

MR images were acquired with a 1.0 Tesla (T) MR-SIM (Panorama High-Field Open Magnetic Resonance System, Philips Medical Systems, Cleveland, OH) using the integrated quadrature coil. The MR-SIM consists of a vertical magnetic field design with 45 cm anterior–posterior clearance of the physical aperture. To measure distortions resulting from GNL, the phantom was scanned with a 3D T1-weighted gradient echo (GE) sequence: TE/TR/flip angle of 5.54 ms/30 ms/28°, FOV 450  ×  450  ×  26 mm³, bandwidth 191 Hz/pixel, acquisition voxel dimensions 1  ×  1  ×  2 mm³, number of signal averages  =  1, and acquisition duration of 5.6 min. Two scans were obtained in each of the three phantom orientations (the first with a positive read gradient polarity 4.48 mT/m and the second with a negative read gradient polarity −4.48 mT/m) so that the reverse gradient technique^14,16,19 could be used to isolate distortions due to GNL in all axes. During standard 3D GE imaging protocols, object dependent and B₀ distortions are only present in the frequency-encoding direction, while gradient distortions are present in all three directions. It is important to note that GNL is a property of the magnet and thus, independent of acquisition sequence. In this manner, the use of a 3D sequence with only one frequency encoding direction was necessary to isolate sequence-dependent distortions to a single axis. While a 3D spin echo (3DSE) sequence could have been used, a 3DSE acquisition would have substantially longer scan times than 3DGE and thus impede clinical efficiency. In addition, our selection of 3DGE is also consistent with the literature.^6,14,16 In the reverse gradient method, the same scan is repeated using opposite read gradient polarities. B₀ distortions will have opposite polarity when the polarity of the read gradient is reversed, while gradient distortions will remain constant. Therefore, the distortion due to GNL can be isolated by taking the average distortion of the two scans. A more detailed discussion of this method can be found in Baldwin et al.¹⁶ Our scanner is equipped with vendor-supplied corrections to correct for gradient-related distortions that are derived from a spherical harmonic model. All scans were acquired with vendor-supplied 3D corrections enabled, which is consistent with our clinical practice.

For the 3D analysis, in order to sample the distortion in a larger superior-inferior (SI) direction, a batch file script was devised that communicated with the scanner to translate the 3D phantom in its axial orientation yielding a total scan extent of 465 × 350 × 400 mm³ (>13 800 landmarks). Two scans with reverse read gradient polarities were taken at each of the three locations within the bore so that the reverse gradient technique could be applied throughout the entire imaging volume.

It has been shown that eddy currents generated by rapidly pulsed gradients may potentially influence image distortion.²⁰ To verify that eddy currents do not adversely impact our distortion characterization, the phantom was scanned as above at four different TE settings (5.5, 13.8, 20.7, and 34.5 ms with TR = 50.9 ms) in three cardinal axes. TEs spanned a range similar to what has been reported in the literature¹⁶ but modified ad hoc to yield acceptable image quality and resolve scanner conflicts. Using 5.5 ms as the baseline value, the mean shift in distortion measurements over all landmarks for each phantom orientation was calculated and plotted as a function of TE to identify possible trends.

2.C. Image analysis

To establish the position of each phantom control point (defined as the centroid), an automated program was developed in-house using matlab^® (Mathworks, Natick, MA). First, images were generated by taking the maximum intensity projection of each of all 13 slices for each scan, which is consistent with our clinical protocol.¹⁵ Control point detection was then conducted on each image with a combination of masking and thresholding, while a connectivity algorithm was used to further separate control points from increased noise at the field boundaries. The x and y positions (horizontal and vertical axes, respectively) were determined by finding the centroid of each control point and were compared to a binary template generated from the factory schematic of the phantom. Similar analysis was performed for the 3D phantom for all three axes. The total distortion of each control point was taken as the difference of the measured centroid positions from the known positions in the template. Once the distortions at each control point were determined, a full distortion map was interpolated by using singular value decomposition (SVD) to fit the data to a sixth-degree polynomial, which is similar to what has been reported in the literature.^21,22 Distortion maps were plotted and compared for each axis (week 1 shown in Fig. 1) and over the entire sampled FOV using the 3D phantom. Figure 3 illustrates a subset of distortion measurements plotted as a function of distance from isocenter.

FIG. 3.

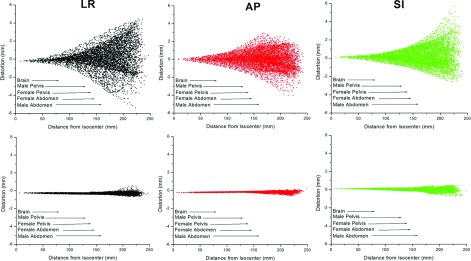
(Top row) Distortion measurements (mm) as a function of distance from magnet isocenter (mm) for one scan. (Bottom row) Residual distortion after postprocessing corrections (mm) as a function of distance (mm). Arrows show the average radius of relevant anatomy of interest taken from the literature (Refs. 26–29 and 31).

2.D. Distortion correction

To correct for the distortion, the derived distortion map was used as a template to warp the distorted image and create a corrected image. However, since there is not necessarily a one-to-one correspondence between pixels in the distorted image and pixels in the corrected image, our algorithm steps through each pixel of the corrected image and determines the pixel’s intensity from the distorted pixels that map to it (inverse warping). This ensures that no pixels in the corrected image are missed, and thus avoids “holes” in the corrected image. Because image distortion may cause compression and expansion of image volumes resulting in intensity changes that may not be fully resolved by pixel mapping, the corrected image was also multiplied by a Jacobian scaling factor as described in Doran et al.⁶

2.E. Temporal stability of distortion corrections

Temporal stability of large FOV distortion corrections and recommended measurement frequency are not currently known. Mah et al. measured distortion at four locations and showed temporal variations of less than 3 pixels over 18 months, although this was not characterized for large FOVs.²³ To characterize the stability of GNL distortion measurements, weekly scans of the 2D distortion phantom in all three axes were acquired over the course of six months (20 time points) using the reverse gradient technique. Differences from baseline (i.e., week 1) were assessed by generating difference maps and evaluating daily statistics.

3. RESULTS AND DISCUSSION

3.A. Distortion characterization at isocenter

Eddy currents were found to be appropriately compensated for with image distortion varying <0.2 mm over all TE settings (less than half of the pixel width and can be considered negligible). These results are in agreement with Baldwin et al. (<0.3 mm for a 3.0 T cylindrical magnet).¹⁶ In 2000, Tanner et al. measured distortions of up to 1.3 mm with varying TE for their 1.5 T cylindrical bore magnet.²⁰ However, this early generation magnet had unshielded gradients; modern hardware and shielded gradients more readily compensate for eddy currents.

Figure 1 shows the maps of residual distortion resulting from GNL for the three cardinal planes at magnet isocenter, and Table I shows the corresponding distortion statistics across the entire 36 × 43 cm phantom. Although negligible near isocenter (less than the 1 mm pixel width), these distortions become greater than 1 mm as close as 9.5 cm from isocenter in the transverse plane, 12.5 cm in the sagittal plane, and 11.7 cm in the coronal plane. The largest distortion magnitudes occurred near the periphery of the usable FOV (∼4 mm distortion at 20 cm from isocenter), where the usable FOV is defined by the furthest extent at which control points can be identified. These distortions are similar in magnitude to those measured without vendor corrections enabled for a 3 T magnet with cylindrical geometry by Baldwin et al.¹⁶ GNL distortions for our vertical magnet were more pronounced in the left–right direction, particularly in the coronal plane as shown in the middle-right panel of Fig. 1. In the vertical magnet orientation, the maximum magnetic field gradient occurs in the right to left direction, which may contribute to the larger GNL distortion in this axis. It is also important to note that our measurements were non-negligible when 3D vendor distortion corrections were enabled, indicating that additional corrections are necessary for our magnet configuration.

TABLE I.

Week 1 gradient nonlinearity distortion statistics for three cardinal planes through isocenter where x and y refer to the horizontal and vertical axes of the respective planes. P5 and P95 describe the 5th and 95th percentiles of the distortion distribution, respectively.

Plane	Mean (mm)	StDev (mm)	P5 (mm)	P95 (mm)	Distortion > 1 mm (total % pixels)	Distortion > 2 mm (total % pixels)
Transverse (x)	0.07	1.10	−1.83	1.92	35	7
Transverse (y)	0.10	1.10	−1.5	2.15
Sagittal (x)	0.03	0.64	−0.93	1.15	14	3
Sagittal (y)	−0.09	0.70	−1.23	1.11
Coronal (x)	0.40	1.16	−1.32	2.50	40	14
Coronal (y)	0.04	0.40	−0.52	0.77

Over six months, the coronal plane had the widest interquartile range, with 50% of the usable FOV having distortions between −0.5 and 1.25 mm, while the sagittal plane had the smallest, with 50% of the usable field of view having distortion between −0.25 and 0.25 mm. The transverse plane consistently has the largest distortions with maximum distortions of 4 mm, and a P95 of 2 mm. For any given daily distortion measurement over the six months, difference maps show 95% of voxels varied <0.6 mm from the baseline measurement (week 1) for all planes. This suggests that for routine QA, a higher frequency of GNL measurement is not necessary and these results support recent recommendations of annual measurement.²⁴

3.B. 3D distortion characterization

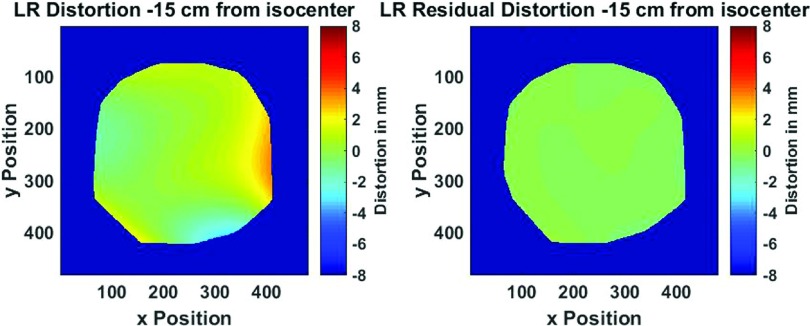
As expected, distortion from GNL is much more pronounced in the peripheral voxels. Over the entire sampled volume, 65% of all voxels had non-negligible distortions (>1 mm), 26% of voxels distorted >2 mm, 9% > 3 mm, and 3% > 4 mm, with the largest distortion observed of ∼7.4 mm at 23 cm radial distance from magnet isocenter. Figure 2 (Multimedia view) illustrates the 3D distortion results over the entire phantom volume before and after postprocessing corrections were applied. In the postcorrection dataset, nearly all measured distortions were reduced to less than 1 pixel width, with the exception of distant field corners up to a radial distance of 25 cm from magnet isocenter. This suggests that with appropriate postprocessing corrections, GNL distortions can be reduced to negligible levels despite substantial initial GNL distortion for large FOVs. Similar results were reported by Doran et al.⁶ and Baldwin et al.¹⁶ with a possible cause of the remaining distortion being divergence of the polynomial fit at the boundaries.

FIG. 2.

Left–right (LR) distortion maps for the 3D phantom in the transverse plane. (Left) Quantified gradient nonlinearity distortion for the 3D phantom at 15 cm inferior of isocenter. (Right) Residual distortion after postprocessing corrections were applied. Results for the entire volume can be observed in Multimedia view. [URL: http://dx.doi.org/10.1118/1.4930245.1]MPHYA6-000042-005955_1-S1.gif ^{(2.9MB, gif)} DOI: 10.1118/1.4930245.1

Figure 3 shows the 3D stepped distortion map data plotted as a function of radial distance from magnet isocenter with the radii of typical anatomical structures also shown.^25–29 Initial vendor-supplied 3D distortion corrections maintained <1 mm distortion up to ∼9.5 cm from isocenter although GNL became non-negligible as distance from isocenter increased. This suggests that to support MR-only RTP, additional corrections are necessary for anatomy >10 cm from isocenter for this magnet configuration. However, in another study by Wang et al., it was suggested that shorter gradient coils could result in significantly higher GNL distortion.¹⁷ This suggests that the GNL distortion measured for vertical magnet designs could be significantly worse than for the more commonly used cylindrical bore configuration.

Another solution to address GNL includes using a “step and shoot” technique where multiple couch longitudinal positions are used to segment large FOVs to facilitate imaging more of the anatomy of interest near isocenter.²⁴ Our open geometry allows for lateral table translation, thus lateral lesions such as breast cancer or sarcomas may be positioned at isocenter to further reduce the impact of GNL.

One limitation of this study is that it focused on GNL and did not address other sources of distortion such as those arising from field inhomogeneity, chemical shift, and magnetic susceptibility differences. Nevertheless, using higher readout bandwidths^14,24,30 and thoughtful sequence selection³¹ have been shown to minimize these effects. A double echo gradient echo phase mapping method^14,32 can be used to measure and calculate sequence-dependent distortion maps which can then be used for corrections. Future work will include characterization of patient-dependent distortions for our magnet, including susceptibility, for relevant regions of interest.

4. CONCLUSION

Inherent distortions due to GNL were non-negligible for large FOVs with 3D vendor corrections enabled, thus necessitating a correction scheme to support MRI only treatment planning for anatomies >10 cm from isocenter. However, with postprocessing corrections, GNL was reduced to <1 mm for large FOVs. GNL measurements were stable over six months of clinical operation, thus supporting the application of correction maps in MR-only RTP.