The Distribution of Fitness Costs of Resistance-Conferring Mutations Is a Key Determinant for the Future Burden of Drug-Resistant Tuberculosis: A Model-Based Analysis

Abstract

Background. Drug resistance poses a serious challenge for the control of tuberculosis in many settings. It is well established that the expected future trend in resistance depends on the reproductive fitness of drug-resistant Mycobacterium tuberculosis. However, the variability in fitness between strains with different resistance-conferring mutations has been largely ignored when making these predictions.

Methods. We developed a novel approach for incorporating the variable fitness costs of drug resistance-conferring mutations and for tracking this distribution of fitness costs over time within a transmission model. We used this approach to describe the effects of realistic fitness cost distributions on the future prevalence of drug-resistant tuberculosis.

Results. The shape of the distribution of fitness costs was a strong predictor of the long-term prevalence of resistance. While, as expected, lower average fitness costs of drug resistance–conferring mutations were associated with more severe epidemics of drug-resistant tuberculosis, fitness distributions with greater variance also led to higher levels of drug resistance. For example, compared to simulations in which the fitness cost of resistance was fixed, introducing a realistic amount of variance resulted in a 40% increase in prevalence of drug-resistant tuberculosis after 20 years.

Conclusions. The differences in the fitness costs associated with drug resistance–conferring mutations are a key determinant of the future burden of drug-resistant tuberculosis. Future studies that can better establish the range of fitness costs associated with drug resistance–conferring mutations will improve projections and thus facilitate better public health planning efforts.

Drug-resistant forms of tuberculosis are a persistent threat to effective control of tuberculosis in many settings and, by any method of accounting, exact a substantial global health and economic toll [1, 2]. Currently, data to evaluate trends in the burden of drug-resistant tuberculosis are limited: in most countries, sufficiently robust surveillance is not available to evaluate whether the incidence of drug-resistant tuberculosis is increasing or decreasing. This lack of trend information makes it difficult to assess whether the epidemiology of drug-resistant tuberculosis is changing over time, to determine whether interventions have been effective at controlling drug-resistant tuberculosis, and to make appropriate plans for future resource needs.

In the absence of robust data on trends, mathematical models have served as a tool to help guide our thinking about how drug-resistant tuberculosis epidemics may progress over time and which factors may influence these trends [3–6]. One of the most important determinants of drug-resistant tuberculosis projections is the reproductive number of drug-resistant forms of tuberculosis, defined as the expected number of secondary cases of drug-resistant tuberculosis that are attributable to a single patient infectious with drug-resistant tuberculosis. When the reproductive number exceeds the critical threshold of 1, each existing case of drug-resistant tuberculosis will cause, on average, at least another case of drug-resistant tuberculosis through transmission, and the drug-resistant tuberculosis epidemic will not be contained. The reproductive number depends on pathogen biological factors, factors impacting the duration of the infectious period, and the degree of vulnerability of the population in which the pathogen is being spread [7].

Drug resistance arises initially in the bacterium that causes tuberculosis disease, Mycobacterium tuberculosis, via chromosomal mutations [8]; these rare sporadic mutants may be selected by suboptimal treatment leading to acquired resistance. After drug resistance emerges among individuals receiving ineffective treatment, these forms of resistant M. tuberculosis may be transmitted directly to others, leading to primary (or transmitted) resistance.

Multiple studies have shown that different mutations can confer similar resistance phenotypes, but may be associated with very different effects on the reproductive capacity (“fitness”) of strains [9–12]. For example, resistance to rifampicin can be encoded by several different mutations in the rpoB gene [13], each of which has a different effect on in vitro growth rates [9–11]. These experimental measures of fitness often correlate well with the apparent reproductive fitness in clinical populations; in several settings, those mutations that are least costly are those that are preferentially transmitted [9, 11, 14, 15]. Worryingly, recent genomic studies have found that in several settings there is already a dominance of multidrug-resistant (MDR) tuberculosis strains with these lowest-cost mutations [16–18], as well as strains with compensatory mutations that can partially ameliorate the initial fitness cost to resistance [19].

Determining the speed with which these different drug-resistant tuberculosis strains arise and spread is vital for understanding the epidemic potential of drug-resistant tuberculosis. Several previous mathematical models have investigated drug-resistant tuberculosis spread [3, 5, 20, 21]; however, most models assume a single reproductive fitness level for drug-resistant tuberculosis strains. This assumption does not allow for the possibility that some strains of drug-resistant tuberculosis will have less costly mutations and may be preferentially transmitted, leading to changes in the mean and distribution of fitness costs within the population of resistant strains over time. A few models have allowed for a small number of fitness levels of drug-resistant tuberculosis strains [22, 23], but consideration of realistic distributions of fitness costs associated with drug resistance–conferring mutations has not been incorporated into a simple modeling framework.

Here we use experimental data to parameterize the distribution of fitness costs at resistance acquisition, and introduce a novel method for dynamically tracking changes in fitness within a population with drug-resistant tuberculosis. Using this new model, we illustrate how heterogeneity in the fitness costs of mutation impacts the expected future burden of drug-resistant tuberculosis.

METHODS

We expanded a standard model for tuberculosis transmission to include a function that tracks the distribution of reproductive fitness costs of drug-resistant forms of M. tuberculosis over time. We considered the effect of realistic distributions of fitness costs on the projected burden of resistance to a new drug over a 20-year time horizon.

Tuberculosis Transmission Model

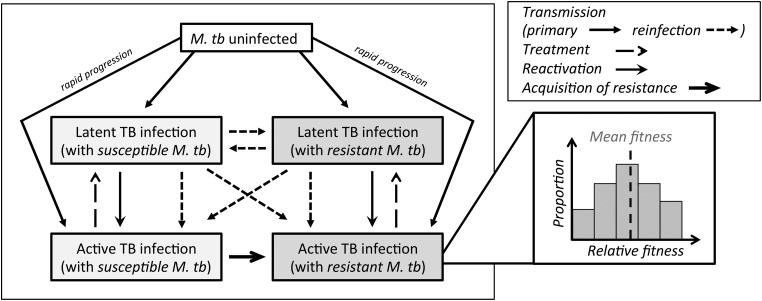
We modified a previously published model [20], which is structured similarly to other tuberculosis models [4, 24]. The model includes 3 basic health states: tuberculosis-uninfected, latent tuberculosis, and active (infectious) tuberculosis disease (Figure 1). Latent tuberculosis is modeled as an asymptomatic and noninfectious state that persists throughout an individual's life and may reactivate to active (symptomatic, infectious) tuberculosis disease at any time. We also allow for rapid progression of disease upon initial infection, reflecting the fact that the majority of individuals who develop active tuberculosis do so within 5 years of their initial infection [25]. The strains causing infection and disease are classified by resistance phenotype to the new drug as either drug-susceptible or drug-resistant tuberculosis. Drug-resistant tuberculosis strains appear first via acquired resistance (ie, sporadic mutation and subsequent selection among individuals ineffectively treated for active drug-susceptible tuberculosis). These resistant strains may then be transmitted at a rate determined by the reproductive fitness associated with the specific mutation responsible for the resistant phenotype.

Figure 1.

Model outline. The tuberculosis (TB) transmission model consists of individuals who are not infected with Mycobacterium tuberculosis (M. tb) and those who are infected with M. tb and in a latent state (noninfectious) or active state (infectious). Drug-resistant M. tb appears first through acquired resistance among those with active, drug-susceptible disease. Drug-resistant M. tb can subsequently be transmitted. The relative transmission potential of strains is dependent on the number of individuals with active disease and the mean fitness of the circulating strains. All susceptible strains have a mean fitness of 1, whereas the resistant strains have a range of relative fitness levels. The changes in this distribution of relative fitness levels are tracked in those with active diseases (as shown) and latent infection (not shown).

We calibrated the model by altering the M. tuberculosis transmission rate to reach a base case steady-state tuberculosis prevalence of 150 per 100 000 population prior to new drug introduction. The probability of acquiring resistance was benchmarked to a baseline scenario of current rifampicin resistance levels and the level of treatment success for drug-resistant tuberculosis set to that for MDR tuberculosis [20]. A table with all parameter values is available in Supplementary Table 1. It was assumed that a new drug was introduced at time zero. The outputs were the prevalence of active cases with resistance to this new drug (drug-resistant tuberculosis) per 100 000 population at 5 and 20 years from the time of drug introduction.

Both a deterministic and stochastic version were implemented in R [26]. The stochastic model allows for exploration of chance events: in particular, this model variant allows us to include the effect that small drug-resistant subpopulations may die out by chance, even when the effective reproductive number exceeds unity. Full details of model implementation are available in the Supplementary Materials.

Modeling the Fitness of New Resistance Mutations

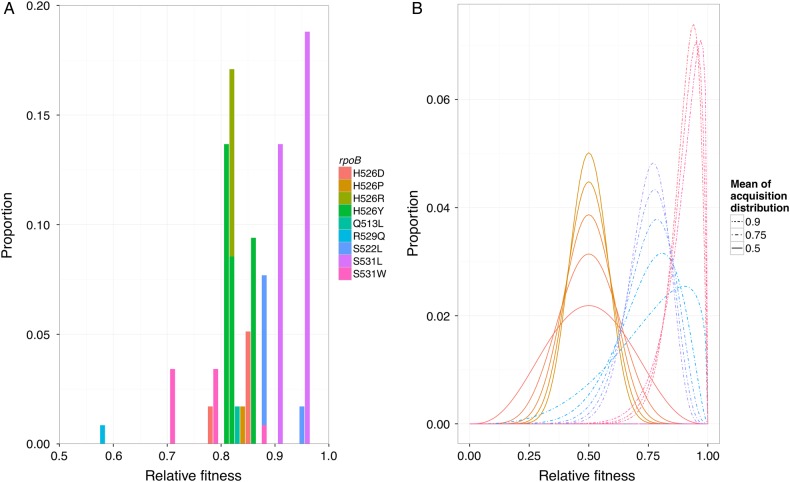
To parameterize the shape of the distribution of fitness costs associated with various drug resistance–conferring mutations, we used previously published data for rifampicin on the frequency of each resistance-conferring mutation in the set of spontaneous mutants derived in vitro and their relative fitness levels from growth competition experiments. The data were available from 2 experimental studies [9, 10] and are shown in Figure 2A and Table 1. This acquisition distribution had a mean relative fitness (vs susceptible strains) of 0.87, with most mutations clustered around a relative fitness of 0.86, and all above 0.5.

Figure 2.

Acquisition distribution. Distributions of fitness costs associated with new resistance mutations from experiments (A) and generalized via β distributions as input for the models (B). A, Distributions of fitness costs from pooled data from Gagneux et al [9] and Mariam [10] show that each different mutation within the rpoB gene conferring resistance to rifampicin has a different relative fitness level as measured by competitive co-culture with a parental, susceptible strain. The different mutations (shown in different colors) are labeled as original amino acid, codon position of mutation, and subsequent new amino acid. The frequency is taken from the number of in vitro spontaneous resistance mutations found to have this mutation (Table 1). B, Examples of the distributions of fitness levels for new mutations that were used as inputs for the deterministic model. Here the examples have 3 mean fitness values (0.5, 0.75, and 0.9), each with several levels of variance. For example, the 2 curves with the lowest peaks have means of 0.5 and 0.75 and have a variance of 0.03. Note that these are β distributions, which are capped at 1 and have an area under the curve capped at 1.

Table 1.

Data on Genetic Background and Mutation, Acquisition Probability, Experimental Condition, and Relative Reproductive Fitness of In Vitro, Spontaneously Acquired Rifampicin Resistance Mutations in Mycobacterium tuberculosis Strains

Strain (No. of Colonies Selected)	No. of Unique Mutations	Mutation in rpoB	Acquisition Probability	Experimental Conditiona	Relative Fitness	Notes	Reference
Harlingen strain (27)	3	S531W	0.12	Competition against parental	0.67 (.61–.73)	1/3 of spontaneous resistances had mutations not in rpoB	[10]
		H526Y	0.65		0.89 (.84–.94)
		S522L	0.23		0.54 (.51–.57)
		S531W	0.12	Independent	0.71 (.62–.80)
		H526Y	0.65		0.86 (.83–.89)
		S522L	0.23		0.95 (.93–.97)
		S531W	0.12	In macrophages	0.28 (.22–.34)
		H526Y	0.65		0.63 (.61–.65)
		S522L	0.23		0.50 (.34–.66)
CDC1551 (52)	12	S531L	0.31	Competition against parental	0.91 (.86–.97)		[9]
		H526Y	0.19		0.82 (.75–.89)
		H526D	0.04		0.78 (.73–.82)
		S531W	0.02		0.88 (.78–.88)
		H526R	0.19		0.82 (.75–.88)
		S522L	0.15		0.88 (.80–.96)
		Q513L	0.04		0.83 (.79–.86)
		H526P	0.04		0.84 (.8–.89)
		R529Q	0.02		0.58 (.55–.61)
T85 (63)	7b	S531L	0.46	Competition against parental	0.96 (.93–.99)
		H526Y	0.33		0.81 (.78–.84)
		H526D	0.13		0.85 (.82–.88)
		S531W	0.08		0.79 (.75–.82)

^a This refers to the experimental condition under which relative fitness was determined.

^b Only 4 were included in the fitness analysis.

In our models, we explored how several β distributions (examples in Figure 2B) of similar shape to the empirical rifampicin data affected the projected trajectory of drug-resistant tuberculosis over time. These distributions are bounded between 0 and 1 and parameterized by 2 shape parameters, which we selected to produce a range of mean fitness levels from 0.5 to 0.9 and a variance between 0.004 and 0.032.

Tracking the Distribution of Fitness Costs Among Drug-Resistant Strains Over Time

To capture the effect of the natural history dynamics (Figure 1) on fitness, we developed a function that tracks the proportion of active and latent cases with drug-resistant tuberculosis strains at each level of relative fitness over time (Supplementary Materials). This function accounts for the distribution of fitness costs associated with new mutations (the acquisition distribution, captured with different β distributions) and the preferential transmission of strains with higher fitness. At each time, the function returns a mean relative fitness of extant drug-resistant tuberculosis strains among active (ie, infectious) tuberculosis cases that is then used in the dynamic transmission model to determine the number of subsequent infections (Figure 1). Hence, relative fitness is here defined as relative ability to transmit (rather than, eg, relative ability to cause disease after transmission).

Impact of Background Force of Tuberculosis Infection

To test the impact of differing forces of tuberculosis infection on projections of drug resistance, we performed analyses where we assumed lower (50/100 000) and higher (1000/100 000) prevalence of tuberculosis than in our base case scenario.

RESULTS

Projected Burden of Drug-Resistant Tuberculosis Is Dependent on the Fitness Cost of Resistance

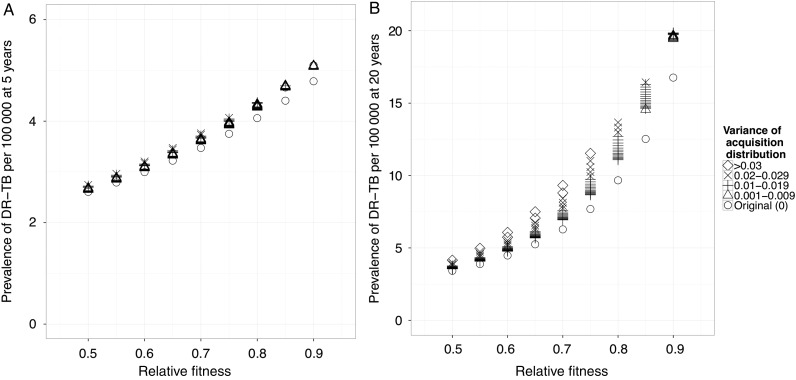
As expected, if we assume that resistance is associated with a single, fixed fitness cost, the projected level of drug-resistant tuberculosis at 5 and 20 years (Figure 3A and 3B) is strongly dependent on this cost. For example, if resistance-conferring mutations confer a 50% fitness cost, then the projected prevalence of drug-resistant tuberculosis 20 years after drug introduction is 3 drug-resistant tuberculosis cases per 100 000 (mean of acquisition distribution: 0.5; Figure 3B). If they confer only a 10% cost, then the projected prevalence of drug-resistant tuberculosis is >5 times higher at 17 drug-resistant tuberculosis cases per 100 000 (mean of acquisition distribution: 0.9; Figure 3B).

Figure 3.

Model results. Fitness distributions with higher variance are associated with higher levels of resistance at 5 (A) and 20 years (B), from the time of drug introduction in the deterministic model. When different levels of variance are included (shape scale), the prevalence of resistance is higher (eg, compare open circles to crosses at a single mean). This effect is more easily appreciated at the 20-year time point (compare results at 5 [A] and 20 years [B]). Abbreviation: DR-TB, drug-resistant tuberculosis.

Projected Burden of Drug-Resistant Tuberculosis Is Also Strongly Dependent on the Variance of Fitness Costs of Resistance

When we include a distribution of costs associated with resistance-conferring mutations (eg, those in Figure 2B), we find that the projected prevalence of drug-resistant tuberculosis is dependent on both the mean and variance of this distribution (Figure 3A and 3B; Supplementary Figure 3).

While this dependence on variation is less evident at the 5-year time horizon, after 20 years, the projected prevalence of resistance is clearly affected by the variance in costs of resistance, especially at intermediate values of the mean fitness cost (Figure 3B). For example, simulations for which we assume a distribution of fitness costs to resistance with a mean fitness cost of 20% (mean of acquisition distribution: 0.8) and a variance of 0.03 produces a 41% higher prevalence at 20 years from drug introduction than simulations in which we assume a constant fixed mean fitness cost of 20% (Figure 3B).

Mean Relative Fitness Increases Over Time

When including a distribution of fitness costs, the mean relative fitness of drug-resistant tuberculosis strains circulating in the population increases over time (Supplementary Figure 3B). The rate of increase was faster when there was a higher variance in the distribution of fitness costs to resistance. This means that it is possible that resistance-conferring mutations associated with high average fitness costs may nonetheless lead to high levels of drug-resistant tuberculosis when associated variation around this average cost is large. For example, the levels of drug-resistant tuberculosis 20 years after drug introduction achieved from an acquisition distribution with a mean fitness cost of 25% (mean of acquisition distribution: 0.75), can exceed the levels from an acquisition distribution with a mean fitness cost of 20% (mean of acquisition distribution: 0.8) when the variance associated with the greater average cost of mutation is higher (Figure 3B). Worryingly, the prevalence of resistance achieved from an acquisition distribution with a given mean fitness cost with no variance is comparable to the prevalence achieved when the mean is 10% smaller but has a reasonable degree of variance.

Stochastic Effects Slightly Reduce the Expected Levels of Resistance, but Exhibit Wide Divergence

As in the deterministic model, the long-term levels of resistance achieved in a stochastic model were dependent on both the mean and variance of the acquisition distribution (Supplementary Figure 4). Whereas the stochastic model allows for chance die out of individual resistant strains, resulting in a slightly lower mean projected drug-resistant tuberculosis level (Supplementary Figure 5), elimination of resistance is unlikely due to the continued acquisition of resistance during treatment of drug-susceptible disease [3]. The stochastic model results are highly divergent and illustrate that while the expected levels of resistance are lower than in the deterministic projections, chance events could also promote even higher levels of resistance (Supplementary Figure 5).

Dependence of Projections in Drug-Resistant Tuberculosis on Variability of Fitness Costs Is Maintained at Very Different Forces of Tuberculosis Infection

Our results supporting the importance of variability of fitness costs are maintained at both much higher (1000 cases/100 000 population) and lower (50 cases/100 000 population) levels of tuberculosis transmission (Supplementary Figures 6 and 7).

DISCUSSION

Improved projections of the spread of drug-resistant tuberculosis must account for the fact that not all strains of drug-resistant tuberculosis have the same epidemic potential. Multiple studies have demonstrated that the same phenotypic resistance can be conferred by different mutations, each of which may be associated with different effects on reproductive fitness [27]. Our results demonstrate that not only the absolute (mean) magnitude of these fitness costs, but also the variation in fitness cost between strains, is an important determinant of future epidemic trajectories of drug-resistant tuberculosis. By better understanding the relationship between mutations and fitness costs, we can improve predictions of future levels of drug-resistant tuberculosis and facilitate enhanced public health planning efforts. Specifically, with this model framework, we can combine laboratory data on fitness and observational studies on the distribution of fitness costs associated with resistance-conferring mutations (eg, [28]) with snapshots of fitness from population studies of clinical isolates (eg, [29]), to better understand the threat of ongoing transmission of resistance. By extending cross-sectional data accordingly, this modeling framework can inform better forecasts of resistance levels and predictions of the impact of interventions for control.

Here, we developed a new approach to model the effects of variation in fitness costs of drug resistance–conferring mutations on short- and longer-term prevalence of drug-resistant tuberculosis. Our model suggests that the shape of this distribution of fitness costs is a key contributor to resistance levels over time; by considering such variation we find that the projected burden of drug-resistant tuberculosis could be nearly 50% higher after 20 years compared to scenarios in which such variation is ignored. Similar to an earlier model [22], we find that wide distributions in the costs of resistance-conferring mutations allow for increasingly frequent generation of relatively fit resistant strains that can be transmitted and subsequently jeopardize drug-resistant tuberculosis control even if the current average drug-resistant tuberculosis fitness within a population is low.

More generally, our finding that a wide variance of fitness costs associated with resistance is associated with greater epidemic potential is closely related to Fisher's fundamental theorem of natural selection, which states that “the rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time” [30]. The link between variation in fitness and the rate of change of a fitness-associated trait in a population has been made more formally by Price [31, 32] and previously applied to models of parasite evolution [33].

Our results suggest that the fraction of resistance mutations that harbor minimal fitness costs (ie, those in the upper tail of a highly variable fitness cost distribution, approaching the fitness of drug-susceptible tuberculosis) is an important determinant of the epidemic potential of drug-resistant tuberculosis. Once strains with mutations that confer resistance without substantial fitness costs appear and are selected for by ineffective treatment, they will become the preferentially transmitted resistant strains and will contribute to increases in mean fitness of drug-resistant tuberculosis over time. Drug-resistant strains with mutations that confer large fitness costs may also accumulate secondary mutations that compensate or ameliorate these initial fitness costs [19, 27, 34], although we have not considered such effects here. Fitness costs of resistance-conferring mutations are conditional on strain genetic background [8, 35], which could influence the relative prevalence of specific lineages under the selective pressure of tuberculosis drug treatment [36, 37]. These mechanisms suggest that the mean fitness of drug-resistant tuberculosis may increase in the long term (>5 years). Hence, population-based studies that estimate relative fitness should regard their estimates as specific to a particular moment in time [29]. This increase in fitness may have already occurred in several settings where MDR strains of tuberculosis appear to be readily transmitted [15–18]. This increases urgency for tuberculosis control programs to improve the detection and treatment of MDR and extensively drug-resistant tuberculosis [15, 38], to minimize the probability that strains with low-cost mutations appear, are selected for, and subsequently spread.

Although our model was designed to investigate the impact of variation in fitness costs of resistance-conferring mutations on short- and longer-term trends on drug-resistant tuberculosis, there are important determinants of the future burden of drug-resistant tuberculosis beyond biological fitness. Most importantly, as tuberculosis control programs improve their ability to rapidly detect and effectively treat individuals with drug-resistant tuberculosis, the duration of infectiousness with drug-resistant tuberculosis strains, and hence the reproductive number of drug-resistant tuberculosis, will be reduced. We did not consider such improvements to tuberculosis control programs. Furthermore, in the interest of simplicity, we aggregated resistance into a single phenotype in the model, which does not reflect the heterogeneity in resistance patterns observed clinically. In addition, we have not considered host susceptibility factors, such as coinfection with human immunodeficiency virus, which have complex and time-varying effects on the incidence of tuberculosis and the spread of drug-resistant tuberculosis [23]. For these reasons, the projection of trends in drug-resistant tuberculosis should not be viewed as quantitative predictions of expected levels of drug resistance in the future. Despite these caveats, our results strongly support the need for additional research to better understand the likelihood of emergence of relatively fit strains of drug-resistant tuberculosis, whether these occur through the sporadic appearance of low-cost resistance-conferring mutations or because of the accumulation of compensatory mutations.

This model suggests that even if the mean fitness cost associated with resistance-conferring mutations is large, if a subset of strains have much smaller fitness costs or harbor costly mutations that can subsequently be compensated, these strains will be preferentially transmitted. This process skews the range of resistance mutations observed and suggests that those mutations with the lowest fitness cost should be prioritized for molecular drug resistance tests if the goal of such testing is to provide an early warning for risk of transmitted resistance. It should be emphasized here that due to the dynamic nature of fitness, the most prevalent mutations in the population may not be associated with the smallest fitness cost—this distribution will depend on time since drug introduction.

In conclusion, we found that, in addition to the mean fitness cost associated with drug resistance appearance, the variance in fitness costs of specific drug resistance–conferring mutations is a key determinant of future trends of drug-resistant tuberculosis. Our results are important both to understand the factors affecting the useful lifespan of existing antituberculosis drugs, but also for projections about the speed at which we expect to observe resistance to new antituberculosis drugs in the development pipeline [39, 40]. Given the importance of the distribution in fitness costs, it would be valuable, although challenging [41], to design additional studies aiming to estimate the ranges of such fitness costs at resistance emergence and in populations with drug-resistant tuberculosis over time. To guard against the appearance and continued selection of fit drug-resistant strains, further investment to improve the capacity of tuberculosis programs to detect and effectively treat individuals with drug-resistant tuberculosis is essential.

Supplementary Data

Supplementary materials are available at Clinical Infectious Diseases online (http://cid.oxfordjournals.org). Supplementary materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supplementary data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.