SCD-HeFT: Use of RR Interval Statistics for Long-term Risk Stratification for Arrhythmic Sudden Cardiac Death

Abstract

Background

In the SCD-HeFT a significant fraction of the congestive heart failure (CHF) patients ultimately did not die suddenly from arrhythmic causes. CHF patients will benefit from better tools to identify if ICD therapy is needed.

Objective

To identify predictor variables from baseline SCD-HeFT patients’ RR intervals that correlate to arrhythmic sudden cardiac death (SCD) and mortality and to design an ICD therapy screening test.

Methods

Ten predictor variables were extracted from pre-randomization Holter data from 475 patients enrolled in the SCD-HeFT ICD arm using novel and traditional heart rate variability methods. All variables were correlated to SCD using Mann Whitney-Wilcoxon test and receiver operating characteristic analysis. ICD therapy screening tests were designed by minimizing the cost of false classifications. Survival analysis, including log-rank test and Cox models, was also performed.

Results

α₁ and α₂ from detrended fluctuation analysis, the ratio of low to high frequency power, the number of PVCs per hour and heart rate turbulence slope are all statistically significant for predicting the occurrences of SCD (p<0.001) and survival (log-rank p<0.01). The most powerful multivariate predictor tool using the Cox Proportional Hazards was α₂ with a hazard ratio of 0.0465 (95% CI: 0.00528 – 0.409, p<0.01).

Conclusion

Predictor variables from RR intervals correlate to the occurrences of SCD and distinguish survival among SCD-HeFT ICD patients. We believe SCD prediction models should incorporate Holter based RR interval analysis to refine ICD patient selection especially in removing patients who are unlikely to benefit from ICD therapy.

Introduction

Implantable Cardioverter-Defibrillator (ICD) therapy decreases mortality in select post-MI and CHF patients.^{1, 2} However, many deaths occur from mechanisms unamenable to ICD therapy. New tools to better identify candidates who would benefit the most from ICD therapy remains a challenge.³ The proof of this can be found In the Sudden Cardiac Death in Heart Failure Trial (SCD-HeFT) where only 182 patients received ICD shocks for ventricular tachycardia (VT) or ventricular fibrillation (VF) over a median follow-up period of 45.5 months out of the 811 congestive heart failure (CHF) patients who received ICD therapy (22.4%).⁴

It has been shown in the past that traditional HRV measures in the time and frequency domains have prognostic power.⁵ However, they are neither measured in well-conducted ICD clinical trials nor harbor significant power to serve as a practical risk predictor. More recently, methods based on non-linear dynamics, such as detrended fluctuation analysis (DFA) and heart rate turbulence (HRT), which looks at the return to equilibrium of heart rate after a premature ventricular contraction (PVC), may yield superior predictive results.^{6, 7} DFA fractal exponents of heart rate time series have been shown to correlate with autonomic tone while HRT parameters correlate with baroreflex sensitivity.^8,9 In this paper, we investigated the effectiveness of these methods, together with traditional Holter methods to predict which SCD-HeFT patients would benefit or not benefit from their ICD over the duration of the study.

Methods

Subjects

SCD-HeFT was a large National Institutes of Health funded clinical trial that was designed to study the effectiveness of ICD and amiodarone therapies in patients with mild to moderate heart failure.¹ From September 16, 1997 to July 18, 2001, 2521 patients were randomly assigned in equal proportions to receive placebo, amiodarone or a single-chamber ICD programmed to shock-only mode (model 7223, Medtronic). All patients were followed until October 31, 2003. The inclusion criteria for the study was that the patients had to be at least 18 years old, have New York Heart Association (NYHA) class II or III chronic, stable congestive heart failure (CHF) due to ischemic or nonischemic causes and a left ventricular ejection fraction (LVEF) of no more than 35 percent.

The Holter monitor sub-study was approved by the human studies committee at the participating institutions. Holters were obtained in the two weeks prior to randomization to placebo, amiodarone, or ICD. Analysis included characterization of non-sustained ventricular tachycardia (NSVT). Holter staff and readers were blinded to clinical parameters, randomization status, and outcomes. Among the 2521 patients enrolled in SCD-HeFT, 2040 (81%) had 24±6 hours of readable data: 687 were randomly assigned to placebo, 674 to amiodarone, and 679 to ICD therapy (664 actually received an ICD).

In this analysis, we were able to study the relationship between baseline Holter data and subsequent ICD therapy in 475 ICD patients in whom high quality Holter recordings were available. These patients were those with at least 16 hours of data and at least 90% readability. Table 1 shows the characteristics of SCD-HeFT patients included in the sample.

Table 1.

Characteristics of the CHF patients from SCD-HeFT in the ICD arm.

Characteristic	CHF patients from SCD-HeFT (n=475)
Age at Enrollment	Average: 59.5 (19–90) Median Ag: 60
Gender	370 males 105 females
Races	372 Caucasians 83 African Americans 15 Latin Americans 1 Native American 4 Asians
NYHA	Class II: 342 Class III: 133
Heart Failure etiology	223 non-ischemic 252 ischemic
Number of patients using β-blocker	327

Predictor Variables derived from Holter Monitor Data

Holter monitor data were transferred from flash cards and magnetic tapes onto the modified Marquette MARS 8000 reader system, and were then reviewed by Core Laboratory staff, and validated. Each tape scan was reviewed for accuracy, and the results tabulated.

MIT annotation files of the ECG recordings were generated using the MARS Ambulatory ECG Analysis System. RR intervals were then extracted from the MIT annotation files using the program ann2rr from Physionet. We analyzed the variability of the RR intervals by DFA, HRT, and traditional heart rate variability measures in frequency domain and time domain.

A) Detrended Fluctuation Analysis

DFA as a predictive tool in heart disease was introduced by Peng et al.¹⁰ The DFA yields a short-term fractal exponent, α₁, and a long-term fractal exponent, α₂. These exponents tell us about the self-similarity of the RR intervals in both the short term and long term and have been considered prognostic in certain disease states.^{11, 12}

In performing DFA, the record of RR intervals of each person were broken into a sequence of segments of 8192 consecutive heartbeats shifted by 10 minutes to find α₁ and α₂ for each segment along the entire record. The segment length of 8192 consecutive heartbeats were chosen as recommended by Peng et al.¹⁰ The short-term and long-term fractal exponents for each segment were then averaged over all segments using the “fastdfa” algorithm.¹³

B) Heart Rate Turbulence

HRT was introduced by Schmidt.⁷ It describes the physiological response of the sinus node to PVCs. It consists of an initial acceleration followed by a deceleration of the heart rate. Turbulence slope (TS) and turbulence onset (TO) are the two parameters associated with the HRT method.

TS is defined as the maximum slope of a regression line over any sequence of five subsequent RR intervals within the first 20 RR intervals after a PVC. TO is the percentage difference between the heart rate immediately following a PVC and the heart rate immediately preceding a PVC.

During the process of computing the HRT, we also determined the number of PVCs/hr for each patient and separately evaluated it as a risk stratification parameter.

C) HRV Frequency-Domain Method – LF/HF ratio

In frequency domain analysis of heart rate variability, high frequency power (HF, 0.15 – 0.4 Hz in adults) broadly reflects vagus nerve activity while low frequency power (LF, 0.04 – 0.15 Hz in adults) reflects sympathetic activity.^14–16 Although not definitive, high LF/HF ratio tends to show the dominance of the sympathetic activity while low LF/HF ratio tends to reflect the dominance of the vagus nerve activity.

The power spectral density function for each subject was obtained through the Lomb periodogram algorithm.^{17, 18} The Lomb periodogram algorithm was chosen because RR intervals are sampled at irregular time intervals and this algorithm performs well in the presence of artifacts and PVCs.

D) HRV Time-Domain Methods – SDNN, mean heart rate, pNN50 and HRVTI

To determine the HRV measures in time domain we deleted all the artifacts and PVCs from the RR intervals so that only normal-to-normal (NN) intervals originated from the sinus nodes were analyzed.

Standard Deviation of NN intervals (SDNN)

SDNN is a measure of the total variability of the NN intervals. Past research has shown that decreased variability in heart rate is a risk factor for mortality in post-myocardial infarction patients and patients with ischemic cardiomyopathy.^{5, 19}

Mean Heart Rate

Mean heart rate for each patient was expressed as the number of beats per minute (bpm). Past research has shown that elevated mean heart rate is a risk factor for mortality, cardiovascular disease and sudden death in patients with known or suspected coronary heart disease, post-myocardial infarction patients and patients with hypertension.²⁰

pNN50

pNN50 is the fraction of NN intervals that have a difference of more than 50ms in consecutive beats. pNN50 is a measure of how often there is a rapid change from one beat to the next one. It is highly correlated with HF in the frequency domain.⁵

Heart Rate Variability Triangular Index (HRVTI)

HRVTI is equal to the total number of NN intervals divided by the number of NN intervals in the modal bin when the NN intervals are plotted in a histogram.²¹ The Holter monitors in this study operated at the sampling rate of 128Hz. Therefore, the NN intervals were measured to the nearest 1/128s and the width of each bin in the histogram was equal to 1/128s.

Outcomes

The final status of patients and their causes of death are documented in SCD-HeFT via a blinded events committee.²² A cardiac arrest was defined as the sudden loss of consciousness requiring transthoracic defibrillation and/or cardiopulmonary resuscitation to stabilize blood pressure and rhythm. Outcomes were SCD, VF and ventricular flutter (VFL) appropriate shock as defined by previous study. SCD-HeFT included a pre-specified protocol for ICD programming. This included a single zone of therapy at a detection rate of ≥188 beats/min. The initial detection interval was for 18 of 24 beats, and the redetect interval was for 12 of 16 beats. Shock-only mode was used with no antitachycardia pacing. Antibradycardia pacing was set to 50 beats/min with hysteresis of 34 beats/min, the minimal allowed heart rate.²³

Based upon the final status, the subjects were separated into a positive group and a negative group. The positive group consisted of subjects who have received at least one appropriate shock for a VF episode or a VFL episode from their ICDs. Also, it included patients who have died from sudden tachy-arrhythmia as determined by the events committee.²² The negative group consisted of all other SCD-HeFT subjects in the ICD patient sample.

Statistical Analysis

In order to find the prognostic power of the predictor variables, we performed a non-parametric two-sample Mann Whitney-Wilcoxon (MWW) test between the positive group and the negative group for each of the predictor variables. The null hypothesis of the MWW test is that the distributions of the two populations are the same.^{24, 25} P-values less than 0.05 are considered statistically significant. Besides p-values from the MWW test, we also quantified the prognostic power of the predictor variables by performing receiver-operator characteristic (ROC) analysis on the subjects.²⁶ We calculated the ROC curves and found the area under the curve (AUC) for each of the predictor variables. Also, bootstrapping was done by getting new samples for the two groups by resampling with replacement for a thousand times.²⁷ A new estimate of AUC was calculated at each bootstrap. Then we found the mean and the standard deviation of these AUC estimates for each predictor variable to provide a distribution of the AUCs.

We combined two or three predictor variables to perform multifactorial ROC analysis in order to examine if the prognostic power could be improved.²⁸ With the combinations that give the highest AUC, we found the operating points by minimizing the cost of false classifications. Cost here can be defined as monetary costs and patient mortality. The cost function is the following:

$$\text{cost}={(1\text{-p})}^{\ast }{\mathrm{\gamma }}^{\ast }\mathrm{x}+{\mathrm{p}}^{\ast }{\mathrm{\delta }}^{\ast }(1\text{-y})$$ (1)

where p is the proportion of positive cases, x is one minus specificity and y is sensitivity. γ is the cost of a false positive and δ is the cost of a false negative. At the operating point that would minimize the cost, we listed the sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV) and percentage of CHF patients excluded.

We plotted the Kaplan-Meier survival plots and performed log-rank test on the ICD-arm subjects on the variables from DFA, HRT, LF/HF and number of PVCs/hr. We also performed univariate and multivariate Cox proportional hazards model analysis on all the variables. Time to event was the number of days to the occurrences of VF, VFL or sudden tachyarrhythmic death.

Lastly, we examined the correlations between all the measures through Pearson product-moment correlation coefficients (PPMCCs) to identify independent predictor variables.²⁹

Results

Prediction of Occurrences of VF, VFL or SCD

Table 2 shows the respective median and interquartile range (IQR) for the positive and negative groups. As seen, α₁, α₂, TS, Number of PVCs/hr and LF/HF are all statistically significant predictor variables (p<.001). Also, TO is a statistically significant predictor variable (p<.05).

Table 2.

Statistical association of predictor variables with the occurrences of VF, VFL or SCD

	Positive group Median (IQR) (n=72)	Negative group Median (IQR) (n=403)	p-value
α1	.4331 (.3505 – .5732)	.6140 (.4762 – .8030)	<.001
α2	.6865 (.6002 – .8497)	.9072 (.7313 – 1.016)	<.001
TS (ms/RRI)*	1.360 (.5421 –2.648)	2.1746 (1.120 – 4.542)	<.001
TO (%)*	.0030 (−.0028 – .0088)	0.000 (−.0084 – .0078)	<.05
Number of PVCs/hr	17.32 (6.255 – 33.99)	5.097 (1.010 – 17.60)	<.001
LF/HF	.4953 (.3890 – .5885)	.6687(.4951-.9365)	<.001
SDNN (ms)	113.3 (76.63 – 154.5)	115.0 (86.98 – 151.5)	.37
Mean heart rate (bpm)	78.70 (69.82 – 85.79)	75.11 (67.68 – 84.20)	.16
pNN50 (%)	19.44 (10.36 – 35.02)	16.81 (7.718 – 29.76)	.21
HRVTI	26.80 (17.55 – 34.15)	28.50 (20.91 – 37.71)	.08

^*n=70 for the Positive group, n=388 for the Negative group

Table 3 shows the AUCs for each predictor variable and each combination of predictor variables in the ROC analysis. Among the univariate ROC analysis, it can be seen that α₁ performs the best with the mean AUC equals to .73. LF/HF performs second best with a mean AUC equal to .71, followed by α₂ with a mean AUC equal to .69. As we combined more variables together and performed multifactorial ROC analysis, the AUCs increased as seen in Table 3. We tried four different combinations each with three different predictor variables. An AUC of .79 was achieved for all combinations. Figure 1A shows the ROC curves of the five predictor variables with the highest prognostic power while Figure 1B shows the five multifactorial ROC curves. From Figure 1B one can observe that the classification performed with α₁ and α₂ has a comparable performance as the classifications performed when one more predictor variable is added.

Table 3.

Results of AUCs from univariate and multifactorial ROC curves for prediction of occurrences of VF, VFL or SCD

	AUC Mean (SD)
α1	.73 (.03)
α2	.69 (.03)
TS	.64 (.04)
TO	.59 (.03)
Number of PVCs/hr	.67 (.03)
LF/HF	.71 (.03)
SDNN	.53 (.04)
Mean heart rate	.55 (.03)
pNN50	.55 (.04)
HRVTI	.57 (.04)
α1, α2	.78
α1, TS	.76
α1, TO	.75
α1, number of PVCs/hr	.75
α1, LF/HF	.76
α1, HRVTI	.76
α1, α2, TS	.79
α1, α2, LF/HF	.79
α1, α2, number of PVCs/hr	.79
α1, α2, HRVTI	.79

Figure 1.

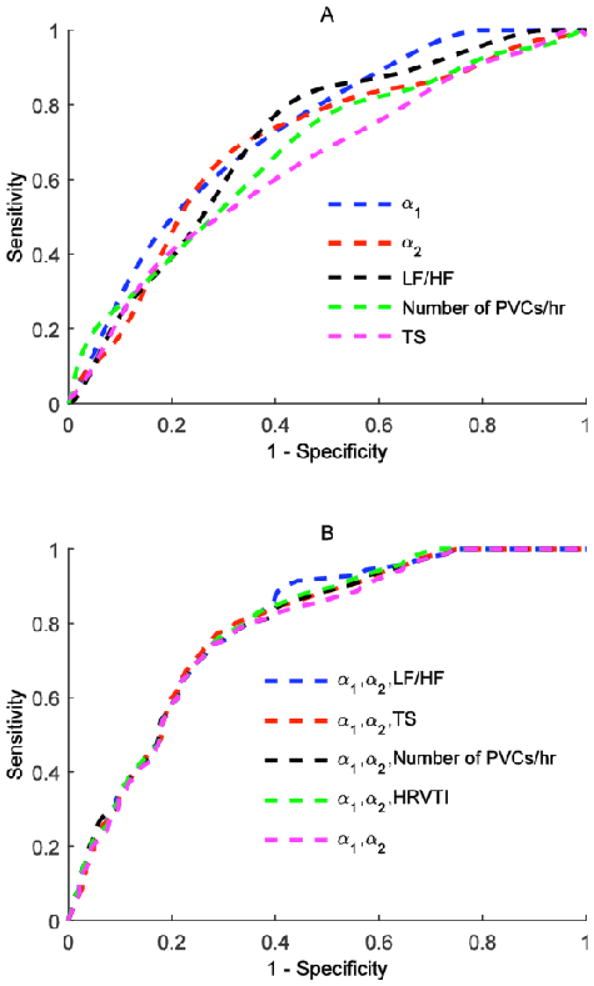
Plot of ROC curves for five predictor variables with the highest prognostic power for occurrences of VF, VFL or SCD (A). Plot of multifactorial ROC curves for occurrences of VF, VFL or SCD (B).

We assumed that the cost of a false negative (δ) was ten times the cost of a false positive (γ). By minimizing the cost of false classifications in each of the multifactorial ROC curves with three predictor variables, we found the corresponding thresholds along with their classification performances (Table 4). It can be observed that for all these tests, they have decent sensitivities and very high NPVs. The outcome of each of these tests is the exclusion of about half of the HF patients from ICD therapy consideration.

Table 4.

Thresholds that give minimum costs and classification performance for prediction of recurrences of VF, VFL and SCD for γ = 1, δ = 10.

Thresholds with minimal costs	Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)	CHF patients excluded (%)
α1≤.43 or α2≤.66 or LF/HF ≤ .60	91.4	55.9	27.2	97.3	48.7
α1≤.40 or α2≤.71 or TS ≤ 1.05	84.3	60.6	27.8	95.5	53.7
α1≤.45 or α2≤.69 or number of PVCs/hr ≤ 19	85.7	57.7	26.8	95.7	51.1
α1≤.48 or α2≤.80 or HRVTI ≤ 15.8	87.1	56.2	26.4	96.0	49.6

Survival Analysis

Figure 2 shows the Kaplan-Meier survival plots for DFA variables, LF/HF, Number of PVCs/hr and HRT variables, each separated by quartiles. From the log-rank test p-values, it can be seen that there are statistically significant differences between the survival functions below and above the median of the predictor variables for α₁, α₂, LF/HF, Number of PVCs/hr and TS. This fact is even more pronounced when one looks at the Kaplan-Meier survival plot by quartiles of α₁. Q1 has a survival rate of 60% at the end of SCD-HeFT while the survival rate of Q4 stays almost at 100%.

Figure 2.

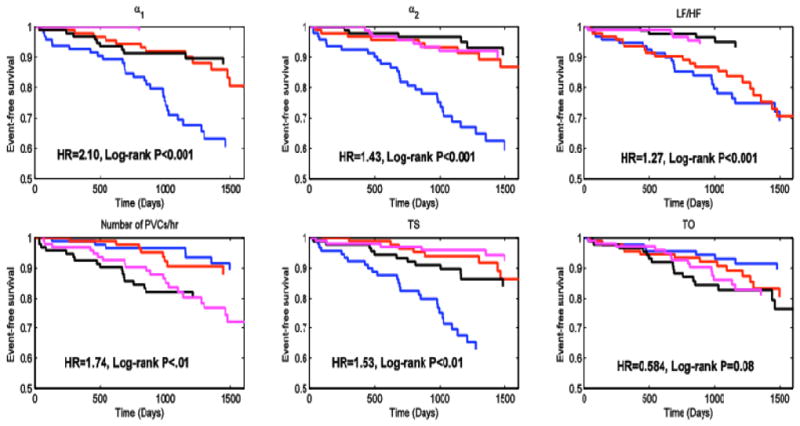
Kaplan-Meier Survival Plots for occurrences of VF, VFL or SCD by quartiles of the six predictor variables. Q1 is blue, Q2 is red, Q3 is black and Q4 is magenta. Log-rank P values were obtained from comparing the survival functions of Q1 and Q2 versus the survival functions of Q3 and Q4.

Table 5 shows the results from both univariate and multivariate Cox proportional-hazards regression performed on the data. From the univariate analysis, by looking at the p-values, it can be seen that α₁, α₂, LF/HF, Number of PVCs/hr and TS are all statistically significant covariates in distinguishing the survival. From the multivariate analysis, it can be seen that α₂ stands out as the only independent and statistically significant covariate in finding the differences in the survivals of the patients with a hazard ratio of 0.0465 (95% CI: 0.00528 – 0.409, p<0.01).

Table 5.

Hazard ratios from the Cox model for Predictions of VF, VFL or SCD.

	Univariate Analysis				Multivariate Analysis
Covariate	Beta	HR [exp(beta)]	95% CI	p-value	beta	HR [exp(beta)]	95% CI	p-value
α1	−4.06	0.0173	(3.83E-3 0.0785)	<0.001	0.367062	1.44	(0.0823 25.3)	0.802
α2	−3.46	0.0316	(7.82E-3 0.127)	< 0.001	−3.06931	0.0465	(0.00528 0.409)	<0.01
TS	−0.242	0.785	(0.672 0.918)	<0.01	−0.11552	0.891	(0.763 1.04)	0.144
TO	12.4	2.45E+05	(0.732 8.2E10)	0.0559	8.649373	5.71E+03	(3.20E-06 1.02E13)	0.426
Number of PVCs/hr	0.032	1.03	(1.02 1.05)	< 0.001	0.018571	1.02	(0.997 1.04)	0.0932
LF/HF	−2.39	0.0919	(0.0277 0.305)	< 0.001	−1.26969	0.281	(0.0479 1.65)	0.160
SDNN	−0.0041	0.996	(0.990 1.00)	0.19	−0.00422	0.996	(0.983 1.01)	0.537
Mean heart rate	0.0201	1.02	(0.996 1.04)	0.097	0.012986	1.01	(0.984 1.04)	0.380
pNN50	0.0015	1.00	(0.989 1.01)	0.817	−0.00421	0.996	(0.970 1.02)	0.752
HRVTI	−0.0213	0.979	(0.955 1.00)	0.088	0.024206	1.02	(0.974 1.08)	0.348

Correlations between Predictor Variables

The correlation between all the predictor variables was investigated using Pearson product-moment correlation coefficients (PPMCCs) and they are shown in Figure 3. PPMCCs are presented in absolute values. Black means perfect linear correlation (PPMCC=1). While white means no correlation (PPMCC=0). From Figure 3, it can be seen that LF/HF and α₁ are highly correlated (PPMCC=0.7160). Therefore, even though LF/HF has decent prognostic power in predicting occurrences of ventricular arrhythmia (AUC=.71, Table 3), it does not add significant prognostic power when combined with α₁. On the other hand, even though TS has smaller prognostic power than LF/HF (AUC=0.64, Table 3), it can still add prognostic power when it is used in combination with α₁ as TS and α₁ have a low correlation (PPMCC=0.2024). From Table 3, it can be seen that α₁, TS has the same AUC as α₁, LF/HF (AUC=.76). Besides, DFA fractal exponents and HRT parameters have low correlation with mean heart rate (PPMCCs<.2) as shown in Figure 3.

Figure 3.

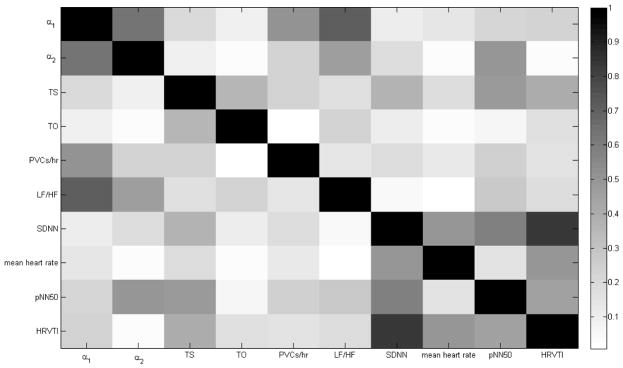
Correlation Plot for All the Predictor Variables expressed through the PPMCCs in Absolute Values.

Discussion

Important Findings

Heart failure has been linked to arrhythmia related sudden death. VT/VF have been the most likely cause of SCD, however reduced ejection fraction has been repeatedly associated as an independent risk factor for sudden death.² Evaluation of R-R intervals with non-linear dynamics in HF patients with ICD might predict which patients are likely to experience appropriate ICD therapy or have SCD. α₁, α₂, LF/HF ratio, number of PVCs/hr and TS have the highest prognostic powers in identifying candidates for ICD therapy independently among all the predictor variables investigated. When we combined α₁, α₂ and one other predictor variable to perform multifactorial ROC analysis we achieved AUCs of 0.79 for the prediction of occurrences of VF, VFL or SCD. Moreover, negative predictive values from the combined DFA and spectral measures were strong enough to allow us to be confident that certain SCD-HeFT ICD patients (approximately half) did not need an ICD with 97.3% certainty.

Setting δ ten times γ was an assumption and it was used to help us find the operating point for the ICD therapy screen test and hence it should only be used as a reference. δ being 10 times γ means that the screen test would rather give unnecessary ICD therapy than fail to give necessary ICD therapy. The changes in the ratio of δ to γ will lead to changes in classification performances.

α₁, α₂, LF/HF ratio, number of PVCs/hr and TS can all distinguish survivals independently (log-rank p-values<0.01, univariate Cox model p-values<0.01). Notably, if α₁ is in Q4, one can have confidence that the patient would not experience a fatal ventricular arrhythmic event for the duration of the trial. In performing the multivariate Cox proportional-hazards regression, α₂ is the only independent and statistically significant covariate in distinguishing the survivals of the patients with a hazard ratio of 0.0465 (95% CI: 0.00528 – 0.409, p<0.01) as seen in Table 5. Therefore, both α₁ and α₂ are powerful variables in distinguishing survivals.

One advantage of DFA over conventional time series methods, such as spectral analysis, is that it is more suited for non-stationary physiological signals. There are many extrinsic trends in a person’s heart rate that arise due to activities or uncorrelated environmental stimuli. DFA discards these trends and focus on the intrinsic dynamics of the autonomic nervous system itself. DFA is also better suited for the investigation of self-similarity in the RR intervals when altered self-similar behaviors are found in patients with cardiovascular diseases and old age.⁶ Its advantage is shown by α₁ from DFA having higher prognostic power than LF/HF ratio.

Our research showed that measures from HRT, especially TS, have decent prognostic power for predicting arrhythmic SCD among subjects in SCD-HeFT. This finding is consistent with results from past researches. For example, HRT measures have been shown to be able to do risk stratification for mortality in CHF patients enrolled in Muerte Subita en Insuficiencia Cardiaca (MUSIC).³⁰ Also, these measures have been shown to stratify risks for serious arrhythmic events in patients with left ventricular dysfunction.³¹

Amiodarone was associated with an overall mortality risk reduction in GESICA where survival benefit appeared to occur in those patients whose pre-treatment resting heart rate was greater than 90 bpm.³² Fractal exponents from DFA and HRT parameters can be used as additional independent predictors for SCD as they have low correlation with the mean heart rate (PPMCCs<.2).

α₁ from DFA has high correlation with the LF/HF ratio as shown by their PPMCC (r=0.7160). This finding is consistent with results from past research.³³ Since measures from DFA are highly correlated with the LF/HF ratio nothing significant is gained by combining them. However, if DFA measures are combined with another predictor variable with decent prognostic power but low correlation, such as TS, it is possible to achieve better classification performances.

Limitations

There are several limitations to consider. First, some of our measures are affected to various degrees by the extent of heart failure. There may be significant deviations from the norm depending on the degree of heart failure (Class II vs. Class III) and the underlying type of heart disease (Ischemic vs. Non-ischemic) as regards to the LF, HF and LF/HF ratio of the spectral and fractal components of HRV. Our findings are interpreted broadly for the entire heart failure population as HRV reference values for stable heart failure subgroups are not yet described. Second, no predictive tool can be expected to provide anything but incremental benefit over the present clinical knowledge base of SCD prediction in heart failure. Clearly, the positive predictive value found in our study will not alter the ability to discern who will be shocked by an ICD and who will not. On the other hand, the negative predictive value is sound, at >95%. This has value as a screen test for the decision to exclude from ICD therapy. Finally, we have endeavored to capture an economic value of this negative predictive methodology. To make any definitive arguments about the economic cost-savings of these statistical tools requires detailed capture of hospital expenditures in a prospective manner tracked against mortality and quality of life adjusted finances using our metrics. As such, our use of a 1 in 10 ratio is meant purely to provide a way to estimate value, not as a firm ratio upon which to make clinical decisions.

Conclusion

Survival in heart failure patients can be improved by placement of ICDs, however less than 25% of patients who receive ICDs experience SCD or appropriate shock therapy. We have shown that variables extracted from non-linear dynamic analysis of SCD-HeFT subjects’ RR interval recordings have prognostic power for predicting SCD and appropriate ICD shocks in HF patients who have ICDs. α₁ and α₂ from DFA, LF/HF ratio, number of PVCs/hr and TS correlate with the occurrences of SCD and distinguish the survivals in the SCD-HeFT subjects in the ICD arm. Perhaps most importantly, the ability to determine who will not benefit from an ICD can be found in these tools. Further work should be done to examine the possibility of utilizing these variables for ICD therapy screen tests.

Clinical Perspectives.

Our research confirms that the short-term and long-term fractal exponents from detrended fluctuation analysis, which describe self-similarity in patients’ RR intervals, contain valuable information about the patients’ cardiovascular health. More specifically, our research shows that both of the fractal exponents can be used to do long-term prediction of the occurrences of sudden death and survivals among class II/III heart failure patients. These measures could be measured and incorporated when a decision has to be made on whether a class II/III heart failure patient should receive an ICD therapy. From SCD-HeFT, it was shown that many of the heart failure patients who received ICDs ended up not benefiting from them. Our research can help eliminate unnecessary ICD therapy and reduce waste of resources. In clinical practice, Holter data would be obtained from heart failure patients to determine the short-term and long-term fractal exponents. High values of these exponents would indicate, if supported by standard ICD screening, a high probability that the patients could be excluded from ICD therapy.

Abbreviations

AUC

area under curve

bpm

beats per minute

CHF

congestive heart failure

CI

confidence interval

DFA

detrended fluctuation analysis

ECG

electrocardiogram

HRT

heart rate turbulence

HF

high frequency power

HRV

heart rate variability

HRVTI

heart rate variability triangular index

ICD

implantable cardioverter-defibrillator

IQR

Interquartile Range

LF

low frequency power

LVEF

left ventricular ejection fraction

MUSIC

Muerte Subita en Insuficiencia Cardiaca

MWW

Mann Whitney-Wilcoxon

NN

normal-to-normal

NSVT

non-sustained ventricular tachycardia

NYHA

New York Heart Association

pNN50

the fraction of consecutive normal-to-normal intervals that differ by more than 50ms

PPMCC

Pearson product-moment correlation coefficient

PVC

premature ventricular contraction

ROC

receiver operating characteristics

SCD

sudden cardiac death

SCD-HeFT

Sudden Cardiac Heart Failure Trial

SDNN

standard deviation of normal-to-normal intervals

TO

turbulence onset

TS

turbulence slope

VF

ventricular fibrillation

VFL

ventricular flutter

VT

ventricular tachycardia