Abstract
Segments of genome inherited from a common ancestor by related individuals are said to be identical by descent (IBD). Modern genetic marker data provide information to infer such segments among multiple related members of a population, even when pedigree relationships are unknown. Previous methods have been proposed for detection of pairwise IBD, but computation of probabilities of trait data under many trait models requires an IBD estimate jointly consistent among individuals and slowly varying across genome locations; we refer to such an estimate as an IBD graph. In this paper, we develop a novel method that builds IBD graphs sequentially among related individuals from a population sample using either phased or unphased genetic marker data. We show how IBD graphs realized conditionally on marker data provide a form of linkage mapping score, analogous to a LOD score, and propose a permutation approach to normalize this mapping score. Using a simulated quantitative trait dependent on the (unobserved) genotype at a major locus, we apply the approach to two samples containing both closely and remotely related individuals, among whom there are complex patterns of IBD. We compare the results of our approach with an alternate approach based on estimation of local kinship. We show that pairwise estimates derived from a joint IBD graph give significant improvements in LOD score estimation over estimates derived from an intrinsically pairwise approach.
Keywords: identity by descent (IBD), detecting IBD segments, joint IBD constraints, sampling joint IBD graphs, likelihood, linkage mapping
Introduction
Segments of genome inherited from a common ancestor by multiple individuals are said to be identical by descent (IBD). Two individuals share a gene copy IBD if they inherited the gene copy from a common ancestor who lived more recently than a specific time point. This time point is understood to be recent relative to the mutation process, so that IBD segments have nearly the same DNA sequence. Moreover, although the probability that two gametes are IBD at a locus declines exponentially with the number of meioses since their common ancestor, given that they are IBD, the expected length of the IBD segment declines as the inverse of the number of meioses [1]. Thus, given some recent IBD between two individuals, the IBD segment is likely to be long enough to detect by modeling sequence similarity reflected in dense genetic marker data [2, 3, 4, 5, 6]. IBD segments detected in groups of individuals not known to be related may be used in a variety of analyses of population data, including questions of disease mapping [3], haplotype phasing [4], and copy number variation [5].
The IBD resulting from the descent of DNA to related individuals also underlies linkage analysis [7]. Segments of shared genome among multiple related affected individuals provide strong evidence of locations of causal genes [8]. Global and local estimates of pairwise kinship, together with clustering of individuals into related sets [9], have provided a basis for mapping of quantitative trait loci (QTL) using the same mixed-model approach as had previously been used in pedigrees [10]. Among close relatives, who share several segments of autosomal genome IBD with high probability, it is more informative to generate detailed realizations of pairwise IBD states across the genome [11], providing estimates of degree of relationship or even information to correct misspecified pedigrees. These realizations can also be used in follow-up mixed-model QTL mapping studies [11].
The classical linkage LOD score [12] also remains a key tool in the genetic mapping of trait loci, and the focus of this paper is in estimating an analogous linkage mapping score using inferred IBD among individuals. The LOD score is a (base-10) log likelihood-ratio comparing the numerator hypothesis of a trait locus (or loci) at given position(s) on a marker map with null hypothesis of the same underlying genetic model for the trait but with causal location(s) unlinked to the genetic markers under consideration [12]. On known pedigrees, the model of Mendelian segregation provides probabilities or realizations of descent that are then used to compute the LOD score [13, 14]. This LOD score computation is feasible for many models for either quantitative or dichotomous traits, including, but not limited to, single-locus trait models with phenotype probabilities or probability densities defined for each modeled but unobservable trait-locus genotype. A single set of realizations of IBD conditional on genetic marker data can be used to estimate the numerator probability in the LOD score, not only for multiple hypothesized trait locus positions [7] but for multiple traits and trait models [14]. If IBD can be inferred from genetic marker data on related individuals in a population sample, the same approach will provide an estimate of this key component of the LOD score in the absence of any assumed pedigree.
The remainder of this paper is as follows. In the Methods section, we first summarize relevant background models and methods for the inference of IBD segments. We then present our new approach to realization of joint IBD among multiple individuals and across the genome, and show how these realizations may be used in linkage inference. We describe two example data sets. In both cases, the simulated quantitative trait is based on a single-locus major gene model. The marker data of the first example is simulated on an extended human pedigree, using real marker data to generate the underlying marker properties. The second example uses real marker data from an animal data set [15]. On the first example, we describe methods used to compare our approach with an alternate approach developed by [9]. In the Results section we present the outcomes of our analyses on the two example data sets. Although the data derive from pedigrees, they are analyzed without reference to the pedigree. We show that in these examples that IBD can be accurately estimated without knowledge of the true pedigree, and that this results in a Monte Carlo estimate of a gene mapping score analogous to a LOD score. We also present results of our comparison analyses. We show that in regions of the genome where there are complex patterns of IBD among sampled individuals, pairwise estimates derived from our joint IBD estimates outperform those based on direct estimation of pairwise IBD. We end with a Discussion.
Methods
IBD in pedigrees and populations
A set of n diploid individuals is most easily considered as the set of their 2n paternal and maternal gametes (haploid genomes). At a locus, the IBD state of a set of gametes is a partition of the set. Gametes are in the same block of the partition if they are IBD: that is, their DNA at the locus descends from DNA in a single ancestral gamete. We denote the space of possible IBD states (partitions) by
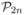 . Table 1 shows the classical 15 states of gene identity among the four gametes of two individuals, A and B. These states are the elements of
. Table 1 shows the classical 15 states of gene identity among the four gametes of two individuals, A and B. These states are the elements of
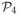 and range from the first where all 4 gametes are IBD, to the last, where none are IBD: grey shading indicates IBD. Each individual has a paternal gamete (subscript p) and a maternal gamete (subscript m). In the depiction of the states, individual A is on the left, and B on the right, and paternal gametes are above and maternal below. Thus, for example, in state numbered 6 in Table 1, the paternal gamete Ap of A is IBD to both gametes of B, but the maternal gamete Am is not IBD to the other three. Also given in Table 1 is the conditional kinship (sometimes referred to as local kinship [9]) corresponding to each state. This is the probability that there is IBD at this locus in gametes segregating from each of A and B. For example, in state-6, this takes the value 1/2, since A segregates Ap or Am each with probability 1/2: Ap is necessarily IBD with either gamete from B, and Am is not.
and range from the first where all 4 gametes are IBD, to the last, where none are IBD: grey shading indicates IBD. Each individual has a paternal gamete (subscript p) and a maternal gamete (subscript m). In the depiction of the states, individual A is on the left, and B on the right, and paternal gametes are above and maternal below. Thus, for example, in state numbered 6 in Table 1, the paternal gamete Ap of A is IBD to both gametes of B, but the maternal gamete Am is not IBD to the other three. Also given in Table 1 is the conditional kinship (sometimes referred to as local kinship [9]) corresponding to each state. This is the probability that there is IBD at this locus in gametes segregating from each of A and B. For example, in state-6, this takes the value 1/2, since A segregates Ap or Am each with probability 1/2: Ap is necessarily IBD with either gamete from B, and Am is not.
Table 1.
The 15 IBD partitions among the four gametes of two individuals
| State | Element of
 (AB) (AB) |
Conditional kinship, ϕ | |
|---|---|---|---|
| 1 |

|
{Ap, Am, Bp, Bm} | 1 |
| 2 |

|
{Ap, Am}, {Bp, Bm} | 0 |
|
|
|
||
| 3 |

|
{Ap, Am, Bp}, {Bm} | 1/2 |
| 4 |

|
{Ap, Am, Bm}, {Bp} | 1/2 |
| 5 |

|
{Ap, Am}, {Bp}, {Bm} | 0 |
|
|
|
||
| 6 |

|
{Ap, Bp, Bm}, {Am} | 1/2 |
| 7 |

|
{Ap}, {Am, Bp, Bm} | 1/2 |
| 8 |

|
{Ap}, {Am}, {Bp, Bm} | 0 |
|
|
|
||
| 9 |
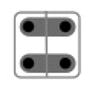
|
{Ap, Bp}, {Am, Bm} | 1/2 |
| 10 |

|
{Ap, Bm}, {Am, Bp} | 1/2 |
|
|
|
||
| 11 |
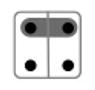
|
{Ap, Bp}, {Am}, {Bm} | 1/4 |
| 12 |

|
{Ap, Bm}, {Am}, {Bp} | 1/4 |
| 13 |

|
{Ap}, {Am, Bp}, {Bm} | 1/4 |
| 14 |

|
{Ap}, {Am, Bm}, {Bp} | 1/4 |
|
|
|
||
| 15 |

|
{Ap}, {Am}, {Bp}, {Bm} | 0 |
IBD is defined relative to a set of founder gametes. In a specified pedigree, the pedigree founders form the relevant set of ancestors; two gametes are considered IBD at a locus if their DNA traces to a common ancestor within the pedigree. In a population, where no relationships among individuals are known, the founder set is the set of gametes of all individuals alive at a fixed point in time. If we consider the (usually unknown) full pedigree ancestry of current individuals back to this time point, the population and pedigree definitions of IBD coincide. In Figure 1 we show a simple example of coancestry between a pair of individuals A and B. The mothers of A and B share common ancestors in the reference founder population, as also do the fathers. At any locus this leads to four possible IBD states: those numbered 9, 11, 14, and 15 in Table 1. The individuals A and B may be IBD in their maternal gametes, their paternal gametes, or both, or neither.
Figure 1.
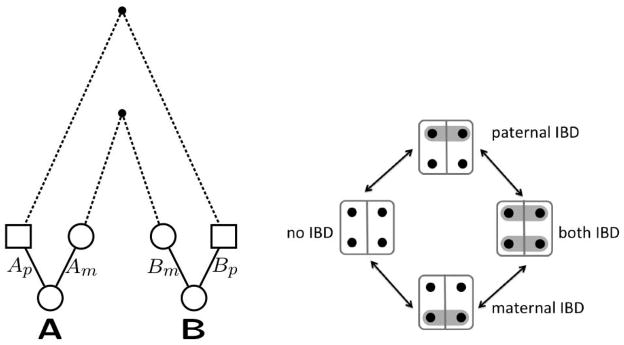
The left figure shows possible coancestry between two individuals A and B. On the right is shown the four possible IBD states at a locus, and possible transitions that could result from recombination events in the ancestral lineages.
In diploid organisms, the IBD state varies across the genome because of recombination. In the example of Figure 1, a state of maternal IBD ({Am, Bm}) will become non-IBD ({Am}, {Bm}) due to any recombination in the meioses in the maternal chain of coancestry, and similarly for paternal IBD ({Ap, Bp}). Once in a state of non-IBD, maternal/paternal IBD will be regained only when all the meioses again align to provide that IBD. With the simple coancestry as depicted in Figure 1, maternal IBD in A and B is independent of their paternal IBD, so transitions among the four possible states occur as shown in the right side of the figure. This process of losing and regaining IBD across a chromosome is not Markov [1], although it is approximately so.
More generally, a natural model for IBD across the genome arises from the coalescent [16] and from the ancestral recombination graph (ARG) of [17] and [18]. The ARG defines the changing coalescents arising along the chromosome as a result of recombination, and the coalescent at a locus defines the IBD partition relative to any fixed ancestral time. Across the genome, the model of changing partitions at a fixed time point induced by the ARG is therefore a natural model for changes in IBD state. Although the coalescent model with recombination is not Markov along the chromosome [19], and thus neither is the induced IBD process at a fixed time point, we approximate this process by a Markov model with a small number of parameters.
Sobel and Lange [20] introduced the descent graph to express the IBD state at a locus among members of a pedigree. The nodes of the graph denote founder genome labels (FGLs) assigned to founder gametes. The edges represent the individuals; each edge connects the two FGL nodes of that individual at that locus. Thus the set of edges at any node denote that the corresponding individuals share that FGL and hence share genome IBD. Note that the node labelling is arbitrary; what is significant is the IBD not the FGL. This enables the descent graph to represent IBD also in a population context, where there are no specified founders. Further, all graphs with the same IBD structure among the labeled edges are equivalent for purposes of analysis of genetic data [21]. Extending this graphical representation of IBD at a locus along the chromosome, we use the term IBD graph for a series of IBD states indexed by genome location.
Model-based IBD detection among individuals in populations
There have been many methods developed for detecting IBD in pairs of gametes or of individuals: for a review see [22]. Model-based approaches are based on a hidden Markov model (HMM), permitting efficient computation [23] and flexible model specification. The hidden space is some specification of the IBD at a locus; for example, for a pair of individuals, the 15 states of Table 1. The genetic marker data at successive loci are assumed to be independent conditional on the hidden IBD state. In a pedigree, the IBD at adjacent marker loci has a transition model determined by the recombination process in the meioses of the specified pedigree. Without a pedigree, there are no explicit constraints on the possible locus-to-locus changes in IBD state among a set of gametes, but the transition model expresses the fact that adjacent states are likely to be similar. For example, in the small example of Figure 1, maternal or paternal IBD may be lost or gained, but loss of both paternal and maternal IBD between two close loci is very improbable.
Here we summarize the HMM model of Brown et al. [6] which we use in our approach. The model is a generalization of the two-gamete model of Leutenegger et al. [24]. The latent HMM process in that model had two parameters: the probability β of IBD between the pair of gametes at any point in the genome, and the rate parameter α of potential changes in IBD state along the chromosome. The more general model of [6] also has these two parameters, with the IBD partition of the gametes at any point having the probability distribution given by the Ewens sampling formula or ESF [25]. Here we reparametrize the ESF in terms of the population kinship, β: that is, β is the prior probability of IBD between any two gametes at any point in the genome.
The HMM transition model across the chromosome is specified as a continuous time Markov chain. That of [6] is based on a modification of the Chinese Restaurant Process (CRP) [26]. This one-parameter stochastic process on set partitions has the ESF as its stationary distribution. Two IBD states have non-zero infinitesimal transition rates if one can be transformed to the other by moving a single gamete among subsets of the partition. The rates of possible transitions are parametrized by the population kinship, β, with an overall scaling of rates given by the rate parameter α and the number of gametes n in the HMM.
In [6], the HMM model was applied to pairs of individuals, using the 15 IBD states among n = 4 gametes. The genetic marker data were were diallelic single nucleotide polymorphisms (SNPs). Over loci, the observed alleles are assumed independent given the underlying IBD state. At any locus, DNA that is IBD is of the same allelic type, while the allelic types of gametes that are not IBD at this locus are independent draws from the population. Population allele frequencies must be provided as input. Genotyping errors are modeled as a small probability that the reported allele differs from the true allele. Differences in allelic types in IBD DNA that are due to mutation are indistinguishable from errors.
The HMM approach can be applied either to phased or unphased genetic marker data. New technologies potentially provide sequence data over long segments of genome [27], so that phased data may be observed, but most current microarray and next-generation sequencing technologies detect variants on short segments of genome, so the data produced are unphased. While statistical phasing methods [28, 4, 29] can be applied, it is also desirable to be able to analyze unphased data directly. The model of [6] accommodated unphased data by redefining the latent Markov chain, conflating IBD states at a locus that are genotypically equivalent [30]. However, in our current approach, we work with the latent state space for 2n identified gametes of n individuals regardless of the form of the data. To use the full latent space with unphased data, we modify the emission model. It is shown in Appendix A that averaging the phased data-probabilities over groups of genotypically equivalent latent states provides the correct model for unphased data.
Probabilities of the IBD states at each locus conditional on the complete (phased or unphased) marker data are computed using the standard forward-backward algorithm for HMMs [23]. A discretization of the hidden process is used to avoid computing matrix exponentials when calculating locus-to-locus transition probabilities. Provided the markers are tightly spaced relative to the rate of state transitions, the prior probability of a change in IBD state between adjacent markers is small and the discrete approximation is accurate. In order that all transitions have non-zero probability locus-to-locus (as they do under the continuous model), a small fraction ε of the stationary distribution is mixed with the discrete jump chain. Using this model, [6] studied the detection of IBD segments among the four gametes of pairs of individuals, under varying levels of linkage disequilibrium in the population, using both phased and unphased genetic marker data.
Although the model of [6] can be extended to an arbitrary number of individuals, the HMM forward-backward calculations are intractable for the model on more than three or four diploid individuals. Time complexity is quadratic in the number of hidden states [23], and the number of partitions grows dramatically with the number of gametes. There are more than 105 IBD states for five individuals, and more than 1013 for ten.
Building joint IBD states from pairwise realizations
It is possible to estimate IBD probabilities between all pairs of individuals, incurring a cost that grows only quadratically in the group size, but in many situations a model for the entire group is necessary. For example, if pairwise IBD estimates are used to calculate covariances among individuals, the resulting matrix may not be positive semi-definite, leading to aberrant results in variance-component analyses. For any major gene model, if a probability of jointly observed trait data is to be computed conditional on inferred IBD, a valid IBD graph is necessary.
Glazner and Thompson [31] presented an attempt at estimating group IBD states by merging IBD inferred among individuals within specified pedigrees with separately inferred IBD resulting from unknown relationships among the distinct pedigrees. The method used two sources of inferred IBD: IBD graphs estimated in the known pedigrees using pedigree-based MCMC methods [14], and pairwise marginal probabilities of IBD estimated among all pairs of individuals using the population-based model of [6]. At each locus, the pedigree IBD graphs were combined to create an initial joint IBD state, and the pairwise states were arranged in descending order of probability. Then, each pairwise state was added to the joint state if it did not conflict with the existing joint state. The aim of this approach was to include as much pairwise information as possible in constructing the joint state, without creating an invalid joint state. The method was shown to be capable of accurately reconstructing LOD scores in a large pedigree using only information about relationships in small subpedigrees. Among the method’s shortcomings were its inability to express uncertainty in the pairwise inferences and the lack of smoothing across marker loci.
Here we propose a new algorithm for building a joint IBD graph incrementally from sampled paths from the pairwise HMM, adding each individual in turn to the IBD graph. As in previous HMM approaches to inferring IBD [6, 31], the hidden states of the pairwise HMM are the 15 states of
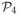 shown in Table 1. However, by conditioning at every stage on the IBD graph across the chromosome sampled among previously considered individuals, we produce joint IBD states consistent among individuals and across the chromosome. That is, at each locus, our output IBD state on a group of n individuals is an element of
shown in Table 1. However, by conditioning at every stage on the IBD graph across the chromosome sampled among previously considered individuals, we produce joint IBD states consistent among individuals and across the chromosome. That is, at each locus, our output IBD state on a group of n individuals is an element of
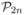 , and we build this element of
, and we build this element of
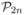 incrementally out of elements of
incrementally out of elements of
 : that is, from pairwise relationships represented by the 15 IBD states of Table 1. This is possible because each element of
: that is, from pairwise relationships represented by the 15 IBD states of Table 1. This is possible because each element of
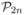 uniquely defines a vector of
elements of
uniquely defines a vector of
elements of
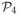 , one for each pair of the n diploid individuals. This space of vectors is denoted
. The target of our inference is the subset of
corresponding to elements of
, one for each pair of the n diploid individuals. This space of vectors is denoted
. The target of our inference is the subset of
corresponding to elements of
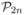 , which we will call valid configurations. Similarly, a collection of
elements of
, which we will call valid configurations. Similarly, a collection of
elements of
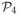 corresponding to the pairs in a set of k individuals is valid if it corresponds to an element of
corresponding to the pairs in a set of k individuals is valid if it corresponds to an element of
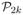 .
.
It is straightforward to check if an element p of
is a valid element of
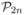 . IBD at a locus is an equivalence relationship on a set of gametes: gametes that are IBD are in the same subset of the IBD partition. Consider the relation R formed by taking the union of all the
states in p, treated as equivalence relations. If R is an equivalence relation, then p is valid and corresponds to an element of
. IBD at a locus is an equivalence relationship on a set of gametes: gametes that are IBD are in the same subset of the IBD partition. Consider the relation R formed by taking the union of all the
states in p, treated as equivalence relations. If R is an equivalence relation, then p is valid and corresponds to an element of
 . Reflexivity and symmetry hold trivially, so the condition is satisfied if R is transitive: i.e. for any three chromosomes a, b, and c, aRb and bRc implies aRc. Conversely, if p is not valid, there is some nontransitive triple {a, b, c}. Any set of three gametes {a, b, c} are in at most three individuals.
. Reflexivity and symmetry hold trivially, so the condition is satisfied if R is transitive: i.e. for any three chromosomes a, b, and c, aRb and bRc implies aRc. Conversely, if p is not valid, there is some nontransitive triple {a, b, c}. Any set of three gametes {a, b, c} are in at most three individuals.
To check validity of p, first any two of the pairwise states composing p that have an individual in common must agree on the IBD status of the two gametes of the common individual. Then, assuming no pairs conflict, we only need to check trios of individuals to ensure that the configuration is valid for all individuals. If the pairwise states in p for all trios of individuals do not create a nontransitive relation, p is a valid configuration. Figure 2 shows an example of an invalid configuration. The IBD of the three pairwise comparisons are shown, with each individual’s paternal gamete above and maternal gamete below. Any two of the three pairs is compatible: in no case is any of A, B, or C implied to have two IBD gametes. However the three pairs are not jointly compatible, since A’s paternal gamete and C’s maternal gamete are both IBD with B’s paternal gamete, but not IBD with each other.
Figure 2.
An example of an invalid configuration in , the space of pairwise IBD states covering a trio of individuals. The grey shading represents IBD gametes. For details see text.
This procedure illustrates that we can determine valid states by considering at most three individuals at a time. This property is used to build a joint state among any number of individuals. Starting from the IBD state inferred for a single pair of individuals, we successively add individuals to the configuration. In adding the k th such individual, we infer the pairwise IBD of this individual with each of the previous k−1 in a way that respects both the constraints of previously inferred IBD and the model for IBD across the chromosome. This is achieved by eliminating from the hidden state space any IBD states which would create an invalid joint configuration, and performing HMM calculations on the reduced state space. This is feasible since only trios involving the current individual and each pair of previous ones need be considered in determining the relevant constraints. A more rigorous specification of the algorithm is given later, but since trios form the core of the method we first consider in detail the case of a single trio.
The case of three individuals
To illustrate the method, we examine the dependence among the pairwise IBD states at locus t among the trio of individuals A, B, and C. Separately, each of the states p4(AB), p4(BC), and p4(AC) can take any value from the fifteen states in
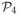 (Table 1). However, there are only |
(Table 1). However, there are only |
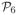 | = 203 IBD states the trio can be in, so the set of consistent pairwise states is a small subset of the 153 = 3375 elements in
| = 203 IBD states the trio can be in, so the set of consistent pairwise states is a small subset of the 153 = 3375 elements in
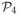 ×
×
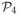 ×
×
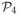 . Fixing p4(AB), the value of p4(BC) can be any state in which the IBD status of B’s two gametes agrees with p4(AB). Once p4(AB) and p4(BC) are fixed, p4(AC) can only be one of a small number of states: at most seven, usually three or less, and sometimes only one. Continuing the example of Figure 2, suppose the states p4(AB) and p4(BC) are as shown. There are then only two possibilities for the IBD state between individuals A and C: the paternal gamete of A must be IBD to the maternal gamete of C, since both are IBD to the paternal gamete of B. Additionally, the maternal gamete of A may or may not be IBD to the paternal gamete of C. This shown in Figure 3. The left part of the figure show the IBD constraints imposed on pairs AB and BC, while the right part shows the two possible states for pair AC. Any other of the 15 states will produce an invalid configuration.
. Fixing p4(AB), the value of p4(BC) can be any state in which the IBD status of B’s two gametes agrees with p4(AB). Once p4(AB) and p4(BC) are fixed, p4(AC) can only be one of a small number of states: at most seven, usually three or less, and sometimes only one. Continuing the example of Figure 2, suppose the states p4(AB) and p4(BC) are as shown. There are then only two possibilities for the IBD state between individuals A and C: the paternal gamete of A must be IBD to the maternal gamete of C, since both are IBD to the paternal gamete of B. Additionally, the maternal gamete of A may or may not be IBD to the paternal gamete of C. This shown in Figure 3. The left part of the figure show the IBD constraints imposed on pairs AB and BC, while the right part shows the two possible states for pair AC. Any other of the 15 states will produce an invalid configuration.
Figure 3.
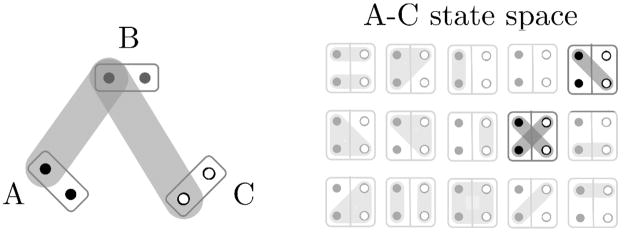
The previously sampled pairwise IBD states p4(AB) and p4(BC) restrict the possible values of p4(AC). For details see text.
The vector p4(ij) of IBD states between two individuals i and j takes values in
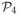 . Suppose that over several consecutive loci p4(AB) and p4(BC) are constant with the values in Figure 3. The transition process for p4(AC) between the two permitted states is exactly that of the full process on
. Suppose that over several consecutive loci p4(AB) and p4(BC) are constant with the values in Figure 3. The transition process for p4(AC) between the two permitted states is exactly that of the full process on
 restricted to the two states; the transition matrix is the full matrix after removing the rows and columns of all but the permitted states. We can do HMM calculations and sample p4(AC) over these loci, conditional not only on the marker data of A and C but also on p4(AB) and p4(BC). This is possible for any fixed values of p4(AB) and p4(BC), although the permitted state space will change accordingly.
restricted to the two states; the transition matrix is the full matrix after removing the rows and columns of all but the permitted states. We can do HMM calculations and sample p4(AC) over these loci, conditional not only on the marker data of A and C but also on p4(AB) and p4(BC). This is possible for any fixed values of p4(AB) and p4(BC), although the permitted state space will change accordingly.
This conditional model for p4(AC) must allow for changes in p4(AB) and p4(BC) along the chromosome. Suppose C stops sharing maternally with B between loci t and t + 1, so that there is no longer any IBD among the four gametes of B and C. Since A and B share paternal gametes, C can no longer share IBD with A’s paternal gamete. The set of permitted states for p4(AC) at locus t + 1 changes to the following: A’s maternal gamete may be IBD to C’s paternal gamete, maternal gamete, or neither, The transition matrix between these two loci is now the full transition matrix restricted to transitions beginning in the two states allowed at locus t and ending in the three states allowed at locus t + 1.
If these sets of states are disjoint, p4(AC) is forced to change states. Such a change is always possible because there is non-zero probability of going from any state to any other under the continuous transition model, and also under the discretized transition model as implemented by [6] (see Model-based IBD detection among individuals in populations). Further, p4(AC) will be able to reach at least one of the new permitted states in a single transition as long as the change in p4(AB) and p4(BC) is due to a change in the ancestral origin of a single gamete. Any single transition in the hidden model can be described (not always uniquely) as a change in the ancestral origin of a single gamete which causes the gamete to jump IBD groups. If the transition in one or both of p4(AB) and p4(BC) is due to a change in one of B’s gametes, the IBD state between C and A is unchanged and no transition is forced. If it is due to a change in A or C, then it can be reached in a single transition in the state between A and C. While this fact is not necessary for specifying a valid conditional model, it does ensure that single transitions in p4(AB) and p4(BC) will not force transitions in p4(AC) which violate the CRP model.
A conditional HMM can also be constructed for sampling p4(BC) conditional on p4(AB). In this case, the only restriction on the state space is that IBD status of B’s two gametes in p4(BC) must match p4(AB). Subject to this restriction, p4(BC) can be in any state, since for any values of p4(AB) and p4(BC) there is at least one consistent value of p4(AC). We reduce the transition matrix accordingly and sample a trajectory for p4(BC).
We can now specify a procedure for generating a sample of p6(ABC), the vector of states in
 for the trio:
for the trio:
simulate p4(AB) unconditionally,
simulate p4(BC) conditional on p4(AB), and
simulate p4(AC) conditional on p4(AB) and p4(BC)
all conditional on the marker data of the two individuals being sampled.
As demonstrated above, this procedure will produce a consistent configuration of pairwise states that specifies a state in
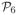 . We now justify its use as an approximation to sampling from the joint distribution Pr(p6(ABC) | xA, xB, xC), with xi the vector of marker data for individual i. The distribution decomposes as:
. We now justify its use as an approximation to sampling from the joint distribution Pr(p6(ABC) | xA, xB, xC), with xi the vector of marker data for individual i. The distribution decomposes as:
The sampled states come from the distribution:
where Q indicates the sampling distribution of the HMM with the state space constrained according to the previously sampled IBD. The difference between the two is that each pair of individuals is sampled conditional only on the data for those two individuals. We are ignoring the dependence of IBD states on other individuals’ data, and the sampling distribution depends on the order in which the individuals are considered. We therefore randomize over orderings of pairs of individuals to obtain a procedure which is exchangeable in the input data.
The case of n individuals
We now return to the general case of n individuals, considering first the sampling approximation to the full joint probability distribution. Li and Stephens [32] used a sequential procedure based on products of approximate conditional likelihoods to calculate likelihoods in a coalescent model with recombination. In similar fashion we decompose the sampling distribution of the trajectory through
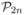 :
:
where x is the data of all individuals. We then replace the terms on the the right side with their approximations: letting x(ij) be the allele data of individuals i and j,
The approximation step is to sample each pairwise configuration conditionally only on the allele data for that pair. The sampling distribution of a pairwise trajectory for a pair of individuals given their allele data and a set of already sampled pairwise trajectories is defined as follows: the hidden trajectory distribution of the basic HMM, with the state space modified to contain only states which do not create (or force the later creation of) an invalid configuration.
The algorithm for any number of individuals is given in Table 2; the references to steps of the algorithm below refer to the numbered lines of this table. As in Li and Stephens [32], the approximate sampling distribution is not exchangeable in the individuals. Thus for each independent iteration of the sampling algorithm, we first randomly permute the individuals (Step 2). Beginning with an empty group state, each individual is added to the group in the permuted order. Additionally, as each individual is added, the individuals already in the group are permuted (Step 5) to obtain the order in which to sample the pairwise trajectories for the new individual each of them. Since many samples must be generated in any case, this resampling over orderings does not create an additional computational burden.
Table 2.
Algorithm to sample an IBD graph on n individuals from SNP data
| 1 | Initialize to the empty IBD graph. |
| 2 | Randomly permute the individuals and label them {A1 … An} |
| 3 | Sample from Q[p4(A1A2)|x(A1A2)] and add the trajectory to . |
| 4 | For 2 < k ≤ n |
| 5 | Randomly permute individuals {A1 … Ak−1} and label them {B1 … Bk−1}. |
| 6 | For 1 ≤ i < k |
| 7 | Sample from , x(BiAk)] and add the trajectory to . |
| 8 | End for I |
| 9 | End for k |
| 10 | Return an IBD graph on n individuals, . |
To build a joint state, we first sample a trajectory of IBD states for a pair of individuals using the basic HMM (Step 3). Then a trajectory for one individual and a third individual is sampled, subject to the constraints imposed by the first pairwise trajectory. We sample a trajectory for the third side of the triangle, conditional on the other two. We now have three compatible pairwise states which form a joint IBD state for the three individuals.
To illustrate we use again the example of Figure 3. Assume now that pairwise trajectories across loci have been sampled for pairs AB and BC. The left part of Figure 3 shows, at a single locus, the incomplete joint state being constructed. The IBD in pairs AB and BC constrain the IBD for pair AC to only the two IBD states shown in the right part of the figure. Constraining the state space in this way is minimal in the sense that the only states ruled out are those which lead to an invalid configuration. That is, the support of the sampling distribution matches that of the true conditional distribution; no possible valid joint configurations are eliminated. Figure 4 shows the sampling of a trajectory between two individuals where some of the 15 states have been precluded by previously inferred IBD. The precluded states are shown in grey while the permitted states are shown in black. The trajectory is sampled according to the relative probabilities of permitted states in the restricted HMM.
Figure 4.
The HMM state space is restricted to the IBD states which are compatible with existing IBD states between other pairs. The solid line indicates a possible trajectory through permitted states along the chromosome.
This restricted HMM process is then repeated for the pairwise IBD between the new individual and each individual already considered (Step 7). The appearance of in the conditioning of the HMM sampling distribution Q indicates that the space of possible states for the pair of individuals under consideration is reduced to only those states which do not conflict with the group IBD state in the process of being constructed. Appendix B demonstrates that the constrained state space when adding an individual k is never empty at any locus. There is always at least one allowed state for a pair to be in, given an existing configuration of all pairwise states for a group and some of the pairs of formed by individual k and the group.
The software package ibd_stitch implements this algorithm, and is available at https://github.com/cglazner/ibd_stitch. Further details of the algorithm are given in Appendix B.
Trait mapping inference using IBD graphs
In order to make inferences about the location of genes affecting a trait, we need to connect IBD graphs to a likelihood model parametrized by a hypothesized trait locus. The traditional mechanism for doing so is the LOD score [12], defined for a particular locus as the log likelihood-ratio between the hypothesis of a trait driven by a gene at the locus and the hypothesis of an unlinked trait.
Given marker data x and trait data y on a group of individuals in a pedigree, we compare the models Γ and Γ0, where Γ(t) hypothesizes a trait location t on the chromosome of the markers, and Γ0 assumes that the trait and marker data are independently distributed on the pedigree. Because it assumes this independence, model Γ0 can be factored into a trait model ΓT and a marker model ΓM:
| (1) |
On large pedigrees, the numerator cannot be calculated exactly. Following [7] we express the likelihood under Γ as an expectation over all possible IBD patterns
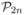 on the pedigree:
on the pedigree:
In this equation, ΓT(t) is the marginal trait model, ΓT, augmented by the trait location hypothesized in Γ(t). Simulating B realizations pi from Pr(p | x) and computing the likelihood of the trait data as a function of p, we obtain a Monte Carlo estimate of L(t):
| (2) |
Tong and Thompson [33] developed methods for efficient MCMC sampling of IBD graphs on large pedigrees, and implemented LOD score estimation using equation (2). Equation (2) also permits the separation of IBD inference and trait likelihood computation: IBD graphs may be realized conditional on marker data, and stored in a compact format. These graphs can be used as input to compute L̂(t) for any t without further reference to the marker data or pedigree structure [14]. Additionally, equivalence of IBD graphs across realizations and across locations can be determined [21], and used to ensure each distinct LOD score contribution is computed once only.
This suggests an approach to estimating a LOD score in the absence of a pedigree. IBD graphs are sampled using ibd_stitch, and then used to calculate trait likelihoods as in equation (2). However, this is insufficient to obtain the LOD score (1). Without a pedigree, there is no basis to compute the denominator of the LOD score. Moreover, in a pedigree, variation in IBD across loci is limited by the tightly constrained changes in descent patterns in the pedigree. When IBD is estimated without pedigrees, the average level of IBD tends to vary across the chromosome, so the variation in L̂(t) is driven more by average relatedness than by concordance between the trait and the estimated IBD pattern at a locus.
To normalize L̂(t) in a way that compares the degree to which different hypothesized causal locations have IBD patterns which accord with the trait, we adopt a permutation approach analogous to that of population-based case-control studies. That is, we permute the trait values assigned to the edges of our sampled IBD graphs. We generate D random permutations σj of the trait data. For a particular IBD graph pi, the term
gives a measure of trait likelihood at t holding fixed the sampled structure of IBD at the locus disassociating the IBD from trait values. Summing this quantity over sampled IBD graphs, we obtain the estimator
| (3) |
which, at each locus, measures the relative likelihood of the trait given the sampled IBD graphs to that given only the sampled IBD structures at the locus. We can view log10(L̃(t)) as analogous to a LOD score because we expect it to be highest when the IBD reflects the allelic similarity driving the trait. The null hypothesis for the permutations at each locus is that the individual-specific joint IBD at the locus is independent of the individuals’ trait values.
Data simulation 1: Simulations on an Iceland pedigree
Two simulated datasets were created to assess ibd_stitch. The aim in both cases was to create realistic study populations with high levels of relatedness and a trait driven by a genome segment shared IBD in the population. For purposes of illustration, we use the same major-gene model for this trait locus as was used by [31].
The first set of test data was one for which the true descent pattern was known. The data were generated using a subset of a large Icelandic pedigree [34]. The pedigree subset spans twelve generations and contains 107 individuals. We assume that this extended pedigree represents unknown relationships that connect several recent 3-generation pedigrees. The members of three such families, with a total of 31 individuals, were designated as “observed” individuals.
The descent pattern and haplotypes for this data were both simulated. A trait locus was chosen, and at this locus one FGL of one founder was designated the “trait allele” q. A descent pattern was generated which propagated this allele to each of the three observed families, but was not otherwise constrained. A quantitative trait on the 31 “observed” individuals was generated by assigning mean trait values according to the presence of allele q or alternate “normal” allele Q. That is, the model for the vector y of trait values for the observed individuals is
| (4) |
For our example, μ = 0, 4, and 5 for trait genotypes QQ, Qq, and qq respectively, and the residual variation e is a vector of independent Normal variables with variance 4.0.
Descent across the rest of the chromosome was simulated according to Mendelian laws and the linkage map, conditional on the pattern at the trait locus. Once the descent within the pedigree is simulated, assigning haplotypes to founders determines haplotypes for the entire pedigree. In order to produce realistic haplotypes, founder haplotypes were simulated using the beaglesim procedure on the BEAGLE model [35] generated by [6] in a real-data analysis. This procedure generates haplotypes that have, probabilistically, the local linkage disequilibrium (LD) structure of original haplotypes input to BEAGLE, but no features of the original haplotypes are identifiable. As described by [6], the beaglesim procedure also allows for relaxation of the LD via a parameter which is the probability that the local haplotype structure is randomly “broken” at each marker. For the current simulation, a value 0.2 was used, limiting LD to a range of 5 markers, on average.
A total of 10,188 markers were simulated over 200 cM of chromosome, and the resulting haplotypes of the 31 “observed” individuals constructed. The methods described above were used to obtain realized IBD graphs across the chromosome. These graphs were used to obtain estimates both of the numerator log-likelihood log10 L̂(t) ( equation ( 2)) and of our LOD-score analogue log10 L̃(t) (equation (3)) based on the trait data y under the trait model (4). In analyzing the trait data y, trait genotypes are of course unobservable. In these analyses, a value 0.2 was used for the allele frequency of hypothetical trait allele q [31].
Data simulation 2: real marker data on a Pig Pedigree
A second study of ibd_stitch was performed using a dataset for which only the trait was simulated, with the marker data and underlying relationships among individuals coming from real data. Genus PIC, a pig genetics firm, provided a data set containing 5772 individuals genotyped at 6973 markers on one chromosome. These data overlap with the genotypes made publicly available by Genus PIC and described in [15]. The data provided by Genus PIC also included a pedigree containing 11,544 members and a genetic map for the chromosome of the markers.
SNPs were filtered as follows: markers were discarded if the genotypes were missing in more than 5% of individuals, as were individuals missing more than 5% of their marker genotypes. The markers were further thinned to speed computations and reduce the level of LD in the dataset, since high LD impacts accuracy of IBD inference [6]. To retain the (on average) most informative markers for which relative allele frequencies can be most accurately estimated, markers with minor allele frequency less than 0.3 were also discarded. The final SNP dataset contained 1034 markers typed on 5742 individuals. Population allele frequencies were estimated from these data.
Five subpedigrees of pigs were chosen for analysis. To obtain closely related genotyped individuals, a pool of subpedigrees was created by choosing random proband individuals and selecting all individuals within three parent/child meioses of the proband. The candidate subpedigrees were then inspected manually, to remove subpedigrees with few genotyped individuals. Five subpedigrees with a high proportion of typed individuals were selected, comprising a total of 69 individuals.
The trait used in the analysis was simulated based on IBD observed in the selected individuals. Preliminary samples of IBD graphs on the individuals were generated. A locus which appeared to show a small number of well-resolved IBD groups was chosen as a good candidate for simulating a trait. Additionally, the cleaned marker data for the selected individuals were analyzed using version 3.3.2 of BEAGLE [36] as an independent method of IBD detection. With the default settings, BEAGLE was also used to fit a model of haplotype clusters in the sample. At the candidate trait locus, only two clusters were detected, defining a diallelic trait locus, with alleles q and Q. This “trait locus” was used as the basis for generation of a quantitative trait y using the same model equation (4) as above. Again, in analysis of trait data, “trait genotypes” are unobservable. As for that example, IBD graphs were realized from the marker data. These IBD graphs then provided estimates of the L̃(t) function (equation (3)), under the trait model (4) for the observed y.
Comparison with a pairwise approach
Our approach provides jointly consistent IBD realizations among individuals and across loci, and thus may be used with any trait model. However, these realizations may also be reduced to estimates of pairwise IBD at each locus and so provide location-specific estimates of “local kinship” (Table 1). Our method may thus be compared with a random-effects QTL mapping approach such at that of [9] who also proposed a method of LOD score estimation for that model using “local kinship” inferred from marker data. We make this comparison using the simulated data of the Iceland example. Since the descent is simulated we have the true IBD state for each pair of individuals at every locus.
The approach of [9] begins with a moment-based estimate of IBD from marker allelic similarities between the two members of each pair of individuals. This provides pairwise estimates of global (genome-wide) and local kinship coefficients (Table 1). These are then used to fit random-effects variance-component models to the quantitative trait data [10]. The full model is
| (5) |
where 1 is a vector of ones, and e is a vector of independent Normal components each with variance . The random effect zj attributable to location j is Normal with mean 0 and variance where Φj is the local kinship matrix at locus j. The global additive genetic effect za is Normal with mean 0 and variance , where Ψ is the global kinship matrix. Since our approach does not assume availability of genome-wide marker data, we have no basis for the marker-based estimation of Ψ. However, since even using the true pedigree-based kinship there was scant evidence for a global additive genetic variance term (see Results), we ignored this component in subsequent analyses.
We first compared estimates of local kinship Φj at locations j chromosome. For the kinships from ibd_stitch, we simply averaged the locus-specific kinship for each pair of individuals and each locus position over the realized IBD graphs. For the allelic similarity (identity-by-state: IBS) approach we followed [9] as closely as feasible. We used a moment-based estimator of local kinship (equation (2) of [9]) over small windows of about 100 Kb to each side of each SNP. These windows are somewhat larger than the 50Kb advocated by [9] due to our more sparse marker data (10,188 markers over 200 cM). As noted by [9] these estimates are quite noisy, so we smoothed over broader windows of about 2 Mb width.
True locus-specific kinship can take only one of the four values in H = {0, 1/4, 1/2, 1} (Table 1 and [9]). We therefore additionally computed estimates constraining the values to one of these four values. This was done both for the estimates from the IBD graphs and for the smoothed IBS-based estimators. Although we did not implement the full joint smoothing and constraining algorithm proposed by [9], it seems our constrained estimates should be comparable to the outcome from that procedure.
We computed a random-effects trait-model LOD scores using the quantitative trait data on the 31 individuals of this Iceland data set [10]. Since we assumed , we reparametrized in terms of and local heritability . For the trait model (5) and at each locus j, this LOD score then compares the base-10 log-likelihood maximized over and , with that for the null model log-likelihood maximized over with . We computed five such LOD score curves over locations j across the 200cM chromosome: one for the local kinships from the true IBD, and one for each of these four estimates (ibd_stitch —raw average and then also constrained; IBS-based —smoothed, and then also constrained).
Results
Results of ibd_stitch on the Iceland example
The ibd_stitch program was used to analyze the simulated datasets with the goal of estimating a mapping score that would inform inference of the location of the trait. In the HMM model, the average prior kinship was set as β = 0.05 and the stationary distribution fraction used to accommodate discretization of the latent process was set equal to ε = 0.1. The genotyping error rate was set 0.01 (although no errors were simulated in the Iceland data). Under this model and the data on 10,188 markers, 200 IBD graphs were realized across the 200 cM chromosome. Since the Iceland marker data were simulated, the haplotypes of each observed individual were known. The above generation of IBD graphs and subsequent computations was therefore done twice: once with the phased haplotypes, and then also assuming only genotypic data.
Using the trait data and trait model, likelihoods were computed at a subset of 334 marker positions across the 200 cM chromosome, at a spacing slightly over 2 per cM. Since the descent pattern was simulated, the true IBD among the individuals was known. The likelihood curve produced by this true IBD was used as a standard against which to measure the sampled IBD graphs. Figure 5 shows estimates of log10 L̂(t) based on the true IBD and the graphs sampled using ibd_stitch. The data for ibd_stitch are the phased haplotypes of the 31 observed individuals. Although no assumptions are made in the analysis about any relationships among the 31 individuals, the estimated curve follows the truth almost exactly, showing that the sampling method accurately reconstructs the simulated IBD on the pedigree. The trait locus is correctly identified by the maximum of the linkage mapping curve.
Figure 5.
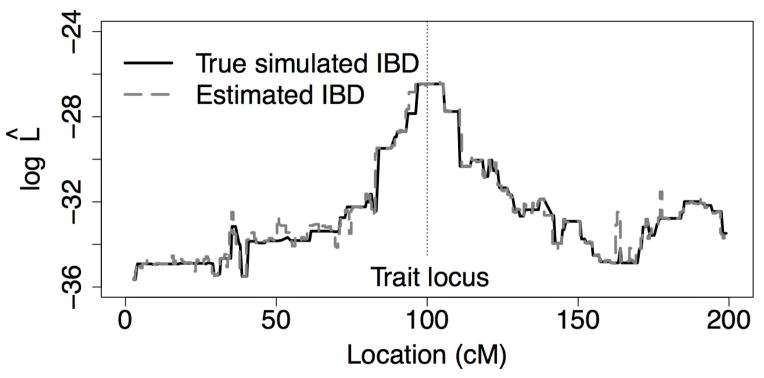
Unnormalized base-10 log-likelihoods for a simulated quantitative trait, calculated using the true IBD graph used to simulate the data and IBD graphs estimated using ibd_stitch.
As discussed in the Methods Section (equation (3)) without the pedigrees of the families composing the dataset we cannot calculate the trait data probability necessary to normalize a LOD score. To produce a linkage score without pedigrees, we calculate L̃(t) (equation (3)). This approach normalizes the likelihood at a locus by an average over likelihoods calculated by permuting the trait among individuals. Figure 6 shows log10 L̃(t) for the IBD graphs sampled on the Iceland pedigree; 200 permutations were used for the normalization. As with the unnormalized likelihoods, the curve achieves a maximum at the simulated trait locus, although the trait is not as cleanly resolved as in the unnormalized case. Away from the trait, where there is no genetic association with the trait, the curve decays towards zero as expected.
Figure 6.
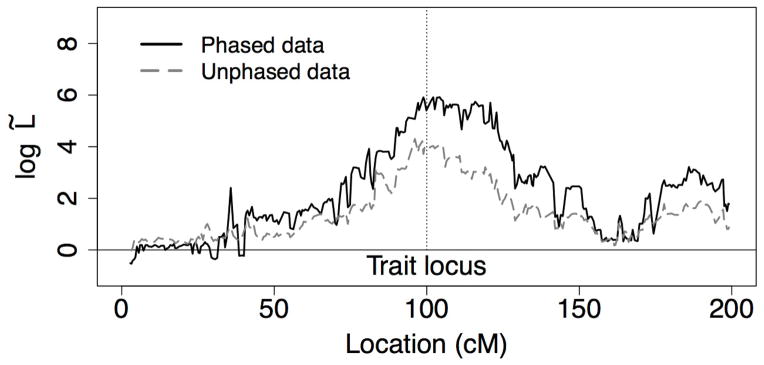
Permutation-normalized log-likelihoods (log10 L̃(t)) calculated at points along the simulated Iceland chromosomes. The vertical line indicates the trait locus.
Figure 6 also shows the result for an analysis using only the unphased genotypes of the 31 observed individuals. Some information is lost, with a generally lower log10 L̃(t) curve, but the trait location is again well-identified.
Results of ibd_stitch on the pig data
In the case of the pig data, the true IBD is unknown and the genotype data at the 1034 selected SNP markers are unphased. Using these unphased marker data and the same prior model in ibd_stitch as for the Iceland data, 1000 IBD graphs across the 300cM chromosome were realized.
Likelihoods for the simulated trait were computed at all 1034 marker positions (about 3 per cM). The same procedures as for the Iceland data were applied with 200 permutations of the trait value used to normalize the likelihood curve. Figure 7 shows the normalized likelihood curve. Without the normalization, there was no signal at the trait locus, and values of L̂(t) were quite noisy. With the locus-dependent normalization provided by the 200 permutations, the log10 L̃(t) curve correctly spikes at the trait locus, showing that the sampled IBD graphs capture the shared genome which drives the trait.
Figure 7.
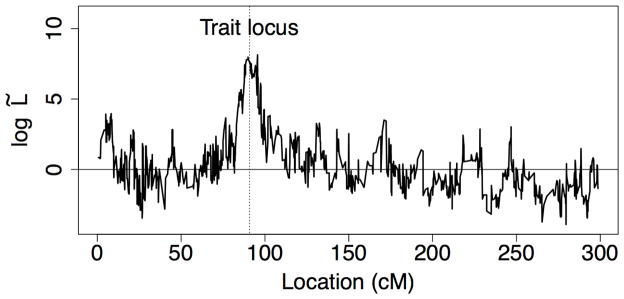
Permutation-normalized log-likelihoods (log10 L̃ (t)) calculated at points along the Genus PIC chromosomes. The vertical line indicates the trait locus.
Results of comparison with a pairwise approach
With this small data set of 31 observed individuals, the random-effects likelihoods (model of equation (5) typically maximized at a heritability of either 0 or 100%. This is particularly so in the case of local heritabilities, , where every local kinship coefficient in Φj is such that the individuals share 0, 1 or 2 genes IBD and are thus as if unrelated (ϕ = 0), parent offspring (ϕ = 1/4), or MZ twins (ϕ = 1/2), or even, in a few cases, inbred MZ twins (ϕ = 1) (See Table 1). Additionally, the matrix of local kinships is typically only positive semi-definite. We therefore restricted both global and local heritability to be ≤ 99%.
Fitting a global polygenic model (5) with , using for Ψ the full true pedigree-based kinship matrix, the heritability estimate was at this upper limit. However, the base-10 log-likelihood relative to 0% heritability ( ) was 0.38. Using only the pedigree clusters of more closely related individuals as in [9], it reduced to 0.27. Given this small impact of global relatedness, we assumed in subsequent analyses. Additionally, as found by others [9, 6], with dense genetic marker data assumptions regarding genome-wide kinship have almost no impact on local kinship estimates.
The local kinship estimates from the true IBD and from each of the four estimates described in the Methods section (ibd_stitch —raw and constrained; IBS-based —smoothed, and then also constrained) were computed at each of the same 334 marker locations as used for the likelihood computations on these data described above. At any locus, there are 496 values of pairwise kinship among 31 individuals (including self-kinships). Figure S1 of the Supplementary material shows the correlation of these 496 values with the simulation truth at each of the 334 test locations across the chromosome. As described more fully in the Supplementary Material, the pairwise kinship estimates from joint IBD graphs estimated by ibd_stitch show higher correlation with the true values than do those from the IBS-based methods. Constraining the pairwise kinship values to the set H = (0, 1/4, 1/2, 1) generally had little impact.
In total over the 334 test positions there are 496×334 = 165, 664 local kinship values estimated by each of the estimators. Of these, under the simulation truth, there are 123,801, 27,949, 13,513 and 401 values of ϕ = 0, 0.25, 0.5 and 1, respectively. Figure S2 of the Supplementary Material shows boxplots of the (unconstrained) ibd_stitch and IBS-based estimators at each of these four true values. Generally, the spread of the distribution is much less for the estimator based on the IBD graphs from ibd_stitch, although there are some extreme outliers especially at ϕ = 0.5. Whereas the estimators from ibd_stitch find the high kinship values quite well, the IBS-based estimator is downward biased at ϕ = 0.5 and fails to find the values ϕ = 1.
The comparative performance of these local kinship estimates then has impact on a randome-effects-model LOD score. In this fitted model, equation (5) with , at each test position j there are two parameters and . Likelihoods typically maximized either at providing a LOD score of 0, or at the upper limit . For several of our local kinship estimators, Figure 8 shows these LOD score curves evakuated at the same 334 marker locations.
Figure 8.
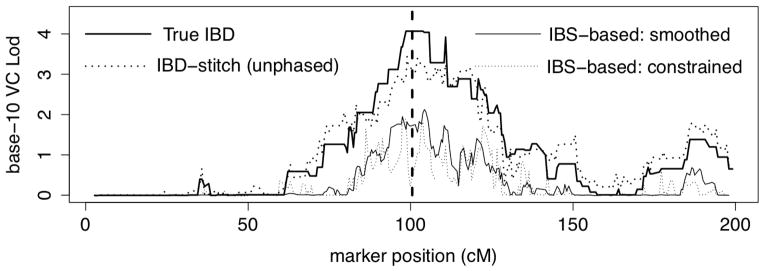
Lod scores under a random-effects model using several alternative estimators of local pairwise kinship across the chromosome. The vertical line indicates the trait locus.
This figure may be compared with Figures 5 and 6. Note that the true pairwise IBD gives a lower LOD score signal at the trait locus than did the true joint IBD graph (Figure 5). In Figure 6 the LOD score from IBD estimate from unphased data was significantly lower than that given by the phased data which effectively represented the signal provided by the true joint IBD. However, in Figure 8 the estimate from ibd_stitch using unphased data is very similar both to that shown in Figure 6 and to that achievable if the true pairwise IBD is known. For the results from ibd_stitch, both the raw average values over IBD-graph realizations and the values constrained to the allowed values in H = (0, 1/4, 1/2, 1) gave almost identical curves, so only the former is shown.
As seen in Figure 8, the IBS-based estimates show a similar LOD score curve but with a much weaker signal. In this example, constraining the IBS-based estimates to H did not improve the estimates. In fact, at the trait locus this constraint destroyed the signal, because the small region with some ϕij values equal to 1 was not found and this high 4-gamete IBD (State-1 of Table 1) contributes to the linkage signal.
Discussion
In this paper, we have shown how an analogue, L̃(t), of a classical linkage LOD score can be computed in the absence of any pedigree information. Although we use only population-based data and models, our approach relies on the inference of IBD and is thus inheritance-based. It stands in contrast to genome-wide association studies (GWAS) [37], which analyze only the allelic variation at genetic marker loci, considering neither the dependence among individuals due to relationships, nor across the genome due to linkage.
The key to our approach is a new method for sampling joint IBD trajectories across a chromosome sequentially among individuals, based on their phased or unphased genetic marker data. These sampled trajectories (IBD graphs) provide a Monte Carlo estimate of the numerator of the classical LOD score: the probability of trait data given the marker-based inheritance at hypothesized trait locations. Although the examples of this paper focus on a quantitative trait, this approach is applicable to any trait model for which probabilities of trait phenotypes can be computed on a specified IBD graph, and so the approach is equally applicable to dichotomous traits. However, since there is no pedigree, there is no basis on which to compute the classical denominator: the probability of trait data unconditioned on genetic markers. To address this, we develop a permutation approach, in which trait values are permuted on the edges of the IBD graph. The resulting joint trait probability is based on the same level and structure of whole-sample IBD as that realized at that locus from the marker data, but with the individual-specific trait values disassociated from the individual-specific IBD.
In both the example data sets, the L̃(t) curve is erratic compared to a traditional pedigree-based LOD score: the constraints on population-inferred IBD are much weaker than those imposed by an assumed pedigree. Like a LOD score, L̃(t) maximizes at true trait locations, but it does not have the negative classical LOD scores that result from marker-based evidence against linkage. Moreover, where the set of individuals contains multiple close relatives, as in the examples of this paper, the score will usually be positive even at locations unlinked to the trait. Given the joint IBD structure at any locus, close relatives are likely those who share genome IBD and these same individuals show phenotypic similarity, but the permutation approach of equation (3) disassociates IBD and phenotypic similarity. The quantitative interpretation of L̃(t) scores requires additional study.
Although our approach focuses on estimation of IBD that is jointly consistent among multiple individuals, these joint realizations can readily be reduced to summary IBD measures such as locus-specific pairwise kinship matrices which may then be used in a random-effects model for a quantitative trait. Our comparisons with smoothed moment-based estimators of pairwise IBD show that our realized IBD graphs provide more accurate estimates. Without further study, we cannot conclude whether this is due to the use of joint IBD per se, or whether another pairwise estimator could perform better. In either case, our results from just 200 realized IBD graphs across the chromosome are very encouraging. Also important is that, in this example, the LOD score estimate from joint IBD using unphased marker data is almost the same for the major gene trait model as for the random-effects model. For a quantitative trait, the latter may be a preferred approach, since there then is no requirement to specify the trait model in order to compute the trait likelihood.
Our IBD estimation approach shares with earlier methods the approximations inherent in discretization on the HMM, with its marker-to-marker transition process. While the approximations are accurate for tightly linked markers, and the latent IBD model is in any case an approximation to the true ancestral processes in the population sample, analyses based on the original continuous genome model might be preferred. Unfortunately such analyses seem computationally intensive, at best. An MCMC approach which samples IBD transition points under the continuous genome model has been implemented for sets of up to 40 gametes over regions of up to 10 Mbp [38], but scalability beyond this is an issue. An alternative MCMC particle filter approach [39] has also been implemented (Glazner PhD thesis: unpublished), but has similar scalability issues.
The method of sequential sampling of IBD developed in this paper can also incorporate pedigree-based IBD information. An IBD graph realized conditional on marker data within small subpedigree units using pedigree-based methods [14], can be taken as initial input into the ibd_stitch process. This approach was applied to the Iceland example, pre-sampling IBD within each of the three small subpedigrees of observed individuals (but not between them). It is interesting that analysis with this additional subpedigree IBD information using unphased genetic marker data recovers almost the IBD of the phased analysis (Figure 5) that assumes no pedigree information at all (data not shown). Essentially, it seems that the specification of the local family structure serves to phase these individuals but provides no broader IBD information.
In conclusion, we believe our population-based linkage scores extend classical analysis to situations where there may be samples of related individuals, but where no pedigree relationships are specified. We emphasize there is no attempt to estimate a pedigree, nor even levels of relatedness among individuals. The process of meiosis has high variance [22], and such estimates would serve no useful gene mapping process. Rather we infer the realized IBD at specific genome locations that is the actual basis of mapping information.
Supplementary Material
Acknowledgments
This work was supported in part by NIH grant R37 GM046255 and T32 GM081062. The authors are grateful to Genus PIC and Dr. Matt Cleveland for providing pedigree, genetic marker genotypes, and genetic marker map information used in our second example data set. We are also grateful to Ellen Wijsman, Steven Lewis, Fiona Grimson and John Ranola for comments on an earlier draft, and to Jesse Raffa and two anonymous referees for comments that improved the revised text.
Appendix A: Phased and unphased data
At any locus, the latent IBD states on a set of 2n gametes of n diploid individuals may be divided into classes, such that all states in a class give the same probability to a given set of n unphased genotypes on the individuals. For example, the fifteen partitions of a set of 4 gametes, give rise to the nine states relevant to the joint genotype probabilities of two diploid individuals. In general, the subdivision of states can be defined by considering the orbits under a group of 2n transformations g generated by interchange of the two gametes of each diploid individual [30].
To accommodate both phased and unphased data into an HMM using the same latent IBD states on 2n gametes, we define the same interchange transformations to the two alleles of an individual’s genotype. At a locus, let R denote the (unknown) ordering of the two alleles of each individual relative to some fixed (e.g. paternal then maternal) ordering, r0. If X is an observed ordered set of 2n alleles at a locus
for any X, any latent IBD state i, any allele ordering R, and any g in the group of transformations. Note also that values of R are equivalent to values g; each individual’s two alleles are either interchanged or not, relative to the fixed order.
Consider now augmenting the state space of the HMM at each locus with the random variable, R. In the case of completely phased data R is known, say R = g*:
That is, the model with augmented haplotype phase is identical to the original model when the data are completely phased.
When data are unphased, there is no prior information about R, so each value g has prior probability 1/2n:
where r0 is the fixed order. That is, averaging the emission probabilities over orbits of states which map to one another over g provides the correct probabilities to model unphased data using the full 2n gamete latent IBD states in the HMM.
The idea of modifying the emission function can be extended to represent more complicated states of partial phase information, but in this paper we restrict attention to genotypes that are either completely phased or completely unphased.
Appendix B: The joint sampling algorithm
The algorithm of Table 2 samples pairwise IBD trajectories from the distribution Q, which is the HMM of [6] with certain states removed from the state space to ensure that a valid joint IBD state will result once all pairs have been sampled. The algorithm assumes that the reduced state space is never empty, so we must demonstrate that this is always the case.
Our proof proceeds by induction. For the first pair of individuals sampled, there are no constraints on the state space. When attaching the kth individual to the joint state, suppose we have already obtained a valid joint IBD trajectory for the first k−1 individuals. In the notation of Table 2, we refer to these individuals as the set β = {B1, …, Bk−1}; let p2(k−1)(β) be the joint IBD state at a locus for these individuals. We sample a pairwise trajectory between individuals Ak and Bi, supposing that we have sampled states between individual Ak and individuals B1 through Bi−1. The joint IBD state composed of these pairwise states at a particular locus is denoted p2i(α), with α = {Ak, B1, …, Bi−1}.
We determine the set of valid choices for the state p4(BiAk). To do so, we examine each possible trio {Ak, Bi, Bj} with j < i. We have sampled pairwise states for two of the three pairs in the trio, and we rule out any states which would create an invalid trio as illustrated in Figure 3. To show that there is at least one allowed pairwise state for p4(BiAk), it suffices to show that there is a valid state p2k(γ) covering the individuals γ = {Ak, B1, …, Bk−1} which is in agreement with p2(k−1)(β) and p2i(α). The pairwise state p4(BiAk) imposed by p2k(γ) cannot have been ruled out in our conditioning step.
To discuss the partitions in question more precisely, we consider the lattice of partitions on n. individuals,
 [40]. A lattice is a set closed under two operations, ∧ and ∨, called meet and join and satisfying certain algebraic properties. Partitions of a set form a lattice with a partial ordering defined by refinement: a ≤ b if and only if a can be derived from b by splitting some blocks. Two elements are in the same block in a∧b if and only if they are in the same block in both a and b. The partition consisting only of singletons is the least element in the lattice, and the partition of all elements into a single block is the greatest. A singular partition 1X is the partition placing all elements of the set X in a single block and all other elements in singleton blocks. We implicitly embed a partition on a subset of the individuals in the lattice by assuming that individuals outside the subset have all gametes in singleton blocks. Conversely, we say a partition aX of the set X induces a partition aS of S ⊂ X if 1S ∧ aX = aS.
[40]. A lattice is a set closed under two operations, ∧ and ∨, called meet and join and satisfying certain algebraic properties. Partitions of a set form a lattice with a partial ordering defined by refinement: a ≤ b if and only if a can be derived from b by splitting some blocks. Two elements are in the same block in a∧b if and only if they are in the same block in both a and b. The partition consisting only of singletons is the least element in the lattice, and the partition of all elements into a single block is the greatest. A singular partition 1X is the partition placing all elements of the set X in a single block and all other elements in singleton blocks. We implicitly embed a partition on a subset of the individuals in the lattice by assuming that individuals outside the subset have all gametes in singleton blocks. Conversely, we say a partition aX of the set X induces a partition aS of S ⊂ X if 1S ∧ aX = aS.
Using this terminology, we must show the existence of some partition p2k(γ) which induces p2(k−1)(β) on β and induces p2i(α) on α. By assumption
That is, the two existing joint states agree where they overlap, on the set δ = {B1, …, Bi−1}. We use a lemma from Ore [41, Theorem 11]:
If a is singular and a ≥ b, then for any c,
| (6) |
Applying equation (6), we have 1β ≥ p2(k−1)(β) by definition and
So the partition p2(k−1)(β) ∨ p2i(α) induces p2(k−1)(β); by the same reasoning, p2(k−1)(β) ∨ p2i(α) induces p2i(α). We conclude that p2(k−1)(β) ∨ p2i(α) meets our requirements for p2k(γ), and therefore at every locus there is some pairwise state which has not been ruled out by the conditioning step.
References
- 1.Donnelly K. The probability that related individuals share some section of genome identical by descent. Theoretical Population Biology. 1983;23:34–63. doi: 10.1016/0040-5809(83)90004-7. [DOI] [PubMed] [Google Scholar]
- 2.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, Sham PC. PLINK: a tool-set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Browning SR, Browning BL. High-resolution detection of identity by descent in unrelated individuals. The American Journal of Human Genetics. 2010;86:526–539. doi: 10.1016/j.ajhg.2010.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kong A, Masson G, Frigge ML, Gylfason A, Zusmanovich P, Thorleifsson G, Olason PI, Ingason A, Steinberg S, Rafnar T, Sulem P, Mouy M, Jonsson F, Thorsteinsdottir U, Gudbjartsson DF, Stefansson H, Stefansson K. Detection of sharing by descent, long-range phasing and haplotype imputation. Nature Genetics. 2008;40:1068–1075. doi: 10.1038/ng.216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gusev A, Lowe JK, Stoffel M, Daly MJ, Altshuler D, Breslow JL, Friedman JM, Pe’er I. Whole population, genome-wide mapping of hidden relatedness. Genome Research. 2009;19:318–326. doi: 10.1101/gr.081398.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brown MD, Glazner CG, Zheng C, Thompson EA. Inferring coancestry in population samples in the presence of linkage disequilibrium. Genetics. 2012;190:1447–1460. doi: 10.1534/genetics.111.137570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lange K, Sobel E. A random walk method for computing genetic location scores. American Journal of Human Genetics. 1991;49:1320–1334. [PMC free article] [PubMed] [Google Scholar]
- 8.Thomas A, Camp NJ, Farnham JM, Allen-Brady K, Cannon-Albright LA. Shared genomic segment analysis mapping predisposition genes in extended pedigrees using SNP genotype assays. Annals of Human Genetics. 2008;72:279–287. doi: 10.1111/j.1469-1809.2007.00406.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Day-Williams AG, Blangero J, Dyer TD, Lange K, Sobel EM. Linkage analysis without defined pedigrees. Genetic Epidemiology. 2011;35:360–370. doi: 10.1002/gepi.20584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Almasy L, Blangero J. Multipoint quantitative-trait linkage analysis in general pedigrees. American Journal of Human Genetics. 1998;62:1198–1211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Han L, Abney M. Identity by descent estimation with dense genome-wide genotype. Genetic Epidemiology. 2011;35:557–567. doi: 10.1002/gepi.20606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morton N. Sequential tests for the detection of linkage. American Journal of Human Genetics. 1955;7:277. [PMC free article] [PubMed] [Google Scholar]
- 13.Abecasis G, Cherny S, Cookson W, Cardon L. Merlin: rapid analysis of dense genetic maps using sparse gene flow trees. Nature Genetics. 2001;30:97–101. doi: 10.1038/ng786. [DOI] [PubMed] [Google Scholar]
- 14.Thompson EA. The structure of genetic linkage data: from LIPED to 1M SNPs. Human Heredity. 2011;71:86–96. doi: 10.1159/000313555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cleveland MA, Hickey JM, Forni S. A common dataset for genomic analysis of livestock populations. G3: Genes— Genomes— Genetics. 2012;2:429–435. doi: 10.1534/g3.111.001453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kingman JFC. On the genealogy of large populations. Journal of Applied Probability. 1982;19:27–43. [Google Scholar]
- 17.Hudson R. Gene genealogies and the coalescent process. Oxford Surveys in Evolutionary Biology. 1990;7:44. [Google Scholar]
- 18.Griffiths R, Marjoram P. Ancestral inference from samples of DNA sequences with recombination. Journal of Computational Biology. 1996;3:479–502. doi: 10.1089/cmb.1996.3.479. [DOI] [PubMed] [Google Scholar]
- 19.McVean GA, Cardin NJ. Approximating the coalescent with recombination. Philosophical Transactions of the Royal Society B: Biological Sciences. 2005;360:1387–1393. doi: 10.1098/rstb.2005.1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sobel E, Lange K. Descent graphs in pedigree analysis: applications to haplotyping, location scores, and marker-sharing statistics. American Journal of Human Genetics. 1996;58:1323–1337. [PMC free article] [PubMed] [Google Scholar]
- 21.Koepke H, Thompson E. Efficient testing operations on dynamic structures using strong hash functions. Journal of Computational Biology. 2013;20:551–570. doi: 10.1089/cmb.2013.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thompson EA. Identity by descent: Variation in meiosis, across genomes, and in populations. Genetics. 2013;194:301–326. doi: 10.1534/genetics.112.148825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rabiner L. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE. 1989;77:257–286. [Google Scholar]
- 24.Leutenegger A, Prum B, Verny C. Estimation of the inbreeding coefficient through use of genomic data. The American Journal of Human Genetics. 2003;73:516–523. doi: 10.1086/378207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ewens W. The sampling theory of selectively neutral alleles. Theoretical Population Biology. 1972;3:87–112. doi: 10.1016/0040-5809(72)90035-4. [DOI] [PubMed] [Google Scholar]
- 26.Aldous D. Exchangeability and related topics. École d’Été de Probabilités de Saint-Flour. 1985;XIII—1983:1–198. [Google Scholar]
- 27.Fan HC, Wang J, Potanina A, Quake SR. Whole-genome molecular haplotyping of single cells. Nature Biotechnology. 2011;29:51–57. doi: 10.1038/nbt.1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Browning SR, Browning BL. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. American Journal of Human Genetics. 2007;81:1084. doi: 10.1086/521987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR. MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genetic Epidemiology. 2010;34:816–834. doi: 10.1002/gepi.20533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Thompson EA. Gene identities and multiple relationships. Biometrics. 1974;30:667–680. [PubMed] [Google Scholar]
- 31.Glazner CG, Thompson EA. Improving pedigree-based linkage analysis by estimating coancestry among families. Statistical Applications in Genetics and Molecular Biology. 2012;11(2):11. doi: 10.2202/1544-6115.1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li N, Stephens M. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics. 2003;165:2213–2233. doi: 10.1093/genetics/165.4.2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tong L, Thompson EA. Multilocus lod scores in large pedigrees: Combination of exact and approximate calculations. Human Heredity. 2008;65:142–153. doi: 10.1159/000109731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Thompson EA. Statistical Inferences from Genetic Data on Pedigrees, vol. 6 of NSF-CBMS Regional Conference Series in Probability and Statistics. Institute of Mathematical Statistics; Beachwood, OH: 2000. [Google Scholar]
- 35.Browning SR. Multilocus association mapping using variable-length Markov chains. The American Journal of Human Genetics. 2006;78:903–13. doi: 10.1086/503876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Browning BL, Browning SR. Efficient multilocus association testing for whole genome association studies using localized haplotype clustering. Genetic epidemiology. 2007;31:365–375. doi: 10.1002/gepi.20216. [DOI] [PubMed] [Google Scholar]
- 37.Burton PR, Clayton DG, Cardon LR, Craddock N, Deloukas P, Duncanson A, Kwiatkowski DP, McCarthy MI, Ouwehand WH, Samani NJ, et al. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zheng C, Kuhner M, Thompson E. Joint inference of identity by descent along multiple chromosomes in population samples. Journal of Computational Biology. 2014;21:185–200. doi: 10.1089/cmb.2013.0140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2010;72:269–342. [Google Scholar]
- 40.Kung JP, Rota GC, Yan CH. Combinatorics: the Rota way. Cambridge University Press; 2009. [Google Scholar]
- 41.Ore O. Theory of equivalence relations. Duke Mathematical Journal. 1942:573–627. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.