Abstract
Combination chemotherapy is standard treatment for pancreatic cancer. However, current drugs lack efficacy for most patients and selection and evaluation of new combination regimens is empirical and time-consuming. The efficacy of gemcitabine, a standard-of-care agent, combined with birinapant, a pro-apoptotic antagonist of Inhibitor of Apoptosis Proteins (IAPs), was investigated in pancreatic cancer cells. PANC-1 cells were treated with vehicle, gemcitabine (6, 10, 20 nM), birinapant (50, 200, 500 nM), and combinations of the two drugs. Temporal changes in cell numbers, cell cycle distribution, and apoptosis were measured. A basic pharmacodynamic (PD) model based on cell numbers, and a mechanism-based PD model integrating all measurements, were developed. The basic PD model indicated that synergistic effects occurred in both cell proliferation and death processes. The mechanism-based model captured key features of drug action: temporary cell cycle arrest in S phase induced by gemcitabine alone, apoptosis induced by birinapant alone, and prolonged cell cycle arrest and enhanced apoptosis induced by the combination. A drug interaction term ψ was employed in the models to signify interactions of the combination when data were limited. When more experimental information was utilized, ψ values approaching 1 indicated that specific mechanisms of interactions were captured better. PD modeling identified the potential benefit of combining gemcitabine and birinapant, and characterized the key interaction pathways. An optimal treatment schedule of pretreatment with gemcitabine for 24-48 h was suggested based on model prediction and was verified experimentally. This approach provides a generalizable modeling platform for exploring combinations of cytostatic and cytotoxic agents in cancer cell cultures.
Keywords: Mathematical model, drug combinations, systems pharmacology, pancreatic cancer, gemcitabine, birinapant
Introduction
Pancreatic cancer is the fourth leading cause of cancer-related deaths in the United States and five year survival is only 6% [1]. The high mortality rate can be attributed to advanced disease and metastasis at the time of diagnosis, and limited efficacy of conventional chemotherapy [2].
Gemcitabine-based therapy has been a standard of treatment for more than a decade, although survival is improved only approximately 6 months [3]. Because of the complexity of disease pathogenesis, numerous efforts have sought to combine either traditional cytotoxic agents or molecular targeted therapies with gemcitabine [2]. Recently, the combination of gemcitabine with nab-paclitaxel [4] and the four-drug combination FOLFIRINOX (lacking gemcitabine) [5] were shown to provide modest improvements in survival compared to gemcitabine alone. Therapeutic challenges arise from the intrinsic resistance of the disease. A comprehensive analysis of 24 pancreatic cancers revealed 63 genetic alterations, mostly point mutations, which were classified into 12 altered signaling pathways, including DNA damage control, the apoptosis pathway, and signaling pathways such as Hedgehog and Wnt/Notch [6]. Tumor stromal cells, cancer stem cells, and factors of the tumor microenvironment (such as hypoxia) also contribute to intrinsic resistance [7].
Gemcitabine (2’,2’-difluoro 2’-deoxycytidine, dFdC) is a deoxycytidine analog that enters cells via the nucleoside transporters (SLC28 and SLC29) and is phosphorylated intracellularly into the active diphosphate (dFdCDP) or triphosphate (dFdCTP) forms. The dFdCTP is incorporated into DNA during replication, inhibits DNA synthesis, and arrests cells in the cell cycle S phase, whereas dFdCDP inhibits ribonucleotide reductase and reduces the production of deoxycytidine diphosphate (dCDP), further enhancing the inhibition of DNA synthesis [8]. Stalled DNA replication activates the checkpoint signaling pathways ATR/Chk1 and ATM/Chk2 [9].
Checkpoint activation causes inhibitory phosphorylation of cyclin-dependent kinases (CDKs) [10] and also leads to cell cycle arrest. However, arrest is temporary at low to medium gemcitabine concentrations, because proteins such as p53 and BRCA1 are also activated by checkpoints and initiate the DNA repair process [11]. In the case of DNA damage that cannot be repaired, p53 initiates the intrinsic apoptosis pathway [12]. Other p53-independent apoptosis pathways affected by gemcitabine have been reported, such as Fas-mediated apoptosis and the MAPK-caspase apoptotic signaling pathway [13]. Genetic mutations and/or abnormal signaling related to cell survival (e.g. PI3K/Akt/NF-κB) and apoptosis (e.g. IAPs, Bcl-2 family) can also contribute to the suboptimal efficacy of gemcitabine [7, 14].
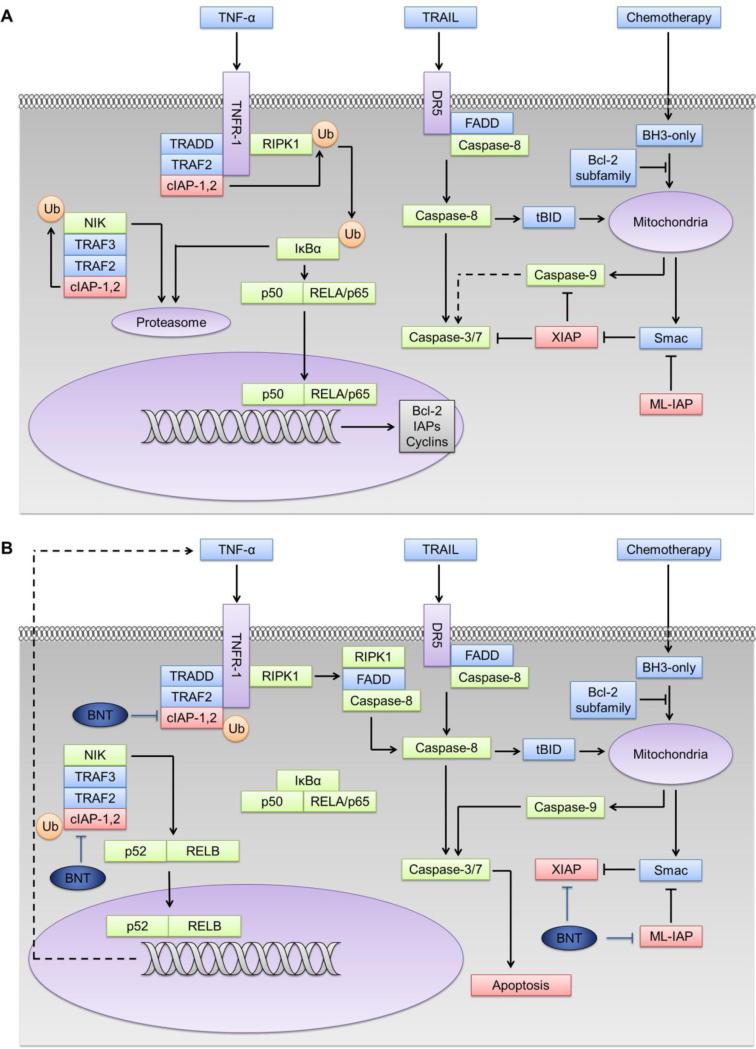
Inhibitor of Apoptosis Proteins (IAPs) are overexpressed in a variety of cancers and contribute to abnormal signaling in apoptosis. The expression of XIAP, cIAP2, and survivin mRNA and protein were higher in pancreatic tissues from pancreatic cancer patients than normal subjects [15]. Co-expression of cIAP1 and cIAP2 in pancreatic tumors was correlated with shorter survival [16], and down-regulation of these IAPs induced greater sensitivity to chemotherapeutic agents [15]. The IAP protein family comprises eight proteins that play a critical role in the regulation of the apoptosis signaling network (Figure 1A). XIAP (X chromosome-linked IAP) binds to and inhibits caspases −3, −7 and −9 via their BIR domains, and negatively regulates the intrinsic and extrinsic apoptosis pathways. The natural antagonist Smac (second mitochondria-derived activator of caspases) counterbalances the anti-apoptotic effect of XIAP. Other IAP proteins such as cIAP1,2 (cellular IAP 1and 2) and ML-IAP (melanoma IAP) are not potent, direct inhibitors of caspases, but bind to Smac with high affinity and inhibit it from blocking XIAP-mediated inhibition of caspases [17]. The cIAP1 and cIAP2 proteins also play a crucial role as positive regulators of the canonical NF-κB pathway and negative regulators of the noncanonical NF-κB pathway (Figure 1A) [18].
Fig.1.
Involvement of IAP proteins and IAP antagonists in the apoptosis and NF-κB pathways [17, 18]. a) Role of IAPs in the apoptosis pathway: IAPs negatively regulate both the intrinsic and extrinsic pathways. Certain chemotherapeutic agents activate intrinsic apoptosis through activation of Bcl-2 homology 3 (BH3)-only proteins, which leads to the release of cytochrome C and Smac from mitochondria and the activation caspase-9 and caspase-3/7. Activation of death receptors such as DR5 or Fas causes receptor trimerization and recruits Fas-associated death domain protein (FADD), triggering the caspase-8-mediated extrinsic pathway. Extrinsic death signals can crosstalk with the intrinsic pathway through truncated BID (tBID). XIAP negatively regulates both intrinsic and extrinsic pathways by inhibiting both caspases-3 and -9. Smac promotes apoptosis by binding XIAP. Melanoma IAP (ML-IAP) blocks apoptosis by depleting Smac from XIAP. IAPs are also involved in the regulation of NF-κB pathway. Activation of tumor necrosis factor receptor 1 (TNFR-1) induces the formation of complex 1, consisting of TNFR-associated via death domain (TRADD), receptor-interacting serine/threonine-protein kinase 1(RIPK1), TNFR-associated factor 2 (TRAF2) and cIAP1/2. cIAPs ubiquitinate but do not degrade RIPK1, which leads to the ubiquitination and proteasomal degradation of Inhibitor of NF-κB (IκB) and the translocation of p50 and the transcription factor RELA (p65) to the nucleus. Thus, cIAPs positively regulate the TNF-α-mediated activation of canonical NF-κB. In the non-canonical NF-κB pathway, cIAPs cause ubiquitination and proteasomal degradation of NF-κB-inducing kinase (NIK) and inhibit the non-canonical NF-kB signaling. b) Birinapant (BNT), as an IAP antagonist, binds to the BIR3 domains of cIAP1/2 and causes auto-ubiquitination and proteasomal degradation of the cIAPs. NIK is stabilized and non-canonical NF-κB signaling is activated. Loss of TRAF2-bound cIAP1/2 causes subsequent inhibition of canonical NF-κB activation, as well as formation of complex II (RIPK1, FADD, caspase-8 complex) and induction caspase-8-mediated apoptosis. Birinapant also releases activated caspases from XIAP and ML-IAP sequestration and induces both intrinsic and extrinsic apoptosis pathways.
Birinapant (TL32711; TetraLogic, Malvern, PA) is a bivalent IAP antagonist that consists of two covalently-linked Smac-mimetic domains, and exhibits higher potency than monovalent Smac mimetics [19]. It binds with high affinity to cIAP1, cIAP2, XIAP, and ML-IAP, and thus releases their target caspases from XIAP inhibition. Birinapant binding to cIAP1 and cIAP2 promotes their dimerization, which increases auto-ubiquitination and proteasomal degradation of the cIAP proteins. Degradation of cIAP1 and cIAP2 can interrupt the positive feedback between TNF-α and NF-κB and thereby switch pro-survival canonical NF-κB signaling into a pro-apoptotic, caspase-8-mediated cell death pathway (Figure 1B) [20]. The IAP antagonists have been shown to sensitize various cancers towards chemotherapy [17] and several reports suggest they can sensitize pancreatic cancer to gemcitabine both in vitro and in xenograft models via an NF-κB-dependent, TNF-α-dependent, and caspase-mediated mechanism [21–23].
We hypothesize that birinapant can increase pancreatic cancer cell sensitivity to gemcitabine by enhancing caspase-mediated apoptotic signaling and suppressing both the canonical NF-κB signaling pathway and NF-κB-regulated proteins. To test this hypothesis, we utilized mathematical modeling to assess the action and interactions of gemcitabine and birinapant. A traditional drug interaction model was applied first to describe the measurements of cell proliferation, and then we extended the empirical model to include more mechanism-based elements. Cell culture data for the concentration- and time-dependent effects of gemcitabinebirinapant combinations were obtained and their interactions were initially described with a quantitative empirical model. The Ariens noncompetitive interaction equation [24] was employed, with addition of an interaction term ψ to signify synergism (ψ<1), additivity (ψ=1), or antagonism (ψ>1) of the combination [25]. The drug interaction equation was extended to include the temporal dimension. To evolve from the empirical model into a more mechanism-based model, data were obtained for key biomarkers of effects mediated by the combinations, and systems or network models were then applied to describe detailed signaling pathways of interactions [26, 27]. The models were developed to describe data obtained for cell proliferation, cell cycle distribution, and apoptosis, and the meaning of ψ was expanded to indicate the degree to which the model components capture the underlying biological mechanisms. The resulting models captured experimental data well, and permitted in-depth understanding and quantitative predictions to optimize the schedules of the two agents in combination.
Methods and materials
Cell culture
The human pancreatic cancer cell line PANC-1 was obtained from the American Type Culture Collections (Rockville, MD). Cells were cultured in Dulbecco's Modified Eagle's Medium (DMEM; Cellgro, Manassas, VA) containing 10% (v/v) fetal bovine serum (FBS; Atlanta Biological, Lawrenceville, VA) in a humidified atmosphere with 5% CO2 at 37°C. Cells were passaged at 80-90% confluence using 0.05% trypsin with 0.53 mM EDTA (Gibco BRL, Gaithersburg, MD).
Reagents
Gemcitabine hydrochloride was purchased from Sequoia Research Products (Pangbourne, UK). The gemcitabine stock solution was 50 mM in sterile double-distilled water and stored at −20°C until use. Birinapant (TL32711) was provided by TetraLogic. The birinapant stock solution was 30 mM in dimethylsulfoxide (DMSO; Sigma-Aldrich, St. Louis, MO) and stored at −20°C until use. When diluted to the final working solutions, the DMSO concentration was below 0.05% v/v and did not perturb cell growth.
Cell counting
Cells were seeded in 6-well plates at a density of 2.5×105 cells per well in a volume of 2 mL. After overnight incubation to allow them to adhere, cells were exposed to 6, 10, 20 nM gemcitabine, 50, 200, 500 nM birinapant, or to combinations of the two drugs over a range of concentrations. The vehicle control was DMSO at a final concentration of 0.05% (v/v), which exceeded the highest concentration present in any drug-treated wells (0.002%). After exposure for 0, 12, 24, 36, 48, 72, and 96 h, attached cells were detached using trypsin, harvested, and counted using a Coulter Counter Z2 (Beckman Coulter, Brea, CA). Detached cells in the culture medium were also collected by centrifugation and counted. Total cells were considered as the sum of attached cells and detached cells. Triplicate samples were used for every concentration and time point.
Analysis of cell cycle distribution
The cell cycle distribution was determined from DNA content by propidium iodide (PI) staining. Cells were seeded in 6-well plates and treated with drugs as described above. At designated time points, attached cells were harvested, washed with Dulbecco's phosphate-buffered saline (PBS; Sigma-Aldrich, St. Louis, MO), fixed in 70 % ice-cold ethanol, and stored at −20°C for up to one week. For analysis, cells were centrifuged at 220 g for 10 min, washed with Staining Buffer (BD Pharmingen, San Diego, CA), resuspended in 500 μL PI/RNase Staining Buffer (BD Pharmingen), and incubated in the dark for 30 min at room temperature. Analysis was performed using a FACSCalibur flow cytometer (Becton-Dickinson, Mansfield, MA) and at least 10,000 events were collected. Cell cycle distributions were obtained using CellQuest software (Becton-Dickinson) and imported into ModFit software (Verity Software House, Topsham, ME) to quantify the fraction of viable cells in G0/G1, S, and G2/M cell cycle phases. Triplicate samples were used for every time point.
Analysis of apoptosis
Apoptosis was quantified using an Annexin V-phycoerythrin (PE) conjugate to stain phosphatidylserine externalized during the early phases of apoptosis, and 7-aminoactinomycin D (7-AAD) to indicate the loss of cell membrane integrity in the late phases of apoptosis. Adherent cells were detached using ACCUTASE (EMD Millipore, Temecula, CA) and combined with detached cells that were harvested from the supernatant by centrifugation. Cells were washed with PBS and resuspended in Annexin V Binding Buffer (BD Pharmingen) at a final concentration of 1.0×106 cells/mL. Four μL of Annexin V-PE (BD Pharmingen) was added to 100 μL of cells and incubated in the dark at room temperature for 15 min. Then 7 μL of 7-amino-actinomycin D (7-AAD; eBioscience, San Diego, CA) was added and incubated for 5 min. Cells were diluted with an additional 400 μL of Binding Buffer and analyzed by flow cytometry immediately. Populations of live cells (Annexin V− / 7-AAD-), and those undergoing early- (Annexin V+ / 7-AAD-) and late apoptosis (Annexin V+ / 7-AAD+), were obtained using CellQuest software and quantified using FCS Express 4 Flow Cytometry software (De Novo Software, Los Angeles, CA). Duplicate samples were used for every time point.
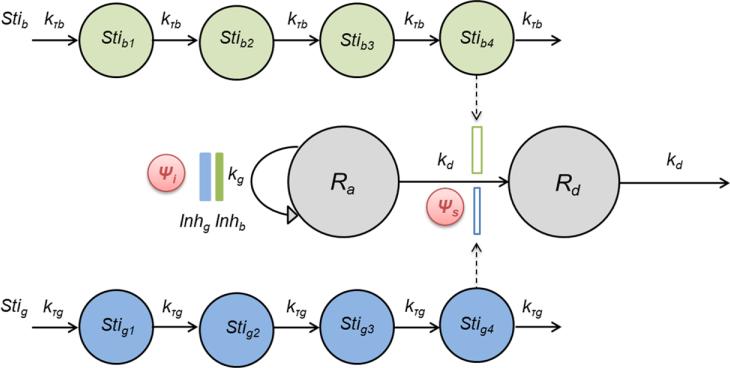
Basic cell growth model
The basic model is shown schematically in Figure 2. Previously it was shown that an apoptotic event is the detachment of adherent cells from the cell culture substrate [28, 29]. Therefore we made the assumption that for PANC-1, an adherent cell line, the attached cells are proliferating and detached cells are undergoing apoptosis. This assumption was confirmed experimentally (Supplementary Figure 1). We assumed that the attached cells proliferate with a first-order rate constant kg and follow logistic growth. They also detach with a first-order rate constant kd, and when apoptosis is complete, they are cleared from the system with the same rate constant kd. Unperturbed cell proliferation and detachment were described as:
| (1) |
| (2) |
where Ra is the number of attached (proliferating) cells, Rd is the number of detached (dead) cells, and Rss is the maximum cell number in the culture system.
Fig.2.
Schematic of the basic PD model to evaluate the interactions of gemcitabine and birinapant based on cell proliferation measurements. Symbols are defined in the text describing Eq. 11-12 and are listed in Table 1. Gemcitabine effects are highlighted in blue and birinapant in green.
We assumed that gemcitabine inhibits cell proliferation according to:
| (3) |
where Inhg is the inhibition of cell proliferation by gemcitabine, Cg is the concentration of gemcitabine in the culture medium, Imaxg is the maximum inhibitory effect of gemcitabine on cell growth, IC50g is the concentration of gemcitabine at which half-maximal effect is achieved, and Hig is the Hill coefficient that modifies the shape of the concentration-response relationship.
Delayed gemcitabine-induced cell death was observed, and the delay between drug exposure and onset of the effect was captured using four transit steps [30, 31]:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where Stig is the stimulation of cell death by gemcitabine, Smaxg is the maximum cell death-stimulating effect of gemcitabine, SC50g is the concentration of gemcitabine at which half-maximal effect is reached, Hsg is the Hill coefficient for the death-induction effect, Stig4 is related to Stig through four transit steps for temporal delay, kτg is the first-order transit rate between transit steps, and τ = 1/kτg refers to the mean transit time of each transit step.
We assumed that birinapant has similar effects on cell growth and death, but with a different intensity and time course. An analogous set of parameters (Imaxb, IC50b, Hib, Smaxb, SC50b, Hsb, kτb) was used to describe the effects of birinapant.
For drug combinations, the sensitivity of cells to one drug may be affected by the second drug in terms of both growth inhibition and death induction. The outcome could be either enhancement or diminution. We applied the interaction terms ψ on both growth and death pathways to account for the effects of drug interactions [32, 33]:
| (9) |
| (10) |
where ψ>1 indicates antagonism, ψ<1 indicates synergism, and ψ=1 indicates additivity.
In general, the dynamics of the proliferating and dead cell populations during treatment with both drugs was described as:
| (11) |
| (12) |
For this model, 21 parameters were fitted as listed in Table 1 to describe approximate 420 observations of Ra and Rb.
Table 1.
Parameters and Coefficients of Variation (%CV) estimated in the basic PD model (Figure 2).
| Drug-specific parameters | |||
|---|---|---|---|
| Cell growth inhibition effect | Gemcitabine | Birinapant | |
| Imax | Maximum inhibition of cell growth | 0.991 (11.1) | 0.375 (29.3) |
| IC50 (nM) | Drug concentration producing half maximal effect | 20.8 (6.66) | 145 (69.7) |
| Hi | Hill coefficient | 3.57 (16.2) | 1.06 (37.7) |
| Cell death induction effect | Gemcitabine | Birinapant | |
|---|---|---|---|
| Smax | Maximum induction of cell death | 4.09 (13.8) | 17.5 (16.0) |
| SC50 (nM) | Drug concentration producing half maximal effect | 14.0 (6.50) | 168 (41.4) |
| Hs | Hill coefficient | 5.00 (fixed) | 0.984 (18.8) |
| kT (h−1) | Transit rate for the delay of drug effect | 0.0860 (11.0) | 0.611 (7.55) |
| Drug interaction parameters | Confidence interval (95%) | ||
|---|---|---|---|
| ψ i | Interaction term for growth inhibition | 0.582 (11.7) | [0.446, 0.718] |
| ψ s | Interaction term for cell death induction | 0.583 (5.03) | [0.524, 0.641] |
| Cell-specific parameters | ||
|---|---|---|
| R0 | Initial number of total cells in the culture system | 2.36 × 105 (1.14) |
| f(G1)0 | Initial fraction of cells in the cell cycle of G0/G1 phase | 48.1 (1.50) |
| f(S)0 | Initial fraction of cells in the cell cycle of S phase | 10.8 (4.41) |
| f(apo)0 | Initial fraction of cells undergoing apoptosis | 5.00 (fixed) |
| f(other)0 | Initial fraction of cells undergoing non-apoptotic cell death | 1.50 (fixed) |
| k1 (h−1) | Rate constant for transition from G0/G1 to S phase | 0.357 (16.0) |
| k2 (h−1) | Rate constant for transition from S to G2/M phase | 0.114 (1.93) |
| k3 (h−1) | Rate constant for transition from G2/M to G0/G1 phase (mitosis) | 0.222 (14.7) |
| kapo (h−1) | Rate constant for progression to apoptosis | 3.94 × 10−3 (3.28) |
| f1 | Ratio of rate constants for progression to apoptosis and cleared from the system | 0.467 (6.91) |
| kother (h−1) | Rate constant for progression to non-apoptotic cell death | 2.97 × 10−4 (12.6) |
| IR50 | Number of cells that cause half maximal growth restriction | 1.23 × 105 (21.3) |
| Imax3 | Ratio of growth restriction on transition rate k3 vs. transition rate k1 | 0.753 (6.34) |
Mechanism-based PD model
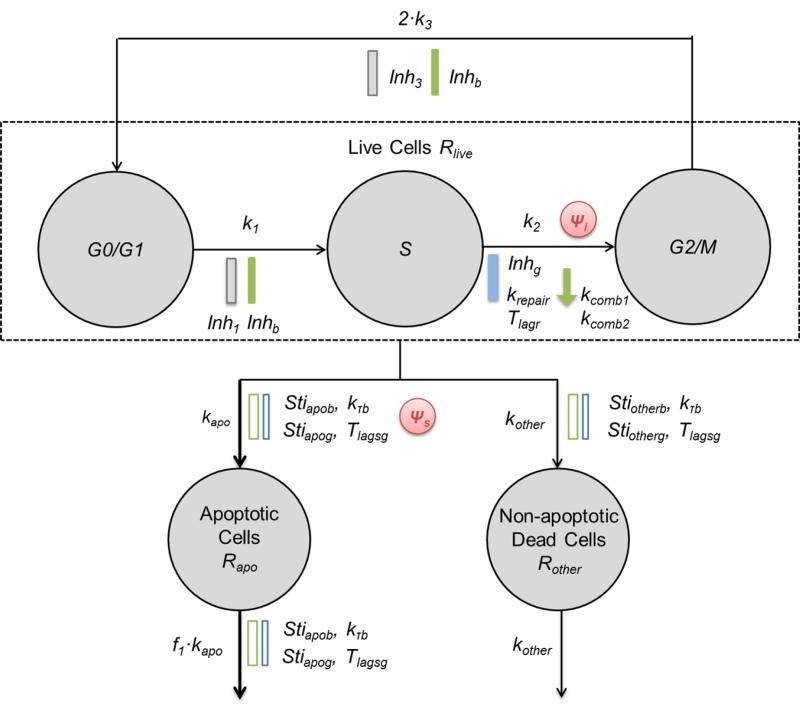
Characterization of cell cycle distribution
To describe drug effects upon cell cycle distribution, three compartments (G0/G1, S, G2/M) represent cells in those phases of cell cycle based upon DNA content, as determined by flow cytometry analysis [34]. Under unperturbed growth conditions, proliferating cells transit through consecutive phases with first-order rate constants k1, k2 and k3. Some cells also undergo apoptosis with rate constant kapo and are cleared from the culture system with the rate constant f1·kapo. We assumed that increasing live cell density restricts cell proliferation because of contact inhibition and limitations in growth factors, leading to cell arrest in the G0/G1 phase [35, 36]. Therefore, inhibition terms were added on the transition from G1 to S phase (k1):
| (13) |
and on mitosis (k3):
| (14) |
where Rlive is the number of proliferating cells, IR50 is the number of cells that causes half maximal growth restriction of transition rates k1 and k3, and Imax3 is the ratio of restriction on transition rate k3 versus that on transition rate k1. The same IR50 was used to describe Inh1 and Inh3 to avoid over-parameterization as they are similar processes.
In the unperturbed condition, cell distribution in the three phases was described as:
| (15) |
| (16) |
| (17) |
where kapo is a first-order rate constant for cell progression to apoptosis.
Low to medium concentrations of gemcitabine (relative to the sensitivity of cells to the drug) cause temporary cell cycle arrest in S phase [37], which will activate the checkpoint proteins and the DNA repair system, and compensate for the drug effect. We assumed that initiation of the DNA repair process is delayed by Tlagr after drug exposure because of the sharp returning of the cell cycle to normal progression (Figure 5D). The inhibition effect can be described as:
| (18) |
where Inhg is the inhibition of cell cycle transition by gemcitabine, Imaxg and IC50g also apply to the cell cycle transition effects of gemcitabine, krepair is a rate constant for cells to recover from cell cycle arrest, and Tlagr is assumed to be proportional to the logarithm of gemcitabine concentration:
| (19) |
where kdelay is a linear coefficient for the delay in initiation of recovery of DNA synthesis. We assumed that birinapant influences cell cycle distribution slightly, by inhibiting the transition from G0/G1 to S and from G2/M to G0/G1 (mitosis) according to:
| (20) |
For the drug combinations, we assumed that birinapant affects DNA repair by postponing initiation of the repair process:
| (21) |
and dampening the repair effect:
| (22) |
where Tlagrc represents the delay in the initiation of DNA repair in the drug combination, kcomb1 and kcomb2 are linear coefficients for the prolonged delay of recovery onset and decreased ability for the recovery of DNA synthesis. The interaction term ψi was multiplied with IC50g to test whether unknown drug interactions remain in the cell proliferation process that are not explained by available data and the hypothesized mechanisms included in the model.
Fig.5.
Effects of gemcitabine and birinapant, alone and in combination, upon cell cycle kinetics. Experimental observations of the fraction of cells in G0/G1, S, and G2/M cell cycle phases over time are indicated by symbols and fittings based on the mechanism-based PD model of Figure 3 are indicated by curves.
Characterization of apoptosis
The transition of cells from early- to late-stage apoptosis could not be discriminated temporally based on our experimental observations. Therefore, apoptotic cells were considered as a single population. Under unperturbed conditions, a small percentage of cells continually undergo programmed cell death (PCD) , mainly through apoptosis [38], to maintain the balance of the system. A small portion of cell death via mechanisms other than PCD was also observed experimentally. Both gemcitabine and birinapant were assumed to induce apoptosis according to a nonlinear function (Eq. 4). The delay in onset of the birinapant effect was described using the same transit steps as in the basic model (Eq. 5-8). However, the delay in onset of the gemcitabine effect could not be captured with transit steps, which would produce gradually-increasing effects (data not shown). Based on experimental data, the effect of gemcitabine to induce apoptosis was modeled as an off/on behavior: gemcitabine effects were minimal within the first 48 h of exposure, and then increased sharply. Thus, a lag time Tlagsg was used to describe the delay:
| (23) |
Both drugs induced a small amount of non-apoptotic cell death, which was described with a simple nonlinear function:
| (24) |
where Kother is a nonlinear coefficient for induction of non-apoptotic cell death and Hother is a Hill coefficient that modifies the shape of the concentration-response relationship. The delay in onset of non-apoptotic cell death was the same as that for onset of apoptosis (Eq. 5-8 and Eq. 23).
For combination treatments, the interaction term ψs was utilized within the apoptosis pathway to test whether unknown interactions remain, similar to the ψi in Eq. 22:
| (25) |
Drug interactions promoting non-apoptotic cell death were not considered because of the relatively small fraction of cells in that population and the high variability of that data.
Model development
The cells were divided into five populations, including proliferating cells progressing through the three cell cycle phases (G0/G1, S, and G2/M), cells undergoing apoptosis, and cells undergoing non-apoptotic cell death. The model is shown schematically in Figure 3.
Fig.3.
Schematic of the mechanism-based PD model to evaluate the interactions of gemcitabine and birinapant in detail. Symbols are defined in the text describing Eq. 26-31 and are listed in Table 2. Gemcitabine effects are highlighted in blue and birinapant in green.
The five populations of cells were described as:
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
The total number of cells was obtained in the model by summing the number of cells in each phase:
| (31) |
where Rapo is the number of cells undergoing apoptosis, Rother is the number of cells undergoing non-apoptotic cell death, and Rtotal is the total number of cells in the culture system.
For this model, 37 parameters were fitted as listed in Table 2 to describe approximate 1200 observations of Rtotal, G1/Rtotal, S/Rtotal, G2/Rtotal, Rapo/Rtotal and Rother/Rtotal.
Table 2.
Parameters and Coefficients of Variation (%CV) estimated in the mechanism-based PD model (Figure 3).
| Drug-specific parameters | |||
|---|---|---|---|
| Inhibition of cell cycle progression | Gemcitabine | Birinapant | |
| Imax | Maximum inhibition of cell cycle progression | 0.878 (0.751) | 0.177 (24.4) |
| IC50 (nM) | Drug concentration producing half maximal effect | 6.00 (2.61) | 154 (68.7) |
| Hi | Hill coefficient | 4.34 (6.71) | 1.00 (fixed) |
| krepair (h−1) | Rate constant for recovery from cell cycle arrest | 0.0495 (15.4) | |
| kdelay (h−1) | Linear coefficient for delay in DNA recovery onset | 38.6 (3.72) | |
| kcomb1 (nM−1) | Linear coefficient for prolongation of delay in DNA recovery onset | 9.19 × 10−4 (25.9) | |
| kcomb2 (nM−1) | Linear coefficient for decreased ability in recovery of DNA synthesis | 7.75 × 10−4 (60.6) | |
| Induction of apoptosis | Gemcitabine | Birinapant | |
|---|---|---|---|
| Smax | Maximum induction of apoptosis | 2.74 (94.9) | 3.72 (10.0) |
| SC50 (nM) | Drug concentration producing half maximal effect | 23.6 (50.6) | 50.1 (17.9) |
| Hs | Hill coefficient | 3.00 (fixed) | 1.24 (31.5) |
| k1 (h−1) | Transit rate for the delay of drug effect | 0.376 (11.6) | |
| Tlags (h) | Delay of apoptosis onset after drug exposure | 38.7 (7.79) |
| Induction of non-apoptotic cell death | Gemcitabine | Birinapant | |
|---|---|---|---|
| Kother | Nonlinear coefficient for induction of non-apoptotic cell death | 1.00 × 10−5 (fixed) | 5.50 × 10−3 (22.2) |
| Hother | Hill coefficient | 0.100 (fixed) | 1.00 (fixed) |
| Drug interaction parameters | Confidence interval (95%) | ||
|---|---|---|---|
| ψ i | Interaction term for cell cycle arrest | 0.949 (3.02) | [0.892, 1.01] |
| ψ s | Interaction term for induction of apoptosis | 1.26 (16.5) | [0.844, 1.68] |
Data analysis
Model fitting and parameter estimation was performed using ADAPT 5 [39] with the maximum likelihood algorithm. Naïve-pooled data from all replicate studies were analyzed using the variance model:
| (32) |
where Vi is the variance of the response at the ith time point (ti), and Y(ti) is the predicted response at time ti. Variance parameters intercept and slope were estimated together with system parameters. Model performance was evaluated by goodness-of-fit criteria, including visual inspection of the fitted curves, sum of squared residuals, Akaike Information Criteria (AIC), Schwarz Criterion (SC), and Coefficients of Variation (CV%) of the estimated parameters.
Results
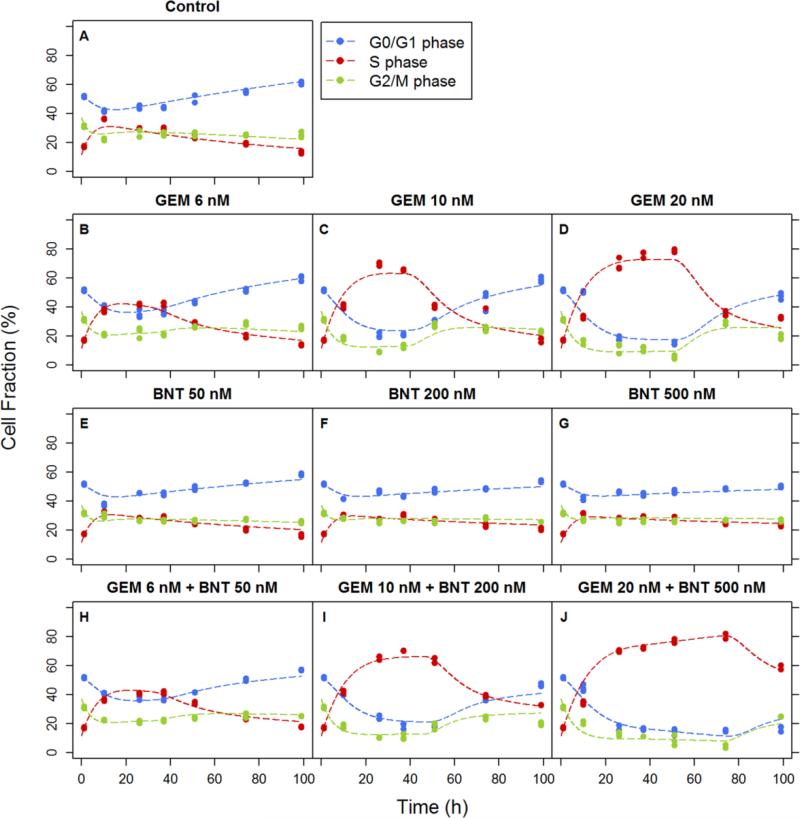
Drug combination effect on dynamics of cell numbers
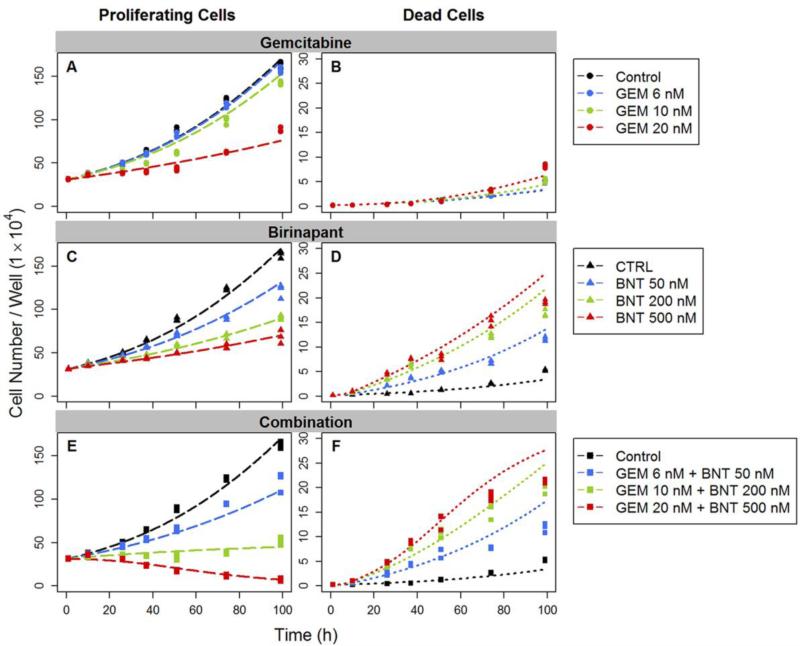
Temporal changes in the numbers of proliferating and dead cells are shown in Figure 4 for the two drugs, alone and in combination. The estimated rate constant for unperturbed cell growth kg was 0.0209 h−1 (Table 1). The doubling time of PANC-1 cells in the exponential growth phase, calculated as ln(2)/kg, was 33.2 h. Based on model fittings of single agent effects, both drugs inhibited cell proliferation (cytostatic effects) and increased the dead cell population (cytotoxic effects). For the combination, gemcitabine mediated the major effect on growth inhibition, with maximum inhibition Imax of approximately 1 and IC50 of 20.8 nM (Table 1). These results are consistent with the common view of gemcitabine as a potent cytostatic agent [37]. Birinapant also exerted some effect on cell growth inhibition, although the effect was minor; Imax was only 0.375 and IC50 was 145 nM. Birinapant contributed primarily to induce cell death, and the maximum induction Smax was 17.5. Gemcitabine also showed a minor death-induction effect, with Smax of 4.09. For both drugs, a delay was observed between exposure and the increase in the number of dead cells. Therefore, a nonlinear, time-dependent signal transduction model was used (Eq. 5-8) to capture the delay. The selection of number of transit steps was based on testing 3, 4, and 5 steps with 4 being optimal. The overall mean transit time was calculated as MTT = N·τ, where N is the number of transit steps and τ is the mean signal transduction time. The propagation of the death-induction signal was approximately 7 h for birinapant and 47 h for gemcitabine.
Fig.4.
Effects of gemcitabine (GEM) and birinapant (BNT), alone and in combination, upon cell proliferation. Numbers of proliferating cells (left) and dead cells (right) were counted over time. Experimental observations are indicated by symbols and fittings based on the basic PD model of Figure 2 are indicated by curves.
The interaction term ψ was used to test whether the two drugs interact on either the cell proliferation or death pathways. The ψi was factored with the IC50 (growth-inhibiting effect) of gemcitabine (Eq. 9) because the majority of growth inhibition was mediated by gemcitabine. A second ψs accompanied the SC50 (death-stimulating effect) of birinapant (Eq. 10) because it was the major contributor to cell death induction. Both estimated ψ values were significantly smaller than 1 (Table 1). Thus when the two agents are combined, there appear to be synergistic or augmented effects on both cell proliferation and death mechanisms.
Drug effects on cell cycle distribution
Cell cycle models have been used to describe tumor growth and cell cycle arrest mediated by chemotherapeutic agents [34]. Therefore we applied a model based upon the cell cycle structure to explore the cytostatic effects of the single and combined agents.
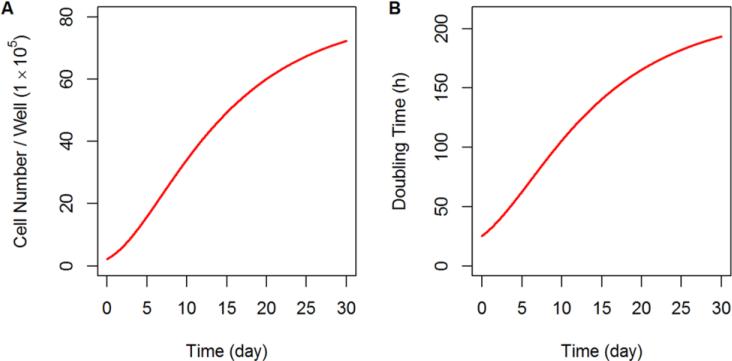
Temporal changes in cell cycle distribution were observed as untreated control cells grew with increasing cell numbers in the G0/G1 phase and decreasing numbers in the S and G2/M phases at later times (Figure 5A). Based on these profiles, we proposed a model for unperturbed cell proliferation in which increasing cell numbers inhibited primarily cell progression from G0/G1 to S phase, and inhibited slightly the G2/M to G0/G1 transition. Growth inhibition mediated by increasing cell number was described with two Hill-function-like equations (Eq. 13-14), and control group data were well-captured (Figure 5A). The doubling time of the cells could be calculated from (1/k1,app + 1/k2 + 1/k3,app), in which the apparent transition rate between G0/G1 and S phases is k1,app = k1 · (1 – Rlive/(IR50 + Rlive)), and the apparent transition rate between G2/M and S phases is k3,app = k3 · (1 – Imax3 · Rlive/(IR50 + Rlive)). Thus, the predicted cell doubling time was 26 h initially, and increased to 53 h after 4 days because of increased cell density (Figure 6B). The estimated IR50, which is the cell number that results in half of the initial transition rate between cell cycle phases, was 1.23 × 105 per well (Table 2).
Fig.6.
a) Simulated growth profile of proliferating cells in the unperturbed control group based on the mechanism-based PD model of Figure 3. b) Simulated change of the cell doubling time resulting from continuous proliferation of the unperturbed control group based on the mechanism-based PD model of Figure 3.
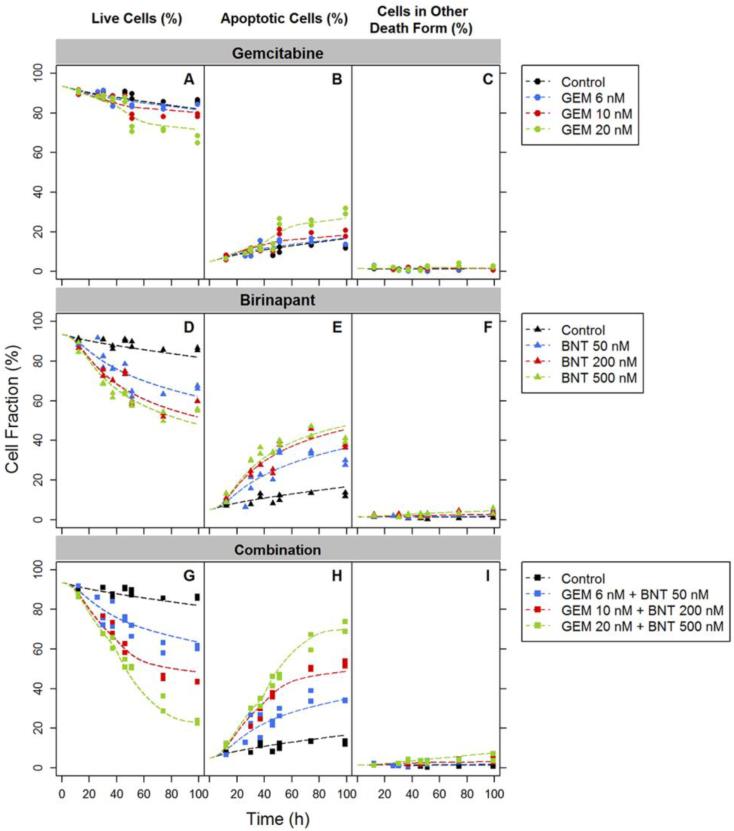
In the gemcitabine treatment group, significant arrest of cells in S phase was observed, and the effect was concentration-dependent. The estimated maximum inhibition of cell cycle progression mediated by gemcitabine Imax was approximately 1 and the estimated IC50 was 6.00 nM (Table 2). However, after the arrest was maintained for a period of time, the cell cycle distribution suggested a return towards normal progression (Figure 5B-D). The recovery from cell cycle arrest was assumed to arise from the initiation of DNA repair mechanisms. Based on model estimation, onset of DNA repair was delayed 30-50 h (Table 2) after initiation of drug exposure, and a longer delay in onset was observed with higher gemcitabine concentrations. The DNA repair was described by multiplying a modification term exp (–krepair · t) with the inhibition term (Eq. 18). The estimated krepair was 0.0495 h−1 (Table 2) and suggests that 90% of the cell cycle arrest recovers within the duration of ln (1/0.1)/krepair, or 48 h after initiation of the recovery process.
Birinapant induced S-phase arrest for a shorter period of time with lower intensity, and reduced cell distribution in the G1 phase in a concentration-dependent manner (Figure 5E-G). The effect was statistically significant but much lower in magnitude than the effect of gemcitabine. If the unperturbed model (Eq. 15-17) was used to describe birinapant treatment, the values of phase transition rates k1 and k3 were decreased (data not shown) compared to the control group, indicating that birinapant may slow progression from G0/G1 to S and from G2/M to G0/G1. Therefore, the birinapant effect on cell cycle progression was described by applying an inhibitory Hill function (Eq. 20) on cycle phase transition rates k1 and k3. The inhibitory contribution of birinapant was slight, with Imax of only 0.177 and IC50 of 154 nM (Table 2).
For the two drugs combined, the effect upon S-phase arrest was prolonged and the intensity was enhanced slightly compared to gemcitabine alone (Figure 5H-J). Although other mechanisms could be postulated, we assumed that birinapant modulates the effect of gemcitabine upon cell cycle distribution by interrupting the DNA repair process. Our empirical model described birinapant modulation of gemcitabine effects on cell cycle distribution by increasing the lag time of repair onset Tlagr, in a manner dependent upon birinapant concentration, to (1 + kcomb1 · Cb) · Tlagr, and decreasing the repair rate krepair to (1 – kcomb2 · Cb) · krepair. The estimated coefficients for the dampened DNA repair, kcomb1 and kcomb2, were 9.19 × 10−4 nM−1 and 7.75 × 10−4 nM−1 (Table 2).
Drug effects on apoptosis
Based upon prior analysis with the basic model, the induction of cell death by the drug combination was mediated principally by birinapant. This finding is consistent with the mechanisms of action of birinapant, in that it antagonizes the IAP family proteins and enhances caspase activity directly. With detailed measurements of apoptosis incorporated into the mechanism-based model, the apoptosis induction effect of gemcitabine appeared to be comparable to that of birinapant, with Smax of 2.74 for gemcitabine versus 3.72 for birinapant (Table 2). However the induction was manifested via very different temporal patterns. Apoptosis induction by birinapant was progressive and relatively rapid (Figure 7E). The delay in onset was described by four transit steps and estimated as 10 h. Apoptosis induction by gemcitabine was very much delayed after drug exposure, and the apoptosis profile appeared to display a threshold pattern (Figure 7B). The estimated delay in gemcitabine-induced apoptosis, described using a lag time Tlagsg instead of transit steps, was 38.7 h (Table 2).
Fig.7.
Experimental observations (symbols) and fittings based on the mechanism-based PD model of Figure 3 (curves) of gemcitabine (GEM), birinapant (BNT), and drug combination effects on apoptosis (percentage of live cells, apoptotic cells and cells dying by other mechanisms) over time.
A small population of cells underwent cell death by mechanisms other than PCD or apoptosis (Figure 7C,F,I). We described drug effects producing this population using a simple nonlinear function. Because of the low fraction of cells in this population and large variability in the data, most parameters describing this process were fixed to values based upon prior model fittings of single drug effects: Kotherg was 1.00 × 10−5, Hotherg was 0.100, and Hotherb was 1.00 (Table 2). These values were selected based on the criteria of a lower AIC value and better capture of the observations. The Kotherb was estimated to be 5.50 × 10−3. For the purpose of model parsimony, we assumed that the delay in onset of both apoptotic and non-apoptotic cell death were equivalent.
Interaction term ψ in the mechanism-based model
In the mechanism-based model, the ψ interaction terms (Eq. 22,25) were incorporated in the cell cycle arrest and apoptosis induction pathways in the same manner as in the basic model (Eq. 9,10) . Neither ψ value was significantly different from 1, with confidence intervals of 0.892 to 1.01 for the cell cycle arrest pathway, and 0.844 to 1.68 for the apoptosis induction pathway (Table 2). This result demonstrates that the mechanism-based PD model is sufficient to capture the major mechanisms of drug interactions related to cell proliferation or death, revealed as synergism in the basic PD model, and little residual unexplained drug effect exists for which a ψ interaction term differing from 1 is required. Other drug mechanisms not included in the model may exist, but are not required to explain the current data.
Simulation of dosing regimens upon efficacy
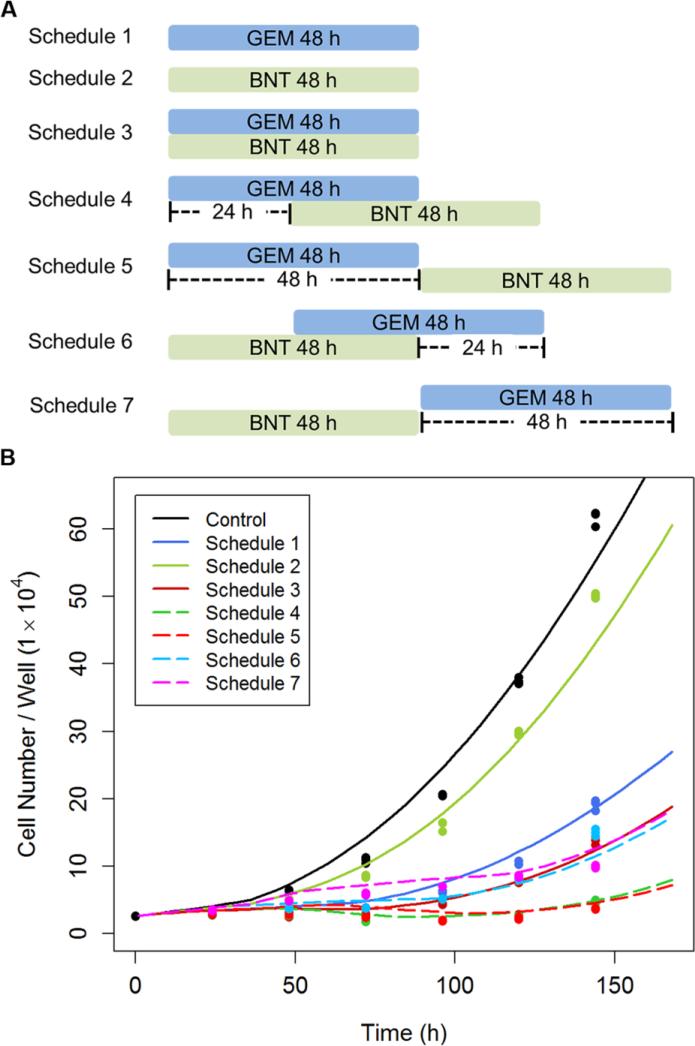
The mechanism-based model described well all data when fit simultaneously, and provided a reasonable estimation of the parameters. Therefore, simulations were performed to investigate the effect of different treatment regimens upon cell growth inhibition. Despite the short plasma half-life of gemcitabine in patients [40, 41], 48 h exposure was simulated because of the prolonged intracellular persistence of the active metabolite [42]. The same period of exposure was simulated for birinapant. Birinapant has a long half-life (~50 h) in solid tumors [43], but the shorter simulated exposure permitted sensitive identification of the exposure window that most affects efficiency of the combination. Cell growth was simulated for the untreated control and 7 treatment regimens (Figure 8A): (i) gemcitabine or (ii) birinapant alone for 48 h, (iii) simultaneous exposure, gemcitabine (iv) 24 or (v) 48 h before birinapant, and birinapant (vi) 24 or (vii) 48 h before gemcitabine. The simulation predicted that pre-exposure of cells to gemcitabine for 24 or 48 h before addition of birinapant would mediate the greatest inhibition of cell proliferation.
Fig.8.
a) Exposure schedules for simulations of effects of combined gemcitabine (GEM) and birinapant (BNT) upon cell proliferation, as well as for the hypothesis-testing experimental design. The duration of exposure to 20 nM gemcitabine and/or 100 nM birinapant was 48 h, and the sequences and inter-dose intervals were as shown. b) Experimental observations (symbols) and model-based simulations (curves) of PANC-1 cell proliferation with different schedules and sequences of exposure to gemcitabine and birinapant.
This simulation-generated hypothesis was tested experimentally. Several parameter values were modified to adapt model estimations to the culture conditions in the hypothesis-testing study. Parameters describing unperturbed cell growth were adjusted to capture data for the control group because somewhat fewer cells were seeded per well in the hypothesis-testing study, which led to a longer lag phase of cell growth. Therefore we assumed that the transition rates between cell cycle phases k1, k2 and k3 were halved before 36 h. In addition, the drug-containing medium was replaced daily for the crossover regimens (iv-vii), partially relieving the cell growth inhibition by increased cell density. Therefore, the IR50 value, which determines cell growth retardation by contact inhibition or medium depletion, was doubled. Parameters related to drug efficacy were also adjusted based upon existing literature or observations from preliminary studies. First, although the gemcitabine exposure was 48 h, we assumed the gemcitabine effects persist after removal. It has been reported that short-term gemcitabine exposure can result in long-term cell growth inhibition [44, 45]. Second, the hypothesis-testing study was performed in the 24-well culture system, whereas data upon which the PD models were developed were generated from a 6-well culture system. The minor changes in culture conditions affected specific parameters that are documented in Supplementary Figure 3. For example, we observed that cells were approximately two-fold more sensitive to gemcitabine or birinapant in 24-well plates than in 6-well plates. Therefore, we assumed that the IC50 and SC50 were half of the estimated values for the simulations. After correction of these parameter values, the model simulations are consistent with, and confirmed by, the observations in the hypothesis-testing study (Figure 8B).
Discussion
Combination chemotherapy is a standard approach in cancer treatment, but the selection and evaluation of drug candidates and treatment regimens often is empirical. Here we have developed a quantitative framework to evaluate combined therapy, in order to explore underlying mechanisms with limited pre-clinical data, evaluate key biomarkers as potential drug targets, and identify factors that require consideration in the design of an exposure regimen. The proposed mechanism-based model merges molecular pharmacology and signal transduction mechanisms with elements of previous mathematical models [30–34]. Identifiability may be of a concern in these complicated models. In our study, the problem is lessened by use of a wide range of drug concentrations, assessment over suitable time courses, and employment of measurements from different assays. The models were also constructed with a minimum number of parameters that were each justified and these parameters were estimated with low or reasonable variability (CV%).
The effects of combined gemcitabine and birinapant on PANC-1 cells were assessed step-by-step. First, drug effects upon cell numbers were measured as a direct endpoint of cell proliferation, and a basic PD model was proposed (Figure 2) to characterize changes in the numbers of adherent and non-adherent cells, with the latter as a surrogate for apoptotic cells. From the basic model, cytostatic vs. cytotoxic drug effects were differentiated, and we identified cell proliferation and cell death as major pathways of drug action and interactions for the two agents. Finally, we measured additional endpoints relevant to these drug mechanisms, including cell cycle distribution and apoptosis, and employed these data to extend the basic model towards a more integrated, mechanism-based model (Figure 3). We observed that gemcitabine impeded cell progression from S to G2/M phase, and caused S-phase arrest. In addition, birinapant had a minor effect of slowing progression of cells from G0/G1 to S phase and mitosis. When birinapant was combined with gemcitabine, the S-phase arrest effect was prolonged and enhanced. Both drugs were observed to stimulate apoptosis, which was mutually reinforcing, but according to different temporal patterns. The empirical drug interaction term ψ has been used in interaction equations to signify the synergism/additivity/antagonism of pharmacological interactions, and to account for the interactions when detailed mechanisms are unknown and therefore not included in the model [25, 32, 33]. Although the ψ term is used here to describe drug interactions in both models, its application and significance is different. In the basic model, the estimated ψ values placed upon the growth-inhibition and death-induction pathways were significantly smaller than 1, suggesting supra-additive interactions. However, the mechanistic basis of these drug interactions is unknown, and the ψ term aggregates those multiple unknown contributions into a single term. In contrast, the mechanism-based model characterizes drug interactions in the two pathways in greater detail. In this case, the estimated ψ values were not significantly different from 1. This does not mean that the interactions no longer exist. Rather, the unknown components represented by ψ are diminished by the additional details that are incorporated quantitatively into the description of the key pathways, and the mechanism-based model characterizes better the mechanisms of drug interactions. Therefore, the ψ term not only can help to account for unknown interactions, but also can indicate how well the model captures important underlying mechanisms.
Key model assumptions could be justified by the pharmacology at the signal transduction level. We assumed that birinapant alone retards slightly the G0/G1- to S-phase cell cycle transition as well as mitosis. Involvement of the birinapant targets cIAP1 and cIAP2 in cell cycle regulation has been reported previously [46–48]. Another target of birinapant, XIAP, was also reported to regulate positively the expression of cyclin D1, which controls the G1-S phase transition [49]. Therefore birinapant likely perturbs the cell cycle via antagonism of the IAP proteins. Birinapant may also modulate the cell cycling indirectly by affecting signaling pathways such as NF-κB, which regulates cell cycle proteins (e.g. cyclins) [50]. Another important assumption was that in the combined treatment, birinapant enhances the effect of gemcitabine upon cell cycle distribution by interrupting the DNA repair process. At low-to-medium concentrations, cell cycle arrest by gemcitabine is temporary and the duration of the effect is concentration-dependent [37]. This is consistent with our experimental observations, and we incorporated this characteristic in our model. Gemcitabine-mediated DNA replication stress activates checkpoint proteins and pathways such as ATM/Chk2, which further activates the NF-κB pathway and initiates DNA repair by homologous recombination [51, 52]. The IAP proteins are involved in the ATM-mediated activation of NF-κB pathway [53]. Thus, degradation of IAP proteins resulting from birinapant exposure may impede the initiation of DNA repair.
Model-based estimation of parameters has clinical implications, especially for parameters such as IC50 and SC50. In the basic PD model, the estimated IC50 for cell growth inhibition by gemcitabine was ~15 nM, and this value was 2-3-fold lower in the mechanism-based model. For birinapant as a single agent, the SC50 (~50 nM) in the mechanism-based model was also lower than the SC50 (~150 nM) estimated from the basic model. Interestingly, the SC50 value in the mechanism-based model is comparable to the dissociation constant Kd of birinapant for the specific IAP proteins (1-45 nM) [20], indicating faithful capture of birinapant interaction with its targets by the mechanism-based model. Furthermore, IC50 and SC50 estimates for gemcitabine obtained from the basic and mechanistic models are much lower than the peak plasma concentrations of gemcitabine achieved clinically (50 μM) [40, 41]. This large discrepancy between high clinical concentrations and lower effective concentrations in vitro suggests that although gemcitabine is a potent cytostatic and cytotoxic agent in pancreatic cancer cells in vitro, the in vivo processes such as drug transport or metabolism [54], and the physiological drug delivery barriers of solid tumors [55], may limit gemcitabine efficacy. The plasma concentration of birinapant at a clinically-relevant dose (17 mg/m2) peaks at ~1 μM, with a long (30 h) terminal half-life. Birinapant also shows high uptake and retention in solid tumors [43]. Therefore, birinapant concentrations relevant to in vitro interactions with gemcitabine (100–1000 nM) are sustained in the both plasma and tumor tissue for 24-48 h after dosing.
A modeling approach such as developed here can provide additional information on the underlying system and help to reconcile conflicts in the literature. For example, reports for the doubling time of PANC-1 cells include 52 h [56], 38 h [57], and 28 h [58], which may also reflect heterogeneity. Over 96 h of culture, we observed a progressive change in cell cycle distribution for the unperturbed control group, which consisted of a small, time-dependent accumulation of cells in the G1 phase. This phenomenon was attributed to contact inhibition and growth factor deprivation, and the model accounts for these changes. The model-predicted cell growth rate decreases for the untreated controls as cell proliferation continues (Figure 6A), and may partially explain the discrepancies in cell doubling times reported in the literature. The model-predicted proliferation of the control group is also consistent with proliferation that is empirically described by the logistic function and Gompertz equation [59].
Quantitative analysis and modeling can also assist in study design. For example, based on model predictions, gemcitabine shows moderate induction of apoptosis and, interestingly, initiation of apoptosis is delayed for approximately 40 h. This delay in effect onset influences selection of gemcitabine concentrations and the time frame over which in vitro experiments involving apoptosis should be conducted, and may explain why apoptosis induction by gemcitabine is under-recognized in the literature. Numerous studies have employed short-duration exposure to high gemcitabine concentrations [23, 60], and thus have the potential to miss cellular responses that could be observed with longer-duration exposure to lower gemcitabine concentrations. Thus model-based analysis can identify key elements of study design for apoptosis-inducing drugs such as gemcitabine.
Although a relatively small number of pharmacodynamic endpoints were measured in this study, the model can implicate key biomarkers of potential targets to enhance gemcitabine efficacy. For example, gemcitabine showed a delayed induction of apoptosis that was comparable in magnitude to that of birinapant. It could be beneficial to sequence other apoptosis inducers within an appropriate time frame to enhance the effect of gemcitabine. An example of such an apoptosis-inducer is paclitaxel. The combination of Abraxane (nab-paclitaxel) and gemcitabine recently has been approved for treatment of pancreatic cancer. Paclitaxel was shown to presensitize cells to gemcitabine through down-regulation of Bcl-2, and the sequence of paclitaxel followed by gemcitabine showed the most benefit, with enhanced apoptosis induction [61]. Alternatively, inhibition of the canonical NF-κB pathway may also contribute to the efficacy of gemcitabine. Gemcitabine can induce activation of the NF-κB pathway as a mechanism for treatment resistance [62]. Our data suggest that birinapant antagonizes the activation of NF-κB pathway and provides extra benefits. Therefore, other agents that suppress NF-κB activity (e.g. curcumin [63]) are potential candidates for combination with gemcitabine. Finally, the delays in DNA repair initiation (30-50 h) and onset of apoptosis (38.7 h) after gemcitabine administration are similar, suggesting that certain proteins or pathways in common may control the induction of both processes. Mediators that influence such functions could be checkpoint proteins such as Chk1 and Chk2, or those interacting directly with checkpoints, such as p53 and ATM/ATR, which are potential switchers between cell cycle arrest and DNA repair vs. commitment to apoptosis [12]. Therefore inhibition of these additional proteins could potentially enhance therapeutic efficacy. The hypothesis that inhibition of the homologous recombination process can slow DNA repair and enhance cytostatic effects of gemcitabine is supported by direct experimental observations [64, 65].
The issue of dosing schedule in combination chemotherapy is an under-studied but potentially important factor to enhance efficacy and reduce toxicity. The design of combination regimens usually is empirical and lacks mechanistic support or evidence. Our mechanism-based model captured the observed data well and largely incorporated the most important mechanisms of drug interactions, as evidenced by the ψ term approaching 1. Simulations were performed with the model to predict the outcomes of different exposure regimens. A delay in birinapant exposure for 24-48 h after initiation of gemcitabine exposure was predicted to have a major positive influence upon the efficacy of the combination, and was confirmed experimentally to be superior to simultaneous drug exposure or the reverse sequence. Although birinapant has a long half-life and can provide extended exposure in patients, aiming for the peak concentrations to occur within the optimal time window after gemcitabine treatment may be beneficial. Mechanisms of drug response supporting sequential dosing are justified in the literature [65], and as hypothesized here, the mechanism for improved efficacy of sequential dosing of gemcitabine and birinapant may arise from the delay of 24-48 h in both apoptosis induction and recovery of DNA synthesis. The model predictions will be further verified in a xenograft mouse model.
Conclusions
The combined effects of gemcitabine and birinapant were assessed using mathematical approaches that consider dimensions of both drug concentration and exposure time. The underlying mechanisms of these agents, alone and in combination, were incorporated into a mechanism-based cellular PD model. Using data acquired for specific biological endpoints, the model integrates quantitatively the dynamic changes in cell numbers, cell cycle distribution, and apoptosis for both untreated control cells and those treated with the single or combined agents. Simulations identified 24-48 h after gemcitabine exposure as an important time window for maximal efficacy of the combination. A novel characteristic of the model is the use of the drug interaction term ψ as an indicator of the degree to which incorporation of mechanistic detail into the model captures key aspects of drug interactions. Although further experiments are required to confirm some assumptions of the model, this approach has potential for assessing diverse drug combinations used in cancer treatment.
Postscript
WJJ was an undergraduate pharmacy student and later a graduate student in the laboratory of Gerhard Levy (GL) in the 1960's during the time of his inspirational PK/PD publications on the kinetics of pharmacologic effects (Clin Pharmacol Ther 7: 362-372, 1966) and pharmacodynamics of warfarin (Clin Pharmacol Ther, 10: 22–35, 1969). GL's invitation to work in his laboratory diverted WJJ from a possible career in hospital pharmacy to graduate studies and academic research and enkindled his enthusiasm for PK/PD. Following GL's canny practice of mining the literature for examples of unexplained phenomena for application of pharmacological relationships, WJJ's earliest publications as an independent scientist dealt with the creation of basic models for the pharmacodynamics of chemotherapeutic effects (J Pharm Sci 60: 862-895, 1971; J Pharmacokin Biopharm 1: 175-200, 1973). It is thus highly fitting that the present article, in serving as a tribute to GL, describes modeling the activities of drugs used for treatment of pancreatic cancer and demonstrates the evolution from simply counting numbers of cells over time to more comprehensive and mechanistic assessments of cell cycling kinetics, quantification of drug interactions, and use of contemporary pharmacometric methodology. WJJ returned to Buffalo as a faculty member in 1972 and RMS, with career-long interests in drug delivery and cancer therapeutics, joined our department in 1989. We flourished with GL's presence and scientific leadership until his retirement in 2000. Our department has maintained world-wide recognition in academic research in PK/PD and pharmaceutics in large part owing to GL's seminal developments in biopharmaceutics and PK/PD, his teaching innovations, his collegial interactions, his attention to evolving professional and scientific needs, and his role in attracting and recruiting synergistic faculty members and outstanding graduate students and post-doctoral fellows. XZ is very highly pleased to be listed as GL's academic granddaughter.
Supplementary Material
Acknowledgments
We thank Nancy Pyszczynski for excellent technical assistance and the Department of Flow Cytometry at Roswell Park Cancer Institute for technical consulting. We also thank Gilbert Koch for his suggestions in model development and manuscript revision. We are grateful to TetraLogic Pharmaceuticals Inc. for providing birinapant. This work was supported by Grants GM57980 and GM24211 from the National Institutes of Health.
Footnotes
Electronic supplementary material
The online version of this article () contains supplementary material, which is available to authorized users.
References
- 1.Siegel R, Ma J, Zou Z, Jemal A. Cancer statistics, 2014. CA Cancer J Clin. 2014;64:9–29. doi: 10.3322/caac.21208. doi: 10.3322/caac.21208. [DOI] [PubMed] [Google Scholar]
- 2.Melisi D, Calvetti L, Frizziero M, Tortora G. Pancreatic cancer: systemic combination therapies for a heterogeneous disease. Curr Pharm Des. 2014;20:6660–6669. doi: 10.2174/1381612820666140826154327. doi: 10.2174/1381612820666140826154327. [DOI] [PubMed] [Google Scholar]
- 3.Burris HA, Moore MJ, Andersen J, Green MR, Rothenberg ML, Modiano MR, Cripps MC, Portenoy RK, Storniolo AM, Tarassoff P, Nelson R, Dorr FA, Stephens CD, Von Hoff DD. Improvements in survival and clinical benefit with gemcitabine as first-line therapy for patients with advanced pancreas cancer: a randomized trial. J Clin Oncol. 1997;15:2403–13. doi: 10.1200/JCO.1997.15.6.2403. [DOI] [PubMed] [Google Scholar]
- 4.Von Hoff DD, Ervin T, Arena FP, Chiorean EG, Infante J, Moore M, Seay T, Tjulandin SA, Ma WW, Saleh MN, Harris M, Reni M, Dowden S, Laheru D, Bahary N, Ramanathan RK, Tabernero J, Hidalgo M, Goldstein D, Van Cutsem E, Wei X, Iglesias J, Renschler MF. Increased survival in pancreatic cancer with nab-paclitaxel plus gemcitabine. N Engl J Med. 2013;369:1691–703. doi: 10.1056/NEJMoa1304369. doi: 10.1056/NEJMoa1304369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Conroy T, Desseigne F, Ychou M, Bouché O, Guimbaud R, Bécouarn Y, Adenis A, Raoul J-L, Gourgou-Bourgade S, de la Fouchardière C, Bennouna J, Bachet J-B, Khemissa-Akouz F, Péré-Vergé D, Delbaldo C, Assenat E, Chauffert B, Michel P, Montoto-Grillot C, Ducreux M. FOLFIRINOX versus gemcitabine for metastatic pancreatic cancer. N Engl J Med. 2011;364:1817–25. doi: 10.1056/NEJMoa1011923. doi: 10.1056/NEJMoa1011923. [DOI] [PubMed] [Google Scholar]
- 6.Jones S, Zhang X, Parsons DW, Lin JC-H, Leary RJ, Angenendt P, Mankoo P, Carter H, Kamiyama H, Jimeno A, Hong S, Fu B, Lin M, Calhoun ES, Kamiyama M, Walter K, Nikolskaya T, Nikolsky Y, Hartigan J, Smith DR, Hidalgo M, Leach SD, Klein AP, Jaffee EM, Goggins M, Maitra A, Iacobuzio-Donahue C, Eshleman JR, Kern SE, Hruban RH, Karchin R, Papadopoulos N, Parmigiani G, Vogelstein B, Velculescu VE, Kinzler KW. Core signaling pathways in human pancreatic cancers revealed by global genomic analyses. Science. 2008;321:1801–6. doi: 10.1126/science.1164368. doi: 10.1126/science.1164368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Long J, Zhang Y, Yu X, Yang J, LeBrun DG, Chen C, Yao Q, Li M. Overcoming drug resistance in pancreatic cancer. Expert Opin Ther Targets. 2011;15:817–28. doi: 10.1517/14728222.2011.566216. doi: 10.1517/14728222.2011.566216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wong A, Soo RA, Yong W-P, Innocenti F. Clinical pharmacology and pharmacogenetics of gemcitabine. Drug Metab Rev. 2009;41:77–88. doi: 10.1080/03602530902741828. doi: 10.1080/03602530902741828. [DOI] [PubMed] [Google Scholar]
- 9.Karnitz LM, Flatten KS, Wagner JM, Loegering D, Hackbarth JS, Arlander SJH, Vroman BT, Thomas MB, Baek Y-U, Hopkins KM, Lieberman HB, Chen J, Cliby WA, Kaufmann SH. Gemcitabine-induced activation of checkpoint signaling pathways that affect tumor cell survival. Mol Pharmacol. 2005;68:1636–44. doi: 10.1124/mol.105.012716. doi: 10.1124/mol.105.012716. [DOI] [PubMed] [Google Scholar]
- 10.Vermeulen K, Van Bockstaele DR, Berneman ZN. The cell cycle: a review of regulation, deregulation and therapeutic targets in cancer. Cell Prolif. 2003;36:131–149. doi: 10.1046/j.1365-2184.2003.00266.x. doi: 10.1046/j.1365-2184.2003.00266.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yoshida K, Miki Y. Role of BRCA1 and BRCA2 as regulators of DNA repair, transcription, and cell cycle in response to DNA damage. Cancer Sci. 2004;95:866–71. doi: 10.1111/j.1349-7006.2004.tb02195.x. doi: 10.1111/j.1349-7006.2004.tb02195.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hill R, Rabb M, Madureira PA, Clements D, Gujar SA, Waisman DM, Giacomantonio CA, Lee PWK. Gemcitabine-mediated tumour regression and p53-dependent gene expression: implications for colon and pancreatic cancer therapy. Cell Death Dis. 2013;4:e791. doi: 10.1038/cddis.2013.307. doi: 10.1038/cddis.2013.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gesto DS, Cerqueira NMFSA, Fernandes PA, Ramos MJ. Gemcitabine: a critical nucleoside for cancer therapy. Curr Med Chem. 2012;19:1076–87. doi: 10.2174/092986712799320682. doi: 10.2174/092986712799320682. [DOI] [PubMed] [Google Scholar]
- 14.Voutsadakis IA. Molecular predictors of gemcitabine response in pancreatic cancer. World J Gastrointest Oncol. 2011;3:153–64. doi: 10.4251/wjgo.v3.i11.153. doi: 10.4251/wjgo.v3.i11.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lopes RB, Gangeswaran R, McNeish IA, Wang Y, Lemoine NR. Expression of the IAP protein family is dysregulated in pancreatic cancer cells and is important for resistance to chemotherapy. Int J Cancer. 2007;120:2344–52. doi: 10.1002/ijc.22554. doi: 10.1002/ijc.22554. [DOI] [PubMed] [Google Scholar]
- 16.Esposito I, Kleeff J, Abiatari I, Shi X, Giese N, Bergmann F, Roth W, Friess H, Schirmacher P. Overexpression of cellular inhibitor of apoptosis protein 2 is an early event in the progression of pancreatic cancer. J Clin Pathol. 2007;60:885–95. doi: 10.1136/jcp.2006.038257. doi: 10.1136/jcp.2006.038257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fulda S, Vucic D. Targeting IAP proteins for therapeutic intervention in cancer. Nat Rev Drug Discov. 2012;11:109–24. doi: 10.1038/nrd3627. doi: 10.1038/nrd3627. [DOI] [PubMed] [Google Scholar]
- 18.Gyrd-Hansen M, Meier P. IAPs: from caspase inhibitors to modulators of NF-κB, inflammation and cancer. Nat Rev Cancer. 2010;10:561–74. doi: 10.1038/nrc2889. doi: 10.1038/nrc2889. [DOI] [PubMed] [Google Scholar]
- 19.Condon SM, Mitsuuchi Y, Deng Y, LaPorte MG, Rippin SR, Haimowitz T, Alexander MD, Kumar PT, Hendi MS, Lee Y-H, Benetatos CA, Yu G, Kapoor GS, Neiman E, Seipel ME, Burns JM, Graham MA, McKinlay MA, Li X, Wang J, Shi Y, Feltham R, Bettjeman B, Cumming MH, Vince JE, Khan N, Silke J, Day CL, Chunduru SK. Birinapant, a smac-mimetic with improved tolerability for the treatment of solid tumors and hematological malignancies. J Med Chem. 2014;57:3666–77. doi: 10.1021/jm500176w. doi: 10.1021/jm500176w. [DOI] [PubMed] [Google Scholar]
- 20.Benetatos CA, Mitsuuchi Y, Burns JM, Neiman EM, Condon SM, Yu G, Seipel ME, Kapoor GS, Laporte MG, Rippin SR, Deng Y, Hendi MS, Tirunahari PK, Lee Y-H, Haimowitz T, Alexander MD, Graham MA, Weng D, Shi Y, McKinlay MA, Chunduru SK. Birinapant (TL32711), a bivalent SMAC mimetic, targets TRAF2-associated cIAPs, abrogates TNF-induced NF-κB activation, and is active in patient-derived xenograft models. Mol Cancer Ther. 2014;13:867–79. doi: 10.1158/1535-7163.MCT-13-0798. doi: 10.1158/1535-7163.MCT-13-0798. [DOI] [PubMed] [Google Scholar]
- 21.Dineen SP, Roland CL, Greer R, Carbon JG, Toombs JE, Gupta P, Bardeesy N, Sun H, Williams N, Minna JD, Brekken RA. Smac mimetic increases chemotherapy response and improves survival in mice with pancreatic cancer. Cancer Res. 2010;70:2852–61. doi: 10.1158/0008-5472.CAN-09-3892. doi: 10.1158/0008-5472.CAN-09-3892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Probst BL, Liu L, Ramesh V, Li L, Sun H, Minna JD, Wang L. Smac mimetics increase cancer cell response to chemotherapeutics in a TNF-α-dependent manner. Cell Death Differ. 2010;17:1645–54. doi: 10.1038/cdd.2010.44. doi: 10.1038/cdd.2010.44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stadel D, Cristofanon S, Abhari BA, Deshayes K, Zobel K, Vucic D, Debatin K-M, Fulda S. Requirement of nuclear factor κB for Smac mimetic-mediated sensitization of pancreatic carcinoma cells for gemcitabine-induced apoptosis. Neoplasia. 2011;13:1162–70. doi: 10.1593/neo.11460. doi: 10.1593/neo.11460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ariens EJ, Van Rossum JM, Simonis AM. Affinity, intrinsic activity and drug interactions. Pharmacol Rev. 1957;9:218–36. [PubMed] [Google Scholar]
- 25.Chakraborty A, Jusko WJ. Pharmacodynamic interaction of recombinant human interleukin-10 and prednisolone using in vitro whole blood lymphocyte proliferation. 2002;91:1334–1342. doi: 10.1002/jps.3000. [DOI] [PubMed] [Google Scholar]
- 26.Harrold JM, Straubinger RM, Mager DE. Combinatorial chemotherapeutic efficacy in non-Hodgkin lymphoma can be predicted by a signaling model of CD20 pharmacodynamics. Cancer Res. 2012;72:1632–41. doi: 10.1158/0008-5472.CAN-11-2432. doi: 10.1158/0008-5472.CAN-11-2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fitzgerald JB, Schoeberl B, Nielsen UB, Sorger PK. Systems biology and combination therapy in the quest for clinical efficacy. Nat Chem Biol. 2006;2:458–66. doi: 10.1038/nchembio817. doi: 10.1038/nchembio817. [DOI] [PubMed] [Google Scholar]
- 28.Au JL, Kumar RR, Li D, Wientjes MG. Kinetics of hallmark biochemical changes in paclitaxel-induced apoptosis. AAPS PharmSci. 1999;1:E8. doi: 10.1208/ps010308. doi: 10.1208/ps010308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lawrence TS, Davis MA, Hough A, Rehemtulla A. The role of apoptosis in 2′,2′-difluoro-2′-deoxycytidine (Gemcitabine)-mediated radiosensitization. Clin Cancer Res. 2001;7:314–319. [PubMed] [Google Scholar]
- 30.Ait-Oudhia S, Straubinger RM, Mager DE. Systems pharmacological analysis of paclitaxel-mediated tumor priming that enhances nanocarrier deposition and efficacy. J Pharmacol Exp Ther. 2013;344:103–12. doi: 10.1124/jpet.112.199109. doi: 10.1124/jpet.112.199109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lobo ED, Balthasar JP. Pharmacodynamic modeling of chemotherapeutic effects: application of a transit compartment model to characterize methotrexate effects in vitro. AAPS PharmSci. 2002;4:E42. doi: 10.1208/ps040442. doi: 10.1208/ps040442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pawaskar DK, Straubinger RM, Fetterly GJ, Ma WW, Jusko WJ. Interactions of everolimus and sorafenib in pancreatic cancer cells. AAPS J. 2013;15:78–84. doi: 10.1208/s12248-012-9417-7. doi: 10.1208/s12248-012-9417-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Koch G, Walz A, Lahu G, Schropp J. Modeling of tumor growth and anticancer effects of combination therapy. J Pharmacokinet Pharmacodyn. 2009;36:179–97. doi: 10.1007/s10928-009-9117-9. doi: 10.1007/s10928-009-9117-9. [DOI] [PubMed] [Google Scholar]
- 34.Hamed SS, Straubinger RM, Jusko WJ. Pharmacodynamic modeling of cell cycle and apoptotic effects of gemcitabine on pancreatic adenocarcinoma cells. Cancer Chemother Pharmacol. 2013;72:553–63. doi: 10.1007/s00280-013-2226-6. doi: 10.1007/s00280-013-2226-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Modiano JF, Ritt MG, Wojcieszyn J, Smith R. Growth arrest of melanoma cells is differentially regulated by contact inhibition and serum deprivation. DNA Cell Biol. 1999;18:357–67. doi: 10.1089/104454999315259. doi: 10.1089/104454999315259. [DOI] [PubMed] [Google Scholar]
- 36.Hayes O, Ramos B, Rodríguez LL, Aguilar A, Badía T, Castro FO. Cell confluency is as efficient as serum starvation for inducing arrest in the G0/G1 phase of the cell cycle in granulosa and fibroblast cells of cattle. Anim Reprod Sci. 2005;87:181–92. doi: 10.1016/j.anireprosci.2004.11.011. doi: 10.1016/j.anireprosci.2004.11.011. [DOI] [PubMed] [Google Scholar]
- 37.Cappella P, Tomasoni D, Faretta M, Lupi M, Montalenti F, Viale F, Banzato F, D'Incalci M, Ubezio P. Cell cycle effects of gemcitabine. Int J Cancer. 2001;93:401–408. doi: 10.1002/ijc.1351. doi: 10.1002/ijc.1351. [DOI] [PubMed] [Google Scholar]
- 38.Taylor RC, Cullen SP, Martin SJ. Apoptosis: controlled demolition at the cellular level. Nat Rev Mol Cell Biol. 2008;9:231–41. doi: 10.1038/nrm2312. doi: 10.1038/nrm2312. [DOI] [PubMed] [Google Scholar]
- 39.D'Argenio DZ, Schumitzky A, Wang X. ADAPT 5 user's guide: pharmacokinetic/pharmacodynamic systems analysis software. Biomedical Simulations Resource; Los Angeles: 2009. [Google Scholar]
- 40.Battaglia MA, Parker RS. Pharmacokinetic/pharmacodynamic modelling of intracellular gemcitabine triphosphate accumulation: translating in vitro to in vivo. IET Syst Biol. 2011;5:34. doi: 10.1049/iet-syb.2009.0073. doi: 10.1049/iet-syb.2009.0073. [DOI] [PubMed] [Google Scholar]
- 41.Zhang L, Sinha V, Forgue ST, Callies S, Ni L, Peck R, Allerheiligen SRB. Model-based drug development: The road to quantitative pharmacology. J Pharmacokinet Pharmacodyn. 2006;33:369–393. doi: 10.1007/s10928-006-9010-8. doi: 10.1007/s10928-006-9010-8. [DOI] [PubMed] [Google Scholar]
- 42.Heinemann V, Xu YZ, Chubb S, Sen A, Hertel LW, Grindey GB, Plunkett W. Cellular elimination of 2′,2′-difluorodeoxycytidine 5′-triphosphate: A mechanism of self-potentiation. Cancer Res. 1992;52:533–539. [PubMed] [Google Scholar]
- 43.Amaravadi R, Schilder R, Dy G, Ma W, Fetterly G, Weng D, Graham M, Burns J, Chunduru S, Condon S, McKinlay M, Adjei A. Phase 1 study of the Smac mimetic TL32711 in adult subjects with advanced solid tumors & lymphoma to evaluate safety, pharmacokinetics pharmacodynamics and anti-tumor activity.. Poster session presented at: 102nd Annual Meeting of the American Association.2011. [Google Scholar]
- 44.Bocci G, Danesi R, Marangoni G, Fioravanti A, Boggi U, Esposito I, Fasciani A, Boschi E, Campani D, Bevilacqua G, Mosca F, Del Tacca M. Antiangiogenic versus cytotoxic therapeutic approaches to human pancreas cancer: an experimental study with a vascular endothelial growth factor receptor-2 tyrosine kinase inhibitor and gemcitabine. Eur J Pharmacol. 2004;498:9–18. doi: 10.1016/j.ejphar.2004.07.062. doi: 10.1016/j.ejphar.2004.07.062. [DOI] [PubMed] [Google Scholar]
- 45.Buchsbaum DJ, Bonner J a., Grizzle WE, Stackhouse MA, Carpenter M, Hicklin DJ, Bohlen P, Raisch KP. Treatment of pancreatic cancer xenografts with Erbitux (IMC-C225) anti-EGFR antibody, gemcitabine, and radiation. Int J Radiat Oncol Biol Phys. 2002;54:1180–1193. doi: 10.1016/s0360-3016(02)03788-4. doi: 10.1016/S0360-3016(02)03788-4. [DOI] [PubMed] [Google Scholar]
- 46.Jin H-S, Lee TH. Cell cycle-dependent expression of cIAP2 at G2/M phase contributes to survival during mitotic cell cycle arrest. Biochem J. 2006;399:335–42. doi: 10.1042/BJ20060612. doi: 10.1042/BJ20060612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Samuel T, Okada K, Hyer M, Welsh K, Zapata JM, Reed JC. cIAP1 Localizes to the nuclear compartment and modulates the cell cycle. Cancer Res. 2005;65:210–8. [PubMed] [Google Scholar]
- 48.Wang H, Tan S, Wang X, Liu D, Yu C, Bai Z, He D, Zhao J. Silencing livin gene by siRNA leads to apoptosis induction, cell cycle arrest, and proliferation inhibition in malignant melanoma LiBr cells. Acta Pharmacol Sin. 2007;28:1968–74. doi: 10.1111/j.1745-7254.2007.00724.x. doi: 10.1111/j.1745-7254.2007.00724.x. [DOI] [PubMed] [Google Scholar]
- 49.Cao Z, Zhang R, Li J, Huang H, Zhang D, Zhang J, Gao J, Chen J, Huang C. X-linked inhibitor of apoptosis protein (XIAP) regulation of cyclin D1 protein expression and cancer cell anchorage-independent growth via its E3 ligase-mediated protein phosphatase 2A/c-Jun axis. J Biol Chem. 2013;288:20238–47. doi: 10.1074/jbc.M112.448365. doi: 10.1074/jbc.M112.448365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Karin M, Cao Y, Greten FR, Li Z-W. NF-κB in cancer: from innocent bystander to major culprit. Nat Rev Cancer. 2002;2:301–310. doi: 10.1038/nrc780. doi: 10.1038/nrc780. [DOI] [PubMed] [Google Scholar]
- 51.Volcic M, Karl S, Baumann B, Salles D, Daniel P, Fulda S, Wiesmüller L. NF-κB regulates DNA double-strand break repair in conjunction with BRCA1-CtIP complexes. Nucleic Acids Res. 2012;40:181–95. doi: 10.1093/nar/gkr687. doi: 10.1093/nar/gkr687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wu Z-H, Miyamoto S. Induction of a pro-apoptotic ATM-NF-κB pathway and its repression by ATR in response to replication stress. EMBO J. 2008;27:1963–73. doi: 10.1038/emboj.2008.127. doi: 10.1038/emboj.2008.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Marivin A, Berthelet J, Plenchette S, Dubrez L. The inhibitor of apoptosis (IAPs) in adaptive response to cellular stress. Cells. 2012;1:711–37. doi: 10.3390/cells1040711. doi: 10.3390/cells1040711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hung SW, Mody HR, Govindarajan R. Overcoming nucleoside analog chemoresistance of pancreatic cancer: a therapeutic challenge. Cancer Lett. 2012;320:138–49. doi: 10.1016/j.canlet.2012.03.007. doi: 10.1016/j.canlet.2012.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Olive KP, Jacobetz M a, Davidson CJ, Gopinathan A, McIntyre D, Honess D, Madhu B, Goldgraben M a, Caldwell ME, Allard D, Frese KK, Denicola G, Feig C, Combs C, Winter SP, Ireland-Zecchini H, Reichelt S, Howat WJ, Chang A, Dhara M, Wang L, Rückert F, Grützmann R, Pilarsky C, Izeradjene K, Hingorani SR, Huang P, Davies SE, Plunkett W, Egorin M, Hruban RH, Whitebread N, McGovern K, Adams J, Iacobuzio-Donahue C, Griffiths J, Tuveson DA. Inhibition of Hedgehog signaling enhances delivery of chemotherapy in a mouse model of pancreatic cancer. Science. 2009;324:1457–1461. doi: 10.1126/science.1171362. doi: 10.1126/science.1171362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lieber M, Mazzetta J, Nelson-Rees W, Kaplan M, Todaro G. Establishment of a continuous tumor-cell line (panc-1) from a human carcinoma of the exocrine pancreas. Int J Cancer. 1975;15:741–747. doi: 10.1002/ijc.2910150505. [DOI] [PubMed] [Google Scholar]
- 57.McIntyre LJ, Kim YS. Effects of sodium butyrate and dimethylsulfoxide on human pancreatic tumor cell lines. Eur J Cancer Clin Oncol. 1984;20:265–71. doi: 10.1016/0277-5379(84)90194-9. [DOI] [PubMed] [Google Scholar]
- 58.Okada G, Watanabe H, Ohtsubo K, Mouri H, Yamaguchi Y, Motoo Y, Sawabu N. Multiple factors influencing the release of hTERT mRNA from pancreatic cancer cell lines in in vitro culture. Cell Biol Int. 2012;36:545–53. doi: 10.1042/CBI20090471. doi: 10.1042/CBI20090471. [DOI] [PubMed] [Google Scholar]
- 59.Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, Germani M, Poggesi I, Rocchetti M. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004;64:1094–101. doi: 10.1158/0008-5472.can-03-2524. doi: 10.1158/0008-5472.CAN-03-2524. [DOI] [PubMed] [Google Scholar]
- 60.Nakashima M, Adachi S, Yasuda I, Yamauchi T, Kawaguchi J, Itani M, Yoshioka T, Matsushima-Nishiwaki R, Hirose Y, Kozawa O, Moriwaki H. Phosphorylation status of heat shock protein 27 plays a key role in gemcitabine-induced apoptosis of pancreatic cancer cells. Cancer Lett. 2011;313:218–25. doi: 10.1016/j.canlet.2011.09.008. doi: 10.1016/j.canlet.2011.09.008. [DOI] [PubMed] [Google Scholar]
- 61.Oliveras-Ferraros C, Vazquez-Martin A, Colomer R, De Llorens R, Brunet J, Menendez JA. Sequence-dependent synergism and antagonism between paclitaxel and gemcitabine in breast cancer cells: the importance of scheduling. Int J Oncol. 2008;32:113–20. [PubMed] [Google Scholar]
- 62.Arlt A, Gehrz A, Müerköster S, Vorndamm J, Kruse M-L, Fölsch UR, Schäfer H. Role of NF-κB and Akt/PI3K in the resistance of pancreatic carcinoma cell lines against gemcitabine-induced cell death. Oncogene. 2003;22:3243–51. doi: 10.1038/sj.onc.1206390. doi: 10.1038/sj.onc.1206390. [DOI] [PubMed] [Google Scholar]
- 63.Kunnumakkara AB, Guha S, Krishnan S, Diagaradjane P, Gelovani J, Aggarwal BB. Curcumin potentiates antitumor activity of gemcitabine in an orthotopic model of pancreatic cancer through suppression of proliferation, angiogenesis, and inhibition of nuclear factor-κB-regulated gene products. Cancer Res. 2007;67:3853–3861. doi: 10.1158/0008-5472.CAN-06-4257. doi: 10.1158/0008-5472.CAN-06-4257. [DOI] [PubMed] [Google Scholar]
- 64.Zabludoff SD, Deng C, Grondine MR, Sheehy AM, Ashwell S, Caleb BL, Green S, Haye HR, Horn CL, Janetka JW, Liu D, Mouchet E, Ready S, Rosenthal JL, Queva C, Schwartz GK, Taylor KJ, Tse AN, Walker GE, White AM. AZD7762, a novel checkpoint kinase inhibitor, drives checkpoint abrogation and potentiates DNA-targeted therapies. Mol Cancer Ther. 2008;7:2955–66. doi: 10.1158/1535-7163.MCT-08-0492. doi: 10.1158/1535-7163.MCT-08-0492. [DOI] [PubMed] [Google Scholar]
- 65.Montano R, Thompson R, Chung I, Hou H, Khan N, Eastman A. Sensitization of human cancer cells to gemcitabine by the Chk1 inhibitor MK-8776: cell cycle perturbation and impact of administration schedule in vitro and in vivo. BMC Cancer. 2013;13:604. doi: 10.1186/1471-2407-13-604. doi: 10.1186/1471-2407-13-604. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.