Objective evaluation of reconstruction methods for quantitative SPECT imaging in the absence of ground truth

Abstract

Quantitative single-photon emission computed tomography (SPECT) imaging is emerging as an important tool in clinical studies and biomedical research. There is thus a need for optimization and evaluation of systems and algorithms that are being developed for quantitative SPECT imaging. An appropriate objective method to evaluate these systems is by comparing their performance in the end task that is required in quantitative SPECT imaging, such as estimating the mean activity concentration in a volume of interest (VOI) in a patient image. This objective evaluation can be performed if the true value of the estimated parameter is known, i.e. we have a gold standard. However, very rarely is this gold standard known in human studies. Thus, no-gold-standard techniques to optimize and evaluate systems and algorithms in the absence of gold standard are required. In this work, we developed a no-gold-standard technique to objectively evaluate reconstruction methods used in quantitative SPECT when the parameter to be estimated is the mean activity concentration in a VOI. We studied the performance of the technique with realistic simulated image data generated from an object database consisting of five phantom anatomies with all possible combinations of five sets of organ uptakes, where each anatomy consisted of eight different organ VOIs. Results indicate that the method provided accurate ranking of the reconstruction methods. We also demonstrated the application of consistency checks to test the no-gold-standard output.

1. INTRODUCTION

Quantitative single-photon emission computed tomography (SPECT) is emerging as an important tool for clinical studies and biomedical research.^{1, 2} In quantitative SPECT, the end task is estimating a certain functional or anatomical parameter about the object of interest from a SPECT image, such as quantifying the total activity or the mean activity concentration within a certain volume of interest (VOI) in a patient image. Quantitative SPECT has several important applications such as in targeted radionuclide therapy (TRT) for treatment planning,^3–5 myocardial perfusion SPECT studies that quantify regional blood flow⁶ or perform dynamic analysis of myocardial perfusion to derive the kinetic parameters or the perfusion volume,⁷ dopamine transporter scan (DaTSCAN) quantification,^{8, 9} and renal Tc-99m dimercaptosuccinic acid (DMSA) SPECT studies.^{10, 11}

Several imaging systems and algorithms have been designed to provide accurate quantitative SPECT imaging. There is a requirement for objective methods to optimize and evaluate these systems and algorithms on the basis of their performance in the task of estimating the parameter of interest accurately and precisely. Such objective evaluation is greatly simplified when we know the true value of the parameter, but this is rarely the case in patient studies. For this reason, animal, physical phantom and simulation studies have become an important tool in this optimization and evaluation process. However, it is highly desirable to ultimately validate these results using clinical studies and human images where the true value, which serves as a gold standard, is known imperfectly or not at all. Thus, in order to objectively compare systems and algorithms for quantitative SPECT, there is a need for evaluation methods that can be implemented in the absence of a gold standard. In this paper, our broad objective is to design such a no-gold-standard method to evaluate quantitative SPECT systems on the task of estimating the mean activity concentration within a VOI.

The objective evaluation of imaging systems or algorithms in the absence of gold standard has been a challenging and important research problem. Henkelman et al.¹² derived a method to perform receiver operating characteristic (ROC) analysis without knowing the true diagnosis. A method to objectively compare the performance of imaging systems and algorithms for estimation tasks in the absence of ground truth was developed by Hoppin et al.¹³ and Kupinski et al.¹⁴ The method was used to compare cardiac-ejection-fraction estimation algorithms in the absence of ground truth.¹⁵ The method was extended to objectively evaluate segmentation algorithms in diffusion-weighted magnetic resonance imaging (DWMRI) when the ground truth segmentation is not known.^16–18

In quantitative SPECT imaging for activity estimation, most current methods to evaluate algorithms assume a gold standard that is obtained either by applying another algorithm on the image or from another imaging modality,¹⁹ and thus is not necessarily accurate. Further, determining the actual gold standard is very complicated in these applications. Thus, there is a great need for a no-gold-standard approach for evaluating systems and algorithms based on the task of activity estimation. The particular problem we consider in this paper is the evaluation of reconstruction methods for quantitative SPECT imaging when the end task is estimating the activity within a VOI.

2. METHODS

2.1 Theory

Consider the case where P patients are imaged using a SPECT imaging system. The acquired projection data are reconstructed using K different reconstruction methods, and the mean activity concentration in the VOI is estimated using the reconstructed images from all the methods. Our objective is to develop a no-gold-standard technique to evaluate these K reconstruction methods based on the task of estimating the mean activity concentration. A schematic illustrating the problem statement is presented in Fig. 1.

Figure 1.

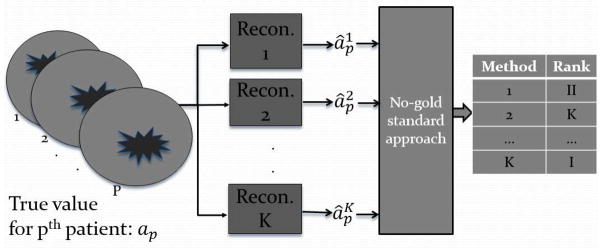
A schematic illustrating the problem statement for the no-gold-standard method

The method that we propose in this paper builds up on the basic framework as proposed previously in Hoppin et al.,¹³ Kupinski et al.¹⁴ and Jha et al.¹⁷ We assume that there is some relationship between the true and estimated activity values, consisting of both deterministic and random components. Using realistic simulation studies described below, and with the aid of measures such as the Akiki information criterion (AIC) and Bayesian information criterion (BIC), we found that a linear model, consisting of a slope, intercept, and zero-mean normally-distributed noise term, could be used to model the relationship between the true and estimated activity values. Thus, denoting the true activity value for the p^th patient by a_p, the estimated activity value for this patient using the k^th reconstruction method by ${\widehat{a}}_k^p$, and the slope, intercept and standard deviation of the noise term for the k^th method by u_k, v_k and σ_k, respectively, we write this model as

$${\widehat{a}}_k^p=u_k{a}_p+v_k+\mathcal{N}(0,{\sigma }_k),$$ (1)

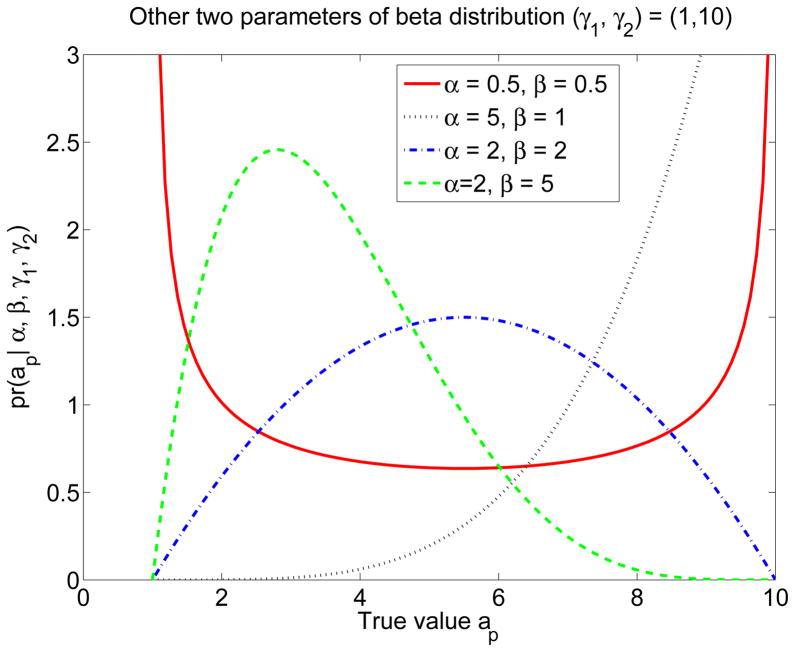
where (0, σ_k) denotes a zero-mean normally distributed random variable with standard deviation σ_k. Let us denote the unknown linear model parameters for all the reconstruction methods, i.e. {u_k, v_k, s_k, k = 1, 2 … K} by Θ. We next assume that the true value a_p arises from some unknown distribution. Based on our empirical studies and in order to accommodate a wide variety of distribution shapes, we choose this distribution to be a four-parameter beta distribution, parameterized by the vector Ω.¹⁷ The beta distribution has the ability to model non-symmetric data, negatively skewed, uni-modal, strictly increasing, strictly decreasing, concave, convex and uniform distributions, as illustrated by some representative beta distributions in Fig. 2. Note that we do not know the values of Ω or Θ.

Figure 2.

Various shapes taken by the beta distribution as the distribution parameters are varied

Let us denote the set of all estimated mean activity concentration values, i.e the set { ${\widehat{a}}_k^p$, k = 1, 2 … K, p = 1, 2, …, P}, by . The no-gold-standard method uses a maximum-likelihood (ML) approach, i.e. it estimates the values of the unknown parameters that maximize the probability of all the observed data. Denoting the estimated values by {Θ̂, Ω̂}, the objective is to determine

$$\{\widehat{\mathbf{\Theta }},\widehat{\mathbf{\Omega }}\}=\mathit{argmax}\text{pr}(\widehat{\mathcal{A}}\mid \mathbf{\Theta },\mathbf{\Omega })$$ (2)

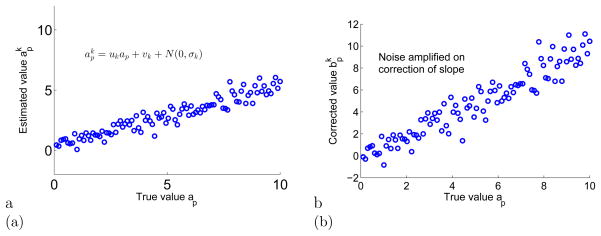
We determined the expression for pr( |Θ, Ω) and subsequently computed the ML solution using a quasi-Newton optimization technique. We used these estimated parameters to compute two figures of merit. The first figure of merit represents the precision of the algorithm when the slope and intercepts are treated as calibration factors and corrected. The correction of the slope amplifies the noise variance, as illustrated by the schematic in Fig. 3. Therefore, thenoise-to-slope ratio σ_k/a_k, was chosen as the first figure of merit. The second figure of merit is the scaled ensemble mean square error (EMSE), denoted by EMSE_SC, and is defined as

Figure 3.

A demonstration of the effect of correcting the data for the bias and slope terms. In (a), we present an example plot of synthetically generated true and estimated mean activity concentration values. The estimated values are corrected for the slope and bias, and in (b), a plot of the true and corrected mean activity concentration values is presented. We observe that the noise is amplified due to the correction of the slope.

$${\text{EMSE}}_{\text{sc}}=\frac{v_k^2+{\sigma }_k^2}{u_k^2}$$ (3)

EMSE_SC is a modified EMSE metric assuming that the data are corrected for the slope factor but not the intercept. This metric measures both the bias and variance of the reconstruction algorithm.

2.2 Consistency checks

The no-gold-standard approach could yield incorrect ranking of the methods due to erroneous estimation of the model parameters. Thus, we developed checks that verify if the estimated no-gold-standard output is consistent with the observed data. These checks test the similarity between the histogram of estimated activity values and the theoretically estimated distribution computed using the no-gold-standard method. The first consistency check computes the correlation coefficient of the quantile-quantile (QQ) plot²⁰ between the two distributions, while the second check is a Pearsons χ² test²¹ with these two distributions.

2.3 Validating the no-gold-standard approach

We simulated a SPECT imaging system that images an I-131 radioisotope distribution modeling the uptake of an I-131 labeled anti-CD20 antibody used for radionuclide therapy of non-Hodgkins Lymphoma. The object database consisted of five patient anatomies with all possible combinations of five sets of organ uptakes. The phantoms were based on the non-uniform rational B-spline (NURBS)-based cardiac-torso (NCAT) phantom with organ sizes and uptakes based on patient data.²² The data were simulated using realistic and previously validated MC simulation methods. The acquired projection data were reconstructed using compensation for three different combinations of model-based compensation implemented using the ordered subsets expectation maximization (OSEM) algorithm. The compensations investigated included attenuation and scatter (AS) compensation, attenuation, scatter and detector response compensation (ADS), and ADS with the addition of explicit compensation for down-scatter from high-energy photons (ADS.DWN).²³ Scatter compensation used the effective scatter source estimation (ESSE) scatter model and detector response compensation included the geometric, septal penetration and septal scatter components.²⁴ The activity in eight different VOIs corresponding to the lungs, liver, heart, spleen, kidneys, pelvis, blood, and background were estimated assuming knowledge of the true organ VOIs. In our simulation study, we computed the noise-to-slope ratio and the EMSE_SC for the different reconstruction methods using the estimated no-gold-standard parameters. We used these estimated parameters to predict the rank of the reconstruction methods. These rankings were then compared to the true rankings obtained using the actual value of the EMSE_SC and noise-to-slope ratio.

3. RESULTS

The true values of the figures of merit and the values estimated using the no-gold-standard method for one of the noise realizations are shown in Table 1. It is observed that both the estimated and the true noise-to-slope ratios yield the same rankings for the three reconstruction methods. The same trend is observed with the rankings predicted using the true and estimated EMSE_SC values. Thus, the ranking predicted using the parameters estimated from the no-gold-standard technique is the same as the rankings from the true figures of merit.

Table 1.

The true and estimated figures of merit for one noise realization. The rankings predicted from the estimated figures of merit are the same as the rankings using the true figures of merit.

Reconstruction method	True noise-to-slope ratio	Estimated noise-to-slope ratio	True EMSESC	Estimated EMSESC
AS	0.299	0.173	0.128	0.056
ADS	0.190	0.099	0.039	0.014
ADS-DWN	0.167	0.002	0.029	0.001

The regression lines obtained using the estimated no-gold-standard parameters were also compared to the scatter plot of the true and estimated activity values for all the reconstruction methods. It is observed, as shown in Fig. 4, that for all the reconstruction methods, the scatter plot coincided with the estimated regression line, thus demonstrating the efficacy of the no-gold-standard technique. It is also observed that the regression line plots reflected the noise in the relation between the true and estimated mean activity concentration values.

Figure 4.

Regression lines estimated using the no-gold-standard method for the three reconstruction methods. The solid line is generated using the estimated linear model parameters, and the dashed line denotes the estimated standard deviation.

Further, when the no-gold-standard method estimated the correct ranking, the correlation coefficient of the Q-Q plot and the p-value returned by the Pearson’s χ² test were both very close to 1. Thus the consistency check correctly predicted that the no-gold-standard method yielded the correct rankings.

4. CONCLUSIONS

We have developed a no-gold-standard method for evaluating reconstruction methods for quantitative SPECT imaging where the end task is estimating the activity concentration in a VOI. The performance of the method has been studied with a realistic simulated image dataset, and results show that the method provides accurate estimate of the rankings of the considered reconstruction methods using two different figures of merit. We are currently repeating these experiments with multiple noise realizations to assess the reliability of the method. An issue with the approach is the amount of patient data required to obtain reliable performance, especially since much paitent data might be unavailable. Currently we are also quantifying this data requirement and investigating methods for its reduction. The method can be extended to objectively evaluate quantitative SPECT systems and algorithms for other quantitative tasks such as VOI segmentation and histogram estimation.