Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Sep 24;5:13956. doi: 10.1038/srep13956

Tunable mid-infrared coherent perfect absorption in a graphene meta-surface

Yuancheng Fan 1,a, Zhe Liu 2, Fuli Zhang 1, Qian Zhao 3, Zeyong Wei 4, Quanhong Fu 1, Junjie Li 2, Changzhi Gu 2, Hongqiang Li 4
PMCID: PMC4585855  PMID: 26400371

Abstract

Graphene has drawn considerable attention due to its intriguing properties in photonics and optoelectronics. However, its interaction with light is normally rather weak. Meta-surfaces, artificial structures with single planar function-layers, have demonstrated exotic performances in boosting light-matter interactions, e.g., for absorption enhancement. Graphene based high efficiency absorber is desirable for its potential applications in optical detections and signal modulations. Here we exploit graphene nanoribbons based meta-surface to realize coherent perfect absorption (CPA) in the mid-infrared regime. It was shown that quasi-CPA frequencies, at which CPA can be demonstrated with proper phase modulations, exist for the grapheme meta-surface with strong resonant behaviors. The CPA can be tuned substantially by merging the geometric design of the meta-surface and the electrical tunability of graphene. Furthermore, we found that the graphene nanoribbon meta-surface based CPA is realizable with experimentally achievable graphene sample.

Recently, graphene is been widely investigated for potential applications in photonics and optoelectronics1,2,3,4,5. It exhibits much stronger binding of surface plasmon polaritons6, and the Dirac fermions provides ultrawideband tunability through electrostatic field, magnetic field or chemical doping7,8. One key feature of graphene is that it is almost transparent to optical waves9 due to the relatively low carrier concentrations in a monolayer atomic sheet. Boosting the light-matter interaction in graphene is one important issue to address to take further advantage of graphene in optoelectronic devices. For example, to realize functionality like optical insulator10 similar to gapped graphene11,12 for nanoelectronics, which is essential for myriad applications in all-optical systems and components of much miniaturized optical circuits13,14.

Artificially engineered photonic structures have been employed as a platform for boosting light-matter interactions for decades15,16. Optical absorption enhancement had been demonstrated in a photonic crystal nanocavity for high-contrast electrooptic modulation17. In the meanwhile, metamaterials18,19 with even miniaturized elements are promising for the manipulation of light in a subwavelength scale. Especially the metamaterials with a single planar function-layer, or meta-surface20,21, has been intensively studied in recent years for various possibilities to manipulate light peculiarly22,23,24,25,26. The meta-surface has also found its close connection to graphene: replacing metals with graphene makes the meta-surface even miniaturized for frequency-agile responses27; and the light-graphene interactions can be significantly modified in an atomically thin graphene meta-surface in return. It was reported that optical absorption enhancement can be achieved in periodically doped graphene nanodisks, in which periodic graphene nanodisks are overlying on a substrate or on a dielectric film coating on metal, the excitation of electric mode of the nanodisks together with multi-reflection from the assistants of total internal reflection and metal reflection can result in a complete optical absorption28. Graphene micro/nanoribbons, ring resonators, mantles, nano-crosses and super-lattices have also been attempted for manipulating the terahertz/infrared waves29,30,31,32,33,34,35,36,37,38,39,40,41. A comparative study37 found that the fundamental electric dipolar mode provides stronger light-graphene interaction at terahertz frequencies than the magnetic and higher-order electric modes, it is also found that the maximum absorption in a monolayer graphene is 50%, which is associated with a real number effective surface conductivity 2/η0 where η0 represents the characteristic impedance of vacuum42. The concept of coherent perfect absorption in structured systems43,44,45,46,47,48,49,50,51,52 was introduced into a suspending monolayer graphene for 100% absorption of terahertz waves53. However, the proposed non-resonant CPA based on the intrinsic Drude response of graphene is realizable only in the few-terahertz range with achievable graphene samples.

In this paper, we propose a tunable mid-infrared coherent perfect absorber with a graphene nanoribbon based meta-surface. It is found that quasi-CPA frequencies, which is the necessary formation condition of coherent absorption, does exist in the mid-infrared regime for properly designed graphene nanoribbon arrays. The scattering of coherent beams can be perfectly suppressed at the quasi-CPA frequencies with proper phase modulations on the input beams. For the case with two crosses on the transmission and reflection spectra, we can achieve coherent perfect absorption at the two quasi-CPA frequencies, simultaneously. The flexible tunabilities of the graphene meta-surface based CPA are of interests for tunable infrared detections and signal modulations.

Results and Discussion

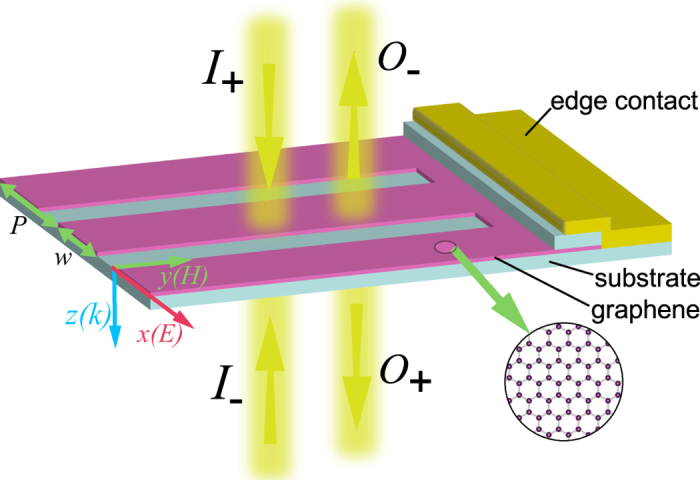
Figure 1 shows the schematic of the proposed graphene nanoribbons based meta-surface and corresponding excitation configuration with two counter-propagating and coherently modulated optical beams (I+ and I−), O+ and O− are the respective output magnitudes, the graphene sheet is illuminated with perpendicularly polarized light (electric vector E is parallel to the x-axis). The meta-atoms, i.e., graphene nanoribbons, are periodically arranged in x-y plane with the lattice (along x axis) constant and ribbon’s width being P and w, respectively. Both lattice constant and width of the graphene nanoribbon meta-atoms play important roles in determining the optical resonant behaviors of graphene meta-surface, the lattice constant is set to be P = 0.7 μm for the study of CPA in the mid-infrared regime.

Figure 1. Schematic of a graphene ribbon meta-surface illustrated by two counter-propagating and coherently modulated input beams (I+ and I−, the electric polarization is along x-axis, and propagate along ±z-directions), O+ and O− represent the amplitudes of output beams.

Figure 1

Open in a new tab

The graphene layer is considered as a sheet material modeled with complex surface conductivity (σg) since a one-atom-thick graphene sheet is sufficiently thin compared with the concerned wavelength. In the theoretical perspective based on random-phase-approximation (RPA)54,55,56, the complex conductivity of graphene can be described by the Drude model as 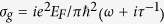Inline graphic, especially in heavily doped region and low frequencies (far below Fermi energy), where EF represents the Fermi energy, 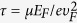Inline graphic is the relaxation rate with the mobility μ = 104 cm2V−1s−1 and Fermi velocity vF ≈ 106 m/s.

We first took EF = 0.5 eV. Figure 2a presents the spectra of the reflection coefficients (r) and transmission coefficients (t) for the case of graphene nanoribbon meta-surface with width of w = 0.33 μm. We can see an obvious resonance around 23.0 THz. The resonance was confirmed to be electric dipolar mode (which will be verified from the effective surface conductivity below), similar to the low-frequency resonance of split-ring-resonators as that in37. The excitation of electric dipolar mode leads to the enhancement of absorption in the graphene sheet, however, the maximum limit is 50%.

Figure 2.

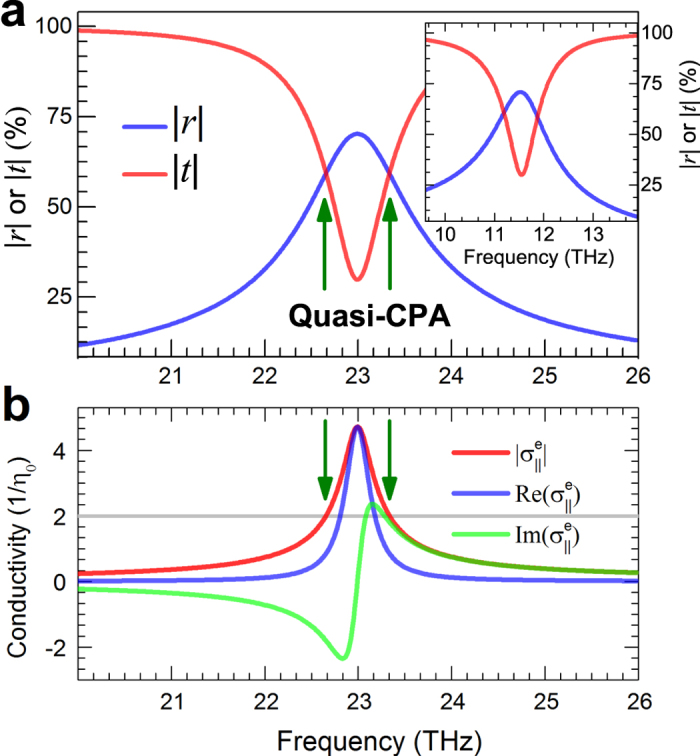
Figure 2

Open in a new tab

(a) Spectra of the reflection and transmission coefficients of a graphene nanoribbon meta-surface (w = 0.33 μm), the quasi-CPA points at the crosses of the scattering spectra are indicated with arrows. (b) Absolute values, real and imaginary parts of the effective surface conductivities of the corresponding graphene nanoribbon meta-surface.

The complex scattering coefficients (O±) of the graphene nanoribbon meta-surface can be related to the two input beams (I±, and in this paper the two input beams are set to be of equal amplitude I) through a scattering matrix, Sg, defined as:

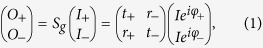graphic file with name srep13956-m3.jpg

where (t/r)+ and (t/r)− are scattering elements of forward (irradiate towards z+, I+) and backward (irradiate towards z−, I−) beams, since the linear monolayer graphene under investigation is of reciprocity and spatial symmetry, the scattering matrix can be simplified with t± = t and r± = r. Then the amplitude of the scattering coefficients would be

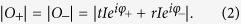graphic file with name srep13956-m4.jpg

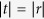The scatterings of the input beams are required to be inhibited to demonstrate a CPA, that is Inline graphic, from which we can get the necessary condition for CPA performance: Inline graphic.

Since the high-order scatterings of the deep-subwavelength graphene nanoribbons are negligible, the graphene meta-surface can be formalized with effective surface conductivities 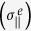Inline graphic and its scattering coefficients of normal incident light can be got with a transfer matrix formalism:

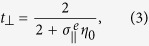graphic file with name srep13956-m8.jpg
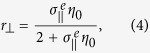graphic file with name srep13956-m9.jpg

where η0 is the wave impedance of free space.

It can be seen from Fig. 2a there exists two frequencies (22.65 THz, and 23.33 THz), which we call quasi-CPA point, where 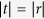Inline graphic implies the necessary condition for suppressing the scattering fields to completely absorb coherent input beams of equal-intensity. In the view of experiments, graphene generally needs to be transferred onto some substrate, we studied the scattering responses of a nanoribbon array [with same geometry as that in Fig. 2a] sandwiched in between two 45 nm-thick hexagonal boron nitride (h-BN) substrates, which was suggested as an exceptionally clean environment for achieving high confinement and low levels of plasmon damping in graphene57 and is suitable for the one-dimensional high-quality electrical contact58 (see the illustration in Fig. 1). The dielectric function of which was taken from experimental studies57,59. As can be seen from the inset of Fig. 2a, the resonant frequency shifts to lower frequency as expected because of the introduction of the substrate, and there keeps two quasi-CPA frequencies. For simplicity and without loss of generality, we will consider free-standing graphene meta-surfaces.

From Eq. (3), we can also get the formation condition for CPA in an effective medium scheme as: 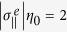Inline graphic. To verify this, we used a recently proposed sheet retrieval method60 to extract the effective surface conductivity 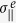Inline graphic of the graphene nanoribbon meta-surface. Figure 2(b) shows the absolute, real and imaginary parts of the effective surface conductivities corresponding to Fig. 2a, It is obvious that there is a Lorentz-resonance around 23.0 THz on the effective electric conductivity spectrum, which confirms the excitation of electric dipolar mode. The extracted magnetic conductivity does not show any resonant feature around this electric resonance, so we have not included the corresponding result here. And it is also seen that the condition 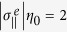Inline graphic is fulfilled at the two quasi-CPA frequencies, which indicate the validity of describing the graphene nanoribbon meta-surface with the effective surface conductivity.

To implement the perfect absorption with the graphene meta-surface, we set a chirped phase modulation 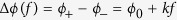Inline graphic on the beams I±, with f being the frequency, and 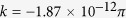Inline graphic being the chirped factor to compensate the frequency dispersion. The plotted false-color map of the normalized spectra of total absorptions in Fig. 3a, shows the detailed dependence on ϕ0. We see that a proper phase modulation (ϕ0 = 1.03π) of the input coherent beams leads to significant suppression of the scattering outputs at the quasi-CPA frequencies. The normalized total absorption as a function of frequency for the phase modulation ϕ0 = 1.03π is plotted in Fig. 3b. We can see total absorption at both the two quasi-CPA frequencies. The significant boosting of the absorption implies destructive interference which prevents the coherent beams from escaping the absorbing channel of the graphene meta-surface, demonstrating completely absorption of the coherent input beams.

Figure 3. A two-dimensional false-color plot of the normalized total absorptions as a function of frequency and phase modulation ϕ0, the exact CPA points are denoted with green arrows.

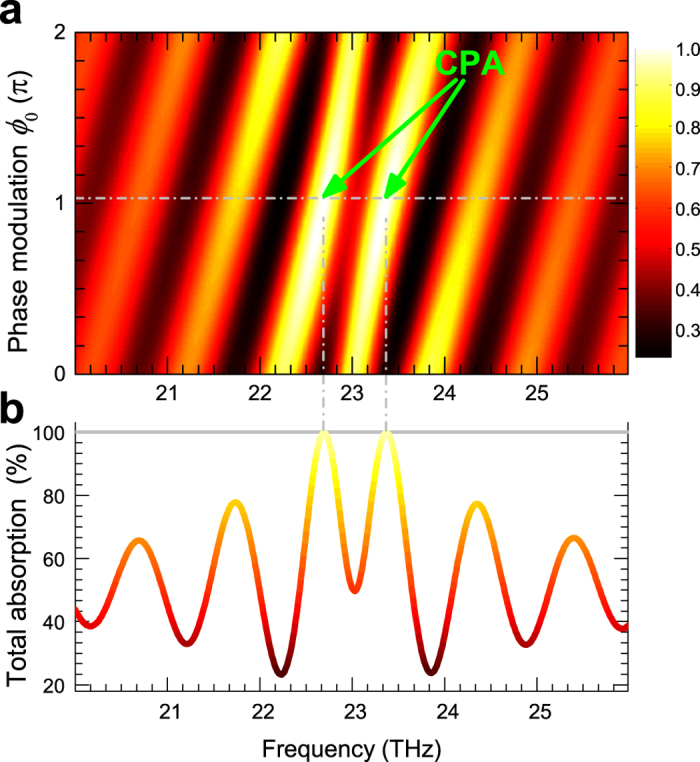
Figure 3

Open in a new tab

(b) Normalized total absorption as a function of frequency for the phase modulation ϕ0 = 1.03π.

The meta-surface structures together with the electrically-controlled graphene will provide more wider tunable space for the design of mid-infrared CPA, we first consider the geometric tunability of the graphene nanoribbon based CPA. Figure 4 shows the dependence of the difference 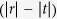Inline graphic of the scattering coefficients (r and t) of the graphene meta-surface on the widths of nanoribbons. We can see that the resonant frequency of the electric dipolar mode shows a monotonous red-shift with the increase of w, which is similar the cut-wire case42 (actually, the ribbon structure is the special situation of cut-wire with graphene covers all the lattice range along x axis. Increasing of the width w or the graphene’ filling factor in the unit cell of the meta-surface leads to stronger light-graphene interaction, i.e. high resonant strength of the electric dipolar resonance, and thus higher r and lower t around the resonance that introduce a regime where 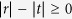Inline graphic starting from w = 0.138 μm, which has its boundary (as the solid line indicated) being the quasi-CPA points. The discrete spheres on top of the solid curve, representing the extracted surface conductivities with 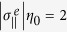Inline graphic, also imply the formation condition of CPA is fulfilled at the boundary. At these quasi-CPA points, we can completely suppress the scatterings of the graphene meta-furface with proper phase modulations as that showed in Fig. 3.

Figure 4. Geometric tunability of the graphene meta-surface CPA: Spectra of the difference 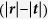Inline graphic of the scattering coefficients (r and t) for the graphene meta-surface width increasing from 0.075 μm to 0.42 μm.

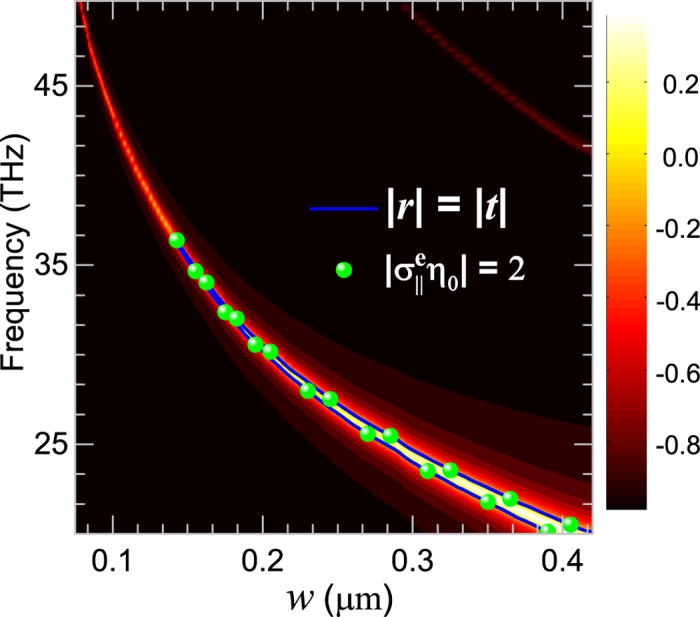
Figure 4

Open in a new tab

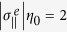The solid line indicates quasi-CPA points where Inline graphic, while the spheres represent the extracted surface conductivities with values Inline graphic.

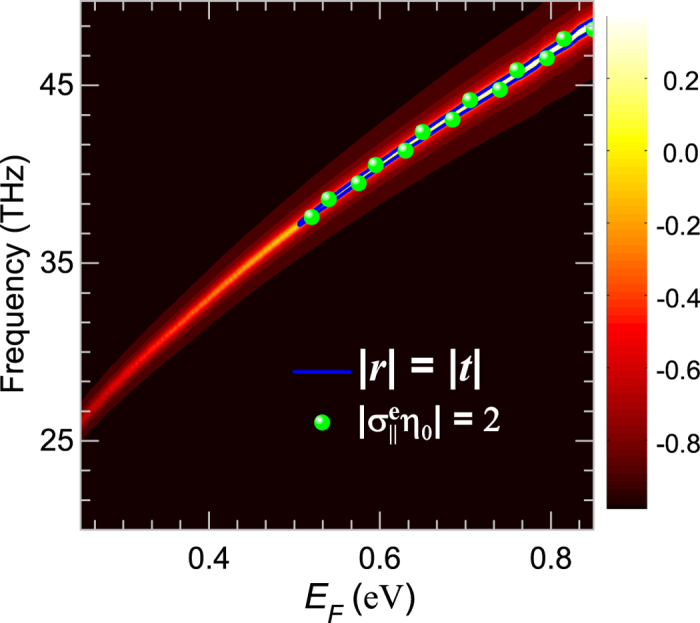
On the other hand, the graphene meta-surface is also expected to have higher resonant strength for graphene with larger Fermi level3,42. The dependence on Fermi energy of the difference 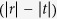Inline graphic of the scattering coefficients are plotted in Fig. 5 [the width of the graphene nanoribbon was set to be 0.138 μm, the left edge of the solid boundary in Fig. 4], it can be seen that the resonant frequency shifts to higher frequencies and the resonant strength becomes higher while the Fermi level changes from to 0.25 eV to 0.85 eV. Similar to the influence of the width of nanoribbons, the light-graphene interaction is enhanced for better resonant behaviors, and thus a regime starting from 0.5 eV where 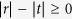Inline graphic with its boundary being the quasi-CPA frequencies. Combining the two functional bands for CPA, we see that it is freely to achieve CPA at desired frequency in an ultra-wide range by merging the geometric and electrical tunabilities. And the discrete spheres representing the extracted surface conductivities in Fig. 5 again confirm that 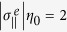Inline graphic is equivalent to the quasi-CPA condition Inline graphic for graphene nanoribbons based meta-surface.

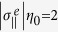Figure 5. Electric tunability of the graphene meta-surface CPA: Spectra of the difference Inline graphic of the scattering coefficients (r and t) for the graphene meta-surface with Fermi energy EF ranging from 0.25 eV to 0.85 eV.

Figure 5

Open in a new tab

The solid line indicates quasi-CPA points where Inline graphic, while the spheres represent the extracted surface conductivities with values Inline graphic.

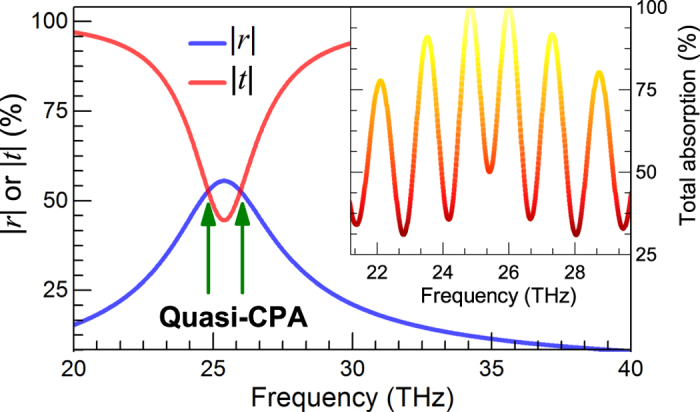
Here, we also consider a graphene nanoribbon array (P = 0.22 μm, w = 0.20 μm) made from experimentally practical graphene, i.e., the Yan et al. graphene with Drude weight 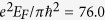Inline graphic GHz/Ω and collision frequency τ−1 = 9.8 THz2,5. The spectra of the scattering coefficients are presented in Fig. 6a, from which, a electric resonance is found around 25.5 THz with two associate quasi-CPA frequencies. The inset shows perfect absorption can be achieved at these two quasi-CPA frequencies with proper phase modulation. This suggest that the graphene nanoribbon meta-surface based CPA is feasible with high-quality Chemical Vapour Deposition (CVD) grown graphene samples.

Figure 6. Scattering coefficients of a graphene nanoribbon array with experimental data (Yan et al. data), the inset shows normalized total absorption for proper phase modulation.

Figure 6

Open in a new tab

Conclusions

In conclusion, we show that graphene nanoribbons based meta-surface can be employed for perfectly suppressing scattering of mid-infrared radiations for CPA. And the quasi-CPA frequency can be found from the effective surface conductivity spectra where 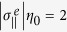Inline graphic. Furthermore, the CPA can be tuned in a ultra-wide frequency band by considering both the geometric tunability and electrically-controlled charge-carrier density in graphene. We expect potential applications of coherent modulations in optical detections and signal processing with structured two-dimensional materials.

Methods

The numerical calculation results were obtained with a finite-integration-technique based electromagnetic solver (CST Microwave Studio). The periodic boundary conditions were set for the simulation of periodic graphene nanoribbon structures. The effective surface conductivities of the graphene nanoribbon based meta-surfaces were carried out using a recently proposed sheet retrieval method60.

Additional Information

How to cite this article: Fan, Y. et al. Tunable mid-infrared coherent perfect absorption in a graphene meta-surface. Sci. Rep. 5, 13956; doi: 10.1038/srep13956 (2015).

Acknowledgments

The authors would like to acknowledge financial support from the NSFC (Grants No. 61505164, 11174221, 11204218, 11372248, 61101044, 61275176, 61390503, and 91323304), the Fundamental Research Funds for the Central Universities (Grant No. 3102015ZY079), and the National 863 Program of China (Grant No. 2012AA030403).

Footnotes

Author Contributions Y.F., Z.L. and Z.W. did the theoretical calculations and the numerical simulations. Q.F., F.Z. and Q.Z. helped the simulations. J.L., C.G. and H.L. contributed to the scientific discussion. Y.F. conceived the idea and wrote the manuscript, all authors commented on the manuscript revisions.

References

  1. Bonaccorso F., Sun Z., Hasan T. & Ferrari A. C. Graphene photonics and optoelectronics. Nat. Photonics 4, 611–622 (2010). [Google Scholar]
  2. Yan H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol 7, 330–334 (2012). [DOI] [PubMed] [Google Scholar]
  3. García de Abajo F. J. Graphene plasmonics: Challenges and opportunities. ACS Photonics 1, 135–152 (2014). [Google Scholar]
  4. Low T. & Avouris P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 8, 1086–1101 (2014). [DOI] [PubMed] [Google Scholar]
  5. Tassin P., Koschny T. & Soukoulis C. M. Graphene for terahertz applications. Science 341, 620–621 (2013). [DOI] [PubMed] [Google Scholar]
  6. Jablan M., Buljan H. & Soljačić M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009). [Google Scholar]
  7. Koppens F. H. L., Chang D. E. & García de Abajo F. J. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett. 11, 3370–3377 (2011). [DOI] [PubMed] [Google Scholar]
  8. Vakil A. & Engheta N. Transformation optics using graphene. Science 332, 1291–1294 (2011). [DOI] [PubMed] [Google Scholar]
  9. Nair R. R. et al. Fine structure constant defines visual transparency of graphene. Science 320, 1308 (2008). [DOI] [PubMed] [Google Scholar]
  10. Yablonovitch E. Photonic crystals: semiconductors of light. Sci. Am. 285, 47–51, 54 (2001). [PubMed] [Google Scholar]
  11. Yao Y., Ye F., Qi X.-L., Zhang S.-C. & Fang Z. Spin-orbit gap of graphene: First-principles calculations. Phys. Rev. B 75, 041401 (2007). [Google Scholar]
  12. Zhang Z. et al. Extend the omnidirectional electronic gap of thue-morse aperiodic gapped graphene superlattices. Appl. Phys. Lett. 101, 252104 (2012). [Google Scholar]
  13. Engheta N. Circuits with light at nanoscales: Optical nanocircuits inspired by metamaterials. Science 317, 1698–1702 (2007). [DOI] [PubMed] [Google Scholar]
  14. Fan Y. et al. Subwavelength electromagnetic diode: One-way response of cascadinig nonlinear meta-atoms. Appl.Phys. Lett. 98, 151903 (2011). [Google Scholar]
  15. Hess O. et al. Active nanoplasmonic metamaterials. Nat. Mater. 11, 573–584 (2012). [DOI] [PubMed] [Google Scholar]
  16. Kauranen M. & Zayats A. V. Nonlinear plasmonics. Nat. Photonics 6, 737–748 (2012). [Google Scholar]
  17. Gan X. et al. High-contrast electrooptic modulation of a photonic crystal nanocavity by electrical gating of graphene. Nano Lett. 13, 691–696 (2013). [DOI] [PubMed] [Google Scholar]
  18. Smith D. R., Pendry J. B. & Wiltshire M. C. K. Metamaterials and negative refractive index. Science 305, 788–792 (2004). [DOI] [PubMed] [Google Scholar]
  19. Soukoulis C. M. & Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5, 523–530 (2011). [Google Scholar]
  20. Kildishev A. V., Boltasseva A. & Shalaev V. M. Planar photonics with metasurfaces. Science 339, 6125 (2013). [DOI] [PubMed] [Google Scholar]
  21. Yu N. & Capasso F. Flat optics with designer metasurfaces. Nat. Mater 13, 139–150 (2014). [DOI] [PubMed] [Google Scholar]
  22. Yu N. et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 334, 333–337 (2011). [DOI] [PubMed] [Google Scholar]
  23. Ni X., Emani N. K., Kildishev A. V., Boltasseva A. & Shalaev V. M. Broadband light bending with plasmonic nanoantennas. Science 335, 427 (2012). [DOI] [PubMed] [Google Scholar]
  24. Sun S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426–431 (2012). [DOI] [PubMed] [Google Scholar]
  25. Yin X., Ye Z., Rho J., Wang Y. & Zhang X. Photonic spin hall effect at metasurfaces. Science 339, 1405–1407 (2013). [DOI] [PubMed] [Google Scholar]
  26. Shitrit N. et al. Spin-optical metamaterial route to spin-controlled photonics. Science 340, 724–726 (2013). [DOI] [PubMed] [Google Scholar]
  27. Chen H.-T. et al. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photonics 2, 295–298 (2008). [Google Scholar]
  28. Thongrattanasiri S., Koppens F. H. L. & García de Abajo F. J. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 108, 047401 (2012). [DOI] [PubMed] [Google Scholar]
  29. Ju L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011). [DOI] [PubMed] [Google Scholar]
  30. Alaee R., Farhat M., Rockstuhl C. & Lederer F. A perfect absorber made of a graphene micro-ribbon metamaterial. Opt. Express 20, 28017–28024 (2012). [DOI] [PubMed] [Google Scholar]
  31. He S., Zhang X. & He Y. Graphene nano-ribbon waveguides of record-small mode area and ultra-high effective refractive indices for future vlsi. Opt. Express 21, 30664–30673 (2013). [DOI] [PubMed] [Google Scholar]
  32. Yan H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photonics 7, 394–399 (2013). [Google Scholar]
  33. Zhang Y., Feng Y., Zhu B., Zhao J. & Jiang T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 22, 22743–22752 (2014). [DOI] [PubMed] [Google Scholar]
  34. Liu P., Cai W., Wang L., Zhang X. & Xu J. Tunable terahertz optical antennas based on graphene ring structures. Appl. Phys. Lett. 100, 153111 (2012). [Google Scholar]
  35. Wang W. Plasmons and optical excitations in graphene rings. J. Phys.: Condens. Matter 24, 402202 (2012). [DOI] [PubMed] [Google Scholar]
  36. Papasimakis N., Thongrattanasiri S., Zheludev N. I. & García de Abajo F. J. The magnetic response of grapheme split-ring metamaterials. Light: Sci. Appl 2, e78 (2013). [Google Scholar]
  37. Fan Y., Wei Z., Zhang Z. & Li H. Enhancing infrared extinction and absorption in a monolayer graphene sheet by harvesting the electric dipolar mode of split ring resonators. Opt. Lett. 38, 5410–5413 (2013). [DOI] [PubMed] [Google Scholar]
  38. Chen P.-Y. & Alù A. Atomically thin surface cloak using graphene monolayers. ACS Nano 5, 5855–5863 (2011). [DOI] [PubMed] [Google Scholar]
  39. Cheng H. et al. Mid-infrared tunable optical polarization converter composed of asymmetric graphene nanocrosses. Opt. Lett. 38, 1567–1569 (2013). [DOI] [PubMed] [Google Scholar]
  40. Fan Y., Wei Z., Li H., Chen H. & Soukoulis C. M. Photonic band gap of a graphene-embedded quarter-wave stack. Phys. Rev. B 88, 241403(R) (2013). [Google Scholar]
  41. Zhu W., Xiao F., Kang M., Sikdar D. & Premaratne M. Tunable terahertz left-handed metamaterial based on multilayer graphene-dielectric composite. Appl. Phys. Lett. 104, 051902 (2014). [Google Scholar]
  42. Fan Y., Shen N.-H., Koschny T. & Soukoulis C. M. Tunable terahertz meta-surface with graphene cut-wires. ACS Photonics 2, 151–156 (2015). [Google Scholar]
  43. Wan W. et al. Time-reversed lasing and interferometric control of absorption. Science 331, 889–892 (2011). [DOI] [PubMed] [Google Scholar]
  44. Zhang J., MacDonald K. F. & Zheludev N. I. Controlling light-with-light without nonlinearity. Light: Sci. Appl 1, e18 (2012). [Google Scholar]
  45. Lin Z. et al. Unidirectional invisibility induced by pt-symmetric periodic structures. Phys. Rev. Lett 106, 213901 (2011). [DOI] [PubMed] [Google Scholar]
  46. Longhi S. Pt-symmetric laser absorber. Phys. Rev. A 82, 031801 (2010). [Google Scholar]
  47. Hao J., Zhou L. & Qiu M. Nearly total absorption of light and heat generation by plasmonic metamaterials. Phys. Rev. B 83, 165107 (2011). [Google Scholar]
  48. Pirruccio G., Martín Moreno L., Lozano G. & Gómez Rivas J. Coherent and broadband enhanced optical absorption in graphene. ACS Nano 7, 4810–4817 (2013). [DOI] [PubMed] [Google Scholar]
  49. Sun Y., Tan W., Li H., Li J. & Chen H. Experimental demonstration of a coherent perfect absorber with pt phase transition. Phys. Rev. Lett. 112, 143903 (2014). [DOI] [PubMed] [Google Scholar]
  50. Kang M., Chong Y. D., Wang H.-T., Zhu W. & Premaratne M. Critical route for coherent perfect absorption in a fano resonance plasmonic system. Appl. Phys. Lett. 105, 131103 (2014). [Google Scholar]
  51. Zheng J., Barton R. A. & Englund D. Broadband coherent absorption in chirped-planar-dielectric cavities for 2dmaterial- based photovoltaics and photodetectors. ACS Photonics 1, 768–774 (2014). [Google Scholar]
  52. Zhang J. et al. Coherent perfect absorption and transparency in a nanostructured graphene film. Opt. Express 22, 12524–12532 (2014). [DOI] [PubMed] [Google Scholar]
  53. Fan Y., Zhang F., Zhao Q., Wei Z. & Li H. Tunable terahertz coherent perfect absorption in a monolayer graphene. Opt. Lett. 39, 6269–6272 (2014). [DOI] [PubMed] [Google Scholar]
  54. Wunsch B., Stauber T., Sols F. & Guinea F. Dynamical polarization of graphene at finite doping. New J. Phys. 8, 318 (2006). [Google Scholar]
  55. Hwang E. H. & Das Sarma S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007). [Google Scholar]
  56. Gusynin V. P., Sharapov S. G. & Carbotte J. P. Magneto-optical conductivity in graphene. J. Phys.: Condens. Matter 19, 026222 (2007). [Google Scholar]
  57. Woessner A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater 14, 421–425 (2015). [DOI] [PubMed] [Google Scholar]
  58. Wang L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013). [DOI] [PubMed] [Google Scholar]
  59. Caldwell J. D. et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 5, 5221 (2014). [DOI] [PubMed] [Google Scholar]
  60. Tassin P., Koschny T. & Soukoulis C. M. Effective material parameter retrieval for thin sheets: Theory and application to graphene, thin silver films, and single-layer metamaterials. Physica B 407, 4062–4065 (2012). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES