Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Sep 28;5:14568. doi: 10.1038/srep14568

A generalized target theory and its applications

Lei Zhao 1,2, Dong Mi 3,a, Bei Hu 1,2, Yeqing Sun 1,2,b
PMCID: PMC4585963  PMID: 26411887

Abstract

Different radiobiological models have been proposed to estimate the cell-killing effects, which are very important in radiotherapy and radiation risk assessment. However, most applied models have their own scopes of application. In this work, by generalizing the relationship between “hit” and “survival” in traditional target theory with Yager negation operator in Fuzzy mathematics, we propose a generalized target model of radiation-induced cell inactivation that takes into account both cellular repair effects and indirect effects of radiation. The simulation results of the model and the rethinking of “the number of targets in a cell” and “the number of hits per target” suggest that it is only necessary to investigate the generalized single-hit single-target (GSHST) in the present theoretical frame. Analysis shows that the GSHST model can be reduced to the linear quadratic model and multitarget model in the low-dose and high-dose regions, respectively. The fitting results show that the GSHST model agrees well with the usual experimental observations. In addition, the present model can be used to effectively predict cellular repair capacity, radiosensitivity, target size, especially the biologically effective dose for the treatment planning in clinical applications.

Instead of the conventional adopted γ or X rays, high energy charged particles are being widely used in cancer therapy1,2. The main advantages over γ or X rays are due to the particular physical and radiobiological properties of charged particle radiation, especially, giving rise to a sharp maximum in ionization near the end of the range (Bragg peak) and an enhanced relative biological effectiveness (RBE) (for heavy ions only)3,4. In the actual radiotherapy, the spread out Bragg peak (SOBP) is used to cover a well defined target volume at a given depth by modulating single peaks5.

Radiotherapy is based on the mechanism of radiation-induced cell killing1. At the molecular level, it is generally considered that cell killing has been mainly attributed to the radiation energy deposition in the DNA within the nucleus, with production of DNA double-strand breaks (DSB)1,6. Hence, the hypothesis is raised that the nuclear DNA is the critical target to induce lethal effects as a result of radiation exposure, which is termed “targeted effects”7,8,9. In addition, some new radiobiological experiments show that, there exist “non-targeted effects”10, such as bystander effect11,12, adaptive response13,14, low dose hyper-radiosensitivity15, etc, which do not depend on the amount of energy deposited in DNA.

Different radiobiological models, including “targeted” and “non-targeted” effects models, have been proposed for RBE estimation of radiotherapy, and even risk assessment of space radiation16. Lea’s target theory is one of the earliest interpretive models for radiation-induced cell killing17. In this theory, the hit probability p0 for N targets to be hit n times followed Poisson distribution, which can be expressed as

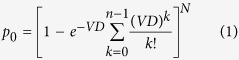graphic file with name srep14568-m1.jpg

where, D represents the radiation dose, and V denotes the target volume. When both N and n are equal to 1, the survival fraction S can be reduced to single-hit single-target (SHST) model,

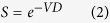graphic file with name srep14568-m2.jpg

The major drawback of target theory is that it can’t describe the induction of damage by radiation and cellular repair effects17,18. Only two states in the theory are distinguished, namely, the undamaged surviving and the damaged death. Nevertheless, the target models still have a certain application in radiotherapy and radiobiology, in particular, for describing cell survival under high-dose radiation18.

To overcome some inconsistencies of target theory, the “Linear-Quadratic (LQ) model” was proposed by the dual radiation action theory19 and molecular theory20. In the LQ model, the cell survival fraction S with dose D is given by

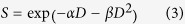graphic file with name srep14568-m3.jpg

where, the dose coefficients α and β are the radiosensitivity parameters. Generally, the LQ model is effective in the low-dose range for low linear energy transfer (LET) radiotherapy, but less effective in fitting the dose-response curves at high-dose range, which are widely used on stereotactic body radiotherapy (SBRT)21,22. In spite of this, the LQ model is still the most commonly used medical theory, which is used to describe the radiation effects for the fractionation schemes at present22,23,24,25.

A number of other cell survival models dedicated to high-LET radiation have also been proposed, such as the amorphous track structure model (ATSM)26,27,28 and the more recent Local Effect Model (LEM)29,30,31,32. Both models are based on the assumptions of simplified biological targets and radiation fields (amorphous particle track)33. The target is assumed to be an infinitely thin disc, its size or cross-section being endpoint dependent. More specifically, it is assumed in the ATSM that a set of cellular subtargets, representing the sensitive site, has been activated or inactivated to induce the effects. Thus, the cross-sectional area is not always equal to the geometrical size of the target. However, there is no concept of subtarget in the LEM, and the response of the biological target (cell nucleus) is assumed to be determined by local dose deposition events. Both models assume that the radiation field is entirely described by its dose distribution due to δ-electrons originating from ionization events, while neglecting the contributions from excitations and nuclear stopping. Under this assumption, there is no LET variation from particles or even stopping particles within the target. Hence, the basic assumptions of the ATSM and the LEM are questioned33,34. Generally, all these models mentioned above can be ascribed to the “targeted effects models”8,35. In addition, a series of non-targeted effects models have been developed36, while generally speaking, their applications can not be taken into account in radiotherapy due to the limited specific data set fitting10.

In fact, the response of different organisms to ionizing radiation depends on the radiation quality and the intrinsic characteristics, which mainly include repair mechanisms of the living organism. Therefore, some authors have proposed a series of repair models from different points of view4,37,38,39,40. Most of these models could better predict the cellular repair capacity for low LET radiation, while they usually become ineffective for high LET radiation. For example, some researchers regarded the ratio α/β in the LQ model as an indicator of cellular repair capacity3,41, while it tends to overestimate the cellular repair capacity for high LET radiation.

In this work, we firstly proposed a simple radiobiological model, which tries to reflect cellular repair effects together with indirect effects of radiation. Then, we discussed the relationships between this model and the target model, as well as the LQ model. After that, we tested this model by fitting the representative and widely used experimental data sets reported in publications. Finally, the present model was used to predict the radiosensitivity and target size of the cell, and calculate the biologically effective dose (BED) for the treatment planning in clinical applications.

Methods and Materials

Theoretical Model

When an organism is subject to irradiation, there is no doubt that “the irradiated tissue (cell set) will be affected by radiation” is a deterministic event, and “the target of a cell in this tissue may be hit by radiation particles” is a stochastic event. However, “the cellular response after its target being hit” should be regarded as a fuzzy event, because the response can be irreversible or reversible change in structure and function (Cell death or inactivation is only the most severe damage response.), depending on radiation characteristics and cell types. Both the stochastic event and the fuzzy event are used to express the characteristics of uncertainty, and the difference between them is the former has its precise boundary, whereas the latter boundary is not sharp42. Thus, the relationship between “hit” and “inactivation” in traditional target theory should be generalized. The negation operator in fuzzy mathematics can provide a way to implement this idea, which carries the sense of complement42.

Let p0 be the hit probability, the survival fraction S in Lea’s target theory is

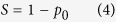graphic file with name srep14568-m4.jpg

which can be regarded a standard negation operator in interval [0, 1]. This implies that “If the target of a cell is hit, it will certainly lead to the cell inactivation”18. If “the cellular response after its target being hit” is a fuzzy event, the standard negation operator defined in equation (4) may be replaced by a more general negation operator,

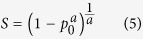graphic file with name srep14568-m5.jpg

which is one of the popular complement functions, i.e., so-called Yager negation operator42,43, where a is the parameter of negation (a > 0). When a = 1, it means that one hit necessarily lead to one inactivation, and equation (5) will be reduced to equation (4) in target theory; a > 1 means that one hit will lead to less than one inactivation, for the cellular repair mechanisms are likely at work strongly; a < 1 implies that one hit will lead to more than one inactivation, because the indirect effects, which are caused by the damage of the radiation-induced free-radical attack to the key target in the cell, are likely to become dominant.

Combining equation (1) and (5), one can obtain the general survival equation, which is called as the generalized multi-hit multi-target (GMHMT) model

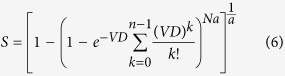graphic file with name srep14568-m6.jpg

when both N and n are equal to 1, the GMHMT model can be simplified to

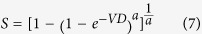graphic file with name srep14568-m7.jpg

which is called as the generalized single-hit single-target (GSHST) model.

Low-dose and high-dose approximation

Taking the natural logarithm of both sides of equation (7), one can obtain

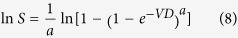graphic file with name srep14568-m8.jpg

In the low-dose region, 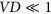Inline graphic. If the logarithmic term in equation (8) is expanded into a Taylor series, neglecting the second and higher order terms, one can get

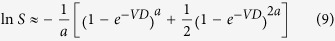graphic file with name srep14568-m10.jpg

Furthermore, using the linear approximation of Taylor series expansion of exponential function and power function, equation (9) can be reduced to the LQ model

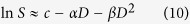graphic file with name srep14568-m11.jpg

where 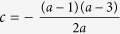Inline graphic, α = (2 − a)V, and 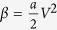Inline graphic. It can be seen that α, β and their ratio α/β all depend on the parameter a and target size V.

On the other hand, in the high-dose region, 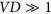Inline graphic. If the power function in logarithmic term in equation (8) is expanded into a Taylor series, again neglecting the second and higher order terms, equation (8) can lead to the same result with the single-hit multi-target model at high-dose

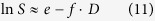graphic file with name srep14568-m15.jpg

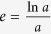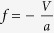where Inline graphic,and Inline graphic. And, the slope of the approximate expression is the reciprocal of the ratio a/V.

Thus, the GSHST model can be naturally reduced to the LQ model and the multitarget model asymptote at low-dose and high-dose ranges, respectively. To unify the LQ model survival curve for the low-dose range and the multitarget model asymptote for high-dose range, it is not necessary to artificially introduce the piecewise-defined function with a transitional discontinuity in the universal survival curve model44,45. In addition, some authors attempt to develop integrated theories in radiobiology45, for example, Sutherland proposed a repair dependent model with the product of a single exponential and an Euler gamma function, which could accurately describe the survival fraction and the probability of transformation46,47. In these models, since curve-fitting is the main issue, the model with smallest number of parameters that fits the data well is the best choice48. However, for example, there are as many as four parameters in the repair dependent model46,47.

So far, the ambiguous descriptions of “target” were used in a variety of different ways7,18. In fact, the detailed concepts of the “target”, which may be the cell nucleus, chromosomes, or DNA, are still open at present7. Therefore, the “number of targets in a cell” was introduced artificially in various target theories. The similar case is for the concept of “the number of hits per target”. In fact, both “number of targets in a cell” and “the number of hits per target” are the parameters of phenomenological target theories, they even not be integers49,50. On the other hand, it was found that different versions of the GMHMT model could give the similar dose-response curves by adjusting the parameter a. In this work, we assume that there is only one “effective target” in a cell, and one hit by radiation on the “effective target” could cause varying degrees of cell death, depending on the characteristics of radiation, the cellular repair abilities and indirect effects, etc. Thus, only the GSHST model was used to describe the general dose-response curves in the theory.

Results and Discussion

Simulated survival fraction

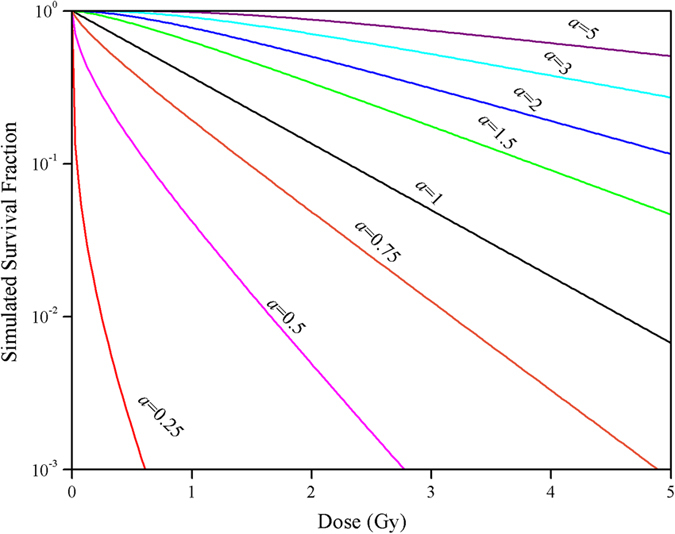
Figure 1 shows the simulation results of the GSHST model to describe the cell survival, where the parameter V takes the value 1 and a ranges from 0.25 to 5. When a is equal to 1, the GSHST model will be reduced to SHST model in Lea’s target theory. It was shown that the dose-response curves changed with parameter a when parameter V was fixed: if a is greater than 1, the dose-response relationship showed a smooth curve with a larger shoulder at the low dose, which means that the survival fraction decreased slowly with increasing a values; on the other hand, if a is less than 1, the dose-response relationship showed a steep tendency, which means that the survival fraction decreased rapidly with decreasing a values.

Figure 1. Simulated survival fraction of the present model on a semilogarithmic scale as the parameter a, assuming that the target volume V = 1.

Figure 1

Open in a new tab

Comparison with experiments

The detailed datasets in the collection of published measurements, and methods of model fitting were listed in Supplementary information (SI). The results of fitting equation (2), (3), and (7) to the cell survival data are shown in Supplementary Fig. S1-S8 (SI), respectively. Regression analysis showed that the GSHST model, the SHST model, and the LQ model all could give significant fits to experimental results (P < 0.05) (Supplementary Table S1 and S2, SI).

Overall, the goodness of fit of the GSHST model is better than that of the SHST model, approximate to that of the LQ model (Supplementary Table S1 and S2, SI). In addition, we will see that, the ratio a/V in the GSHST model is a more effective indicator than the ratio α/β in the LQ model to reflect the cellular repair capacity.

RBE and cellular repair capacity

Based on the results of the GSHST model fitting the experimental data, the RBE37 (see Supplementary equation (S3) to (S5) in SI for more details) for different LET radiations could be calculated in five cell lines (Supplementary Fig. S9, SI). It can be seen that, in general, the RBE37 values firstly increased with LET, after reached a peak at around 150 ~ 200 keV/μm, then decreased with LET. However, for xrs5 mutant cells, the maximum of RBE37 was significantly less than that of other cells. It should be pointed out here that, because the experimental data was deficient when LET > 252 keV/μm, there was no significant decline in the higher-LET region for T1 cells. If the corresponding experiments had been done, it is inferred that a significant RBE37 decline in the higher-LET region for T1 cells may appear. So, the relationships between RBE and LET are similar for different cell lines. This conclusion is consistent with the previous reports51.

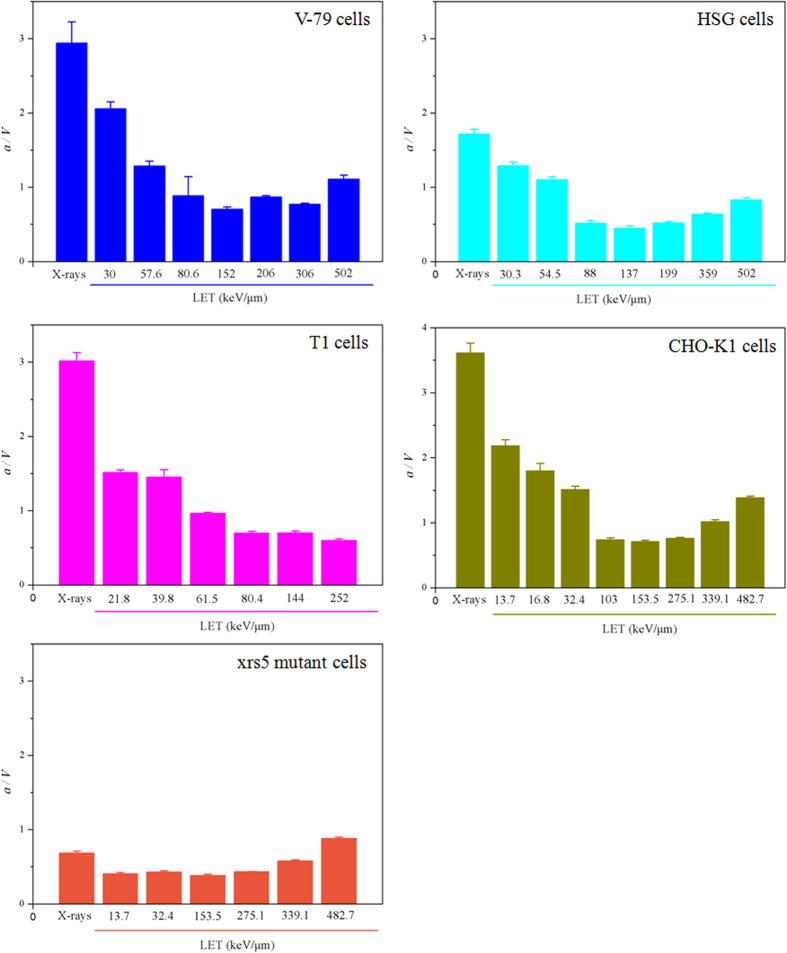
The ratios a/V for different LET radiations in the five cell lines could be calculated, the results were listed in Fig. 2. It can be seen that the relationship between a/V and LET is generally dependent on the cell-line types: for Chinese hamster cells (V-79), human salivary gland tumor cells (HSG), and Chinese hamster ovary cells (CHO-K1), the a/V decreased with increasing LET and the minimum was attained at around 150 keV/μm, then increased slightly with increasing LET. For the T1 cell, the a/V gradually decreased with increasing LET. Whereas all of the a/V are less than 1 in xrs5 mutant, which are obvious lower than that of other cells.

Figure 2. Ratios a/V (unit: Gy) in five cell lines as a function of LET using the present model for regression analysis.

Figure 2

Open in a new tab

Values represent the arithmetic mean ± standard error.

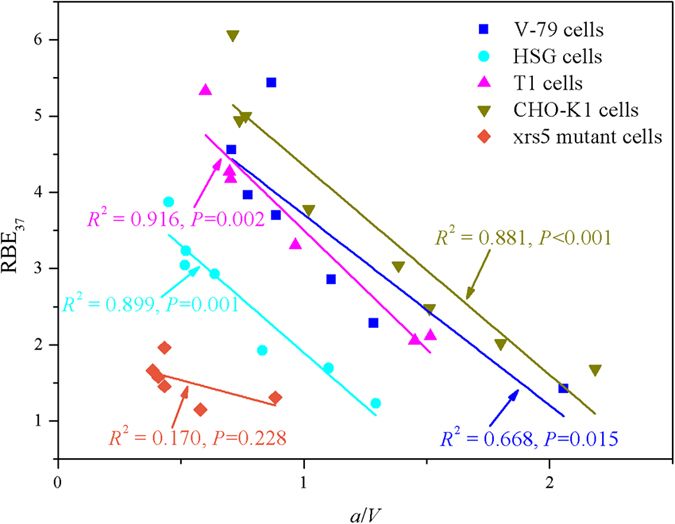
Combining the discussion in the last two paragraphs, one can see that RBE and a/V for different cell lines exhibit the opposite trend with increasing LET. As shown in Fig. 3, indeed, the significant linear correlations were observed between RBE37 and the ratios a/V for V-79, HSG, T1, and CHO-K1 cells (P < 0.05). However, there was no significant correlation between RBE37 and a/V for xrs5 mutant (Adj. R2 = 0.170, P = 0.228). The absence of Ku80 component makes the xrs5 mutant difficult to recruit DNA-PKcs, which is followed by other repair proteins in the repair pathway of non-homologous end-joining (NHEJ)52, and this can result in the lack of cellular repair capacity.

Figure 3. Linear regressions of RBE and the ratios a/V (unit: Gy) together with the corresponding values in five cell lines irradiated by 12C with different LETs in this study.

Figure 3

Open in a new tab

The above analysis shows that the ratio a/V in the present model could reflect the cellular repair capacity. The ratio decreases with increasing LET, after reaches a nadir at around 150 ~ 200 keV/μm, then increases with LET. The above results also imply that RBE is probably related to the cellular repair capacity. So, the declining of RBE at high LET region (>100 ~ 200 keV/μm) observed in radiobiology experiments may be due to the increasing cellular repair capacity. Previous studies also show that the very end of range (largest LETs) for certain particles (such as helium with LET = 123 keV/μm) can induce less unrepaired damages than those of low LET (such as helium with LET = 40 ~ 81 keV/μm)53, which is consistent with the present hypothesis. In other words, the high-LET radiation can activate the repair mechanisms or enhance the cellular repair capacity. So far, the declining effects had been described by several mechanisms54, such as “overkill effects”, “thindown”, etc. Each of these speculations considered the saturation mechanism of detriment, while neglected the repair mechanism in organisms. In the case of high LET radiation, more than 90% lesions are associated with very complex damages. Several repair pathways, including NHEJ, homologous recombination, microhomology-mediated end-joining, and alternative nonhomologous end-joining, may sequentially attempt to recover it55. The choice of the appropriate pathway is regulated by three major factors, which include the damage complexity, cell cycle phase, and the speed of different repair mechanisms56.

It was interesting to find that significant differences of a/V values under X-rays, low and high LET 12C radiations were observed (P < 0.05) (Supplementary Fig. S10, SI). In addition, significant linear correlations between two sets of the a/V values under X-rays and low, and high LET 12C radiations were both found (P < 0.001) (Fig. 4). In the LQ model, the ratio α/β can be used as an indicator to reflect the cellular repair capacity. This indicator works well except for the A-172 cell line in the case of low LET 12C radiation. However, it does not work in high LET 12C radiation41. In contrast with these results, the previous results showed that the ratio a/V in the GSHST model maybe considered a robust indicator to reflect the cellular repair capacity, which is suitable for both low and high LET radiotherapy.

Figure 4. Linear correlations between two sets of the a/V (unit: Gy) values under X-rays and low LET 12C radiation (13.3 keV/μm, pink), X-rays and high LET 12C radiation (77 keV/μm, cyan).

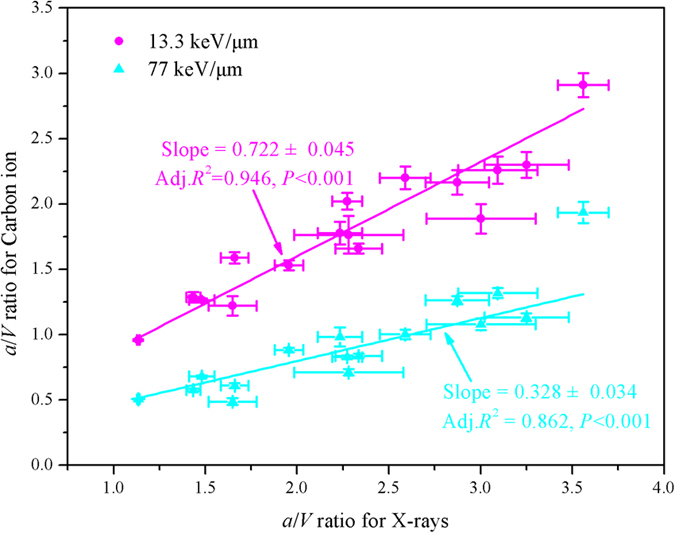
Figure 4

Open in a new tab

It can be seen that the low LET slope was 2.20 times higher than the high LET slope (Fig. 4), which suggested that the cellular repair capacity was mainly dependent on LET. Furthermore, the above results also indicated that the cellular repair capacity should be a complex function of LET, and there should exist the threshold to strengthen or activate the repair mechanism for different cell lines.

Cellular repair capacity dependent radiosensitivity

The ratios a/V for various human cell lines with X-rays, low and high LET 12C radiations were shown in Supplementary Fig. S10 (SI). The ratios a/V fluctuate in various cell lines under the same irradiation conditions, indicating that the cellular repair capacity was also dependent on cell types. Furthermore, the mean RBE37 under high LET 12C radiation (2.247 ± 0.333) were 1.70-fold higher than those under low LET 12C irradiation significantly (P < 0.05) (Supplementary Fig. S11, SI).

The D10 (dose required for 10% survival) in the present model could be calculated by the following equation

graphic file with name srep14568-m18.jpg

where S is equal to 0.1, and D10 is regarded as a classic indicator for radiosensitivity41. By linear regression analysis, it was found that a/V was linearly correlated well with the D10 for X-rays, low and high LET 12C radiations, respectively (P < 0.001) (Fig. 5). These results indicated that the radiosensitivity of a particular cell type was dominated by the cellular repair capacity.

Figure 5. Linear regressions of the ratios a/V (unit: Gy) and D10 (unit: Gy) together with the corresponding values in sixteen cell lines under X-rays, low and high LET 12C radiations (13.3 and 77 keV/μm) in this study.

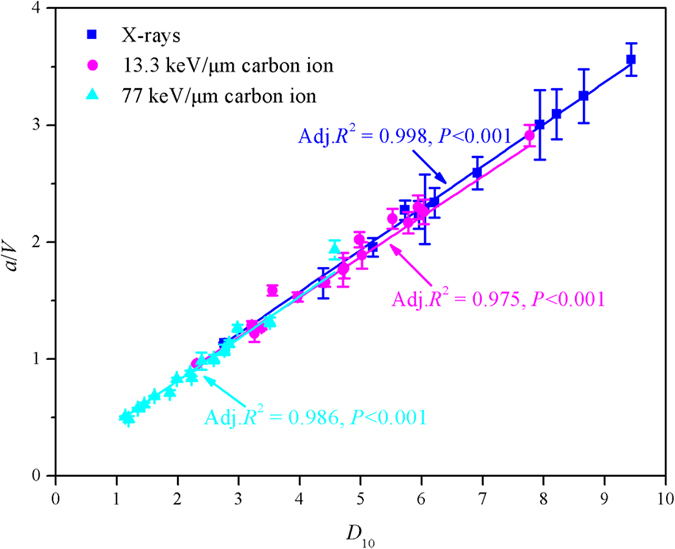
Figure 5

Open in a new tab

Under X-rays, low and high LET 12C radiation conditions, all the maximum and minimum of a/V appeared in the case of Becker and KS-1 cells. These results imply that the Becker cells has strong radioresistance and the KS-1 cells has strong radiosensitivity, which is consistent with the variation of the RBE37 in Supplementary Fig. S11 (SI) and the conclusion coming from Suzuki et al.41.

Target size prediction

The size of some biological macromolecules could be calculated by using Lea’s target theory, and the effectiveness of this method had been confirmed57,58. In the present model, the target size can also be calculated easily. Given the average energy E0 deposited per “hit” event, the target size (Mr, Da) can be calculated by

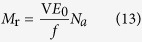graphic file with name srep14568-m19.jpg

where f = 6.2 × 1015 eV · g−1 · Gy−1, is the conversion factor from unit dose to energy deposition events, and Na is Avogadro’s number. In the present work, we take E0 = 75 eV, as known empirically from experiment59. Supplementary Fig. S12 (SI) depicted that the every target size of sixteen human cell lines has no significant difference under three different treatments (P = 0.101). The mean target weight of every sixteen cell lines is (1.12 ± 0.76) × 1010 Da, which is in the similar order of magnitude of DNA (the typical mass of a DNA molecule is 3.7 × 1010 ~ 1.7 × 1011 Da), and obviously bigger than the molecular weights of RNA (approximate to 106 Da) and protein (about 104 Da)60. The reason why the predicted values by the present model are less than the typical mass of a DNA molecule is possible associated with the selected average energy E0 deposited per “hit” event. If E0 takes a larger value, the estimated target size will be closer to the actual order of magnitude of DNA. The GSHST model indicated that DNA should be the critical and sensitive “effective target” in cell under both low and high LET radiations, which is consistent with the mainstream view that the supposed damage to genomic DNA is the main event of radiation induced9,10,18,61. The interaction of radiation with cells can occur through direct interaction of radiation with the “effective target” or through indirect damage caused by elevated radiation - induced ROS production9. Nevertheless, the direct and/or indirect effects that depend on radiation quality, will ultimately cause a change that leads to loss of biological activity in the molecule of DNA, and activate different repair mechanisms.

Calculation and optimization of BED

To show the actual implementation of this model to the treatment planning of carbon ion therapy, we performed a calculation and optimization of BED, which is a characteristic dose value that facilitates comparisons between the effects of different dose-fractionation schemes44. The calculation and optimization followed the similar procedures as described by Krämer et al.62, where BED is defined by the absorbed dose multiplied with the local RBE factors evaluated for a mixed radiation field. Briefly, when applying the present model to therapy planning, the first and most important input data are physical dose distribution profiles D(F(x)), generated by an ensemble of pencil beams at locations x with number of particles F(x) in the water-equivalent material. If the tumor type and size are certain, then the relationships between RBE and a/V, as well as a/V and LET can be obtained relatively easy for cultivated cell lines, as shown in Figs. 2 and 3. According to the present model, BED can be got by

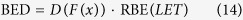graphic file with name srep14568-m20.jpg

with the physical dose D (F(x)) and RBE (LET)

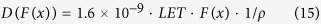graphic file with name srep14568-m21.jpg
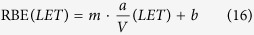graphic file with name srep14568-m22.jpg

where, as the function of depth, LET can be modulated by a heavy ion beam of energy Ebeam63,64, ρ is the density of targeted tissue (or biological material), and the coefficients m and b can be obtained via the large number of dose-effect curves in vitro.

The mean BED are estimated to be 12.2 and 7 GyE at the 3 cm SOBP by depth-dose profile and depth-LET distribution for a 200 MeV u−1 12C beam by the LQ and present model, respectively (Fig. 6A). RBE for 37% survival was calculated according to equation (S8) in SI for the LQ model, and equation (16) for the present model, where m and b could be obtained by the linear regressions of RBE and the ratios a/V in CHO-k1 cells, as shown in Fig. 3. As an example, Supplementary Fig. S13 in SI showed the comparison of depth RBE distributions obtained directly from the depth LET profiles according to equation (16), where the depth a/V profiles were derived from the relationship between a/V and LET in the CHO-K1 cells by linear interpolation.

Figure 6. Calculation and optimization of biologically effective dose (BED) (A), and its corresponding cell survival fraction predicted (B) for CHO-K1 cells.

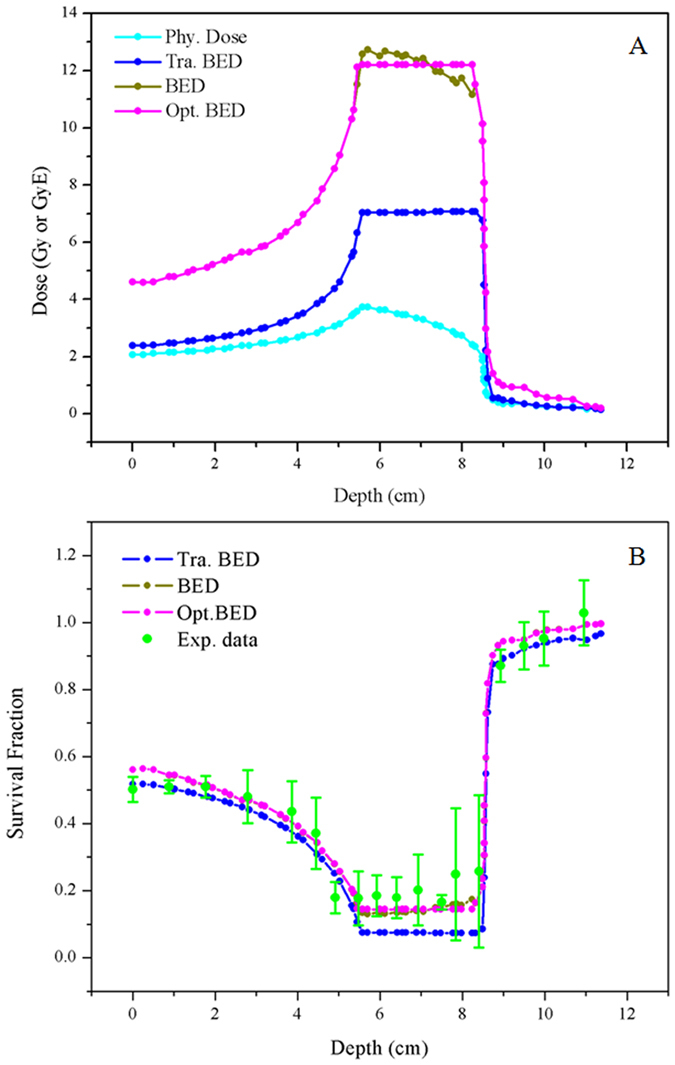
Figure 6

Open in a new tab

Experimental data from reference (59) is adjusted to depth-survival distribution for a 200 MeV u−1 12C beam. Phy. dose, Tra. BED, and Opt. BED in the figures represent physical dose, BED calculated by the LQ model and the GSHST model, respectively.

In order to optimize with respect to BED in the region of SOBP, the same techniques as described by Krämer et al.65 can be applied, with

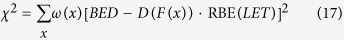graphic file with name srep14568-m23.jpg
graphic file with name srep14568-m24.jpg

with appropriately chosen weight factors ω(x) which can be modulated by particles F(x) at locations x, the dose D (F(x)) and RBE (LET) are given by equation (15) and (16), respectively. The optimized BED predicted by this method is shown in Fig. 6A. It can be seen that the optimized BED was relatively homogeneous in the region of SOBP, while higher than that of the traditional method, which was in consistent with the clinical practice66,67. BED was used to predict cell survival fraction by the LQ model, present model, and its optimizing (Fig. 6B), according to the fitted parameters in CHO-K1 cells (Supplementary Table S4 in SI). Comparison with the measured cell survival fraction in experiment shows that the calculated results of the GSHST model is better than that of the LQ model (Supplementary Table S5 in SI).

Conclusions

In this study, a simple radiobiological model, i.e. GSHST model, is presented. In theory, it overcomes some defects in traditional targeted effects models by considering cellular repair capacity and indirect effects of radiation, and makes the linear quadratic model and multitarget model the low-dose and high-dose limits. In applications, the GSHST model firstly could predict the cell-killing effects accurately and be suitable for various dose and LET ranges, and many cell types. Secondly, the parameter a/V could well reflect the cellular repair capacity, radiosensitivity, and target size. Thirdly, the present model has a simple mathematical structure for fast computation in radiotherapy, especially the calculation of BED in the treatment planning of clinical applications.

Additional Information

How to cite this article: Zhao, L. et al. A generalized target theory and its applications. Sci. Rep. 5, 14568; doi: 10.1038/srep14568 (2015).

Supplementary Material

Supplementary Information
srep14568-s1.doc (1.7MB, doc)

Acknowledgments

This research was supported by grants from the Institute of Environmental Systems Biology of Dalian Maritime University, National Natural Science Foundation of China (No. 31270903), the Strategic Priority Research Program on Space Science in the Chinese Academy of Sciences (No. XDA04020202-12) and Fundamental Research Funds for the Central Universities (No. 3132014306 and 2015YB07).

Footnotes

Author Contributions L.Z., D.M., B.H. and Y.S. have set up the study concept and design, performed research, analysis and interpretation of data, were responsible for the draft of the manuscript. D.M. and Y.S. jointly supervised this work.

References

  1. Prise K. M., Schettino G., Folkard M. & Held K. D. New insights on cell death from radiation exposure. Lancet Oncol 6, 520–528 (2005). [DOI] [PubMed] [Google Scholar]
  2. Schulz-Ertner D. & Tsujii H. Particle radiation therapy using proton and heavier ion beams. J Clin Oncol 25, 953–964 (2007). [DOI] [PubMed] [Google Scholar]
  3. Weyrather W. K., Ritter S., Scholz M. & Kraft G. RBE for carbon track-segment irradiation in cell lines of differing repair capacity. Int J Radiat Biol 75, 1357–1364 (1999). [DOI] [PubMed] [Google Scholar]
  4. Wada M. et al. Modeling the biological response of normal human cells, including repair processes, to fractionated carbon beam irradiation. J Radiat Res 54, 798–807 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Belli D. B. et al. Inactivation of human normal and tumour cells irradiated with low energy protons. Int J Radiat Biol 76, 831–839 (2000). [DOI] [PubMed] [Google Scholar]
  6. Prise K. M. & O’Sullivan J. M. Radiation-induced bystander signalling in cancer therapy. Nat Rev Cancer 9, 351–360 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Goodhead D. T. Energy deposition stochastics and track structure: what about the target? Radiat Protect Dosim 122, 3–15 (2006). [DOI] [PubMed] [Google Scholar]
  8. Ballarini F. et al. Radiation risk estimation: Modelling approaches for “targeted” and “non-targeted” effects. Adv Space Res 40, 1392–1400 (2007). [Google Scholar]
  9. Arena C., De Micco V., Macaeva E. & Quintens R. Space radiation effects on plant and mammalian cells. Acta Astronaut 104, 419–431 (2014). [Google Scholar]
  10. Sjostedt S. & Bezak E. Non-targeted effects of ionising radiation and radiotherapy. Australas Phys Eng Sci Med 33, 219–231 (2010). [DOI] [PubMed] [Google Scholar]
  11. Mothersill C. & Seymour C. B. Radiation-induced bystander effects and the DNA paradigm: An “out of field” perspective. Mutat Res-Fund Mol M 597, 5–10 (2006). [DOI] [PubMed] [Google Scholar]
  12. Morgan W. F. & Sowa M. B. Non-targeted bystander effects induced by ionizing radiation. Mutat Res-Fund Mol M 616, 159–164 (2007). [DOI] [PubMed] [Google Scholar]
  13. Wolff S. The adaptive response in radiobiology: Evolving insights and implications. Environ Health Persp 106, 277 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Iyer R. & Lehnert B. E. Low dose, low-LET ionizing radiation-induced radioadaptation and associated early responses in unirradiated cells. Mutat Res-Fund Mol M 503, 1–9 (2002). [DOI] [PubMed] [Google Scholar]
  15. Joiner M. C., Marples B., Lambin P., Short S. C. & Turesson I. Low-dose hypersensitivity: Current status and possible mechanisms. Int J Radiat Oncol 49, 379–389 (2001). [DOI] [PubMed] [Google Scholar]
  16. Durante M. & Cucinotta F. A. Heavy ion carcinogenesis and human space exploration. Nat Rev Cancer 8, 465–472 (2008). [DOI] [PubMed] [Google Scholar]
  17. Ballarini F. From DNA radiation damage to cell death: Theoretical approaches. J Nucleic Acids 2010, 1–8 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Friedland W. & Kundrát P. In Comprehensive Biomedical Physics 105–142 (Elsevier, 2014). [Google Scholar]
  19. Kellerer A. M. & Rossi H. H. A generalized formulation of dual radiation action. Radiat Res 75, 471–488 (1978). [DOI] [PubMed] [Google Scholar]
  20. Chadwick K. H. & Leenhouts H. P. A molecular theory of cell survival. Phys Med Biol 18, 78 (1973). [DOI] [PubMed] [Google Scholar]
  21. Partridge M., Ramos M., Sardaro A. & Brada M. Dose escalation for non-small cell lung cancer: Analysis and modelling of published literature. Radiother Oncol 99, 6–11 (2011). [DOI] [PubMed] [Google Scholar]
  22. Antonovic L., Brahme A., Furusawa Y. & Toma-Dasu I. Radiobiological description of the LET dependence of the cell survival of oxic and anoxic cells irradiated by carbon ions. J Radiat Res 54, 18–26 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sheu T. et al. Use of the LQ model with large fraction sizes results in underestimation of isoeffect doses. Radiother Oncol 109, 21–25 (2013). [DOI] [PubMed] [Google Scholar]
  24. Chapman J. D. & Gillespie C. J. The power of radiation biophysics—Let’s use it. Int J Radiat Oncol Biol Phys 84, 309–311 (2012). [DOI] [PubMed] [Google Scholar]
  25. Kong C. et al. A new index comparable to BED for evaluating the biological efficacy of hypofractionated radiotherapy schemes on early stage non-small cell lung cancer: Analysis of data from the literature. Lung Cancer 84, 7–12 (2014). [DOI] [PubMed] [Google Scholar]
  26. Katz R., Ackerson B., Homayoonfar M. & Sharma S. C. Inactivation of cells by heavy ion bombardment. Radiat Res 47, 402–425 (1971). [PubMed] [Google Scholar]
  27. Cucinotta F. A. Effects of track structure and cell inactivation on the calculation of heavy ion mutation rates in mammalian cells. Int J Radiat Biol 69, 593–600 (1996). [DOI] [PubMed] [Google Scholar]
  28. Cucinotta F. A., Nikjoo H. & Goodhead D. T. Applications of amorphous track models in radiation biology. Radiat Environ Biophys 38, 81–92 (1999). [DOI] [PubMed] [Google Scholar]
  29. Scholz M. & Kraft G. Track structure and the calculation of biological effects of heavy charged particles. Adv Space Res 18, 5–14 (1996). [DOI] [PubMed] [Google Scholar]
  30. Scholz M., Kellerer A. M., Kraft-Weyrather W. & Kraft G. Computation of cell survival in heavy ion beams for therapy. Radiat Environ Biophys 36, 59–66 (1997). [DOI] [PubMed] [Google Scholar]
  31. Elsässer T. & Scholz M. Cluster effects within the local effect model. Radiat Res 167, 319–329 (2007). [DOI] [PubMed] [Google Scholar]
  32. Elsässer T., Krämer M. & Scholz M. Accuracy of the local effect model for the prediction of biologic effects of carbon ion beams in vitro and in iivo. Int J Radiat Oncol 71, 866–872 (2008). [DOI] [PubMed] [Google Scholar]
  33. Paganetti H. & Goitein M. Biophysical modelling of proton radiation effects based on amorphous track models. Int J Radiat Biol 77, 911–928 (2001). [DOI] [PubMed] [Google Scholar]
  34. Elsässer T. in Ion Beam Therapy Vol. 320 Biological and Medical Physics, Biomedical Engineering (ed. Linz Ute) Ch. 8, 117–133 (Springer Berlin Heidelberg, 2012). [Google Scholar]
  35. Ballarini F., Facoetti A., Mariotti L., Nano R. & Ottolenghi A. Cellular communication and “non-targeted effects”: Modelling approaches. Adv Space Res 44, 917–925 (2009). [Google Scholar]
  36. Little M., Heidenreich W., Moolgavkar S., Schöllnberger H. & Thomas D. Systems biological and mechanistic modelling of radiation-induced cancer. Radiat Environ Bioph 47, 39–47 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tobias C. A. The repair-misrepair model in radiobiology: comparison to other models. Radiat Res 104, 77–95 (1985). [PubMed] [Google Scholar]
  38. Curtis S. B. Lethal and potentially lethal lesions induced by radiation—A unified repair model. Radiat Res 106, 252–270 (1986). [PubMed] [Google Scholar]
  39. Stewart R. D. Two-lesion kinetic model of double-strand break rejoining and cell killing. Radiat Res 156, 365–378 (2001). [DOI] [PubMed] [Google Scholar]
  40. Wedenberg M., Lind B. K., Toma-Dasu I., Rehbinder H. & Brahme A. Analytical description of the LET dependence of cell survival using the repairable-conditionally repairable damage model. Radiat Res 174, 517–525 (2010). [DOI] [PubMed] [Google Scholar]
  41. Suzuki M., Kase Y., Yamaguchi H., Kanai T. & Ando K. Relative biological effectiveness for cell-killing effect on various human cell lines irradiated with heavy-ion medical accelerator in Chiba (HIMAC) carbon-ion beams. Int J Radiat Oncol Biol Phys 48, 241–250 (2000). [DOI] [PubMed] [Google Scholar]
  42. Lee K. H. First course on fuzzy theory and applications. Vol. 27 (Springer Science & Business Media, 2006). [Google Scholar]
  43. Batyrshin I. On the structure of involutive, contracting and expanding negations. Fuzzy Set Syst 139, 661–672 (2003). [Google Scholar]
  44. Park C., Papiez L., Zhang S., Story M. & Timmerman R. D. Universal survival curve and single fraction equivalent dose: useful tools in understanding potency of ablative radiotherapy. Int J Radiat Oncol Biol Phys 70, 847–852 (2008). [DOI] [PubMed] [Google Scholar]
  45. McKenna F. W. & Ahmad S. Fitting techniques of cell survival curves in high-dose region for use in stereotactic body radiation therapy. Phys Med Biol 54, 1593 (2009). [DOI] [PubMed] [Google Scholar]
  46. Sutherland J. C. Repair-dependent cell radiation survival and transformation: an integrated theory. Phys Med Biol 59, 5073–5090 (2014). [DOI] [PubMed] [Google Scholar]
  47. Sutherland J. C. Repair dependent radiation survival: a stochastic model with Euler gamma function solutions. Phys Med Biol 51, 4883 (2006). [DOI] [PubMed] [Google Scholar]
  48. Rahmanian S., Taleei R. & Nikjoo H. Radiation induced base excision repair (BER): A mechanistic mathematical approach. DNA Repair 22, 89–103 (2014). [DOI] [PubMed] [Google Scholar]
  49. Waligórski M. P. R., Hollmark M., Lind B. & Gudowska I. Cellular parameters for track structure modeling of radiation hazard in space. Adv Space Res 34, 1378–1382 (2004). [DOI] [PubMed] [Google Scholar]
  50. Zhou L. B. et al. Linear energy transfer dependence of the effects of carbon ion beams on adventitious shoot regeneration from in vitro leaf explants of Saintpaulia ionahta. Int J Radiat Biol 82, 473–481 (2006). [DOI] [PubMed] [Google Scholar]
  51. Thacker J., Stretch A. & Stephens M. A. Mutation and inactivation of cultured mammalian cells exposed to beams of accelerated heavy ions. II. Chinese hamster V79 cells. Int J Radiat Biol 36, 137–148 (1979). [DOI] [PubMed] [Google Scholar]
  52. Taccioli G. E. et al. Ku80: product of the XRCC5 gene and its role in DNA repair and V(D)J recombination. Science 265, 1442–1445 (1994). [DOI] [PubMed] [Google Scholar]
  53. Carabe-Fernandez A., Dale R. G. & Paganetti H. Repair kinetic considerations in particle beam radiotherapy. Brit J Radiol 84, 546–555 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Cucinotta F. A., Kim M. & Chappell L. J. Space radiation cancer risk projections and uncertainties–2012. NASA TP 217375 (2013). [Google Scholar]
  55. Belov O. V., Krasavin E. A., Lyashko M. S., Batmunkh M. & Sweilam N. H. A quantitative model of the major pathways for radiation-induced DNA double-strand break repair. J Theor Biol 366, 115–130 (2015). [DOI] [PubMed] [Google Scholar]
  56. Shibata A. et al. Factors determining DNA double‐strand break repair pathway choice in G2 phase. EMBO J 30, 1079–1092 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Kempner E. Novel predictions from radiation target analysis. Trends Biochem Sci 18, 236–239 (1993). [DOI] [PubMed] [Google Scholar]
  58. Verkman A., Skorecki K. & Ausiello D. Radiation inactivation of oligomeric enzyme systems: theoretical considerations. P Natl Acad Sci USA 81, 150–154 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Alpen E. L. In Radiation Biophysics (Second Edition) (ed. Alpen Edward L.) 104–131 (Academic Press, 1998). [Google Scholar]
  60. Michaels H. B. & Hunt J. W. A model for radiation damage in cells by direct effect and by indirect effect: a radiation chemistry approach. Radiat Res 74, 23–34 (1978). [PubMed] [Google Scholar]
  61. Friedland W., Dingfelder M., Kundrát P. & Jacob P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat Res-Fund Mol M 711, 28–40 (2011). [DOI] [PubMed] [Google Scholar]
  62. Krämer M. et al. Treatment planning for heavy-ion radiotherapy: physical beam model and dose optimization. Phys Med Biol 45, 3299 (2000). [DOI] [PubMed] [Google Scholar]
  63. Sternheimer R. M. & Peierls R. F. General Expression for the Density Effect for the Ionization Loss of Charged Particles. Phys Rev B 3, 3681–3692 (1971). [Google Scholar]
  64. Kraft G., Krämer M. & Scholz M. LET, track structure and models. Radiat Environ Biophys 31, 161–180 (1992). [DOI] [PubMed] [Google Scholar]
  65. Krämer M. & Scholz M. Treatment planning for heavy-ion radiotherapy: calculation and optimization of biologically effective dose. Phys Med Biol 45, 3319 (2000). [DOI] [PubMed] [Google Scholar]
  66. Ugo A. & Gerhard K. Radiotherapy with beams of carbon ions. Rep Prog Phys 68, 1861 (2005). [Google Scholar]
  67. Tsuji H. et al. Carbon-ion radiotherapy for locally advanced or unfavorably located choroidal melanoma: A Phase I/II dose-escalation study. Int J Radiat Oncol Biol Phys 67, 857–862 (2007). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep14568-s1.doc (1.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES