Optimization of retinotopy constrained source estimation constrained by prior

Abstract

Studying how the timing and amplitude of visual evoked responses (VERs) vary between visual areas is important for understanding visual processing but is complicated by difficulties in reliably estimating VERs in individual visual areas using noninvasive brain measurements. Retinotopy constrained source estimation (RCSE) addresses this challenge by using multiple, retinotopically mapped stimulus locations to simultaneously constrain estimates of VERs in visual areas V1, V2, and V3, taking advantage of the spatial precision of fMRI retinotopy and the temporal resolution of magnetoencephalography (MEG) or electroencephalography (EEG). Nonlinear optimization of dipole locations, guided by a group‐constrained RCSE solution as a prior, improved the robustness of RCSE. This approach facilitated the analysis of differences in timing and amplitude of VERs between V1, V2, and V3, elicited by stimuli with varying luminance contrast in a sample of eight adult humans. The V1 peak response was 37% larger than that of V2 and 74% larger than that of V3, and also ∼10–20 ms earlier. Normalized contrast response functions were nearly identical for the three areas. Results without dipole optimization, or with other nonlinear methods not constrained by prior estimates were similar but suffered from greater between‐subject variability. The increased reliability of estimates offered by this approach may be particularly valuable when using a smaller number of stimulus locations, enabling a greater variety of stimulus and task manipulations. Hum Brain Mapp 35:1815–1833, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

Despite significant advances in non‐invasive measurement of brain activity over the last two decades, it remains quite challenging to reliably measure, or even estimate, the time course of visual evoked responses (VERs) in individual visual cortical areas in humans. Functional magnetic resonance imaging (fMRI) has provided the means to study the response properties of individual visual areas with relatively good spatial resolution, but the sluggish hemodynamic response severely limits the temporal resolution of fMRI, such that it cannot offer meaningful information about the relative latency of responses in visual areas or the timing of response modulation caused by various stimulus or task‐related parameters. Magnetoencephalography (MEG) and electroencephalography (EEG) have excellent temporal resolution, on the order of a millisecond, but the ill‐posedness of the inverse problem presents a challenge for accurate localization of current sources and makes it extremely difficult to confidently estimate the time course of activity for a given visual area.

The use of additional constraints derived from structural or functional magnetic resonance imaging (MRI) provides a way to specify which, of all possible combinations of dipoles, are most relevant to the experiment at hand [Dale and Halgren, 2001; Dale et al., 2000; Dale and Sereno, 1993; Hamalainen et al., 1993; Scherg and Berg, 1991]. Cortical surface reconstructions from structural MRI are used to restrict potential sources to cortical gray matter and the orientation of each current dipole can be assumed to be perpendicular to the cortical sheet [Dale et al., 2000; Dale and Sereno, 1993]. To further constrain source locations for visual evoked responses, fMRI data has been used as either an initial estimate or fixed localization constraint in equivalent current dipole (ECD) modeling [Di Russo et al., 2005; Vanni et al., 2004], or as a Bayesian prior for distributed source estimation [Auranen et al., 2009; Dale et al., 2000; Yoshioka et al., 2008]. The assumption of self‐similarity of the responses within visual areas is another promising approach for improving source localization and separation of responses [Cottereau et al., 2012a].

Despite these advances in multimodal integration, limitations related to crosstalk and separation of sources remain for visual areas such as V2 and V3 [Auranen et al., 2009; Cottereau et al., 2012b; Di Russo et al., 2005; Vanni et al., 2004; Yoshioka et al., 2008]. Source estimation with a few ECDs is problematic, usually requiring that multiple visual areas be modeled by a single dipole, even when fMRI and MRI data are used to determine dipole locations or orientations [Di Russo et al., 2005; Vanni et al., 2004]. Distributed source estimation methods in which thousands of ECDs are spread evenly across the cortical surface have limited spatial precision as well, so that despite apparently excellent localization accuracy [Moradi et al., 2003; Sharon et al., 2007], the estimated waveform for a given location contains a mixture of activity from neighboring locations within ∼20 mm, making it impossible to generate reliably independent source estimates for areas such as V1, V2, and V3 [Bonmassar et al., 2001; Dale et al., 2000; Hagler et al., 2009; Kajihara et al., 2004; Liu et al., 2002; Moradi et al., 2003].

A fundamental limitation is that occipital cortex contains several visual areas in close proximity that become active with near simultaneity [Schmolesky et al., 1998; Schroeder et al., 1998]. When the current dipole generated by an active patch of cortex produces a similar spatial distribution of MEG and EEG sensor amplitudes as another, nearby patch of cortex, there is inherent ambiguity between them, resulting in crosstalk between the estimated source waveforms for the two dipoles [Liu et al., 1998]. Depending on cortical folding, the predicted dipole orientations for two areas may be nearly parallel for particular stimulus locations, making it impossible to separate their actual time courses. Even if the dipoles for two areas happen to be orthogonal, small inaccuracies in specifying dipole orientations result in blending of the two time courses.

In two previous studies in which fMRI retinotopy and cortical surface reconstructions were used to precisely determine the predicted location and orientation of current dipoles in V1, V2, and V3 for various stimulus locations, the estimated source waveforms exhibited implausible variation within a given visual area if calculated independently for each location [Hagler and Dale, 2013; Hagler et al., 2009]. If responses to multiple stimulus locations were instead used to simultaneously constrain the inverse solution, crosstalk between areas—and the effect of small, random errors in specifying dipole orientations—was greatly reduced [Hagler et al., 2009]. This method, which we have called retinotopy constrained source estimation (RCSE), provides more independent source estimates than can be obtained with conventional equivalent current dipole or distributed source estimation methods. It is not limited by the proximity of these visual areas because it relies upon the distinct pattern of dipole orientation as a function of multiple stimulus locations for each visual area, which is determined by an individual subject's retinotopy and cortical folding pattern [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009; Slotnick et al., 1999].

RCSE is limited, however, in that it requires accurate representations of the cortical generators for each stimulus location. This can be affected by a number of factors [Hagler and Dale, 2013], including spatial and intensity distortion in MRI and fMRI images that require special corrections [Holland et al., 2010; Jovicich et al., 2006]. The quality of fMRI retinotopy data is also important, but even subjects with superior retinotopy data can present difficulties in obtaining sensible RCSE waveforms. Subjects with highly folded cortex could make it more likely that a small displacement along the cortical surface would result in a large change in dipole orientation from reality, thus contaminating the resulting source estimates. This possibility is mitigated by the use of a large number of stimulus locations. Ales et al. attempted to further reduce the influence of such errors through an exhaustive neighborhood search, in which a single cortical surface mesh vertex was chosen from a defined cortical neighborhood for each stimulus location and visual area to obtain the best possible fit to their EEG data [Ales et al., 2010a]. In another recent study, Hagler and Dale used a robust estimation technique known as iteratively reweighted least squares (IRLS) to reduce the contribution of outliers [Holland and Welsch, 1977; Huber, 1981]; that is, stimulus locations with particularly high residual error [Hagler and Dale, 2013].

In this study, this same robust estimation approach was used with a group of subjects, in order to find the consensus estimate of the visual evoked responses for V1, V2, and V3; the group‐constrained solutions can be viewed as a probabilistic atlas of visual area time courses. To improve the reliability of individual subject RCSE waveforms, a probabilistic atlas‐based, nonlinear search for better fitting dipole locations was developed for this study. In this method, small displacements along the cortical surface are tested for each stimulus location to find the one that provides a better fit to both the data and the time course atlas. The atlas serves as an a priori estimate to guide the dipole optimization for individual subjects and avoid implausible results that can result from less constrained nonlinear optimization. This method may be particularly valuable when using a small number of stimulus locations.

METHODS

Participants

Eight healthy adults were included in this study (6 females, mean age: 25.2 ± 3.0 SD, age range, 22–30). One additional subject (female) was excluded because fMRI retinotopy data were extremely noisy and therefore unusable. Subjects were right handed, had normal vision, with no history of neurological disorders. The experimental protocol was approved by the UCSD institutional review board, and informed consent was obtained from all participants.

Data Collection

MEG signals were measured with an Elekta/Neuromag Vectorview 306 channel whole head neuromagnetometer (Elekta, Stockholm, Sweden), with two planar gradiometers and one magnetometer at each of 102 locations. Electrooculogram electrodes were used to monitor eye blinks and movements. The sampling frequency for the MEG recording was 601 Hz with an anti‐aliasing low‐pass filter of 200 Hz. The locations of the nasion, preauricular points, and additional locations on the scalp were measured using a FastTrack 3‐D digitizer (Polhemus, Colchester, VT). Head position indicator (HPI) coils were used to establish the position of the head relative to the MEG device. Visual stimuli were presented with a three‐mirror DLP projector and the maximum visual angle (top to bottom of displayable area) was fixed at 25°. For recording behavioral responses, a finger lift device was used with a laser and light sensor (Elekta/Neuromag).

Magnetic resonance images of brain were collected using a GE 3T scanner with a GE 8‐channel phased array head coil (General Electric). High‐resolution T₁‐weighted images were acquired to generate cortical surface models (TR = 10.5 ms, flip angle = 15°, bandwidth = 20.83 kHz, 256 x 256 matrix, 180 sagittal slices, 1 x 1 x 1 mm³ voxels). Echo‐planar imaging (EPI) was used to obtain T₂ ^*‐weighted functional images in the axial plane with 2.5 mm isotropic resolution (TR = 2,500 ms, TE = 30 ms, flip angle = 90°, bandwidth = 62.5 kHz, 32 axial slices, 96 x 96 matrix, FOV = 240 mm, fractional k‐space acquisition, with fat saturation pulse). For each of the gradient‐echo EPI scans, a pair of spin‐echo EPI images with opposing phase‐encode polarities was collected for estimating the B0 distortion field (TR = 10,000 ms, TE = 90 ms, identical slice prescription as gradient‐echo images). Dental impression bitebars were used to reduce head motion. Stimuli were presented via a mirror reflection of a plastic screen placed inside the bore of the magnet, and a standard video projector with a custom zoom lens was used to project images onto this screen from a distance. The maximum visual angle was measured for each session and ranged from 26° to 29° due to practical limitations in our ability to adjust the visual distance for fMRI experiments. The individualized maximum visual angle measurements were used as input parameters in fMRI retinotopic map fitting and MEG dipole modeling, allowing for consistent mapping between MEG stimuli and the cortical surface for each subject. An MRI‐compatible fiber‐optical button box was used to record behavioral responses (Current Designs, Philadelphia, PA).

Data Processing

MEG and MRI/fMRI data were processed using an automated processing stream written with MATLAB (The Mathworks, Natick, MA) and C++ by D. Hagler, A. Dale, and other members of the UCSD Multimodal Imaging Laboratory, which also uses software from AFNI [Cox, 1996], FreeSurfer [Dale et al., 1999; Dale and Sereno, 1993; Fischl et al., 2001; Fischl et al., 2002; Fischl et al., 1999; Segonne et al., 2004; Segonne et al., 2007], and Fiff Access (Eleckta/Neuromag, Stockholm Sweden). Very noisy or flat channels were excluded from analysis. Magnetometers were excluded because they are often noisy, depending on environmental noise, and have less focal spatial sensitivity profiles (i.e., lead fields). After rejecting trials containing artifacts such as eye blinks and movements, data from remaining trials for a given stimulus location were used to calculate average time series time‐locked to stimulus onset, with a 100 msec pre‐stimulus baseline and 350 msec post‐stimulus response. Before averaging, individual trials were band‐pass filtered between 0.2 and 120 Hz with a 60 Hz notch filter, using buffer periods of at least 450 ms duration before and after each trial to reduce filter artifacts. In addition, the periods from −100 to 350 ms relative to each stimulus were linearly detrended, and the average of the baseline period, from −100 to 0 ms, was subtracted to correct for baseline shifts.

fMRI data were corrected for slice timing differences and head motion with AFNI's 3dvolreg. B0‐inhomogeneity distortions in fMRI data were corrected using the reversing gradient method [Chang and Fitzpatrick, 1992; Holland et al., 2010; Morgan et al., 2004]. Displacement fields estimated from paired spin‐echo test images with opposite phase‐encode polarity were applied to each frame of the motion‐corrected gradient‐echo EPI fMRI images [Holland et al., 2010]. In‐plane and through‐plane gradient warping in structural and functional MRI images was corrected by applying a predefined, scanner specific nonlinear transformation [Jovicich et al., 2006]. Two or more T₁‐weighted structural MRI volumes for each subject were coregistered, averaged, and rigidly resampled into alignment with an atlas brain. Automated registration between T₂‐weighted (fMRI and dMRI) and T₁‐weighted structural images was performed using mutual information [Wells et al., 1996] with coarse prealignment based on within‐modality registration to atlas brains. The FreeSurfer software package version 4.5.0 (http://surfer.nmr.mgh.harvard.edu) was used to create cortical surface models from T₁‐weighted MRI images [Dale et al., 1999; Dale and Sereno, 1993; Fischl et al., 2001, 2002, 1999; Segonne et al., 2004, 2007]. The resulting surfaces were thoroughly checked for errors in occipital cortex, and manual editing of the white matter segmentation was performed to correct local defects.

Stimuli for MEG Sessions

Visual stimuli were portions of a black and white dartboard pattern presented for 100 msec at three levels of luminance contrast on a gray background (15%, 71%, and 95% Michelson contrast). There were 36 total stimulus locations, divided between 3 eccentricities (3.6, 5.3, 8.2° visual angle, with sizes 1.2, 2.2, 3.6° visual angle, respectively) and 12 polar angles (22° polar angle wide, contiguous, non‐overlapping portions of the visual field, excluding 24° polar angle centered on each horizontal or vertical meridian) (Fig. 1A). The spatial frequency of the stimuli was varied with eccentricity, according to a log scale, with spatial frequency decreasing from ∼2.5 to ∼1 cycles per degree, although such square wave stimuli contain a broad range of spatial frequencies. To ensure that subjects maintained a stable level of alertness and maintained central fixation, subjects performed a simple task in which they made a finger lift response upon rare dimming of the central fixation cross (approximately once every 5–10 s). Trials within 700 ms before or after a button press were excluded. The interval between successive stimulus onsets was fixed at 117 ms. Ten percent of trials were “null” events in which no stimulus was presented. The average of these null events reflects the average, ongoing activity that overlaps with the response to stimulus trials. This overlap was removed by subtracting the averaged null event from the other stimulus condition averages. In a single MEG session with up to 45 min of stimulus presentation (separated into 2.5‐min blocks with rest periods of 30 s or more), up to ∼16,000 total trials were acquired, divided approximately equally across all stimulus locations and contrast levels.

Figure 1.

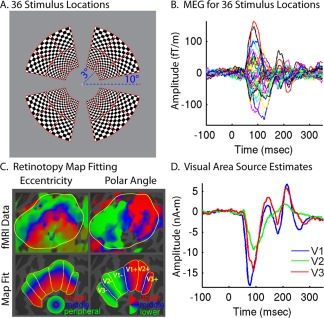
Retinotopy constrained source estimation. A: Stimuli were displayed at one of 36 visual field locations. B: MEG was used to measure VERs in an individual subject, and time courses for each location are shown for a selected mid‐line occipital gradiometer. C: A map template was fitted to fMRI retinotopy data to identify cortical patches for each stimulus location and construct retinotopy constrained forward models. D: Source estimates were generated for V1, V2, and V3, simultaneously constrained by all 36 stimulus locations. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Retinotopic Mapping and Map Fitting

Procedures for the acquisition and analysis of phase‐encoded fMRI data were similar to previous, detailed descriptions [DeYoe et al., 1996; Engel et al., 1994; Hagler et al., 2009, 2007; Hagler and Sereno, 2006; Sereno et al., 1995]. Retinotopic maps of polar angle were measured using a black and white dartboard wedge revolving around a central fixation cross (12° polar angle wide). Eccentricity was mapped using an expanding or contracting ring. To ensure a stable level of alertness and maximize attention, subjects performed a peripheral detection task, in which they pressed a button upon rare (∼5–10 s inter‐stimulus interval) presentation of a gray circle at pseudo‐random locations occluding the flickering dartboard pattern [Bressler and Silver, 2010]. For each subject, there were equal numbers of scans with counterclockwise or clockwise stimulus revolutions. Similarly for eccentricity mapping, expansion and contraction scans were counterbalanced. fMRI time series data were normalized by mean intensity for each voxel. Linear regression was used with the motion estimates from 3dvolreg and a quadratic polynomial to remove drift and head motion artifacts. Fourier transforms of the fMRI time series were computed to estimate the amplitude and phase of periodic signals at the stimulus frequency, with phase corresponding to the preferred stimulus location for a given voxel. For 5 subjects, a 32‐s cycle was used, with 10 cycles /scan, and for 3 subjects, a 64‐s cycle was used with 5 cycles/scan. Real and imaginary components were averaged across scans, with phases for clockwise polar angle and contracting eccentricity scans reversed before averaging. Phase delays of ∼3 s were subtracted from the Fourier components before averaging to account for hemodynamic delays, and the combination of opposite direction scans removes residual bias due to spatially varying hemodynamic delays [Hagler et al., 2007; Hagler and Sereno, 2006; Warnking et al., 2002]. For each subject, four polar angle scans (two clockwise and two counterclockwise) and two eccentricity scans (one outward, one inward) were collected in a single MRI session.

Nonlinear optimization methods were used to fit a template map including V1, V2, and V3 to polar angle and eccentricity mapping data derived from fMRI [Dougherty et al., 2003; Hagler and Dale, 2013]. The template maps were initialized as rectangular grids, and each grid node was assigned a preferred polar angle and eccentricity and a unique area code, corresponding to the lower or upper field portions of V1, V2, and V3 (Fig. 1C). V3 is often treated as two separate areas, V3 and VP, but for simplicity, these will be referred to as the lower and upper field portions of V3. To align the template map with the cortical surface, regions of interest (ROIs) were first manually drawn for each cortical hemisphere of each subject to encompass all of V1, V2, and V3, up to the maximum eccentricity measured with fMRI; a buffer zone was included, extending to the middle field representations of V3A and V4 (Fig. 1C). A two part fitting procedure was then performed. First, a coarse fitting step with 21 parameters determined the overall shape and location of the template map that best fit the data. Second, a fine‐scale fitting step smoothly deformed the template to better match the data. Unlike the previous description of this map fitting method [Hagler and Dale, 2013], additional free parameters were added to allow for greater flexibility in the fitting, including 5 to model a polynomial curve and 6 to vary the length of each upper and lower field sub‐area.

Retinotopy Constrained Source Estimation

Retinotopy constrained forward and inverse matrices were calculated as described previously [Hagler et al., 2009], with cortical patch models derived from retinotopic map fits [Hagler and Dale, 2013] (Fig. 1). Lead fields were calculated using the boundary element method (BEM) [Mosher et al., 1999; Oostendorp and van Oosterom, 1989]. Unlike EEG, MEG signals are relatively insensitive to the conductivity profile of the head because of the low conductivity of the skull that confines almost all the current within it, and so only the inner skull boundary was used for the MEG forward solution, which was approximated by filling and dilating FreeSurfer's automated brain segmentation [Fischl et al., 2002]. Brain conductivity was assumed to be 0.3 S/m. Gain matrices, specifying the predicted sensor amplitudes for a set of cortical surface locations, were calculated for dipoles oriented perpendicularly to the cortical surface. To determine the rigid body transformation between MRI and MEG reference frames, 100 or more digitized locations on the scalp were manually aligned to a surface representation of the outer scalp surface (obtained with the FreeSurfer watershed program) using a graphical interface written with MATLAB.

Models of the cortical sources of evoked visual responses, limited to visual areas V1, V2, and V3, were generated for each subject by selecting weighted cortical surface patches based on the retinotopic map fit, as described in detail previously [Hagler and Dale, 2013]. For each stimulus presented during an MEG session, weighting factors for each cortical surface vertex (∼0.8 mm inter‐vertex distance) in V1, V2, and V3 were calculated based on the preferred stimulus location derived from the fMRI retinotopy template fit. Realistic receptive field size estimates were used to define the extent of cortical activation for each stimulus. Values of 0.66, 1.03, and 1.88 (degrees visual angle) were used for V1, V2, and V3, respectively, with slopes as a function of eccentricity of 0.06, 0.10, and 0.15 (degrees visual angle/eccentricity degrees visual angle), derived from published group averages of receptive field sizes estimated from fMRI data [Dumoulin and Wandell, 2008]. The vertex weights were normalized so that the sum across visual field locations equaled one, and values less than 0.01 times the maximum for each cortical location were set to zero. Vertices in ipsilateral cortex were allowed (e.g., near vertical meridians) as was crossover between the upper and lower field sub‐areas (e.g., near horizontal meridians). Each vertex was treated as a separate dipole, with orientation assumed to be perpendicular to the cortical surface.

Retinotopy constrained forward matrices were constructed from the gain matrices described above and the cortical patch weighting factors for each stimulus location. The gain vectors for all 36 stimulus locations—or alternatively a subset of four locations—were arranged into a single column, assuming that a given visual area has the same evoked response regardless of stimulus location [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009; Slotnick et al., 1999]. The size of the forward matrix was the number of measurements (# of sensors X # of stimulus locations) by the number of sources (visual areas). An inverse matrix was calculated from the forward matrix using a regularized pseudo‐inverse with an identity matrix as the sensor noise covariance matrix. Separate source estimates were calculated for each contrast level using the same, time invariant inverse matrix. Normalized residual error was calculated as the ratio between the across‐sensor variance of the residual error and the maximum variance of the data over time. To exclude potential interactions with the other nonlinear dipole optimization methods used in this study, IRLS was not used for individual subject RCSE solutions.

Group‐Constrained RCSE

RCSE waveforms were calculated using MEG data and retinotopy constrained forward solutions from multiple subjects to simultaneously constrain the solution. To construct a group retinotopy constrained forward matrix, the retinotopy constrained forward solutions for multiple subjects were concatenated into a single matrix with a column for each of the three visual areas and ∼58,000 rows for ∼204 gradiometers (excluding bad channels), 36 stimulus locations, and 8 subjects. An inverse matrix was then calculated and applied to the event‐related MEG data concatenated across sensors, stimulus locations, and subjects.

IRLS was used to reduce the contribution of individual subject responses to particular stimulus locations with large residual error relative to other locations and subjects [Hagler and Dale, 2013; Holland and Welsch, 1977; Huber, 1981]. The absolute value of residual error was summed across all time points, contrast levels, and sensors, to provide absolute residual error (ARE) values for each subject and stimulus location combination. The minimum ARE value across all subjects and stimulus locations was subtracted from each ARE value, and these offset values were then normalized by their median absolute deviation (MAD), a robust estimator of the standard deviation [Hampel, 1974]. Weighting factors were calculated from the normalized residual using Tukey's bisquare function [Tukey, 1960]. These weights were used to scale both the sensor data and retinotopy constrained forward matrix before calculating the inverse operator and source estimates. Predicted sensor waveforms were calculated using the revised source estimates and the unweighted forward matrix. This process was repeated for at most 100 iterations or until the solution converged (i.e., source estimates change less than 10⁻⁷), which typically occurred within 10 iterations.

Optimization of Cortical Patch Locations Constrained by Prior

An iterative, random search procedure was used to find optimal cortical patch locations. At each of 1,000 iterations, cortical patches were slightly displaced across the cortical surface using a 2‐dimensional grid defined to encompass the occipital ROI used for the retinotopy map fit. In units relative to the width of the grid, the step size for each optimization step was 0.002 and the maximum displacement was 0.02. This corresponded to a maximum displacement of ∼5 mm across the cortical surface and a mean displacement of 2.4 ± 0.2 mm (see Supporting Information Table 1). With patches in four visual field quadrants of three visual areas and either 4 or 36 stimulus locations, there were a total of 96 or 864 parameters, respectively. The optimization procedure required 10–20 min to complete with 4 stimulus locations and 1–2 h with 36 locations.

The optimized solution was constrained to be similar to a group‐constrained RCSE solution, which served as an a priori estimate of the shapes of V1, V2, and V3 waveforms. The cost function to be minimized is described by Eq. (1):

$$c=\lambda ·e_{\text{prior}}+(1-\lambda )·e_{\text{data}}$$ (1)

where c is the cost function, λ is a weighting factor between 0 and 1, e _prior is the normalized difference between the source estimates and the prior waveform, and e _data is the normalized residual error, or the difference between the data and fit. A weighting factor of 0.5 would represent equal weighting between correspondence to the atlas prior and goodness of fit to the data, whereas a value of 1.0 would rely solely on the atlas prior. In this study, the prior weighting factor was chosen to be 0.8, a value that was large enough to prevent clearly wrong source estimates, such as can happen with no atlas prior, particularly with few stimulus locations (Figs. 2B and 5B), but less than 1 so that the individual's data still contributed to the solution.

Figure 2.

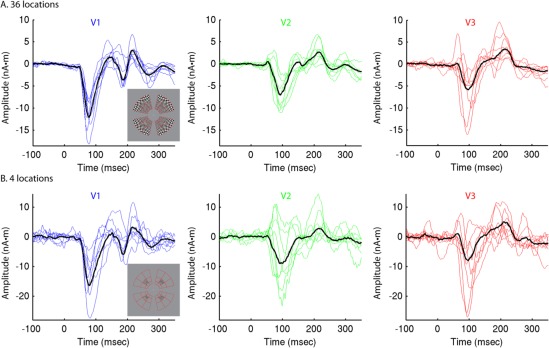
Group‐constrained RCSE. RCSE time courses calculated from responses to high contrast (95%) stimuli for eight subjects are shown in blue (V1), green (V2), or red (V3), with group‐RCSE solutions superimposed in black. A: RCSE solutions with 36 stimulus locations. B: RCSE with 4 stimulus locations. Locations of the 4 stimuli were at 5.3° visual angle and 45° from the horizontal and vertical meridians, as indicated by the inset image of stimulus locations. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 5.

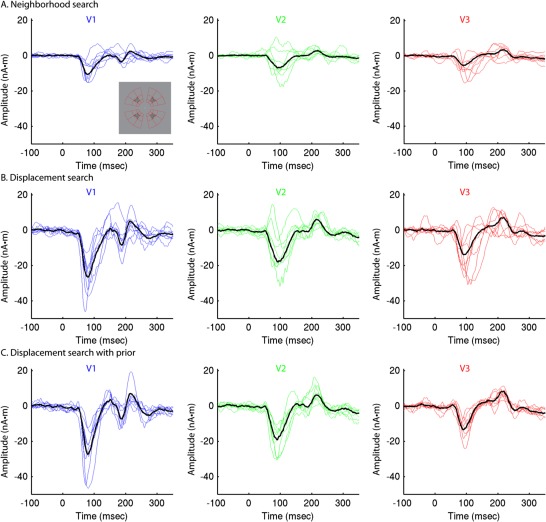
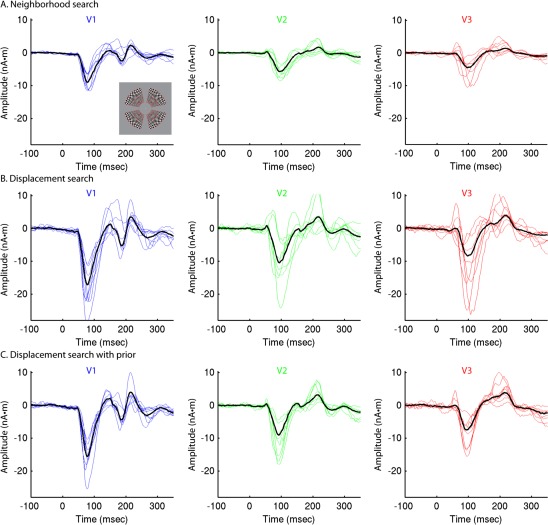
Group‐constrained RCSE after nonlinear optimization. RSCE time courses calculated from responses to high contrast (95%) stimuli at four locations for eight subjects after three methods of nonlinear optimization shown in blue (V1), green (V2), or red (V3), with recalculated group‐RCSE solutions superimposed in black. A: Neighborhood search. B: Displacement search without prior. C: Displacement search constrained by group‐RCSE prior. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

To use only the shape of the prior to constrain the solution and allow the optimized waveform amplitudes to vary between subjects, for each iteration of the optimization procedure, the amplitude of the prior was linearly scaled to optimally match the source estimate amplitude. To avoid making any assumptions about the relative amplitudes of V1, V2, or V3, the prior was scaled independently for each visual area. To avoid circularity issues related to self‐bias, the prior estimate for each subject was the group‐constrained RCSE solution calculated from the other seven subjects. Similarly, to avoid the possibility of biasing the contrast response functions, only the responses to high contrast stimuli and the group‐constrained RCSE solutions computed from them were used to determine the optimal dipole locations; these locations were then used to estimate waveforms for each contrast level.

Exhaustive Neighborhood Search

A related nonlinear optimization method, previously introduced by Ales and colleagues [Ales et al., 2010a], was also implemented for comparison. That method, herein referred to as a neighborhood search, performs an exhaustive search for the single cortical surface mesh vertex within a defined cortical neighborhood for each stimulus location and visual area that minimizes residual error. In this study, the cortical neighborhood was defined based on the weighted cortical patches determined by the fMRI retinotopic map fit used for the non‐optimized RCSE solution. To make the problem tractable, the search is performed in serial for each cortical neighborhood, during which the dipoles for all other stimulus locations are held constant [Ales et al., 2010a]. Only the primary cortical patch was used, excluding the additional patches for ipsilateral and opposing upper/lower hemifields. To reduce the size of the neighborhood to be similar to the allowed range for the patch displacement search described above (see Supporting Information Table 1), vertices with weights less than 70% of the maximum weight for a given patch were excluded. The neighborhood search optimization required 2–3 h to complete with 36 stimulus locations.

Waveform Analysis

Peak latency and amplitude were derived from group average RCSE waveforms. This approach, rather than finding peaks in individual subject waveforms, was chosen because some subjects exhibited responses with double peaks, particularly at lower contrast, resulting in elevated variance of peak latency. Peaks were detected using Eli Billauer's peakdet (http://www.billauer.co.il/peakdet.html), which finds minima and maxima that are a minimum difference from surrounding extrema (0.5 nA·m). The peak with the largest amplitude between 50 and 150 ms post‐stimulus was chosen for analysis. Bootstrap resampling was used to calculate 95% confidence intervals for average waveforms and peak latencies and amplitudes [Efron, 1979, 1987]. For each of 2,000 iterations, a sample of eight subjects was selected with replacement, average waveforms were calculated, and peak latencies and amplitudes were determined. Confidence intervals and p‐value upper bounds were then derived from the distribution of observed values, using the bias correction and acceleration method to correct for bias due to finite sampling [Efron, 1987]. To control for multiple comparisons involved in the latency and amplitude comparisons between V1, V2, and V3 at low, medium and high contrast, a p‐value threshold of 0.0175 or less was determined to result in a 0.05 false discovery rate [Benjamini and Hochberg, 1995].

RESULTS

Between Subject Variability of RCSE Waveforms

In previous descriptions of RCSE, the V1, V2, and V3 waveforms have shown similarities across studies and between subjects, although only two subjects were included in each [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009]. The typical V1 response to high contrast pattern stimuli was dominated by a large negative peak at ∼80 ms post‐stimulus, which reflects a current dipole pointing from gray matter toward the underlying white matter [Hagler et al., 2009]. For V2 and V3, the initial negative peaks were delayed by several milliseconds (Fig. 1D). In this study, with a larger sample of eight subjects, there were again similarities common to all subjects, but substantial variation was observed as well. Examples of this were differences in the relative peak amplitudes of each area, inverted or biphasic initial responses for one or more areas in some subjects, and simultaneous responses in V1 and V2 or V3 in some subjects (Fig. 2).

The source of this variation is presumably at least partly artifactual, due to slight errors in the specification of dipole locations and orientations [Hagler and Dale, 2013; Hagler et al., 2009]; these unusual waveform features occurred more often when fewer stimulus locations were used to constrain the solutions (Fig. 2B). That waveforms estimated with a small number of stimulus locations exhibit greater sensitivity to dipole specification errors was confirmed through additional simulations (Supporting Information Fig. 1). If dipole locations were shifted across the cortical surface, a variety of waveform shapes resulted (Fig. 3). For individual subjects, the use of many stimulus locations reduces the sensitivity to errors specific to one or a few stimulus locations [Hagler and Dale, 2013; Hagler et al., 2009], and robust estimation with IRLS can further reduce the contribution of outliers [Hagler and Dale, 2013; Holland and Welsch, 1977; Huber, 1981]. Similarly, the larger group of subjects in the current study provided the opportunity to obtain multi‐subject consensus estimates of the V1, V2, and V3 VER time courses, using IRLS to reduce the contribution of outliers (Fig. 2; see Group‐constrained RCSE in Methods).

Figure 3.

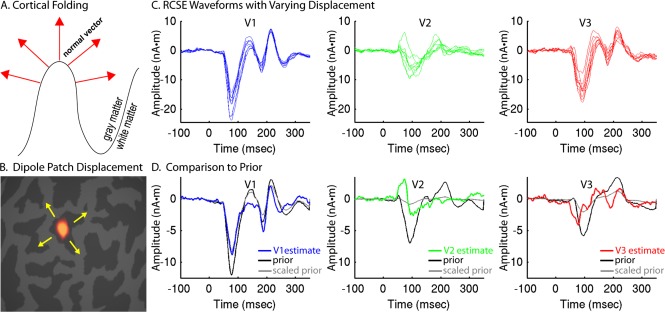
RCSE dipole optimization constrained by group‐RCSE prior. A: Schematic depiction of the relationship between cortical folding, dipole location, and predicted dipole orientation. B: Dipole patches were displaced across the cortical surface in search of better fitting locations. C: For an individual subject, cortical displacement of dipole patches can result in a variety of V1, V2, and V3 RCSE waveforms, some of which provide a better fit to the measured MEG data. D: To constrain dipole optimization, waveform estimates (blue, green, or red traces) are compared with the prior estimate derived from group‐constrained RCSE (black traces) that have been scaled in amplitude (gray traces) to best match the estimate at each iteration. RCSE waveforms shown were derived from responses to high contrast (95%) stimuli. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Optimization of RCSE Constrained by Prior

To improve the reliability of RCSE for individual subjects, particularly when using a smaller number of stimulus locations, an optimization method was developed to correct for inaccurately specified dipole locations and orientations (Supporting Information Fig. 2). This method works by nonlinearly searching for displacements along the cortical surface of the cortical patches for each stimulus location, in order to provide a better fit to the sensor data (Fig. 3A–C). An exhaustive neighborhood search was also tested for comparison [Ales et al., 2010a]. Because of the introduction of many free parameters, it is possible to obtain solutions with reduced residual error (Supporting Information Fig. 3) that are nonetheless quite implausible (Fig. 4A,B), particularly with a small number of stimulus locations (Fig. 5A,B). To prevent this, the group‐constrained RCSE solution was used as a priori information about the timing and shape of the response of each area—essentially a probabilistic atlas of visual area time courses—in order to constrain the individual subject solution (Fig. 3D). To avoid circularity issues, a leave‐one‐out approach was used for computing the group‐constrained RCSE solutions, so that an individual's own initial RCSE waveforms did not contribute to the prior used to constrain the optimization. Using this method, the types of waveform abnormalities described above were generally avoided, and the variance of RCSE waveforms across subjects was substantially reduced (Figs. 4C and 5C). These different optimization methods were constrained such that they resulted in dipole displacements no greater than 6 mm that were less than 2.5 mm on average (Fig. 6, Supporting Information Table 1).

Figure 4.

Group‐constrained RCSE after nonlinear optimization. RSCE time courses calculated from responses to high contrast (95%) stimuli at 36 locations for eight subjects after three methods of nonlinear optimization shown in blue (V1), green (V2), or red (V3), with recalculated group‐RCSE solutions superimposed in black. A: Neighborhood search. B: Displacement search without prior. C: Displacement search constrained by group‐RCSE prior. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 6.

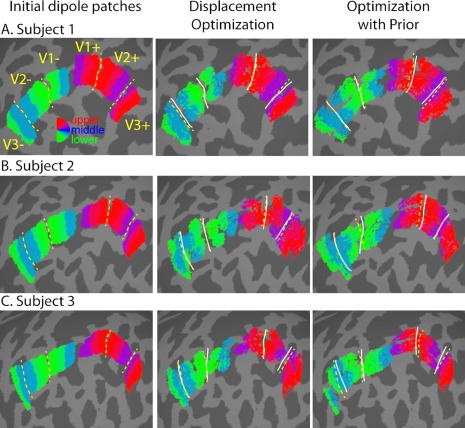
Cortical patch dipoles before and after optimization constrained by prior for three representative subjects (A–C). Colors for each cortical patch (excluding those with weights < 0.2 relative to maximum) correspond to the central polar angle of the matching stimulus, using the same color scheme as in Figure 1C. The small holes in the patches after optimization are related to how patches were displaced across the cortical surface. For each vertex in the original patch, a single vertex was chosen closest to the original location plus the 2‐dimensional displacement. Dashed, yellow lines represent approximate, manually drawn borders between V1, V2, and V3. Solid white lines represent approximate, manually drawn borders after optimization. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Differences between V1, V2, and V3 Responses and the Effects of Luminance Contrast

RCSE with prior‐constrained dipole optimization was used to measure V1, V2, and V3 responses as a function of luminance contrast (Fig. 7). Stimuli at 36 locations were presented one at a time, using three different luminance contrast values (15%, 71%, 95%; Fig. 7D). RCSE waveforms averaged across the eight subjects show that both the amplitude and latency of the responses vary with luminance contrast in expected ways (Fig. 7A–C). At low contrast, the responses were both smaller and later (Fig. 7E,F). The contrast latency functions were similarly shaped for V1, V2, and V3, but with significantly earlier peak responses in V1 for each contrast level, ranging from ∼10 to ∼20 ms (Fig. 7E, Tables 1 and 2). Peak latencies of V2 and V3 were quite similar, although a small difference of ∼4 ms was found to be significant for 71% and 95% contrast stimuli (Fig. 7E, Tables 1 and 2). Peak amplitudes for V1 were larger than those of V2 by 37%—though significant only for 71% and 95% contrast—and larger than those of V3 by 74% (Fig. 7F; Tables 1 and 2). Peak amplitudes for V2 were 27% larger than for V3, but these differences were not significant. Normalized contrast response functions were nearly indistinguishable for the three visual areas (Fig. 7G). The overall shape of the estimated response was similar for the three areas, but V1 displayed a second negative peak at ∼190 ms—about the time expected for a response to the stimulus offset. A similarly prominent peak was not observed in the V2 or V3 waveforms.

Figure 7.

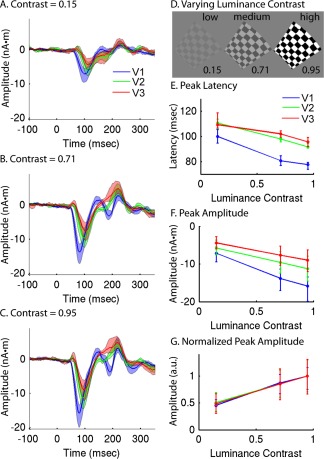
Group averages of V1, V2, and V3 responses to stimuli with varying luminance contrast. A: V1, V2, and V3 RCSE waveforms after dipole optimization for low luminance contrast (15%) stimuli. B: Medium contrast (71%). C: High contrast (95%). D: Images of stimuli with three levels of luminance contrast. E: Peak latency as a function of luminance contrast for V1, V2, and V3. F: Peak amplitude relative to the pre‐stimulus baseline. G: Normalized peak amplitude, relative to mean amplitude at high contrast. 95% confidence intervals derived from bootstrap resampling are shown as shaded regions (A–C) or error bars (E–G). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Peak latencies and amplitudes obtained from group mean RCSE waveforms after dipole optimization constrained by prior for V1, V2, and V3, and three levels of luminance contrast

Visual area	Contrast (%)	Peak latency		Peak amplitude
		Mean (msec)	95% confidence	Mean (nAm)	95% confidence
	15	99.9	94.8–105.6	7.1	5.5–9.4
V1	71	80.7	76.8–84.6	13.8	11.3–17.1
	95	77.6	73.9–79.4	15.9	13.4–19.9
	15	110.8	106.4–113.7	5.7	3.6–7.6
V2	71	98.1	95.8–99.2	9.6	6.7–12.4
	95	91.8	90.6–94.4	11.3	7.9–14.6
	15	109.4	106.8–118.9	4.4	2.7–6.0
V3	71	102.1	96.5–104.6	7.7	5.2–10.3
	95	95.6	92.0–99.2	9.0	6.2–12.0

95% confidence intervals were derived from bootstrap resampling. Peak amplitudes correspond to negative (inward) currents, but for simplicity are shown without negative signs.

Table 2.

Differences in peak latencies and amplitudes obtained from group mean RCSE waveforms after dipole optimization constrained by prior for V1, V2, and V3, and three levels of luminance contrast

Visual areas	Contrast (%)	Peak latency difference			Peak amplitude difference
		Mean (msec)	95% confidence	P‐value	Mean (nAm)	95% confidence	P‐value
	15	10.9	6.9–17.8	0.0005	1.4	−0.2–4.6	0.1050
V2 vs. V1	71	17.4	14.7–21.9	0.0005	4.2	1.8–8.7	0.0005
	95	14.1	10.6–16.4	0.0005	4.6	1.8–9.8	0.0005
	15	9.5	3.6–26.5	0.0005	2.8	1.4–4.2	0.0005
V3 vs. V1	71	21.4	17.1–26.9	0.0005	6.1	3.5–7.8	0.0005
	95	18.0	15.7–24.6	0.0005	6.9	3.6–9.1	0.0005
	15	−1.4	−6.5–6.1	0.4835	1.4	−0.7–4.0	0.2145
V3 vs. V2	71	4.0	0.9–6.1	0.0175	1.9	−1.1–4.7	0.1975
	95	3.9	2.1–12.6	0.0040	2.3	−0.4–5.4	0.0960

95% confidence intervals were derived from bootstrap resampling. p‐values less than or equal to 0.0175, providing a false discovery rate of 0.05, are in bold.

These results, obtained using the prior‐constrained dipole optimization described above, were qualitatively compared to results without optimization, with neighborhood search, and with displacement search unconstrained by a prior, using either 36 or 4 stimulus locations (Figs. 8 and 9, Supporting Information Fig. 3). The average response amplitudes were generally larger when using four stimulus locations instead of 36, as was the proportion of explained variance. Response amplitudes increased after optimizing dipole location via displacement search. Explained variance was increased when the search was not constrained by a prior, but roughly unchanged when a prior was used. Curiously, response amplitudes were relatively small with neighborhood search, despite increases in the explained variance. This may be due to reduced cancellation when using single vertices to model dipoles rather than distributed cortical patches [Ahlfors et al., 2010]. Aside from these differences, the functions of peak latency and amplitude relative to luminance contrast were similar for the different sets of results. There was, however, greater inter‐subject variability for the non‐optimized estimates and the estimates using neighborhood search or displacement search unconstrained by a prior. This resulted in larger 95% confidence intervals, particularly with only four stimulus locations (Fig. 9), thereby reducing power to detect differences between conditions or visual areas.

Figure 8.

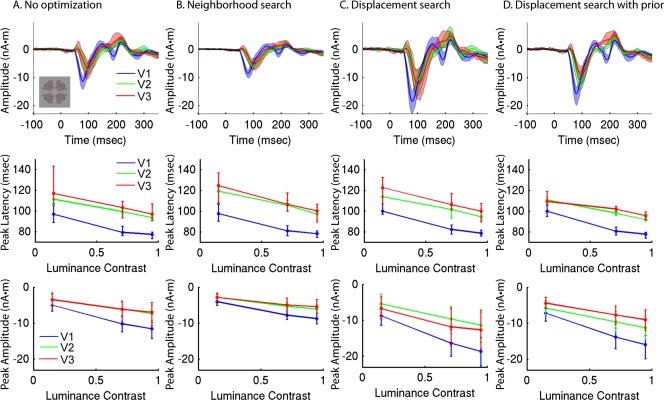
Group average responses for 36 stimulus locations, with and without dipole optimization. A: Group average RCSE waveforms for high contrast (95%) stimuli (top), peak latency versus contrast (middle), and peak amplitude versus contrast (bottom) for initial RCSE estimates without optimization. B: Neighborhood search. C: Displacement search without prior. D: Displacement search constrained by group‐RCSE prior. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 9.

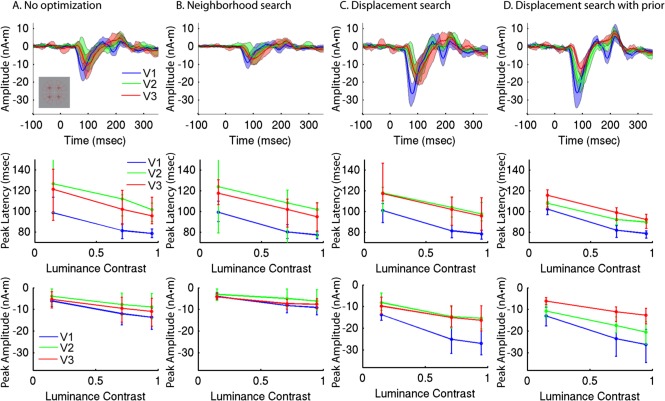
Group average responses for four stimulus locations, with and without dipole optimization. A: Group average RCSE waveforms for high contrast (95%) stimuli (top), peak latency versus contrast (middle), and peak amplitude versus contrast (bottom) for initial RCSE estimates without optimization. B: Neighborhood search. C: Displacement search without prior. D: Displacement search constrained by group‐RCSE prior. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

A potential explanation for the lack of substantial differences between V2 and V3 is that their sensor topographies are too similar to properly distinguish between them [Ales et al., 2010b]. The patterns of MEG sensor topography predicted by the retinotopy constrained forward solutions as functions of stimulus location were reviewed for each visual area [Supporting Information Figs. 4–6]. Although topography for several stimulus locations may in fact be similar for V2 and V3, such that the angular difference between their dipoles was consistently less than for V1 and V2 or V1 and V3 (Supporting Information Table 2), the collection of multiple stimulus locations appeared to allow for adequate separation between visual areas. This was quantified using the crosstalk measure [Hagler et al., 2009; Liu et al., 1998], which was quite low between V2 and V3, both before and after prior‐constrained dipole optimization, even for only four stimulus locations (Supporting Information Table 3).

DISCUSSION

Estimation of visual evoked responses in individual visual areas based on noninvasive recordings is a challenge for a number of reasons; chief among them, the close proximity of early visual areas and the convoluted cortical surface upon which retinotopic maps lie. RCSE accounts for the mapping of the visual field to the folded cortical surface, and through the use of multiple stimulus locations to constrain the solutions, resolves the proximity issue [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009]. The primary limitation of RCSE is related to the inherent imprecision of mapping between the visual field and visual cortex. To compensate for small errors in the specification of dipole locations and improve the reliability of RCSE, a dipole optimization procedure was developed, constrained by prior information about the time courses of activity in V1, V2, and V3. This is the first study using RCSE to include results from more than two subjects, and while the sample size of eight subjects was not large, it was sufficient to answer some basic questions about differences between the responses of V1, V2, and V3. The V1 peak response was ∼10–20 ms earlier than that of V2 and V3, as well as ∼30–70% larger in amplitude. Normalized contrast response functions were, however, nearly identical for the three visual areas.

General Limitations of RCSE

One of the key, simplifying assumptions of RCSE is that time courses within a visual area are identical for stimuli at different visual field locations. This is likely a reasonable approximation, and there is some evidence to suggest that estimated responses are quite similar within eccentricity bands [Slotnick et al., 1999] and across left and right hemifields [Ales et al., 2010a]. There is, however, evidence that visual evoked potential peak latencies decrease with increasing eccentricity [Baseler and Sutter, 1997]. Furthermore, differences between responses to stimuli in the upper and lower visual fields may be predicted based on previous demonstrations of a behavioral advantage for lower field stimuli [Levine and McAnany, 2005; McAnany and Levine, 2007; Previc, 1990; Skrandies, 1987], as well as much larger visual evoked fields [Portin et al., 1999]. The potential for variation of the responses across the visual field is, therefore, a real concern, as discrepancies between visual field locations will contribute to greater residual error. Despite this, it seems appropriate to view the RCSE estimates as consensus solutions that, in the event of latency variations across the visual field, will have intermediate timing. In any case, future work should include a detailed analysis of the variation across the visual field by comparing the responses estimated from subsets of stimulus locations.

The ability of RCSE to correctly distinguish between one visual area and another depends on the accuracy of the forward model. For example, because of cortical curvature, small displacements along the cortical surface can result in large changes in the predicted dipole orientation [Hagler et al., 2009]. If multiple stimulus locations are used, and the displacements are small and randomly distributed, the estimated waveforms may not be substantially altered, although residual error will be increased [Hagler et al., 2009]. Larger or systematic discrepancies in the mapping between MEG stimulus locations and fMRI retinotopic maps could result in highly inaccurate source estimates, particularly when fewer stimulus locations are used (Fig. 3, Supporting Information Fig. 1).

There appears to be an inverse relationship between the estimated response amplitude and residual error, such that estimated waveforms with small amplitudes are accompanied by high residual error. Consistent with this, increased response amplitudes were observed for estimates using only four stimulus locations (Figs. 8 and 9) as well as a corresponding increase in the proportion of variance explained by the RCSE fit (Supporting Information Fig. 3). The use of many stimulus locations tends to reduce the amount of variance that can be explained, since noise that is independent for the different stimulus locations is excluded from the fitted solution [Hagler and Dale, 2013]. For example, RCSE fit variance during the pre‐stimulus baseline period was nearly zero, compared with substantial, non‐zero variance of the data during this period (Supporting Information Fig. 3). Also, the cumulative effect of inaccurately specified cortical patch locations increases residual error more when using many stimulus locations (Supporting Information Fig. 7). In contrast, source estimation methods using a single stimulus location can account for a greater fraction of variance—even in baseline periods without actual neural activity—although this does not imply a more accurate solution [Hagler and Dale, 2013; Hagler et al., 2009].

Another limitation of current and previous implementations of RCSE is that only the early visual areas V1, V2, and V3 were modeled. Using multiple stimulus locations does impose a strong constraint on the RCSE solution and reduces the likelihood of contamination between visual areas [Hagler et al., 2009], but to the extent that other visual areas are activated by these stimuli, the omission of such areas contributes to elevated residual error, presumably more so at later time points. If only to gain more comprehensive information about the properties of the visual system, it would be desirable to include additional visual areas. Creating retinotopy constrained dipole models for areas such as V3A, V4, or V5 would be relatively straightforward, but the results would require careful validation, particularly given the small size of these areas, their large receptive fields, and their close proximity to other, related visual areas.

Between Subject Variability of RCSE Waveforms

Some degree of heterogeneity among human subjects in the latency of visual evoked responses is expected, for example, due to differences in axonal conduction speed [Berman et al., 2009]. Other large variations in RCSE waveforms across subjects, such as polarity inversions, are more likely artifactual in origin. The quality of fMRI retinotopy data and map fits, cortical surface reconstructions, and the signal‐to‐noise‐ratio (SNR) of MEG/EEG data each contribute to the variability of RCSE waveforms [Hagler and Dale, 2013]. Also, variation in the complexity of cortical folding, which has been previously observed [Palaniyappan et al., 2011; Penttila et al., 2009; Rogers et al., 2010; Toro et al., 2008], may contribute to greater discrepancies in particular subjects. In the current sample, there were positive, but nonsignificant correlations between the variability of orientations within cortical patches and RCSE residual error (Supporting Information Table 4). Additional variability could arise from the mapping between the visual fields used for separate MEG and fMRI measurements. In this work, the maximum visual angle was held constant for MEG sessions and precisely measured for fMRI sessions so that they could be taken into account in retinotopic map fitting and RCSE dipole modeling, thus fully accounting for variation in the size of the stimulated visual field for fMRI sessions across subjects.

Another potential source of variability between subjects, particularly for a small number of stimulus locations, is the extent to which the collection of dipoles chosen for V1, V2, and V3 are orthogonal to each other. Also, because of dipole cancellation and the insensitivity of MEG to radial dipoles, some source locations for particular subjects may result in smaller MEG signals, potentially making estimated responses noisier. Given knowledge of the predicted dipole locations and orientations for multiple visual areas and visual field locations, it should be possible to choose a small set of stimulus locations that provide superior separation between V1, V2, and V3, tailored to each subject. For example, one could choose locations where the differences in dipole orientation for V1 and V2 (or V1 and V3, or V2 and V3) are closest to 90 degrees (see Supporting Information Table. 2). Similarly, one could choose the combination of locations that collectively result in the lowest cross‐talk between V1, V2, and V3. In addition, locations with relatively weak, predicted sensor amplitudes could be avoided. A caveat is that if the retinotopic maps used to calculate the forward models are slightly wrong, the stimulus locations chosen for a particular subject may not be truly optimal. Given that, it would be advisable to prefer stimulus locations corresponding to relatively smooth cortical locations, so that small inaccuracies in the modeled location would be less problematic. Even so, retinotopic map fitting errors would likely necessitate dipole optimization. Another concern is that if VERs vary as a function of visual field location, for example, reduced latency in the periphery [Baseler and Sutter, 1997], choosing different stimulus locations for each subject could introduce unnecessary variation.

The simultaneous constraint of many stimulus locations helps to reduce the influence of modeling imperfections [Hagler and Dale, 2013; Hagler et al., 2009]. Similarly, RCSE constrained by multiple subjects yields a consensus solution, with IRLS to minimize the contribution of outliers. For hypothesis testing and describing the between‐subject variability of source estimates, non‐parametric resampling methods were used because they do not require the assumption of normal distributions, which could, in principle, be violated for RCSE waveforms and derived measures, particularly with a relatively small sample. Also, peak latencies and amplitudes were more reliably derived from group average waveforms rather than those of individual subjects, and bootstrap resampling allowed the estimation of confidence intervals for those measures.

Nonlinear Optimization of Dipole Locations

Nonlinear optimization of dipole locations for RCSE is a way to relax the strong constraints provided by fMRI retinotopy, with the knowledge that those constraints could be slightly inaccurate. This general approach was used previously by Ales et al., who performed a neighborhood search for the best fitting vertex, iterating through each stimulus location and visual area in turn, holding dipoles for all other stimulus locations constant [Ales et al., 2010a]. A conceptually similar method would be to first linearly estimate source waveforms and then use those estimates to linearly estimate better fitting dipole orientations.

A limitation of both approaches is strong dependence on the initial waveform estimates. Also, the sequential nature of the neighborhood search reduces the likelihood of obtaining an optimal solution. Furthermore, using a single vertex, rather than weighted cortical patches, to model the source of visual evoked responses for a particular visual area and stimulus location fails to account for the extent of cortex activated or the fact that stimuli near the vertical and horizontal meridians evoke responses in each of the four sub‐areas of V1, V2, and V3 [Hagler and Dale, 2013]. In the current study, the vertical and horizontal meridians themselves were not stimulated, primarily to minimize cross‐over contributions and avoid parts of V1 that are more sharply curved than others. It is likely, however, that the methods described here would be applicable to stimuli presented at the meridians because these cross‐over contributions may be modeled explicitly with weighted cortical patches and dipole optimization can compensate for problems related to curvature.

A more general concern about nonlinear optimization, which also affects the cortical patch displacement search described in this paper, is that the introduction of many free parameters erodes the highly over‐determined nature of the RCSE method. Although the goal is to obtain more accurate source estimates, reductions in residual error provided by multi‐parameter nonlinear optimization do not guarantee this. While dipole optimization without the group‐RCSE prior generally reduced residual error (Supporting Information Fig. 3), the resulting waveforms were sometimes implausible (Figs. 4 and 5). A potential explanation is that if some of the poorer fitting dipoles of V1, V2, or V3 were reoriented to align with other, un‐modeled visual areas, estimated time courses would be more inaccurate, even though residual error would be reduced. The use of prior estimates of visual area time courses to guide the optimization is a way to correct for incorrectly specified cortical patch locations while imposing constraints on the solution that may prevent contamination between visual areas that would otherwise result from dipole optimization. With the group‐RCSE prior, results tended to be more sensible, but residual error was reduced to a lesser degree [Supporting Information Fig. 3]. This might suggest that there were substantial differences between individual subjects and the group‐RCSE solution, such that forcing the waveforms to be similar to the group‐RCSE did not improve the goodness of fit for individuals. Alternatively, it may be that there is a limit to the proportion of variance that can be explained with the multi‐location V1, V2, and V3 cortical patch models, and that unconstrained optimization methods reduce the residual error artifactually; for example, by capturing the variance of additional, un‐modeled visual areas.

The greatest potential benefit of prior‐constrained dipole optimization is to improve the reliability of RCSE when using a small number of stimulus locations, such as one in each quadrant. With few locations, small inaccuracies in retinotopic mapping and fMRI to MEG registration become particularly influential (Supporting Information Fig. 1) [Hagler and Dale, 2013]. Using a small number of locations, however, would make the use of RCSE more practical for a wider range of applications by allowing for parametric manipulation of stimulus or task conditions while maintaining a sufficiently large number of trials per condition within a feasible recording duration. Regardless of the number of stimulus locations, about 200 or more trials per condition are required for RCSE source waveforms with acceptable SNR.

Because the timing and waveform shape of VERs depend on stimulus properties, it is necessary to select an appropriately similar prior, considering luminance contrast, spatial frequency, and other factors. Assuming that the locations of the cortical dipole patches are invariant with respect to stimulus properties other than visual field location, optimized dipole locations obtained for a single stimulus condition—i.e., the one most similar to the prior—may be applied to other conditions with identical visual field locations but varied stimulus or task properties. The prior may be derived from group‐constrained RCSE, as in the current study, or from a previous recording session for the same subject using a large number of stimulus locations. Using a subject‐specific prior would allow for the possibility of greater, true variation between subjects in waveform shape or timing, although this approach would also be more vulnerable to inaccuracies in the original estimates. In the current study, a leave‐one‐out approach was used to avoid circularity issues, but in general it is likely preferable to use as a prior group‐constrained RCSE waveforms derived from as many subjects as possible.

A characteristic of the optimization approach used for the current study was that the cortical patches corresponding to each stimulus location were simply displaced across the cortical surface, limiting the number of free parameters to two per patch. At the expense of greater computation time, additional parameters could possibly be used to increase the goodness of fit. For example, the patches could be rotated, or the diameter varied. A more complex nonlinear estimation procedure could even allow for changes to the shape of the cortical patches, although it would require further study to establish the feasibility of such an approach. It is difficult to know whether additional parameters would make a substantial improvement, given that MEG or EEG sensors detect dipolar sources at a distance, such that subtle changes to the shape of the patches could be insignificant. On the other hand, if a patch is the wrong size or incorrectly oriented, this could increase residual error by under‐ or over‐estimating the degree of cancellation. Also, the inclusion or omission of particular vertices from a patch could, because of cortical folding, dramatically change the equivalent dipole orientation. Not including additional parameters could, therefore, have precluded some dipole displacements that would otherwise have produced better fits to the data.

A finite search radius was used for both displacement search and neighborhood search (Supporting Information Table 1). For neighborhood search, this was implemented by only including vertices with high weighting factors (≥70% of the maximum for each patch). The size of the range allowed is a somewhat arbitrary choice, balancing the ability to correct for retinotopic mapping errors with the need to avoid artifactually large displacements. Dipole search with larger ranges produced similar results, but sometimes resulted in implausible patterns of patch displacements (not shown). For neighborhood search, including more vertices in the search neighborhoods—which increased computation time by as much as 10 times if using the full set of vertices in a patch—reduced residual error, but did not improve overall performance in terms to preventing implausible waveform abnormalities such as polarity inversions (not shown).

Differences Between Visual Areas

Invasive recordings in monkeys have shown that the early visual areas first become active nearly simultaneously [Schmolesky et al., 1998; Schroeder et al., 1998], and whether there is a substantial difference in timing between V1, V2, and V3 in humans has been recently debated [Ales et al., 2010b; Kelly et al., 2012]. In previous studies using the RCSE method [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009], the number of subjects tested has been too small to draw firm conclusions on this issue. In the current study, the peak responses of both V2 and V3 were found to be significantly delayed relative to V1, by ∼10–20 ms. Interestingly, the peak V3 response was nearly coincident with that of V2. This suggests that direct input from V1 plays an important role in the V3 response, bypassing V2. At the least, the short delay indicates that local processing in V2 is not required before signals are passed to V3 for further processing.

Peak amplitudes were significantly larger for V1 than for V2 and V3. These amplitude differences may reflect higher levels of activity within individual neurons or a greater number of active neurons, but other explanations are possible as well. For example, the strength of a current dipole depends on the geometry of neuronal populations in different layers of cortex [Einevoll et al., 2007; Gratiy et al., 2011]. Also, systematic differences in the accuracy of the forward models for each visual area, which could contribute to under‐ or over‐estimation of response amplitudes, cannot be ruled out. No apparent differences between V1, V2, and V3 were found in the relative peak amplitudes as a function of luminance contrast. This finding is similar to the results of previous fMRI studies [Avidan et al., 2002; Buracas et al., 2005; Kastner et al., 2004], although it conflicts with one early fMRI study that found a large difference between the contrast response functions of V1 and V3 [Tootell et al., 1995]. The discrepancy may reflect imprecise labeling of V3 or differences in stimulus properties such as spatial frequency.

In previous studies using RCSE, large, positive deflections were observed in the estimated V2 and V3 waveforms [Ales et al., 2010a; Hagler and Dale, 2013; Hagler et al., 2009], roughly coincident with the onset of the V1 response. Although this type of biphasic pattern is consistent with the shape of cortical surface electrode recordings in monkeys [Schroeder et al., 1991], and the positive peak can be potentially explained by depolarization of layer 2/3 pyramidal neurons [Barth and Di, 1991; Einevoll et al., 2007; Hagler et al., 2009], such polarity inversions are also potentially explained by incorrectly specified dipole locations (Fig. 3, Supporting Information Fig. 1). In the current study, these peaks were sufficiently small and variably timed across subjects—they were not observed at all in some subjects—that they were barely noticeable in the group‐constrained RCSE solutions (Figs. 2, 4, and 5). In group average V2 and V3 waveforms, they were quite small, particularly after prior‐constrained dipole optimization (Figs. 7, 8, and 9). If, for some reason, a large, positive peak were actually present in an individual but not the group‐constrained solution, the use of the group‐RCSE prior could be expected to slightly reduce the amplitude of this peak but not eliminate it after optimization (Supporting Information Fig. 8). Thus, without ruling out early, small amplitude, positive currents, it seems that the large, positive peaks observed previously in V2 and V3 waveforms were likely artifacts of displaced dipole locations.

CONCLUSIONS

RCSE allows for the separation of activity in individual visual areas despite their close proximity, but it is limited by the accuracy of the retinotopy‐defined dipole locations. Group‐constrained RCSE was developed to obtain consensus response waveforms for V1, V2, and V3. Using such group‐constrained RCSE solutions as prior estimates for nonlinear optimization of dipole locations improved the robustness of RCSE for individual subjects, avoiding artifacts such as polarity inversions that were sometimes observed without optimization or with optimization methods unconstrained by a prior. This was particularly the case when using a small number of stimulus locations, which is desirable for applications involving the parametric manipulation of stimulus or task conditions. Using these methods and RCSE solutions obtained from a group of subjects, the V1 peak response was, not surprisingly, found to be significantly larger and earlier than V2 and V3, which were relatively similar in amplitude and latency. The relationship between luminance contrast and normalized peak amplitudes was nearly identical for the three areas.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information